2. 西安测绘研究所地理信息工程国家重点实验室, 陕西 西安 710054;
3. 东南大学仪器科学与工程学院, 江苏 南京 210096;
4. 香港理工大学, 香港 999077
2. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
3. Master of Instrument and Meter Engineering, Southeast University, Nanjing 210096, China;
4. Hong Kong Polytechnic University, Hongkong 999077, China
当卫星按圆轨道、赤道轨道以及圆赤道轨道运动时,某些卫星开普勒(Kepler)轨道根数发生退化,用于表达卫星轨道的拉格朗日运动方程和源于拉格朗日运动方程的高斯运动方程发生数学奇异,即为奇点问题,它一直是天体力学和N体问题研究中的核心问题之一[1-4]。卫星轨道理论研究主要基于二体问题的摄动理论[5-7],二阶摄动理论解研究近年来取得了长足进步[8-12],为奇点问题的进一步研究奠定了基础。众多学者在理论研究方面做了很多努力[13-16],也取得了不少成果。第1类和第2类奇点问题为解决卫星导航领域的奇点问题提供了可能,但其表达复杂且解决思路和最终表达很难统一[17-18]。文献[19-20]提出参量代换和坐标系旋转等方法,分别从圆轨道,赤道轨道和极轨道的情况,对其方法进行论证和阐述,为奇点问题的解决提供了新的思路。但其忽略了代换参量实际的物理和几何意义,以及转换过程对整个轨道系统求解的可逆性。2012年,文献[21]以不定积分解的形式提出无奇点理论,并于2013年有了以微分方程描述的公式版本[22]。但其公式推导主要是逻辑推理,2014年给出了拉格朗日无奇点运动方程纯数学的严格推导与证明[23]。2015年又给出了高斯无奇点运动方程纯数学的严格推导与证明[24]。上述论文主要是从纯数学角度进行推导证明,参数的物理意义和方程的连续性有待进一步分析。
为了解决上述问题,本文充分考虑参数的实际几何物理意义、总体方程的统一性以及与原始方程的一致性,从拉格朗日无奇点运动方程出发,对奇点问题作了进一步的分析和探索。奇点情况时,某些Kepler轨道根数发生退化,本文基于原始拉格朗日和高斯运动方程及其物理意义,对卫星无奇点方程的判据进行推导与分类,并分别对拉格朗日/高斯无奇点卫星运动方程在圆轨道、赤道轨道和圆赤道轨道情况下存在奇异的轨道参数(升交点赤经、近地点角距和平近点角)赋予新的实际物理和几何意义。在拉格朗日-许与高斯-许卫星运动方程的基础上,根据参数定义对奇异项进行加和变换,从而消除奇异因子,最后给出一种新的拉格朗日/高斯无奇点卫星运动方程的统一表达式。
1 卫星无奇点方程的判据卫星运动方程的奇点问题源于某些特定情况时Kepler根数的物理意义的模糊,导致拉格朗日运动方程出现小分母或分母为零的问题。拉格朗日卫星运动方程可表示为[7, 14]
 (1)
(1)
式中,函数R称为摄动位函数,包括了除中心引力位以外的全部项,6个开普勒根数a、e、ω、i、Ω、M,即半长轴、偏心率、近地点角距、倾角、升交点赤经、平近点角。文献[21]将其改写成
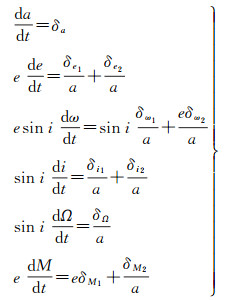 (2)
(2)
式中,δ及其下标表示式(1)的右边各项。当e或者sin i趋近于0时,即可能发生奇点问题。奇点问题解决的前提是需要对奇点域做具体的判断。首先,定义径向和赤道方向的误差如下[22]
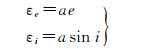 (3)
(3)
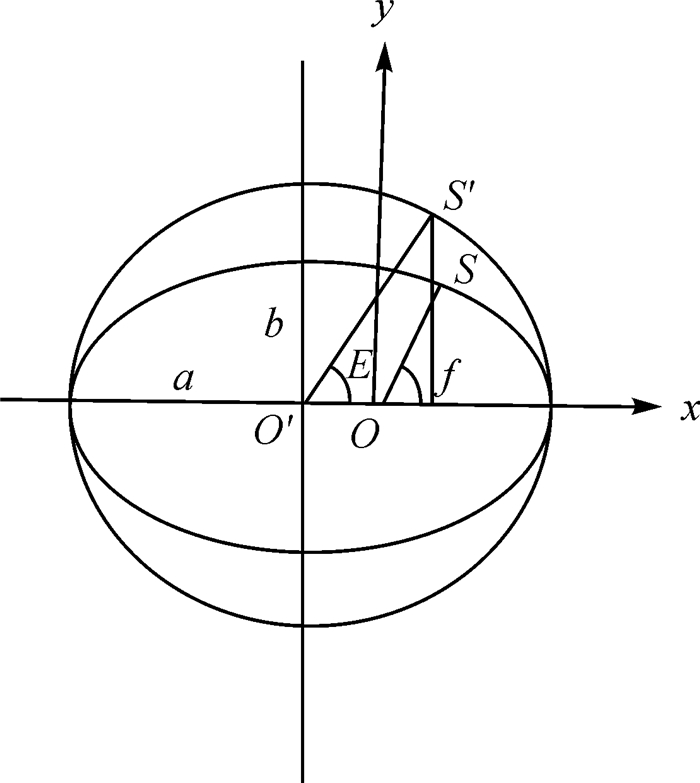
此处径向误差ae是轨道几何中心O′与地心O的距离,如图 1所示,也是e引起的最大径向误差。赤道偏差a sin i≈ai表示卫星由i引起的垂直于赤道的最大距离(倾角i是卫星的最大纬度)。在积分时刻t0=0,e或者/和i接近于0,则在积分时刻t,偏差e和i就为Δe和Δi。式(3)可写成
|
| 图 1 卫星的扁心率和近点角 Fig. 1 The eccentricity and anomalies of a satellite |
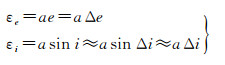 (4)
(4)
圆轨道、赤道轨道以及圆赤道轨道的轨道偏差定义为
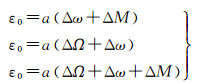 (5)
(5)
式中,ε0表示在卫星运动方向上由ΔΩ、Δω、ΔM引起的最大偏差。径向偏差、赤道方向偏差和轨道方向偏差是轨道最大误差的3个组成部分。3个偏差表示(e, ω, i, Ω, M)扰动对轨道产生的最大误差域。实际应用中,假定轨道3个方向偏差εe、εi和ε0分别为1 m,即这里定义的εe、εi和ε0可以作为判据标准。对于不同轨道,判据条件如表 1所示,用于对奇点问题的判断与进一步分析。
| 奇点类型 | 判断条件 |
| 非奇点 | ae≥εe=1, asin i≥εi=1 |
| 圆轨道奇点 | ae < εe=1, asin i≥εi=1 |
| 赤道轨道奇点 | ae≥εe=1, asin i < εi=1 |
| 圆赤道轨道奇点 | ae < εe=1, asin i < εi=1 |
2 拉格朗日无奇点卫星运动方程推导分析
拉格朗日无奇点运动方程的数学推导已在文献[21]中详细给出。对于通常非奇点情况拉格朗日方程[15, 22]可写为
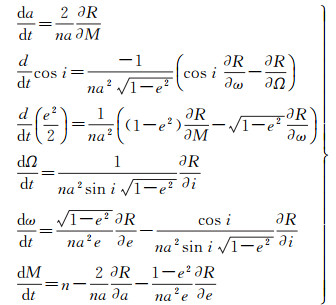 (6)
(6)
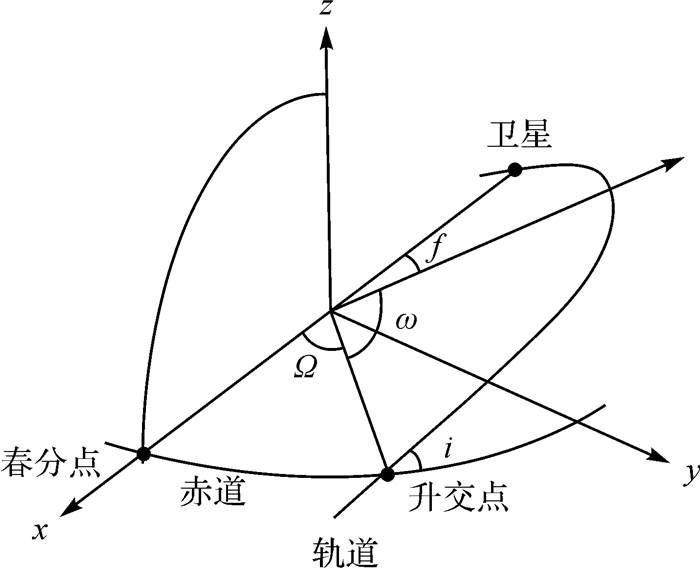
对于奇点情况还需进一步分析。由轨道参数的原始定义有:Ω表示在地球赤道平面上,升交点与春分点之间的地心夹角称为升交点赤经;ω表示在轨道平面上近地点与升交点之间的地心角距称为近地点角距;f表示卫星到近地点之间的地心角距,如图 2所示。为计算真近点角,二体问题中引入偏近点角和平近点角的定义,3种近点角(真近点角f、平近点角M、偏近点角E)均是时间的函数,用来表述卫星在ECI坐标系中的位置随着时间的变化。其中,平近点角M采用平均角速度n来描述卫星绕地球的轨道运动,广泛用于解析轨道的理论推导和应用,本文的推导也是基于此。
|
| 图 2 轨道几何图 Fig. 2 Orbital geometry |
奇点情况分为圆轨道、赤道轨道和圆赤道轨道3种情况。当为圆轨道时,e=0近地点失去意义,无法确定。此时开普勒轨道根数发生退化,平近点角M和近地点角距ω意义发生改变。因此,从卫星实际运动情况分析,可定义新的平近点M′表示卫星与升交点的夹角,即
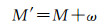 (7)
(7)
当为赤道轨道时,sin i=0,升交点失去意义,无法确定。此时开普勒轨道根数发生退化,升交点赤经Ω和近地点角距ω意义发生改变。因此,可定义新的近地点角距ω′表示近地点与春分点的夹角,即
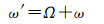 (8)
(8)
当为圆赤道轨道时,e=0且sin i=0,近地点和升交点均失去意义,无法确定。此时开普勒轨道根数发生退化,平近点角M和近地点角距ω以及升交点赤经Ω意义均发生变化。因此,定义一个新的平近点M″表示卫星与春分点的夹角,即
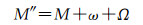 (9)
(9)
对于上述变化过程,并未引入新的参数而是考虑特殊情况下,根据实际轨道使发生变化的参数仍具有实际意义。从轨道运行连续性以及力的连续性分析,整个轨道的变化过程是缓慢连续变化的,奇点情况下组合后的对应的量存在且连续。所有引起ω、Ω、M变化的力模型都保持不变,也即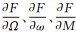
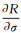
圆轨道情况ae < εe=1、a sin i≥εi=1时,从物理意义分析,近地点无法确定,相关轨道参数对时间的偏导数也无法确定。从数学角度分析e除到式(2)右边,分母存在零因子,即发生奇点。由式(7),可得
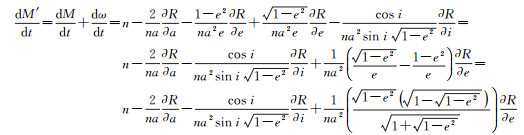 (10)
(10)
因此,圆轨道奇点情况的运动方程由式(6)中一、二、三、四式,以及下式组成
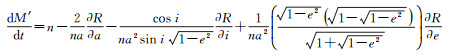 (11)
(11)
赤道轨道情况ae≥εe=1、asin i < εi=1时,从物理意义分析,升交点无法确定,相关轨道参数对时间的偏导数也无法确定。从数学角度分析,sin i除到式(2)右边,分母存在零因子,即发生奇点。由式(8)可得
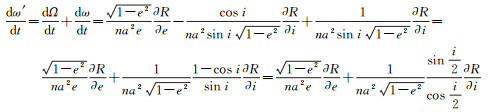 (12)
(12)
因此,赤道轨道奇点情况的运动方程由式(6)中一、二、三、六式,以及下式组成
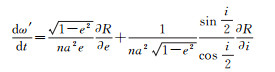 (13)
(13)
圆赤道轨道情况ae < εe=1、asin i < εi=1时,从物理意义分析,升交点和近地点无法确定,相关轨道参数对时间的偏导数也无法确定。从数学角度分析,sin i、e除到式(2)右边,分母存在零因子,即发生奇点。由式(9),可得
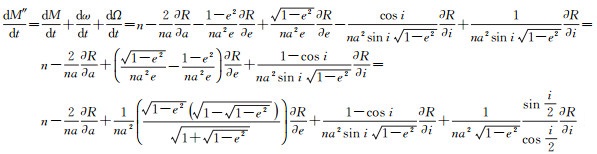 (14)
(14)
因此,圆赤道轨道奇点情况的运动方程由式(6)中一、二、三式,以及下式组成
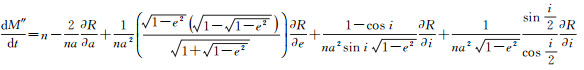 (15)
(15)
非奇点情况下高斯运动方程为[24]
 (16)
(16)
式中,fa、fh、fr分别表示轨道坐标系的3个方向的摄动力。对于奇点情况下的高斯运动方程做进一步推导。
3.1 圆轨道情况ae < εe=1、asin i≥εi=1,根据拉格朗日圆轨道运动方程,得
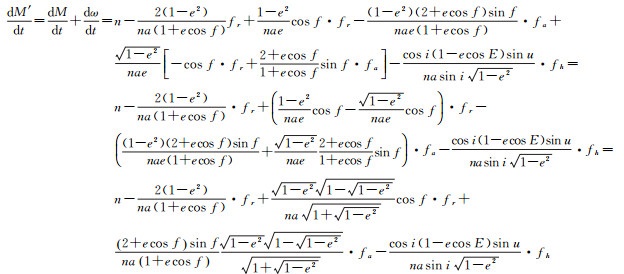 (17)
(17)
因此,圆轨道奇点情况的运动方程由式(16)中一、二、三、五式,以及下式组成
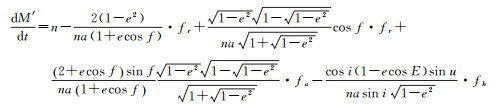 (18)
(18)
ae≥εe=1、asin i < εi=1,根据拉格朗日赤道轨道运动方程,得
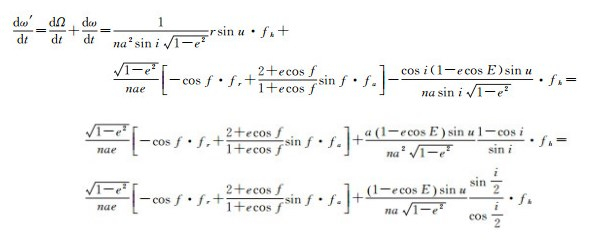 (19)
(19)
因此,赤道轨道奇点情况的运动方程由式(16)中一、二、三、六式,以及下式组成
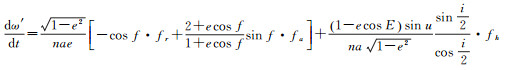 (20)
(20)
ae < εe=1, asin i < εi=1,根据拉格朗日圆赤道轨道运动方程,得
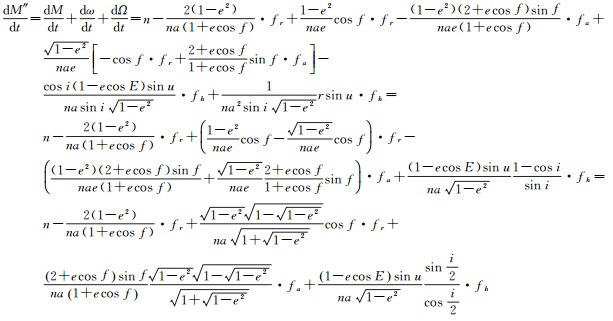 (21)
(21)
因此,圆赤道轨道奇点情况的运动方程由式(16)中一、二、三式,以及式(22)组成
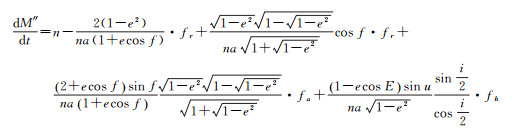 (22)
(22)
总结上述非奇点与奇点的各种情况,最终统一的拉格朗日无奇点卫星运动方程为

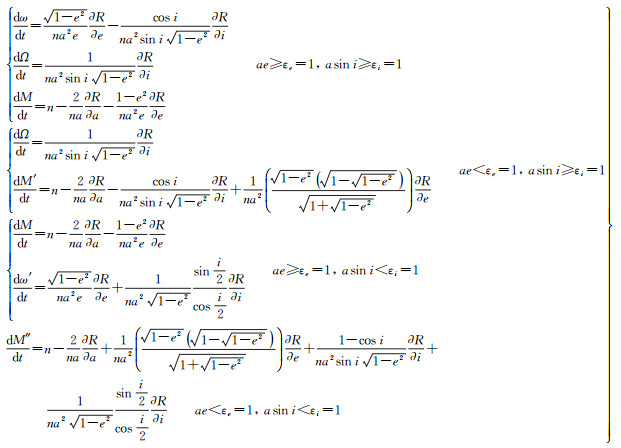 (23)
(23)
最终统一的高斯无奇点卫星运动方程为

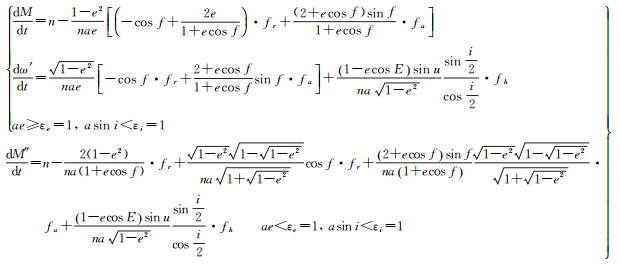 (24)
(24)
卫星的运动和力模型是连续的,进一步分析卫星运动方程的连续性可知,式(23)、(24)对于任何一种奇点情况(圆轨道奇点、赤道轨道奇点、圆赤道轨道奇点)方程是非间断的,奇点情况下运动方程中重新定义的组合量及非奇点情况下运动方程的轨道参数在其对应的判据域内均是连续的。因此,新的拉格朗日和高斯无奇点卫星运动方程具有连续性。
5 仿真与分析为进一步验证本文所做的推导,分别针对3种奇点情况开展仿真与分析。假设卫星处于二体运动,奇点情况下,摄动力对各项轨道根数的偏导数为0,但拉格朗日卫星运动方程中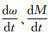
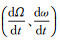
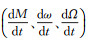
(1) 圆轨道情况。轨道坐标系下状态矢量进行一次旋转,分析角度物理意义为
 (25)
(25)
(2) 赤道轨道情况。轨道坐标系下旋转矩阵,分析角度物理意义可知
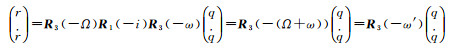 (26)
(26)
式中,R1、R3为x和z中的旋转矩阵[16],圆赤道轨道两点兼有。
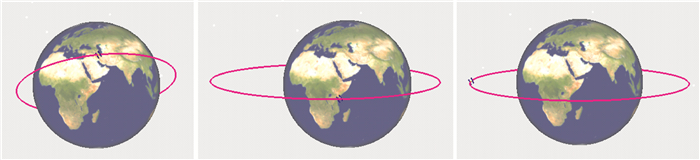
下面利用本文推导的拉格朗日无奇点卫星运动方程描述卫星运动,轨道初值如表 2所示(其中后3个可表示新定义的根数)。首先基于式(23)求出各时刻的卫星的轨道根数,然后利用式(25)、(26)将其转换成卫星状态矢量,最后利用自主编写的卫星轨道三维可视化仿真软件分别绘制二体运动圆轨道、赤道轨道以及圆赤道轨道轨迹[25],如图 3所示。将计算轨道与积分轨道对比,轨道差在厘米级。高斯方程同理。
|
| 图 3 圆轨道、赤道轨道以及圆赤道轨道卫星轨迹 Fig. 3 The circular/equatorial/circular and equatorial satellite orbit |
| 轨道类型 | a/km | e/(°) | i/(°) | Ω/(°) | ω/(°) | M/(°) |
| 圆轨道 | 8000 | 0 | 30 | 0 | — | 80 |
| 赤道轨道 | 12 000 | 0.3 | 0 | — | 60 | 20 |
| 圆赤道轨道 | 11 000 | 0 | 0 | — | — | 10 |
从上述过程与结果可知,本文推导的无奇点卫星运动方程,可描述二体运动中的圆轨道、赤道轨道以及圆赤道轨道卫星运动,且计算精度与非奇点二体运动相当,可用于解决二体运动中的奇点问题,从而在一定程度上证明本文推导公式的正确性和可用性。
6 结论本文推导了卫星拉格朗日/高斯无奇点运动方程,无任何近似,与原始拉格朗日/高斯运动方程具有逻辑一致性;奇点情况下,对参数含义重新定义,所得方程在奇点情况下仍具有几何和物理意义;圆轨道、赤道轨道和圆赤道轨道下的卫星运动方程的表达更加简洁,便于理解和计算;轨道方程右端完全消除了零因子,从根本上解决卫星运动方程的奇点问题,并且该卫星运动方程具有连续性。
| [1] | XIA Zhihong. The Existence of Noncollision Singularities in Newtonian Systems[J]. Annals of Mathematics, 1992, 135(3): 411–468. DOI:10.2307/2946572 |
| [2] | DIACU F. The Solution of The N-body Problem[J]. The Mathematical Intelligencer, 1996, 18(3): 66–70. DOI:10.1007/BF03024313 |
| [3] | DIACU F, HOLMES P. Celestial Encounters:the Origins of Chaos and Stability[M]. Princeton, NJ: Princeton University Press, 1996. |
| [4] | WANG Qiudong. The Global Solution of the N-body Problem[J]. Celestial Mechanics and Dynamical Astronomy, 1990, 50(1): 73–88. |
| [5] | XU Guochang. Sciences of Geodesy-Ⅰ:Advances and Future Directions[M]. Berlin: Springer, 2010: 105-154. |
| [6] | BROUWER D, CLEMENCE G M. Methods of Celestial Mechanics[M]. Burlington, MA: Elsevier, 2013. |
| [7] | CHOBOTOV V A. Orbital Mechanics[M]. . |
| [8] | XU Guochang, XU Tianhe, YEH T K, et al. Analytical Solution of a Satellite Orbit Disturbed by Lunar and Solar Gravitation[J]. Monthly Notices of the Royal Astronomical Society, 2011, 410(1): 645–653. DOI:10.1111/mnr.2010.410.issue-1 |
| [9] | XU Yan, YANG Yuanxi, ZHANG Qin, et al. Solar Oblateness and Mercury's Perihelion Precession[J]. Monthly Notices of the Royal Astronomical Society, 2011, 415(4): 3335–3343. DOI:10.1111/mnr.2011.415.issue-4 |
| [10] | XU Guochang, XU Jia. On Orbital Disturbing Effects of the Solar Radiation[J]. Monthly Notices of the Royal Astronomical Society, 2013, 432(1): 584–588. DOI:10.1093/mnras/stt483 |
| [11] |
张兵兵, 聂琳娟, 吴汤婷, 等.
SWARM卫星简化动力学厘米级精密定轨[J]. 测绘学报, 2016, 45(11): 1278–1284.
ZHANG Bingbing, NIE Linjuan, WU Tangting, et al. Centimeter Precise Orbit Determination for SWARM Satellite via Reduced-dynamic Method[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(11): 1278–1284. DOI:10.11947/j.AGCS.2016.20160284 |
| [12] |
邹贤才, 李建成, 姜卫平, 等.
卫星重力资料分析的同解法研究及其仿真[J]. 测绘学报, 2010, 39(4): 344–348.
ZOU Xiancai, LI Jiancheng, JIANG Weiping, et al. Research on the Simultaneous Solution Method for Satellite Gravity Data Analysis and Its Simulation[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 344–348. |
| [13] | HAVEL K. N-body Gravitational Problem:Unrestricted Solution[M]. Brampton, ON, Canada: Grevyt Press, 2008. |
| [14] | BATTIN R H. An Introduction to the Mathematics and Methods of Astrodynamics[M]. Reston, VA: AIAA, 1999. |
| [15] | KAULA W M. Theory of Satellite Geodesy:Applications of Satellites to Geodesy[M]. Mineola, NY: Dover Publications Inc, 2000. |
| [16] | XU Guochang. Orbits[M]. Berlin: Springer, 2008. |
| [17] |
韩星远, 向开恒, 王海红.
第一类无奇点变量的广播星历参数拟合算法[J]. 航天器工程, 2011, 20(4): 54–59.
HAN Xingyuan, XIANG Kaiheng, WANG Haihong. Research on Broadcast Ephemeris Parameters Fitting Algorithm Based on the First Class of No Singularity Variables[J]. Spacecraft Engineering, 2011, 20(4): 54–59. |
| [18] |
张中凯, 杜兰, 旦增曲英, 等.
基于第二类无奇点根数的改进根数[J]. 测绘科学技术学报, 2012, 29(4): 257–261.
ZHANG Zhongkai, DU Lan, DAN Zengquying, et al. Improved Elements Based on Second Class of No-singularity Variables[J]. Journal of Geomatics Science and Technology, 2012, 29(4): 257–261. |
| [19] | BROUCKE R A, CEFOLA P J. On the Equinoctial Orbit Elements[J]. Celestial Mechanics, 1972, 5(3): 303–310. DOI:10.1007/BF01228432 |
| [20] | BATTIN R H. An Introduction to the Mathematics and Methods of Astrodynamics[M]. New York: American Institute of Aeronautics and Astronautics, 1987. |
| [21] | XU Guochang, XU Jia. On the Singularity Problem in Orbital Mechanics[J]. Monthly Notices of the Royal Astronomical Society, 2013, 429(2): 1139–1148. DOI:10.1093/mnras/sts403 |
| [22] | XU Guochang, XU Jia. Orbits:2nd Order Singularity-free Solutions[M]. Berlin: Springer, 2013. |
| [23] | XU G, LV Z P, SHEN Y Z, et al. A Mathematical Derivation of Singularity-free Lagrange Equations of Planetary Motion, Special Issue for Celebration 80th Birthday of Academician Houze Xu[J]. Journal of Surveying and Mapping, 2014. |
| [24] |
许国昌, 陈武, 沈云中, 等.
高斯无奇点卫星运动方程的数学推导——谨以本文恭贺师兄欧吉坤教授七十寿辰[J]. 导航定位学报, 2015, 3(3): 5–12.
XU Guochang, CHEN Wu, SHEN Yunzhong, et al. A Mathematical Derivation of Singularity-free Gaussian Equations of Planetary Motion[J]. Journal of Navigation and Positioning, 2015, 3(3): 5–12. |
| [25] |
杜玉军. 卫星轨道的三维可视化程序设计[D]. 武汉: 武汉大学, 2008. DU Yujun. 3D Visualization Programming of Satellite Orbiting[D]. Wuhan:Wuhan University, 2008. |



