在测量领域,定向可理解为确定基准点与目标点所成几何矢量相对基准方向的夹角。目前主要的绝对定向手段可分为磁定向法、陀螺经纬仪定向法、卫星定向法以及天文定向法[1]。其中,磁定向法、卫星定向法均容易受到电磁干扰导致定向精度严重漂移,陀螺经纬仪定向法存在误差累积的问题,长时间使用后需要对仪器校准。天文定向是一种通过观测自然天体获取目标方向与测量仪器参考基准间的夹角关系进而进行绝对定向的手段,具有自主无源、抗干扰、无误差累积的优良特性[2]。目前国内外主要通过将恒星作为观测天体实现地面天文定向,存在受气候条件影响严重的缺点,在阴天、浓雾的夜晚不能持续观测[3-6]。月球是夜间最亮的自然天体,在轻薄云雾条件下,仍然具有较好的可见性,是理想的观测天体。文献[7-8]提出了基于月球边沿采样的月球视面中心拟合算法及球面圆拟合算法,较好地解决了月球视面中心的确定问题,并由此实现了优于±2″的定向精度。然而该方法需要用肉眼通过经纬仪的十字丝中心对月球边沿进行多次精确照准,对作业员提出了一定技能要求,且不同作业员存在人仪差的问题。随着天体成像技术和数字图像处理技术的发展,人们开始尝试使用CCD敏感天体成像,建立CCD量度坐标系与天球坐标系的关系,进而实现没有人为干预的自动化天文定位定向[9]。文献[10]设计了一套基于图像处理的测月定向装置,将CCD摄像头精确固定在经纬仪卡槽,拍摄月球后在像面坐标系计算月球中心与经纬仪十字丝中心的夹角,避免了人为照准月球,最终实现了±0.28密位(±60.48″)左右的定向精度。然而该方法依赖于CCD摄像头与经纬仪水平视轴的精确校准,且获取目标方向度盘值时仍需肉眼照准,这两个过程均不能脱离人为干预。
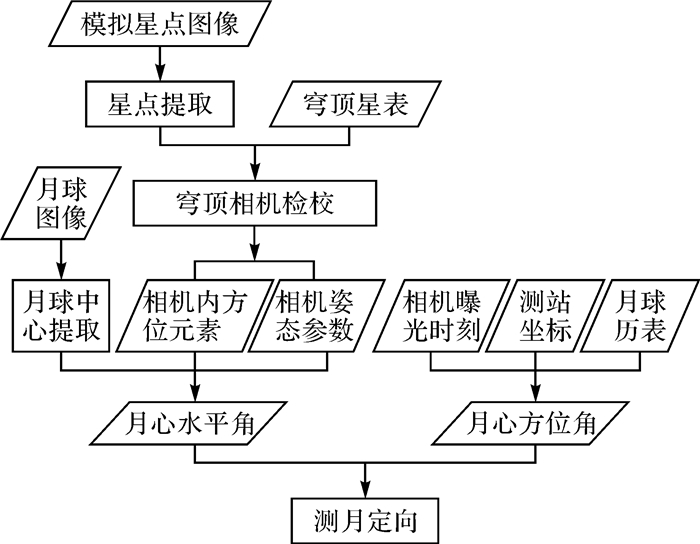
本文使用美国Apogee公司生产的Alta U9000 CCD和日本尼康公司生产的AF Fisheye-Nikkor 16 mm f/2.8D鱼眼镜头组成鱼眼相机,即超大视场月球敏感器,视场角可达139.96°×360°,既可避免拍摄受大气折射影响严重的低高度角月球,又可在无须伺服控制装置调整相机姿态的情况下对月球进行连续跟踪拍摄。为构建天文定向装置,本文使用德国徕卡公司生产的Nivel230二维水平仪与相机固连,使用GPS OEM板通过卫星授时校准笔记本电脑晶振从而组成天文计时器,使用德国PI公司的H840.G1x六自由度并联机器人作为高精度外部检核敏感载体。如图 1所示,本文基于室内全物理仿真星空穹顶实现相机标校,通过图像处理提取月球中心像面坐标,结合时间、位置和历表信息实现快速自动化天文定向。
|
| 图 1 测月定向整体流程 Fig. 1 The whole process of orientation by lunar observing |
1 像点-物方点坐标转换
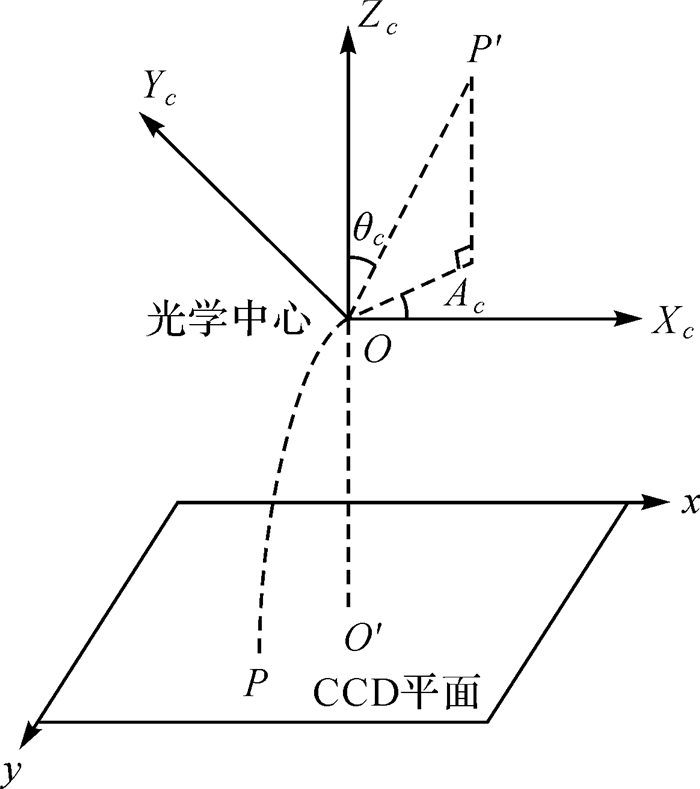
如图 2,定义O-XcYcZc为相机坐标系,原点O位于相机的光学中心,Zc轴指向主光轴方向,Xc轴与Zc轴垂直,且与CCD平面坐标系的x轴平行,Yc轴按右手定则确定。主光轴与CCD平面的交点O′为像主点,P为像点,P′为物方点。P′在相机坐标系下的坐标可采用方位角Ac和半视场角θc表示。Ac定义为通过O和月心的垂直面与XcOZc面的夹角,从XcOZc面起算,范围为0~360°;θc定义为物方点的方向矢量与Zc轴的夹角,从Zc轴正向起算,范围为0~90°。
|
| 图 2 镜头投影原理 Fig. 2 Principle of lens projection |
本文选用的AF Fisheye-Nikkor 16 mm f/2.8D鱼眼镜头,其投影模型标称为等立体角投影模型。针对畸变模型,鱼眼镜头的光学畸变分为径向畸变、偏心畸变和平面内畸变,相对径向畸变,偏心畸变和平面内畸变在10-7~10-5量级上,可忽略不计[11]。可采用4阶多项式描述成像径向畸变,已知月心像点P坐标(x, y),根据镜头投影模型和畸变模型、像主点O′坐标(x0, y0)、焦距f、径向畸变参数(k1, k2, k3),可计算出物方空间点P′在相机坐标系下的半视场角[11-12]
 (1)
(1)
式中,r为像点至像主点的距离,即
 (2)
(2)
根据前文,镜头切向畸变极小,且一般情况下主光轴与CCD平面垂直,故像面上像点P与像主点O′构成的向量PO′与x轴的夹角和物方空间物点P′在相机坐标系下的方位角相等,即
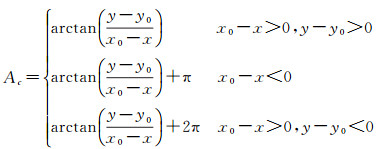 (3)
(3)
将(Ac, θc)化为直角坐标
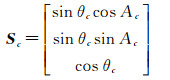 (4)
(4)
至此,像点图像坐标即转化为物方点相机坐标系下三维坐标。
2 室内相机标校利用鱼眼相机进行天文定向,需要事先对其进行标校以获取相机参数,包括6个内方位元素(包括像主点坐标(x0, y0)、焦距f及CCD像面径向畸变参数(k1, k2, k3))和2个外方位元素(包括滚动角γ和俯仰角ψ),即相机相对水平面的2个姿态参数。为此建立了全物理仿真星空穹顶作为室内相机标校平台,可实现对穹顶星空一次成像实现相机参数标校。如图 3所示,建设穹顶时,从依巴谷星表中挑选出全天区5.2等以上的恒星1853颗,利用导光光纤模拟星点光源,精确放样标定在穹幕上。

|
| 图 3 穹顶及星空仿真效果 Fig. 3 Dome and star simulation effect |
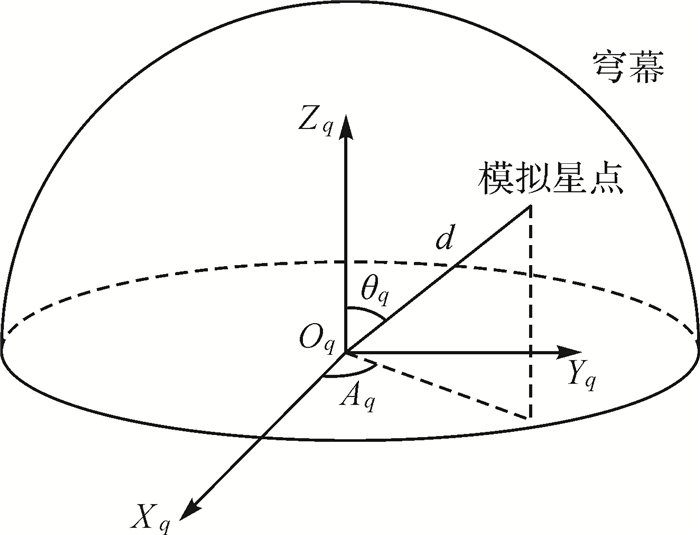
如图 4所示,定义Oq-XqYqZq为穹顶坐标系,Oq为穹顶球心,Xq轴指向仿真星空的春分点,Zq轴指向天顶,Yq轴按右手定则确定。为编制穹顶星表,使用徕卡TS50i全站仪精确测量每颗星点的位置并归算至穹顶坐标系,经多次复测验证,每颗星方向精度优于±2″,完全满足相机标校的精度需求。
|
| 图 4 穹顶坐标系示意图 Fig. 4 Dome coordinate system |
2.1 相机标校模型
室内相机标校模型需要求解12个相机参数,分别为像主点坐标(x0, y0)、焦距f、畸变参数(k1, k2, k3)、旋转参数(a, b, c)和平移参数(X0, Y0, Z0),其中旋转参数采用罗德里格参数表示,避免了复杂的三角函数运算,可简化标校误差方程。
设模拟星点在穹顶星表中的球面坐标为(θq, Aq, d),转化为穹顶坐标系下三维坐标
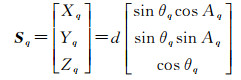 (5)
(5)
设S0为穹顶球心至相机光学中心的平移向量
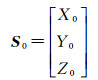 (6)
(6)
将Sq平移至相机光学中心
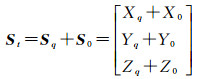 (7)
(7)
将St单位化
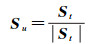 (8)
(8)
鱼眼相机拍摄得到的星图经星点提取可得星点图像坐标,进而可根据第2节方法转化为相机坐标系下星点三维坐标向量Sc。Su与Sc之间有旋转关系
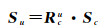 (9)
(9)
所有旋转矩阵均可由反对称矩阵Q和单位矩阵I表示[13],则
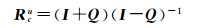 (10)
(10)
式中
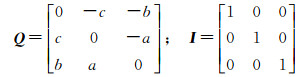 (11)
(11)
构建误差方程
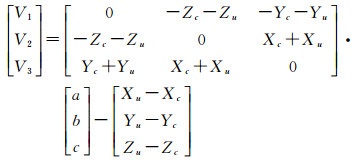 (12)
(12)
设未知参数的初值为
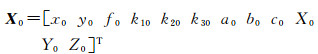 (13)
(13)
对误差方程线性化并写为矢量形式可得
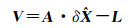 (14)
(14)
根据最小二乘法可求解未知参数的改正数为
 (15)
(15)
相机参数估值为
 (16)
(16)
如果有n个模拟星点及其对应的像点,则有3n个误差方程,单位权中误差为
 (17)
(17)
未知参数的权逆阵为
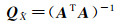 (18)
(18)
相机参数的精度估计公式为[14]
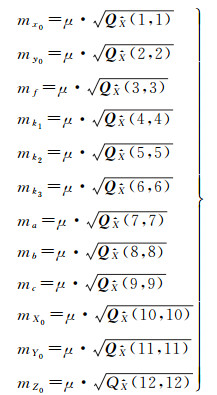 (19)
(19)
至此即得到了相机的6个内方位元素。
2.2 相机姿态标定定义O-XIYIZI为水平仪坐标系,XI轴、YI轴随水平仪出厂固定,ZI轴按右手定则确定。由于水平仪可实时输出自身XI轴、YI轴和当地水平面的夹角,且水平仪与相机固连,水平仪坐标系与相机坐标系相对位置关系不变,因此可将水平仪作为媒介将野外月球中心在相机坐标系下坐标改正至当地水平面。理论上,只要保证水平仪读数在穹顶标校时和野外测月时一致,则相机坐标系相对当地水平面的旋转关系就会保持一致,在实际操作中,不妨将水平仪保持整平状态。
图 5所示为穹顶标校时各坐标系位置关系,O-XuYuZu为平移、单位化后的穹顶坐标系,O-XIYIZI为水平仪坐标系,O-XcYcZc为相机坐标系,定义O-XchYchZch为相机水平坐标系,Xch轴为相机坐标系的Xc轴在水平面的投影,Zch轴指向天顶,Ych轴按右手定则确定。图中显示的是水平仪整平时的状态,即ZI轴、Zu轴、Zch轴三轴重合,指向天顶,统一表示为Z轴。

|
| 图 5 穹顶相机姿态标定各坐标系示意图 Fig. 5 Coordinate systems when calibrating camera attitude in the dome |
将O-XcYcZc转换到O-XuYuZu需要经过以下3次旋转:
(1) 绕Xc轴旋转γ角,旋转矩阵记作RX(γ)。
(2) 绕Yc轴旋转ψ角,旋转矩阵记作RY(ψ)。
(3) 绕Zc轴旋转ξ角,旋转矩阵记作RZ(ξ)。
定义Rcu为O-XcYcZc转换到O-XuYuZu的旋转矩阵,则
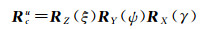 (20)
(20)
展开后得
 (21)
(21)
而Rcu根据式(10)得到,故
 (22)
(22)
第(1)、(2)次旋转可将O-XcYcZc转换为O-XchYchZch,定义Rcch为相应的旋转矩阵,则
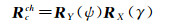 (23)
(23)
至此即实现了相机坐标系与相机水平坐标系的空间关系标定。由于相机水平坐标系是建立在当地水平面上的坐标系,因此标定了Rcch即相当于找到了当地的水平基准,可将相机坐标系下月球中心的方位角改正到水平面上,进而计算月心方向的水平角L。
3 月球中心位置提取月球平均扁率约为1/3476,且在严格意义上,月球的几何中心与质心并不重合,重心偏向地球方向约2 km。然而地月距离遥远,地球上观测月球的角半径仅约15′,因此,可近似认为地球上观测的月球圆盘为正圆面,圆心与月球质心位置重合[15-16]。此外,在地球上观测月球,其存在月相的周期性变化,一般呈现由晨昏分界线与真实边缘线构成的缺面,其中仅有圆形的真实边缘线可用于拟合提取月心位置。
3.1 月相边缘检测及月心拟合方法为在像面准确提取月球中心位置,本文采用文献[17]推导的9×9尺寸Zernike矩模板,组成Sobel-Zernike矩算子,对月相边缘进行亚像素级检测,检测效果如图 6所示。

|
| 图 6 月相边缘检测效果 Fig. 6 Effect of moon phase edge detection |
鱼眼相机对圆形目标投影成像时,由于镜头带来的桶形畸变,目标在像面会呈现近似椭圆,且随着半视场角增大,目标越来越接近视场边缘,椭圆性愈发明显[18-19]。因此,经镜头投影和畸变,月球真实边缘线在像面形成近似椭圆,为拟合月心位置,本文引入直接最小二乘椭圆拟合算法[20],基本思想如下:
椭圆的一般方程为
 (24)
(24)
为计算方便,不妨取4ac-b2=1,令
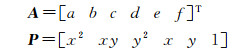 (25)
(25)
则F(x, y)可改写为向量形式
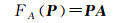 (26)
(26)
定义|FA(Pi)|为坐标(xi, yi)到拟合椭圆曲线F(x, y)=0的代数距离,反映了点(xi, yi)处的拟合残差,因此,所有参与拟合点的代数距离向量模可作为拟合精度指标,使得模最小的向量A即为椭圆系数直接最小二乘拟合值。
设有M个点(x1, y1)、(x2, y2)、…、(xM, yM)参与椭圆拟合,令
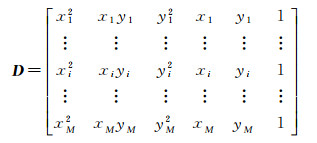
 (27)
(27)
则拟合求解问题可改写为[21]
 (28)
(28)
该约束条件下的最小化问题可以依据广义特征值问题求解
 (29)
(29)
可以证明,该广义特征值系统有且仅有一个正特征值[22],该特征值对应的特征向量即为所求椭圆系数向量。
3.2 月球真实边缘点筛选方法基于3.1节检测出的月相边缘,需要区分月球真实边缘线与晨昏分界线。为准确而充分地筛选月球真实边缘点,本文提出先粗后精的思想,通过取半搜索初步筛选,通过循环搜索精化筛选。
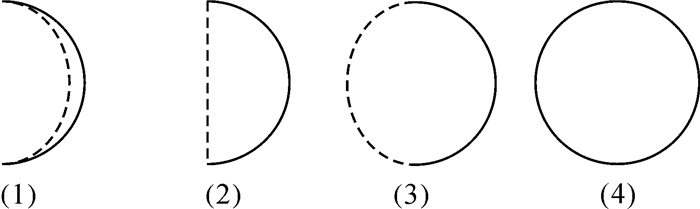
3.2.1 取半搜索初步筛选如图 7所示,对于月相来说,月球真实边缘线长度始终大于晨昏分界线长度,图中实线部分为月球真实边缘线,虚线部分为晨昏分界线。
|
| 图 7 月相示意图 Fig. 7 Moon phase |
由于月球真实边缘线在像面成像为椭圆线,晨昏分界线成像为不规则曲线,这样,取月相边缘点总数的一半作为搜索步长,以代数距离向量模(式(28)中DA)作为边缘点集合椭圆拟合精度指标,对应模最小的一半点理论上必属于月球真实边缘线的一部分。具体实施步骤如下:
(1) 任取检测出的边缘点总量N的连续一半点[N/2](取整)作椭圆拟合。
(2) 以[N/2]为搜索步长,逐次往前搜索,直到搜索点与第一次所取重合,这样需要作N次椭圆拟合。
(3) 计算N次椭圆拟合的代数距离向量模。
(4) 取模最小的一个点集,该点集即位于月球真实边缘线对应图像上。
3.2.2 循环搜索精化筛选初步筛选可得到月球真实边缘线上的一部分点,然而并不完全。如果仅用这些点去拟合月心坐标,会损失部分精度,需要进一步搜索可用的月球真实边缘点。为此本文提出基于代数距离均值的循环搜索法,其基本思想为:在剩余月相边缘点中,以代数距离均值为度量,取代数距离小于均值的点为月球真实边缘点并循环筛选。具体实施步骤如下:
(1) 设边缘点总数为N,用取半搜索法初步筛选出的[N/2]个月球真实边缘点为(x1, y1)、(x2, y2)、…、(xi, yi)、…、(x[N/2], y[N/2]),拟合得到的椭圆系数向量为A1,令向量
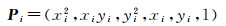 (30)
(30)
则这些点到拟合椭圆的代数距离均值为
 (31)
(31)
(2) 设剩余某点为(xt, yt),则
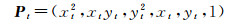 (32)
(32)
该点到(1)中拟合椭圆的代数距离为
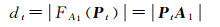 (33)
(33)
(3) 若dt < d1,则可认为点(xt, yt)属于月球真实边缘点。
(4) 假如步骤(3)筛选出了W个符合条件的点,则至此可得到[N/2]+W个月球真实边缘点,令其分别为(x1, y1)、(x2, y2)、…、(xi, yi)、…、(x[N/2]+W, y[N/2]+W)。设用这些点进行第二次椭圆拟合得到的系数向量为A2。同理,这些点到拟合椭圆的代数距离均值为
 (34)
(34)
(5) 类似步骤(2)、步骤(3),求剩余边缘点到第2次拟合椭圆的代数距离并判断其是否为月球真实边缘点。依次类推,直至所有剩余边缘点到拟合椭圆的代数距离均大于已筛选出的月球真实边缘点到拟合椭圆的代数距离均值。此时的月球真实边缘点可视为筛选完全。
图 8为上述过程的程序流程。

|
| 图 8 循环搜索流程 Fig. 8 Flow chart of cyclic search |
4 测月定向原理
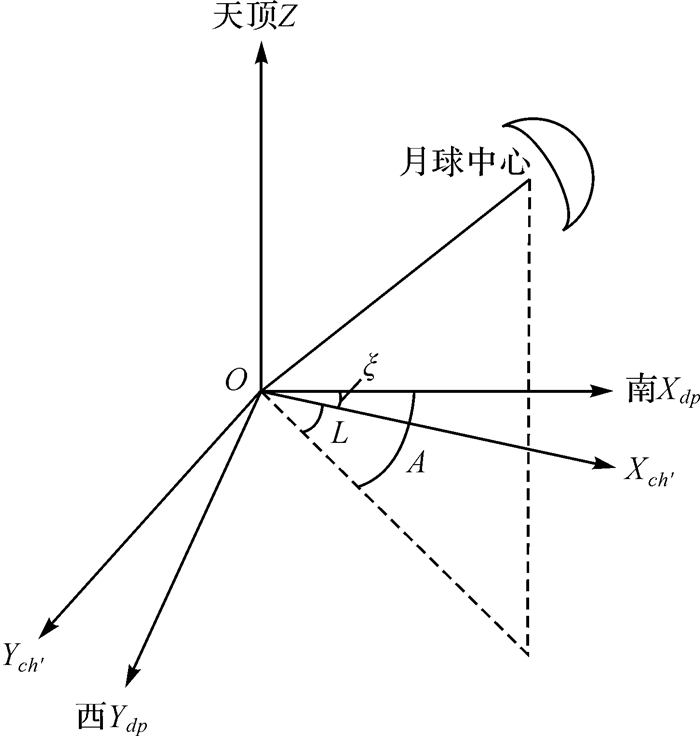
月心图像坐标经投影模型计算、畸变模型改正、水平改正即可转换为月心物方点在相机水平坐标系下的坐标。本文规定地平坐标系为左手系,因此需要将相机水平坐标系Ych轴反向变为左手系。图 9所示为测月定向基本原理,O为相机光学中心,O-XdpYdpZ为地平坐标系,O-Xch′Ych′Z为变为左手系的相机水平坐标系,二者共用指向天顶的Z轴。L为相机曝光瞬间月球在相机水平坐标系(左手系)下的水平角,从XM′轴起算,顺时针量取;A为相机曝光瞬间月球在地平坐标系下的方位角,从Xdp轴起算,顺时针量取;ξ为航向角,即相机水平坐标系Xch′轴与地平坐标系Xdp轴的夹角,也即相机坐标系Xc轴(或CCD平面坐标系的x轴)在水平面的投影与真南方向的夹角。
|
| 图 9 测月定向原理 Fig. 9 Principle of orientation by lunar observing |
故航向角计算公式为
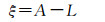 (35)
(35)
下面介绍水平角L的计算过程:
令Sch′为月心在相机水平坐标系下的方向向量,则
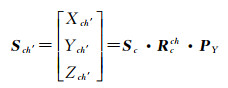 (36)
(36)
式中,Sc由式(4)可得;Rcch由式(23)可得;PY为Y轴反向矩阵。
进而,水平角L计算公式为
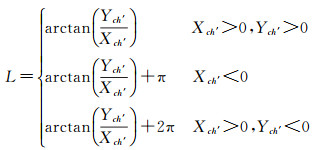 (37)
(37)
方位角A需要根据观测时刻、月球历表以及测站位置计算得到。一般可根据时角法计算月球方位角[23]
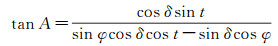 (38)
(38)
式中,φ为测站天文纬度; δ为月球的站心观测赤纬; t为月球的时角,计算公式为
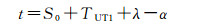 (39)
(39)
式中,α为月球的站心观测赤经,需要说明的是,月球的站心观测位置(α, δ)是根据月球历表经岁差、章动、视差、光行差以及大气折射改正计算得到的;λ为测站天文经度;TUT1为相机曝光瞬间对应的格林尼治UT1时刻,需要通过对应的UTC时刻TUTC进行化算,进而需要查阅IERS定期发布的Bulletina公报。S0为世界时0时对应的格林尼治恒星时,计算公式为
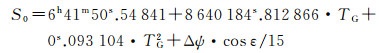 (40)
(40)
式中,Δψ为黄经章动;ε为黄赤交角;TG为格林尼治日期对应的儒略世纪数。
理论上,采用鱼眼相机测月定向,只需对月球一次成像即可获得航向角,实际操作中可对月球多次成像,得到多个航向角取均值以提高定向精度。
需要说明的是,针对月球历表,本文采用2000年第24届IAU大会决议的JPL的数值历表DE405/LE405[24]。针对岁差-章动模型,为提高计算效率,本文采用美国海军天文台提供的NOVAS 2000K岁差-章动模型代替精确的IAU 2000A模型,此时月球视位置计算精度可优于±3.5 mas,完全满足天文定向的精度需求[25]。针对相机曝光时刻,本文使用的天文计时器利用计算机内部计时芯片的晶振守时,计时精度优于±0.5 ms,完全满足天文定向的精度需求[26]。
5 试验为检核测月定向方法的外符合精度,如图 10,本文选用德国PI公司的H840.G1x六自由度并联机器人作为定向装置敏感载体,其绕Z轴旋转精度优于±12 urad(±2.48″)[27]。

|
| 图 10 H840.G1x六自由度并联机器人 Fig. 10 H840.G1x 6-axis hexapod |
如图 11所示,由于机器人基座坐标系OB-XBYBZB与水平仪坐标系OI-XIYIZI并非严格平行,当水平仪整平时,水平仪XIOIYI面与水平面平行,而机器人基座平面XBOBYB与水平面不平行。设水平仪坐标系ZI轴与机器人基座坐标系ZB轴夹角为i,则当机器人基座坐标系绕ZB轴旋转θ时,水平仪坐标系随之在水平方向旋转θ′,其转换关系为

|
| 图 11 机器人基座平面与水平面关系示意图 Fig. 11 Relation between hexapod base plane and horizontal plane |
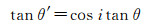 (41)
(41)
经出厂检测,水平仪ZI轴与整体定向装置垂直轴的夹角小于±1″。实际作业时,装置下表面紧贴于机器人基座平面,其垂直轴与机器人基座坐标系ZB轴基本重合,因此不妨将水平仪坐标系ZI轴与机器人基座坐标系ZB轴夹角i放宽到±10′。若机器人基座坐标系绕ZB轴旋转角度θ与水平仪坐标系在水平方向旋转角度θ′差值为Δθ,则
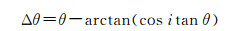 (42)
(42)
当θ=5°,i∈[0′, 10′],Δθ与i的关系如图 12所示。

|
| 图 12 Δθ随i变化关系图 Fig. 12 Relation between Δθ and i |
由图 12可知,在机器人基座平面旋转5°,水平仪坐标系ZI轴与机器人基座坐标系ZB轴夹角小于±10′时,机器人基座坐标系绕ZB轴旋转角度与水平仪坐标系在水平方向旋转角度的差值小于0.08″。因此,机器人在水平方向上提供的外符基准精度优于±2.56″,基本满足需求。
为实测检验测月定向方法的可靠性,制定了以下试验方案,分为室外拍摄与室内标校两部分:
(1) 通过调整镜头对焦环、光圈及相机快门速度试拍摄月球,直至月球图像轮廓清晰。
(2) 将定向装置置于六自由度机器人承载平面,通过控制机器人绕XB、YB轴旋转整平水平仪,使得水平仪XI、YI轴读数均小于±2″。
(3) 设置相机采样率为0.083 Hz,拍摄75幅月球图像,同时利用计时器记录每幅图像相机曝光瞬间时刻。
(4) 控制机器人绕ZI轴旋转5°,并整平水平仪,操作同步骤(2)。
(5) 设置相机采样率为0.083 Hz,拍摄75幅月球图像,并利用计时器记录每幅图像相机曝光瞬间时刻。
(6) 将仪器搬运至室内穹顶标校场,通过调整镜头光圈及相机快门速度试拍摄模拟星点,直至星点成像清晰。
(7) 整平水平仪,操作同步骤(2)。
(8) 拍摄模拟星点图像。
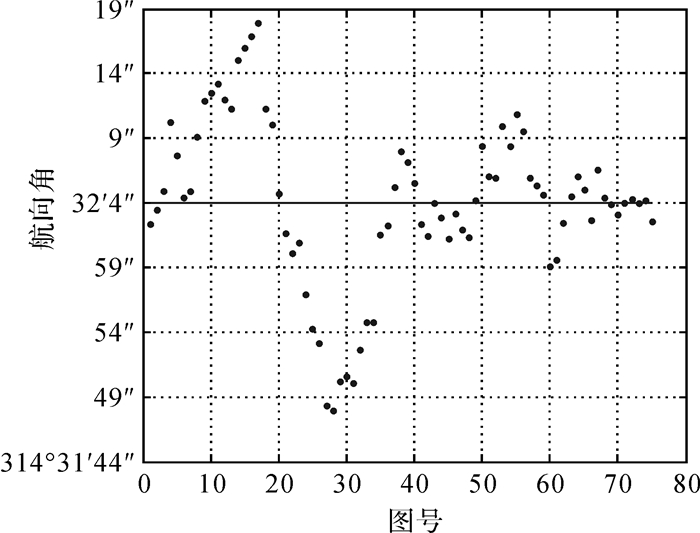
2017年5月12日晚,天气状况良好,有少量薄云,月球可见性较好,在中国华北地区某测站,按照上述方案进行了测月定向试验。方向1拍摄时间为23:45—00:00,方向2拍摄时间为00:18—00:33。两个方向定向结果如图 13、14所示,其中实线为定向均值。需要说明的是,方向2剔除了3幅被云层遮挡严重,成像质量较差的图像。
|
| 图 13 方向1航向角统计图 Fig. 13 Heading angles of direction one |
|
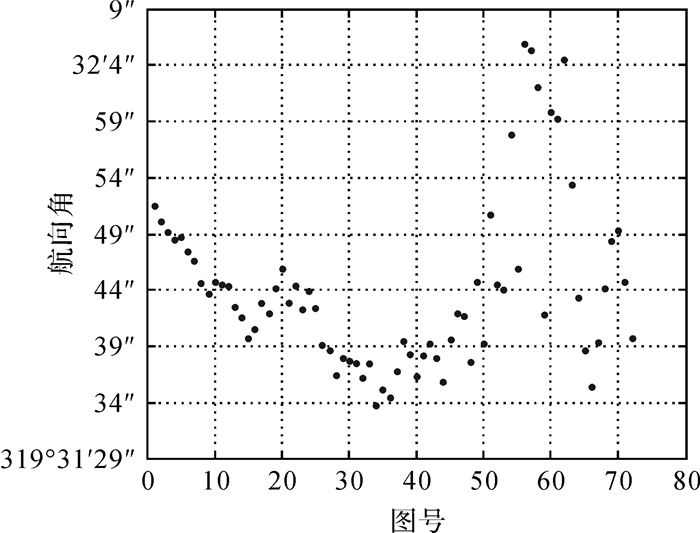
| 图 14 方向2航向角统计图 Fig. 14 Heading angles of direction two |
方向1定向误差小于±20″,标准差为±6.5″,定向均值为314°32′4″,方向2定向误差小于±25″,标准差为±7.5″,定向均值为319°31′44″,两个方向定向均值外符合精度为±20″。
由图 13、14可知,两个方向的航向角总体来看具有一定的随机性,这是由于月球中心提取误差造成的。事实上,本文使用的月球中心提取方法在除新月外的月相情况下精度基本相当,这是因为新月的晨昏分界线与月球真实边缘线相距很近,较难区分,可能出现较大的月心位置提取误差甚至提取失败。
两个方向的航向角在局部存在较为明显的趋势性,其原因可能有以下3点:
(1) 测站坐标不准确导致月球方位角A的计算存在系统偏差,包括对中误差及测站天文坐标的误差。
(2) 标校的相机参数不准确,导致水平角L的计算存在误差,由于焦距f与畸变参数(k1, k2, k3)均为径向相机参数,实际主要影响源为像主点坐标(x0, y0)与相机姿态参数(滚动角γ和俯仰角ψ)。
(3) 相机受温度、湿度、气压等环境因素的影响,其像主点坐标、姿态参数等在试验过程中可能发生变化。
6 结论(1) 本文提出的超大视场测月定向方法与传统天文定向方法相比,不需肉眼照准,定向结果没有人为干预,且对云雾天气具有一定的适应性。此外,利用鱼眼镜头的超大视场可对月球连续跟踪观测,不需伺服控制装置。需要说明的是,目前在应用该方法之前还需要对装置进行人工置平。
(2) 单幅图像定向内符合精度优于±25″,连续跟踪测月15 min,75幅图像定向内符合精度优于±7.5″,外符合精度约为±20″,可满足导弹、火炮等阵地测量的精度需求。
(3) 由于月球也有重力场,且在月球上观测地球也有地相变化,因此后期研究如能解决人工置平的影响,本文测月定向方法可扩展到月球车测地定向。
| [1] |
许其凤, 丛佃伟, 董明.
主要定向技术比较与GNSS快速定位定向仪研制进展[J]. 测绘科学技术学报, 2013, 30(4): 349–352, 408.
XU Qifeng, CONG Dianwei, DONG Ming. Comparison Among the Main Orientation Technologies and the Research Progress of GNSS Rapid Positioning and Orientation Device[J]. Journal of Geomatics Science and Technology, 2013, 30(4): 349–352, 408. |
| [2] |
王安国.
现代天文导航及其关键技术[J]. 电子学报, 2007, 35(12): 2347–2353.
WANG Anguo. Modern Celestial Navigation and the Key Techniques[J]. Acta Electronica Sinica, 2007, 35(12): 2347–2353. DOI:10.3321/j.issn:0372-2112.2007.12.023 |
| [3] | VONDEROHE A P, MEZERA D F. Astro-azimuth Using Time Difference[J]. Journal of Surveying Engineering, 1984, 110(2): 112–118. DOI:10.1061/(ASCE)0733-9453(1984)110:2(112) |
| [4] | BUONOCORE B, VASSALLO A. Astronomical Determination of Azimuth and Latitude by Observation of Two Unknown Stars Without Time Measurement and Knowledge of Astronomy[J]. Survey Review, 1991, 31(242): 233–237. DOI:10.1179/sre.1991.31.242.233 |
| [5] | BALODIMOS D D, KORAKITIS R, LAMBROU E, et al. Fast and Accurate Determination of Astronomical Coordinates φ, Λ and Azimuth, Using a Total Station and GPS Receiver[J]. Survey Review, 2003, 37(290): 269–275. DOI:10.1179/sre.2003.37.290.269 |
| [6] |
张超, 郑勇, 李长会.
用任意星进行天文定向的研究[J]. 测绘科学, 2005, 30(4): 30–32.
ZHANG Chao, ZHENG Yong, LI Changhui. Research on Astronomy Orientation by Using the Random Star[J]. Science of Surveying and Mapping, 2005, 30(4): 30–32. |
| [7] |
詹银虎, 张超, 郑勇, 等.
月球视面中心拟合算法及其在测月快速定向中的应用[J]. 测绘学报, 2012, 41(3): 353–358.
ZHAN Yinhu, ZHANG Chao, ZHENG Yong, et al. A Fitting Algorithm of the Apparent Moon Center and Its Application on Fast Orientation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 353–358. |
| [8] |
詹银虎, 郑勇, 张超, 等.
球面圆拟合算法及其在测月定向中的应用[J]. 武汉大学学报(信息科学版), 2015, 40(11): 1514–1519.
ZHAN Yinhu, ZHENG Yong, ZHANG Chao, et al. Spherical Circle Fitting Algorithm and Its Application on Azimuth Determination by Observing the Moon[J]. Geomatics and Information Science of Wuhan University, 2015, 40(11): 1514–1519. |
| [9] |
何炬.
国外天文导航技术发展综述[J]. 舰船科学技术, 2005, 27(5): 91–96.
HE Ju. Survey of Overseas Celestial Navigation Technology Development[J]. Ship Science and Technology, 2005, 27(5): 91–96. |
| [10] |
韩永琪. 基于图像处理的天文定向装置设计[D]. 北京: 北京理工大学, 2015: 60-64. HAN Yongqi. Design of the Astronomical Orientation Device Based on Image Processing[D]. Beijing:Beijing Institute of Technology, 2015:60-64. |
| [11] |
原玉磊. 恒星法鱼眼相机恒星法检校技术研究[D]. 郑州: 信息工程大学, 2012: 206-217. YUAN Yulei. Research on Fish-eye Camera Stellar Calibration Technology[D]. Zhengzhou:Information Engineering University, 2012:206-217. |
| [12] |
王永仲.
鱼眼镜头光学[M]. 北京: 科学出版社, 2006: 37-39.
WANG Yongzhong. Fisheye Lens Optics[M]. Beijing: Science Press, 2006: 37-39. |
| [13] |
姚吉利, 韩保民, 杨元喜.
罗德里格矩阵在三维坐标转换严密解算中的应用[J]. 武汉大学学报(信息科学版), 2006, 31(12): 1094–1096, 1119.
YAO Jili, HAN Baomin, YANG Yuanxi. Applications of Lodrigues Matrix in 3D Coordinate Transformation[J]. Geomatics and Information Science of Wuhan University, 2006, 31(12): 1094–1096, 1119. |
| [14] | SUI Lifen, SONG Lijie, CHAI Hongzhou. Error Theory and Foundation of Surveying Adjustment[M]. Beijing: Surveying and Mapping Press, 2010: 66-70. |
| [15] |
欧阳自远.
月球科学概论[M]. 北京: 中国宇航出版社, 2005: 224-225.
OUYANG Ziyuan. Introduction to Lunar Science[M]. Beijing: China Astronautic Publishing House, 2005: 224-225. |
| [16] |
李茂登, 荆武兴武, 黄翔宇.
考虑月球扁率修正的月球卫星自主导航[J]. 宇航学报, 2012, 33(7): 896–902.
LI Maodeng, JING Wuxingwu, HUANG Xiangyu. Autonomous Navigation for Lunar Satellite with Lunar Oblateness Correction[J]. Journal of Astronautics, 2012, 33(7): 896–902. |
| [17] |
曲迎东, 李荣德, 白彦华, 等.
高速的9×9尺寸模板Zernike矩边缘算子[J]. 光电子·激光, 2010, 21(11): 1683–1687.
QU Yingdong, LI Rongde, BAI Yanhua, et al. A High-speed Zernike Moments Edge Operator Based on 9×9 Masks[J]. Journal of Optoelectronics·Laser, 2010, 21(11): 1683–1687. |
| [18] |
李崇辉, 杜兰, 韩建, 等.
圆形目标的鱼眼相机成像模型推导[J]. 河南科学, 2013, 31(7): 975–979.
LI Chonghui, DU Lan, HAN Jian, et al. Imaging Model Derivation of Circular Target Based on Fish-eye Camera[J]. Henan Science, 2013, 31(7): 975–979. |
| [19] |
詹银虎, 郑勇, 张超, 等.
超大视场太阳敏感器图像质心提取算法[J]. 测绘学报, 2015, 44(10): 1078–1084.
ZHAN Yinhu, ZHENG Yong, ZHANG Chao, et al. Image Centroid Algorithms for Sun Sensors with Super Wide Field of View[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1078–1084. DOI:10.11947/j.AGCS.2015.20150118 |
| [20] | FITZGIBBON A W, PILU M, FISHER R B. Direct Least Squares Fitting of Ellipses[C]//Proceedings of the 13th International Conference on Pattern Recognition. Vienna, Austria:IEEE, 1996. |
| [21] | HALÍŘ R, FLUSSER J. Numerically Stable Direct Least Squares Fitting of Ellipses[C]//Proceedings of the 6th International Conference in Central Europe on Computer Graphics and Visualization. Berlin:[s.n.], 1998. |
| [22] | GANDER W. Least Squares with a Quadratic Constraint[J]. Numerische Mathematik, 1980, 36(3): 291–307. DOI:10.1007/BF01396656 |
| [23] |
詹银虎. 基于自然天体的快速定向理论及技术研究[D]. 郑州: 信息工程大学, 2012: 12-13. ZHAN Yinhu. Theory and Technology Research on Fast Orientation Based on Celestial Bodies[D]. Zhengzhou:Information Engineering University, 2012:12-13. |
| [24] |
夏一飞, 金文敬.
新参考系的引入对天体测量学的影响[J]. 天文学进展, 2004, 22(3): 200–2087.
XIA Yifei, JIN Wenjing. Impacts of the New Reference System on Astrometry[J]. Progress in Astronomy, 2004, 22(3): 200–2087. |
| [25] | BANGERT J, PUATUA W, KAPLAN G, et al. User's Guide to NOVAS Version C3.0[M]. Washington:USA Naval Observatory, 2009, 12:31-32. |
| [26] |
张超. 基于电子经纬仪的天文测量系统及应用研究[D]. 郑州: 信息工程大学, 2009: 86-89. ZHANG Chao. System-level Development and Application Research on Astronomic Surveying System Based on Electronic Theodolites[D]. Zhengzhou:Information Engineering University, 2009:86-89. |
| [27] | PI. PI Datasheet H-840[R/OL]. (2016-01-11)[2017-06-09] Physik Instrumente, 2016. http://www.physikinstrumente.com/en/products/parallel-kinematic-hexapods/hexapods-with-motor-screw-drives/h-840-6-axis-hexapod-700810/. |



