2. 武汉大学海洋研究院, 湖北 武汉 430078;
3. 国家海洋局第一海洋研究所, 山东 青岛 266061
2. Marine Research Institute, Wuhan University, Wuhan 430078, China;
3. The First Institute of Oceanography, Qingdao 266061, China
海底控制网是海底板块运动、水下导航定位、水下建筑物稳定性监测等应用的参考[1]。为获得监测对象的绝对坐标,需在控制网点布设完成后确定各点的绝对坐标。为此,国内外学者提出了组合定位方法,即利用GNSS和水声测距设备结合,借助多艘测量船测距交会确定海底控制点绝对坐标[2-8]。文献[9]借助该方法在台湾海峡东部开展了试验,并将确定的海底点间距同SATS(seafloor acoustic transponder system)数据比较,验证了该方法的有效性。文献[10]对该方法进行了分析,认为存在如下不足:①需多艘测量船同步作业,交会确定水下点绝对坐标,作业成本较高;②测距以及定位精度受声速误差影响较大[11-12],尤其在深海,难以满足高精度监测需要。为提高作业效率、绝对坐标确定精度以及降低成本,文献[13]提出了一种借助船载换能器围绕待定水下点实施圆走航来确定海底点绝对坐标方法。相对于组合定位方法,圆走航方法只需一艘测量船即可完成定位。同时,因采用圆走航,测量波束入射角近似相等,声速带来的测距误差近似相等,且具有对称性,借助最小二乘解可很好地消除其影响,因此提高了水下点平面坐标精度。圆走航方法简化了作业,提高了精度,节约了成本,但当待确定点数较多时该方法仍费时费力。上述方法均存在一个普遍问题,即确定的垂直解精度不高甚至不稳定。文献[14-15]利用压力传感器对1500 m至2000 m海底点水深进行了持续观测,监测了Lucky Strike火山岩浆和大洋中脊的构造运动,认为监测精度远高于现有声学测距精度[16-20]。该研究为高精度垂直解的确定提供了一种解决方案,但因声学定位需要在一段时间内完成,期间波浪因素会对压力传感器实测深度带来显著误差,波浪影响需在测量中给予充分考虑和消除。
为解决上述问题,实现海底控制点绝对坐标的高精度、快速确定,本文提出了一种考虑波浪影响和深度约束的水下控制网点精确确定方法。本文主要包括如下内容:首先,研究了波浪的特征,实现了点间高差及点高程的确定;其次,提出了一种顾及波浪影响及深度约束的海底控制网点精确确定方法,包括附加深度约束的三维坐标基准传递法、深度约束的水下控制网点无约束平差法以及海底控制网的组合约束平差法和三维联合约束平差法。在此基础上,对该方法进行了试验验证,并对试验结果进行了分析;最后,结合理论方法研究及试验验证结果,得出一些有益的结论。
1 波浪影响及点间高差确定海底控制点上应答器内置有压力传感器,可测量该点到海面的垂直距离(深度)[21-22]。水面平静时该深度为常数。受波浪和潮汐等综合影响,实际海面是变化的,水深D为
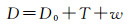 (1)
(1)
式中,D为观测水深;D0为多年平均海面至海底的深度,是潮汐起伏的基准面;T为潮位的振幅;w为波浪影响。
通常,波浪周期只有几秒到几分钟;水位周期较长,10 min内可认为几乎不变。因此,短时内,借助滑动平均便可将w影响滤除
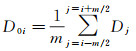 (2)
(2)
式中,D0i为第i个水深数据滤波结果;m为滤波窗口大小。
短时(10 min)内,借助式(2)可得一个稳定水面。考虑相邻点间距离约为几公里,开阔水域两点间潮位可认为近似相同,即认为小区域内水面平行。因此,式(2)计算得到的相邻两点D0差也即两点间高差
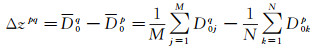 (3)
(3)
式中,相邻两点p和q高差为Δzpq;对应的平均水深为D0p和D0q;时序长度为N和M。
声学定位中,常借助船载换能器与海底点上应答器相互测距,船载GNSS同步作业。借助测量船的姿态、罗经等参数及GNSS天线、换能器在船体坐标系下的坐标,将GNSS天线实时测量的三维解归算至换能器,获得换能器T在地理坐标系下的绝对坐标[23]
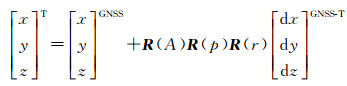 (4)
(4)
式中,[x, y, z]T和[x, y, z]GNSS分别为船载换能器和GNSS天线地理坐标;[dx, dy, dz]GNSS-T为二者在船体坐标系下的坐标差,其中,船载坐标系原点位于船重心,龙骨方向为x轴,船艏为正,垂直于龙骨并平行于船面的方向为y轴,右舷为正,垂直于x、y轴的方向为z轴,向下为正。A、p和r分别为测量船的方位、纵摇和横滚,对应旋转矩阵为R(A)、R(p)和R(r)。
若船载换能器吃水为ΔD,则瞬时海面高程为
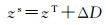 (5)
(5)
式中,zs为瞬时海面高程;ΔD为换能器T的吃水。
借助FFT低通滤波,可从zs序列中消除波浪影响,得到稳态水位z0s(文献[24])。短时内可认为海面变化较小,此时的稳态水位面z0s与前面通过压力传感器得到的平静水面D0相同。z0s为绝对高程,D0为相对海底点的水深,则海底点的高程zR为
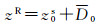 (6)
(6)
式中,zR为海底点高程。
以上推导建立在短时间小区域内。对于观测时间较长的情况,可以按固定时间间隔分段处理,最终的海底点高程为所有时段内海底点高程的平均。对于水下控制网点数多且范围大的情况,可求得一定基线长以内的所有点间高差,相距较远的点间高差可利用相距较近的点间高差得到。
2 顾及波浪影响和深度约束的海底控制网点坐标确定 2.1 附加深度约束的水下绝对基准传递方法绝对基准传递目的在于获得满足水下控制网平差所需必要起算点数的控制点绝对坐标,可利用圆走航方法实现[9]。圆走航时,船载换能器与海底应答器实测空间距离可表示为
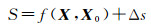 (7)
(7)
式中,f(X, X0)为船载换能器到海底应答器间的空间几何距离;S为带有误差Δs的观测距离;X和X0分别为海底点和换能器的真实坐标(x, y, z)和(x0, y0, z0)。
利用压力传感器在圆走航期间实测深度、船载GNSS实测海面高,借助式(4)—(6)可得海底点高程zR。根据式(4)所得换能器高程zT,可得实时换能器相对海底应答器的高差ΔzTR
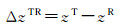 (8)
(8)
式中,ΔzTR为应答器R和换能器T高差,二者对应的高程分别为zR和zT。
在不同历元,构建如式(7)和式(8)所示方程,形成如下方程组,其矩阵形式为
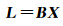 (9)
(9)
借助最小二乘,解算得到海底点坐标X,并评估其中误差。
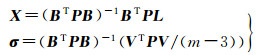 (10)
(10)
式中,m为圆走航的点数。
以上方程组构建中,消除波浪影响后的深度约束体现在式(8)中。去除式(8),则为传统的圆走航距离交会水下绝对基准传递方法。
2.2 深度约束的海底控制网无约束平差方法获得了部分海底点绝对坐标后,可开展海底控制网相互测距,利用声剖、测量时间等声线跟踪得到点间距离。为检验和剔除不合格观测距离或基线,需开展海底控制网无约束平差。
测量时,海底应答器内置压力传感器同步观测水深。借助上文方法,利用式(1)—(3),得到点间深度差。由于深度差具有较高的精度,可作为无约束平差中的约束条件,表现为:
(1) 视压力传感器提供的点间深度差为真值,将点间空间距离转换为水平距离,也即将三维网平差问题转变为二维网平差问题。
(2) 考虑压力传感器提供的点间深度差仍存在误差,视为观测量,与空间距离方程联合构建方程组开展解算,此时的平差问题即为附加深度约束的三维网平差。
以上两种约束皆可用于控制网无约束平差和约束平差。考虑无约束平差主要实现不合格基线的剔除及內符合精度的评估,这里采用深度约束的二维网平差方法。
设k、j为相邻两点,Skj和Δzkj为点间空间观测距离和高差,则点间平距skj为
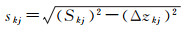 (11)
(11)
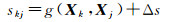 (12)
(12)
式中,g(Xk, Xj)表示两点间真实水平距离;Xk和Xj分别为k、j点坐标;Δs为观测误差。
对式(12)作泰勒展开。若有n条基线,可构建如下方程组
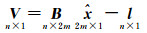 (13)
(13)
式中,B为秩亏系数矩阵;x为待求坐标改正数。令N=BTPB,N同样秩亏。选择重心基准的无约束平差[25],点的权阵Px为单位阵,基准阵S如下式
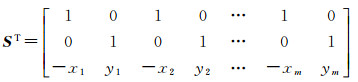
令K=PxSSTPx,则法方程系数阵为N′=N+K,此时N′满秩。改正数为
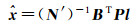 (14)
(14)
单位权中误差σ0和各kj基线中误差σkj为
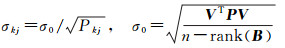 (15)
(15)
式中,rank(B)表示系数矩阵B的秩。
基于如下原则实现不合格基线的剔除
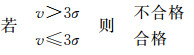 (16)
(16)
式中,v为基线改正数;σ为其单位权中误差。剔除不合格基线后,再按上述过程进行无约束重心基准网平差,直至所有基线合格。
2.3 附加深度信息的海底控制网约束平差方法无约束网平差给出了所有合格基线。要获得各水下点绝对坐标,需联合2.1节给出的部分水下点绝对坐标,开展附加深度信息的水下控制网约束平差。如2.2节所述,点间深度差Δz具有较高精度,可作为观测信息一并参与控制网约束平差。Δz的作用体现如下。
2.3.1 组合约束平差组合平差包括二维网约束平差和一维水准网约束平差。
将点间高差Δz作为已知值,利用式(11)将所有点间空间距离转换为平距;以圆走航确定的满足必要起算点数的水下点绝对坐标为起算数据,构建平距观测方程,形成平距方程组;借助式(9)和式(10)所示间接平差模型,解算得到各待求点平面坐标及其中误差。
以点间高差Δz为观测量,构建高差观测方程;利用所有基线高差方程,形成方程组;以已知点高程为起算,采用间接平差,获得各待求点高程及高程中误差。
2.3.2 三维联合约束平差以点间高差Δz为带有误差的观测量,构建高差观测方程;以点间空间距离为观测量,圆走航所得部分水下点坐标为起算,构建距离观测方程;联合所有基线的上述两类观测方程形成方程组,采用间接平差解算得到各待求点的三维坐标及其中误差。
以上平差处理中,各基线权为其距离倒数,深度权为观测水深倒数乘上平均水深同平均基线距离的比值。
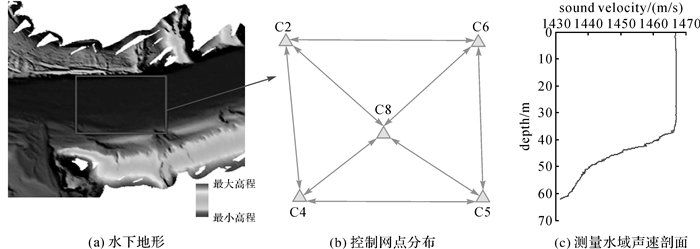
3 试验及分析 3.1 试验概况为检验本文给出的海底控制网点绝对坐标确定方法的正确性,在松花湖开展了水下试验。试验水域平均水深约60 m,水下地形平坦如图 1(a)所示。在湖底布设5个应答器,作为水下控制点如图 1(b)所示,编号分别为C2、C4、C5、C6和C8,分布在134 m×102 m范围内。测量前,严格测定船载换能器、GNSS RTK(real-time kinematic)天线在船体坐标系下的坐标。测量时,对5个水下点开展圆走航测量,水下点上应答器间相互测距,期间还开展了声速剖面测量,对所有换能器和应答器之间及应答器相互间测距进行声速改正,如图 1(c)所示。
|
| 图 1 水下试验 Fig. 1 Underwater experiment |
3.2 数据处理及分析 3.2.1 附加深度约束的绝对基准传递
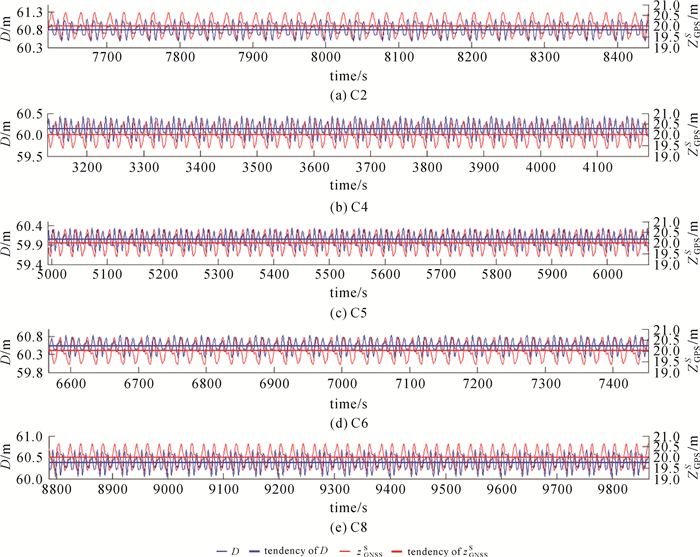
对所有原始观测数据滤波,消除异常观测。在此基础上,借助不同时刻GNSS RTK解、船姿、换能器和RTK天线在船体坐标系下的坐标,计算船载换能器绝对坐标。其中,RTK流动站与基准站间最大距离为15 km,流动站高程精度为±45 mm+1 ppm。借助换能器高程及其吃水,形成海面高程zGNSSs序列。借助圆走航时各应答器上压力传感器提供的深度D形成水深序列。序列D和zGNSSs均反映了瞬时水面变化。由图 2可知,受波浪、走航时动吃水等影响,D序列变幅在-0.2~0.2 m,zGNSSs序列在-0.6~0.6 m。以30 min为截止周期。用FFT低通滤波消除波浪影响,得到各自趋势线即平均水面如图 2所示。可以看出,两个序列的平均水面几乎平行。试验在湖上进行,该结论与实际相符,也验证了短时内两种方法得到的平均水面相同的假设成立。由于各自起算基准不同,为得到水下点的绝对高程,以GNSS平均水面为参考,结合二者水面差,可得C2、C4、C5、C6和C8高程分别为-40.8、-40.146、-40.044、-40.536和-40.374 5 m。
|
| 图 2 圆走航应答器内置压力传感器观测水深和GNSS观测水面高程 Fig. 2 Observation depth of all transponders and corresponding GNSS elevation of circle navigation |
借助船载换能器到水下应答器间测量距离,结合不同测距时刻换能器的绝对三维坐标,采用空间距离交会法(定义为方法1)确定水下应答器三维坐标;以前面根据水面差求得的水下点高程为观测量,与空间距离交会中各观测方程联合,利用2.1节方法开展深度约束的水下点绝对坐标解算(定义为方法2)。两种方法解算结果如表 1所示。可以看出两种方法得到的水下点平面坐标几乎相同,高程存在差异。以上述水面差求得的水下点高程为参考,可看出方法1所得高程偏差变化较大,最大达到16 cm;方法2所得高程偏差小且稳定,最大偏差为8 cm,因此将方法2所得三维坐标作为最终的水下点绝对坐标。
| 控制点 | 方法 | x/m | y/m | z/m | σx/cm | σy/cm | σz/cm | σ/cm | |dz|/cm |
| C2 | 方法1 | 315 690.39 | 4 841 955.13 | -40.96 | 2 | 2 | 1 | 3 | 16 |
| 方法2 | 315 690.39 | 4 841 955.12 | -40.88 | 2 | 2 | 1 | 3 | 8 | |
| C4 | 方法1 | 315 697.79 | 4 841 835.08 | -40.11 | 1 | 1 | 0 | 1 | 3 |
| 方法2 | 315 697.79 | 4 841 835.08 | -40.13 | 1 | 1 | 1 | 2 | 2 | |
| C5 | 方法1 | 315 792.61 | 4 841 865.00 | -39.97 | 1 | 1 | 0 | 1 | 8 |
| 方法2 | 315 792.60 | 4 841 865.00 | -40.02 | 2 | 2 | 1 | 3 | 2 | |
| C6 | 方法1 | 315 787.11 | 4 841 969.78 | -40.63 | 2 | 2 | 1 | 3 | 9 |
| 方法2 | 315 787.07 | 4 841 969.80 | -40.60 | 2 | 2 | 1 | 3 | 6 | |
| C8 | 方法1 | 315 736.47 | 4 841 896.68 | -40.47 | 1 | 1 | 0 | 1 | 5 |
| 方法2 | 315 736.48 | 4 841 896.68 | -40.44 | 2 | 2 | 1 | 3 | 2 |
3.2.2 附加深度约束的控制网无约束平差
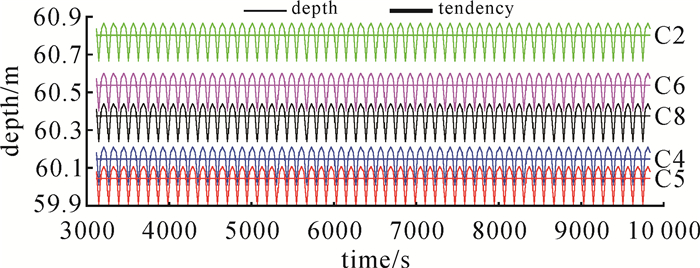
提取5个水下应答器相互测距期间各自压力传感器实测深度序列如图 3所示。可以看出,受波浪影响,序列中存在波动。此外,因应答器投放位置不同,各序列水深值存在差异。取30 s大小窗口对各序列滑动平均,得到消除波浪影响后的趋势面或平均水面。5个应答器上方的平均水面几乎平行。因在湖上试验,各应答器上方的平均水面理应相同。图 3中平均水面互差也即对应的两水下点间高差。由表 2统计结果可看出,相对圆走航期间所得水下点高程计算得到的点间高差,相互测距期间所得点间高差与之最大偏差为3 cm,表明消除波浪影响后得到的水下点高程及点间高差具有较高的稳定性,再次证明了短期平距水面具有较好的稳定性以及基于平均海面确定水下点高程及点间高差方法的合理性。
|
| 图 3 水下应答器相互测距期间各压力传感器提供的水面变化序列 Fig. 3 Water surface's change provided by transponders in distance measuring |
| cm | ||||||||||
| 时段 | C2-C4 | C2-C5 | C2-C6 | C2-C8 | C4-C5 | C4-C6 | C4-C8 | C5-C6 | C5-C8 | C6-C8 |
| 点间测距 | -66.4 | -72.6 | -23.4 | -43.6 | -12.2 | 39.0 | 22.9 | 49.3 | 35.0 | -16.0 |
| 圆走航 | -65.4 | -75.6 | -26.4 | -42.6 | -10.2 | 39.0 | 22.8 | 49.2 | 33.1 | -16.2 |
| 高差之差 | -1.0 | 3.0 | 3.0 | -1.0 | -2.0 | 0.0 | 0.0 | 0.1 | 1.9 | 0.2 |
对观测的2828条测线开展声线跟踪,获得点间空间距离;利用以上得到的点间高差,将空间距离换算为平距并构建距离方程,采用2.2节所示方法对水下网点开展无约束网平差;将式(16)中σ倍数改为2并据其剔除1529条不合格基线,最终得到1299条合格基线。可见,剔除比例较高。分析认为有两方面原因:其一是受应答器性能限制、测量环境及测量条件影响,水下应答器间互相应答时测量所得时间跳变较大所致;其二是在平差时采用2倍中误差作为门限参数来剔除不合格基线所致。图 4给出了各基线的最终改正量。所有基线改正数均小于1.5 cm,表明最终所得基线内符合精度较高。

|
| 图 4 深度约束的相对校准中各基线改正数 Fig. 4 Baseline corrections of relative calibration with depth constraint |
3.2.3 附加深度观测信息的控制网约束平差
获得高精度基线后,以部分已知点坐标为起算,对水下控制网开展约束平差。为分析本文给出的不同约束平差方法的精度及相对传统方法的优势,采用以下3种方法处理:
方法1:任选3个水下控制点(共8组),开展传统三维约束网平差处理。
方法2:任选两个水下控制点(共10组),开展三维联合约束网平差处理。
方法3:任选两个水下控制点(共10组),开展组合约束网平差处理。
以表 1中方法2给出的水下点坐标为参考,3种方法平差所得各点坐标与参考比较,表 3和表 4给出了各方法偏差的统计结果。
| cm | ||||||||||||||||||||
| 方法 | 控制点 | C2 | C4 | C5 | C6 | C8 | ||||||||||||||
| |dx| | |dy| | |dz| | |dx| | |dy| | |dz| | |dx| | |dy| | |dz| | |dx| | |dy| | |dz| | |dx| | |dy| | |dz| | ||||||
| 方法1 | C2 C4 C5 | — | — | — | — | — | — | — | — | — | 13 | 8 | 30 | 1 | 3 | 51 | ||||
| C2 C4 C6 | — | — | — | — | — | — | 7 | 3 | 38 | — | — | — | 6 | 0 | 21 | |||||
| C2 C4 C8 | — | — | — | — | — | — | 19 | 0 | 45 | 23 | 8 | 41 | — | — | — | |||||
| C2 C5 C6 | — | — | — | 11 | 11 | 11 | — | — | — | — | — | — | 7 | 6 | 35 | |||||
| C2 C6 C8 | — | — | — | 4 | 9 | 57 | 8 | 3 | 70 | — | — | — | — | — | — | |||||
| C4 C5 C6 | 6 | 0 | 89 | — | — | — | — | — | — | — | — | — | 4 | 6 | 45 | |||||
| C4 C5 C8 | 5 | 14 | 62 | — | — | — | — | — | — | 9 | 18 | 47 | — | — | — | |||||
| C5 C6 C8 | 22 | 3 | 99 | 16 | 11 | 50 | — | — | — | — | — | — | — | — | — | |||||
| 方法2 | C2 C4 | — | — | — | — | — | — | 15 | 0 | 2 | 15 | 9 | 6 | 8 | 4 | 1 | ||||
| C2 C5 | — | — | — | 10 | 8 | 1 | — | — | — | 12 | 7 | 6 | 5 | 1 | 1 | |||||
| C2 C6 | — | — | — | 10 | 12 | 1 | 5 | 10 | 2 | — | — | — | 3 | 7 | 1 | |||||
| C2 C8 | — | — | — | 5 | 9 | 1 | 8 | 8 | 3 | 15 | 1 | 6 | — | — | — | |||||
| C4 C5 | 6 | 11 | 9 | — | — | — | — | — | — | 11 | 11 | 6 | 3 | 11 | 1 | |||||
| C4 C6 | 12 | 2 | 7 | — | — | — | 10 | 3 | 3 | — | — | — | 0 | 2 | 0 | |||||
| C4 C8 | 0 | 8 | 8 | — | — | — | 13 | 1 | 3 | 14 | 10 | 6 | — | — | — | |||||
| C5 C6 | 16 | 1 | 9 | 11 | 11 | 1 | — | — | — | — | — | — | 11 | 2 | 2 | |||||
| C5 C8 | 11 | 3 | 8 | 12 | 5 | 1 | — | — | — | 3 | 9 | 6 | — | — | — | |||||
| C6 C8 | 13 | 6 | 8 | 5 | 14 | 2 | 6 | 7 | 2 | — | — | — | — | — | — | |||||
| 方法3 | C2 C4 | — | — | — | — | — | — | 15 | 1 | 2 | 15 | 9 | 6 | 8 | 4 | 2 | ||||
| C2 C5 | — | — | — | 9 | 5 | 2 | — | — | — | 11 | 5 | 6 | 6 | 1 | 2 | |||||
| C2 C6 | — | — | — | 8 | 11 | 2 | 6 | 9 | 2 | — | — | — | 5 | 10 | 2 | |||||
| C2 C8 | — | — | — | 5 | 9 | 2 | 8 | 8 | 2 | 15 | 1 | 6 | — | — | — | |||||
| C4 C5 | 6 | 11 | 8 | — | — | — | — | — | — | 11 | 11 | 6 | 3 | 11 | 2 | |||||
| C4 C6 | 12 | 2 | 8 | — | — | — | 10 | 3 | 2 | — | — | — | 3 | 0 | 2 | |||||
| C4 C8 | 0 | 8 | 8 | — | — | — | 13 | 1 | 2 | 14 | 10 | 6 | — | — | — | |||||
| C5 C6 | 16 | 1 | 8 | 11 | 11 | 2 | — | — | — | — | — | — | 12 | 2 | 2 | |||||
| C5 C8 | 11 | 3 | 8 | 12 | 5 | 2 | — | — | — | 3 | 9 | 6 | — | — | — | |||||
| C6 C8 | 13 | 6 | 8 | 5 | 14 | 2 | 6 | 7 | 2 | — | — | — | — | — | — | |||||
| cm | ||||||||||||||
| 方法 | |dx| | |dy| | |dz| | |||||||||||
| max | min | mean | STD | max | min | mean | STD | max | min | mean | STD | |||
| 方法1 | 23 | 1 | 10 | 6 | 18 | 0 | 6 | 5 | 99 | 11 | 49 | 22 | ||
| 方法2 | 16 | 0 | 9 | 5 | 14 | 0 | 6 | 4 | 9 | 0 | 4 | 3 | ||
| 方法3 | 16 | 0 | 9 | 4 | 14 | 0 | 6 | 4 | 8 | 2 | 4 | 3 | ||
由表 3和表 4可看出:在z方向,方法1所得z偏差普遍偏大,所有组合的平差结果中dz均为分米级,最大为99 cm,分析认为主要由于在绝对基准传递和海底网测量时未顾及海面起伏、较差的海底控制网网型空间分布等因素所致,也印证了前述传统三维网平差结果中垂直解精度不高的问题。方法2和方法3的垂直解偏差皆为厘米级,最大偏差分别为9 cm和8 cm,精度远高于传统方法。分析认为,方法1以带有较多误差的空间距离为观测量开展平差,而方法2和3均以消除波浪后的高精度点间高差为观测量参与平差,因此在整体上改善了观测数据的质量。在x、y方向,3种方法所得点位偏差大部分在厘米级。方法1最大偏差为23 cm,方法2和方法3最大偏差皆为16 cm。相同理由,本文方法相对传统方法的平面解精度略有提高。
比较发现,方法2和方法3结果精度近似。分析认为,方法2利用高精度高差将空间距离换算为平距,再开展二维平面网平差和一维高差网平差,改善了空间距离精度的同时,顾及了点间高差在网内的一致性;方法3则将空间距离与高差联合平差,一体化确定水下点三维坐标。高差在两种方法中的作用近似,因此二者的网平差结果一致。
4 结论本文提出的顾及波浪影响和深度约束的海底控制网点精确确定方法,消除了波浪影响,获得了准确的水下点高程及点间高差;基于圆走航实现了绝对平面和垂直基准从水面到水下传递;以消除波浪影响后的点间高差为约束,利用水下点间相互测距信息实施无约束网平差,获得了高精度基线;以高精度点间高差为观测信息,提出了组合约束平差法和三维联合平差法,解决了传统基于距离的约束平差带来的水下点位解算精度不高和高程确定不稳定问题,因此实现了水下控制网点的高精度确定。试验也验证了本文方法的正确性。
| [1] | BIALIK R, MAJDAN'SKI M, MOSKALIK M. Achievements, History and Challenges in Geophysics[M]. Cham: Springer, 2014. |
| [2] | SPIESS F N, CHADWELL C D, HILDEBRAND J A, et al. Precise GPS/Acoustic Positioning of Seafloor Reference Points for Tectonic Studies[J]. Physics of the Earth and Planetary Interiors, 1998, 108(2): 101–112. DOI:10.1016/S0031-9201(98)00089-2 |
| [3] | FUJITA M, ISHIKAWA T, MOCHIZUKI M, et al. GPS/Acoustic Seafloor Geodetic Observation:Method of Data Analysis and Its Application[J]. Earth, Planets and Space, 2006, 58(3): 265–275. DOI:10.1186/BF03351923 |
| [4] | GAGNON K L, CHADWELL C D. Relocation of a Seafloor Transponder-Sustaining the GPS-acoustic Technique[J]. Earth, Planets and Space, 2007, 59(5): 327–336. DOI:10.1186/BF03352692 |
| [5] | IKUTA R, TADOKORO K, ANDO M, et al. A New GPS-acoustic Method for Measuring Ocean Floor Crustal Deformation:Application to the Nankai Trough[J]. Journal of Geophysical Research:Solid Earth, 2008, 113(B2): B02401. |
| [6] |
蔡艳辉, 杨新红.
差分GPS水下定位系统的解析法分析[J]. 大地测量与地球动力学, 2008, 28(6): 101–106.
CAI Yanhui, YANG Xinhong. Underwater Positioning System's Baseline Network Analyzing Based on Analytical Method[J]. Journal of Geodesy and Geodynamics, 2008, 28(6): 101–106. |
| [7] |
兰华林. 深海水声应答器定位导航技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2008. LAN Hualin. Research on Poistioning and Navigation Technique with Underwater Acoustic Transponder in Deep Sea[D]. Harbin: Harbin Engineering University, 2008. |
| [8] |
兰华林, 孙大军, 张殿伦, 等.
海底应答器绝对位置快速校准[J]. 计算机工程与应用, 2007, 43(22): 191–193.
LAN Hualin, SUN Dajun, ZHANG Dianlun, et al. Rapid Calibration of Absolute Position of Transponder on Seabed[J]. Computer Engineering and Applications, 2007, 43(22): 191–193. DOI:10.3321/j.issn:1002-8331.2007.22.057 |
| [9] | CHEN H H, WANG C C. Accuracy Assessment of GPS/Acoustic Positioning Using a Seafloor Acoustic Transponder System[J]. Ocean Engineering, 2011, 38(13): 1472–1479. DOI:10.1016/j.oceaneng.2011.07.002 |
| [10] | YAMADA T, ANDO M, TADOKORO K, et al. Error Evaluation in Acoustic Positioning of a Single Transponder for Seafloor Crustal Deformation Measurements[J]. Earth, Planets and Space, 2002, 54(9): 871–881. DOI:10.1186/BF03352435 |
| [11] | ISSHIKI H. Precise Positioning of a Transponder Placed on a Sea Floor[C]//Proceedings of the 2000 International Symposium on Underwater Technology. Tokyo: IEEE, 2000: 334-339. |
| [12] | YANG Fanlin, LU Xiushan, LI Jiabiao, et al. Precise Positioning of Underwater Static Objects Without Sound Speed Profile[J]. Marine Geodesy, 2011, 34(2): 138–151. DOI:10.1080/01490419.2010.518501 |
| [13] | CHEN H H, WANG C C. Optimal Localization of a Seafloor Transponder in Shallow Water Using Acoustic Ranging and GPS Observations[J]. Ocean Engineering, 2007, 34(17-18): 2385–2399. DOI:10.1016/j.oceaneng.2007.05.005 |
| [14] | BALLU V, BOUIN M N, CALMANT S, et al. Absolute Seafloor Vertical Positioning Using Combined Pressure Gauge and Kinematic GPS Data[J]. Journal of Geodesy, 2010, 84(1): 65–77. DOI:10.1007/s00190-009-0345-y |
| [15] | BALLU V, AMMANN J, POT O, et al. A Seafloor Experiment to Monitor Vertical Deformation at the Lucky Strike Volcano, Mid-atlantic Ridge[J]. Journal of Geodesy, 2009, 83(2): 147–159. DOI:10.1007/s00190-008-0248-3 |
| [16] | LEE P M, JUN B H. Pseudo Long Base Line Navigation Algorithm for Underwater Vehicles with Inertial Sensors and Two Acoustic Range Measurements[J]. Ocean Engineering, 2007, 34(3-4): 416–425. DOI:10.1016/j.oceaneng.2006.03.011 |
| [17] | MAJUMDER S, SCHEDING S, DURRANT-WHYTE H F. Multisensor Data Fusion for Underwater Navigation[J]. Robotics and Autonomous Systems, 2001, 35(2): 97–108. DOI:10.1016/S0921-8890(00)00126-3 |
| [18] | OBANA K, KATAO H, ANDO M. Seafloor Positioning System with GPS-acoustic Link for Crustal Dynamics Observation:A Preliminary Result from Experiments in the Sea[J]. Earth, Planets and Space, 2000, 52(6): 415–423. DOI:10.1186/BF03352253 |
| [19] | XU Peiliang, ANDO M, TADOKORO K. Precise, Three-dimensional Seafloor Geodetic Deformation Measurements Using Difference Techniques[J]. Earth, Planets and Space, 2005, 57(9): 795–808. DOI:10.1186/BF03351859 |
| [20] |
赵建虎, 邹亚靖, 吴永亭, 等.
深度约束的海底控制网点坐标确定方法[J]. 哈尔滨工业大学学报, 2016, 48(10): 137–141.
ZHAO Jianhu, ZOU Yajing, WU Yongting, et al. Determination of Underwater Control Point Coordinate Based on Constraint of Water Depth[J]. Journal of Harbin Institute of Technology, 2016, 48(10): 137–141. DOI:10.11918/j.issn.0367-6234.2016.10.020 |
| [21] |
白鑫, 钱志博, 陈洁.
一种水声应答器电子系统的设计[J]. 电子测量技术, 2009, 32(10): 8–11.
BAI Xin, QIAN Zhibo, CHEN Jie. Design of Underwater Acoustic Transponder Electronic System[J]. Electronic Measurement Technology, 2009, 32(10): 8–11. DOI:10.3969/j.issn.1002-7300.2009.10.003 |
| [22] |
吴永亭, 周兴华, 杨龙.
水下声学定位系统及其应用[J]. 海洋测绘, 2003, 23(4): 18–21.
WU Yongting, ZHOU Xinghua, YANG Long. Underwater Acoustic Positioning System and Its Application[J]. Hydrographic Surveying and Charting, 2003, 23(4): 18–21. |
| [23] |
田坦.
水下定位与导航技术[M]. 北京: 国防工业出版社, 2007.
TIAN Tan. Underwater Acoustic Localization and Navigation Technology[M]. Beijing: National Defense Industry Press, 2007. |
| [24] |
赵建虎.
现代海洋测绘[M]. 武汉: 武汉大学出版社, 2008.
ZHAO Jianhu. Modern Marine Surveying and Charting[M]. Wuhan: Wuhan University Press, 2008. |
| [25] |
崔希璋, 於宗俦, 陶本藻, 等.
广义测量平差[M]. 2版. 武汉: 武汉大学出版社, 2009.
CUI Xizhang, YU Zongchou, TAO Benzao, et al. Generalized Surveying Adjustment[M]. 2nd ed. Wuhan: Wuhan University Press, 2009. |



