2. 广州大学地理科学学院, 广东 广州 510006;
3. 广州市城市规划勘测设计研究院, 广东 广州 510060;
4. 武汉大学资源与环境科学学院, 湖北 武汉 430072
2. School of Geographical Sciences of Guangzhou University, Guangzhou 510006, China;
3. Guangzhou Urban Planning and Design Survey Research Institute, Guangzhou 510060, China;
4. School of Resources and Environment Science, Wuhan University, Wuhan 430072, China
空间数据现势性作为数据质量的基本特征,直接影响地图数据空间分析、挖掘及决策的准确性。随着基础地理设施数据库建设不断完善,基础测绘工作重心由数据生产转向数据维护[1],特别是对现有多比例尺矢量地图数据库的现势性更新与一致性维护[2]。常规方法是以影像、局部实测数据为参考,对不同比例尺地图数据集进行独立式更新。一方面耗时耗力,另一方面容易导致不同比例尺数据间产生表达不一致[3]。为了提高多比例尺地图数据更新的效率,文献[4-6]研究了增量式更新模式,即将不同比例尺地图数据组织为多重表达数据库[7],建立纵向跨比例尺地图目标间的对应关系,使得大比例尺数据中发生的更新内容能够以增量形式传递到后续小比例尺数据中。然而,受生产单位、生产任务以及时间周期差异等因素影响,实践中不同比例尺地图数据通常割裂式组织,难以满足上述条件。考虑到当前地图数据组织管理现状,采用新旧数据叠加更新策略更为合理[8]。该方法首先依据各种更新数据源对大比例尺地图数据实施动态实时更新,然后定期将更新后的大比例尺地图数据作为参考,探测并更新邻近小比例尺数据的变化目标,依次执行直至完成整个多比例尺地图数据库的更新。这种叠加式更新策略产生的关键问题之一是如何识别新旧地图数据间隐含的变化信息。
变化是指由于地理实体发生改变而导致的新旧地图目标间的差异。变化识别受实体世界地物演化行为、地图数据采集精度、地图数据处理误差等多方面影响,一直是GIS领域的难点问题,对地图数据更新、变化建模及时空分析有重要意义[9]。针对该问题,相关学者从不同角度展开了深入研究。如文献[10]提出通过匹配处理建立新旧地图同名目标关联关系,然后基于匹配关系类型、几何形状及属性信息一致性等指标确定目标是否发生变化。文献[11]设计了相似性度量模型计算线状道路目标间的相似度,通过研究道路变化与对应新旧目标间的相似度关系,最终建立道路数据的变化发现模型。针对新旧目标间几何差异信息可能由成图精度、测量时间、投影变形等因素影响导致的“伪变化”,文献[12-13]以面状水系为例分别提出了拓扑量化的“伪变化”剔除方法和顾及时空目标边界不一致性的变化识别模型。上述方法主要面向同比例尺新旧地图数据的变化发现,无法直接应用于跨比例尺情形。原因是多尺度地图目标改变除由地物实体演化而引起外,不同比例尺表达上的尺度变换(即数据综合)也会导致。这一问题已经引起研究人员的注意,如文献[14]提出在获取新旧地图目标变化差异的基础上,结合地图综合知识过滤尺度表达不一致引起的变化部分;文献[15]以跨比例尺面目标为例,将目标基本变化类型归纳为出现、消失、扩张、收缩等9种类型,并提出基于4交差拓扑模型的变化判别方法等。文献[16]在目标叠置运算的基础上通过数据增强方法提炼居民地目标间的真实变化信息。
在上述工作基础上,本文对跨比例尺新旧地图数据间的变化分析与识别展开更为深入的研究。研究动机包括两个方面:①对新旧地图目标间的变化进行梳理分析,包括变化产生的缘由、变化表现的形式;②综合考虑几何、拓扑、上下文关系等多种因子,引入决策树方法通过学习方式构建准确的变化识别模型。
1 多尺度新旧地图目标变化分析实施变化识别以及后续更新操作,首先需要理解新旧地图数据间隐含的目标变化信息。下文首先从表层形式和内在缘由两个角度对面状居民地目标的变化进行剖析。
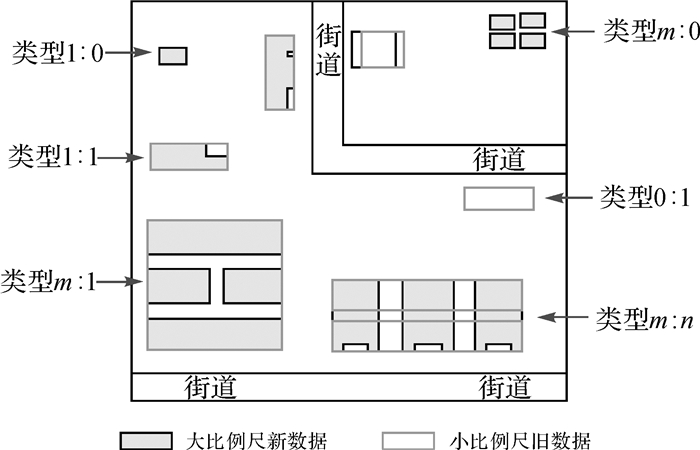
1.1 目标变化的类型从表层形式上看,新旧地图目标间的变化包括积极的正向变化(如目标新增、目标轮廓扩张)和消极的负向变化(如目标消失、目标轮廓收缩)。同时,也表现为个体变化(如单个目标的增加、消失、扩张、收缩)和群体变化(即目标群的新增、扩张、收缩等)。假设大比例尺新地图数据为D1,小比例尺旧地图数据为D2,依据新旧目标间的匹配对应关系将面状居民地目标变化归纳为以下6种类型(图 1):
|
| 图 1 新旧跨比例尺地图间居民地目标变化类型 Fig. 1 Types of building change between two map datasets at different scales |
类型1:0,D1中某个目标在D2中没有与之匹配的对象,表现为单个房屋目标新增;
类型1:1,D1和D2中两个目标匹配对应,但是在目标局部存在扩张、收缩现象;
类型0:1,D2中某个目标在D1中没有与之匹配的对象,表现为单个房屋目标消失;
类型m:1(m>1),D1中多个相邻目标与D2中单个目标匹配对应,表现为相邻目标的合并;
类型m:n(m≥1,n>1),D1中单个或多个相邻目标与D2中多个目标匹配对应,房屋目标间的结构关系发生改变;
类型m:0(m>1),该类型变化将D1中多个相邻目标作为整体看待,在D2中没有与之匹配对应的目标或目标群,表现为房屋群的新增。
1.2 真实变化与表达变化新旧地图目标发生变化的直接原因是所表达的地物发生了改变。这种由于地物实体改变而导致的地图目标变化称为真实变化。面状居民地目标变化信息可归纳为以下类型(图 2)。

|
| 图 2 房屋实体变化情形及引起的目标变化 Fig. 2 Buildings' evolution in real word and their impacts on object change |
房屋新建:在空地上建造新房屋,表现为新地图数据中新增房屋目标(1:0类型);
房屋拆除(局部拆除):由于道路改造等原因对原有房屋进行完整(或局部)拆除,表现为旧地图数据中的居民地目标在新数据表达中完整消失(0:1类型)或者局部消失(1:1类型);
房屋扩建:对原有的房屋进行扩建,表现为居民地目标几何轮廓的扩张(1:1类型);
房屋重建:即将原有房屋拆除后重新建造,表现为旧房屋目标被新房屋目标所替代,可能的变化类型包括1:1、m:1、m:n。
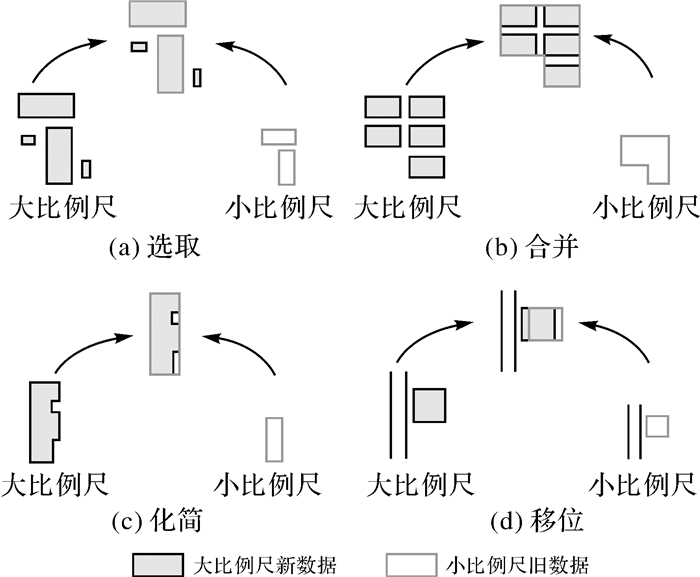
除真实变化外,新旧地图数据表达上的差异同样会影响变化信息的产生,包括数据采集精度、建库方式、表达比例尺等。对于同一数据库中的不同比例尺数据,小比例尺地图数据通常由大比例尺地图数据综合缩编获得, 包括目标合并[17]、形状化简[18]等操作。因此,表达变化可以忽略数据精度、建库方式等因素影响,主要是指不同比例尺地图数据间由于尺度变换导致的差异信息。对于城市区域1:2000和1:10 000两个比例尺的新旧居民地数据,综合操作及对变化信息的影响包括以下情形(图 3)。
|
| 图 3 不同尺度变换操作导致的目标变化情形 Fig. 3 Scale transformation operations and their impacts on object change |
选取:舍弃尺寸小于最小上图面积的房屋目标,表现为房屋目标在小比例尺表达中消失(0:1类型);
合并:将相邻房屋目标合并为一个房屋目标,合并前后呈m:1变化类型;
化简:对目标多边形轮廓进行化简,化简后目标局部轮廓扩张或者收缩(1:1变化类型);
移位:为保证房屋与道路(或其他要素目标)间的间隔大于可辨析距离,轻微地改变房屋目标的分布位置,属1:1变化类型。
2 决策树支持下的变化信息识别模型构建上文从表现形式和发生缘由两个方面,对新旧地图居民地目标变化进行了分析归纳。严格意义上,变化识别的目标是提取由地理实体改变而引起的目标变化。但是在缺乏参考数据(如遥感影像)情况下,仅依据新旧不同比例尺地图间表达差异很难实现上述目标。例如,大比例尺新数据中的一个小面积房屋在小比例尺旧数据中消失(1:0类型),这一变化可能是实地新建房屋导致,也可能是由于房屋面积过小而在数据综合过程中被舍弃。对于跨比例尺地图数据更新,幅度较小的真实变化由于尺度变换因素无需更新,因此变化识别主要任务是探测超出地图数据综合操作范围的目标变化信息。
跨比例尺新旧地图变化识别是一个复杂的决策过程。一方面,地图综合产生的变化受多种因素影响,综合算法/算子选择、参数设置、综合流程组织等与区域环境特点、数据应用需求、比例尺范围密切相关;另一方面,变化识别本身需要考虑变化类型、变化幅度、变化关联目标的几何、结构信息等多重上下文条件。在此背景下,引入机器学习领域的决策树方法构建跨比例尺新旧地图数据间的变化识别模型,采用的技术路线如图 4所示。

|
| 图 4 跨比例尺新旧地图数据变化识别决策树模型构建流程 Fig. 4 The framework of decision tree based model for change detection between datasets at different points both in time and scale |
2.1 匹配关系构建
识别变化,首先需要建立新旧地图目标间匹配关系。针对这一问题,相关学者围绕居民地[19-20]、道路[21-23]等要素提出多种方法。这些方法依据要素对象特点、应用需求,采取不同相似性指标组合(包括长度、面积、距离、方向、拓扑结构等)与匹配策略(如概率统计、全局寻优、层次化匹配)。考虑大比例尺居民地数据特点及效率,本文采用一种迭代式的目标匹配方法。假设大比例尺新数据和小比例尺旧数据包含的居民地目标集合分别为OL={OL1, OL2, …, OLm}和OS={OS1, OS2, …, OSn},TL和TS定义为临时集合分别存储来自OL和Os的目标,初始化TL=Φ,TS=Φ。步骤如下:
步骤1:若OS≠Φ,取OS中任一目标并存储到TS,转步骤4,否则,转步骤2;
步骤2:若OL≠Φ,转步骤3,否则结束匹配过程;
步骤3:对OL中抱团分布且邻近距离小于dm的目标群,记录为m:0(m>1)匹配关系,其余目标记录为1:0匹配关系,结束匹配过程;
步骤4:遍历TS中每个目标Oi,
查询OL中与Oi拓扑相交的目标,从OL取出查询结果并保存到数组A中;
按式(1)计算A中每个目标Oj与Oi间的重叠系数λ,若λ小于阈值λ0,将Oj从list取出放回OL
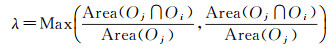 (1)
(1)
式中,Area(Oj∩Oi)表示两个目标相交部分面积,Area(Oj)和Area(Oi)表示目标面积,Max取最大值。
若A为空,转步骤6;否则清空TL,并将A中目标转移到TL中;
步骤5:遍历TL中的每个目标Oi,
查询OS中与Oi拓扑相交的目标,从OS取出查询结果并保存到数组A中;
按式(1)计算A中每个目标Oj与Oi间的重叠系数λ,若λ小于阈值λ0,将Oj从A取出放回OS;
若A为空,转步骤6;否则清空TS,将A中目标转移至TS中,转步骤4;
步骤6:分别取出TL和TS中的目标记录为匹配对,同时清空TL和TS,转步骤1。
2.2 变化描述与计算以建立的匹配组为基本单元,对新旧目标变化进行特征描述,为后期决策树分类模型的形成提供参数。考虑人工变化识别过程中涉及的基本判断依据,采用以下5个特征指标:
(1) 变化关系类型(nType):如上文所述,变化关系包括1:0、0:1、1:1、m:1、m:0、m:n 6种类型。它们不仅蕴含了变化发生的范围信息(如个体变化、群体变化),同时也揭示了变化产生的效应(如1:0为目标消失、0:1为目标新增),是变化识别的基础性依据。
(2) 重叠差异度(ov_diff):假设某一匹配组包含m个来自新数据的目标OL1, OL2, …, OLm和n个来自旧数据的目标OS1, OS2, …, OSn,m≥1,n≥1,重叠差异度φ计算如下
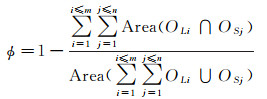 (2)
(2)
式中,∩表示交运算,∪表示并运算。重叠差异度反映了新旧目标分布范围上的差异,是衡量目标发生扩张或收缩程度的重要特征。
(3) 形状相似性(sim_shape),即新旧目标间形状上的相似性程度。采用形状指数描述单个目标(如Oi)的形状信息(式(3)),其中Perimeter(Oi)和Area(Oi)分别表示目标的周长和面积。两个目标形状指数的比值定义为形状相似度。形状相似度对于识别由尺度变换(如移位)引起的变化信息有参考价值。
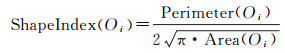 (3)
(3)
(4) 大小相似性(sim_size),定义为匹配组中新旧目标间的面积比率。
(5) 几何面积,包括新目标面积(new_area)和旧目标面积(old_area)。该指标是1:0和m:0两种变化的重要识别依据。对于面积较小的新增目标或目标群,由于处于综合选取引起的变化范围内,不作为变化信息用于更新。
2.3 变化识别决策树模型及实施过程变化识别可以看作是“变化”和“非变化”的分类过程。决策树因数据处理简单(非参数化算法,数据无需标准化处理)、效率高(线性分类模型)、分类规则可解译性强等特点而被广泛应用[24-27]。决策树本质是一个有向无环树,内部节点(包括根节点)表示在一个属性上的测试,后继分支则代表该属性测试的输出,每个叶节点代表一种类别。利用决策树分类时,待分类对象按属性特征由上到下遍历树结构即可预测其类别。C4.5算法是目前应用最为广泛的决策树构建方法,基本思想是对样本数据属性特征构成的多维空间进行分割,分割能力最好的属性项作为根节点的测试,样本数据按该属性测试分割为多个子集作为后继分支,重复该过程直至形成最终的树结构。C4.5算法采用信息增益率标准确定当前最佳分组属性及分割点[22]。基于决策树的跨比例尺新旧居民地目标变化识别方法实施过程描述如下:
(1) 选择样本区域的新旧居民地目标,按2.1节方法建立匹配关系,将相互匹配的新旧目标作为一条样本记录;
(2) 对每一条样本记录,计算2.2节定义的特征参量;
(3) 由专家在交互式平台上对每一条样本记录进行变化识别,标识为“Yes”(属于变化)和“No”(不属于变化),并将样本数据输出为表 1所示格式;
| 编号(ID) | 变化类型(nType) | 新目标面积(new_area) | 旧目标面积(old_area) | 重叠差异度(ov_diff) | 面积相似性(sim_size) | 形状相似性(sim_shape) | 是否变化(class) |
| 1 | 1:1 | 246.4 | 275.3 | 0.14 | 0.90 | 0.93 | No |
| 2 | m :1 | 2560.7 | 2900.4 | 0.16 | 0.88 | null | No |
| 3 | 1:0 | 400.4 | null | null | null | null | Yes |
| 4 | 0:1 | unll | 488.6 | null | null | null | Yes |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
(4) 基于样本数据构建决策树模型,并结合测试数据评估相关性能。
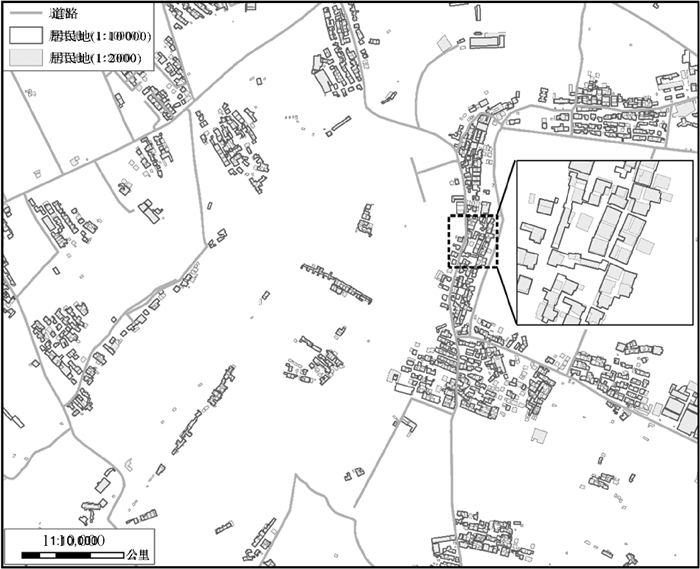
3 试验分析及评价(1) 试验数据。采用广州市1:2000和1:10 000的居民地数据,对应更新时间节点分别是2009年和2007年。如图 5所示,试验数据来自A、B、C 3个区域。A区域覆盖城区及城乡结合部,作为训练数据使构建的决策树模型获取不同区域环境下的变化识别知识; B区域和C区域分别位于城区和城乡结合部,作为测试数据以检验模型在不同区域类型数据上的表现。表 2描述了训练及测试数据基本情况。其中,样本及测试记录的变化标识由广州市城市规划勘测设计研究院地图所3名具备丰富数据更新经验的作业人员完成。为保证变化标识结果的准确性,取3名作业人员变化标识结果相一致的记录作为最终样本及测试数据。
|
| 图 5 试验数据示例 Fig. 5 Experimental data |
| 数据 | 房屋数量 | 新旧目标匹配对数目(变化|非变化) | ||
| 1:2000 | 1:10 000 | |||
| 训练数据 | 区域A | 9146 | 5037 | 5908(1665|4243) |
| 测试数据 | 区域B | 4591 | 1523 | 1714(321|1393) |
| 区域C | 3646 | 1613 | 2156(434|1722) | |
(2) 试验环境。利用ArcGIS平台通过二次开发建立数据分析准备功能,包括新旧居民地目标匹配关系构建、变化参量计算、交互式变化识别及标注等;然后,采用数据挖掘与分析软件SPSS Clementine基于训练数据构建变化识别决策树模型,同时结合测试数据进行模型评价。
(3) 参数设置。包括:①构建新旧目标匹配关系时,通过多次试验反馈,设置λ0=0.3、dm=5 m(即1:10 000比例尺下图面0.5 mm);②为避免决策树构建时“过拟合”问题,采用“减少-误差”法进行后剪枝操作,设置节点剪枝alpha值0.55,子节点最小样本数量50。考虑到不同类型的新旧目标变化参量描述上存在差异,如重叠差异度、大小相似性等对1:0型变化关系没有意义(样本记录中标识为Null),建模过程中分别对不同变化类型的训练样本子集构建决策树,最后合并形成一棵完整的决策树模型。
图 6是基于训练数据导出的决策树图,包括4个层级、12个叶子节点。具体描述如下:①对于1:0型样本子集,利用新目标面积进行分割,new_area≤145.5时样本判别为“非变化”(推理置信度98.9%),new_area>145.5时判别为“变化”(置信度97.2%);②对于1:1型样本子集,首先采用重叠差异度进行分割,ov_diff≤0.18时判别为“非变化”(置信度98.0%),剩余样本则进一步依据形状及面积相似性属性进行分类,如符合规则sim_shape≤0.67的样本为“变化”(推理置信度89.7%),sim_shape>0.67并且sim_size≤0.84的样本为“变化”(置信度86.4%),sim_shape>0.67并且sim_size>0.84的样本划分为“非变化”(置信度86.7%);③0:1型样本判定为“变化”(置信度100%),该类型目标变化对应于真实地理世界中的房屋消失,不受地图综合的影响;④m:1型样本符合规则ov_diff≤0.26判定为“非变化”(置信度92.4%),ov_diff>0.26判定为“变化”(置信度89.3%);⑤m:n型样本直接判定为“变化”(置信度92.3%);⑥m:0型样本与1:0型相似,当new_area>137.3时样本判定为“变化”(置信度92.1%),反之判定为“非变化”(置信度96.2%)。

|
| 图 6 训练数据生成的决策树 Fig. 6 The constructed decision tree based on training data |
表 3是建立的决策树模型在训练数据获得的分类结果混淆矩阵。通过计算得到整体分类精度(即分类正确的样本数量除以样本总数)和kappa系数分别为96.1%、90.5%,表明建立的决策树模型具有较高的分类精度。考虑到训练数据中实际“变化”样本数量明显少于“未变化”样本数量,进一步分析“变化”样本的误检率和漏检率。误检率α和漏检率β定义如式(4)和式(5)所示。
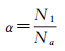 (4)
(4)
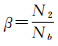 (5)
(5)
| 分类 | 决策树分类 | 总计 | ||
| Yes | No | |||
| 人工识别分类 | Yes | 1539 | 126 | 1665 |
| No | 99 | 4144 | 4243 | |
| 总计 | 1638 | 4270 | 5908 | |
式中,Na表示决策树分类为“变化”的样本数量,N1表示实际“非变化”但是误判为“变化”的样本数量,Nb表示集合样本中人工判断为“变化”的样本数量,N2表示实际“变化”但是漏判为“非变化”的样本数量。依据式(4)(5)得到整体变化信息的误检率α=8.0%,漏检率β=10.5%。表 4统计了不同变化类型样本子集中决策树表现出的分类及变化识别性能指标。从分类精度上看,决策树在不同类型样本子集中均达到90%以上。从变化识别精度上看,m:1型样本的漏检率较高(β=22.1%),其他类型变化的误检率和漏检率均低于15%。
| (%) | ||||||
| 结果 | 变化类型 | |||||
| 1:0 | 1:1 | 0:1 | m:1 | m:n | m:0 | |
| 整体分类精度 | 98.6 | 95.9 | 100 | 91.7 | 92.3 | 95.0 |
| 变化误检率 | 6.7 | 11.5 | 0 | 10.7 | 7.7 | 3.2 |
| 变化漏检率 | 2.8 | 13.2 | 0 | 22.1 | 0 | 4.3 |
(4) 试验分析评价。利用区域B和C数据对构建的决策树模型进行分析评价。理由包括:①训练数据与测试数据不同,能够避免训练数据可能带来的偏见;②不同区域环境类型的数据测试结果及比较能够为后续应用提供参考。表 5列出了测试数据分类及变化识别结果。可以发现,决策树模型在新数据上的表现接近于训练数据。进一步地,可以发现城乡结合部(区域C)的分类及变化识别效果优于城区区域(区域B)。结合图 7分析,导致的原因主要包括:
| (%) | |||
| 区域 | 整体分类精度 | 变化误检率 | 变化漏检率 |
| 区域B(城区) | 92.1 | 12.4 | 25.3 |
| 区域C(城乡结合部) | 98.2 | 6.9 | 8.1 |

|
| 图 7 决策树模型变化识别结果示例 Fig. 7 Samples of change detection using the constructed decision tree on test data |
构建的决策树模型对于m:1型变化关系的识别成功率相对其他变化类型较低。这是由于决策树模型对m:1型变化的判定只考虑了重叠差异度指标,无法准确反映关联新旧居民地目标间局部的变化性质。如图 7中M1、M2以及M4处的居民地分别存在局部扩建和局部拆除的变化,但是新旧目标间的重叠差异度并不大(分别是0.23、0.25和0.22),因此误判为“非变化”;而M3处从尺度变换的角度属合并操作引起的变化范畴,但是由于重叠差异度较大误判为“变化”。
城区居民地分布密集,跨比例尺新旧房屋目标间对应关系相对复杂。目标变化以群体式的扩展、收缩为主,尺度表达上的合并操作产生大量m:1型变化关系;而城乡结合部房屋分布较为稀疏,目标以单一分布为主,对象性强,大量的变化关系表现为1:0、1:1、0:1等类型,变化识别难度系数相对较低。此外,部分城区居民地变化的产生涉及多种尺度变换组合情形,如M5处存在合并与移位两种操作,增大了变化识别的难度。
上述问题的解决,一方面需要从方法本身出发,引入新的变化描述特征、提升模型构建策略以及选取更多实际数据进行训练。另一方面,实际应用中可对不同区域特点的规则阈值进行适度调整,如城区可适当提高重叠度阈值以增强对居民地局部区域发生变化的识别能力。虽然部分“非变化”可能识别为“变化”,一定程度上增加了后续更新操作的工作量,但是能够保证变化更新的完整性。基于决策树的变化识别模型对变化条件判断综合性强,多种判断规则通过逻辑与、或、差集成,同时各规则的阈值设定又能根据区域环境差异适应性地设定。本文方法与文献[16]叠置运算方法识别跨比例尺间的居民地变化相比,在变化条件的集成上得到加强,不是简单通过多边形叠置运算后基于面积大小关系判断是否有变化,同时顾及了形状、空间关系参量等在变化判断中的作用。
4 结论本文以居民地数据为例,从发生缘由和表现形式两个主要角度,对跨比例尺新旧地图数据间的变化信息进行了系统梳理。以数据更新为目标,引入决策树方法建立变化信息识别模型,并采用真实数据验证了方法的可行性。决策树模型在判断新旧数据变化过程中,考虑了数据本身的变化和上下文邻域变化,同时顾及了映射关系上的单目变化和多目变化。多因素的变化条件通过决策树不同规则及其逻辑运算集成,保障本方法在实际地理环境下变化识别的可行性。同时,本决策树方法的规则条件、阈值设定,可通过不同样区的训练获得,从而适应不同区域环境条件下的变化识别(如居民地分布的城市中心区CBD、城乡结合部、远郊区等)。
结合试验结果,以下工作需要进一步完善:①强化复杂变化特征描述。从试验结果上看,m :1型及部分1:1型变化关系的识别有待提高。特别是目标局部发生扩张或收缩变化,仅通过目标间的重叠差异度无法精确判断是真实变化还是表达变化。这一问题需要在获得新旧目标图形差异的基础上进行局部形态分析,并定义相关描述参量;②变化识别推理规则的组织与完善。决策树模型能够导出学习得到的规则,通过加工提炼后可融入到专业的地图数据管理软件,进而形成专门的数据更新模块;③本文仅探讨了大比例尺段(1:2000至1:10 000)面状居民地目标间的变化分析与识别,需要进一步扩展至其他比例尺范围(如1:10 000新数据与1:50 000旧数据)、目标几何维度(点、线目标)以及多种语义要素目标(居民地与道路)混合等其他变化情形。
| [1] | FRITSCH D. GIS Data Revision-visions and Reality[R]. Keynote Speech in Joint ISPRS Commission Workshop on Dynamic and Multi-Dimensional GIS. Beijing: NGCC, 1999. |
| [2] |
陈军, 王东华, 商瑶玲, 等.
国家1:50000数据库更新工程总体设计研究与技术创新[J]. 测绘学报, 2010, 39(1): 7–10.
CHEN Jun, WANG Donghua, SHANG Yaoling, et al. Master Design and Technical Development for National 1:50 000 Topographic Database Updating Engineering in China[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 7–10. |
| [3] | ZHOU Qi, LI Zhilin. Use of Artificial Neural Networks for Selective Omission in Updating Road Networks[J]. The Cartographic Journal, 2014, 51(1): 38–51. DOI:10.1179/1743277413Y.0000000042 |
| [4] | KILPELÄINEN T, SARJAKOSKI T. Incremental Generalization for Multiple Representations of Geographic Objects[M]//MULLER J C, LAGRANGE J P, WEIBEL R. GIS and Generalization. London: Taylor & Francis, 1995: 209-218. |
| [5] | HARRIE L, HELLSTRÖM A K. A Prototype System for Propagating Updates between Cartographic Data Sets[J]. The Cartographic Journal, 1999, 36(2): 133–140. DOI:10.1179/caj.1999.36.2.133 |
| [6] | HAUNERT J H, SESTER M. Propagating Updates between Linked Datasets of Different Scales[C]//Proceedings of the XXⅡ International Cartographic Conference. A Coruña, Spain: ICC, 2005. |
| [7] | DEVOGELE T, TREVISAN J, RAYNAL L. Building a Multi-scale database with Scale-transition Relationships[C]//Proceedings of the 7th International Symposium on Spatial Data Handling. London: Taylor & Francis, 1996: 337-351. |
| [8] |
胡云岗, 陈军, 李志林, 等.
地图数据缩编更新的模式分类与选择[J]. 地理与地理信息科学, 2007, 23(4): 22–24.
HU Yungang, CHEN Jun, LI Zhilin, et al. Study on Modes of Map Data Updating Based on Generalization[J]. Geography and Geo-information Science, 2007, 23(4): 22–24. |
| [9] |
陈军, 林艳, 刘万增, 等.
面向更新的空间目标快照差分类与形式化描述[J]. 测绘学报, 2012, 41(1): 108–114.
CHEN Jun, LIN Yan, LIU Wanzeng, et al. Formal Classification of Spatial Incremental Changes for Updating[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 108–114. |
| [10] |
张新长, 郭泰圣, 唐铁.
一种自适应的矢量数据增量更新方法研究[J]. 测绘学报, 2012, 41(4): 613–619.
ZHANG Xinchang, GUO Taisheng, TANG Tie. An Adaptive Method for Incremental Updating of Vector Data[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 613–619. |
| [11] |
唐炉亮, 杨必胜, 徐开明.
基于线状图形相似性的道路数据变化检测[J]. 武汉大学学报(信息科学版), 2008, 33(4): 367–370.
TANG Luliang, YANG Bisheng, XU Kaiming. The Road Data Change Detection Based on Linear Shape Similarity[J]. Geomatics and Information Science of Wuhan University, 2008, 33(4): 367–370. |
| [12] |
林艳, 陈军, 刘万增, 等.
面状水系伪增量剔除的拓扑量化法[J]. 武汉大学学报(信息科学版), 2012, 37(12): 1504–1507.
LIN Yan, CHEN Jun, LIU Wanzeng, et al. Topological Quantitatively Method for Spurious Increments Removed of Area Water[J]. Geomatics and Information Science of Wuhan University, 2012, 37(12): 1504–1507. |
| [13] |
林艳, 陈军, 赵仁亮, 等.
顾及时空目标边界不一致性的增量识别计算[J]. 测绘学报, 2014, 43(4): 411–418.
LIN Yan, CHEN Jun, ZHAO Renliang, et al. Increments Recognition and Calculation Considering the Inconsistency of Spatio-temporal Boundaries[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 411–418. DOI:10.13485/j.cnki.11-2089.2014.0061 |
| [14] | QI H B, LI Z L, CHEN J. Automated Change Detection for Updating Settlements at Smaller-scale Maps from Updated Larger-Scale Maps[J]. Journal of Spatial Science, 2010, 55(1): 133–146. DOI:10.1080/14498596.2010.487855 |
| [15] |
简灿良, 赵彬彬, 王晓密, 等.
多尺度地图面目标变化分类、描述及判别[J]. 武汉大学学报(信息科学版), 2014, 39(8): 968–973.
JIAN Canliang, ZHAO Binbin, WANG Xiaomi, et al. A Methodology of Change Classification, Formal Description and Identification between Corresponding Areas in Multi-scale Maps[J]. Geomatics and Information Science of Wuhan University, 2014, 39(8): 968–973. |
| [16] |
杨敏, 艾廷华, 晏雄锋, 等.
叠置运算支持下的跨比例尺城区居民地数据变化发现与更新[J]. 测绘学报, 2016, 45(4): 466–474.
YANG Min, AI Tinghua, YAN Xiongfeng, et al. Change Detection and Updating by Using Map Overlay for Buildings on Multi-scale Maps[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 466–474. DOI:10.11947/j.AGCS.2016.20150302 |
| [17] |
艾廷华, 郭仁忠.
基于格式塔识别原则挖掘空间分布模式[J]. 测绘学报, 2007, 36(3): 302–308.
AI Tinghua, GUO Renzhong. Polygon Cluster Pattern Mining Based on Gestalt Principles[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 302–308. |
| [18] | AI Tinghua, KE Shu, YANG Min, et al. Envelope Generation and Simplification of Polylines Using Delaunay Triangulation[J]. International Journal of Geographical Information Science, 2017, 31(2): 297–319. DOI:10.1080/13658816.2016.1197399 |
| [19] |
童小华, 邓愫愫, 史文中.
基于概率的地图实体匹配方法[J]. 测绘学报, 2007, 36(2): 210–217.
TONG Xiaohua, DENG Susu, SHI Wenzhong. A Probabilistic Theory-based Matching Method[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 210–217. DOI:10.3321/j.issn:1001-1595.2007.02.017 |
| [20] |
黄智深, 钱海忠, 郭敏, 等.
面状居民地匹配骨架线傅里叶变化方法[J]. 测绘学报, 2013, 42(6): 913–921, 928.
HUANG Zhishen, QIAN Haizhong, GUO Min, et al. Matching Algorithm of Polygon Habitations Based on Their Skeleton-lines Using Fourier Transform[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6): 913–921, 928. |
| [21] |
赵东保, 盛业华.
全局寻优的矢量道路网自动匹配方法研究[J]. 测绘学报, 2010, 39(4): 416–421.
ZHAO Dongbao, SHENG Yehua. Research on Automatic Matching of Vector Road Networks Based on Global Optimization[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 416–421. |
| [22] |
张云菲, 杨必胜, 栾学晨.
利用概率松弛法的城市路网自动匹配[J]. 测绘学报, 2012, 41(6): 933–939.
ZHANG Yunfei, YANG Bisheng, LUAN Xuechen. Automated Matching Urban Road Networks Using Probabilistic Relaxation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 933–939. |
| [23] |
田文文, 朱欣焰, 呙维.
一种VGI矢量数据增量变化发现的多层次蔓延匹配算法[J]. 武汉大学学报(信息科学版), 2014, 39(8): 963–967, 973.
TIAN Wenwen, ZHU Xinyan, GUO Wei. A VGI Vector Road Data Increment Distinguishing Research Based on Multilevel Spreading Algorithm[J]. Geomatics and Information Science of Wuhan University, 2014, 39(8): 963–967, 973. |
| [24] |
田晶, 艾廷华, 丁绍军.
基于C4.5算法的道路网网格模式识别[J]. 测绘学报, 2012, 41(1): 121–126.
TIAN Jing, AI Tinghua, DING Shaojun. Grid Pattern Recognition in Road Networks Based on C4.5 Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 121–126. |
| [25] | QUINLAN J R. Induction of Decision Trees[J]. Machine Learning, 1986, 1(1): 81–106. |
| [26] | QUINLAN J R. C4.5:Programs for Machine Learning[M]. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc., 1993. |
| [27] | BREIMAN L, FRIEDMAN J H, OLSHEN R A, et al. Classification and Regression Trees[M]. Belmont, CA, USA: Wadsworth, 1984. |



