2. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079;
3. 中国测绘科学研究院, 北京 100830
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
3. Chinese Academy of Surveying and Mapping, Beijing 100830, China
色彩是重要的地图语言,在地图设计中作用不可忽视[1]。行政区划单元是常用的底图要素,通常用颜色进行区分,这些大面积分布的色彩往往决定了一幅地图的配色风格[2]。因此,行政区划图的色彩配置需要格外关注。
目前,国内外的研究主要涉及着色区域计算和色彩设计。行政区划图着色要求相邻行政区划单元颜色不相同,若将行政区划单元看成是图节点,着色区域计算可抽象为经典的“四色问题”,即对于任一地图,只用不多于4种颜色,就能使相邻的行政区划单元颜色不相同。传统的递归、回溯和贪心算法可以用来解决该问题[3],但是若将颜色数限定为4,这些方法有时并不一定能找到满足条件的解。另外,随着计算机技术的发展,智能化算法也被应用于解决这个问题,如遗传算法、蚁群算法、模拟退火算法、禁忌搜索算法等[3-4],但是智能化方法有时效率不高。
当设计地图色彩时,出于不同的目的可能抽象出不同的规则。若保证所选颜色之间具有较好的区分度,可以在给定颜色集中选择一组最大颜色区间最小差异的配色模板[5],也可以直接选择色彩空间中距离较大的颜色[6-7]。基于色彩与表达信息的一致性,并顾及颜色之间的搭配规则,文献[8-13]设计了适宜于地图着色的多种配色模板。地图色彩设计还需要顾及色彩的语义特征,文献[14]研发了相应的地图色彩设计工具。另外,色彩的对比与调和是地图色彩设计中广泛遵循的理论,相关色彩设计的方法和工具有很多,如HCS Generator、Color Schemer Online[15-17]等。若从受众角度出发,色彩设计还需要顾及特定人群的视觉规律,如制作服务色弱人群的地图时,需要选择一些特殊的颜色;另外,不同地域的人群对于色彩的视觉感受也不一致[18-19]。
常用的着色区域计算方法只能找到一个满足相邻行政区划单元颜色不相同条件下的解,没有较好顾及着色区域间的面积均衡。另外,着色区域计算只顾及了地图要素间的空间关系,而色彩设计也只顾及了颜色之间的搭配原则。但是,行政区划图着色时,还需要考虑色彩在空间上的配置,不同的空间配置方案会引起人不同的地图色彩视觉感受。针对以上两个问题,本文详细研究了行政区划图着色过程中需要顾及的视觉规律,并建立了相应的着色效果评价模型;在着色区域计算中,添加了面积均衡约束,设计并实现了顾及面积均衡的着色区域计算方法。
1 顾及面积均衡约束的回溯法行政区划图着色需要计算着色区域,即对行政区划单元进行分组,找到一个着色区域的分组方案A={A1, A2, …, An},表示将行政区划单元分成n组,用不同的n种颜色对这n组区域着色时,能保证相邻行政区划单元颜色不相同。
回溯法是一种优选搜索法,按优选条件向前搜索,直至达到目标。当探索到某一步,发现选择并不优或达不到目标时,就退回一步重新选择。因此,利用回溯法求解的问题可以表达为:已知n元组{x1, x2, …, xn}组成状态空间P={(x1, x2, …, xn)|xi∈N, i=1, 2, …, n},给定n元组的一个分量约束集D,求P中满足约束集D的一个n元组。行政区划图着色要求邻接行政区划单元颜色不相同,若将行政区划单元看成是图节点,相邻行政区划单元对应两个图节点连接,那么,行政区划图的着色区域计算就可以抽象为图着色问题:给定无环图G=(V, E)和配色模板C={C1, C2, …, Cm},其中V={v1, v2, …, vn}为图顶点集,E={e1, e2, …, en}为图边集,从配色模板C中用尽可能少的颜色对顶点集V进行着色,且相邻节点颜色不相同。因此,行政区划图的着色区域可以利用回溯法进行计算。
但是,利用回溯法计算行政区划图着色区域时,若将颜色数目限定为4,回溯法有时不能找到满足相邻行政区划单元颜色不相同条件下的解。另外,地图着色时,需要顾及人的视觉效果,应尽量保证图上用色相对均匀[1],因此,行政区划图着色区域计算时,也需要顾及各色块间的面积均衡。行政区划图着色通常使用3—7种颜色为宜[1],若不将着色数目限定为4,分别利用3—7种颜色数依次对可能的解进行探测,直至找到满足条件的解才停止探测,就更可能找到满足条件的解;此外,在回溯法中,如果能添加相应的面积均衡约束,就能在着色区域计算时,较好地顾及各色块间的面积均衡。
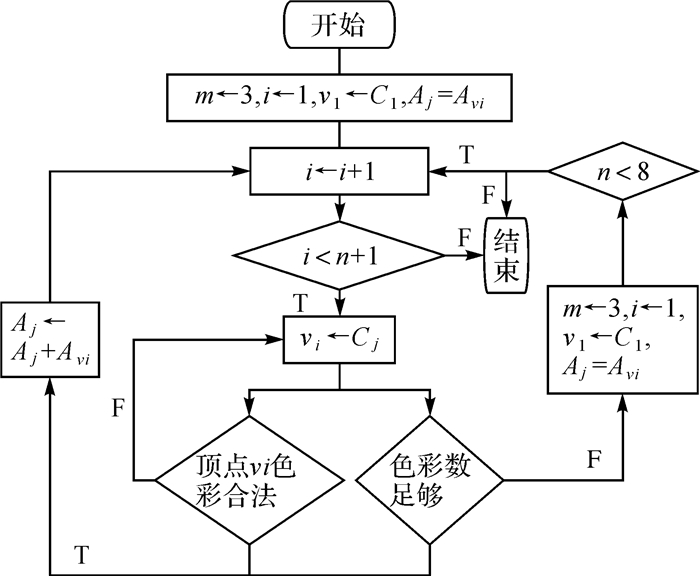
基于以上两个认识,设计顾及面积均衡约束的回溯法。设置初始颜色数m为3,构成颜色集合C={C1, C2, …, Cm};行政区划单元集合对应顶点集V={v1, v2, …, vn},顶点对应的颜色存入一个二维数组中,记为Colors(n),分别存储顶点和顶点对应的颜色,设置初始颜色为空;颜色为Cj的行政区划单元面积和记为Aj,每个顶点对应的行政区划单元面积记为Avi。那么,求解m着色问题的数据处理流程见图 1。
|
| 图 1 回溯法数据处理流程图 Fig. 1 Data processing procedure of backtracking method |
(1) 在颜色集合C={C1, C2, …, Cm}中任取一种颜色Cj,对顶点集中第一个顶点vi进行着色,记i=1,颜色Cj对应的行政区划单元面积和Aj=Avi,并将Colors(n)中顶点vi对应的颜色修改为Cj;
(2) i=i+1,若i < n+1,表明仍存在未着色的顶点,转至步骤(3);否则,表明所有顶点已着色,输出着色区域计算结果Colors(n);
(3) 依次选择颜色集合C={C1, C2, …, Cm}中行政区划单元面积和最小的颜色Cj,对顶点vi着色;若顶点vi着色后与其他顶点颜色不冲突,则Aj=Aj+Avi,并将Colors(n)中顶点vi对应的颜色修改为Cj,转至步骤(2);否则,搜索下一个颜色;
(4) 若步骤(3)中,在当前颜色集合C={C1, C2, …, Cm}中无法找到一种颜色使得顶点vi着色后与其他顶点颜色不冲突,且m < 8,表明无法找到m种颜色条件下满足相邻行政区划单元颜色不相同的解,则m=m+1,构成新的颜色集合C={C1, C2, …, Cm},转至步骤(1)。
2 地图着色的评价模型在地图编制机构已经积累有大量优秀的行政区划图配色模板,在实际应用中,也存在大量可供参考的配色模板和色彩设计工具。因此,色彩设计时可以相对容易地获得符合要求的配色模板。对于一个着色区域方案A={A1, A2, …, An},给定配色模板C={C1, C2, …, Cn},利用配色模板C中的颜色对着色区域A进行着色时,即找到一个从A到C的映射,需要考虑色彩在空间上的配置,使其能较好地顾及地图着色过程中的视觉规律。其中,从A到C映射的优劣需要建立相应的评价模型。
2.1 色彩协调颜色是光从物体反射到人眼睛时所引起的视觉心理印象,协调的颜色搭配和合理的色彩空间分布,能让人感觉舒适[20-21]。试验心理学中建立了大量的数学模型,使得不同颜色之间的协调程度能够被量化,如文献[22-24]的学术成果。另外,图面的色彩协调程度还需要考虑要素的空间特征,如两邻接区域共享边的长度[25-26]等。本文采用文献[22]提出的Η模型对两颜色间的协调程度进行量化,它将RGB色彩转化到基于人眼色彩感知度量建立的颜色-对立色彩空间(CIELab)中,保证了色彩变换的均匀性,且与设备无关。其中,L表示明暗度,a和b表示颜色对立维度。两颜色之间的协调程度由两种颜色的明暗度协调、色相协调和色调协调确定,并将两颜色的协调程度从-5到5进行量化,数值越大,说明两种颜色之间越协调。另外,在两颜色协调程度相同的情况下,若两个行政区划单元共享边长度越长,两行政区划单元间的色彩协调程度也越大[25]。若行政区划单元Ai的颜色为Ci,行政区划单元Aj的颜色为Cj,则这两行政区划单元间的色彩协调程度C(Ai, Aj)计算如下
 (1)
(1)
式中,H(Ci, Cj)为利用Η模型计算出的两种颜色间协调程度;wij为两行政区划单元共享边长度。对任意两个行政区划单元都计算其色彩协调程度,那么,图面的色彩协调程度Sc计算如下
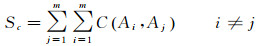 (2)
(2)
式中,m为行政区划单元个数。
2.2 色彩对比试验心理学研究表明,好的色彩对比有助于快速捕捉和识别信息[21]。地图以图解的方式表达空间事物,因而行政区划图着色需要考虑色彩的对比。色彩对比通常在邻近区域或景前与景后的对比中产生,局部邻近区域中,色彩对比需要综合考虑颜色间的差异、要素面积与形状等[7, 20, 25]。颜色间差异可以划分为明暗度差异、色相差异和色调差异,其中,明暗度差异最为重要,因此两种颜色间差异可以用明暗度差异近似度量[16]。另外,在两种颜色间差异程度相同的情况下,若两行政区划单元共享边长度越长,两行政区划单元间的局部区域色彩对比程度也越大。因此,若行政区划单元Ai的颜色为Ci,行政区划单元Aj的颜色为Cj,则这两个行政区划单元间的局部区域色彩对比程度P(Ai, Aj)计算如下
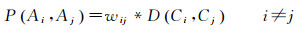 (3)
(3)
D(Ci, Cj)为两颜色在CIELab色彩空间中的明暗度数值差异,wij为两行政区划单元共享边长度。对任意两个行政区划单元都计算其局部区域色彩对比程度,那么图面的局部色彩对比程度Sp计算如下
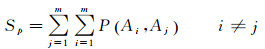 (4)
(4)
式中,m为行政区划单元个数。
在考虑景前与景后的对比关系时,人们往往希望相对于背景,地图内容具有更亮的颜色[20, 25],即面积越大的区域明度越低时,其全局色彩对比度越好。因此,图面的背景色彩对比度Sb计算如下
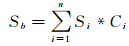 (5)
(5)
式中,n为配色区域个数;Ci为区域Si对应的颜色在CIELab色彩空间中的明暗度数值[26]。图面的色彩对比需要综合考虑局部区域的色彩对比程度和图面背景的色彩对比程度。
2.3 视觉平衡地图的图面设计需要保持图面的均衡,读者读图时往往有一个视觉中心,约比图面图廓几何中心高出5%,图面均衡要求所有的图形都应围绕视觉中心进行配置[1]。地图图形由于所处的位置、颜色等,往往给人轻重的感觉[1, 27]。研究表明,越暗的颜色视觉重力越大[25],因此,参考几何中心的计算方法,图面视觉中心的计算如下
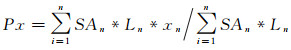 (6)
(6)
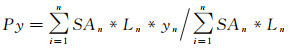 (7)
(7)
式中,SAn为行政区划单元An面积;xn和yn分别是对应行政区划单元An重心的x、y坐标;Ln见公式(8)。
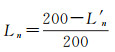 (8)
(8)
式中,L′n为对应行政区划单元An的颜色在CIELab色彩空间中的明暗度数值,取值范围为[0, 100]。若行政区划图视觉中心越靠近理论视觉中心,那么说明它视觉平衡程度越好,因此,图面的视觉平衡程度Pb可以用图面视觉中心与理论视觉中心的距离来定义
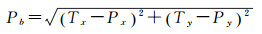 (9)
(9)
式中,Tx与Ty为理论视觉中心的x、y坐标。若Pb越大,说明其离理论视觉中心越远,那么其视觉平衡程度越差。
2.4 行政区划图着色效果评价行政区划图着色效果评价需要综合考虑图面的色彩协调、色彩对比和视觉平衡3个因素。统计学中提供了很多多指标综合分析的方法,本文采用Topsis方法对行政区划图着色效果进行综合评价[28]。其基本原理是通过检测评价对象与最优解、最劣解的距离来进行排序,若评价对象最靠近最优解的同时又最远离最劣解,则为最优;其中最优解各指标值都达到各评价指标的最优。当计算得到一个着色区域方案A={A1, A2, …, Am},将配色模板C={C1, C2, …, Cm}中的颜色分配到A中指定区域共存在Amm种可能组合方案,能分别计算这Amm种颜色分配方案下的4个图面着色效果评价指标。利用Topsis方法,首先将评价指标标准化,这里对各指标值进行排序,用指标的排序来相对度量指标值的优劣程度。其次,要保证指标的同趋势性,其中图面色彩协调程度越大,图面越协调;图面局部色彩对比程度越大,图面局部色彩对比度越好;图面背景色彩对比程度越小,图面背景色彩对比越好;图面视觉平衡程度越小,图面越平衡。因此,分别对图面色彩协调程度和图面局部色彩对比程度按从大到小排序,图面背景色彩对比程度和图面视觉平衡程度按从小到大排序,排序越前,说明该指标越优。图面着色效果的理论最优色彩分配方案即图面色彩协调程度最大,图面局部色彩对比程度最大,图面背景色彩对比程度最小且图面视觉平衡程度最小。最后,计算各方案与理论最优方案的距离来表示图面的着色效果。距离计算需要确定各指标的权重,不同地图侧重点不一样,如风险地图往往需要强调色彩间的对比。本文中,3个因素同等重要,权重取值相等。因此,若颜色分配方案δ对应的四个指标中,色彩协调程度排序为RSc,色彩对比程度中的图面局部色彩对比程度排序为RSp,图面背景色彩对比程度排序为RSb,视觉平衡程度的排序为RPb,那么图面着色效果综合性满意度为f(δ),f(δ)表示不同颜色分配方案满意度的相对值,见公式(10)。
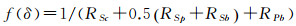 (10)
(10)
对于颜色分配方案δ,若其满意程度越高,则其越能较好地顾及行政区划着色过程中的视觉规律。若对满意程度f(δ)按从大到小排序,能知道每一个颜色分配方案的着色效果排名。
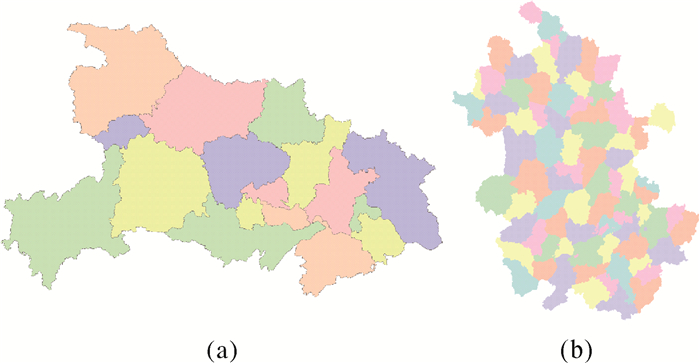
3 试验视觉认知易受人类个体差异和主观影响,如环境、性别、年龄、教育背景和生长环境等,因而行政区划着色的优劣,难以用定量的方式客观评价。但是,优秀的地图作品被广泛接受且符合视觉认知,首先利用本文的图面着色效果评价方法对已有优秀作品进行评价,验证方法的合理性。选择2013年湖北省领导工作用图和2011年公开出版的安徽省地图集中行政区划图作为试验数据,如图 2所示。2013湖北省领导工作用图选用5种颜色进行配色,最终其颜色分配方案的图面着色效果满意度在120种可能的颜色分配方案中排名26;安徽省行政区划图选用6种颜色进行配色,最终其颜色分配方案的图面着色效果满意度在720种可能的颜色分配方案中排名129。这两幅图中,其颜色分配的图面着色效果满意度均处于该方法排序的前25%,这证明了本方法的有效性,图面着色效果的各指标详细说明见表 1。
|
| 图 2 行政区划图色彩设计 Fig. 2 Color design for administrative maps |
| 地图 | RSc | RSp | RSb | RPb | f(δ) | 排序 |
| 2013湖北省领导工作用途 | 50 | 20 | 1 | 64 | 1/124.5 | 26/120 |
| 2011安徽省行政区划图 | 183 | 94 | 37 | 445 | 1/693.5 | 129/720 |
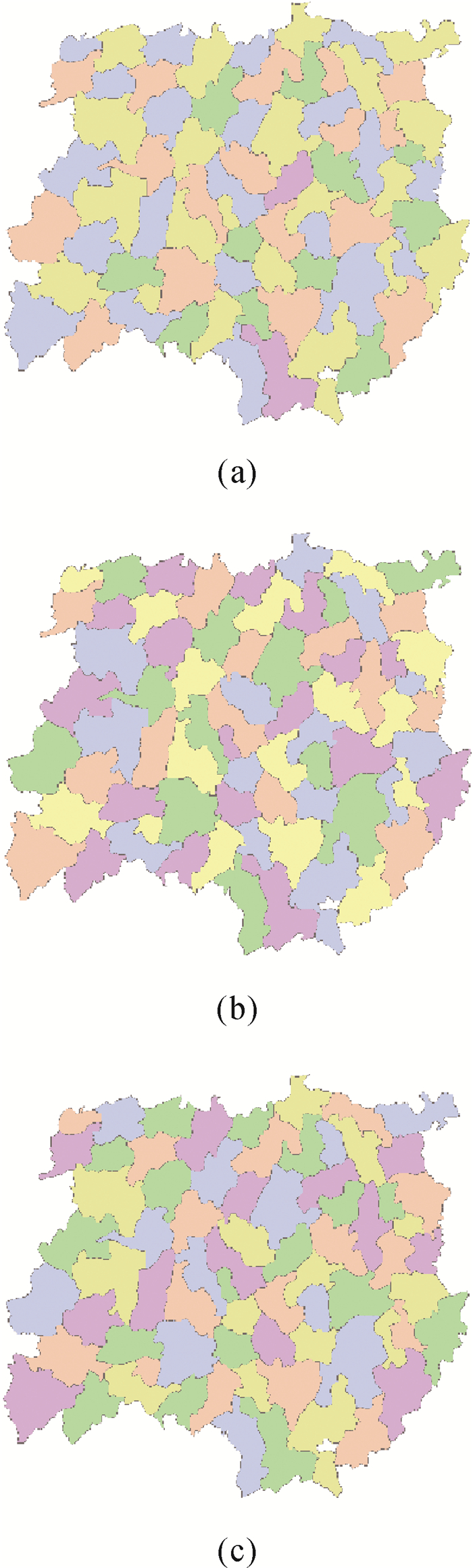
选择中国1:400万县级行政区划中某区域为试验数据验证本文提出的方法,试验区域行政区划单元个数共计72个。利用回溯法计算着色区域,试验结果见图 3(a)和图 3(b)。其中,图 3(a)为未添加面积均衡约束回溯法计算得到的着色区域,图 3(b)为添加了面积均衡约束回溯法计算得到的着色区域,图 3(a)与图 3(b)的对比结果见表 2。由表 2可以看出,当利用回溯法计算着色区域时,5种颜色就能对已有的72个行政区划单元进行着色,而行政区划图着色通常采用3—7种颜色为宜[1];另外,添加了面积均衡约束后,图 3(b)相较于图 3(a)各色块数目与总面积的标准差更小,即添加面积均衡约束后,图 3(b)在各色块行政区划单元数目和各色块总面积上更为均衡。
|
| 图 3 行政区划图色彩设计 Fig. 3 Color design for administrative maps |
给定一个包含5种颜色的配色模板,将这5种颜色分配到利用顾及面积均衡回溯法计算得到的着色区域中,一共存在120中颜色分配方案。利用2.3中提出的地图着色效果评价模型分别计算每一种颜色分配方案下的图面着色效果满意度,并对其进行排序,排序结果见表 3。图 3(b)与图 3(c)分别为图面着色效果排序为1和120的两种配色方案结果图,各指标的详细说明见表 3。考察图 3(b)可知,其具有较好的图面协调和图面均衡程度,且图面对比程度适中,因此图面着色效果最好;考察图 3(c)可知,其图面协调程度很差,且图面均衡程度与对比程度也较差,因此图面着色效果最差。
| 排序 | RSc | RSp | RSb | RPb | f(δ) |
| 1 | 6 | 19 | 30 | 2 | 1/32.5 |
| 2 | 1 | 20 | 3 | 39 | 1/51.5 |
| ⋮ | |||||
| 50 | 8 | 53 | 116 | 65 | 1/157.5 |
| ⋮ | |||||
| 119 | 106 | 116 | 109 | 87 | 1/305.5 |
| 120 | 117 | 110 | 100 | 102 | 1/324 |
4 结论
为解决行政区划图的着色问题,本文在回溯法基础上添加了面积均衡约束,较好地顾及了行政区划图着色过程中着色区域间的图面面积均衡;另外,在计算图面色彩协调程度、图面色彩对比程度和图面视觉平衡程度的基础上,建立了行政区划图着色效果评价的模型。试验表明,本文提出的方法,能有效评价行政区划图图面着色效果的优劣,并辅助自动提高行政区划图图面着色的效果和效率。但是,综合考虑地图着色过程中的视知觉规律与语义特征是后续研究的重点。另外,考虑色彩在不同图种空间上的不同配置要求以拓展本文提出的图面着色效果评价模型也是值得研究的问题。
| [1] |
何宗宜, 宋鹰.
普通地图编制[M]. 武汉: 武汉大学出版社, 2015: 61-78.
HE Zongyi, SONG Ying. General Map Compilation[M]. Wuhan: Wuhan University Press, 2015: 61-78. |
| [2] |
高建军, 关焱, 王友亮.
专题地图基调色设计研究[J]. 武汉大学学报(信息科学版), 2008, 33(7): 766–769.
GAO Jianjun, GUAN Yan, WANG Youliang. Design of Basic Tone of Thematic Map Color[J]. Geomatics and Information Science of Wuhan University, 2008, 33(7): 766–769. |
| [3] |
韩云, 郭庆胜, 章莉萍, 等.
行政区划图自动着色的混合遗传算法[J]. 武汉大学学报(信息科学版), 2007, 32(8): 748–751.
HAN Yun, GUO Qingsheng, ZHANG Liping, et al. Hybrid Genetic Algorithm for Coloring Administrative Map[J]. Geomatics and Information Science of Wuhan University, 2007, 32(8): 748–751. |
| [4] |
彭珊鸰, 何宗宜, 宋鹰, 等.
图着色的混合遗传算法研究[J]. 武汉大学学报(信息科学版), 2009, 34(12): 1499–1501.
PENG Shanling, HE Zongyi, SONG Ying, et al. A Hybrid Genetic Algorithm for Coloring Map[J]. Geomatics and Information Science of Wuhan University, 2009, 34(12): 1499–1501. |
| [5] | STEINRVCKEN J, PLVMER L. Identification of Optimal Colours for Maps from the Web[J]. The Cartographic Journal, 2013, 50(1): 19–32. DOI:10.1179/1743277412Y.0000000017 |
| [6] | BREWER C A. Prediction of Simultaneous Contrast between Map Colors with Hunt's Model of Color Appearance[J]. Color Research and Application, 1996, 21(3): 221–235. DOI:10.1002/(ISSN)1520-6378 |
| [7] | CHESNEAU E. A Model for the Automatic Improvement of Colour Contrasts in Maps:Application to Risk Maps[J]. International Journal of Geographical Information Science, 2011, 25(1): 89–111. DOI:10.1080/13658811003772926 |
| [8] | BREWER C A. The Development of Process-Printed Munsell Charts for Selecting Map Colors[J]. The American Cartographer, 1989, 16(4): 269–278. DOI:10.1559/152304089783813945 |
| [9] | BREWER C A. Spectral Schemes:Controversial Color Use on Maps[J]. Cartography and Geographic Information Systems, 1997, 24(4): 203–220. DOI:10.1559/152304097782439231 |
| [10] | SUCHAN T A, BREWER C A. Qualitative Methods for Research on Mapmaking and Map Use[J]. The Professional Geographer, 2000, 52(1): 145–154. DOI:10.1111/0033-0124.00212 |
| [11] | BREWER C A, PICKLE L. Evaluation of Methods for Classifying Epidemiological Data on Choropleth Maps in Series[J]. Annals of the Association of American Geographers, 2002, 92(4): 662–681. DOI:10.1111/1467-8306.00310 |
| [12] | HARROWER M, BREWER C A. ColorBrewer.org:An Online Tool for Selecting Colour Schemes for Maps[J]. The Cartographic Journal, 2003, 40(1): 27–37. DOI:10.1179/000870403235002042 |
| [13] | BREWER C A. Basic Mapping Principles for Visualizing Cancer Data Using Geographic Information Systems (GIS)[J]. American Journal of Preventive Medicine, 2006, 30(2 Suppl): S25–S36. |
| [14] | CHRISTOPHE S. Creative Colours Specification Based on Knowledge (COLorLEGend system)[J]. The Cartographic Journal, 2011, 48(2): 138–145. DOI:10.1179/1743277411Y.0000000012 |
| [15] |
郭礼珍, 李霖.
政区地图设色方案的自动实现[J]. 武汉大学学报(信息科学版), 2004, 29(11): 1025–1029.
GUO Lizhen, LI Lin. Automatic Implementation of Color Design in Administrative Map[J]. Geomatics and Information Science of Wuhan University, 2004, 29(11): 1025–1029. |
| [16] |
黄丽娜, 郑斌, 何亮.
利用Munsell-HCV模型进行顾及土地利用专题信息的多色等高线配色研究[J]. 测绘学报, 2013, 42(5): 752–759.
HUANG Lina, ZHENG Bin, HE Liang. Color Matching of Polychromatic Contour Lines Considering the Land-use Thematic Information Based on the Munsell-HCV Color Harmony Rule[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 752–759. |
| [17] | HU Guosheng, PAN Zhigeng, ZHANG Mingmin, et al. An Interactive Method for Generating Harmonious Color Schemes[J]. Color Research and Application, 2014, 39(1): 70–78. DOI:10.1002/col.v39.1 |
| [18] | CULP G M. Increasing Accessibility for Map Readers with Acquired and Inherited Colour Vision Deficiencies:A Re-colouring Algorithm for Maps[J]. The Cartographic Journal, 2012, 49(4): 302–311. DOI:10.1179/1743277412Y.0000000030 |
| [19] | OLSON J M, BREWER C A. An Evaluation of Color Selections to Accommodate Map Users with Color-vision Impairments[J]. Annals of the Association of American Geographers, 1997, 87(1): 103–134. DOI:10.1111/0004-5608.00043 |
| [20] | BURCHETT K E. Color harmony[J]. Color Research and Application, 2002, 27(1): 28–31. DOI:10.1002/(ISSN)1520-6378 |
| [21] | FRANCIS G, BIAS K, SHIVE J. The Psychological Four-color Mapping Problem[J]. Journal of Experimental Psychology:Applied, 2010, 16(2): 109–123. DOI:10.1037/a0019095 |
| [22] | OU Lichen, LUO M R. A Colour Harmony Model for Two-colour Combinations[J]. Color Research and Application, 2006, 31(3): 191–204. DOI:10.1002/(ISSN)1520-6378 |
| [23] | SZABÓ F, BODROGI P, SCHANDA J. Experimental Modeling of Colour Harmony[J]. Color Research and Application, 2010, 35(1): 34–49. DOI:10.1002/col.v35:1 |
| [24] | NEMCSICS A. Experimental Determination of Laws of Color Harmony.Part 6:Numerical Index System of Color Harmony[J]. Color Research and Application, 2012, 37(5): 343–358. DOI:10.1002/col.v37.5 |
| [25] | KIM H R, YOO M J, KANG H, et al. Perceptually-based Color Assignment[J]. Computer Graphics Forum, 2014, 33(7): 309–318. DOI:10.1111/cgf.2014.33.issue-7 |
| [26] | CHRISTOPHE S, ZANIN C, ROUSSAFFA H. Colours Harmony in Cartography[C]//Proceedings of the 25th International Cartographic Conference. Paris, France: [s. n. ], 2011. |
| [27] |
马俊, 王光霞, 崔秀飞, 等.
采用力矩平衡原理建立地图视觉平衡模型[J]. 武汉大学学报(信息科学版), 2013, 38(1): 116–120.
MA Jun, WANG Guangxia, CUI Xiufei, et al. Using the Principle of Moment Balance Establishing Map's Visual Balance Modle[J]. Geomatics and Information Science of Wuhan University, 2013, 38(1): 116–120. |
| [28] |
苏为华. 多指标综合评价理论与方法问题研究[D]. 厦门: 厦门大学, 2000. SU Weihua. Research on Multiple-objective-comprehensive-Evaluation[D]. Xiamen: Xiamen University, 2000. |



