2. 中国科学院遥感与数字地球研究所遥感科学国家重点实验室, 北京 100101;
3. 中国科学院大学, 北京 100049;
4. 佛山市城市规划勘测设计研究院, 广东 佛山 528000
2. State Key Laboratory of Remote Sensing Science, Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100101, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. Foshan Urban Planning Design and Surveying Research Institute, Foshan 528000, China
矢、栅空间数据理论和方法是地理信息系统(GIS)中两种重要理论和方法[1-2],它们各有特点,优势互补。相对而言,矢量定义在连续的实数域,对于相当多问题,对于点的计算,可通过矢量计算得到精确解。然而对于复杂的地理信息系统诸多问题,尤其是空间组合优化问题,对于点及集合的计算,或对于网格的计算,无限精确的实数解的获取往往是极困难的,并且在大多数情况下也是不必要的。实际中通常采用一定精度的近似解来解决,而其本质就是栅格方法,采用离散的、近似的解来解决各种实际问题,可能更为广义[3-4]。很明显,二维情况下,当栅格尺寸趋于0×0,解的正确性和准确性没有任何问题,但关键问题是栅格最大尺寸dx×dy多大才能确保计算的精确性,同时又能保证计算的最高效率。而在较大的空间范围内,栅格方法能否保证解决问题所必要的空间精确度也需要证明。其中最可能的解决途径是多重网格计算。传统的多重网格法是一种“近乎最优”的特殊迭代途径,是一种通用的非常有效的特殊类型的迭代法[5-9],成为数值计算领域一种加速迭代收敛的技术,已被广泛应用于微分方程求解[10]、曲面建模[11]、三维数值模拟[12-13]、流体力学[14-15]等方面。本文提出的双重网格计算方法有别于广泛应用于微分方程和积分方程数值求解中的多重网格法,它主要针对大区域高分辨率空间距离变换的快速运算。
目前,地理空间大型度量分析问题真正采用栅格方法的尚不多,并且GIS领域至今尚未见到多重网格方法的具体应用。本文主要讨论欧氏空间和地球信息度量空间下的距离变换的双重网格方法。首先讨论其基础度量,即欧氏和地球信息度量下的计算公式、微分公式及误差,作为双重网格计算的原理,然后再讨论分层计算的组织以及实施方案。
本文中的多重网格方法主要针对正方形剖分的栅格(设dx=dy),全空间等剖分为N1×N2粗网格,在粗网格中剖分成N3×N3个细栅格,并且粗栅格中心距离计算足够严密准确(这也是地图代数理论和实践所严密保证了的)。
1 主要距离变换公式及简化计算原理 1.1 欧氏距离的计算公式、微分公式及误差水平面上a、b两点间欧氏距离公式为
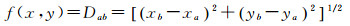 (1)
(1)
顾及二元泰勒展开公式[16]
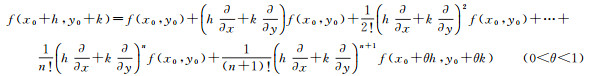 (2)
(2)
设起点a不变,仅终点b有微小增量Δxa、Δyb,可视重要粗栅格内需重新计算各重要细部细栅格为b点的微小增量,在式(2)中取n=1,有全微分公式进行各细栅格计算
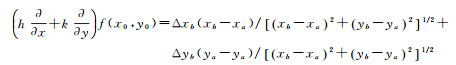 (3)
(3)
其误差余项R2为
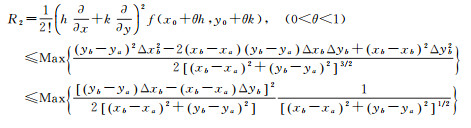 (4)
(4)
若顾及一般[(xb-xa)2+(yb-ya)2]≥4000 km;|Δxb|,|Δyb|均≤0.5 km,第一次粗栅格可有8000×8000规模(一般微机都可承担的计算规模),经分析,根据式(4)可得
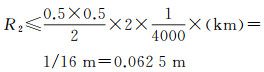 (5)
(5)
以上是假设a点不变,仅b点微小变化的微分公式。倘若a点变动,公式类同,仅仅Δxa、Δyb符号方向取反。综合两者,式(3)则变为
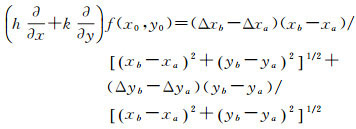 (6)
(6)
故若顾及实际中不仅b点会有微小位移,a点也会有微小位移,这时式(2)的R2会放大为式(5)的2倍,即用微分简化计算其下细栅格,其距离计算精度不低于0.125 m。同理当[(xb-xa)2+(yb-ya)2]1/2≥8000 km,|Δxa|、|Δxb|、|Δya|、|Δyb|均≤0.5 km,则R2 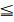
大地线度量的第一类微分公式指的是由于大地起始数据的微小变化(起、终点的大地坐标dBa、dLa、dBa、dLa变化,起始边的大地坐标、方位角及长度的变化)而引起的大地坐标和方位角的改正值的计算公式[17-18]。所谓反算公式,是指端点变化对大地线长度s和方位角A影响的计算式。由于双重网格计算往往涉及两端点都发生变化的情况,有关微分公式如下[19]
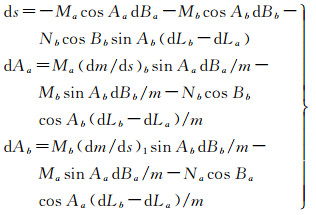 (7)
(7)
式中,M、N、m为子午圈、卯酉圈半径及大地线s的归化长度,下标a、b分别代表起、终端点,dm/ds由式(8)严密计算给出
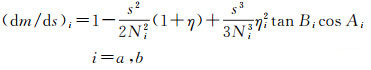 (8)
(8)
微分公式(7)是由大地主题计算严密公式推出,用于较高精度的大地计算。但上述微分公式(7)的严密误差尚不能事先精确控制实施,只能大致估计后,在实践中验后给出。
上述1.1、1.2论述表明:在欧氏及地球椭球面度量中,在适当的小范围内或粗栅格内,原始端点栅格内的微小变化引起距离和方向的变化主要是线性的,可以通过始终端点粗栅格内的局部简化计算完成。因此,通过大区域内的各粗栅格中心间的规范精密计算,结合适当的小范围内(粗栅格内)细栅格中心间微分计算,可实现目标区域距离的准确计算。这种双重网格计算方法,计算对象分割严密,组合对象完整覆盖全区分辨率单元。
1.3 欧氏度量下计算实例 1.3.1 具体算例平面上有远距a、b两点,a点xa=1 564 000,ya=26 000,b点xb=7 989 000,yb=6 218 000,则dab=8 923 087.414。令a点固定,b点微动,范围±500 m,这时,b点在2级栅格(1001×1001)阵4个角点,距离dab直接计算和用微分计算分別如下:
(1) 当xb=7 988 500,yb=6 217 500;即Δxb=-500,Δyb=-500;dab=8 922 380.428,
采用双重网格计算,dab=8 923 087.414-360.021-346.965=8 922 380.428;Δ=0.000。
(2) 当xb=7 989 500,yb=6 217 500;即Δxb=500,Δyb=-500;dab=8 923 100.498,
采用双重网格计算,dab=8 923 087.414+360.021-346.965=8 923 100.470;Δ=-0.028。
(3) 当xb=7 989 500,yb=6 218 500;即Δxb=500,Δyb=500;dab=8 923 794.400,
采用双重网格计算,dab=8 923 087.414+360.021+346.965=8 923 794.400;Δ=0.000。
(4) 当xb=7 988 500,yb=6 218 500;即Δxb=-500,Δyb=500;dab=8 923 074.386,
采用双重网格计算,dab=8 923 087.414-360.021+346.965=8 923 074.358;Δ=-0.028。
1.3.2 分析与讨论由1.3.1中算例可见,在16 000 km范围内,为获得相对最远6000~8000 km处的比例线或中间线达1 m的距离变换精度,不必要实施16 000 000×16 000 000栅格阵的距离变换,而仅需实施16 000×16 000的栅格阵的距离变换;微分计算距离波前沿(或所需目标区域)的微小(米级)栅格距离。上述情况下,在1000 m大小的初始栅格计算下,仅采用一阶微分公式,仅2点在粗栅格中微动(±500 m),双重网格距离计算精度可不低于1/32 m(上例实际是0.028 m)。类同的道理,若a点也在粗栅格中微动,则双重网格距离计算精度可不低于0.062 5 m。而若采用32 000×32 000栅格阵进行距离变换,则双重网格距离计算可达4倍远处,精度仍可不低于0.062 5 m。
类此,原则上也可采用具有多级精度的多阶微分公式多重栅格系列。
1.4 大地线度量下的计算实例 1.4.1 两点间大地线长计算算例a点纬度Ba=20.0,经度La=120.0;2点纬度Bb=49.0,b点经度Lb=147.0。a到b点的大地线长度dab=4 017 429.518 844 56。粗栅格约用1′×1′。a点与b点定位在粗栅格中心。若b点纬度±0.5′或经度±0.5′位移,则大地线长dab精密计算与微分计算的相差均小于0.044 m。具体算例如下:
(1) 到粗栅格左上角:
精密距离=4 017 626.654 256 730 3
微分距离=4 017 429.518 844 56+197.360 787 551 097
差值=0.225 375 379 901 379
(2) 到粗栅格右上角:
精密距离=4 018 510.011 246 322 2
微分距离=4 017 429.518 844 56+1 080.449 002 431 3
差值=0.043 399 330 694 228 4
(3) 到粗栅格左下角:
精密距离=4 016 348.939 659 628 1
微分距离=4 017 429.518 844 56-1 080.622 568 768 07
差值=0.043 383 837 211 877 1
(4) 到粗栅格右下角:
精密距离=4 017 232.834 246 171 6
微分距离=4 017 429.518 844 56-196.459 160 007 337
差值=0.225 438 379 682 601
1.4.2 分析与讨论大地度量下双重网格计算原理已由式(7)、式(8)予以阐明。实例验证由上述算例可知,当地球上距离长达4000 km以上时,端点b在±0.5′内微动时,可由微分公式简易重算更动后的距离,精度可达0.25 m;顾及端点a具有同样大小的微动时,更动后的距离精度或许不超0.5 m,一般可达1 m精度。当然,以验后计算为准。鉴此,也可采用线性递缩微动区间(即依次按粗栅格的0.5间距缩小)的法则,以实现所需精度。若a、b两点是相距4000 km以上的±0.5′粗栅格的中心,且a中有一条精细栅格的线,这时由点b对该线上各精细栅格连线段,并取最短线段,可认为它是b到该线精细距离,以点b为中心的粗栅格中各精细栅格就可通过各自与点b的坐标差(一个粗栅格内)与点b到该线距离,得到(b中精细栅格)各自到该线精细距离。若将a、b对调,结论也同样正确。
2 双重网格距离变换实施双重网格方法一般分基础(粗)栅格及在基础栅格中嵌套细栅格来实行。上述欧氏空间距离变换方法比较明确,故下面主要讨论地球空间的距离变换。实施第一步时一般把对象区域划为M1×N2个基础栅格,先进行粗栅格运算,与通常有序传播的地图代数外距(离)变换[20]完全一样。假设距离变换是对各大洲陆地外缘的低潮线作为起算基线,使洋中任一栅格都标记了距最近大陆外缘线的距离(即距该点最近大陆栅格点)[20-21],然后第二步再进行相应有关粗栅格下细栅格的精细计算。例如图 1所示10 800×5400粗栅格阵表示的太平洋等距圆柱投影图中(南纬45°—北纬45°,东经120°—西经60°),假定该图形足够正确,在此基础上求太平洋的“洋心”(“洋心”指离陆地外缘线最远处)或澳洲、南美洲、北美洲相互中间线。

|
| 图 1 太平洋洋心和邻近大洲的外距变换及Voronoi图 Fig. 1 The center of the Pacific Ocean and distance transform of nearby continents and Voronoi diagram |
2.1 第一次(粗)栅格距离变换
第一次进行距离变换时,采用长距离大地主题反算公式—白塞尔公式[19]计算第一次栅格划分时粗栅格中心的离陆距离,得到全球各陆地外缘线距离波的前沿,得到最大海洋“太平洋”中离陆地最远的地方—“洋心”,这时对于澳洲O、北美N、南美S陆地而言,其变换结果如图 1、2所示,“洋心”栅格离陆地5 147 641 m(小数点后数据略去)。

|
| 图 2 距澳洲、北美洲、南美洲最远处的太平洋“洋心” Fig. 2 The center of the Pacific Ocean with the furthest distance from Australia, North America, South America's |
设O1是距澳洲最近栅格集中最远栅格,N1是距北美洲最近栅格集中最远栅格,S1是距南美洲最近栅格集中最远栅格。如图 2、图 3所示,三大洲的Voronoi线和其上的“洋心”,就在距离呈“T”形的V线最近且各分属两洲的双排栅格上。设洲O陆地外缘线上距离O1最远栅格为O′1栅格,N洲为N′1,S洲为S′1。这时,O1上标识距离为dO1′O1,N1上标识距离为dN1′N1,S1上标识距离为dS1′S1。比较,dO1′O1≥dN1′N1,且dO1′O1≥dS1′S1,故称O1为“洋心”,这是粗栅格距离变换结果。若要求真正精细到米,还必须进一步把栅格划细到0.03″×0.03″以下的细栅格,并确保它们的距离计算达到米级精度。
2.2 第二次(细)栅格距离精细计算把分辨率扩大,每一基础栅格划为M3×N3个细栅格,比如图 3中,N3=2000,相当于1 m×1 m或相当于0.03″×0.03″大小的栅格。这时陆地相当于1:1万比例尺栅格化地形图,且陆地外沿的陆地外缘线精确地通过该图幅。显然,距“洋心”最近的精细栅格与粗栅格所属是不同的。采用以下计算过程进行所需要粗栅格内的精细运算:

|
| 图 3 “洋心”栅格及其相邻栅格与V线的距离关系 Fig. 3 The center grid of the Pacific Ocean and the distance relationship between its adjacent grids and V line |
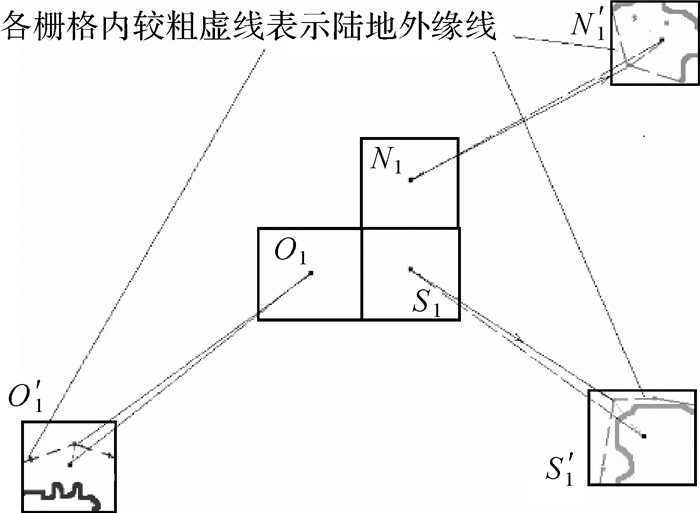
(1) 参见图 4,用微分公式,分别计算Voronoi线或“洋心”所在或毗邻粗栅格O1、N1、S1中心到相应陆地澳洲O、北美洲N、南美洲S的栅格O′1、N′1、S′1中各陆地外缘线上细栅格距离,分别取其最小者,作为高分辨率下O1、N1、S1各中心到O′1、N′1、S′1中精细陆地外缘线栅格的距离,根据点与点集(线)间距离的定义,可以认为是各中心到O′1、N′1、S′1中精细陆地外缘线的距离。
|
| 图 4 若O′1、N′1、S′1中心到O1、N1、S1中心精密距离已知,通过O′1、N′1、S′1中任一细栅格对粗栅格中心位移,运用微分公式,近似计算得到O1、N1、S1中心到O′1、N′1、S′1中最近精细陆地线(即精细陆地细栅格)距离 Fig. 4 Distance calculation from the centers of O1, N1, S1 to the land line in O′1, N′1, S′1 based on the differential equation |
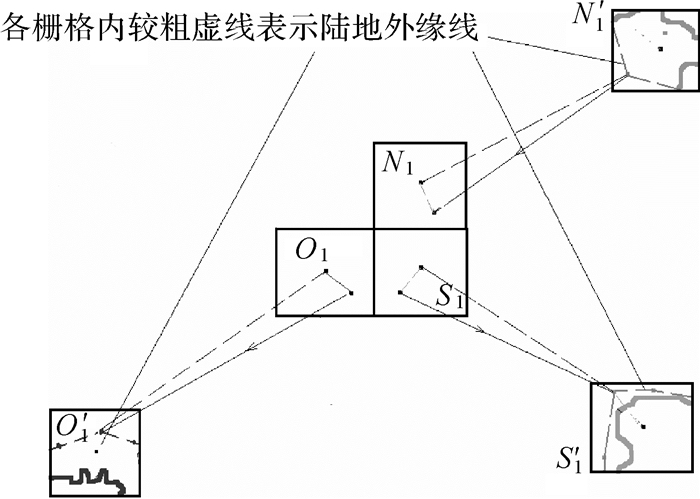
(2) 参见图 5,通过O1、N1、S1中每一细栅格对O1、N1、S1中心的微小坐标位移,再用微分公式,顾及(1)的计算结果,分别计算得到各O1、N1、S1中各细栅格直接到O′1、N′1、S′1中相应实际的精细陆地外缘线距离。
|
| 图 5 由O1、N1、S1中心到O′1、N′1、S′1中精细陆地线距离,O1、N1、S1中任一细栅格可通过对粗栅格中心位移,运用微分公式,近似算得它到精细陆地线距离 Fig. 5 Fine-grid distance calculation from the O′1, N′1, S′1 to the land line in O′1, N′1, S′1 based on the differential equation |
(3) 由于O1粗栅格虽属离澳洲最近集合,但又是最远个体粗栅格,其细栅格不会全属离澳洲最近。故计算O1中心坐标与N1中心的距离起点N′1中心的距离,并类同(2),计算O1每一细栅格相对于N′1精细陆地外缘线栅格的距离。
(4) 类同(3),计算O1中心与S1中心的距离起点S′1中心的距离,并类同(2),计算O1每一细栅格相对于S′1精细陆地外缘线栅格的距离。
(5) 比较O1中各细栅格到O′1、N′1、S′1的3个距离值,每一细栅格取(2)、(3)、(4)同位值的最小值作为O1各细栅格距离值。
(6) 类同(3)、(4)、(5),分别计算N1及S1各细栅格的距离。
(7) 上述(5)、(6)计算结果,即是“洋心”及邻域的细栅格距离变换结果,其中距离最大距离值的细栅格,即是“洋心”所在。
2.3 双重网格计算的复杂性讨论第一次(粗)栅格距离变换:时间复杂性是传统的O(10×N1×N2)。由于此距离变换由正序和逆序两个序贯变换过程组成[3],正序变换序贯访问每一栅格点本身及其左、下左、下中、下右数值及计算而成,故为O(5×N1×N2),逆序变换序贯访问每一栅格点本身及其右、上左、上中、上右数值及计算而成,故合并为O(10×N1×N2),此阶段得到所有粗栅格中心(O1)到相应陆地线(粗栅格中心(O′1))距离。
第二次(细)栅格距离精细计算中(1),是O1中心到O′1中精细陆地线各细栅格(约不大于21/2×N3个)距离,若需计算的O1中心有21/2×Max(N1, N2)个,最后得到各O1中心到各相应O′1中精细栅格陆地线的距离计算,则时间复杂性是O((21/2×N3)×21/2×Max(N1, N2)),此阶段得到各O1中心到相应栅格中精细陆地线的距离。
第二次(细)栅格距离精细计算中(2),若需计算的O1中心有不大于21/2×Max(N1, N2)个,而每个O1粗栅格有N3×N3个细栅格要微分距离计算,则时间复杂性为O(N3×N3×21/2×Max(N1, N2)),联系上阶段计算,此阶段将得到O1中心中各精细栅格到相应O′1中精细陆地线的测地距离。
第二次(细)栅格距离精细计算中(3)、(4),均类同(3)的复杂性O(N3×N3×21/2×Max(N1, N2))。需要说明的是对于“洋心”计算须用O′1、N′1、S′1三方,计算中间线或双方界线仅需计算两方。
第二次(细)栅格距离精细计算中(5)、(6),对于三方计算为3×N3×N3,但“洋心”O1点只是1个或2个,N1、S1类同;对两方计算则是2×N3×N3,但对双边界线,O1将达21/2×Max(N1, N2)个。N1、S1类同。
总括上述,本计算的时间复杂性为O(N3×N3×Max(N1, N2)),只有计算规模的一阶复杂性,并且除(1)外,计算规模也不大,可实时完成并可视化。很明显,空间复杂性也与之相匹配,也不再必须是O(N3×N3×N1×N2)的序贯运算,大大缩减了复杂性。
3 分析和讨论本扩展计算主要准确度依据是微分公式(2)—(8),因而在第一次准确粗栅格变换基础上,保证了第二次粗栅格内的微小位移的细栅格距离计算具有确定的准确性。在保证必要准确度和距离源属情况下,最为准确的最短路径及其上栅格的序贯衔接也就没有太多考虑,或者可认为在这个精度下是正确的。地球空间计算由本文第二部分双重网格距离变换实施一节可知,(1)后的0.06″×0.06″细栅格计算误差约0.086 m,而(2)及(3)、(4)、(5)、(6)后的误差均约为0.17 m,此方法可保证最重要部位细栅格计算准确性。由于粗、细栅格的尺寸可以根据区域大小和精度要求灵活设计,而目前微机一般均具有30 000×30 000栅格计算能力,还留有足够余地,因而全球计算dm级(甚至更高)精度可以保证。
欧氏及地球空间两种度量空间的地理计算中,双重网格计算的精度决定于:①空间度量性质;②初始网格大小,也即微分区间大小,区间越小,精度越高。这就要求第一次网格尽可能高的均衡密度;③计算精度与基量大小有关(如同dO1O1′),也即基量越大,同样大位移产生的变化越小。
双重网格计算原则上也适合于多重网格计算,也即第二层可适合于多种分辨率,并具有多重精度。这对多尺度空间信息产品具有相当大意义,其本质适合于多尺度观察与运算。定义在多尺度空间上的度量信息可以这样,其他信息在一定范围内也可仿照。它甚至完全能够摒弃人的主观因素影响很大的图形概括,而直接利用多尺度的实测、实用地形图,使界限划分更加客观、公平,摒弃直接人为因素。
基于双重(或多重)网格计算上的多尺度可视系统具有普遍意义:它将是一个大尺度全域可视的、各重要的、特征部分(点、线)可随机双尺度或各种多尺度显示,并实时给出各种满足m级、dm级以上精度的特征数据显示系统(类同图 5)。这对重要界线绘制等一类信息系统甚至是必须的。本文采用的多尺度度量和多尺度窗口,有别于通常状况下的单尺度多窗口,对于空间的多尺度效应是有较大意义的。
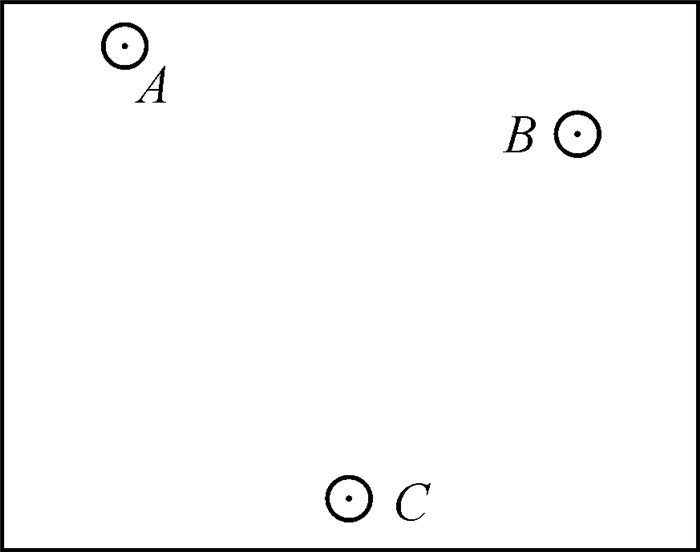
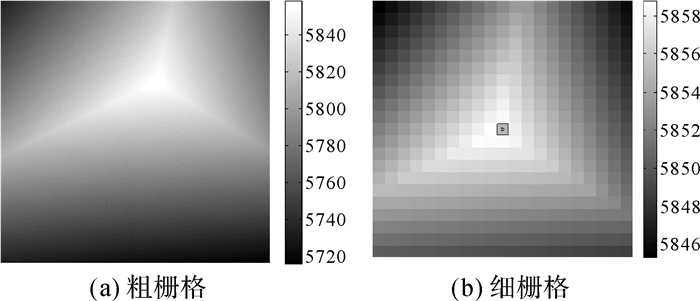
对整个双重网格计算途径进行算法复核及常规检验:按图 6实施了距离变换,其中左上角陆地代号为A,右上角陆地代号为B,下方陆地代号为C,其余区域均为海洋。粗栅格为100×100,每个栅格长宽均为100 m,每个粗栅格内分为100×100个小栅格,细栅格长宽均为1 m,具体陆地的栅格坐标设置如表 1所示。这时,距A、B、C等距的外心可计算确定,粗、细栅格及两重计算结果见图 7、表 2。
|
| 图 6 平面区域陆地分布示图 Fig. 6 Distribution map of A, B and C |
| 陆地 | 粗栅格坐标系 | 细栅格坐标系(左下角及右上角坐标) |
| A | (1,100) | (1,9901)-(100,10000) |
| B | (100,81) | (9900,8001)-(10000,8100) |
| C | (50,1) | (4900,1)-(5000,100) |
|
| 图 7 计算结果 Fig. 7 Results of coarse |
| 方法 | X坐标 | Y坐标 | 距离/m |
| 粗栅格变换 | 5 950.5 | 4 350.5 | 5 872.82 |
| 双重网格变换 | 5 938.5 | 4 416.5 | 5 858.78 |
| 细栅格变换 | 5939 | 4417 | 5 858.85 |
上述距离变换中各方距离可视为等权距离,倘若引入加权距离概念,同样可得到加权距离的“海心”、“陆心”,权比的V线(即比例线)等。
4 结论地球空间的运算,在数万公里的幅员内实施是不可避免的,而当要求两点间距离空间精度达到米级或更高时,矢量计算没有问题的,但它对某些空间问题而言,比如自然图形(点集形态)间的中间线和比例线类型的组合优化问题往往相当困难[22],故很少见诸于文献。由于自然图形具有普遍性,而各种点集间距离恰恰与度量空间最短线程问题相连,也即往往是组合优化问题,计算复杂性较高;采用面向空间的地图代数(距离变换)栅格算法,理论上只需一阶时间复杂性[21, 23],具有解决一些困难问题的能力[24-26],但当空间本质上是几百万个栅格相乘的绝对计算量,或更大、更多维时,其空间、时间开销仍是现今计算能力难以承担,是地图代数和所有栅格方法传统短板。采用本双重网格途径,原理可靠,对象局部化,运算简单(用微分式),第一次栅格计算绝对计算量只数千或数万栅格阵的计算是通常栅格软件现代计算能力均能轻松承担的;第二次栅格计算只需离散计算所需有关各粗栅格中的细栅格集,也即各方距离波最前方,距各方距离最大、数值大小相均衡的粗栅格中的细栅格,而不再必须进行全域的序贯运算,极大地降低了计算开销,突破了大区域度量计算的传统禁区,使高精度空间栅格方法能够明确实施,并且可在指定的相关区域内实时实施,得到理论上精细栅格计算的同样效果,具有重要意义。另外,本方法串接了栅格的多重运算与多分辨率几何关系,对于多分辨率图形图像科学问题的演绎和分析也将有重要的辅助作用。
| [1] |
LONGLEY P A, GOODCHILD M F, MAGUIRE D J, 等. 地理信息系统(上卷)—原理与技术[M]. 唐中实, 译. 2版. 北京: 电子工业出版社, 2004: 99-109, 113-142, 163-173. LONGLEY P A, GOODCHILD M F, MAGUIRE D J, et al. Geographical Information Systems. Volume 1: Principles and Technical Issues[M]. TANG Zhongshi, trans. 2nd ed. Beijing: Publishing House of Electronics Industry, 2004: 99-109, 113-142, 163-173. |
| [2] |
史文中.
空间数据与空间分析不确定性原理[M]. 北京: 科学出版社, 2015.
SHI Wenzhong. Principles of Modeling Uncertainties in Spatial Data and Spatial Analyses[M]. Beijing: Science Press, 2015. |
| [3] |
胡鹏, 杨传勇, 胡海, 等.
GIS的基本理论问题—地图代数的空间观[J]. 武汉大学学报(信息科学版), 2002, 27(6): 616–621.
HU Peng, YANG Chuanyong, HU Hai, et al. Space View of Map Algebra[J]. Geomatics and Information Science of Wuhan University, 2002, 27(6): 616–621. |
| [4] |
蒋会平, 谭树东, 胡海.
椭球面三角形外心的地图代数解法[J]. 测绘学报, 2016, 45(2): 241–249.
JIANG Huiping, TAN Shudong, HU Hai. Determination of Circumcenter of Triangle on Ellipsoidal Surface Based on Map Algebra[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(2): 241–249. DOI:10.11947/j.AGCS.2016.20140503 |
| [5] |
《现代数学手册》编纂委员会.
现代数学手册·计算机数学卷[M]. 武汉: 华中科技大学出版社, 2001: 265.
Editorial Committee of Handbook of Modern Mathematics. Handbook of Modern Mathematics[M]. Wuhan: Huazhong University of Science and Technology Press, 2001: 265. |
| [6] | HACKBUSCH W. Multi-grid Methods and Applications[M]. Berlin, Heidelberg: Springer, 1985: 558-575. |
| [7] | BRANDT A. Multi-level Adaptive Solutions to Boundary-value Problems[J]. Mathematics of Computation, 1977, 31(138): 333–390. DOI:10.1090/S0025-5718-1977-0431719-X |
| [8] | NICOLAIDES R A. On Multiple Grid and Related Techniques for Solving Discrete Elliptic Systems[J]. Journal of Computational Physics, 1975, 19(4): 418–431. DOI:10.1016/0021-9991(75)90072-8 |
| [9] |
宋印军, 岳天祥.
基于多重网格法求解的高精度曲面建模模型[J]. 武汉大学学报(信息科学版), 2009, 34(6): 711–714.
SONG Yinjun, YUE Tianxiang. An Ontology-driven Discovering Model of Geographical Information Services[J]. Geomatics and Information Science of Wuhan University, 2009, 34(6): 711–714. |
| [10] | HIPTMAIR R. Multigrid Method for Maxwell's Equations[J]. Siam Journal on Numerical Analysis, 1998, 36(1): 204–225. DOI:10.1137/S0036142997326203 |
| [11] |
史文娇, 杜正平, 宋印军, 等.
基于多重网格求解的土壤属性高精度曲面建模[J]. 地理研究, 2011, 30(5): 861–870.
SHI Wenjiao, DU Zhengping, SONG Yinjun, et al. High Accuracy Surface Modeling of Soil Properties Based on Multi-grid[J]. Geographical Research, 2011, 30(5): 861–870. |
| [12] | MATVEEV A D. Multigrid Finite Element Method in Calculation of 3D Homogeneous and Composite Solids[M]. Kazan: Kazan University, 2016: 530-543. |
| [13] | CHEN Chao, BIRO O. Geometric Multigrid With Plane Smoothing for Thin Elements in 3D Magnetic Fields Calculation[J]. IEEE Transactions on Magnetics, 2012, 48(2): 443–446. DOI:10.1109/TMAG.2011.2175203 |
| [14] | ARNONE A, LIOU M S, POVINELLI L A. Multigrid Calculation of Three-dimensional Viscous Cascade Flows[J]. Journal of Propulsion and Power, 1993, 9(4): 605–614. DOI:10.2514/3.23664 |
| [15] | CORNELIUS C, VOLGMANN W, STOFF H. Calculation of Three Dimensional Turbulent Flow with a Finite Volume Multigrid Method[J]. International Journal for Numerical Methods in Fluids, 1999, 31(4): 703–720. DOI:10.1002/(ISSN)1097-0363 |
| [16] |
渡部隆一. 泰勒展开[M]. 胡复, 译. 北京: 科学普及出版社, 1980. Du Bulonglong. Talyor Expansion[M]. HU Fu, trans. Beijing: Popular Science Press, 1980. |
| [17] |
刘经南.
三维基线向量与大地坐标差间的微分公式及其应用[J]. 武汉大学学报(信息科学版), 1991, 16(3): 70–78.
LIU Jingnan. The Formula Eetween 3D Baseline Vector and Geodetic Coordinate Differences and Its Application[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1991, 16(3): 70–78. |
| [18] |
施一民, 朱紫阳.
测地坐标系中大地线的微分方程及微分关系式[J]. 同济大学学报, 2003, 31(1): 40–43.
SHI Yimin, ZHU Ziyang. Differential Equations and Differential Relationship of Geodesic Lines in Geodesic Coordinate System[J]. Journal of Tongji University, 2003, 31(1): 40–43. |
| [19] |
陈健, 晁定波.
椭球大地测量学[M]. 北京: 测绘出版社, 1989: 81-262.
CHEN Jian, CHAO Dingbo. Ellipsoid Geodesy[M]. Beijing: Surveying and Mapping Press, 1989: 81-262. |
| [20] |
胡鹏, 游涟, 杨传勇, 等.
地图代数[M]. 武汉: 武汉大学出版社, 2002: 1-297.
HU Peng, YOU Lian, YANG Chuanyong, et al. Map Algebra[M]. Wuhan: Wuhan University Press, 2002: 1-297. |
| [21] |
胡鹏, 游涟, 胡海.
地图代数概论[M]. 北京: 测绘出版社, 2008: 167-189.
HU Peng, YOU Lian, HU Hai. The Introduction of Map Algebra[M]. Beijing: Surveying and Mapping Press, 2008: 167-189. |
| [22] |
胡海, 杨传勇, 胡鹏.
自然图形间的中间线和比例线方法[J]. 海洋测绘, 2009, 29(5): 15–18.
HU Hai, YANG Chuanyong, HU Peng. Methods of Midline and Scale Line Between Nature Figures[J]. Hydrographic Surveying and Charting, 2009, 29(5): 15–18. |
| [23] |
胡海. 自然图形k阶Voronoi图生成和应用[D]. 武汉: 武汉大学, 2007: 1-120. HU Hai. Generation and Application of Natural Graph K-order Voronoi Diagram[D]. Wuhan: Wuhan University, 2007: 1-120. |
| [24] |
胡鹏, 杨传勇, 胡海.
障碍空间最短路径的地图代数解法[M]. 北京: 测绘出版社, 2007.
HU Peng, YANG Chuanyong, HU Hai. Solution on ESPO Using Map Algebra[M]. Beijing: Surveying and Mapping Press, 2007. |
| [25] |
杨传勇, 胡海, 胡鹏, 等.
欧氏障碍空间的最短路径问题解法[J]. 武汉大学学报(信息科学版), 2012, 37(12): 1495–1499.
YANG Chuanyong, HU Hai, HU Peng, et al. Solution of Euclidean Shortest Path Problem Space with Obstacles[J]. Geomatics and Information Science of Wuhan University, 2012, 37(12): 1495–1499. |
| [26] | HU Hai, LIU Xiaohang, HU Peng. Voronoi Diagram Generation on the Ellipsoidal Earth[J]. Computers & Geosciences, 2014, 73: 81–87. |



