2. 地球空间信息技术协同创新中心, 湖北 武汉 430079;
3. 中国天绘卫星中心, 北京 102102;
4. 武汉大学资源与环境科学学院, 湖北 武汉 430079
2. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China;
3. TH Satellite Center of China, Beijing 102102, China;
4. School of Resource and Environmental Science, Wuhan University, Wuhan 430079, China
卫星影像的精度不仅取决于影像测量精度, 而且取决于事后处理控制点的几何分布和精度。然而, 全球测图难免遇到无控制点或少控制点区域, 如我国青藏高原、云贵高山峡谷、西北沙漠等外业测控困难区域以及境外大量无可用控制点区域。所以, 近年来, 立体卫星影像无控区域网平差逐渐引起了广泛的关注。卫星影像无控区域网平差是指在缺少外业控制的条件下, 实现卫星影像定位精度的相对一致性且尽可能地提高对地定位精度。
无控区域网平差的对地定位精度受到卫星影像质量、初始定位精度、地形起伏等因素的影响。为了提高对地定位精度, 国内外研究人员开展了一系列的相关研究。文献[1]研究了采用多次覆盖的卫星影像进行无控区域网平差方法, 可改善卫星影像无控定位精度; 文献[2]研究并实现了覆盖全国范围的8802个资源三号三线阵立体像对在无控制条件下整体一张网的平差, 达到无控制测图精度优于5 m的目标; 文献[3]利用更高定位精度的高分辨率卫星影像(如GeoEye、WorldView等)或航空影像作为控制条件, 也取得了较好的效果。除此之外, 已有的地理信息数据, 如数字正射影像(digital orthophoto map, DOM)和数字高程模型(digital elevation model, DEM), 也可以作为控制数据, 辅助卫星影像区域网平差[4]。随着公众地理信息数据种类的多样化和精度的提升, 平差过程中引入公开且可稳定获取的公众地理信息数据(如Google Earth影像、SRTM DEM)也逐渐成为卫星影像无控平差的可选择方式。其中ICESat卫星获取的激光高程点数据就是一种重要的公众地理信息数据。ICESat卫星是NASA于2003年发射的一颗地球观测卫星, 星上携带有NASA设计的地面高程激光测量系统(geoscience laser altimeter system, GLAS), ICESat卫星兼顾了地形及地面植被高度测量、云层高度及其垂直结构测量、海洋高程测量等科研任务。虽然ICESat卫星已于2009年10月停止了工作, 但是所获取的大量的激光观测数据仍然具有重要的应用价值, 这些观测数据已经被广泛应用于冰川高度变化监测[5-7]、湖泊河流水位高度变化监测、植被高度统计[8-9]、数字高程模型的精度评价等方面[10-11]。
虽然ICESat激光高程点具有较高的测量精度, 但是利用其辅助卫星影像区域网平差方面的研究才刚刚起步。文献[12]开展了ICESat激光高程控制点自动提取方法的研究, 取得了初步的成果, 能有效保证提取的高程控制点的绝对高程精度。文献[13-14]讨论了二线阵影像联合激光测距数据进行光束法平差的可行性, 并进行了模拟数据试验, 结果表明, 利用激光测距数据参与二线阵影像光束法平差, 能有效改善航线模型系统变形并保持较小的上下视差。文献[15]利用嫦娥一号卫星三线阵光学影像和激光测高数据, 采用局部表面约束的联合平差思想进行集成处理, 最终生成了月球表面三维数字表面模型, 为探测器落月选址奠定基础。文献[16-17]采用经过筛选后的ICESat激光测高数据作为广义高程控制点, 将平面和高程控制分离, 辅助资源三号进行三线阵立体区域网平差, 验证了ICESat激光点辅助卫星影像区域网平差的正确性和可行性; 其试验结论为未来我国发射激光测高卫星, 开展卫星激光测高与光学立体影像联合处理提供了很好的参考。
综上所述, 在卫星影像摄影测量处理中引入ICESat激光测高数据是十分有意义的。然而, 激光高程点辅助卫星影像区域网平差, 目前仅停留在平差原理和模型的研究以及小范围数据试验阶段。本文设计了一种ICESat激光高程点自动筛选提取方案, 并提出了一种模型法卫星影像立体区域网平差方法。为验证该方法的有效性和可行性, 本文采用山东全省的天绘一号卫星三线阵影像和ICESat激光测高数据进行了区域网平差试验, 利用外业检查点对其进行精度评定, 并讨论了不同激光高程控制点布设方案对区域网平差结果的影响。
1 ICESat/GLAS激光高程点的自动提取虽然GLAS标称的测距精度为15 cm[9](测距方向为近似垂直方向, 在平坦地区地形高度变化较小, 测距精度近似于高程精度), 但在实际测量过程中, 由于激光脉冲往返经过大气层, 大气分子及气溶胶会对激光脉冲产生散射、能量衰减、光斑漂移、波形展宽等多重影响, 地表的高反射率和云层的前向散射也会引起回波波形的过饱和, 使得测距精度下降。因此, 有必要从庞大的点数据库中提取出适用于高程控制的GLAS激光点。文献[12]研究发现, 利用GLAS L14数据记录的激光点质量评价参数(如饱和度改正标记i_satCorrFlg, 反射率参数i_reflctUncor等)和其他地表测量数据(如SRTM DEM, ASTER DEM)组合对GLAS点进行筛选, 可以达到较好的筛选效果。但是该研究采用90 m分辨率的SRTM DEM(SRTM 3″)作为参考标准, 而GLAS光斑本身只有70 m直径, 在最好的情况下, 单个GLAS光斑也只能覆盖4个参考DEM格网, 导致地面的坡度与粗糙度估计困难, 给GLAS点筛选造成不确定性。从2014年起美国陆续向全球用户免费开放30 m分辨率的SRTM DEM数据SRTM 1″, 与SRTM 3″一样, SRTM 1″覆盖了全球56°S-60°N范围, 标称的绝对高程精度为16 m(LE90), 相对高程精度为10 m(LE90), 但是具有更高的分辨率和数据质量[18]。针对以上问题, 本文采用30 m分辨率的SRTM数据计算得到的地表坡度作为限制条件, 同时根据GLAS本身的质量评价信息进行控制点筛选, 具体流程如图 1所示。
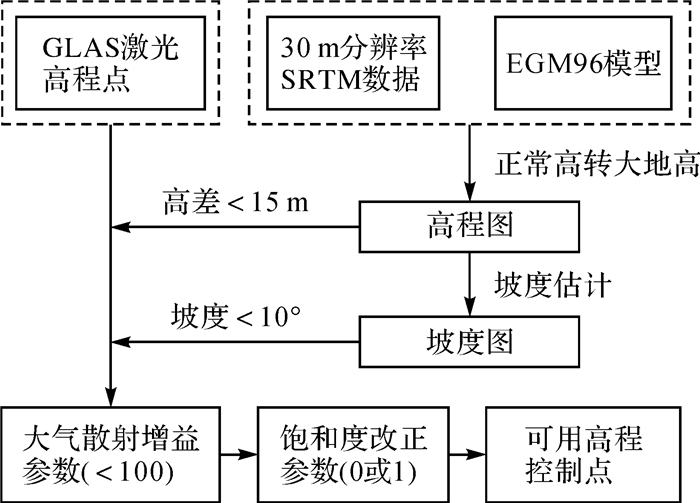
|
| 图 1 GLAS激光高程点自动提取流程 Fig. 1 The workflow of automatic extraction of GLAS laser points |
在实际使用中发现, 很多GLAS激光高程点与SRTM的高程之差达1000多米, 部分原因是GLAS发射的脉冲遇到厚云即反射, 导致测量高度异常; 此外, 地面坡度较大的地区, 如果星下点误差较大, 也导致高程点精度异常, 于是, 必须首先进行坡度估计, 并剔除两类高程异常点。最后, 通过GLAS点本身记录的点质量评价信息对剩余的点做进一步筛选, 即可获取较为可靠的高程控制点。本文采用上述方法对山东测区的ICESat原始数据进行了可用点提取, 并以1:10 000比例尺的DEM产品为参考, 对提取的可用点进行高程精度评定。参考DEM覆盖山东全省约15.8万km2, 地形以平地为主(约占55%), 丘陵和山地为辅(各占13%和16%), 其余为其他地形, 评价的GLAS激光高程点共11 395个。高程点筛选情况如表 1所示, 利用SRTM高差、SRTM坡度、大气散射增益和饱和度改正参数4个限制条件各剔除了3.6%、43.2%、26.2%和10.6%, 利用最终保留的1836个高程点进行精度评定, 与参考DEM的高差的均值为0.296 m, 中误差为1.223 m, 评定结果充分证明了可用点提取方法的有效性。
| 约束项 | 数据保留个数 | 数据剔除率/(%) |
| SRTM高差 | 10 985 | 3.6 |
| SRTM坡度 | 6033 | 43.4 |
| 大气散射增益 | 3045 | 26.2 |
| 饱和度改正参数 | 1836 | 10.6 |
| 与DEM的高差/m | 均值 | 0.296 |
| 中误差 | 1.223 |
从表 1也可以看出, 利用SRTM坡度条件剔除的比例最高, 达到了43.2%, 因此, 保留的高程点都位于地形平缓的平地区域, 将其作为高程控制点更加合理。
2 激光高程点辅助的卫星影像立体区域网平差模型 2.1 卫星影像有理函数模型由于具有传感器参数保密性、成像模型简单性与通用性的优点[19], 目前高分辨率卫星影像的成像模型一般采用有理函数模型(rational function model, RFM)。RFM是将像点坐标(Sample, Line)表示为以相应地面点空间坐标(P, L, H)(其中P为纬度,L为经度, H为高程)为自变量的多项式的比值
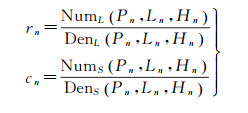 (1)
(1)
式中
 (2)
(2)
式中, b0和d0通常为1;(Pn, Ln, Hn)为正则化的地面坐标; (cn, rn)为正则化的影像坐标
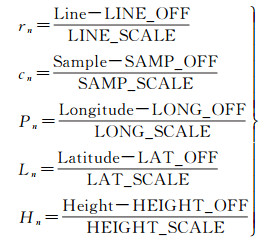 (3)
(3)
式中, LINE_OFF、SAMP_OFF、LONG_OFF、LAT_OFF、HEIGHT_OFF为正则化平移参数; LINE_SCALE、SAMP_SCALE、LONG_SCALE、LAT_SCALE、HEIGHT_SCALE为正则化比例参数。上述式(2)中多项式的系数ai、bi、ci、di(0≤i≤19)和式(3)中的正则化系数称为有理多项式系数(rational polynomial coefficient, RPC)。
综合式(1)与式(3), 有理函数模型建立的像素坐标(Sample, Line)与空间坐标(P, L, H)的关系式如式(4)所示
 (4)
(4)
一般情况下, 卫星影像的RPC参数是由在轨几何标定后的轨道和姿态数据拟合计算获得, 虽然卫星轨道和姿态数据经过在轨几何标定后精度有了很大提高, 但是依然会残留一定的系统误差, 所以由此拟合得到的RPC参数往往也具有系统误差。研究表明, 该系统误差可通过定义在像方的一个仿射变换来进一步改正[20]
 (5)
(5)
式中, Line和Sample是连接点或控制点的像方量测坐标; Line′和Sample′则是根据式(4)计算的连接点或控制点的投影坐标; a0、as、aL、b0、bs、bL为像方仿射变换参数。
卫星影像立体区域网平差的目的在于:①消除卫星影像立体像对内部各影像之间的上下视差; ②使得不同立体像对之间的同名观测具有相同的空间坐标; ③在有控的条件下, 平差解算的加密点空间坐标与其控制点空间坐标差异性最小。也就是通过平差调整卫星影像的定向参数, 使得同名光线相交至一致位置, 且与实际地面的差异性最小。
与文献[20]提出的卫星影像光束法区域网平差方法不同, 本文提出卫星影像模型法立体区域网平差方法。其基本原理为:以卫星立体像对(模型)为单元, 在原始RPC的基础上, 通过空间前方交会计算连接点在所有立体像对中的空间坐标, 并将空间坐标的均值作为其空间加密坐标, 然后使用式(5)逐一计算每张影像的像方仿射变换参数; 重复以上过程, 直至前后两次迭代的像点中误差变化量小于一定的阈值为止。其原理示意如图 2所示。
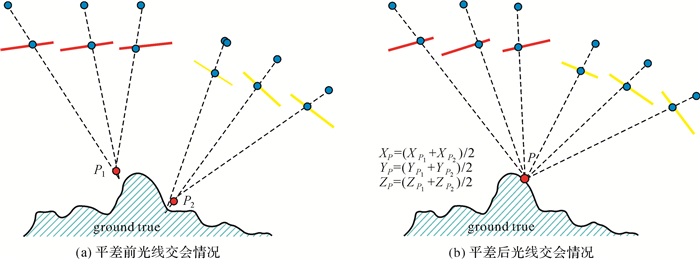
|
| 图 2 卫星影像模型法区域网平差原理示意 Fig. 2 The principle of block adjustment based on stereo model of satellite images |
图 2中3条红线和黄线分别表示两个三视卫星立体像对的3张影像, 分别组成模型1和模型2。在平差之前, 对于两个立体像对上的一个连接点利用原始RPC参数进行空间前方交会, 由于各影像的RPC参数具有一定系统误差, 导致模型1和模型2中像点的对应光线不能交会至一致位置。如图 2(a)所示, 连接点在模型1和模型2中, 最优交会空间点分别为P1和P2两点。平差过程中, 计算P1和P2两点的平均位置P, 并将其作为控制点, 根据式(5)调整每张影像的定向参数(即像方的仿射变换参数, 相当于空间后方交会), 从而使得同名光线相交至点P所在位置。
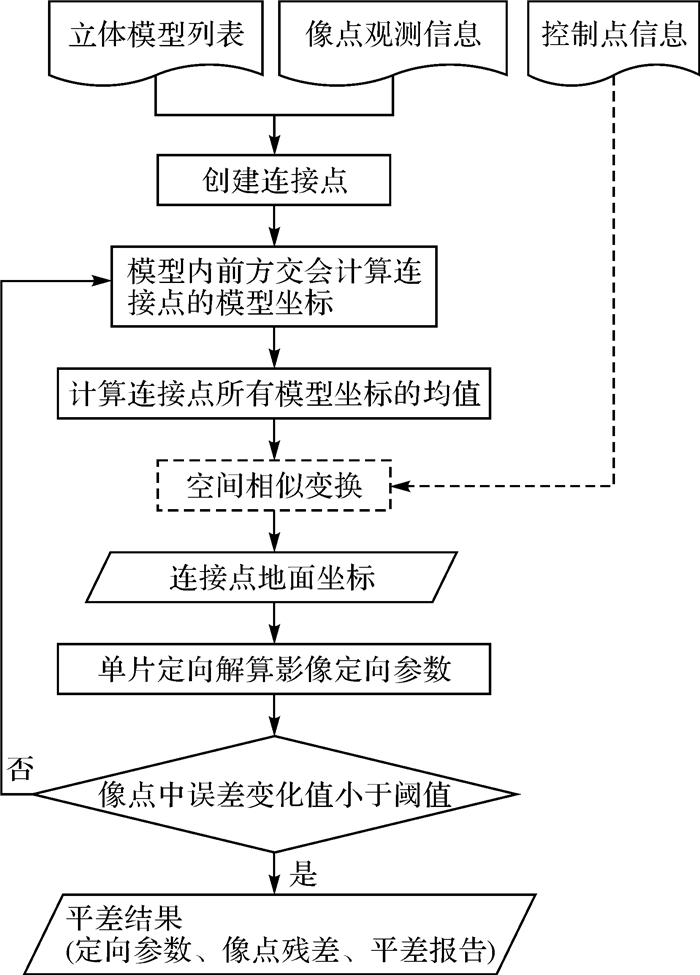
卫星影像模型法立体区域网平差的流程如图 3所示。
|
| 图 3 卫星影像模型法区域网平差流程 Fig. 3 The workflow of block adjustment based on stereo model of satellite images |
该流程可概括为“空间前方交会”-“均值化连接点地面坐标”-“单片定向”3个关键性步骤, 具体如下:
(1) 空间前方交会:以立体模型为单位, 使用影像的原始RPC参数和仿射变换改正参数(每张影像的像方仿射变换改正参数初值为0), 对连接点进行空间前方交会, 计算连接点在每个模型中的空间坐标(本文称为模型坐标)。将式(3)代入式(1), 然后将其按照泰勒公式展开至一次项, 得到式(6)
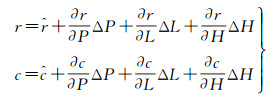 (6)
(6)
于是, 空间前方交会的误差方程式为式(7), 利用多个像点观测联立方程式(7), 即可解算像点的物方空间坐标
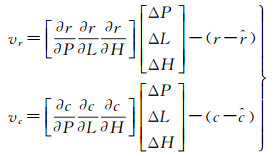 (7)
(7)
(2) 均值化连接点地面坐标:由于不同立体模型的直接对地定位精度不同, 所以步骤(1)计算的同一连接点在不同模型中的前方交会坐标各不相同。通过计算连接点在所有立体模型的模型坐标均值, 并将其作为连接点的地面坐标, 从而逐步消除模型坐标的不一致。在有控的情况下, 通过空间相似变换, 将连接点地面坐标转换为绝对地面坐标。由于测区范围较大, 空间相似变换使用地心地固坐标。
(3) 单片定向:根据式(5)可得单片定向的误差方程式(8), 将步骤(2)得到的连接点作为“虚拟控制点”, 按式(8)逐影像进行单片定向, 计算每张影像的仿射变换改正参数
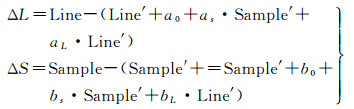 (8)
(8)
式中, ΔL和ΔS为像点残差。
采用迭代计算, 每次迭代结束后更新影像的仿射变换参数。计算相邻两次像点中误差的变化值, 若中误差变化小于预定阈值, 迭代结束。
从上述过程可以看出, 本文提出的卫星影像模型法区域网平差的实质为:通过一致化连接点在各立体模型中前方交会的地面坐标, 实现自由网定向(卫星影像区域网内部一致性); 通过一致化连接点的地面坐标与对应控制点的外业坐标, 实现绝对定向(卫星影像区域网与地面控制点间的外部一致性)。
2.3 ICESat激光高程点辅助的平差精化ICESat激光高程点标称的高程精度为15 cm, 该精度是现有国内外高分辨率立体卫星影像无控定位所难以达到的。天绘一号01星的无控定位的平面和高程中误差分别为10.3 m和5.7 m[21], 资源三号卫星三线阵立体影像经过在轨几何标定之后无控定位的平面和高程中误差约为15 m和8 m[22-23], GeoEye-1卫星GeoStereo级别立体像对无控定位的LE90精度为6 m[24]。因此, ICESat激光高程点可以用来作为高程控制进行辅助卫星影像的区域网平差。
ICESat激光高程点辅助的平差精化的核心是自动提取ICESat高程控制点。考虑到ICESat光斑直径约70 m, 平面精度为10.6±4.5 m[25], 当卫星影像(自由网平差后)平面精度较高(优于15 m), 可认为激光点与影像区域网平面位置套合较好, 此时, 在平坦区域, 由于高程变化小, 可将激光点高程赋予其光斑范围内空三加密点, 作为高程控制条件。本文提取ICESat高程控制点的原理如图 4所示。
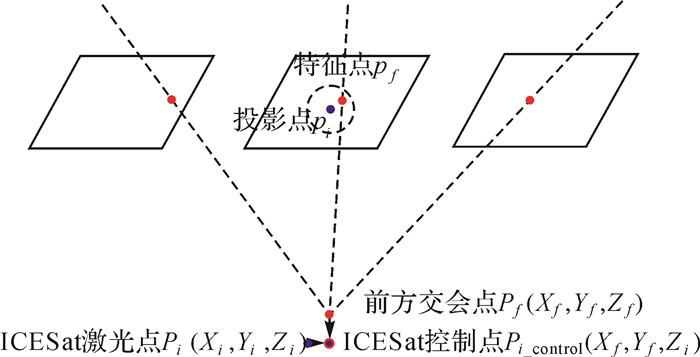
|
| 图 4 ICESat高程控制点提取原理示意 Fig. 4 The principle of the extraction of ICESat laser control points |
对于ICESat激光高程点Pi, 其地面坐标为(Xi, Yi, Zi), 首先, 将其投影至基准卫星影像的pi点, 由于点pi不一定为显著特征点, 因此以点pi为中心, 在ICESat激光高程点光斑对应的影像范围内提取影像特征点pf; 其次, 通过影像匹配自动获取特征点pf在其他影像上的同名像点, 通过多张影像的前方交会计算该同名像点对应地面点Pf的坐标(Xf, Yf, Zf); 最后, 使用ICESat激光高程点Pi的高程取代点Pf的高程, 形成地面控制点Pi_control(Xf, Yf, Zi)。
根据以上方法依次处理测区范围内的所有ICESat激光高程点, 得到多个ICESat高程控制点, 重新进行有控条件下的区域网平差, 计算ICESat激光高程点辅助条件下的影像定向参数。
3 试验数据与结果分析 3.1 试验数据介绍天绘一号是我国第一代传输型立体测绘卫星, 主要用于科学研究、国土资源普查、地图测绘等领域的科学试验任务。天绘一号01星、02星、03星分别于2010年8月24日、2012年5月6日和2015年10月26日发射成功, 现已组网运行。天绘一号卫星采用GPS进行定轨, 其中01星与02星采用单频GPS, 定轨精度为2~3 m, 03星采用双频GPS, 定轨精度优于1 m。
本文试验数据为天绘一号卫星三线阵立体(正视与前后视之间的交会角为25°)影像数据和ICESat/GLAS激光测高数据, 其中影像地面分辨率为5 m, 共2166张(包含01星、02星、03星3颗卫星的数据, 初始定位精度不一致), 组成了722个立体模型。影像摄自2010年至2016年间, 涉及不同时相与不同季节, 平均同一个地方有3次覆盖, 地面范围覆盖整个山东省(约15.8万km2)。试验区域地形复杂, 中部山地突起, 东部主要为丘陵, 西部主要为平原。为评定本文平差方法处理后影像的绝对定位精度, 通过外业GPS测量了96个高精度的野外控制点(平面精度与高程精度均优于0.1 m), 作为检查点使用。
天绘一号卫星影像和ICESat/GLAS激光高程控制点的地理位置如图 5所示, 其中蓝色方框表示影像中心, 黑色实心点表示激光高程控制点。
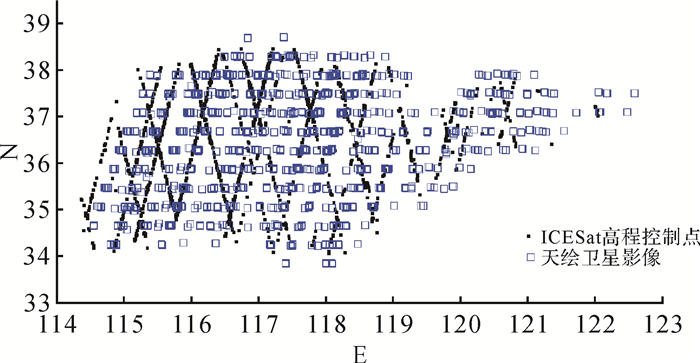
|
| 图 5 天绘一号卫星影像和ICESat/GLAS激光高程点位分布 Fig. 5 The distribution of Mapping Satellite-1 images and ICESat/GLAS laser points |
3.2 试验方案
(1) 自动匹配连接点:采用多级金字塔物方连接点匹配方法[26]匹配影像间的连接点, 在匹配过程中使用SRTM数据进行辅助。SRTM的作用为:首先, 用于改正地形引起的影像几何变形, 提高匹配的精度和成功率; 其次, 用于预测匹配点的初始位置, 对于两张待匹配影像中基准影像上的像点, 将其前方交会至SRTM获得地面点坐标, 然后再投影至匹配影像, 投影位置即为匹配位置的初值。
(2) 无控自由网平差:使用自动匹配获得连接点, 进行无控制条件下的模型法区域网平差, 计算影像像方仿射变换改正参数和连接点的地面坐标(即空三加密坐标)。
(3) ICESat高程控制点自动选取与辅助平差:按前文介绍的ICESat激光高程点辅助平差精化方法, 自动选择ICESat高程点并将其高程赋予对应连接点, 作为控制点, 进行有控条件下的区域网平差。
(4) 精度验证:以外业实测控制点作为平差精度评定的检查点, 分别检查无控条件和ICESat激光高程点辅助条件下两种平差模式的高程精度。
3.3 试验结果及分析 3.3.1 ICESat高程控制点辅助区域网平差试验试验1:完全无控条件下的区域网平差。
试验2:ICESat高程控制点辅助的区域网平差。利用全测区内自动提取的1839个激光高程控制点辅助区域网平差。
以上两组试验均使用96个外业检查点进行精度评定, 两种情况下检查点的高程残差分布分别如图 6与图 7所示, 其中X轴为经度, Y轴为纬度, 单位为度, 红色方向表示高程残差方向, 朝上为正(红色), 朝下为负(蓝色), 箭头矢量长度表示高程残差的大小。
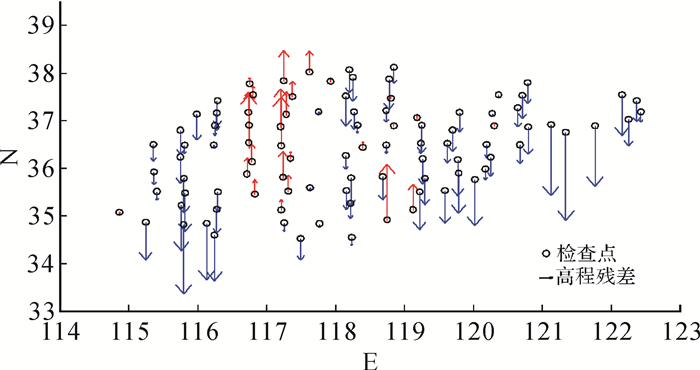
|
| 图 6 无控情况下检查点高程残差分布 Fig. 6 The distribution of vertical errors of check points without ground control points |
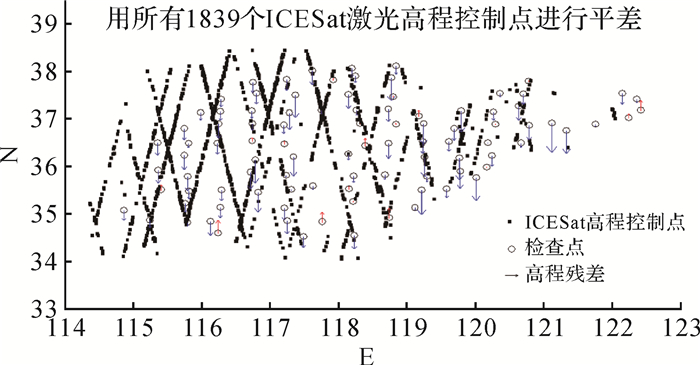
|
| 图 7 ICESat激光高程控制点辅助条件下检查点高程残差分布 Fig. 7 The distribution of vertical errors of check points with ICESat laser control points |
两种情况下检查点的精度比较见表 2。
| m | |||||||
| 误差项 | 完全无控 | ICESat高程点辅助 | |||||
| X | Y | Z | X | Y | Z | ||
| 中误差 | 8.45 | 6.86 | 5.88 | 8.14 | 6.68 | 2.51 | |
| 误差均值 | -7.84 | -5.65 | -2.98 | -7.63 | -5.58 | -1.21 | |
试验结果表明:
(1) ICESat激光高程点辅助区域网平差可显著提高高程定位精度。在完全无控条件下, 检查点的平面精度X、Y方向分别为8.45 m和6.86 m, 高程精度为5.88 m; ICESat激光高程点辅助区域网平差后, 检查点平面精度基本保持不变, 高程精度则有显著改善, 提高至2.51 m。
(2) 可有效消除无控区域网内部扭曲。如图 6所示, 在完全无控情况下, 测区左右两端检查点高程残差为负, 而中部检查点高程残差为正, 且残差值较大, 说明在完全无控情况下, 区域网内部具有一定程度的扭曲; ICESat激光高程点辅助区域网平差后, 整个测区检查点的高程残差大小基本一致, 见图 7, 且与所处的区域无关, 由此说明区域网内部扭曲问题得到有效消除。
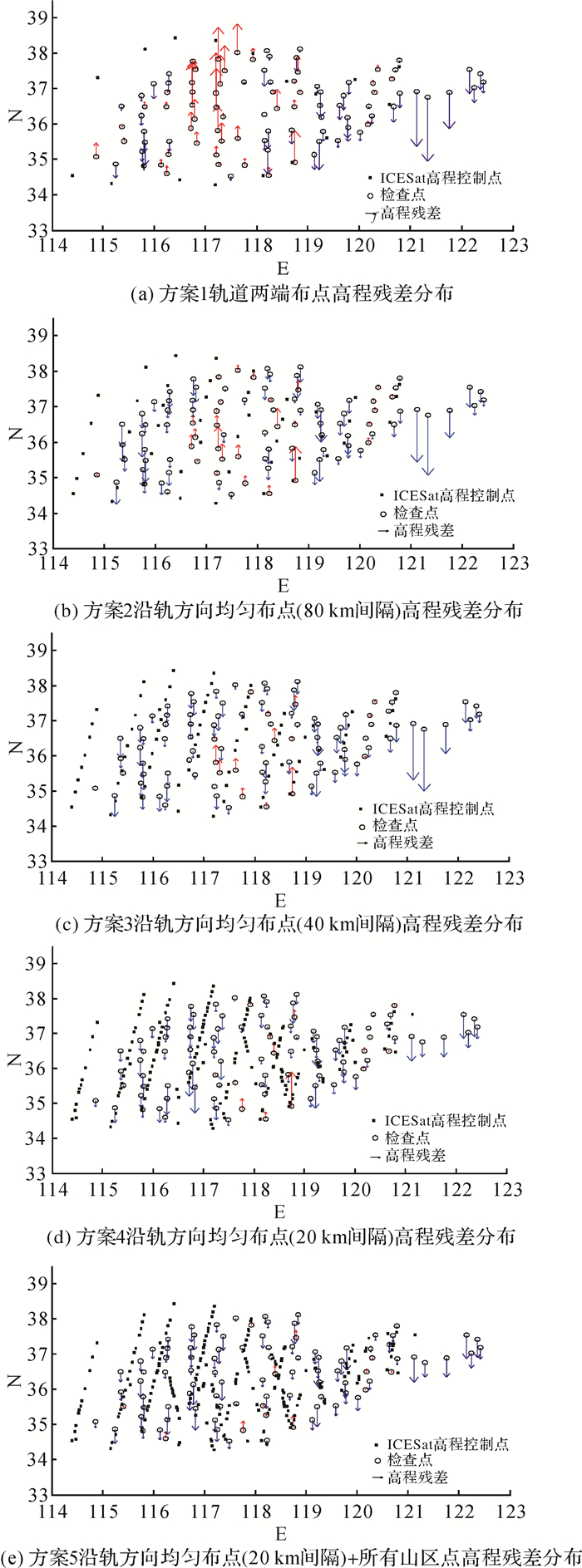
3.3.2 不同ICESat高程控制点布设方案的平差试验采用不同的ICESat激光高程控制点布设方案, 采用23个GLAS条带的激光高程点进行辅助区域网平差试验。提取了1839个激光高程点, 垂直条带方向以100 km间隔, 选取9个GLAS条带, 对于每个条带沿轨道方向按不同间隔选取激光高程点, 共选取5个布设方案, 其点位分布情况和平差结果统计见表 3, 高程残差分布见图 8。
| ICESat激光高程控制点布设方案 | 高程控制点个数 | 控制点高程中误差/m | 检查点高程中误差/m |
| 1 轨道两端布点 | 18 | 3.61 | 5.05 |
| 2 沿轨方向均匀布点(80 km间隔) | 46 | 3.06 | 4.14 |
| 3 沿轨方向均匀布点(40 km间隔) | 78 | 2.39 | 4.14 |
| 4 沿轨方向均匀布点(20 km间隔) | 160 | 2.16 | 3.46 |
| 5 沿轨方向均匀布点(20 km间隔)+所有山区点 | 237 | 1.92 | 3.18 |
|
| 图 8 5种不同高程控制点布设方案的高程残差分布 Fig. 8 The distributions of vertical errors of five layout schemes for ICESat laser control points |
从上述对比试验可以得出以下结论:
(1) 在轨道两端布点时, 全测区高程控制点仅分布在测区边缘, 虽然检查点的高程精度从5.88 m提升至5.05 m, 但是提升幅度不大, 且由于测区内部没有高程控制点, 平差后仍然会出现局部扭曲(图 8(a)中部偏左处红色箭头区域)。
(2) 随着ICESat激光高程点数量增多, 检查点的高程精度将会提高(如图 8(b)、(c)、(d)所示), 而且区域网的内部扭曲也会得到抑制; 当采用沿轨方向以20 km间隔均匀布点时, 区域网内部扭曲基本消除。然而, 以上选点方案所能达到的高程精度都不及使用全测区所有的1839个激光高程点进行整体平差的精度, 因此, 建议在实际生产中使用满足质量要求的所有ICESat激光高程点。
(3) 增加山区激光高程控制点对高程精度有较大改善作用。方案5在方案4基础上增加了位于山区的激光高程点, 检查点的高程精度由3.46 m提升至3.18 m, 且区域网的局部扭曲得到进一步抑制, 图 8(d)中部偏下区域的最大正误差(最长的红色箭头)在图 8(e)中明显变小。
4 结论为了改善卫星影像无控区域网平差的高程精度, 本文使用ICESat/GLAS激光高程点作为辅助, 提出了一种ICESat激光高程点辅助的卫星影像模型法立体区域网平差方法, 并利用山东全省的天绘一号卫星三线阵影像进行了多组区域网平差试验, 试验表明:①无控情况下, 检查点高程精度为5.88 m; 利用测区内自动提取的1839个ICESat高程控制点辅助区域网平差时, 高程精度可提升至2.51 m; ②在测区内选择布设ICESat高程控制点时, 平坦地区沿轨道方向间隔80 km即可, 而在山区需要布设尽可能多的ICESat高程控制点。
本文方法对于未来改善国产高分辨率立体测绘卫星无控测图精度和提高生产效率具有参考价值。然而, 目前将激光测高数据用于高分辨率卫星影像区域网平差仍然存在着一些问题, 例如, ICESat与天绘一号卫星轨道不一致, 不能保证参与平差的激光高程控制点均匀分布。随着未来ICESat-2卫星和高分七号(GF-7)卫星的发射, 我们将有机会使用更多的激光测高数据和国产高分辨率立体测绘卫星数据进行试验, 以进一步验证和提高本文方法的稳定性。
| [1] |
刘昆波. 提高天绘卫星影像无控区域网平差定位精度的研究[D]. 武汉: 武汉大学, 2015. LIU Kunbo. The Research of Improving the Positioning Accuracy of Block Adjustment without GCPs for Images from Mapping Satellite-I[D]. Wuhan: Wuhan University, 2015. |
| [2] |
王密, 杨博, 李德仁, 等.
资源三号全国无控制整体区域网平差关键技术及应用[J]. 武汉大学学报(信息科学版), 2017, 42(4): 427–433.
WANG Mi, YANG Bo, LI Deren, et al. Technologies and Applications of Block Adjustment Without Control for ZY-3 Images Covering China[J]. Geomatics and Information Science of Wuhan University, 2017, 42(4): 427–433. |
| [3] | LI Rongxing, DESHPANDE S, NIU Xutong, et al. Geometric Integration of Aerial and High-Resolution Satellite Imagery and Application in Shoreline Mapping[J]. Marine Geodesy, 2008, 31(3): 143–159. DOI:10.1080/01490410802265310 |
| [4] | ZHANG Zuxun, LU Luping, TAO Pengjie, et al. Registration of CBERS-02B Satellite Imagery in Quick GIS Updating[C]//Proceedings of SPIE 8006, MIPPR 2011: Remote Sensing Image Processing, Geographic Information Systems, and Other Applications. Guilin: SPIE, 2011, 8006: 80060C. |
| [5] |
黄海兰, 王正涛, 金涛勇, 等.
利用ICESat激光测高数据确定极地冰盖高程变化[J]. 武汉大学学报(信息科学版), 2012, 37(10): 1221–1223.
HUANG Hailan, WANG Zhengtao, JIN Taoyong, et al. Determination of Polar Ice Sheet Height Change from ICESat Altimetry Data[J]. Geomatics and Information Science of Wuhan University, 2012, 37(10): 1221–1223. |
| [6] |
李建成, 范春波, 褚永海, 等.
ICESAT卫星确定南极冰盖高程模型研究[J]. 武汉大学学报(信息科学版), 2008, 33(3): 226–228.
LI Jiancheng, FAN Chunbo, CHU Yonghai, et al. Using ICESAT Altimeter Data to Determine the Antarctic Ice Sheet Elevation Model[J]. Geomatics and Information Science of Wuhan University, 2008, 33(3): 226–228. |
| [7] |
鄂栋臣, 沈强, 徐莹, 等.
基于ASTER立体数据和ICESat/GLAS测高数据融合高精度提取南极地区地形信息[J]. 中国科学D辑:地球科学, 2009, 52(5): 714–722.
E Dongchen, SHEN Qiang, XU Ying, et al. High-accuracy Topographical Information Extraction Based on Fusion of ASTER Stereo-data and ICESat/GLAS Data in Antarctica[J]. Science in China Series D-Earth Sciences, 2009, 52(5): 714–722. |
| [8] | WANG Xianwen, CHENG Xiao, GONG Peng, et al. Earth Science Applications of ICESat/GLAS:A Review[J]. International Journal of Remote Sensing, 2011, 32(23): 8837–8864. DOI:10.1080/01431161.2010.547533 |
| [9] | ZWALLY H J, SCHUTZ B, ABDALATI W, et al. ICESat's Laser Measurements of Polar Ice, Atmosphere, Ocean, and Land[J]. Journal of Geodynamics, 2002, 34(3-4): 405–445. DOI:10.1016/S0264-3707(02)00042-X |
| [10] | GONZALEZ J H, BACHMANN M, SCHEIBER R, et al. Definition of ICESat Selection Criteria for Their Use as Height References for TanDEM-X[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(6): 2750–2757. DOI:10.1109/TGRS.2010.2041355 |
| [11] |
万杰, 廖静娟, 许涛, 等.
基于ICESat/GLAS高度计数据的SRTM数据精度评估-以青藏高原地区为例[J]. 国土资源遥感, 2015, 27(1): 100–105.
WAN Jie, LIAO Jingjuan, XU Tao, et al. Accuracy Evaluation of SRTM Data based on ICESat/GLAS Altimeter Data:A Case Study in the Tibetan Plateau[J]. Remote Sensing for Land & Resources, 2015, 27(1): 100–105. DOI:10.6046/gtzyyg.2015.01.16 |
| [12] |
李国元, 唐新明, 张重阳, 等.
多准则约束的ICESat/GLAS高程控制点筛选[J]. 遥感学报, 2017, 21(1): 96–104.
LI Guoyuan, TANG Xinming, ZHANG Chongyang, et al. Multi-criteria Constraint Algorithm for Selecting ICESat/GLAS Data as Elevation Control Points[J]. Journal of Remote Sensing, 2017, 21(1): 96–104. |
| [13] |
王任享, 王建荣.
二线阵CCD卫星影像联合激光测距数据光束法平差技术[J]. 测绘科学技术学报, 2014, 31(1): 1–4.
WANG Renxiang, WANG Jianrong. Technology of Bundle Adjustment Using Two-line-array CCD Satellite Image Combined Laser Ranging Data[J]. Journal of Geomatics Science and Technology, 2014, 31(1): 1–4. |
| [14] |
王建荣, 王任享, 胡莘, 等.
利用激光测距数据处理线阵卫星摄影测量影像[J]. 测绘科学, 2013, 38(2): 15–16.
WANG Jianrong, WANG Renxiang, HU Xin, et al. Application of Laser Distance Measurement Data in Linear Array Satellite Photogrammetry[J]. Science of Surveying and Mapping, 2013, 38(2): 15–16. |
| [15] | WU Bo, GUO Jian, HU Han, et al. Co-registration of Lunar Topographic Models Derived from Chang'E-1, SELENE, and LRO Laser Altimeter Data Based on a Novel Surface Matching Method[J]. Earth and Planetary Science Letters, 2013, 364: 68–84. DOI:10.1016/j.epsl.2012.12.024 |
| [16] |
唐新明, 李国元, 高小明, 等.
卫星激光测高严密几何模型构建及精度初步验证[J]. 测绘学报, 2016, 45(10): 1182–1191.
TANG Xinming, LI Guoyuan, GAO Xiaoming, et al. The Rigorous Geometric Model of Satellite Laser Altimeter and Preliminarily Accuracy Validation[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(10): 1182–1191. DOI:10.11947/j.AGCS.2016.20150357 |
| [17] |
李国元, 唐新明, 王华斌, 等. GLAS激光测高数据辅助的资源三号三线阵区域网平差研究[C]//第三届高分辨率对地观测学术年会. 北京: 高分辨率对地观测系统重大专项管理办公室, 2014: 586-600. LI Guoyuan, TANG Xinming, WANG Huabin, et al. Research on the ZY-3 Block Adjustment Supported by the GLAS Laser Altimetry Data[C]//Proceedings of the 3rd China High Resolution Earth Observation Conference. Beijing: Major Special Management Office of High Resolution to Earth Observation System, 2014: 586-600. |
| [18] | HU Zhihua, PENG Jianwei, HOU Yaolin, et al. Evaluation of Recently Released Open Global Digital Elevation Models of Hubei, China[J]. Remote Sensing, 2017, 9(3): 262. DOI:10.3390/rs9030262 |
| [19] | TAO C V, HU Y. A Comprehensive Study of the Rational Function Model for Photogrammetric Processing[J]. Photogrammetric Engineering & Remote Sensing, 2001, 67(12): 1347–1357. |
| [20] | GRODECKI J, DIAL G. Block Adjustment of High-resolution Satellite Images Described by Rational Polynomials[J]. Photogrammetric Engineering & Remote Sensing, 2003, 69(1): 59–68. |
| [21] |
付勇, 邹松柏, 刘会安.
"天绘一号"01星立体影像定位精度检测[J]. 遥感学报, 2012(S1): 94–97.
FU Yong, ZOU Songbai, LIU Hui'an. Evaluation of the Location Accuracy of the Mapping Satellite-1 Stereo Image[J]. Journal of Remote Sensing, 2012(S1): 94–97. DOI:10.11834/jrs.20120019 |
| [22] |
潘红播, 张过, 唐新明, 等.
资源三号测绘卫星影像产品精度分析与验证[J]. 测绘学报, 2013, 42(5): 738–744, 751.
PAN Hongbo, ZHANG Guo, TANG Xinming, et al. Accuracy analysis and verification of ZY-3 Products[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 738–744, 751. |
| [23] |
蒋永华, 张过, 唐新明, 等.
资源三号测绘卫星三线阵影像高精度几何检校[J]. 测绘学报, 2013, 42(4): 523–529, 553.
JIANG Yonghua, ZHANG Guo, TANG Xinming, et al. High Accuracy Geometric Calibration of ZY-3 Three-Line Image[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 523–529, 553. |
| [24] | GeoEye I. GeoEye Product Guide[EB/OL]. [2011-12-21]. http://www.geoeye.com/CorpSite/assets/docs/brochures/GeoEye_Product_Guide.pdf. |
| [25] | MAGRUDER L A, WEBB C E, URBAN T J, et al. ICESat Altimetry Data Product Verification at White Sands Space Harbor[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(1): 147–155. DOI:10.1109/TGRS.2006.885070 |
| [26] | TAO Pengjie, LU Luping, ZHANG Yong, et al. On-Orbit Geometric Calibration of the Panchromatic/Multispectral Camera of the ZY-102C Satellite Based on Public Geographic Data[J]. Photogrammetric Engineering & Remote Sensing, 2014, 80(6): 505–517. |



