2. 安徽大学电子信息工程学院, 安徽 合肥 230601;
3. 偏振光成像探测技术安徽省重点实验室, 安徽 合肥 230031
2. School of Electronics and Information Engineering, Anhui University, Hefei 230601, China;
3. Anhui Key Laboratory of Polarization Imaging Detection Technology, Hefei 230031, China
卫星遥感图像现已被广泛应用于工业、农业、林业、资源、气象、环境和国防等多个领域。卫星遥感传感器在获取地面图像时, 极易受到天气影响。云层覆盖遥感图像使得图像上的地物信息模糊或者缺失, 严重影响图像的判读和分析。在现有条件下, 寻找一种有效的遥感图像云覆盖下地物信息恢复方法, 是增强有云遥感图像可用性的重要途径。
根据所用的遥感图像数量, 从薄云图像中恢复地物信息的方法大致可以分为两类:第1类是对单幅薄云图像进行滤波或边缘增强达到去除薄云恢复地物信息的目的; 第2类是利用多时相、多光谱遥感图像之间的互补信息来恢复薄云图像中的地物信息。同态滤波法和小波变换法是较为经典的从单幅薄云遥感图像中恢复地物信息的方法。同态滤波法是一种把频率过滤和灰度变换结合起来的处理方法[1-3], 先将图像通过傅里叶变换转换到频率域, 然后使用高频滤波器对图像进行空间滤波去除薄云恢复地物信息。同态滤波法在每个通道的最佳截止频率可以半自动确定[4]。小波变换法对薄云图像进行小波分解, 得到不同分辨率的小波近似系数和细节系数, 通过对近似系数和细节系数的处理和重构, 得到地物信息恢复图像[5-6]。除了小波变换之外, 轮廓波变换、对偶树复小波变换等图像变换方法也被用于从单幅薄云图像中恢复地物信息[7-8]。同态滤波法和图像变换法虽然能够去除薄云恢复地物信息, 但是也会对地物信息造成损伤, 同时由于先验条件的缺失和辅助信息的匮乏, 利用单幅薄云图像恢复地物信息的效果有限。多光谱图像法利用多光谱图像传感器的某些波段分别对云层或地物较敏感这一特性来区分云层或地物, 达到去云恢复地物信息的目的[9-10], 其中Landsat-8 OLI的卷云波段已被广泛应用于Landsat-8多光谱图像的云层检测和去除[11]。多光谱图像法需要有冗余的波段, 在有限光谱分辨率的情况下, 薄云很难用多光谱的方法去除。多时相图像融合法利用不同传感器获得相同地区不同时相的图像, 通过图像融合技术插补薄云区域的数据, 得到无云图像, 恢复地物信息[12-13]。图像融合法可以移除云和云阴影[14], 有效恢复地物信息, 但现有的融合算法对图像噪声和不同图像的辐射差异较为敏感[15]。
本文给出一种融合引导滤波和迁移学习的薄云图像中地物信息恢复算法。该算法利用多方向非抽样对偶树复小波变换对多源多时相遥感图像进行多分辨率分解, 对分解后的图像低频成分分别利用支持向量引导滤波方法和域自适应的迁移学习方法初步去除图像上的薄云, 再对这两种方法处理后的图像低频成分利用基于区域能量的选择和加权相结合的方法进行融合, 最终获取地物细节清晰的无云遥感图像。由于支持向量引导滤波能有效保留地物的细节信息, 还具有较好的抗噪声能力, 域自适应的迁移学习模型能使得可利用的多源多时相遥感图像范围大大扩展, 本文将这两种方法恢复地物信息的图像进行融合, 充分利用支持向量引导滤波和迁移学习方法的优势, 在恢复薄云下地物信息的同时有效去除薄云, 获得好的地物信息恢复效果。
1 地物信息恢复算法 1.1 多方向非抽样对偶树复小波变换由于遥感图像中的地物与薄云一般占用不同的频带, 薄云遥感图像经过多尺度变换分解之后, 地物信息主要分布在高频子带, 薄云信息主要分布在低频子带, 因而小波变换等多尺度分解方法已被应用于遥感图像薄云去除算法中[6]。小波变换处理图像时存在两个方面的缺点:一是移位方差的存在, 即输入信号发生较小的平移, 会造成小波变换的系数发生剧烈变化; 二是方向选择性不足, 只能捕获信号在水平、垂直以及对角3个方向上的细节信息。为此, 文献[16]提出了对偶树复小波变换。对偶树复小波变换由两棵平行的小波树组成, 两棵小波树提供了多分辨率分析的每层必要的信号延迟, 并将采样间隔扩大1倍, 从而消除混叠效应, 实现近似平移不变性。二维对偶树复小波变换把图像在每个尺度上分解成两个低频子带和6个方向的高频子带, 其中低频子带用来继续下一尺度的分解。在二维对偶树复小波滤波器组之前再增加沙漏滤波器组以增加方向选择性[17], 并且在每层小波分解树不进行下采样以实现完全的平移不变性, 这样就构成了多方向非抽样对偶树复小波变换[18]。
多方向非抽样对偶树复小波变换分解二维图像I(n1, n2)可通过式(1)表示
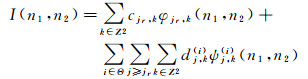 (1)
(1)
式中, Z为自然数集; j和k分别表示平移和膨胀的系数; cjr, k表示尺度系数; dj, k(i)表示第i个方向上的复小波系数; Θ是总的分解方向。
1.2 支持向量引导滤波由于薄云具有缓慢变化的特性, 薄云遥感图像经过多方向非抽样对偶树复小波变换分解之后, 薄云信息主要分布在低频子带。为了去除薄云恢复地物信息, 本文利用引导滤波方法对薄云图像的低频子带进行处理, 引导滤波的输入包括薄云图像和引导图像经多方向非抽样对偶树复小波变换分解后的低频子带图像。
假设p是一个待滤波图像, I是一个无云引导图像, q是引导滤波输出图像。在本文中, 待滤波图像即为薄云图像经多方向非抽样对偶树复小波变换分解后的低频子带图像, 无云引导图像是事先选定的和薄云图像地理位置相同的无云图像经多方向非抽样对偶树复小波变换分解后的低频子带图像。引导滤波输出是引导图像的一个线性变换[19]
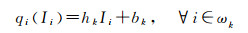 (2)
(2)
式中, ωk是以像素k为中心的一个窗口; i是像素索引; hk、bk是当窗口中心位于像素k时该线性函数的权重和偏置。权重和偏置可以利用待滤波图像p的约束条件来求取, 其中一个较为合理的约束条件是在保持式(2)线性关系的同时最小化输入输出图像间的差异, 比如可以通过最小化下面的损失函数来确定hk、bk的值
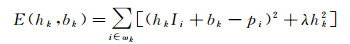 (3)
(3)
式中, (hkIi+bk-pi)2是滤波结果的平方损失; λ是均衡常数; 正则项λhk2起着平滑该线性函数权重hk的作用, 防止输入输出图像之间过拟合。
根据式(2)可得▽q=hk▽I, 因而引导滤波输出图像能够有效保持引导图像的边缘特性, 该特性在图像去雾方面非常有用[20]。
由于引导滤波输出是引导图像的一个线性变换, 虽具有良好的边缘保持特性, 但其抗噪声性能不足。本文利用支持向量回归模型的强泛化能力, 给出一种支持向量引导滤波代替现有的引导滤波, 以便在恢复地物信息的同时能有效去除图像噪声。支持向量引导滤波输出是引导图像的一个非线性变换
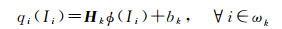 (4)
(4)
式中, φ(·)是将线性不可分样本点变换到线性可分高维特征空间的非线性映射。为了求解该非线性变换的权重Hk和偏置bk, 需要最小化下面的结构风险
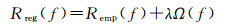 (5)
(5)
式中, Remp(f)是经验风险函数, 度量输入输出图像间的差异, 其作用类似于式(3)中的平方损失; Ω(f)是提高函数泛化能力的正则项, 其作用类似于式(3)中的正则项, 防止输入输出图像之间过拟合。根据支持向量机理论, 最小化式(5)等价于下面的约束优化问题[8]
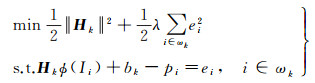 (6)
(6)
定义拉格朗日函数
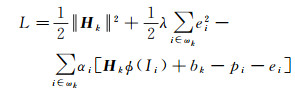 (7)
(7)
式中, αi∈R是拉格朗日乘子。
由KKT(Karush-Kuhn-Tucker)条件得到下列线性方程组
 (8)
(8)
式中, 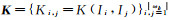
根据表示定理, 式(4)有如下表示形式的解
 (9)
(9)
因而将式(8)的求解结果代入式(9), 就可以得到支持向量引导滤波输出值。式(9)所给出的引导滤波输出是引导图像的一个非线性变换, 该非线性变换的加权系数和偏置由式(8)所定义的线性方程组确定。
利用支持向量引导滤波方法恢复薄云图像低频子带中地物信息的算法流程见图 1。

|
| 图 1 支持向量引导滤波方法流程示意 Fig. 1 Diagram of support vector guided filter method |
1.3 迁移学习
传统机器学习方法有一个共同的假设:训练数据和测试数据均来自同一特征空间或具有同一概率分布, 当两者概率分布发生较大变化时, 尽管源域中有大量可用的训练数据, 但是通过训练这些数据得到的预测模型来测试目标域数据的性能并不稳健。迁移学习方法是解决训练样本与测试样本分布不一致问题的有效方法, 本文采用域自适应的迁移支持向量回归模型将多源多时相图像的地物轮廓信息添加进目标图像中, 以获得好的地物信息恢复效果[8]。
选取多源多时相无云图像经多方向非抽样对偶树复小波变换分解后的低频子带图像构建源域数据集。记源域数据集为DA={(Iia, pia)}i=1M, 其中pia是源域数据集里与薄云图像相同传感器所获取的无云图像的低频子带系数, Iia是源域数据集里由不同传感器所获取的对应位置的无云图像的低频子带系数。选取与薄云图像相同地理位置的无云图像经多方向非抽样对偶树复小波变换分解后的低频子带图像构建目标域数据集。记目标域数据集为DP={(Ii, pi)}i=1N, 其中pi是目标域数据集里与薄云图像相同传感器所获取的无云图像的低频子带系数, Ii是目标域数据集里由不同传感器获取的对应位置的无云图像的低频子带系数。在源域数据集上建立的支持向量回归模型的决策函数为qia(x)=waTΦ(x)+ba, 则最优化问题为
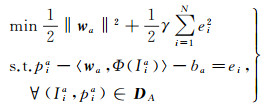 (10)
(10)
迁移支持向量回归模型的决策函数是在标准支持向量回归模型决策函数的基础上增加一个“Δ函数”, 使其在不同域中能更好地自适应[21], 即
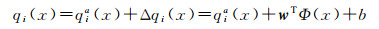 (11)
(11)
可以通过下面的约束优化模型来学习Δqi(x)中的参数w与b
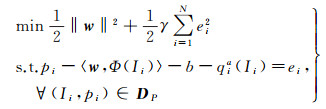 (12)
(12)
利用拉格朗日乘子法得到
 (13)
(13)
式中, αi∈R为拉格朗日乘子。
由KKT条件得到下列线性方程组
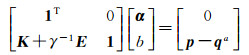 (14)
(14)
式中, 核函数K={Ki, j=K(Ii, Ij)}i, j=1N; 1=(1, …, 1)T; p=(p1, …, pN)T; α=(α1, …αN)T; qa=(qia(I1), qia(I2), …, qia(IN))。
因而, 式(11)可以表示为
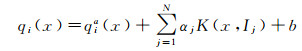 (15)
(15)
同理, 若有M种源域样本, 则迁移支持向量回归模型的决策函数为
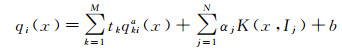 (16)
(16)
式中, qkia(x)是第k个源域数据集上的决策函数。将式(14)的求解结果代入式(15)或式(16), 就可以得到迁移支持向量回归模型的决策值。
利用迁移学习方法恢复薄云图像低频子带中地物信息的算法流程见图 2。

|
| 图 2 迁移学习方法流程示意 Fig. 2 Diagram of transfer learning method |
1.4 高低频子带的处理
薄云遥感图像经多方向非抽样对偶树复小波变换后, 图像分解成低频子带和多尺度多方向高频子带。由于地物信息主要占据了图像的高频频带, 需要对薄云图像的高频方向子带系数进行增强处理。文献[22]提出了一个如下所示的增强函数
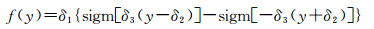 (17)
(17)
式中, -1≤y≤1;δ1={sigm[δ3(1-δ2)]-sigm[-δ3(1+δ2)]}-1, 0 < δ2 < 1, sigm(y)=(1+e-y)-1; 参数δ3用于控制增强强度。由于多方向非抽样对偶树复小波变换具有很强的方向信息, 对噪声点来说, 它的分解系数会较小, 而图像中地物边缘的分解系数会较大, 但对一些较弱的边缘来说, 在部分方向子带里的系数会较大, 在另外一些方向子带里的系数会较小。为了避免对图像中地物的边缘系数进行增强的同时也放大了噪声系数, 需要对方向子带的不同系数分别进行处理, 因而本文采用如下的增强函数[23-24]
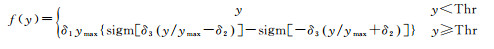 (18)
(18)
式中, ymax是高频方向子带的最大系数; Thr是阈值。假设含噪声信号模型可以表示为
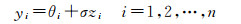 (19)
(19)
式中, 
 (20)
(20)
因而本文中阈值的大小取为
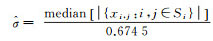
由于薄云占据图像的低频频带, 为了去除薄云恢复地物信息, 需要对低频子带进行处理。利用目标图像和引导图像(源域图像)的低频子带系数求解式(8)、式(9), 获取引导滤波输出的低频子带系数, 求解式(15)、式(16), 获取迁移支持向量回归模型预测的低频子带系数, 再利用图像融合法把引导滤波输出和迁移支持向量回归模型预测的低频子带系数进行融合, 使得融合子带具有更多的地物轮廓信息。本文采用基于区域能量的选择和加权相结合的方法融合低频子带系数。
设所选的区域为Ω, 区域Ω的中心像素点坐标为(s, t), 则该区域Ω的能量表示为
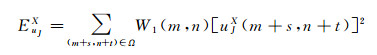 (21)
(21)
式中, X表示区域所在的图像; uJX(m+s, n+t)表示图像X在像素点(m+s, n+t)的低频子带系数; W1为权重系数。
定义两幅图像A、B在区域Ω范围内的匹配度如下[27]
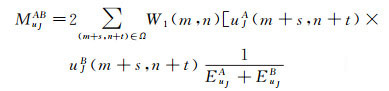 (22)
(22)
式中, EAuJ和EBuJ分别是图像A、B在区域Ω上计算的能量。
定义加权归一化差异指数为
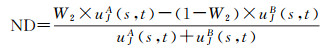 (23)
(23)
式中, W2是权重系数, 大小由式(24)决定
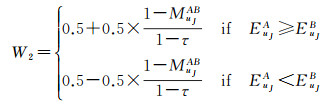 (24)
(24)
式中, τ是加权归一化差异指数的阈值。ND值用来度量待融合图像区域之间的差异程度, 其绝对值越小, 表明待融合图像区域之间的差异程度越小, 融合规则采用加权形式, 反之则表明待融合图像区域之间的差异程度越大, 融合规则采用选择形式。本文根据多次模拟薄云图像试验结果将阈值τ取为0.3。如果-τ < ND < τ, 则融合采用加权形式
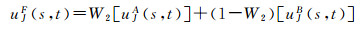 (25)
(25)
如果ND≥τ或ND≤-τ, 则融合采用选择形式
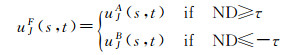 (26)
(26)
为了恢复薄云遥感图像上的地物信息, 本文算法步骤如下:
(1) 选取薄云目标图像和不同时相无云引导图像(源域图像)并进行空间配准。
(2) 对目标图像和引导图像(源域图像)进行多方向非抽样对偶树复小波变换分解, 并提取高低频子带系数。
(3) 利用目标图像和引导图像的低频子带系数求解式(8)、式(9), 获取支持向量引导滤波输出的低频子带系数; 利用目标图像和源域图像的低频子带系数求解式(15)、式(16), 获取迁移学习方法预测的低频子带系数。
(4) 利用式(25)或式(26)的融合规则把支持向量引导滤波方法和迁移学习方法分别处理后的低频子带系数进行融合。
(5) 采用式(18)的增强函数对高频方向子带进行增强处理。
(6) 利用多方向非抽样对偶树复小波逆变换, 把经过融合后的低频子带和经过增强后的高频方向子带进行重构, 获得地物信息恢复图像。
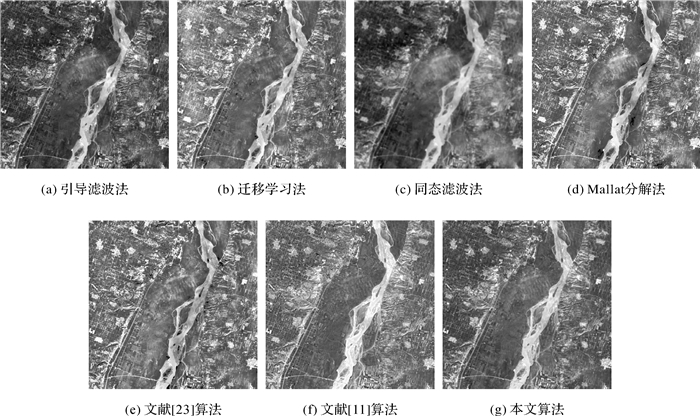
2 试验结果及分析为了验证本文算法的有效性, 本部分进行仿真试验。试验选取的多光谱图像来自于Landsat-8 OLI传感器。试验是对波段1—7进行处理的, 为了更好地显示处理结果, 文中仅给出由4、3、2波段合成的真彩色图像, 定量评价结果也是对这3个波段分别进行定量评价后取平均值。引导滤波法[19]、迁移学习法[8]、同态滤波法[2]、Mallat分解法[6]、文献[23]和文献[11]所提算法被用来与本文算法进行对比分析。由于多方向非抽样对偶树复小波变换的分解级数对处理结果有一定的影响, 分解级数较少时, 薄云图像的低频子带中携带较多的地物细节信息, 对低频子带的处理会损伤地物的边缘, 分解级数较多时, 薄云图像的高频子带中携带较多的薄云信息, 对高频子带的增强处理会增大云噪声, 因此分解级数一般为3~5级, 本文采用较为适中的4级分解。
2.1 模拟薄云图像试验由于薄云图像中的地物信息模糊, 为了对不同方法恢复地物信息的效果进行定量评价, 选取两幅不同时相的南京市无云遥感图像, 将薄云叠加到无云遥感图像获得模拟薄云图像, 见图 3, 其中目标图像获取时间为2017年2月18日, 源域图像获取时间为2017年3月6日。不同方法恢复地物信息的结果见图 4。

|
| 图 3 南京市多光谱图像 Fig. 3 Multi spectral images of Nanjing |
本文选用空间频率、平均梯度、峰值信噪比、偏差指数和结构相似度5个指标对不同方法恢复地物信息的效果进行定量评价。
(1) 空间频率(SF)定义为
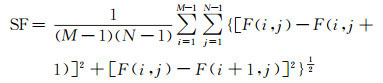 (27)
(27)
式中, F(i, j)表示地物信息恢复图像F在点(i, j)的灰度值, 空间频率值越大表明图像越清晰, 空间质量越好。
(2) 平均梯度(AG)定义为
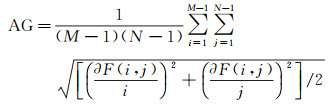 (28)
(28)
式中: 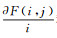
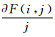
(3) 峰值信噪比(PSNR)定义为
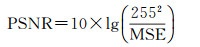 (29)
(29)
式中, MSE为源图像与地物信息恢复图像之间的均方误差。峰值信噪比指标可用来衡量算法的抗噪声的能力, 峰值信噪比越大, 表示去噪能力越强。
(4) 偏差指数(DI)定义为
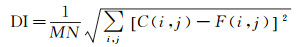 (30)
(30)
式中, C(i, j)为源图像在点(i, j)的灰度值。偏差指数反映地物信息恢复图像与源图像之间的背离程度, 其值越小则偏差越小, 所得结果越优。
(5) 结构相似度(SSIM)定义为
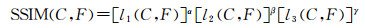 (31)
(31)
式中, l1(C, F)描述的是亮度比较, 其表达式为
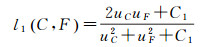 (32)
(32)
l2(C, F)描述的是对比度比较, 其表达式为
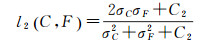 (33)
(33)
l3(C, F)描述的是结构比较, 其表达式为
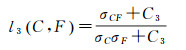 (34)
(34)
式中, uC和uF分别表示去云前后图像的均值; σC和σF为去云前后图像的方差; σCF为去云前后图像的协方差, C1、C2、C3为自行设定的3个较小的常量, 本文中参数α=-1、β=-1和γ=1。图像与源图像结构相似度越高, 薄云去除效果越好[23]。
不同方法恢复地物信息的定量评价指标如表 1所示。
| 引导滤波法 | 迁移学习法 | 同态滤波法 | Mallat分解法 | 文献[23]算法 | 文献[11]算法 | 本文算法 | |
| SF | 20.634 3 | 14.692 8 | 7.282 2 | 16.705 0 | 17.245 8 | 17.398 6 | 19.364 5 |
| AG | 14.590 7 | 10.389 4 | 5.149 3 | 11.812 2 | 12.194 6 | 12.302 7 | 13.692 8 |
| PSNR | 71.686 6 | 72.213 2 | 73.068 2 | 82.254 4 | 64.815 0 | 73.068 2 | 82.316 2 |
| DI | 0.110 2 | 0.082 6 | 0.060 1 | 0.061 4 | 0.062 5 | 0.075 0 | 0.058 2 |
| SSIM | 0.875 1 | 0.953 6 | 0.717 5 | 0.870 3 | 0.826 3 | 0.772 0 | 0.967 3 |
从表 1中可以看出, 本文算法的峰值信噪比指标和结构相似度指标都高于其他6种方法, 空间频率指标和平均梯度指标低于引导滤波法但高于其他5种方法, 引导滤波法恢复地物信息的结果图像含有较多的残留薄云造成其空间频率指标和平均梯度指标较高, 而本文算法去除薄云较为彻底, 所获得的地物信息恢复图像保留了目标图像中更多的地物信息。本文算法的偏差指数指标低于其他6种方法, 说明本文算法恢复的地物信息失真度更小, 地物信息的恢复效果更好。
2.2 真实薄云图像试验图 5所示为丽江市多光谱图像, 其中目标图像获取时间为2016年3月18日, 源域图像获取时间为2016年5月5日。图 7所示为西安市多光谱图像, 其中目标图像获取时间为2016年8月29日, 源域图像获取时间为2016年7月28日。图 5(a)选取的目标图像有少量薄云, 图 7(a)选取的目标图像有大量薄云。不同方法恢复地物信息的结果如图 6和图 8所示。

|
| 图 5 丽江市多光谱图像 Fig. 5 Multi spectral images of Lijiang city |

|
| 图 7 西安市多光谱图像 Fig. 7 Multi spectral images of Xi'an |
从图 6和图 8可以看出, 引导滤波法、Mallat分解法和文献[23]算法能增强地物信息, 但残留了部分薄云。迁移学习法和文献[11]算法能去除大部分云信息, 但是地物信息有一定的损伤。同态滤波法能去除一部分薄云信息, 但对稍厚的云层去除效果不佳, 且地物信息损失较重。本文算法恢复地物信息后的图像更加清晰和流畅。
为了更好地评价不同方法恢复地物信息的效果, 本文借助ENVI的光谱库, 将地物恢复图像中各地物的光谱反射率与光谱库中各地物光谱反射率进行比较, 选择光谱反射率误差指标对真实图像试验进行定量评价。光谱反射率误差SRE的计算公式如下[8]
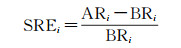 (35)
(35)
式中, AR和BR分别是地物恢复图像中各地物的光谱反射率和ENVI光谱库中各地物光谱反射率; i代表地物类别。
分别选取植被、土壤、岩石和村庄各100个样本点, 根据式(35)计算不同方法恢复地物的平均光谱反射率误差, 见图 9和图 10。可以看出, 本文算法恢复地物的平均光谱反射率误差最小, 地物信息恢复效果相较于其他6种方法更好。
3 结论
由于遥感图像中的地物与薄云一般占用不同的频带, 利用多方向非抽样对偶树复小波变换对薄云遥感图像进行多分辨率分解后, 图像中的地物信息主要分布在高频子带, 薄云信息主要分布在低频子带。通过对高频子带的地物细节信息进行增强, 对低频子带的薄云信息进行抑制, 能有效恢复薄云图像中的地物信息。本文分别采用支持向量引导滤波方法和域自适应的迁移学习方法处理薄云图像的低频子带。由于支持向量回归模型具有强泛化能力, 用支持向量引导滤波代替线性引导滤波, 所获得的滤波输出图像既能保持地物细节信息又能有效去除图像噪声, 获得好的泛化性能。而迁移学习方法是解决训练样本与测试样本分布不一致问题的有效方法, 利用迁移学习能使得可利用的多源多时相遥感图像范围大大扩展。本文利用融合法综合了支持向量引导滤波和迁移学习方法恢复地物信息的优势, 因而能更好地恢复薄云遥感图像中的地物信息, 获得较好的地物信息恢复效果。
| [1] | CAI Wenting, LIU Yongxue, LI Manchun, et al. A Self-adaptive Homomorphic Filter Method for Removing Thin Cloud[C]//Proceedings of 201119th International Conference on Geoinformatics. Shanghai: IEEE, 2011: 1-4. |
| [2] | WU Xiaoping, YANG Wunian, LI Guoming. Thin Cloud Removal of ZY-3 Image based on Improved Homomorphism Filtering Method[C]//Proceedings of 201321st International Conference on Geoinformatics. Kaifeng: IEEE, 2013: 1-4. |
| [3] | WANG Xia, LI Minmin, TANG Hongmei. A Modified Homomorphism Filtering Algorithm for Cloud Removal[C]//Proceedings of 2010 International Conference on Computational Intelligence and Software Engineering. Wuhan: IEEE, 2010: 1-4. |
| [4] | SHEN Huandeng, LI Huifang, QIAN Yan, et al. An Effective Thin Cloud Removal Procedure for Visible Remote Sensing Images[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 96: 224–235. DOI:10.1016/j.isprsjprs.2014.06.011 |
| [5] | ZHU Xifang, WU Feng, TAO Chunkan. A New Algorithm of Cloud Removing for Optical Images Based on Wavelet Threshold Theory[J]. Acta Photonica Sinica, 2009, 38(12): 3312–3317. |
| [6] | ZHU Xifang, WU Feng, ZHUANG Yanbin. An Improved Approach to Remove Cloud and Mist from Remote Sensing Digital Images Based on Mallat Algorithm[J]. Journal of Remote Sensing, 2007, 11(2): 241–246. |
| [7] |
梁栋, 孔颉, 胡根生, 等.
基于支持向量机的遥感影像厚云及云阴影去除[J]. 测绘学报, 2012, 41(2): 225–331, 238.
LIANG Dong, KONG Jie, HU Gensheng, et al. The Removal of Thick Cloud and Cloud Shadow of Remote Sensing Image Based on Support Vector Machine[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 225–331, 238. |
| [8] | HU Gensheng, LI Xiaoyi, LIANG Dong. Thin Cloud Removal from Remote Sensing Images Using Multidirectional Dual Tree Complex Wavelet Transform and Transfer Least Square Support Vector Regression[J]. Journal of Applied Remote Sensing, 2015, 9(1): 095053. DOI:10.1117/1.JRS.9.095053 |
| [9] | JEDLOVEC G J, HAINES S L, LAFONTAINE F J. Spatial and Temporal Varying Thresholds for Cloud Detection in GOES Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(6): 1705–1717. DOI:10.1109/TGRS.2008.916208 |
| [10] | EL-ARABY E, EL-GHAZAWI T, LE MOIGNE J, et al. Reconfigurable Processing for Satellite on-Board Automatic Cloud Cover Assessment[J]. Journal of Real-Time Image Processing, 2009, 4(3): 245–259. DOI:10.1007/s11554-008-0107-8 |
| [11] | SHEN Yang, WANG Yong, LV Haitao, et al. Removal of Thin Clouds in Landsat-8 OLI Data with Independent Component Analysis[J]. Remote Sensing, 2015, 7(9): 11481–11500. DOI:10.3390/rs70911481 |
| [12] | GABARDA S, CRIST? BAL G. Cloud Covering Denoising through Image Fusion[J]. Image and Vision Computing, 2007, 25(5): 523–530. DOI:10.1016/j.imavis.2006.03.007 |
| [13] | YANG Jun, ZHAO Zhongming, MA Jianglin, et al. Image Fusion for Automatic Detection and Removal of Clouds and Their Shadows[C]//Proceedings of SPIE Volume 6419, Geoinformatics 2006: Remotely Sensed Data and Information. Wuhan: SPIE, 2006, 6419: 64191X. |
| [14] | MENG Xiangchao, SHEN H, YUAN Qiangqiang, et al. An Integrated Fusion Framework for Joint Information Reconstruction and Resolution Enhancement[J]. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2017, 42: 831–835. |
| [15] |
许宁, 肖新耀, 尤红建, 等.
HCT变换与联合稀疏模型相结合的遥感影像融合[J]. 测绘学报, 2016, 45(4): 434–441.
XU Ning, XIAO Xinyao, YOU Hongjian, et al. A Pansharpening Method based on HCT and Joint Sparse Model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 434–441. DOI:10.11947/j.AGCS.2016.20150372 |
| [16] | KINGSBURY N Q, Kingsbury N. The Dual-Tree Complex Wavelet Transform: A New Technique for Shift Invariance and Directional Filters[C]//Proceedings of the 8th IEEE Digital Signal Processing Workshop. Bryce Canyon: IEEE. 1998: 2543-2560. |
| [17] | CELIK T, TJAHJADI T. Image Resolution Enhancement Using Dual-tree Complex Wavelet Transform[J]. IEEE Geoscience and Remote Sensing Letters, 2010, 7(3): 554–557. DOI:10.1109/LGRS.2010.2041324 |
| [18] |
胡根生, 査慧敏, 梁栋, 等.
结合分类与迁移学习的薄云覆盖遥感图像地物信息恢复[J]. 电子学报, 2017, 45(12): 2856–2862.
HU Gensheng, ZHA Huimin, LIANG Dong, et al. Ground Object Information Recovery for Thin Cloud Contaminated Remote Sensing Images by Combining Classification with Transfer Learning[J]. Acta Electronica Sinica, 2017, 45(12): 2856–2862. |
| [19] | HE Kaiming, SUN Jian, TANG Xiaoou. Guided Image Filtering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(6): 1397–1409. DOI:10.1109/TPAMI.2012.213 |
| [20] | HE Kaiming, SUN Jian, TANG Xiaoou. Single Image Haze Removal Using Dark Channel Prior[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(12): 2341–2353. DOI:10.1109/TPAMI.2010.168 |
| [21] | PAN S J, YANG Qiang. A Survey on Transfer Learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2010, 22(10): 1345–1359. DOI:10.1109/TKDE.2009.191 |
| [22] | LAINE A F, ZONG Xuli. Multiscale Suboctave Wavelet Transform for Denoising and Enhancement[C]//Proceedings of SPIE Volume 2825, Wavelet Applications in Signal and Image Processing Ⅳ. Denver, CO: SPIE, 1996, 2825: 238-249. |
| [23] | KONG Jie, HU Gensheng, LIANG Dong. Thin Cloud Removing Approach of Color Remote Sensing Image based on Support Vector Machine[C]//Proceedings of 2010 Asia-Pacific Conference on Wearable Computing Systems. Shenzhen: IEEE, 2010: 131-135. |
| [24] | HU Gensheng, SUN Xiaoqi, LIANG Dong, et al. Cloud Removal of Remote Sensing Image based on Multi-Output Support Vector Regression[J]. Journal of Systems Engineering and Electronics, 2014, 25(6): 1082–1088. DOI:10.1109/JSEE.2014.00124 |
| [25] | DONOHO D L. De-noising by Soft-thresholding[J]. IEEE Transactions on Information Theory, 1995, 41(3): 613–627. DOI:10.1109/18.382009 |
| [26] | HASHEMI M, BEHESHTI S. Adaptive Noise Variance Estimation in Bayes Shrink[J]. IEEE Signal Processing Letters, 2010, 17(1): 12–15. DOI:10.1109/LSP.2009.2030856 |
| [27] |
胡根生, 梁栋, 孔颉.
基于支持向量值轮廓波变换的遥感影像融合[J]. 电子学报, 2010, 38(6): 1287–1292.
HU Gensheng, LIANG Dong, KONG Jie. Remote Sensing Image Fusion Based on Support Vector Value Contourlet Transform[J]. Acta Electronica Sinica, 2010, 38(6): 1287–1292. |