2. 宇航动力学国家重点实验室, 陕西 西安 710043;
3. 西安卫星测控中心, 陕西 西安 710043
2. State Key Laboratory of Astronautic Dynamics, Xi'an 710043, China;
3. Xi'an Satellite Control Center, Xi'an 710043, China
精密卫星轨道能够为用户导航定位提供高精度的空间基准, 轨道精度是衡量卫星导航系统服务能力的重要性能指标[1]。北斗卫星精密定轨方法按照使用的数据来划分可分为[2]仅依靠北斗数据的单系统定轨[3-7]和多系统数据融合处理[8-14]。第1类方法不需要其他导航系统观测数据, 数据处理复杂度小, 但在北斗导航系统全球组网尚未完成, 地面观测站较少的情况下, 定轨精度受限。第2类方法能有效借助成熟GNSS系统对北斗卫星轨道参数形成更强的约束, 提高对流层、测站坐标等公共参数解算精度, 进而有效提高北斗定轨精度。
固定载波相位双差模糊度在导航卫星精密定轨过程中同样至关重要, 它能显著提高导航卫星的定轨精度[15-17]。然而, 由于北斗卫星本身诸多限制因素, 特别是IGSO和GEO[18]卫星高轨、观测几何构型不佳[19]、非常缓慢的相对地面运动等, 北斗模糊度固定效果并不理想[20]。因此多数学者在研究北斗精密定轨时都采用浮点解, 对北斗模糊度固定方法鲜有提及。随着北斗系统的发展, 包含有效BDS观测数据的MGEX测站从原来的30多个增加到80多个, 一定程度上改善了北斗系统的观测条件, 也为北斗模糊度固定创造了条件。
本文探讨了利用全球实测的GPS/GLONASS/BDS/Galileo多模接收机双差数据实现多GNSS融合精密定轨方法, 并与北斗单系统定轨结果进行比较, 分析多系统融合解算对提高北斗定轨精度的影响。同时, 针对北斗导航系统特点, 给出了有别于GPS的北斗双差模糊度固定策略, 并分析比较模糊度固定对北斗定轨精度的影响。
1 北斗卫星多系统融合精密定轨 1.1 双差解算模型GNSS观测值中一般采用两种最基本的观测量, 即伪距和载波相位观测值。对于多系统融合定轨, 多模接收机采集的是多个导航系统多频的码和相位数据, 载波相位和伪距码观测值基本非差观测方程[21]可简写为
 (1)
(1)
式中, 下标F表示频率, i表示卫星, k表示测站; LF, ki为载波相位观测值(以距离表示); PF, ki为伪距观测值; ρki为站星几何距离; λF为相应频率波长; NF, ki为模糊度; δk为接收机钟差; δi为卫星钟差; IF, ki为电离层延迟; Tki为对流层延迟; εΦ和εP分别为载波相位和伪距的多路径、测量噪声等影响。
通过将观测数据二次差分, 可以形成双差观测数据。双差观测数据可以用式(2)表达
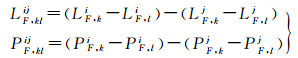 (2)
(2)
在精密定轨中, 采用相位和伪距消电离层组合, 其双差观测方程可表示为
 (3)
(3)
式中, BCklij为宽窄巷相位模糊度组合。
1.2 数据处理流程本文主要讨论基于GPS/GLONASS/BDS/Galileo多系统数据融合的北斗卫星双差动力学精密定轨方法。多GNSS两步法精密定轨流程如下:
(1) 将IGS、MGEX跟踪网的GPS和GLONASS数据联合处理, 形成GPS和GLONASS混合双差, 解算GPS和GLONASS卫星轨道, 估计测站坐标、对流层参数和地球自转参数;
(2) 将MGEX的4系统数据联合处理, 形成4个卫星系统混合双差, 引入并固定上一步解算得到的GPS和GLONASS卫星轨道、地球自转参数、测站坐标和对流层参数, 解算BDS卫星轨道。

|
| 图 1 多系统融合精密定轨流程 Fig. 1 Flow chart of multi-GNSS integrated precise orbit determination |
| 类别 | 模型和参数 |
| 观测量 | 消电离层伪距(只含BDS数据)和 相位双差观测量 |
| 截止高度角 | 3° |
| 采样间隔 | 300 s |
| 码和相位数据权重比 | 1:100 |
| 模糊度 | S1, S2:浮点解 S3, S4:固定解 |
| 接收机天线相位中心 | PCO&PCV(igs08) |
| 卫星天线相位中心 | PCO&PCV(igs08) |
| 对流层 | GPT+GMF |
| 卫星/接收机钟差 | 双差消除 |
| 测站坐标 | S1:IGS14先验坐标, 最小约束解 S2, S3, S4:固定为GPS解算的测站坐标 |
| 初始轨道 | BDS广播星历 |
| 太阳光压 | ECOM模型 |
| 重力场 | EGM2008_SMALL |
| 质心引力 | DE405 |
| 潮汐改正 | solid earth, pole tide, ocean loading (IERS 2010) |
| 轨道动力学参数 | 6个卫星状态参数+9个光压参数 |
| 定轨弧长 | 3 d |
2 双差模糊度固定
模糊度固定策略[22]是指根据基线长度、观测数据类型和时长确定合适的频率线性组合和模糊度固定算法。图 2中实线框部分是Bernese 5.2版本软件推荐的GPS系统模糊度固定策略, 具体说明见表 2。

|
| 图 2 模糊度固定流程 Fig. 2 Flow chart of ambiguity fixing |
| 流程步骤 | 模糊度固定算法 | 频率组合 | 使用数据 |
| L1/L2模糊度固定 | SIGMA | L1&L2 | 相位 |
| L5宽巷模糊度固定 | SIGMA | L5(宽巷组合) | 相位 |
| MW宽巷模糊度固定 | SIGMA | MW | 相位+码 |
| L3窄巷模糊度固定 | SIGMA | L3(无电离层延迟组合) | 相位 |
| QIF模糊度固定 | QIF | L1&L2 | 相位 |
对于BDS系统, 由于GEO卫星“静地”特性引起的较差的观测几何结构和较大的轨道迹向误差, 且卫星迹向轨道分量与双差模糊度强相关, GEO卫星模糊度固定较为困难。借鉴文献[23—25]建议, 为避免GEO卫星模糊度固定对定轨精度可能带来的负面影响, 本文在模糊度固定时不考虑GEO卫星, 只固定IGSO和MEO卫星双差模糊度。BDS系统模糊度固定策略在GPS基础上增加图 2所示虚线框中的步骤, 即对于长基线(>200 km)增加了L5宽巷模糊度固定步骤。试验表明, 增加此步骤后, 长基线模糊度固定成功率大幅提高(具体见下节算例分析), 有效改善了BDS模糊度固定整体效果。
3 算例分析本文采用全球分布的IGS(约90个站)和MGEX(Multi-GNSS Experiment)(约80个站)跟踪网2017年年积日70—81共12 d的多模观测数据进行试验分析。处理中以3 d数据为一个定轨弧段, 共形成10个定轨弧段, 采用单天重叠弧段比较作为定轨精度评定依据, 即一个定轨弧段的第3 d轨道与后续一个定轨弧段的第2 d轨道重叠比较, 如图 3所示。

|
| 图 3 重叠弧段轨道差值比较方法 Fig. 3 Method of overlapped-arc comparison |
为比较单系统和多系统融合两种处理方法在精密定轨精度上的优劣, 分析双差模糊度固定对精密定轨精度的影响, 分别采取如下4种方案进行定轨实验:方案1(S1), BDS单系统精密定轨; 方案2(S2), 多GNSS融合实现BDS精密定轨; 方案3(S3), 模糊度固定(采用Bernese 5.2推荐策略)的多GNSS融合实现BDS精密定轨; 方案4(S4), 模糊度固定(采用本文优化策略)的多GNSS融合实现BDS精密定轨。表 3给出了4种定轨方案下各卫星在所有9 d重叠弧段上径向(R)、切向(T)、法向(N)和三维位置(P)轨道差值的平均RMS情况。为方便比较分析, 图 4给出了其图示形式。
| m | ||||||||||||||||||||
| 卫星类型 | PRN | R | T | N | P(3D) | |||||||||||||||
| S1 | S2 | S3 | S4 | S1 | S2 | S3 | S4 | S1 | S2 | S3 | S4 | S1 | S2 | S3 | S4 | |||||
| GEO | C01 | 0.063 | 0.078 | 0.080 | 0.075 | 0.414 | 0.284 | 0.307 | 0.311 | 0.101 | 0.069 | 0.071 | 0.091 | 0.431 | 0.302 | 0.325 | 0.333 | |||
| C02 | 0.025 | 0.053 | 0.050 | 0.031 | 1.030 | 1.091 | 1.054 | 0.912 | 0.081 | 0.064 | 0.060 | 0.066 | 1.034 | 1.094 | 1.056 | 0.915 | ||||
| C03 | 0.028 | 0.036 | 0.035 | 0.041 | 0.280 | 0.415 | 0.425 | 0.466 | 0.082 | 0.053 | 0.051 | 0.067 | 0.293 | 0.420 | 0.429 | 0.473 | ||||
| C04 | 0.064 | 0.086 | 0.086 | 0.087 | 0.595 | 0.247 | 0.236 | 0.364 | 0.103 | 0.089 | 0.089 | 0.106 | 0.607 | 0.276 | 0.267 | 0.389 | ||||
| C05 | 0.033 | 0.153 | 0.154 | 0.042 | 0.719 | 1.184 | 1.008 | 0.552 | 0.067 | 0.083 | 0.084 | 0.090 | 0.723 | 1.197 | 1.023 | 0.561 | ||||
| mean | 0.046 | 0.091 | 0.091 | 0.059 | 0.661 | 0.762 | 0.701 | 0.563 | 0.088 | 0.073 | 0.072 | 0.085 | 0.668 | 0.771 | 0.710 | 0.572 | ||||
| IGSO | C06 | 0.021 | 0.026 | 0.031 | 0.015 | 0.183 | 0.109 | 0.066 | 0.032 | 0.153 | 0.085 | 0.070 | 0.036 | 0.240 | 0.141 | 0.101 | 0.050 | |||
| C07 | 0.019 | 0.010 | 0.020 | 0.016 | 0.140 | 0.031 | 0.057 | 0.025 | 0.151 | 0.034 | 0.057 | 0.029 | 0.207 | 0.047 | 0.083 | 0.041 | ||||
| C08 | 0.026 | 0.019 | 0.014 | 0.014 | 0.159 | 0.070 | 0.046 | 0.024 | 0.143 | 0.031 | 0.046 | 0.033 | 0.216 | 0.079 | 0.067 | 0.043 | ||||
| C09 | 0.022 | 0.020 | 0.018 | 0.018 | 0.162 | 0.070 | 0.053 | 0.025 | 0.144 | 0.050 | 0.052 | 0.032 | 0.218 | 0.088 | 0.076 | 0.044 | ||||
| C10 | 0.025 | 0.016 | 0.020 | 0.016 | 0.154 | 0.042 | 0.057 | 0.034 | 0.157 | 0.036 | 0.052 | 0.040 | 0.221 | 0.058 | 0.080 | 0.055 | ||||
| C13 | 0.021 | 0.034 | 0.020 | 0.018 | 0.179 | 0.094 | 0.064 | 0.032 | 0.139 | 0.051 | 0.045 | 0.034 | 0.227 | 0.112 | 0.081 | 0.050 | ||||
| mean | 0.022 | 0.022 | 0.021 | 0.016 | 0.163 | 0.074 | 0.058 | 0.029 | 0.148 | 0.051 | 0.054 | 0.034 | 0.222 | 0.093 | 0.082 | 0.048 | ||||
| MEO | C11 | 0.030 | 0.015 | 0.019 | 0.017 | 0.117 | 0.046 | 0.053 | 0.050 | 0.081 | 0.038 | 0.049 | 0.028 | 0.145 | 0.061 | 0.074 | 0.059 | |||
| C12 | 0.033 | 0.015 | 0.016 | 0.017 | 0.141 | 0.060 | 0.042 | 0.037 | 0.102 | 0.030 | 0.034 | 0.041 | 0.177 | 0.069 | 0.057 | 0.058 | ||||
| C14 | 0.046 | 0.037 | 0.055 | 0.031 | 0.174 | 0.141 | 0.129 | 0.060 | 0.078 | 0.047 | 0.047 | 0.038 | 0.197 | 0.153 | 0.148 | 0.078 | ||||
| mean | 0.037 | 0.025 | 0.035 | 0.023 | 0.146 | 0.093 | 0.084 | 0.050 | 0.088 | 0.039 | 0.044 | 0.036 | 0.174 | 0.103 | 0.100 | 0.066 | ||||

|
| 图 4 北斗卫星定轨精度对比 Fig. 4 Comparison of BeiDou satellites orbit precision |
(1) 在方案1中, GEO、IGSO和MEO卫星3维定轨平均精度分别达到0.668 m、0.222 m和0.174 m; 在方案2中分别达到0.771 m、0.093 m和0.103 m。可以看出相比单系统定轨, 多系统融合定轨对IGSO和MEO卫星定轨精度改进作用明显, 且R、T、N方向上精度均有所提高。对于GEO卫星, 方案2与方案1定轨精度量级相当, 在R方向和T方向有所降低, 这是因为GEO卫星的“静止”特性决定了它的精密定轨需要引入码数据, 而本文在轨道解算时采用的码数据只包含BDS系统, GEO卫星码数据只能在系统内组差, 所以本文的多系统融合定轨对GEO定轨精度提升并无帮助。
(2) 在方案3中, 通过对IGSO和MEO卫星双差模糊度固定, 其T方向精度相比方案2有所提高, 但是由于方案3采取的模糊度固定策略固定成功率不高, 对3维轨道精度提高并不明显, 其3维轨道精度与方案2大体相当。
(3) 在方案4中, 采用优化策略对IGSO和MEO卫星双差模糊度进行固定, 其三维定轨精度分别达到0.048 m和0.066 m, 相比方案2精度分别提高48%和36%。IGSO卫星R、T、N方向精度分别达到0.016 m、0.029 m和0.034 m, 比方案2分别提高27%、61%和33%;MEO卫星分别达到0.023 m、0.050 m和0.036 m, 提高8%、46%和8%。由此可见, 模糊度固定能有效提高卫星定轨精度, 特别是对T方向精度改进效果尤为明显。由于并未固定GEO卫星模糊度, 因此其定轨精度与方案2相当。
(4) 方案4与方案3相比, IGSO和MEO卫星三维定轨平均精度分别提高41%和34%, 这主要归功于改进的模糊度固定策略提高了模糊度固定成功率。
分析模糊度固定效果, 表 4统计了不同模糊度固定策略解算的年积日74 d-76 d的模糊度固定结果。
| 日期 | 基线长度/km | 固定前模糊度数 | 固定后模糊度数 | 固定率/(%) | |||
| Bernese 5.2推荐策略 | 优化策略 | Bernese 5.2推荐策略 | 优化策略 | ||||
| 74 | < 20 | 71 | 5 | 5 | 93.0 | 93.0 | |
| 20~200 | 149 | 36 | 36 | 75.8 | 75.8 | ||
| 200~2000 | 874 | 550 | 318 | 37.1 | 63.6 | ||
| >2000 | 303 | 233 | 193 | 23.1 | 36.3 | ||
| total | 1397 | 824 | 552 | 41.0 | 60.5 | ||
| 75 | < 20 | 77 | 6 | 6 | 92.2 | 92.2 | |
| 20~200 | 140 | 21 | 21 | 85.0 | 85.0 | ||
| 200~2000 | 877 | 533 | 305 | 39.2 | 65.2 | ||
| >2000 | 347 | 283 | 228 | 18.4 | 34.3 | ||
| total | 1441 | 843 | 560 | 41.5 | 61.1 | ||
| 76 | < 20 | 81 | 5 | 5 | 93.8 | 93.8 | |
| 20~200 | 112 | 21 | 21 | 81.3 | 81.3 | ||
| 200~2000 | 601 | 348 | 188 | 42.1 | 68.7 | ||
| >2000 | 226 | 187 | 147 | 17.3 | 35.0 | ||
| total | 1020 | 561 | 361 | 45.0 | 64.6 | ||
由表 4可见, 采用本文的模糊度固定策略, IGSO和MEO卫星模糊度固定率整体达到60%以上。200 km以上的长基线固定率达到50%以上, 相比策略改进前提高20%左右。
4 结论本文研究了北斗卫星多系统融合定轨方法和双差模糊度固定策略, 并利用实测数据进行了对比分析。
(1) 多系统融合定轨能有效改进IGSO和MEO卫星定轨精度, 各方向分量重叠轨道精度(模糊度浮点解)均优于10 cm, 相比于单系统定轨, 轨道精度平均提高一倍以上。但对于GEO卫星, 多系统融合处理并无优势。
(2) 根据试验数据分析, 对原有模糊度固定策略进行了优化, 提出了适合北斗卫星的模糊度固定策略, 使IGSO和MEO卫星200 km以上基线模糊度固定率从30%提高到50%以上, 整体固定率达到60%以上。但是, 相比较而言, 2000 km以上长基线模糊度固定率仍然不高, 只有35%左右, 如何提高长基线模糊度固定率还有待进一步深入研究。
(3) 模糊度固定是影响定轨精度的重要因素。采用本文策略对IGSO和MEO卫星双差模糊度固定后, 定轨精度在多系统融合处理模糊度浮点解基础上有明显改进, 各方向分量重叠轨道精度均优于5 cm, 特别是T方向轨道精度提高近一倍。
(4) 改变模糊度固定策略后北斗模糊度固定率得到较大幅度提升的机理目前尚不明确, 还需要后续做进一步研究。
| [1] |
杨元喜.
北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6.
YANG Yuanxi. Progress, Contribution and Challenges of Compass/Beidou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1–6. |
| [2] |
刘伟平, 郝金明, 魏伟, 等.
两种北斗卫星精密定轨方法的对比[J]. 大地测量与地球动力学, 2016, 36(3): 211–215.
LIU Weiping, HAO Jinming, WEI Wei, et al. Comparison of Two Methods of Precise Orbit Determination of BeiDou Satellites[J]. Journal of Geodesy and Geodynamics, 2016, 36(3): 211–215. |
| [3] | STEIGENBERGER P, HUGENTOBLER U, HAUSCHILD A, et al. Orbit and Clock Analysis of Compass GEO and IGSO Satellites[J]. Journal of Geodesy, 2013, 87(6): 515–525. DOI:10.1007/s00190-013-0625-4 |
| [4] | GE Maorong, ZHANG Hongping, JIA Xiaolin, et al. What is Achievable with the Current Compass Constellation[J]. GPS World, 2012, 23(1): 29–34. |
| [5] | ZHOU Shanshi, HU Xiaogong, WU Bin, et al. Orbit Determination and Time Synchronization for a GEO/IGSO Satellite Navigation Constellation with Regional Tracking Network[J]. Science China Physics, Mechanics and Astronomy, 2011, 54(6): 1089–1097. DOI:10.1007/s11433-011-4342-9 |
| [6] | ZHU Jun, WANG Jiasong, ZENG Guang, et al. Precise Orbit Determination of BeiDou Regional Navigation Satellite System Via Double-difference Observations[M]//SUN Jiadong, JIAO Wenhai, WU Haitao, et al. China Satellite Navigation Conference (CSNC) 2013 Proceedings. Berlin Heidelberg: Springer, 2013: 77-88. |
| [7] | ZHAO Qile, GUO Jing, LI Min, et al. Initial Results of Precise Orbit and Clock Determination for COMPASS Navigation Satellite System[J]. Journal of Geodesy, 2013, 87(5): 475–486. DOI:10.1007/s00190-013-0622-7 |
| [8] |
施闯, 赵齐乐, 李敏, 等.
北斗卫星导航系统的精密定轨与定位研究[J]. 中国科学:地球科学, 2012, 55(7): 1079–1086.
SHI Chuang, ZHAO Qile, LI Min, et al. Precise Orbit Determination of BeiDou Satellites with Precise Positioning[J]. Science China Earth Sciences, 2012, 55(7): 1079–1086. |
| [9] | MAO Yue, DU Yu, SONG Xiaoyong, et al. GEO and IGSO Joint Precise Orbit Determination[J]. Science China Physics, Mechanics and Astronomy, 2011, 54(6): 1009–1013. DOI:10.1007/s11433-011-4343-8 |
| [10] | LI Min, ZHAO Qile, SHI Chuang, et al. Precise Orbit Determination of BeiDou Satellites Based on BeiDou/GPS Data[C]//第三届中国卫星导航学术年会电子文集—S03精密定轨与精密定位. 北京: 第三届中国卫星导航学术年会, 2012: 1-10. |
| [11] |
李敏. 多模GNSS融合精密定轨理论及其应用研究[D]. 武汉: 武汉大学, 2011: 30-58. LI Min. Research on Multi-GNSS Precise Orbit Determination Theory and Application[D]. Wuhan: Wuhan University, 2011: 30-58. |
| [12] | MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P, et al. Initial Assessment of the COMPASS/BeiDou-2 Regional Navigation Satellite System[J]. GPS Solutions, 2013, 17(2): 211–222. DOI:10.1007/s10291-012-0272-x |
| [13] |
刘伟平, 郝金明, 李建文, 等.
多GNSS融合的北斗卫星精密定轨[J]. 测绘学报, 2014, 43(11): 1132–1138, 1143.
LIU Weiping, HAO Jinming, LI Jianwen, et al. Multi-GNSS Joint Precise Orbit Determination of BeiDou Navigation Satellite System[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1132–1138, 1143. DOI:10.13485/j.cnki.11-2089.2014.0186 |
| [14] | STEIGENBERGER P, HUGENTOBLER U, HAUSCHILD A, et al. Orbit and Clock Analysis of Compass GEO and IGSO Satellites[J]. Journal of Geodesy, 2013, 87(6): 515–525. DOI:10.1007/s00190-013-0625-4 |
| [15] | MERBART L. Ambiguity Resolution Techniques in Geodetic and Geodynamic Applications of the Global Positioning System[D]. Berne: University of Berne, 1995. |
| [16] | GE Maorong, GENDT G, DICK G, et al. Improving Carrier-phase Ambiguity Resolution in Global GPS Network Solutions[J]. Journal of Geodesy, 2005, 79(1/3): 103–110. |
| [17] | GE Maorong, GENDT G, ROTHACHER M, et al. Resolution of GPS Carrier-phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations[J]. Journal of Geodesy, 2008, 82(7): 389–399. DOI:10.1007/s00190-007-0187-4 |
| [18] |
杜兰. GEO卫星精密定轨技术研究[D]. 郑州: 解放军信息工程大学, 2006: 1-6. DU Lan. A Study on the Precise Orbit Determination of Geostationary Satellites[D]. Zhengzhou: The PLA Information Engineering University, 2006: 1-6. |
| [19] |
文援兰, 柳其许, 朱俊, 等.
测控站布局对区域卫星导航系统的影响[J]. 国防科技大学学报, 2007, 29(1): 1–6.
WEN Yuanlan, LIU Qixu, ZHU Jun, et al. The Effect of TT&C Deployment on the Regional Satellite Navigation System[J]. Journal of National University of Defense Technology, 2007, 29(1): 1–6. |
| [20] |
刘伟平, 郝金明, 田英国, 等.
北斗卫星导航系统双差动力法精密定轨及其精度分析[J]. 测绘学报, 2016, 45(2): 131–139.
LIU Weiping, HAO Jinming, TIAN Yingguo, et al. Solution Method and Precision Analysis of Double-difference Dynamic Precise Orbit Determination of BeiDou Navigation Satellite System[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(2): 131–139. DOI:10.11947/j.AGCS.2016.20150190 |
| [21] | DACH R, LUTZ S, WALSER P, et al. Bernese GNSS Software Version 5.2[M]. Bern: University of Bern, 2015. |
| [22] |
刘经南, 邓辰龙, 唐卫明.
GNSS整周模糊度确认理论方法研究进展[J]. 武汉大学学报(信息科学版), 2014, 39(9): 1009–1016.
LIU Jingnan, DENG Chenlong, TANG Weiming. Review of GNSS Ambiguity Validation Theory[J]. Geomatics and Information Science of Wuhan University, 2014, 39(9): 1009–1016. |
| [23] | HE Lina, GE Maorong, WANG Jiexian, et al. Experimental Study on the Precise Orbit Determination of the BeiDou Navigation Satellite System[J]. Sensors, 2013, 13(3): 2911–2928. DOI:10.3390/s130302911 |
| [24] | GE Maorong, ZHANG Hongping, JIA Xiaolin, et al. What is Achievable with the Current Compass Constellation?[J]. GPS World, 2012, 23(1): 29–34. |
| [25] | LIU Yang, LOU Yidong, SHI Chuang, et al. BeiDou Regional Navigation System Network Solution and Precision Analysis[M]//SUN Jiadong, JIAO Wenhai, WU Haitao, et al. China Satellite Navigation Conference (CSNC) 2013 Proceedings. Berlin Heidelberg: Springer, 2013: 173-186. |



