2. 地球空间信息技术协同创新中心, 湖北 武汉 430079
2. Collaborative Innovation Center for Geospatial Technology, Wuhan 430079, China
GPS精密单点定位(precise point positioning, PPP)模糊度固定技术缩短了传统PPP的收敛时间, 提高了PPP的定位精度, 已成为精密定位领域的研究热点[1-4]。中国的北斗卫星导航定位系统(BeiDou satellite navigation system, BDS)是中国独立发展、自主建设的卫星导航定位系统, 截至2017年6月, 共有5颗地球静止轨道(geostationary earth orbiting, GEO)卫星, 6颗倾斜轨道(inclined geosynchronous orbiting, IGSO)和3颗中地球轨道(medium earth orbiting, MEO)卫星在轨正常运行, 为亚太区域的用户提供连续稳定的导航定位服务[5-6]。将PPP模糊度固定技术引入北斗卫星导航定位系统, 实现单北斗系统的PPP模糊度固定, 对提高北斗系统导航定位精度和应用性能有着重要意义。
与GPS、GLONASS、Galileo等系统不同, 北斗卫星伪距观测值中存在显著的系统偏差, 该伪距偏差与卫星高度角和信号频率相关, 最大可以达到1 m, 对北斗卫星相位小数偏差(uncalibrated phase delay, UPD)的估计和模糊度固定有重大的影响[7-11]。文献[12—16]采用Wanninger和Beer的高度角模型消除了IGSO/MEO观测值伪距偏差后, 估计得到稳定的IGSO/MEO卫星的UPD产品, 从而实现了北斗IGSO和MEO卫星的模糊度固定, 有效地缩短GPS/BDS双系统PPP固定解的收敛时间, 提高定位精度[12-16]。文献[14]研究发现GEO卫星伪距偏差和轨道误差在小区域内具有一致性, 因此可以被吸收到卫星UPD中, 利用区域网的数据可以有效地估计北斗GEO卫星的UPD, 并应用于区域网测站的GPS/BDS模糊度固定。然而在全球范围内, GEO卫星的伪距偏差和轨道误差无法被卫星UPD吸收, 参考站之间UPD估值的互差较大造成GEO卫星的UPD难以正确估计, GEO卫星的模糊度难以正确固定。因此国内外大部分研究主要针对北斗IGSO/MEO卫星模糊度固定, 北斗GEO卫星的UPD估计和模糊度固定技术仍局限于区域网, 对于利用全球网测站进行北斗GEO卫星的UPD估计问题, 以及联合GEO、IGSO和MEO卫星的单北斗系统的PPP固定解的性能评估, 国内外尚无相关的系统研究与分析。
本文针对GEO卫星的伪距偏差问题, 利用小波变换[17-18]的方法削弱伪距偏差和多路径误差的影响。基于窄巷UPD短时间内的稳定特性, 本文改进了窄巷UPD估计的策略, 利用上一历元成功估计的窄巷UPD对当前历元的浮点模糊度进行改正, 然后剔除精度较差的模糊度信息, 修正固定错误的整周模糊度, 从而提高了窄巷UPD的精度和稳定性。利用全球62个测站15 d的观测数据进行北斗GEO、IGSO和MEO卫星的UPD产品估计, 分析比较了伪距偏差改正前后的宽巷窄巷UPD估计结果; 最后对北斗GEO、IGSO和MEO卫星进行非差模糊度固定, 并通过首次固定时间、收敛时间和定位误差对其定位性能进行评估。
1 北斗卫星UPD估计策略和模糊度固定算法北斗卫星的UPD产品分为宽巷UPD和窄巷UPD两种类型, 其中宽巷UPD由于具备较高的时间稳定性[19], 一天通常只估计一个值, 由于窄巷UPD稳定性较低, 本文对窄巷UPD采用逐历元估计方法。在估计宽巷UPD过程中, 宽巷模糊度通过MW组合计算得到, 如式(1)所示[20-21]
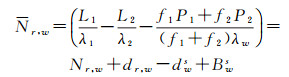 (1)
(1)
式中, Nr, w和Nr, w分别为北斗卫星宽巷浮点模糊度和整周模糊度; f1和f2, λ1和λ2分别对应北斗B1和B2信号的频率和波长; λw为宽巷波长; P和L为伪距和相位观测值; dr, w与dws对应于接收机端和卫星端宽巷UPD; Bws则为北斗卫星端伪距偏差。
由于北斗宽巷模糊度的小数部分既包含了卫星端和接收机端的UPD, 同时也包含了北斗卫星端的伪距偏差。该伪距偏差与卫星高度角和信号频率相关, 最大可以达到1 m, 给宽巷模糊度的UPD估计引入了额外的系统偏差。因此北斗卫星伪距偏差的改正对于北斗卫星UPD估计和模糊度固定至关重要。针对伪距偏差与高度角相关特性, 北斗IGSO和MEO卫星的伪距观测值可以通过Wanninger和Beer提出了高度角模型进行改正[10]。由于受到伪距偏差和测站端多路径影响较为严重, GEO卫星的伪距观测值存在若干分米量级的抖动, 已有改正模型难以准确描述卫星伪距偏差变化。本文通过小波变换的方式提取伪距多路径组合中的低频项, 最后通过低频分量对伪距观测值进行系统误差的改正。该方法不仅改正了GEO卫星的伪距偏差, 也削弱了GEO卫星的多路径影响, 从而可以估计得到稳定的宽巷UPD序列。
在窄巷UPD估计过程中, 首先使用IGS精密轨道和钟差产品对参考站中的每个基准站进行GPS/BDS PPP定位解算得到所有站的所有实数无电离层模糊度参数, 窄巷模糊度则可以通过整周宽巷模糊度和浮点无电离层模糊度组合得到, 如下式[22]
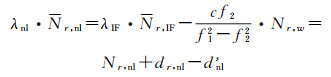 (2)
(2)
式中, λnl和λIF分别为窄巷模糊度和无电离层模糊度的波长; c为光速; dr, w与dws对应于接收机端和卫星端窄巷UPD; Nr, nl和Nr, IF分别对应浮点窄巷模糊度和浮点无电离层模糊度。
由式(1)和式(2)可知, 浮点宽巷模糊度和浮点窄巷模糊度均可以表示为整周模糊度和小数偏差之和, 如下式
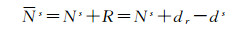 (3)
(3)
式中, Ns为浮点模糊度; Ns为整周模糊度; dr与ds分别为接收机和卫星UPD; R为接收机端和卫星端UPD之和, R可以通过浮点模糊度和取整后整数模糊度做差初步得到。
获得宽巷模糊度和窄巷模糊度的小数部分R后, 宽巷UPD和窄巷UPD可以利用n个测站的模糊度信息通过最小二乘法估计得到[23-24], 如式(4)
 (4)
(4)
式中, Ri对应于测站i上模糊度小数部分(即卫星端和接收机端UPD之和)向量; dr为测站UPD向量; ds是北斗卫星UPD向量; C为接收机UPD的系数矩阵; S则对应于卫星UPD的系数矩阵。
利用式(4)进行宽巷和窄巷UPD估计时, 法方程是秩亏的, 因此选择将其中一个测站的接收机UPD设为0, 以此作为基准。在最小二乘估计过程中, 通过对残差超过阈值的观测值进行降权或剔除, 反复迭代直至参与估计的观测值残差均符合阈值标准。
在宽巷UPD估计过程中, 首先对北斗卫星端伪距偏差改正, 得到正确的MW组合, 为了削弱MW组合伪距多路径和噪声的影响, 对MW组合进行逐历元平滑, 平滑后的MW组合在一个完整的弧段中具有近似的小数部分, 该弧段小数部分的均值即可代表该弧段宽巷模糊度的小数部分。由于周跳、信号中断等因素的影响, 在一天时间内一颗卫星可能存在多个弧段, 对此卫星多个弧段的MW组合小数部分取均值, 合并小数部分相对接近的弧段, 剔除小数部分互差较大的短弧段。最后将每个测站每颗卫星的小数部分代入式(4), 即可得到每颗卫星的UPD估计值。
在窄巷UPD估计过程中, 由于窄巷的波长相对较短, 受观测数据质量和未模型化误差的影响较大, 尤其是对于轨道精度较差的GEO卫星, 各参考站之间UPD估值的互差较大而无法正确估计UPD。因此在逐历元估计过程, 每个历元均能估计得到一组UPD估值, 对于当前历元的每个UPD估计值, 当参与估计该UPD的模糊度个数超过5个, 且估值精度小于0.1周则判定为合格。将合格的UPD估计值代入下一个历元, 对相应的浮点模糊度进行卫星端和接收机端的UPD改正。若改正后该模糊度的小数部分仍大于0.25周, 则认为该模糊度存在较大的偏差, 该模糊度将不会进一步参与UPD估计; 若小数部分不超过0.25周, 则对改正后的模糊度取整固定, 如下式
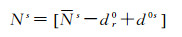 (5)
(5)
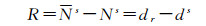 (6)
(6)
式中, dr0和d0s为上个历元的接收机端和卫星端的UPD; 符号[·]表示取整算子。将固定的模糊度代入式(6), 进一步得到当前历元模糊度的小数部分, 并用于后续的最小二乘估计。
利用全球分布测站网的观测数据解算得到的北斗卫星端小数部分, 与钟差和轨道产品联合提供给PPP用户, PPP用户即可利用UPD产品对模糊度进行改正, 在宽巷窄巷固定模式中, 首先对宽巷模糊度进行宽巷UPD改正, 然后通过取整方式固定宽巷模糊度, 之后对窄巷模糊度进行窄巷UPD改正, 然后通过LAMBDA算法[25]搜索正确的整周模糊度, 最终恢复模糊度的整数特性, 从而实现了北斗PPP整数解。值得注意的是, 用户在对北斗卫星进行PPP模糊度固定的过程中, 需要对北斗卫星的伪距偏差进行改正, IGSO和MEO卫星通过高度角模型进行改正, 而GEO卫星需要通过小波变换提取低频分量后去低频分量的方法进行改正, 与对应的UPD产品配套使用, 最终实现宽巷窄巷模糊度的正确固定。
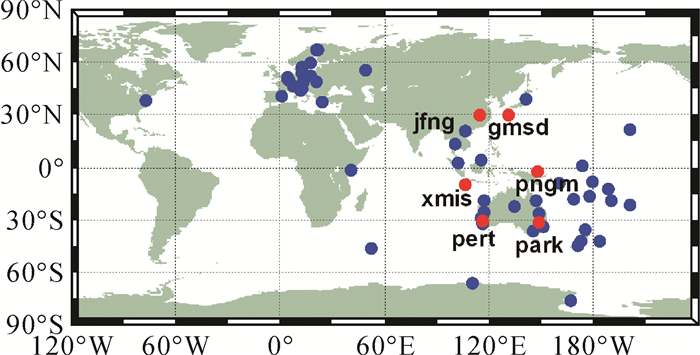
2 北斗GEO、IGSO和MEO卫星的UPD结果为了得到稳定可靠的北斗UPD产品, 本文选取全球62个可以观测到较多北斗卫星的测站2017年1月15日—1月30日共计15 d的数据进行UPD估计。图 1给出了参与北斗UPD估计的62个测站的全球分布图, 其中大部分测站分布于亚太地区, 少数测站分布于欧洲区域。图中蓝色的测站参与了北斗卫星的UPD估计, 红色的6个测站将作为用户站来评估单北斗系统的PPP固定解性能。
|
| 图 1 参与北斗UPD估计的参考站的全球分布图 Fig. 1 The distribution of stations to estimate BDS UPDs |
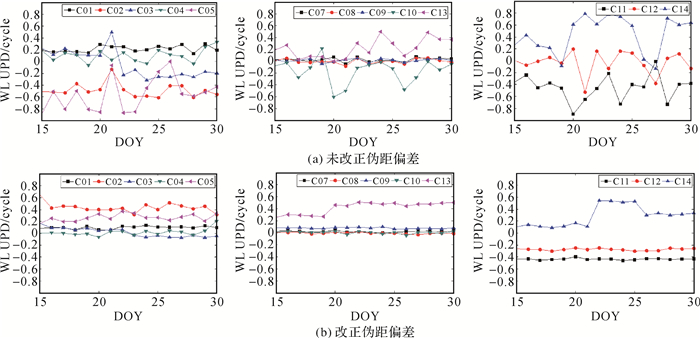
图 2给出了北斗GEO, IGSO和MEO卫星2017年1月15日—2017年1月30日的改正伪距偏差前后的WL UPD结果。可以看出, 未改正伪距偏差时, 由于宽巷模糊度中存在与高度角相关的系统偏差, 从而导致估计得到的北斗GEO、IGSO和MEO卫星的WL UPD均存在显著的波动。对于GEO卫星, 改正伪距偏差后, 15 d的宽巷UPD标准差分别从0.157周提高到0.101周, 提高了35.6%;IGSO和MEO卫星的宽巷UPD标准差分别从0.093周, 0.229周提高到0.021周和0.025周, 分别提高了77.9%和88.9%。伪距偏差改正后, 北斗GEO、IGSO和MEO卫星的WL UPD均有显著的提升, 改正后的WL UPD产品具有较高的稳定性, 符合模糊度固定的要求。图 2中部分天出现了较为明显的跳变, 如2017年1月23日的C03卫星, 2017年1月19日的C13卫星, 1月21日、1月26日的C14卫星, 通过分析钟差文件发现这些天的钟差产品也出现不同量级的基准跳跃现象, 其中的联系与原因仍需要进一步的分析研究。
|
| 图 2 北斗2017年1月15日—1月30日伪距偏差改正前后的WL UPD产品 Fig. 2 The BDS WL UPDs from January 1 to 30 of 2017 before and after the code bias correction |
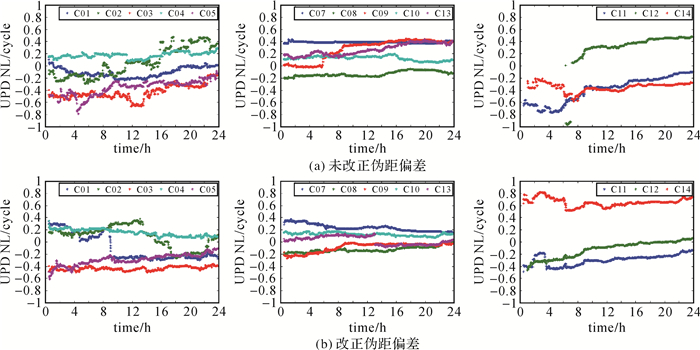
对宽巷模糊度进行UPD改正后取整得到固定后的宽巷模糊度, 联合无电离层浮点模糊度得到浮点窄巷模糊度, 再利用式(4)求得窄巷UPD结果。图 3给出了北斗卫星2017年1月21日伪距偏差改正前后的NL UPD序列。未改正伪距偏差时, 北斗GEO、IGSO和MEO卫星单天的平均标准差分别为0.158、0.099、0.147周, 伪距偏差改正后GEO, IGSO和MEO的单天标准差为0.120、0.043、0.092周, 分别提高了24.0%、59.5%和37.4%。伪距偏差改正后, 估计得到的宽巷UPD结果更加可靠, 因此对于北斗卫星窄巷UPD的结果也有较明显的改进, 尤其是IGSO和MEO卫星。尽管GEO卫星的窄巷UPD的估计结果没有IGSO和MEO卫星稳定, 其0.1周左右的标准差依然满足PPP模糊度固定的需求。
|
| 图 3 北斗2017年1月21日伪距偏差改正前后的NL UPD产品 Fig. 3 The BDS NL UPDs on January 3, 2017 before and after the code bias correction |
3 北斗卫星固定解定位结果分析
一旦获得了稳定可靠的卫星UPD产品, 即可利用UPD产品对北斗卫星进行模糊度固定, 得到PPP固定解的结果, 固定解的定位性能也可以进一步验证北斗UPD产品的有效性。为了评估单北斗系统固定解的定位性能, 本文将从首次固定时间、收敛时间和定位误差多个方面进行评估。本文选取亚太区域6个基准站2017年1月15日—2017年1月30日共计15 d的数据评估北斗PPP模糊度固定解定位性能。表 1给出了6个基准站的测站信息, 包括接收机类型、天线类型、可观测到的卫星数。由表 1可以看出, 大部分测站可以观测到5~6颗IGSO和MEO卫星, 加入GEO卫星后, 可视的北斗卫星有明显的提升, 平均观测到的卫星数目增加到10颗左右。
| 测站名 | 接收机类型 | 天线类型 | 平均观测到卫星数目 (IGSO+MEO) |
平均观测到卫星数目 (GEO+IGSO+MEO) |
| GMSD | TRIMBLE NETR9 | TRM59800.00 SCIS |
6.0 | 10.5 |
| PARK | TRIMBLE NETR9 | ASH701945C_M NONE |
5.2 | 8.2 |
| PERT | TRIMBLE NETR9 | TRM59800.00 NONE |
5.5 | 10.6 |
| PNGM | TRIMBLE NETR9 | TRM59800.00 NONE |
6.9 | 10.8 |
| XIMS | TRIMBLE NETR9 | TRM59800.00 NONE |
7.1 | 12.2 |
| JFNG | TRIMBLE NETR9 | TRM59800.00 NONE |
5.72 | 10.7 |
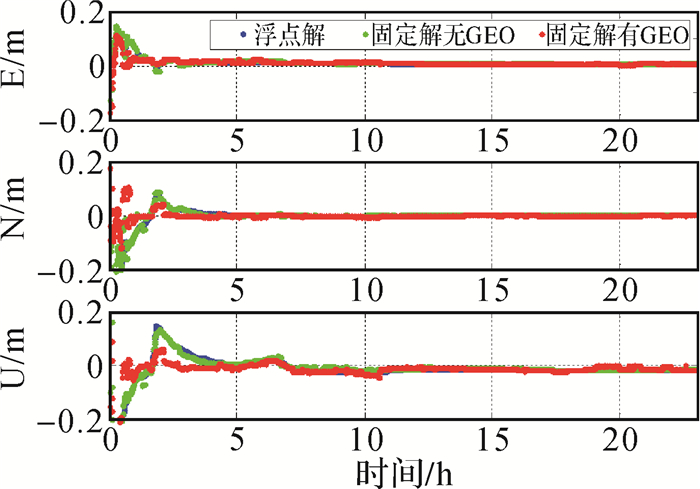
图 4给出了pert测站北斗PPP浮点解和固定解的坐标偏差序列。其中固定解分为两种模式, 第1种模式为仅固定IGSO和MEO卫星的模糊度, 第2种模式对GEO、IGSO和MEO卫星均进行模糊度固定。由图 4可以看出, 相比于PPP浮点解的结果, 仅固定IGSO和MEO卫星模糊度的定位结果略有提升, 对GEO卫星进行模糊度固定后, 其收敛时间和定位精度方面均有显著的提升。结果说明加入GEO卫星后, 随着可视北斗卫星的数目显著增加, 可用于固定的候选模糊度随之增加, 从而可以显著提高固定解的首次固定时间和定位精度。
|
| 图 4 pert测站2017年1月3日北斗PPP浮点解和固定解的坐标偏差 Fig. 4 The coordinate bias of BDS PPP float and fixed solutions for pert station |
进一步统计了6个测站共计15 d的数据(2017年1月15日—2017年1月30日)在不同固定解模式下的平均首次固定时间, 如表 2所示。相对于仅固定IGSO和MEO卫星的结果, 固定GEO卫星后, 所有的测站PPP固定解的首次固定时间均有明显的提升, 平均首次固定时间由54 min提升到28 min, 其中gmsd测站的提升最为明显, 首次固定时间由49 min缩短到20 min, 提高了59.18%。可以看出, 对GEO卫星的模糊度进行固定后, BDS固定解的首次固定时间可以缩短至30 min以内, 部分测站如xims测站, 在16 min以内即可固定模糊度。
| 测站 | 首次固定时间/min | 提升百分比/(%) | |
| IGSO+MEO | IGSO+MEO+GEO | ||
| gmsd | 49 | 20 | 59.18 |
| park | 67 | 39 | 41.79 |
| pert | 42 | 28 | 33.33 |
| pngm | 100 | 42 | 58.00 |
| xmis | 18 | 16 | 11.11 |
| jfng | 53 | 26 | 50.94 |
| average | 54 | 28 | 47.78 |
表 3给出了6个参考站北斗浮点解和两种固定解模式下的平均收敛时间。本文中的收敛时间定义为水平方向上的定位误差均优于10 cm且其后的10个历元的位置偏差均在该范围内。可以看出, 6个参考站北斗浮点解的收敛时间在60 min左右, 对IGSO和MEO卫星进行模糊度固定后, 平均收敛时间减少到45.5 min。对于联合GEO、IGSO和MEO卫星的PPP固定解, 其收敛时间可以缩短到30 min以内, 相较于PPP浮点解提升了49.7%, 相较于只固定IGSO和MEO卫星的PPP固定解, 提升了34.5%。
| 测站 | BDS收敛时间/min | ||
| 浮点解 | 固定解 IGSO+MEO |
固定解 IGSO+MEO+GEO |
|
| gmsd | 82.5 | 57 | 36 |
| park | 28 | 24 | 22 |
| pert | 62.5 | 42 | 26 |
| pngm | 74.5 | 67.5 | 40 |
| xmis | 35 | 27.5 | 21 |
| jfng | 71 | 55 | 33 |
| average | 58.9 | 45.5 | 29.6 |
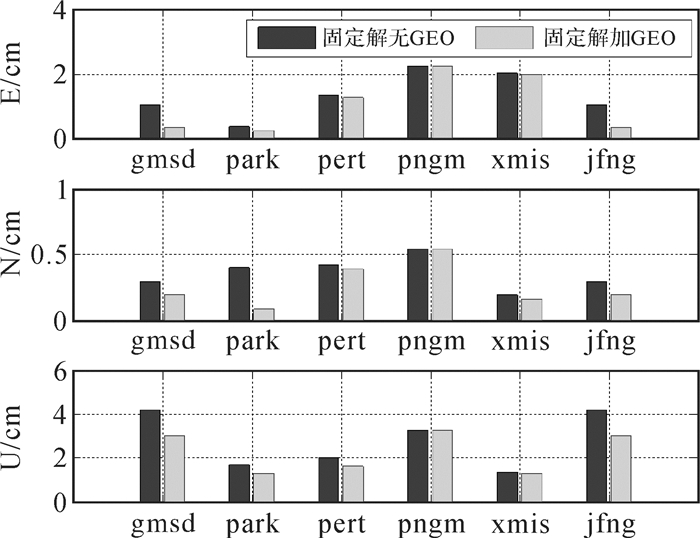
表 4统计了6个参考站北斗PPP固定解6 h后的定位误差, 对应的结果如图 5所示。结合图表可以看出, 固定GEO卫星后, 大部分测站的定位误差均有明显的改善, 在E、N、U 3个方向上的平均定位误差由(1.35, 0.35, 2.75)cm减少到(1.07, 0.26, 2.24)cm, 分别减少了20%、27%和18%, 其中jfng测站的定位误差减少得最为明显, 在E、N、U 3个方向上分别减少了68%、37%和26%。
| cm | |||||||
| BDS(IGSO+MEO) | BDS(GEO+IGSO+MEO) | ||||||
| E | N | U | E | N | U | ||
| gmsd | 1.04 | 0.29 | 4.16 | 0.34 | 0.19 | 3.02 | |
| park | 0.39 | 0.40 | 1.67 | 0.24 | 0.08 | 1.28 | |
| pert | 1.36 | 0.42 | 2.04 | 1.28 | 0.39 | 1.61 | |
| pngm | 2.25 | 0.54 | 3.26 | 2.24 | 0.54 | 3.25 | |
| xmis | 2.02 | 0.19 | 1.32 | 2.00 | 0.16 | 1.30 | |
| jfng | 1.02 | 0.27 | 4.06 | 0.33 | 0.17 | 3.00 | |
| average | 1.35 | 0.35 | 2.75 | 1.07 | 0.26 | 2.24 | |
|
| 图 5 6个基准站北斗PPP 6h的定位误差对比 Fig. 5 The positioning error of PPP AR for 6h observations |
4 结论
针对北斗GEO卫星的多路径误差和伪距偏差, 本文采用小波变换修正伪距观测值的方法进行削弱。在窄巷UPD估计过程中, 本文改进了窄巷UPD估计的策略, 利用上个历元成功估计的窄巷UPD改正当前历元的模糊度, 然后剔除精度较差的模糊度信息, 修正固定错误的整周模糊度, 从而提高了窄巷UPD的精度和稳定性。本文利用全球分布的62个测站对北斗卫星GEO、IGSO和MEO卫星的UPD进行估计, 并比较分析了伪距偏差改正前后的宽巷和窄巷UPD结果。结果表明, 改正伪距偏差并改进UPD估计策略后, 利用全球网测站同时估计北斗GEO、IGSO和MEO卫星的宽巷和窄巷UPD具有可行性。其中北斗GEO卫星宽巷和窄巷UPD标准差分别为0.101和0.120周, IGSO和MEO卫星的UPD的标准差均小于0.1周。相对于未改正伪距偏差的结果, GEO、IGSO和MEO卫星的宽巷标准差分别提高了35.6%、77.9%和88.9%, 其窄巷UPD的标准差分别提高了24.0%、59.5%和37.4%。基于稳定可靠的UPD产品, 本文实现了联合GEO、IGSO和MEO卫星的单北斗系统的PPP模糊度固定, 结果表明:联合GEO、IGSO和MEO卫星的PPP固定解的首次固定时间和收敛时间均可以缩短到30 min以内; 对于6 h的观测数据, E、N、U方向的定位误差由(1.35、0.35、2.75)cm减少到(1.07、0.26、2.24)cm, 分别减少了20%, 27%和18%。
| [1] | 李星星. GNSS精密单点定位及非差模糊度快速确定方法研究[D]. 武汉: 武汉大学, 2013. LI Xingxing. Rapid Ambiguity Resolution in GNSS Precise Point Positioning[D]. Wuhan: Wuhan University, 2013. |
| [2] | GE Maorong, GENDT G, ROTHACHER M, et al. Resolution of GPS Carrier-phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations[J]. Journal of Geodesy, 2008, 82(7): 389–399. DOI:10.1007/s00190-007-0187-4 |
| [3] | COLLINS P, LAHAYE F, HÉROUX P, et al. Precise Point Positioning with Ambiguity Resolution Using the Decoupled Clock Model[C]//Proceedings of ION GNSS 21st International Technical Meeting of the Satellite Division. Savannah, GA: ION GNSS, 2008: 1315-1322. |
| [4] | GENG Jianghui, TEFERLE F N, SHI Changhong, et al. Ambiguity Resolution in Precise Point Positioning with Hourly Data[J]. GPS Solutions, 2009, 13(4): 263–270. DOI:10.1007/s10291-009-0119-2 |
| [5] | 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1–6. |
| [6] | MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P, et al. A COMPASS for Asia: First Experience with the BeiDou-2 Regional Navigation System[C]//IGS Workshop. Olsztyn: IGS, 2012. http://www.igs.org/presents/poland2012/posters.Accessed10July2014. |
| [7] | PERELLO GISBERT J V, BATZILIS N, RISUEÑO G L, et al. GNSS Payload and Signal Characterization Using a 3 m Dish Antenna[C]//Proceedings of the 25th International Technical Meeting of The Satellite Division of the Institute of Navigation. Nashville, TN: ION GNSS, 2012: 347-356. |
| [8] | HAUSCHILD A, MONTENBRUCK O, SLEEWAEGEN J M, et al. Characterization of Compass M-1 Signals[J]. GPS Solutions, 2012, 16(1): 117–126. DOI:10.1007/s10291-011-0210-3 |
| [9] | HAUSCHILD A, MONTENBRUCK O, THOELERT S, et al. A Multi-technique Approach for Characterizing the SVN49 Signal Anomaly, Part 1:Receiver Tracking and IQ Constellation[J]. GPS Solutions, 2012, 16(1): 19–28. DOI:10.1007/s10291-011-0203-2 |
| [10] | WANNINGER L, BEER S. BeiDou Satellite-induced Code Pseudorange Variations:Diagnosis and Therapy[J]. GPS Solutions, 2015, 19(4): 639–648. DOI:10.1007/s10291-014-0423-3 |
| [11] | LI Jinlong, YANG Yuanxi, XU Junyi, et al. GNSS Multi-Carrier Fast Partial Ambiguity Resolution Strategy Tested with Real BDS/GPS Dual-and Triple-frequency Observations[J]. GPS Solutions, 2015, 19(1): 5–13. DOI:10.1007/s10291-013-0360-6 |
| [12] | WANG Min, CHAI Hongzhou, LI Yu. Performance Analysis of BDS/GPS Precise Point Positioning with Undifferenced Ambiguity Resolution[J]. Advances in Space Research, 2017, 60(12): 2581–2595. DOI:10.1016/j.asr.2017.01.045 |
| [13] | LIU Yanyan, YE Shirong, SONG Weiwei, et al. Integrating GPS and BDS to Shorten the Initialization Time for Ambiguity-Fixed PPP[J]. GPS Solutions, 2017, 21(2): 333–343. DOI:10.1007/s10291-016-0525-1 |
| [14] | 雍雯. 北斗高精度定位模糊度解算方法研究[D]. 南京: 东南大学, 2014. YONG Wen. Research on Approach of Beidou High Precision Positioning Ambiguity Resolution[D]. Nanjing: Southeast University, 2014. |
| [15] | LI Pan, ZHANG Xiaohong, GUO Fei. Ambiguity Resolved Precise Point Positioning with GPS and BeiDou[J]. Journal of Geodesy, 2017, 91(9): 25–40. |
| [16] | ANTONINI M, BARLAUD M, MATHIEU P, et al. Image Coding Using Wavelet Transform[J]. IEEE Transactions on Image Processing, 1992, 1(2): 205–220. DOI:10.1109/83.136597 |
| [17] | 王广兴. 北斗观测值特性分析及其在PPP模糊度固定应用中的研究[D]. 武汉: 武汉大学, 2016. WANG Guangxing. On the Analysis of Beidou Observations' Characteristics and Its Application in PPP Integer Ambiguity Resolution[D]. Wuhan: Wuhan University, 2016. |
| [18] | 张小红, 李盼, 李星星, 等. 宽巷载波相位模糊度小数偏差时变特性分析[J]. 测绘学报, 2013, 42(6): 798–803, 809. |
| [19] | MELBOURNE W G. The Case for Ranging in GPS-Based Geodetic Systems[C]//Proceedings of the first International Symposium on Precise Positioning with Global Positioning System. Rockville, MD: International Symposium on Precise Positioning, 1985: 373-386. |
| [20] | WVBBENA G. Software Developments for Geodetic Positioning with GPS Using TI-4100 Code and Carrier Measurements[C]//Proceedings of the First International Symposium on Precise Positioning with the Global Positioning System. Rockville, MD: International Symposium on Precise Positioning, 1985: 403-412. |
| [21] | LI Pan, ZHANG Xiaohong, REN Xiaodong, et al. Generating GPS Satellite Fractional Cycle Bias for Ambiguity-fixed Precise Point Positioning[J]. GPS Solutions, 2016, 20(4): 771–782. DOI:10.1007/s10291-015-0483-z |
| [22] | LI Xingxing, GE Maorong, ZHANG Hongping, et al. A Method for Improving Uncalibrated Phase Delay Estimation and Ambiguity-fixing in Real-time Precise Point Positioning[J]. Journal of Geodesy, 2013, 87(5): 405–416. DOI:10.1007/s00190-013-0611-x |
| [23] | LI Xingxing, ZHANG Xiaohong. Improving the Estimation of Uncalibrated Fractional Phase Offsets for PPP Ambiguity Resolution[J]. Journal of Navigation, 2012, 65(3): 513–529. DOI:10.1017/S0373463312000112 |
| [24] | TEUNISSEN P J G. The Least-squares Ambiguity Decorrelation Adjustment:a Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65–82. DOI:10.1007/BF00863419 |


