Download PDF  
文章快速检索  
  高级检索
引用本文
刘清超, 孙和平, 王泽民, 等. 南极中山站的重力和区域海洋潮汐特征[J]. 测绘学报，2018，47(3)：316-323. DOI: 10.11947/j.AGCS.2018.20170123
LIU Qingchao, SUN Heping, WANG Zemin, et al. The Characteristics of Gravity and Regional Ocean Tides at Zhongshan Station in Antarctic[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(3): 316-323. DOI: 10.11947/j.AGCS.2018.20170123
南极中山站的重力和区域海洋潮汐特征
刘清超1,2 , 孙和平1,2 , 王泽民3 , 陈晓东1 , 张胜凯3 , 徐建桥1     
1. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室, 湖北 武汉 430077;
2. 中国科学院大学, 北京 100049;
3. 武汉大学中国南极测绘研究中心, 湖北 武汉 430079
收稿日期：2017-03-16；修回日期：2017-07-24
基金项目：国家自然科学基金(41621091;41674083;41531069;41374084;41574072)
第一作者简介：刘清超(1990-), 男, 博士生, 研究方向为重力场理论、方法及应用。E-mail:liuqch1990@163.com
摘要：本文利用中山站弹簧重力仪记录的重力潮汐时间序列、验潮站数据、CATS2008区域和Eot11a全球海潮模型研究重力和海洋潮汐特征。结果表明，在周日频段，潮波O1的海潮振幅达到28 cm，4个主要潮波(Q1、O1、P1和K1)的全球模型与验潮站潮高差之和为4.2 cm，区域模型与验潮站潮高差之和为4.4 cm; 在半日频段，潮波M2的海潮振幅达到20 cm，4个主要潮波(N2、M2、S2和K2)的潮高差之和分别为7.7 cm和5.1 cm，说明利用区域模型修正全球模型的重要性。经区域模型修正的全球海潮负荷改正后，重力主波K1、M2和S2的最终残差振幅分别下降了9.84%、56.14%和37.08%，说明区域海潮模型更能反映海洋潮汐的真实特征，用区域模型修正全球海潮模型的有效性得到验证。
关键词：南极    重力潮汐    区域和全球海潮模型    
The Characteristics of Gravity and Regional Ocean Tides at Zhongshan Station in Antarctic
LIU Qingchao1,2 , SUN Heping1,2 , WANG Zemin3 , CHEN Xiaodong1 , ZHANG Shengkai3 , XU Jianqiao1     
1. State Key Laboratory of Geodesy and Earth's Dynamics, Institute of Geodesy and Geophysics, CAS, Wuhan 430077, China;
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Chinese Antarctic Center of Surveying and Mapping, Wuhan University, Wuhan 430079, China
Foundation support: The National Natural Science Foundation of China (Nos.41621091;41674083;41531069;41374084;41574072)
First author: LIU Qingchao(1990—), male, PhD candidate, majors in gravity field theory, methods and applications.E-mail:liuqch1990@163.com
Abstract: This study investigates the characteristics of gravity and ocean tides using time series recorded with the spring gravimeter and tide gauge at Zhongshan station, CATS2008 regional ocean tide model, and Eot11a global ocean tide model. The results show that the ocean tidal amplitude of O1 wave reaches 28 cm in the diurnal tidal bands. The sum of four tidals (Q1, O1, P1 and K1) difference between the global model and the tide gauge station is 4.2 cm, and that between the regional model and the tide gauge station is 4.4 cm. In contrast, the tidal amplitude of M2 wave reaches 20 cm in the semi-diurnal bands, and the sum of four tidals (N2, M2, S2 and K2) difference are 7.7 cm and 5.1 cm, respectively. This shows that correcting global ocean tide model using regional models is important. Subsequent to the correction of global oceanic loading using the regional model, the amplitudes of final residuals for the main gravity waves K1, M2, and S2 decreased by 9.84%, 56.14%, and 37.08%, respectively, which indicates that the regional ocean tide model can better reflect the true characteristics of ocean tides. Moreover, the validity of correcting global ocean tide model using the regional model is verified.
Key words: Antarctic     tidal gravity     regional and global ocean tide model    

南极冰盖质量的变化主要发生在浮冰区的边缘, 对全球海平面的变化起着至关重要的作用, 而且是全球气候变化的一个重要指标。利用测高卫星及GRACE重力卫星研究冰盖表面高或体积长期项变化时, 必须去掉观测资料中的海潮信号[1-2]。

国际同行基于流体动力学方程、有限元计算方法, 以验潮站、卫星测高观测资料等作为限制条件, 编制了一系列海潮模型[3]。但南极地区缺少高精度的卫星测高和验潮站资料, 造成模型精度较低, 如文献[4]利用中山站重力资料测定的主要潮波振幅因子经全球海潮模型作负荷改正后与理论值的相对差异高达5%。验潮站可以提供高精度的局部海洋潮汐特征, 进而提高模型精度, 如文献[5]利用昭和验潮站资料代替全球海潮模型TPXO7.2中相应区域的潮高数据, 主要潮波的最终残差下降了5%。高精度的区域海潮模型可以用于修正全球海潮模型, 文献[6]基于11个全球海潮模型与中国东海及南海潮汐观测资料研究了近海潮汐资料对中国及邻区重力场的影响; 文献[7]发表了南极区域海潮模型CATS, 随着验潮站、GPS和ICESat等观测数据的积累, 模型精度进一步得到优化。

验潮站资料可用于评价海潮模型的适定性, 重力固体潮的潮汐参数有利于研究地球内部构造、地壳的运动等地球动力学现象[8]。南极中山固体潮站于1989年2月26日开始建造, 坐落于东南极大陆的拉斯曼丘陵。1991年3月起, 中国科学院测量与地球物理研究所使用LCR型弹簧重力仪ET20/21在南极中山站(69.371°S, 76.365°E)进行连续重力观测[9]。中山验潮站(69.383°S, 76.380°E)始建于1999年, 位于东南极的Nella峡湾, 由于每年的3月初至11月底一直被冰覆盖[10], 因此, 使用了压力式验潮仪。因验潮仪老化等导致验潮站无法记录海洋潮汐资料, 2010年2月, 中国第26次南极科考队综合南极已有验潮站的建站方法及中山站的实际情况, 采用新的海底压力式验潮仪成功建设了我国在南极的首个永久性自动验潮站系统[11], 为研究南极海洋潮汐特征提供实测数据。

本文首先对中山站2009年至2013年观测资料进行调和分析处理, 获取该地区重力及海洋潮汐参数; 其次, 利用验潮站及重力潮汐资料检验南极区域海潮模型CATS2008修正全球海潮模型Eot11a在南极地区的有效性; 最后, 利用修正后的海潮模型对重力潮汐参数作负荷效应改正。

1 数据处理 1.1 重力固体潮

本文使用的重力固体潮资料为安装在中山站的弹簧重力仪ET21记录所得, 区间为2009年12月1日至2013年12月12日, 原始采样间隔为1 s; 气压观测数据由中山气象站提供, 原始采样间隔为10 min。为了便于处理观测资料, 分别采用整点采样法和三次样条内插法将重力及气压数据的采样间隔转换为1 min。由于弹簧重力仪为相对重力仪, 其输出值是与重力变化对应的电压值, 根据格值因子将其转化为重力单位。然后, 利用国际地球潮汐中心推荐的重力潮汐观测数据预处理软件“T-Soft”[12], 移去理论合成潮, 根据标准大气重力导纳值去掉大气效应, 利用修正器删掉突跳、尖峰和由地震等引起的异常信号, 对由仪器故障、断电等造成的间断进行插值拟合, 利用IERS(international earth rotation service)提供的极移资料计算出极移重力效应[13], 从而扣除观测资料中的极移效应, 再加上上文移除的理论合成潮及大气效应即得到预处理后的重力潮汐数据。最后, 采用低通数字滤波器将高密度采样资料变换为每小时采样。基于Eterna3.30标准分析软件[14]对预处理后的重力潮汐序列作调和分析, 并利用台站气压与重力潮汐残差的线性拟合去除大气效应, 采用切比雪夫多项式拟合漂移, 获取高精度的重力潮汐参数(振幅因子和相位滞后), 具体数值结果列于表 1。其中, δth为文献[15]给出的基于旋转椭球体、非流体静力平衡地球建立的理论潮汐模型值。研究表明, O1和M2潮波振幅因子观测的相对精度分别为0.06%和0.08%, 但与理论值的相对差异分别为13.63%和19.50%, 这主要由海潮负荷效应引起, 因为中山站距海岸线很近, 仅10 m左右。

表 1 中山站重力潮汐参数 Tab. 1 Gravity tidal parameters at Zhongshan station
潮波 理论振幅/(nm/s2) δ σ(δ) Δφ/(°) σ(Δφ)/(°) δc δth
MM 55.253 8 1.209 12 0.109 41 -0.735 8 5.196 2 1.1550 4 1.159 41
MF 104.608 0 1.160 66 0.033 04 -0.415 3 1.633 4 1.1097 4 1.159 41
SGQ1 1.514 4 1.206 44 0.086 08 4.604 9 4.089 3 1.151 12
2Q1 5.197 9 1.337 20 0.027 44 6.003 2 1.174 1 1.151 07
SGM1 6.268 1 1.348 79 0.024 00 4.206 5 1.022 7 1.151 06
Q1 39.279 7 1.335 48 0.003 91 3.397 8 0.168 0 1.209 84 1.150 96
RO1 7.455 6 1.330 19 0.022 04 1.328 4 0.949 6 1.150 94
O1 205.153 6 1.307 58 0.000 81 1.797 7 0.035 5 1.204 09 1.150 76
TAU1 2.674 1 1.386 43 0.054 33 1.309 3 2.245 7 1.150 71
NO1 16.126 1 1.257 98 0.009 67 1.960 6 0.440 8 1.150 16
CHI1 3.085 8 1.265 17 0.055 08 0.496 9 2.494 0 1.149 98
PI1 5.579 0 1.152 77 0.030 09 10.421 7 1.496 0 1.146 85
P1 95.441 7 1.237 83 0.001 76 -0.418 0 0.081 8 1.171 18 1.145 23
K1 288.405 9 1.237 32 0.000 59 0.791 4 0.027 6 1.167 17 1.129 75
PSI1 2.257 2 1.362 49 0.073 68 26.161 0 3.098 5 1.129 75
PHI1 4.106 8 1.272 63 0.039 61 -7.051 7 1.782 7 1.235 45
TET1 3.084 9 1.221 42 0.055 69 -2.885 9 2.612 5 1.165 67
J1 16.131 9 1.236 65 0.009 60 0.793 5 0.444 8 1.153 00
SO1 2.675 5 1.276 36 0.061 13 0.922 9 2.744 1 1.152 77
OO1 8.824 0 1.216 02 0.018 61 1.919 6 0.877 4 1.152 10
NU1 1.689 8 1.261 90 0.088 00 2.697 7 3.997 0 1.152 05
EPS2 0.690 2 1.153 73 0.088 52 -36.338 9 4.396 2 1.151 82
2N2 2.366 7 1.118 40 0.027 34 -20.771 5 1.400 8 1.155 57
MU2 2.856 5 0.911 14 0.025 11 -14.804 1 1.579 3 1.155 57
N2 17.885 1 0.924 94 0.003 88 -15.714 7 0.240 6 1.127 54 1.155 57
NU2 3.397 4 0.929 60 0.021 46 -18.339 8 1.322 6 1.155 57
M2 93.411 4 0.930 23 0.000 78 -4.780 5 0.048 3 1.116 42 1.155 57
L2 2.640 5 1.103 24 0.037 10 25.750 8 1.927 1 1.155 57
T2 2.540 1 1.236 07 0.028 63 21.569 7 1.327 5 1.155 57
S2 43.455 9 1.230 29 0.001 68 13.427 7 0.078 1 1.201 75 1.155 57
K2 11.807 7 1.186 70 0.006 51 12.309 0 0.314 5 1.135 14 1.155 57
ETA2 0.660 5 1.395 53 0.101 33 11.365 6 4.160 1 1.155 57
M3 0.647 9 0.835 17 0.058 37 -102.691 9 4.004 8 1.067 10
注:δ和σ(δ)分别为潮波的重力振幅因子及其标准偏差; Δφ和σ(Δφ)分别为相位滞后及其标准偏差; δth为文献[15]中潮汐理论模型给出的重力振幅因子; δc为经海潮负荷效应改正后的重力振幅因子。
表选项

各潮波振幅是与纬度相关的, 长周期潮波振幅的最大值出现在两极地区, 振幅越大, 越容易从观测信号中分离出来[16], 且求解精度越高。因此, 相对于其他纬度的台站, 当利用相同观测质量、相同观测区间的重力固体潮资料时, 中山站获得的长周期重力潮汐参数精度更高, 其中, MM(月潮)和MF(半月潮)为主要的长周期潮波, 表 1给出了对应的重力潮汐参数。数值结果表明, MM和MF潮波振幅因子观测的相对精度分别为9.05%和2.85%, 低于主要周日及半周日潮波的观测精度, 这是因为长周期潮波周期较长、受到干扰信号影响较大, 例如, 弹簧重力仪的零漂、南极冰盖的变化及其他环境因素等。由于MM和MF的观测相对精度较低, 在后续海潮模型修正的有效性检验中并未参与计算。

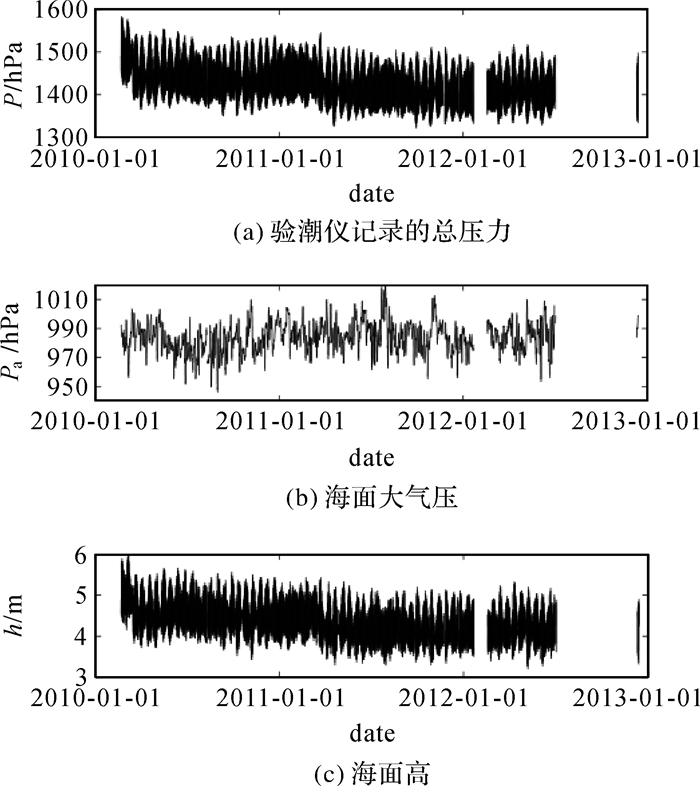
1.2 验潮站

本文分析的验潮资料观测区间为2010年2月21日至2012年12月13日, 采样间隔为1 h。压力式验潮仪给出的原始数据是压力值, 即验潮仪上方海水产生的压力和大气压的总和, 如图 1(a)所示。为了将其转化为真实的海面高, 首先在总压力资料中去除大气压得到海水产生的压力, 然后根据液压公式计算海面高h(如图 1(c)所示)

(1)
图 1 中山验潮站观测资料 Fig. 1 Observation data at Zhongshan tide gauge station
图选项

式中, P是验潮仪记录的总压力; Pa为海面大气压(如图 1(b)所示), 由中山气象观测站提供; ρ为海水密度; G为中山站重力加速度。

某时刻的海面高(潮高)可以表示为[17]

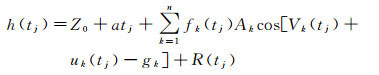(2)

式中, h(tj)为tj时刻的潮高; Z0为常数; a为线性项系数; n为潮波数; Ak和gk分别为潮波k的振幅与相位延迟; fk(tj)和uk(tj)分别为潮波k在tj时刻振幅与相位的节点改正; Vk(tj)为天文参数; R(tj)为非潮汐残差信号; 节点改正及天文参数的计算见文献[18]。与传统调和分析相比, 该方法既消除了将天文参数假定为随时间线性变化而引起的误差, 又克服了将节点改正视为常数的问题, 且加入了随时间变化的线性趋势项。

令

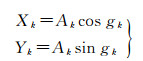(3)

那么, 方程(2)转化为线性方程

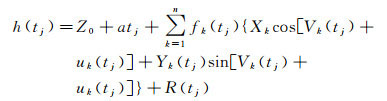(4)

将海面高资料代入式(4), 基于versatile_tidana调和分析软件, 结合文献[19]给出的潮波选择顺序表, 利用奇异值分解(SVD)算法[20]求出各分潮的调和常数(Ak和gk), 可反映该地区的区域海洋潮汐特征, 具体数值结果列于表 2。在长周期频段, 潮波MF的海潮振幅最大, 数值为3.50 cm; 在周日频段, Q1、O1、P1和K1的振幅分别为6.55、28.21、8.82和27.37 cm, 其他潮波的振幅均未达到1.5 cm; 在半周日频段, N2、M2、S2和K2的振幅分别为5.68、19.99、17.92和5.03 cm, 而其他潮波均未超过1.7 cm。与文献[21]的研究结果相比, 主要潮波Q1、O1、P1、K1、N2、M2、S2和K2的振幅差异分别为0.13、0.21、0.28、0.23、0.20、0.13、0.28和0.09 cm, 这与观测时段有关, 也可归因于浅水非线性效应等。

表 2 中山验潮站各分潮的调和常数 Tab. 2 Tidal harmonic constants of constituents at Zhongshan tide gauge station
潮波 潮波频率/cph Ak/m gk/(°) σ(Xk)/m σ(Yk)/m σ(Ak)/m
MSM 0.001 309 781 0.013 08 144.817 0.001 0.001 0.001
MM 0.001 512 152 0.015 07 205.824 0.001 0.001 0.001
MF 0.003 050 092 0.035 04 179.493 0.001 0.001 0.001
ALP1 0.034 396 570 0.003 91 213.600 0.001 0.001 0.001
2Q1 0.035 706 352 0.009 15 247.970 0.001 0.001 0.001
SIG1 0.035 908 721 0.011 48 248.194 0.001 0.001 0.001
Q1 0.037 218 504 0.065 54 262.181 0.001 0.001 0.001
RHO1 0.037 420 873 0.010 70 262.802 0.001 0.001 0.001
O1 0.0387 306 55 0.282 14 270.959 0.001 0.001 0.001
TAU1 0.038 958 814 0.003 58 286.980 0.001 0.001 0.001
NO1 0.040 268 596 0.019 26 275.230 0.001 0.001 0.001
CHI1 0.040 470 965 0.004 11 279.275 0.001 0.001 0.001
P1 0.041 552 588 0.088 16 276.899 0.001 0.001 0.001
S1 0.041 666 672 0.006 86 194.516 0.002 0.002 0.002
K1 0.041 780 747 0.273 72 278.034 0.001 0.001 0.001
PHI1 0.042 008 907 0.003 48 256.494 0.001 0.001 0.001
J1 0.043 292 899 0.011 67 273.834 0.001 0.001 0.001
SO1 0.044 602 677 0.003 82 269.114 0.001 0.001 0.001
OO1 0.044 830 836 0.006 58 252.273 0.001 0.001 0.001
EPS2 0.076 177 314 0.004 34 155.554 0.001 0.001 0.001
2N2 0.077 487 096 0.009 22 147.839 0.001 0.001 0.001
MU2 0.077 689 469 0.010 60 180.253 0.001 0.001 0.001
N2 0.078 999 251 0.056 79 176.115 0.001 0.001 0.001
NU2 0.079 201 616 0.011 14 169.099 0.001 0.001 0.001
M2 0.080 511 399 0.199 90 209.741 0.001 0.001 0.001
LDA2 0.081 821 181 0.003 22 223.888 0.001 0.001 0.001
L2 0.082 023 554 0.016 87 254.805 0.001 0.001 0.001
S2 0.083 333 336 0.179 17 312.417 0.001 0.001 0.001
K2 0.083 561 495 0.050 27 314.804 0.001 0.001 0.001
ETA2 0.085 073 642 0.003 79 358.718 0.001 0.001 0.001
MO3 0.119 242 057 0.004 01 301.594 0.001 0.001 0.001
M3 0.120 767 102 0.016 33 93.054 0.001 0.001 0.001
注:Ak和gk分别为对应潮波的潮高及相位延迟; Xk和Yk均为求解Ak和gk时的中间变量。
表选项

2 全球海潮模型的修正

重力的海潮负荷效应可根据海潮潮高与重力负荷格林函数的褶积积分计算[22-23], 当考虑目标台站的近海效应时, 用区域海潮模型修正全球海潮模型中相应区域的计算公式如下

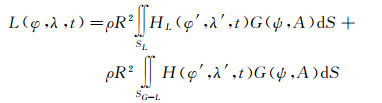(5)

式中, L为负荷矢量; λ、φ为球坐标系下观测台站的经纬度; λ′、φ′分别是球坐标系下海洋潮汐负荷点的经纬度; HL、H分别为近、远区海潮瞬时潮高; SL和SG-L分别代表台站的近和远海区域; ρ为海水密度; R为地球半径; G(ψ, A)为重力负荷格林函数。

全球海潮模型Eot11a是德国DGFI(Deutsches Geodätisches Forschungs Institut)以FES2004模型为基础, 依据1992年至2010年的TOPEX/Poseidon(T/P)、Jason-1/2、ERS-2和Envisat等测高卫星的调和分析资料作经验性改正而得到的模型, 分辨率为1/8°×1/8°(见文献[24])。CATS2008是包含整个南大洋的高精度南极区域海潮模型, 范围是56°S以南的整个区域, 网格分辨率为4 km×4 km, 以天文引潮位和全球海潮模型TPXO7.1的海潮高作为求解线性浅水方程的限制条件, 其同化数据包括:无冰区的T/P雷达测高资料, 50个高精度潮汐记录数据集(底部气压计、沿岸验潮站和GPS记录等, 具体信息参考Antarctic Tide Gauge Database)以及ICESat激光测高卫星获取的罗斯和龙尼-菲尔希纳冰架的表面高资料[25]。其中, 卫星T/P和Jason-1/2可观测的最南端为66.2°S, ERS-2和Envisat为81.5°S, 而ICESat为86.0°S。而南极最大的两个冰架(龙尼-菲尔希纳和罗斯冰架)的浮冰区分别延伸到83.0°S和85.4°S, 因此只有ICESat测高卫星的观测范围可以覆盖整个南极冰盖的浮冰区, 为精化海潮模型提供必要的观测资料。

海潮模型Eot11a和CATS2008均给出了主要潮波在网格节点上的潮高信息(振幅及相位), 考虑到长周期潮波振幅较小且容易受区域环境因素的影响, 因此, 计算了4个周日(Q1、O1、P1和K1)及4个半周日(M2、N2、S2和K2)潮波潮高模型振幅与验潮站观测振幅之间的差异diffi, 具体数值结果见表 3。此外, 还计算了周日潮与半日潮几个主要潮波潮高模型振幅与验潮站观测振幅之差的和, 分别用diffD和diffSD表示。由表 3可知, 在周日频段, 对于Q1和O1潮波, Eot11a模型值比CATS2008更接近潮汐的实际观测值, P1与K1潮波则相反, 但两模型的diffD值基本相当。而在半周日频段中, 除N2潮波外, 其他潮波的CATS2008模型值比Eot11a更接近潮汐的实际观测值, 其中M2波的差值从3.7 cm(Eot11a-TGOTP)下降到1.6 cm(CATS2008-TGOTP)。

表 3 潮高模型振幅与验潮站观测振幅之差 Tab. 3 The tidal amplitude's difference between model values and observations of the tide gauge
cm
模型与观测值差 Eot11a-TGOTP CATS2008-TGOTP
diffQ1 0.092 0.110
diffO1 0.093 0.962
diffP1 1.150 0.466
diffK1 2.885 2.842
diffD 4.220 4.380
diffN2 0.542 1.041
diffM2 3.718 1.589
diffS2 1.909 1.345
diffK2 1.567 1.131
diffSD 7.736 5.106
注:diff表示两者间的差异; TGOTP为通过验潮站资料获得的海潮潮高参数; Eot11a和CATS2008分别为海潮潮高模型值; diffD为4个周日潮波的潮高模型振幅与验潮站观测振幅之差的和; diffSD为4个半周日潮波的潮高模型振幅与验潮站观测振幅之差的和。
表选项

根据式(5), 利用SPOTL软件[26], 计算了南极中山站主要潮波的重力海潮负荷效应, 为方便后文讨论, 将Eot11a全球海潮模型记为模型1, 将Eot11a全球海潮模型经CATS2008区域海潮模型修正后记为模型2, 将验潮站潮高资料替换模型2中以验潮站为中心的1/16°×1/16°网格区域后记为模型3, 具体数值结果列于表 4。可以看出, 利用模型2和模型3计算得到的重力海潮负荷效应相差很小(小于0.001 μGal)。这是因为模型CATS2008同化了中山站附近的戴维斯验潮站的观测资料, 而模型1和模型2计算得到的海潮对K1、M2和S2潮波的负荷效应的振幅之差达到0.1 μGal, 其他主要潮波振幅之间的差异小于0.1 μGal, 相位差异最大值为3.8°(K2)。

表 4 中山站主要潮波的重力海潮负荷矢量 Tab. 4 Gravity loading vectors for main waves at Zhongshan station
潮波 模型1 模型2 模型3
L/μGal α/(°) L/μGal α/(°) L/μGal α/(°)
Q1 0.533 2 -154.63 0.543 0 -153.22 0.542 7 -153.22
O1 2.249 8 -161.45 2.229 2 -161.19 2.228 2 -161.18
P1 0.665 3 -166.28 0.666 2 -163.63 0.665 9 -163.63
K1 1.994 0 -164.85 2.102 9 -163.84 2.101 8 -163.83
N2 0.547 8 -133.17 0.589 9 -135.93 0.589 7 -135.93
M2 1.678 9 -160.60 1.848 4 -163.02 1.847 7 -163.01
S2 0.787 5 89.83 0.945 0 90.83 0.944 2 90.85
K2 0.222 8 79.84 0.264 1 83.66 0.263 9 83.67
注:L为振幅; α为相位; 1 μGal=10-8 m/s2。
表选项

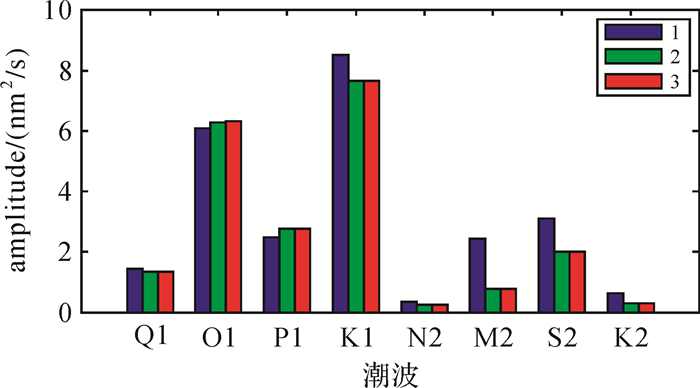
文献[27]利用超导重力仪器的潮汐观测资料研究了海潮模型的适定性问题, 为比较海潮模型CATS2008和Eot11a在南极地区的精度, 计算了主要潮波重力潮汐参数的最终残差, 其振幅越小, 说明模型精度越高。本文利用与验潮站相同观测区间的中山站固体潮观测资料获得重力潮汐参数, 根据矢量叠加原理, 减掉理论重力潮汐参数, 并作海潮负荷效应改正, 即得到各潮波的最终残差, 具体数值结果列于表 5, 振幅如图 2所示。结果表明, 在周日频段内, K1波经模型2作海潮负荷改正后, 最终振幅残差比经模型1作负荷改正时下降了0.8 nm/s2, 下降幅度为9.84%, 其他潮波的最终残差变化不明显; 在半周日频段, N2、M2、S2和K2潮波的最终残差振幅均减小, 其中, M2和S2最终残差振幅分别下降了1.6和1.2 nm/s2, 下降幅度分别为56.14%和37.08%。综上, 可证明南极区域海潮模型CATS2008计算的重力海潮负荷效应比全球海潮模型Eot11a的计算值更接近实际观测值, 即模型CATS2008修正模型Eot11a在南极地区是有效的。这是因为前者同化了南极地区多个高精度验潮站资料以及ICESat测高卫星获取的罗斯和龙尼-菲尔希纳冰架浮冰区的数据信息。但O1、K1潮波残差矢量仍然较大, 原因是其对应的理论振幅大, 分别达到了205和288 nm/s2, 经模型2作海潮负荷效应改正得到的最终残差振幅与理论振幅的比值分别为3.24%和2.60%, 相应的, Q1、P1、N2、M2、S2和K2的比值分别为3.83%、3.24%、2.08%、1.29%、4.54%和2.45%。这表明经海潮负荷效应改正后, 各主要潮波观测振幅与理论值的相对差异在同一个量级。

表 5 中山站主要潮波最终残差矢量 Tab. 5 The final residual vectors for main waves at Zhongshan station
潮波 模型1 模型2 模型3
L/μGal ph/(°) L/μGal ph/(°) L/μGal ph/(°)
Q1 0.154 5 6.70 0.150 5 0.70 0.150 7 0.75
O1 0.641 8 2.86 0.664 4 2.50 0.665 5 2.49
P1 0.278 5 -66.02 0.308 8 -68.07 0.308 8 -67.01
K1 0.833 0 -7.52 0.751 0 -13.34 0.752 1 -13.32
N2 0.074 8 -13.90 0.037 2 -50.66 0.037 1 -50.35
M2 0.275 4 14.91 0.120 8 47.30 0.121 2 47.00
S2 0.313 4 64.09 0.197 2 39.14 0.197 9 39.26
K2 0.060 4 -49.97 0.028 9 -6.09 0.028 8 -6.49
注:L为最终残差振幅; ph为最终残差的相位。
表选项

图 2 中山站主要潮波最终残差振幅 Fig. 2 Amplitudes of the final residual vectors for main waves at Zhongshan station
图选项

最后, 利用模型2对本文1.1节中相应的主要重力潮汐参数作海潮负荷效应改正, 得到主要长周期(MM和MF)、周日(O1、K1、P1和Q1)和半周日(M2、S2、N2和K2)潮波的振幅因子, 具体数值结果见表 1。相应的, 与文献[15]给出的理论振幅因子的相对差异分别为0.38%、4.28%、5.12%、4.63%、2.27%、3.31%、2.43%、3.39%、4.00%和1.77%, 这主要由海潮模型的不确定性、仪器观测误差及区域环境等引起。

3 结语

基于南极中山站重力潮汐及海洋潮汐观测序列, 采用调和分析方法精密确定了重力潮汐参数及潮高值, 分别反映了该地区的重力和海洋潮汐特征。计算结果表明, O1和M2潮波的重力振幅因子观测相对精度分别为0.06%和0.08%, 而MM和MF潮波的对应值分别为9.05%和2.85%, 说明虽然在两极地区长周期潮波振幅大, 但由于容易受到干扰信号(弹簧重力仪的漂移、冰盖的消融和凝固等)的影响, 造成观测精度不高。计算了全球海潮模型Eot11a和区域海潮模型CATS2008在中山验潮站的潮高模型值, 进而计算了潮高模型振幅与验潮站实际观测振幅的差值, 使用CATS2008对Eot11a相应区域作了修正(记为模型2), 并对其进行了有效性检验。研究表明, 在周日频段, 模型Eot11a和CATS2008提供的4个潮波潮高模型振幅与验潮站观测振幅之差的和基本相当, 而在半周日频段, 对应值分别为7.7 cm和5.1 cm, 与利用模型Eot11a作海潮负荷效应改正相比, 使用模型2时, Q1、K1、N2、M2、S2和K2潮波的最终残差振幅均减小, 其中, 潮波K1、M2和S2分别下降了0.82、1.55和1.16 nm/s2, 证明了在南极地区用区域模型修正全球海潮模型的有效性, 因此, 今后在研究该地区的区域动力学问题时, 必须使用区域海潮模型修正后的全球模型计算海潮负荷效应。


参考文献
[1] SHEPHERD A, PEACOCK N R. Ice Shelf Tidal Motion Derived from ERS Altimetry[J]. Journal of Geophysical Research, 2003, 108(C6): 3189. DOI:10.1029/2001JC001130
[2] VELICOGNA I, WAHR J. Measurements of Time-variable Gravity Show Mass Loss in Antarctica[J]. Science, 2006, 311(5768): 1754–1756. DOI:10.1126/science.1123785
[3] 张胜凯, 雷锦韬, 李斐. 全球海潮模型研究进展[J]. 地球科学进展, 2015, 30(5): 579–588.
ZHANG Shengkai, LEI Jintao, LI Fei. Advances in Global Ocean Tide Models[J]. Advances in Earth Science, 2015, 30(5): 579–588. DOI:10.11867/j.issn.1001-8166.2015.05.0579
[4] 刘清超, 孙和平, 徐建桥, 等. 南极中山与昭和站重力海潮负荷效应及背景噪声研究[J]. 地球物理学报, 2016, 59(8): 2773–2782.
LIU Qingchao, SUN Heping, XU Jianqiao, et al. The Research of Ocean Tide Loading Effects on Gravity and Ambient Noise at Zhongshan and Syowa Station in Antarctic[J]. Chinese Journal of Geophysics, 2016, 59(8): 2773–2782. DOI:10.6038/cjg20160805
[5] KIM T H, SHIBUYA K, DOI K, et al. Validation of Global Ocean Tide Models Using the Superconducting Gravimeter Data at Syowa Station, Antarctica, and in Situ Tide Gauge and Bottom-pressure Observations[J]. Polar Science, 2011, 5(1): 21–39. DOI:10.1016/j.polar.2010.11.001
[6] 周江存, 孙和平. 用东海和南海潮汐资料修正全球海潮模型对中国及邻区重力场负荷计算的影响[J]. 地震学报, 2005, 27(3): 332–338.
ZHOU Jiangcun, SUN Heping. Influence of the Modified Global Ocean Tide Model with Local Tides of East and South China Seas on Load Gravity in China and Its Neighbor Area[J]. Acta Seismologica Sinica, 2005, 27(3): 332–338.
[7] PADMAN L, KOTTMEIER C. High-frequency Ice Motion and Divergence in the Weddell Sea[J]. Journal of Geophysical Research, 2000, 105(C2): 3379–3400. DOI:10.1029/1999JC900267
[8] 孙和平, 许厚泽, 徐建桥, 等. 重力场的潮汐变化观测及其研究[J]. 地球科学进展, 2000, 15(1): 53–57.
SUN Heping, XU Houtze, XU Jianqiao, et al. Observation and Study of the Tidal Variation in Gravity Field[J]. Advance in Earth Sciences, 2000, 15(1): 53–57.
[9] 徐建桥, 孙和平, 周江存. 南极中山站重力潮汐观测的海潮负荷效应[J]. 测绘学报, 2002, 31(3): 228–233.
XU Jianqiao, SUN Heping, ZHOU Jiangcun. Loading Effects of the Ocean Tides on the Tidal Gravity Observations at Zhongshan Station in the Antarctic[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(3): 228–233.
[10] 胡胜利. 南极中山站天气系统和气象要素变化[J]. 海洋预报, 2001, 18(1): 34–39.
HU Shengli. The Variation of Weather System and Meteorological Elements[J]. Marine Forecasts, 2001, 18(1): 34–39. DOI:10.11737/j.issn.1003-0239.2001.01.005
[11] 黄继锋, 鄂栋臣, 张胜凯, 等. 南极中山验潮站的数据处理与分析[J]. 大地测量与地球动力学, 2012, 32(5): 63–67.
HUANG Jifeng, E Dongchen, ZHANG Shengkai, et al. Processing and Analysis of Tidal Data for Zhongshan Station, East Antarctica[J]. Journal of Geodesy and Geodynamics, 2012, 32(5): 63–67.
[12] VAN CAMP M, VAUTERIN P. Tsoft:Graphical and Interactive Software for the Analysis of Time Series and Earth Tides[J]. Computers & Geosciences, 2005, 31(5): 631–640.
[13] WAHR J M. Deformation Induced by Polar Motion[J]. Journal of Geophysical Research, 1985, 90(B11): 9363–9368. DOI:10.1029/JB090iB11p09363
[14] WENZEL H G. The Nanogal Software:Earth Tide Data Processing Package ETERNA 3.30[J]. Bulletin d'Informations Mareés Terrestres, 1996, 124: 9425–9439.
[15] DEHANT V, DEFRAIGNE P, WAHR J M. Tides for a Convective Earth[J]. Journal of Geophysical Research, 1999, 104(B1): 1035–1058. DOI:10.1029/1998JB900051
[16] IWANO S, FUKUDA Y, SATO T, et al. Long-period Tidal Factors at Antarctica Syowa Station Determined from 10 Years of Superconducting Gravimeter Data[J]. Journal of Geophysical Research, 2005, 110(B10): B10403. DOI:10.1029/2004JB003551
[17] FOREMAN M G G, CHERNIAWSKY J Y, BALLANTYNE V A. Versatile Harmonic Tidal Analysis:Improvements and Applications[J]. Journal of Atmospheric and Oceanic Technology, 2009, 26(4): 806–817. DOI:10.1175/2008JTECHO615.1
[18] CARTWRIGHT D E, TAYLER R J. New Computations of the Tide-generating Potential[J]. Geophysical Journal International, 1971, 23(1): 45–73.
[19] FOREMAN M G G. Manual for Tidal Heights Analysis and Prediction[R]. Victoria: Institute of Ocean Sciences, 1977.
[20] GOLUB G H, VAN LOAN C F. Matrix Computations[M]. Baltimore: The Johns Hopkins University Press, 1983.
[21] 鄂栋臣, 黄继锋, 张胜凯. 南极中山站潮汐特征分析[J]. 武汉大学学报(信息科学版), 2013, 38(4): 379–382, 464.
E Dongchen, HUANG Jifeng, ZHANG Shengkai. Analysis of Tidal Features of Zhongshan Station, East Antarctic[J]. Geomatics and Information Science of Wuhan University, 2013, 38(4): 379–382, 464.
[22] FARRELL W E. Deformation of the Earth by Surface Loads[J]. Reviews of Geophysics, 1972, 10(3): 761–797. DOI:10.1029/RG010i003p00761
[23] 许厚泽. 固体地球潮汐[M]. 武汉: 湖北科学技术出版社, 2010.
XU Houze. Solid Earth Tide[M]. Wuhan: Hubei Science and Technology Press, 2010.
[24] SAVCENKO R, BOSCH W. EOT11A-empirical Ocean Tide Model from Multi-mission Satellite Altimetry[R]. München: Deutsches Geodätisches Forschungs Institut (DGFI), 2012.
[25] PADMAN L, EROFEEVAR L, FRICHER H, et al. CATS2008a_opt: Circum-Antarctic Tidal Simulation Inverse Model Version 2008a. 2008.
[26] AGNEW D C. SPOTL: Some Programs for Ocean-tide Loading[R]. [S. l. ]: Scripps Institution of Oceanography, 2012.
[27] 孙和平, 许厚泽, 罗少聪, 等. 用超导重力仪的潮汐观测资料研究海潮模型[J]. 测绘学报, 1999, 28(2): 115–120.
SUN Heping, XU Houze, LUO Shaocong, et al. Study of the Ocean Models Using Tidal Gravity Observations Obtained with Superconducting Gravimeter[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(2): 115–120.
http://dx.doi.org/10.11947/j.AGCS.2018.20170123
中国科学技术协会主管、中国测绘地理信息学会主办。
0

文章信息

刘清超，孙和平，王泽民，陈晓东，张胜凯，徐建桥
LIU Qingchao, SUN Heping, WANG Zemin, CHEN Xiaodong, ZHANG Shengkai, XU Jianqiao
南极中山站的重力和区域海洋潮汐特征
The Characteristics of Gravity and Regional Ocean Tides at Zhongshan Station in Antarctic
测绘学报，2018，47(3)：316-323
Acta Geodaetica et Cartographica Sinica, 2018, 47(3): 316-323
http://dx.doi.org/10.11947/j.AGCS.2018.20170123

文章历史

收稿日期：2017-03-16
修回日期：2017-07-24

相关文章

工作空间