BDS系统在2012年宣布正式提供区域服务后发展迅速, 预计于2020年建成覆盖全球的卫星导航系统[1]。随着全球导航卫星系统(global navigation satellite system, GNSS)的快速发展, 多系统精密单点定位(precise point positioning, PPP)体现出显著的优势, 已经成为当前的研究热点[2-11]。在多系统条件下, 非差非组合PPP处理多频数据更为灵活, 避免了观测量组合引起的噪声放大, 并且可以获得电离层延迟估计值, 有助于电离层建模研究[12-17]。因此, 研究多系统非差非组合PPP电离层延迟参数处理方法对于提高PPP的定位性能和电离层建模研究具有重要意义。
全球电离层图(global ionospheric map, GIM)的相关科研成果为进一步研究GNSS电离层延迟误差提供了有力支持。文献[18]研究了总电子含量(total electron content, TEC)参数和电离层图预测方法, 并对欧洲定轨中心(Center for Orbit Determination in European, CODE)提供的电离层图进行了验证。文献[19]总结了垂直总电子含量(vertical total electron content, VTEC)图的生成方法, 验证了VTEC图的可用性和典型VTEC变化周期。在此基础上不少学者开展了利用电离层先验改正模型提高GNSS定位性能的研究。文献[20]通过试验分析了电离层先验改正模型对单频GPS接收机的有效性并推荐采用GIM模型。文献[21]验证了利用区域电离层图提高单频PPP定位精度的可行性。文献[22]提出一种历元差分电离层延迟模型, 使用该电离层延迟模型能够将单频数据转换成双频数据, 有助于单频接收机估计对流层天顶延迟。文献[23]研究了非差非组合PPP电离层参数处理方法, 在使用电离层先验改正模型约束的基础上, 提出利用二阶平稳过程的变异函数描述电离层随机参数在历元间的相关性, 该方法可以提高单频PPP定位精度和收敛时间。文献[24]提出一种区域电离层建模方法, 该方法对每颗卫星的电离层延迟进行建模, 能够提高单频PPP定位精度和缩短双频PPP收敛时间。文献[25]采用电离层空间约束和电离层先验改正模型约束的方法进行了多系统非差非组合PPP试验, 结果表明多系统PPP能够有效缩短收敛时间和提高定位精度。
GIM电离层延迟改正量的精度较低, 一般仅有2~8 TECU(total electron content unit)[16], 传统电离层约束方法难以确定电离层先验改正量与实际观测量之间合适的权比关系。利用GIM进行电离层延迟约束时, 如果电离层先验改正量和实际观测量的权比配置不合理会对平差结果造成负面影响。本文提出一种电离层约束权因子搜索算法, 采用权因子对先验电离层改正量的方差进行调整, 根据验后残差加权平方和最小原则通过搜索找出较优的权因子。试验结果表明, 搜索算法可以提高静态PPP定位精度和收敛速度。
1 数学模型采用精密卫星钟差和差分码偏差(differential code bias, DCB)产品消除卫星钟差和卫星码硬件延迟后, 基于原始观测量的GPS/BDS精密单点定位伪距和相位观测方程可以表示为
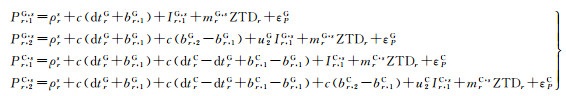 (1)
(1)
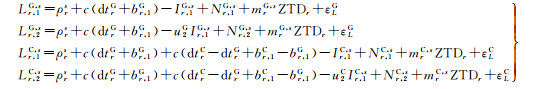 (2)
(2)
式中, 上标G和C分别表示GPS和BDS系统, 为方便叙述用上标T统一表示GPS和BDS系统; f为卫星信号的频率; Pr, fT, s和Lr, fT, s分别为接收机r和卫星s在频率f上的伪距和相位观测量, 单位为m; ρrs为卫星s天线相位中心至接收机r天线相位中心的几何距离; c为光在真空中的速度; dtrT为接收机钟差; br, fT为频率f上的接收机码硬件延迟; Ir, 1T, s=FrsIvr, 1T, s为卫星s在第1个频率上的斜电离层延迟, 可以用投影函数Frs和穿刺点处垂直电离层延迟Ivr, 1T, s的乘积表示, 实际参与平差的待估参数为Ivr, 1T, s; u2T=(λ2T/λ1T)2为频率相关的比例因子; λfT为频率f上的波长; ZTDr为接收机r的天顶对流层延迟; mrT, s为对流层延迟映射函数; Nr, fT, s为频率f上的相位模糊度, 模糊度吸收了相位硬件延迟和卫星码硬件延迟以及第1个频率上的接收机码硬件延迟br, 1T, 单位为m; εPT和εLT分别为伪距和相位观测误差包括观测噪声和多路径误差。
对式(1)和式(2)的参数进行合并, 新的参数可以表示为
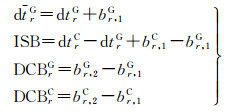 (3)
(3)
式中, dtrG为包含了偏差项的GPS接收机钟差; ISB为BDS相对GPS的系统间偏差, DCBrT为接收机差分码偏差。式(3)隐含的约束条件是令第1个频率上的接收机码硬件延迟br, 1T为零, 使其与接收机钟差dtrT合并。该模型改正了卫星端伪距硬件延迟, 分别估计接收机端伪距DCB和电离层参数, 使得估计出的电离层参数不再受硬件延迟的影响, 为电离层建模及附有电离层约束的PPP提供了一种新的参数估计方法。
1.1 传统电离层先验改正模型约束方法CODE提供的GIM每1 h给出1幅TEC图, 定义了格网点处的垂直方向总电子含量, 通过内插计算可以得到穿刺点处的垂直电离层延迟改正量。将GIM给出的垂直电离层延迟改正量作为虚拟观测量引入平差系统, 虚拟观测量的观测方程可以表示为
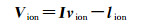 (4)
(4)
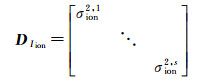 (5)
(5)
式中, Vion为虚拟观测量残差向量; Ivion=[Ivr, 1T, 1Ivr, 1T, 2…Ivr, 1T, s]为垂直电离层延迟参数向量, 上标s为该历元的卫星数; lion为垂直电离层延迟虚拟观测量向量; DIion为虚拟观测量的方差阵; σion2, s=σVTEC2(40.28×1016/(f1s)2)2为虚拟观测量的方差; f1s为卫星s的第1个频率; σVTEC2为穿刺点处垂直方向总电子含量的方差。
1.2 电离层约束权因子搜索算法电离层约束权因子搜索算法的基本思路是, 在传统电离层先验改正模型约束的基础上, 使用权因子对电离层虚拟观测量的方差阵进行调整, 采用该方差阵进行电离层延迟约束和平差计算, 以验后残差加权平方和最小为原则通过搜索找出较优的权因子, 利用验后残差动态调整电离层虚拟观测量的方差从而达到改善定位结果的目的。
搜索算法的具体流程为:第1步, 首次搜索时权因子从k=1开始; 第2步, 用权因子k乘以虚拟观测量方差阵, 采用该方差阵进行电离层延迟约束; 第3步, 在平差计算后记录下验后残差加权平方和的大小, 权因子k按搜索步长累加, 搜索步长为1;重复第2—3步直到找出搜索区间内验后残差加权平方和最小的权因子k, 利用该权因子得到的平差结果即为本历元的最终结果。下一历元从第1步开始重复该过程。验后残差加权平方和最小原则可以表示为
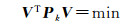 (6)
(6)
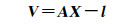 (7)
(7)
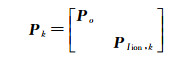 (8)
(8)
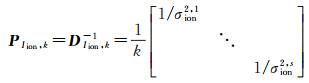 (9)
(9)
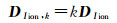 (10)
(10)
式中, V为实际观测量和虚拟观测量的残差向量; A为设计矩阵; X为待估参数向量; l为实际观测量和虚拟观测量; Pk为所有观测量的权阵包括实际观测量权阵Po和虚拟观测量权阵PIion, k; DIion, k为虚拟观测量方差阵DIion和权因子k相乘得到的方差阵。设单位权方差为1, 由于DIion, k为正定对角矩阵, PIion, k可以直接由DIion, k求逆获得。实际观测量的方差由高度角相关模型确定σo2=a2+a2/sin2(E), σo2为实际观测量的方差, E为卫星高度角, 对于伪距观测量a=0.6 m, 对于相位观测量a=0.003 m[26]。
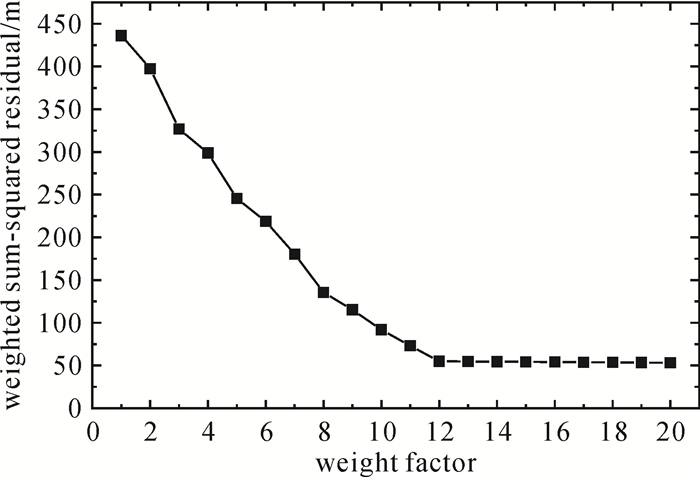
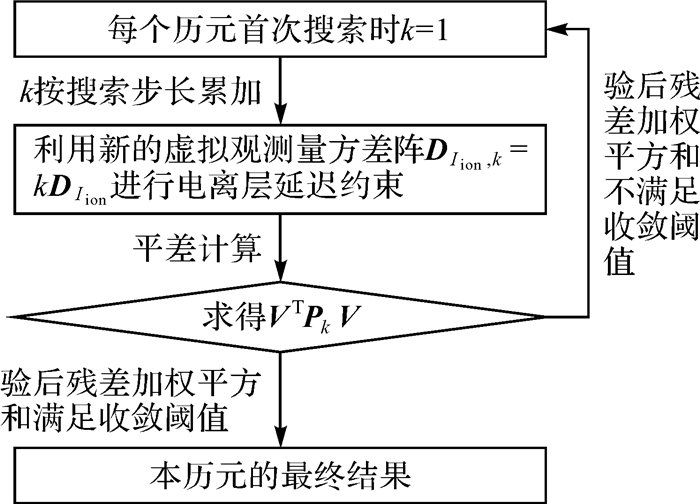
为确定高效的权因子搜索区间, 对权因子与验后残差加权平方和的关系进行试验分析, 试验结果见图 1。由图 1可知, 随着权因子的增加, 验后残差加权平方和逐步减小然后趋于平稳, 在收敛后如果权因子继续增加, 加权平方和的变化并不明显。由于GIM电离层延迟改正量的精度较低, 如果给定的改正量方差过小会导致验后残差增大。随着权因子的增加, 外部约束逐步减弱, 通过搜索算法得到虚拟观测量与实际观测量较优的权比关系后, 验后残差加权平方和趋于稳定。为了提高搜索效率, 在加权平方和收敛后停止搜索, 较优权因子为最后一次搜索时的数值, 设置收敛标准为相邻残差加权平方和的变化小于0.5 m。图 2给出了电离层约束权因子搜索算法的整体流程。此外, 由于残差二次型易受粗差的影响, 采用搜索算法时需进行粗差探测, 剔除受到粗差影响的观测量。
|
| 图 1 权因子与验后残差加权平方和的关系 Fig. 1 Relationships between the weight factors and the weighted sum-squared residuals |
|
| 图 2 电离层约束权因子搜索算法流程 Fig. 2 Flow chart for the weight factor searching algorithm based on ionospheric delay constraint |
2 试验与分析
为验证算法的有效性, 采用8个MGEX跟踪站(CUT0、KRGG、MOBS、NNOR、PERT、UCAL、YAR2和YEL2)2016年年积日21 d的数据进行试验。使用3种试验方案进行对比分析, 3种方案均使用GPS/BDS双频原始观测量, 数据处理策略基本相同, 详见表 1, 仅在电离层参数约束方法上有所区别:
| 类别 | 处理策略 |
| 观测量 | GPS+BDS伪距和相位原始观测量 |
| 估计方法 | 卡尔曼滤波 |
| 信号 | GPS:L1, L2;BDS:B1, B2 |
| 采样间隔 | 30 s |
| 截止角 | 7° |
| 观测值加权 | 采用高度角定权模型 |
| 卫星天线相位中心 | GPS的PCO和PCV采用IGS08.ATX提供的改正值; BDS的PCO和PCV采用ESA提供的改正值 |
| 接收机天线相位中心 | GPS的PCO和PCV采用IGS08.ATX提供的改正值; BDS采用与GPS相同的PCO和PCV改正值 |
| 相位缠绕 | 改正 |
| 潮汐效应 | 改正固体潮、海潮和极潮 |
| 卫星轨道和钟差 | 采用GFZ提供的精密轨道和精密钟差产品 |
| 卫星差分码偏差 | 采用MGEX提供的产品 |
| 对流层延迟 | Saastamoinen模型和随机游走过程 |
| 电离层延迟 | 作为白噪声估计 |
| 全球电离层图 | 采用CODE提供的GIM产品 |
| 接收机坐标 | 作为常数估计 |
| 接收机钟差 | 作为白噪声估计 |
| 接收机ISB | 在一天中作为常数估计 |
| 接收机DCB | 在一天中作为常数估计 |
| 模糊度 | 在连续弧段作为常数估计, 采用浮点解 |
方案1, 不采用电离层约束(简称为无约束方法)。
方案2, 采用传统电离层先验改正模型约束方法(简称为传统约束方法)。
方案3, 采用本文提出的电离层约束权因子搜索算法(简称为搜索算法)。
接收机DCB在静态模式下的估计精度较高, 因此选择进行静态PPP试验。试验分析部分从定位精度、收敛时间和接收机DCB估计精度三方面进行了详细分析。收敛标准为水平和高程定位精度均优于0.1 m, 对收敛后定位误差的均方根误差(root mean square, RMS)进行统计。以IGS发布的DCB产品作为接收机DCB参考值, 统计了接收机DCB估计值与参考值的差值。
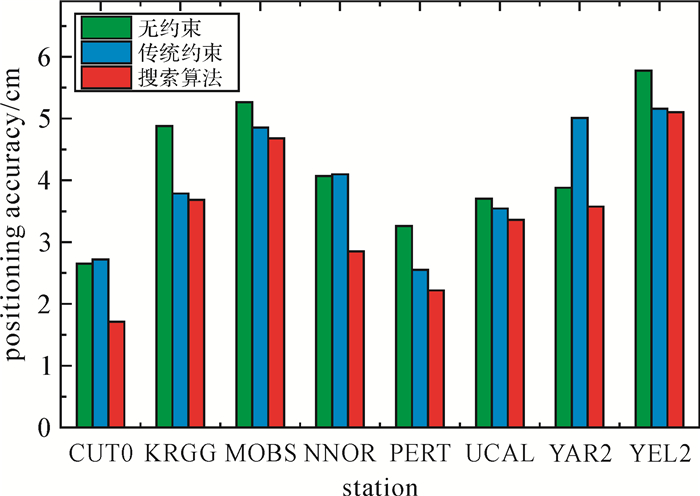
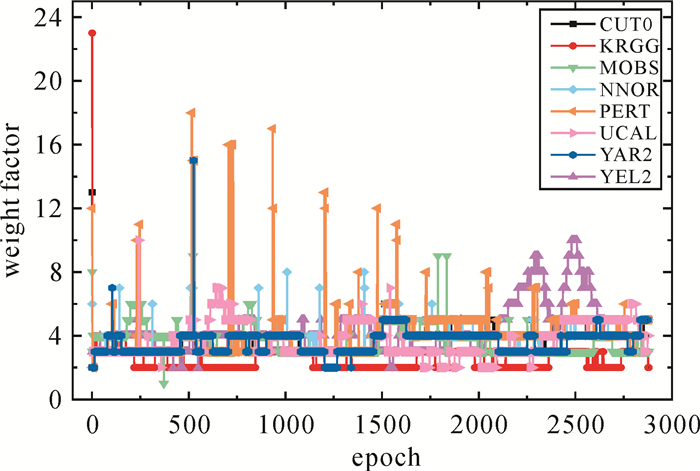
表 2对比了不同方案试验结果, 图 3给出了测站三维定位精度。由表 2可知, 无电离层约束方法的平均三维定位精度为4.19 cm。由图 3可知, 与无电离层约束相比, 传统约束方法的定位精度改进较小, 平均三维定位精度为3.96 cm, 而搜索算法的定位精度明显提高, 平均三维定位精度为3.40 cm。采用传统约束方法时, 部分测站的东向和北向定位精度变差, 东向平均定位精度由2.02 cm降低为2.14 cm。电离层延迟变化与空间水平梯度和电离层活跃程度密切相关, 因此GIM模型精度受到了一定限制[27]。由于GIM的精度较低, 仅为2~8 TECU, 在进行电离层约束时如果给定的电离层虚拟观测量的方差过小, 可能会引入较大误差。GIM模型误差和投影函数误差是部分分量定位精度变差的主要原因。图 4给出了搜索算法确定的权因子。由图 4可知, 权因子在不同历元能够动态调整, 基本稳定在2~6, 搜索算法采用的虚拟观测量方差大于传统约束方法。根据验后残差加权平方和最小原则, 采用搜索算法动态调整虚拟观测量方差的大小可以避免外部约束引起的残差过大, 对于改善平差结果具有显著作用。
| 测站 | 无约束 | 传统约束 | 搜索算法 | |||||||||||
| E/cm | N/cm | U/cm | 收敛时间/min | E/cm | N/cm | U/cm | 收敛时间/min | E/cm | N/cm | U/cm | 收敛时间/min | |||
| CUT0 | 1.32 | 1.69 | 1.56 | 29.0 | 1.27 | 1.89 | 1.49 | 38.5 | 1.16 | 0.82 | 0.96 | 26.5 | ||
| KRGG | 1.75 | 3.46 | 2.96 | 181.5 | 2.22 | 2.82 | 1.21 | 158.0 | 1.81 | 2.92 | 1.33 | 155.0 | ||
| MOBS | 2.44 | 2.10 | 4.17 | 20.5 | 2.61 | 2.39 | 3.32 | 26.0 | 2.28 | 2.03 | 3.55 | 11.0 | ||
| NNOR | 0.99 | 1.58 | 3.62 | 16.5 | 1.77 | 1.47 | 3.39 | 22.5 | 1.18 | 0.61 | 2.52 | 15.5 | ||
| PERT | 2.31 | 1.49 | 1.75 | 24.0 | 1.18 | 1.28 | 1.86 | 36.5 | 1.41 | 0.70 | 1.56 | 26.5 | ||
| UCAL | 2.03 | 0.85 | 2.98 | 116.5 | 2.56 | 1.14 | 2.17 | 105.5 | 2.15 | 0.91 | 2.42 | 88.0 | ||
| YAR2 | 2.00 | 1.35 | 3.04 | 27.0 | 3.53 | 0.97 | 3.42 | 9.0 | 2.21 | 0.53 | 2.76 | 6.5 | ||
| YEL2 | 3.32 | 4.62 | 0.99 | 207.5 | 1.94 | 3.44 | 3.32 | 214.0 | 1.35 | 4.51 | 1.97 | 150.5 | ||
| 平均 | 2.02 | 2.14 | 2.63 | 77.8 | 2.14 | 1.93 | 2.52 | 76.3 | 1.69 | 1.63 | 2.13 | 59.9 | ||
|
| 图 3 3种方案的三维定位精度 Fig. 3 3D positioning accuracies of PPP for the three strategies |
|
| 图 4 搜索算法确定的权因子 Fig. 4 Weight factors generated by the searching algorithm |
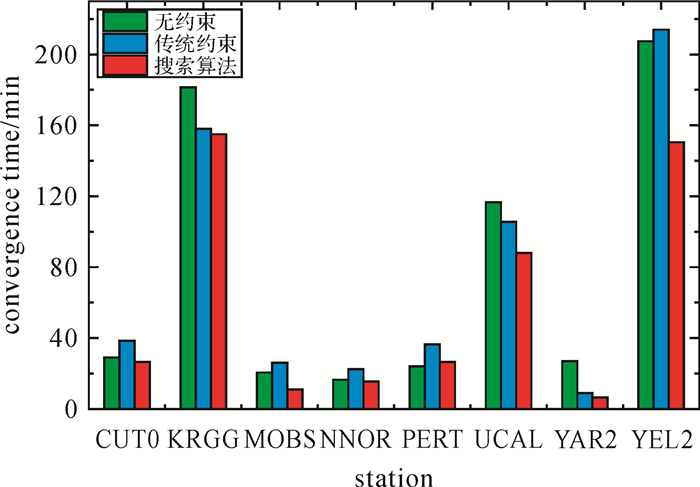
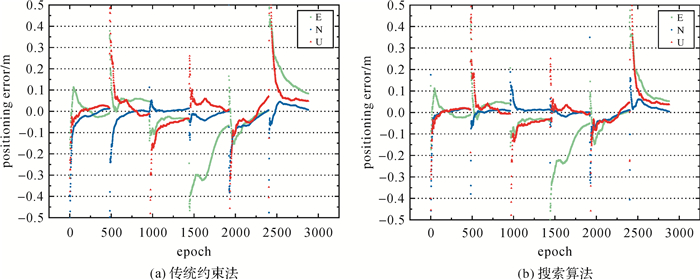
图 5给出了不同方案单天解的收敛时间。由图 5可知, 无电离层约束的平均收敛时间为77.8 min。与无电离层约束相比, 传统约束方法的改进较小, 平均收敛时间为76.3 min, 而搜索算法的收敛时间明显缩短, 平均收敛时间为59.9 min。电离层延迟约束为卡尔曼滤波提供了更多的新息向量, 搜索算法确定了虚拟观测量与实际观测量之间较优的权比关系, 二者可以加快状态参数分离, 提高收敛速度。为进一步验证传统约束方法和搜索算法在不同时段的收敛性能, 每隔4 h重置一次卡尔曼滤波器, 将一天分为6个时段, 对多时段的平均收敛时间进行统计。各测站多时段结果表明, 采用搜索算法后平均收敛时间由87.2 min缩短为68.6 min。以CUT0站为例, 图 6给出了多时段PPP收敛过程。由图 6可知, 搜索算法的收敛速度优于传统约束方法, 且各个时段的收敛时间并不相同, 其中第4时段(12:00—16:00)的收敛时间最长, 原因是电离层在地方时14:00左右最为活跃, 该时段GIM的改正效率较低。
|
| 图 5 不同方案单天解的收敛时间 Fig. 5 PPP convergence time of daily solutions with different strategies |
|
| 图 6 CUT0站多时段PPP收敛过程 Fig. 6 PPP convergence processin different time periodsat station CUT0 |
表 3给出了接收机DCB估计精度。当无电离层约束时, GPS-DCB和BDS-DCB的平均估计精度分别为1.49 ns和0.96 ns。传统约束方法的GPS-DCB和BDS-DCB平均估计精度分别为0.56 ns和0.68 ns, 搜索算法的GPS-DCB和BDS-DCB平均估计精度分别为0.53 ns和0.65 ns。IGS提供的接收机DCB参考值浮动范围约为1.0 ns[28]。3种方法接收机DCB平均估计精度的差异均小于1.0 ns, 处于参考值的浮动范围内。搜索算法和传统约束方法的DCB估计精度基本相当, 略优于无约束方法。
| ns | |||||||
| 测站 | GPS-DCB | BDS-DCB | |||||
| 无约束 | 传统约束 | 搜索算法 | 无约束 | 传统约束 | 搜索算法 | ||
| CUT0 | 1.96 | 0.64 | 0.59 | 0.48 | 0.61 | 0.61 | |
| KRGG | 0.92 | 0.81 | 0.70 | 0.58 | 0.80 | 0.77 | |
| MOBS | 2.12 | 0.44 | 0.49 | 2.17 | 0.25 | 0.27 | |
| NNOR | 2.12 | 0.36 | 0.31 | 0.20 | 0.50 | 0.48 | |
| PERT | 2.05 | 0.53 | 0.48 | 0.59 | 0.47 | 0.47 | |
| UCAL | 1.12 | 0.42 | 0.43 | 1.90 | 1.07 | 0.84 | |
| YAR2 | 1.59 | 0.49 | 0.45 | 0.68 | 0.67 | 0.66 | |
| YEL2 | 0.06 | 0.78 | 0.78 | 1.06 | 1.10 | 1.10 | |
| 平均 | 1.49 | 0.56 | 0.53 | 0.96 | 0.68 | 0.65 | |
3 结论
电离层先验改正模型约束是非差非组合PPP常用的电离层参数处理方法。针对GIM电离层改正量与实际观测量之间权比关系难以确定的问题, 本文提出一种电离层约束权因子搜索算法, 利用权因子对先验电离层改正量的方差阵进行调整, 使用该方差阵进行电离层延迟约束, 以验后残差加权平方和最小为原则通过搜索找出较优的权因子。采用8个MGEX跟踪站的GPS/BDS观测数据对该算法进行验证。静态试验结果表明:对比传统约束方法, 采用搜索算法后平均三维定位精度由3.96 cm提高到3.40 cm, 平均收敛时间由76.3 min缩短为59.9 min。
在非组合PPP电离层约束中, 要根据电离层改正模型精度进行合理定权。将先验电离层改正量作为虚拟观测量引入平差系统, 可认为实际观测量和虚拟观测量为两类观测量。搜索算法借鉴了方差分量估计方法的基本思想, 是该方法的一种简化形式。搜索算法的步骤较为简单, 具有易于实现、稳定性好的优点, 但缺点是搜索耗时较多, 占用计算资源。
| [1] |
朱永兴, 冯来平, 贾小林, 等.
北斗区域导航系统的PPP精度分析[J]. 测绘学报, 2015, 44(4): 377–383.
ZHU Yongxing, FENG Laiping, JIA Xiaolin, et al. The PPP Precision Analysis Based on BDS Regional Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4): 377–383. DOI:10.11947/j.AGCS.2015.20140082 |
| [2] | LOU Yidong, ZHENG Fu, GU Shengfeng, et al. Multi-GNSS Precise Point Positioning with Raw Single-frequency and Dual-frequency Measurement Models[J]. GPS Solutions, 2016, 20(4): 849–862. DOI:10.1007/s10291-015-0495-8 |
| [3] |
张小红, 左翔, 李盼, 等.
BDS/GPS精密单点定位收敛时间与定位精度的比较[J]. 测绘学报, 2015, 44(3): 250–256.
ZHANG Xiaohong, ZUO Xiang, LI Pan, et al. Convergence Time and Positioning Accuracy Comparison between BDS and GPS Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(3): 250–256. DOI:10.11947/j.AGCS.2015.20130771 |
| [4] |
任晓东, 张柯柯, 李星星, 等.
BeiDou、Galileo、GLONASS、GPS多系统融合精密单点[J]. 测绘学报, 2015, 44(12): 1307–1313.
REN Xiaodong, ZHANG Keke, LI Xingxing, et al. Precise Point Positioning with Multi-constellation Satellite Systems:BeiDou, Galileo, GLONASS and GPS[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1307–1313. DOI:10.11947/j.AGCS.2015.20140568 |
| [5] | LIU Yanyan, YE Shirong, SONG Weiwei, et al. Integrating GPS and BDS to Shorten the Initialization Time for Ambiguity-fixed PPP[J]. GPS Solutions, 2017, 21(2): 333–343. DOI:10.1007/s10291-016-0525-1 |
| [6] | CHEN Junping, WANG Jungang, ZHANG Yize, et al. Modeling and Assessment of GPS/BDS Combined Precise Point Positioning[J]. Sensors, 2016, 16(7): 1151. DOI:10.3390/s16071151 |
| [7] | CAI Changsheng, GAO Yang. Modeling and Assessment of Combined GPS/GLONASS Precise Point Positioning[J]. GPS Solutions, 2013, 17(2): 223–236. DOI:10.1007/s10291-012-0273-9 |
| [8] | CHOY S, BISNATH S, RIZOS C. Uncovering Common Misconceptions in GNSS Precise Point Positioning and Its Future Prospect[J]. GPS Solutions, 2017, 21(1): 13–22. DOI:10.1007/s10291-016-0545-x |
| [9] | TEGEDOR J, ØVSTEDAL O, VIGEN E. Precise Orbit Determination and Point Positioning Using GPS, GLONASS, Galileo and BeiDou[J]. Journal of Geodetic Science, 2014, 4(1): 65–73. |
| [10] | CHEN Junping, ZHANG Yize, WANG Jungang, et al. A Simplified and Unified Model of Multi-GNSS Precise Point Positioning[J]. Advances in Space Research, 2015, 55(1): 125–134. DOI:10.1016/j.asr.2014.10.002 |
| [11] | TU Rui, GE Maorong, ZHANG Hongping, et al. The Realization and Convergence Analysis of Combined PPP Based on Raw Observation[J]. Advances in Space Research, 2013, 52(1): 211–221. DOI:10.1016/j.asr.2013.03.005 |
| [12] | LIU Teng, YUAN Yunbin, ZHANG Baocheng, et al. Multi-GNSS Precise Point Positioning (MGPPP) Using Raw Observations[J]. Journal of Geodesy, 2017, 91(3): 253–268. DOI:10.1007/s00190-016-0960-3 |
| [13] |
王利, 张勤, 涂锐, 等.
基于原始观测值的单频精密单点定位算法[J]. 测绘学报, 2015, 44(1): 19–25.
WANG Li, ZHANG Qin, TU Rui, et al. A Kind of Single-frequency Precise Point Positioning Algorithm Based on the Raw Observations[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(1): 19–25. DOI:10.11947/j.AGCS.2015.20130315 |
| [14] |
张宝成, 欧吉坤, 袁运斌, 等.
基于GPS双频原始观测值的精密单点定位算法及应用[J]. 测绘学报, 2010, 39(5): 478–483.
ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Precise Point Positioning Algorithm Based on Original Dual-frequency GPS Code and Carrier-phase Observations and its Application[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 478–483. |
| [15] |
张宝成, 欧吉坤, 袁运斌, 等.
利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差[J]. 测绘学报, 2011, 40(4): 447–453.
ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Calibration of Slant Total Electron Content and Satellite-receiver's Differential Code Biases with Uncombined Precise Point Positioning Technique[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 447–453. |
| [16] |
章红平, 高周正, 牛小骥, 等.
GPS非差非组合精密单点定位算法研究[J]. 武汉大学学报(信息科学版), 2013, 38(12): 1396–1399.
ZHANG Hongping, GAO Zhouzheng, NIU Xiaoji, et al. Research on GPS Precise Point Positioning with Un-differential and Un-combined Observations[J]. Geomatics and Information Science of Wuhan University, 2013, 38(12): 1396–1399. |
| [17] |
张小红, 左翔, 李盼.
非组合与组合PPP模型比较及定位性能分析[J]. 武汉大学学报(信息科学版), 2013, 38(5): 561–565.
ZHANG Xiaohong, ZUO Xiang, LI Pan. Mathematic Model and Performance Comparison Between Ionosphere free Combined and Uncombined Precise Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 561–565. |
| [18] | SCHAER S. Mapping and Predicting the Earth's Ionosphere Using the Global Positioning System[D]. Bern, Swiss: University of Bern, 1999. |
| [19] | HERNÁNDEZ-PAJARES M, JUAN J M, SANZ J, et al. The IGS VTEC Maps:A Reliable Source of Ionospheric Information Since 1998[J]. Journal of Geodesy, 2009, 83(3-4): 263–275. DOI:10.1007/s00190-008-0266-1 |
| [20] | ØVSTEDAL O. Absolute Positioning with Single-frequency GPS Receivers[J]. GPS Solutions, 2002, 5(4): 33–44. DOI:10.1007/PL00012910 |
| [21] | CHOY S. Investigation into the Accuracy of Single Frequency Precise Point Positioning (PPP)[D]. Melbourne: RMIT University, 2009. |
| [22] | DENG Z, BENDER M, DICK G, et al. Retrieving Tropospheric Delays from GPS Networks Densified with Single Frequency Receivers[J]. Geophysical Research Letters, 2009, 36(19): L19802. DOI:10.1029/2009GL040018 |
| [23] | SHI Chuang, GU Shengfeng, LOU Yidong, et al. An Improved Approach to Model Ionospheric Delays for Single-frequency Precise Point Positioning[J]. Advances in Space Research, 2012, 49(12): 1698–1708. DOI:10.1016/j.asr.2012.03.016 |
| [24] | YAO Yibin, ZHANG Rui, SONG Weiwei, et al. An Improved Approach to Model Regional Ionosphere and Accelerate Convergence for Precise Point Positioning[J]. Advances in Space Research, 2013, 52(8): 1406–1415. DOI:10.1016/j.asr.2013.07.020 |
| [25] | LI Xingxing, ZHANG Xiaohong, REN Xiaodong, et al. Precise Positioning with Current Multi-constellation Global Navigation Satellite Systems:GPS, GLONASS, Galileo and BeiDou[J]. Scientific Reports, 2015, 5(1): 83–90. |
| [26] |
李盼. GNSS精密单点定位模糊度快速固定技术和方法研究[D]. 武汉: 武汉大学, 2016. LI Pan. Research on Methodology of Rapid Ambiguity Resolution for GNSS Precise Point Positioning[D]. Wuhan: Wuhan University, 2016. |
| [27] | TU Rui, ZHANG Hongping, GE Maorong, et al. A Real-time Ionospheric Model Based on GNSS Precise Point Positioning[J]. Advances in Space Research, 2013, 52(6): 1125–1134. DOI:10.1016/j.asr.2013.06.015 |
| [28] | ZHANG Hongping, GAO Zhouzheng, GE Maorong, et al. On the Convergence of Ionospheric Constrained Precise Point Positioning (IC-PPP) Based on Undifferential Uncombined Raw GNSS Observations[J]. Sensors, 2013, 13(11): 15708–15725. DOI:10.3390/s131115708 |


