2. 中国科学院上海天文台, 上海 200030;
3. 61876部队, 海南 三亚 572022
2. Shanghai Astronomical Observatory, the Chinese Academy of Sciences, Shanghai 200030, China;
3. 61876 Armies, Sanya 572022, China
北斗卫星导航系统提供广播星历和历书参数两种类型的卫星轨道参数[1], 广播星历参数通常用于导航定位解算, 历书参数通常用于辅助信号捕获[2-3]。高质量的历书数据能给出高精度的卫星运动状态信息, 减小接收机对初始码相位预估值和载波多普勒频移的搜索范围[4]。由于参数个数少、有效时间长, 历书参数还广泛应用于卫星可见性预报、星座性能评估[5]。历书参数包括钟差参数和用于计算卫星位置和速度的轨道参数, 接收机通过这两类参数估计拟捕获卫星信号的传播时延和视距多普勒, 从而大大缩短卫星信号捕获、跟踪的时间。本文仅讨论历书参数中的轨道参数。历书参数的设计可以在星历模型的基础上简化而来。描述北斗卫星轨道的历书参数为8个, 包括参考时刻toa, 6个参考时刻的开普勒根数(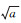
利用星间观测和通信实现的自主导航是新一代全球卫星导航系统的发展趋势, 为了保证星间测量和数据传输的实时性, 星间链路通常采用时分工作模式, 要求在每个短暂的时隙内, 要求每条测量链路完成信号的捕获、跟踪和解调, 由于星上资源受限, 给信号捕获时间和可靠性带来较大的挑战[8]。对于常规导航定位用户, 用户设备在跟踪捕获卫星信号后处于连续跟踪的状态, 历书精度只影响首次定位时间, 而对于时分体制的星间链路每个时隙可能需要切换跟踪不同卫星, 因此高精度的历书参数模型对于星间链路信号快速捕获显得尤为重要, 结合目前卫星软硬件条件, 要求历书精度优于10 km。目前历书参数的有效时长为7 d, 为了满足自主导航连续运行的需求, 需要地面系统采用一次注入多组历书参数, 增加了历书参数注入和卫星使用的复杂性, 同时占用较多星上存储资源。本文在北斗混合星座实际轨道基础上, 以一个自主运行周期90 d为时间尺度, 研究适当增加摄动参数达到增大拟合弧长、减少注入卫星的历书组数, 节约星上储存资源的目的。鉴于历书辅助跟踪捕获除了需要卫星位置外还需要计算卫星速度用于减少多普勒频移的不确定度, 本文将同时对卫星位置和速度的历书拟合精度进行评估, 以期满足星间链路测量和常规导航应用的需求, 为导航系统优化设计提供技术参考。
1 北斗长弧高精度历书参数设计和拟合 1.1 历书参数设计历书参数的设计原则是利用尽量少的参数实现尽量高精度的卫星位置拟合, 通常千米量级的拟合精度能满足信号捕获的需求。对于导航卫星, 由于其轨道高度较高, 因此历书参数设计时地球的非球型引力J2项和月球引力是主要考虑的摄动力。在主要摄动力的影响下, 存在长期变化和长周期变化的轨道根数具有如下规律:
(1) 升交点赤经Ω, 近点角距ω, 平近点角M存在长期变化, 其中影响最大的是J2项, 见式(1)[9]。其次为日月引力摄动, 同时这3个轨道根数具有一阶长周期变化, 最大项为日月引力摄动
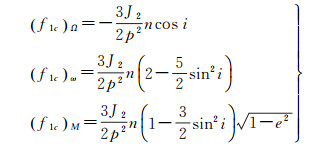 (1)
(1)
式中, (f1c)Ω、(f1c)ω、(f1c)M分别为J2项引起的升交点赤经Ω、近点角距ω和平近点角M的长期变化率; n为平均角速度; i为轨道倾角; e为轨道偏心率; p=a(1-e2); J2=1.082 63×10-3。
(2) 轨道倾角i存在一阶长周期项, 最大项为日月引力摄动, 见式(2)[10], 与文献[9]相比, 式(2)省略了量级较小的项。由于GEO卫星和IGSO卫星轨道高度较高, 在第三体引力摄动作用下其轨道倾角的长周期变化更为显著
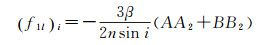 (2)
(2)
式中, (f1l)i为日月引力引起的轨道倾角长周期变化; β=m′Re3/Mer′3; m′为月球或太阳质量; Me为地球质量; r′为月地距离或日地距离; Re为地球半径。A、A2、B、B2与卫星轨道根数、日月轨道根数以及日月位置相关[10]。
利用平均角速度的修正值Δn主要吸收M和ω的长期项和长周期项, 利用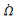
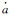

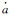
由于长期项随时间增长具有累积效应, 通过初步量级归算[16], 对于GEO和IGSO卫星, 忽略Δn, idot长期项的影响, 在90 d的弧长内能引起几百公里量级的位置误差。对于GEO和IGSO卫星, 最大的共振田谐项J22使得定点在标称经度的静止卫星受到额外的切向引力加速度, 引起定点经度关于赤道稳定点的长周期平动点振动(类似单摆运动), 周期为1000~2000 d, 半长轴的变化则达到±35 km[17]。文献[18]计算了在主要几项田谐项影响下, 静止轨道半长轴的漂移速率与定点经度相关, 数值范围约为0~155 m/d, 北斗导航系统的GEO卫星的定点经度分布范围决定了大部分GEO卫星的半长轴的漂移速率大于100 m/d。忽略GEO卫星的半长轴漂移速率, 在90 d的弧长内能引起上千千米的位置误差。
设新的开普勒轨道根数历书模型为σ0, 根据上文的分析, 定义σ0为
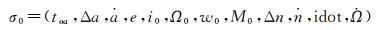 (3)
(3)
式中, i0为参考时刻的轨道倾角(北斗ICD中δi表示参考时间的轨道参考倾角的改正量), Δa为相对于轨道半径的参考值aref的变化值[13-14], 不同卫星类型具有不同的参考值aref。
1.2 历书用户算法利用历书计算卫星位置的方法与利用广播星历计算卫星位置的过程基本相同, 主要差异在于减少6个短周期摄动参数。其算法如下:
(1) 计算卫星平近点角
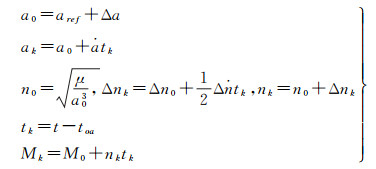 (4)
(4)
式中, μ为地球引力常数。
(2) 迭代计算偏近点角Ek
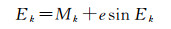 (5)
(5)
(3) 计算卫星矢径rk
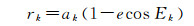 (6)
(6)
(4) 计算真近点角fk及纬度幅角
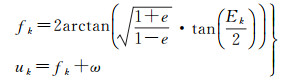 (7)
(7)
(5) 计算卫星在轨道平面坐标系的坐标。
卫星在轨道平面坐标系(X轴指向升交点)中的坐标为
 (8)
(8)
(6) 计算观测时刻升交点经度及轨道倾角
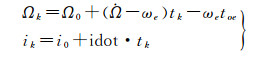 (9)
(9)
其中, Ω0参数为卫星历书在本周0时升交点到格林尼治子午线之间的经度。
(7) 计算卫星在cgcs2000中的位置
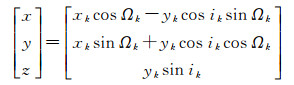 (10)
(10)
对式(10)求11个历书参数的一阶偏导数, 可得线性化的观测方程为
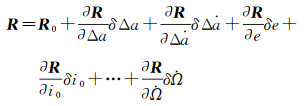 (11)
(11)
式中, R为观测历元t时刻地固坐标系下的卫星位置向量; R0为利用式(10)计算的卫星位置向量近似值; δΔa、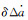
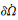
历书参数的正确拟合, 关键是对式(10)表达的地固下位置向量求历书参数的偏导数, 将拟合参数分为两组, 关于轨道面的参数(Δa, 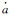

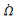
按照1.2节中的历书用户算法, 第一组参数与第二组参数之间相互独立, 对第一组参数求偏导数时, 所有第二组参数为常数。令P和Q分别为近地点单位矢量和半通径单位矢量(由地心处与轨道拱线垂直)[9]
 (12)
(12)
则卫星位置和速度矢量分别为[9]
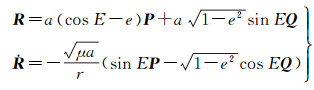 (13)
(13)
根据式(13)和(4)可得
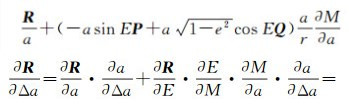 (14)
(14)
其中, 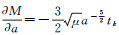
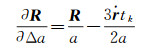 (15)
(15)
根据式(13)和式(4), 可得
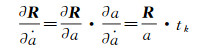 (16)
(16)
将式(8)代入式(10)可得
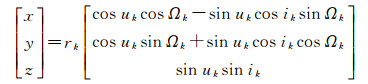 (17)
(17)
rk只与轨道面参数相关, 与轨道定向参数不相关, 因此认为rk为常数。利用式(7)、式(9)及式(17)即可求出卫星位置矢量对轨道定向参数的偏导数。
GEO卫星存在高轨道、小倾角等特点, 导致Δn与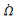
无论是广播星历还是历书参数, 参数只在拟合弧段内有效, 若超过拟合弧段, 卫星轨道位置精度会下降[6]。笔者尝试利用短期拟合的历书模型预报卫星轨道时, 出现轨道精度迅速衰减的现象。因此, 考虑延长历书参数的使用期限时, 需要先利用动力学方法对卫星轨道积分, 然后再进行历书拟合。
将国内区域监测网事后精密轨道拼接为弧长为10 d的数值轨道, 采用动力学平滑方法对离散轨道进行平滑, 得到高精度的动力学参数, 再通过轨道积分获取弧长为90 d的卫星的连续轨道。轨道动力学平滑与轨道改进过程相同, 二者的差别在于:轨道改进是利用实际观测量修正动力学参数, 而轨道拟合则是不需要实际观测量, 只需要已知一组卫星的状态矢量, 并将它们看成虚拟观测量来求解轨道参数[23]。这里利用6个初始轨道根数和伯尔尼模型的5个太阳光压参数[24]来描述整个弧段的轨道信息。通过对北斗三类卫星轨道预报90 d的精度进行评估, 发现轨道预报引起的URE小于600 m, 在90 d预报弧段内历书拟合过程引起的误差是主要因素, 本文主要分析历书拟合过程造成的误差。
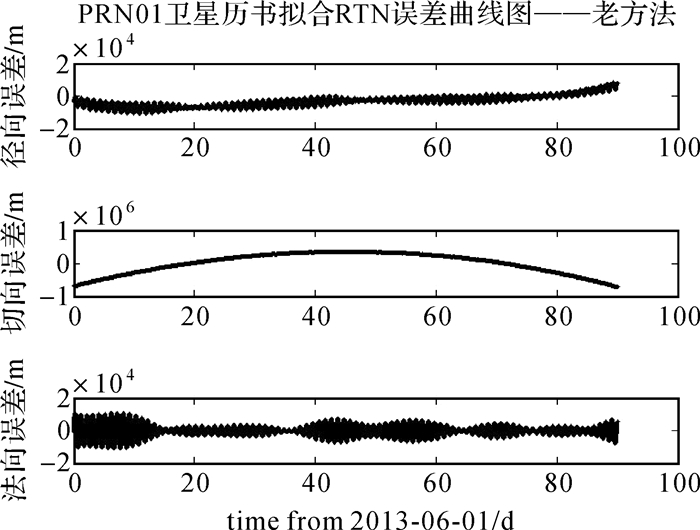
2.1 常规历书参数长弧拟合精度分析 2.1.1 卫星位置拟合精度常规历书拟合模型采用6个轨道根数和1个升交点赤经变率作为待估计的未知参数, 采用90 d拟合弧长考察该模型的长弧拟合性能。忽略数值轨道自身的预报误差, 以数值轨道的历书拟合内符合残差为统计对象。图 1—图 3描述了各类卫星的历书拟合在径向、沿迹和法向方向的误差细节图。对于GEO和IGSO卫星沿迹方向误差最大, 90 d拟合弧段内该方向最大拟合误差达到百公里量级, 而径向和法向两方向误差较小; 对于MEO卫星沿迹和法向方向拟合误差较大, 90 d拟合弧段内最大拟合误差达到10千米量级, 径向拟合误差较小; 总体而言GEO和IGSO卫星的拟合误差比MEO卫星的拟合误差大一个数量级。对于星间测量, 历书参数用于辅助搜星和信号捕获的性能主要受卫星位置误差在观测方向的投影的影响, 最大的影响为两颗卫星的位置误差之和; 对于地面的导航定位用户, 主要取决于卫星位置误差在用户距离方向的投影即用户距离误差(user range error, URE)。普通意义上的URE是指利用导航卫星广播的卫星星历和钟差计算的卫星位置误差和钟差误差在用户和卫星视线方向的投影, 这里的URE是指广播星历拟合过程中产生的拟合位置误差在用户距离方向的投影。拟合URE的计算公式为
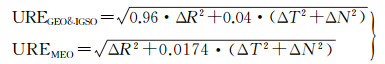 (18)
(18)
|
| 图 1 GEO卫星常规历书拟合三维位置误差曲线图 Fig. 1 The almanac fitting position error curve of GEO satellite with conventional model |
|
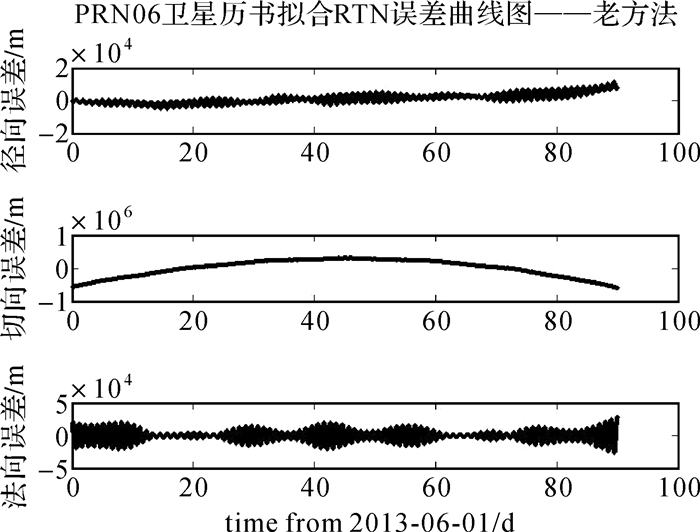
| 图 2 IGSO卫星常规历书拟合三维位置误差曲线图 Fig. 2 The almanac fitting position error curve of IGSO satellite with conventional model |
|
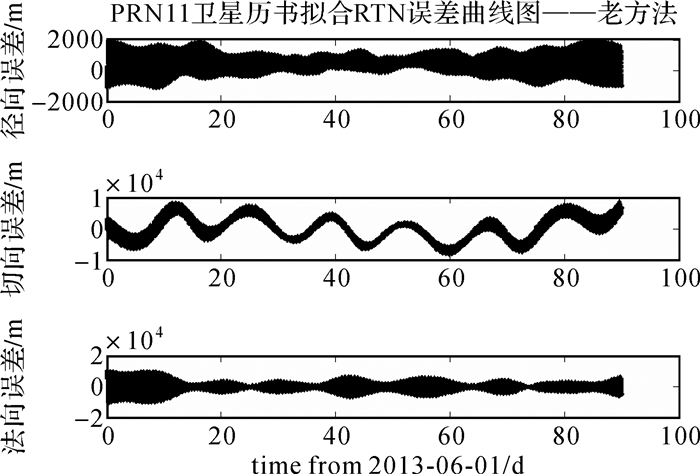
| 图 3 MEO卫星常规历书拟合三维位置误差曲线图 Fig. 3 The almanac fitting position error curve of MEO satellite with conventional model |
表 1列出了采用常规历书拟合模型对北斗在轨卫星进行90 d弧长的历书拟合的URE和位置误差。其中SAT01-05为GEO卫星, 06-10为IGSO卫星, 11-14为MEO卫星。GEO和IGSO卫星平均拟合位置误差约为200 km, URE约为40 km, MEO卫星平均的拟合位置误差约5 km。显然对于GEO卫星和IGSO卫星, 采用常规历书拟合模型拟合误差过大, 导致星间、星地辅助捕获的计算时间大幅度增加。
| km | ||||||||
| PRN | 位置误差 | 拟合URE | PRN | 位置误差 | 拟合URE | PRN | 位置误差 | 拟合URE |
| 01 | 314.4 | 63.0 | 06 | 259.2 | 51.9 | 11 | 5.2 | 1.1 |
| 02 | 82.6 | 16.7 | 07 | 255.7 | 51.2 | 12 | 5.2 | 1.1 |
| 03 | 413.4 | 82.8 | 08 | 230.8 | 46.2 | 14 | 6.3 | 1.1 |
| 04 | 35.5 | 12.2 | 09 | 171.5 | 34.4 | — | ||
| 05 | 216.9 | 43.6 | 10 | 143.2 | 28.7 | — | ||
| 平均 | 212.6 | 43.7 | 平均 | 212.1 | 42.5 | 平均 | 5.5 | 1.1 |
2.1.2 卫星速度拟合精度
利用式(4)—式(10)依次对偏近点角、卫星矢径、纬度幅角、轨道平面坐标、地固系坐标计算变率, 可计算任意历元的卫星速度, 具体过程可参考文献[25—26]。历书拟合采用的数值轨道通常包含卫星在地固下的速度信息, 以数值轨道的速度信息为基准, 考察卫星速度的计算误差。表 2列出了采用常规拟合模型90 d弧长的速度拟合精度统计。总体而言, GEO和IGSO卫星的速度误差比MEO卫星的速度误差大一个数量级。GEO和IGSO卫星速度误差RMS平均值约为15 m/s, 最大值约为35 m/s。对于MEO卫星速度误差RMS平均值约为0.7 m/s, 最大值约为1.7 m/s。
| m/s | ||||||||
| PRN | RMS | 最大值 | PRN | RMS | 最大值 | PRN | RMS | 最大值 |
| 01 | 22.92 | 52.04 | 06 | 18.90 | 43.23 | 11 | 0.69 | 1.51 |
| 02 | 6.02 | 13.78 | 07 | 18.65 | 41.66 | 12 | 0.69 | 1.52 |
| 03 | 30.13 | 68.02 | 08 | 16.82 | 38.22 | 14 | 0.85 | 2.29 |
| 04 | 2.51 | 5.60 | 09 | 12.51 | 28.74 | — | ||
| 05 | 15.81 | 36.37 | 10 | 10.44 | 24.04 | — | ||
| 平均 | 15.31 | 35.17 | 平均 | 15.46 | 35.18 | 平均 | 0.74 | 1.77 |
2.2 新历书模型长弧拟合精度分析 2.2.1 卫星位置拟合精度
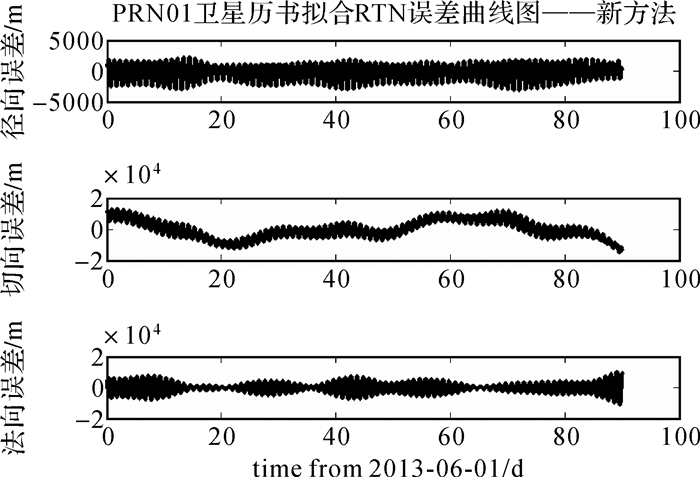
新历书拟合模型采用6个轨道根数和5个摄动参数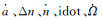
|
| 图 4 GEO卫星新历书拟合三维位置误差曲线图 Fig. 4 The almanac fitting position error curve of GEO satellite with the new model |
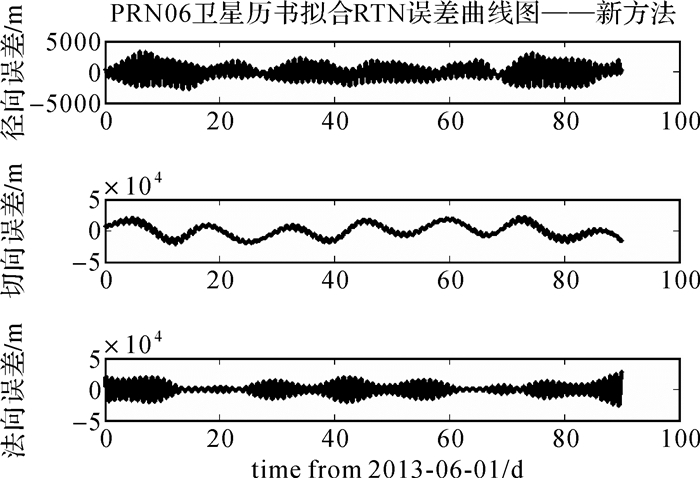
|
| 图 5 IGSO卫星新历书拟合三维位置误差曲线图 Fig. 5 The almanac fitting position error curve of IGSO satellite with the new model |
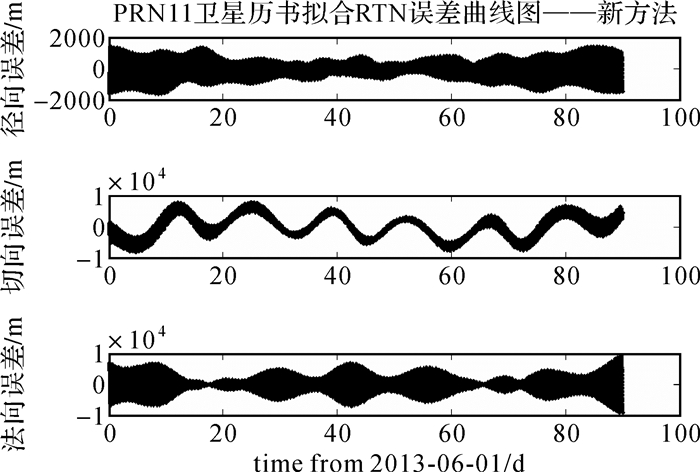
|
| 图 6 MEO卫星新历书拟合三维位置误差曲线图 Fig. 6 The almanac fitting position error curve of MEO satellite with the new model |
表 3列出了采用新历书模型对北斗在轨卫星进行90 d弧长的历书拟合的URE和位置误差。GEO卫星平均拟合位置误差约为6 km, URE约为1.5 km; IGSO卫星平均拟合位置误差约为11 km, URE约为2 km; MEO卫星平均拟合位置误差约为5 km, URE约为900 m。对于时分体制的星间链路观测, 要求接收设备能够快速捕获信号, 因此历书参数用于信号捕获和轨道预报时, 不但关心统计意义的拟合精度, 更关心任意时刻的拟合最大误差。表 3同时列出了新拟合方法90 d弧长拟合最大误差统计。GEO卫星的最大拟合位置误差为22 km, IGSO卫星的最大拟合位置误差为32 km, MEO卫星的最大拟合位置误差为12 km。
| km | ||||||||||||||
| PRN | 位置误差 | 拟合URE | PRN | 位置误差 | 拟合URE | PRN | 位置误差 | 拟合URE | ||||||
| RMS | MAX | RMS | MAX | RMS | MAX | RMS | MAX | RMS | MAX | RMS | MAX | |||
| 01 | 6.9 | 18 | 1.5 | 3.7 | 06 | 13.8 | 32 | 2.2 | 6.4 | 11 | 4.7 | 11 | 0.9 | 2.5 |
| 02 | 5.5 | 13 | 1.4 | 3.3 | 07 | 7.5 | 19 | 1.5 | 3.8 | 12 | 4.7 | 11 | 0.9 | 2.6 |
| 03 | 7.1 | 20 | 1.6 | 4.3 | 08 | 12.2 | 28 | 2.0 | 5.6 | 14 | 4.9 | 12 | 0.7 | 2.4 |
| 04 | 5.3 | 14 | 1.5 | 4.0 | 09 | 13.5 | 30 | 2.1 | 6.1 | — | ||||
| 05 | 8.0 | 22 | 1.6 | 4.5 | 10 | 9.6 | 24 | 1.7 | 4.9 | — | ||||
| 平均 | 6.6 | 22 | 1.5 | 4.5 | 平均 | 11.3 | 32 | 1.9 | 6.4 | 平均 | 4.8 | 12 | 0.9 | 2.4 |
2.2.2 卫星速度拟合精度
表 4列出了采用新历书拟合模型90 d弧长的速度拟合精度统计, 对比表 2, 新模型比常规模型的历书拟合精度大幅度提高, 且3类卫星的速度计算误差相当, RMS平均值约为0.6 m/s, 最大值约为2 m/s。单颗卫星的捕获时间同时与码相位搜索不确定度和载波多普勒搜索不确定度相关, 二者的乘积反映了一定硬件条件下的信号捕获时间[4]。式(19)表示由卫星速度误差引入的多普勒频移误差
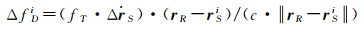 (19)
(19)
| m/s | ||||||||
| PRN | RMS | 最大值 | PRN | RMS | 最大值 | PRN | RMS | 最大值 |
| 01 | 0.48 | 1.24 | 06 | 0.99 | 2.28 | 11 | 0.63 | 1.50 |
| 02 | 0.37 | 1.01 | 07 | 0.53 | 1.40 | 12 | 0.63 | 1.47 |
| 03 | 0.50 | 1.51 | 08 | 0.88 | 1.93 | 14 | 0.67 | 1.69 |
| 04 | 0.36 | 0.88 | 09 | 0.97 | 2.22 | — | ||
| 05 | 0.57 | 1.48 | 10 | 0.68 | 1.70 | — | ||
| 平均 | 0.46 | 1.22 | 平均 | 0.81 | 1.90 | 平均 | 0.64 | 1.53 |
式中, ΔfDi为第i颗卫星的多普勒频移误差; rR为接收机的位置矢量; rSi和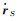
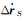
以星间链路的中心频率为例, 将表 2中卫星速度的最大误差68.02 m/s代入式(19), 得出常规历书模型计算出的多普勒频移误差为6 012.6 Hz, 将表 4中卫星速度的最大误差2.28 m/s代入式(19), 得出新历书模型计算出的多普勒频移误差为201.5 Hz。表明在90 d弧段内利用新历书模型的信号捕获时间比常规历书模型提高约30倍。
2.3 讨论 2.3.1 新老历书模型不同拟合弧长拟合精度比较上文的分析表明, 对于GEO和IGSO卫星, 在90 d拟合弧段条件下, 常规历书模型的拟合位置误差在几百千米量级, 而新历书模型由于考虑了主要长期项的影响, 位置拟合误差降低至十几千米甚至几千米。由于不同的用户对历书模型的拟合精度的需求不同, 采用1组历书参数描述90 d弧段的卫星轨道, 即使采用新历书模型, 也不能满足某些特殊用户的需求。这里以减少卫星历书注入组数为目的, 同时兼顾保证一定的拟合精度, 对比了常规历书模型和新历书模型在不同拟合弧长拟合精度的差异, 见表 5。表 5给出了常规历书模型7 d、14 d弧段的拟合精度, 同时给出了新历书模型30 d、45 d和90 d弧段的拟合精度, 以10 km位置误差为上限, 对于常规历书模型只能采用14 d的拟合弧段, 而新模型的拟合弧段可以扩展至45 d。
| m | ||||||||
| 拟合方法/弧长 | GEO卫星 | 拟合方法/弧长 | IGSO卫星 | 拟合方法/弧长 | MEO卫星 | |||
| 位置误差 | 拟合URE | 位置误差 | 拟合URE | 位置误差 | 拟合URE | |||
| 老方法/7 d | 3261 | 998 | 老方法/7 d | 2936 | 939 | 老方法/7 d | 1081 | 569 |
| 老方法/14 d | 7979 | 2275 | 老方法/14 d | 7930 | 1861 | 老方法/14 d | 2975 | 719 |
| 新方法/30 d | 3509 | 1274 | 新方法/30 d | 7289 | 1385 | 新方法/30 d | 3069 | 513 |
| 新方法/45 d | 3851 | 1316 | 新方法/45 d | 7665 | 1394 | 新方法/45 d | 3302 | 574 |
| 新方法/90 d | 6553 | 1531 | 新方法/90 d | 11319 | 1889 | 新方法/90 d | 4798 | 852 |
2.3.2 不同摄动参数对长弧历书拟合的影响分析
为了验证新历书模型是否为适合长弧段拟合的最简模型, 笔者在考虑升角点赤经变化率的常规历书模型基础上, 设计了历书模型A和B, 并将历书拟合精度与常规模型及本文提出的模型进行对比。历书模型A在常规历书模型基础上增加Δn及idot参数(σ0=(toa, Δa, e, i0, Ω0, w0, M0, Δn, idot, 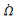
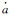
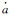
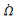
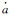
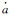
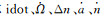
| m | ||||||||
| 历书模型 | GEO卫星 | 历书模型 | IGSO卫星 | 历书模型 | MEO卫星 | |||
| 位置误差 | 拟合URE | 位置误差 | 拟合URE | 位置误差 | 拟合URE | |||
| 历书模型 A | 210 112 | 27 914 | 历书模型 A | 212 082 | 28 104 | 历书模型 A | 4916 | 864 |
| 历书模型 B | 218 295 | 28 921 | 历书模型 B | 212 073 | 28 038 | 历书模型 B | 4916 | 864 |
| 常规模型 | 212 567 | 43 672 | 常规模型 | 212 100 | 42 497 | 常规模型 | 5531 | 1070 |
| 新模型 | 6553 | 1531 | 新模型 | 11 319 | 1889 | 新模型 | 4798 | 852 |
2.3.3 新历书模型工程实现可行性分析
在满足星间链路信号捕获的需求下, 新历书模型可将历书期限从现有7 d扩展至45 d, 辅助星间链路运行的长期历书单次注入信息量减少约76%, 只需修改地面控制系统和卫星以及卫星之间的接口即可; 对于常规导航, 延长有效期的新历书模型可以使接收机启动时充分利用历史历书数据, 减少接收机的首次定位时间。由于新历书模型增加了4个摄动参数, 在下行导航电文中需要增加中等精度历书的信息编排量。新发布的北斗全球CNAV1导航电文中子帧3页面类型4中具有47比特预留位[27], 以1 km为历书最小表达精度初步估算, 新增加的摄动参数可以在预留位中表达, 从而实现不改变导航电文结构, 又增加了下行导航电文中的历书使用期限, 新增参数占用比特位较少, 对用户导航电文解析与解算负担的影响可忽略不计。对于GEO卫星, 由于存在大约频度为1月的轨道机动, 轨道机动后, 原来的历书参数将失效, 因此无论对星间链路还是常规用户, 都需要额外获取卫星的机动标识; 若GEO卫星在自主运行期间没有机动发生, 则新历书模型在有效期内都有效。
3 结论本文以延长历书参数有效期为目的, 分析了北斗GEO、IGSO和MEO 3类导航卫星主要摄动力及其对轨道根数的长期项和长周期项的影响, 以此为基础设计了以6个轨道根数和5个摄动参数为播发参数的历书拟合模型, 并详细推导了新历书模型的参数拟合方法。比较了常规历书模型和新历书模型在90 d拟合弧长条件下的位置和速度拟合精度, 得出新的历书模型提高了历书拟合的精度, 尤其对于GEO和IGSO卫星, 拟合精度提高显著。对于GEO和IGSO卫星, 位置拟合误差大约从200 km降低至十几千米甚至几千米, 速度拟合误差大约从15 m/s降低至0.6 m/s, 新方法拟合精度提高了约20~30倍; 对于MEO卫星, 无论采用哪种历书模型, 位置拟合误差均在5 km左右, 速度拟合误差都在0.6 m/s左右, 新方法拟合精度提高约15%。
针对星间链路卫星10 km位置误差上限的使用需求, 通过实际拟合计算表明常规模型最大拟合弧长约为14 d, 而新历书模型的最大拟合弧长可延长至45 d。通过比较考虑不同摄动力模型的历书拟合精度, 得出考虑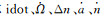
| [1] |
中国卫星导航系统管理办公室. 北斗卫星导航系统空间信号接口控制文件: 公开服务信号(2. 0版)[R]. 北京: 中国卫星导航系统管理办公室, 2013. China Satellite Navigation Office. BeiDou Navigation Satellite System Signal in Space Interface Control Document Open Service Signal (Version 2. 0)[R]. Beijing: China Satellite Navigation Office, 2013. |
| [2] | VAN DIERENDONK A J. 全球定位系统的导航电文[C]//导航星全球定位系统. 北京: 测绘出版社, 1994: 64-87. |
| [3] | KAPLAN E D. Understanding GPS:Principles and Applications[M]. New York: Artech House, 1996. |
| [4] |
王陆潇, 黄智刚, 赵昀.
多类型历书对首次定位性能的影响研究[J]. 武汉大学学报(信息科学版), 2013, 38(2): 140–143.
WANG Luxiao, HUANG Zhigang, ZHAO Yun. Two Sets of GPS Almanac on Time-to-First-Fix Influence[J]. Geomatics and Information Science of Wuhan University, 2013, 38(2): 140–143. |
| [5] |
王梦丽, 陈华明, 王飞雪.
GPS历书数据的有效龄期[J]. 遥测遥控, 2007, 28(3): 31–35.
WANG Mengli, CHEN Huaming, WANG Feixue. Effective Age of GPS Almanac Data[J]. Journal of Telemetry, Tracking, and Command, 2007, 28(3): 31–35. |
| [6] |
刘利, 时鑫, 栗靖, 等.
北斗基本导航电文定义与使用方法[J]. 中国科学(物理学力学天文学), 2015, 45(7): 079509.
LIU Li, SHI Xin, LI Jing, et al. The Definition and Using Method of the COMPASS Basic Navigation Message[J]. Scientia Sinica (Physica, Mechanica & Astronomica), 2015, 45(7): 079509. |
| [7] |
何峰, 王刚, 刘利, 等.
地球静止轨道卫星广播星历参数拟合与试验分析[J]. 测绘学报, 2011, 40(S1): 52–58.
HE Feng, WANG Gang, LIU Li, et al. Ephemeris Fitting and Experiments Analysis of GEO Satellite[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S1): 52–58. |
| [8] |
李献斌, 王跃科, 陈建云.
导航星座星间链路信号捕获搜索策略研究[J]. 宇航学报, 2014, 35(8): 946–952.
LI Xianbin, WANG Yueke, CHEN Jianyun. Research on the Acquisition Search Strategy of Navigation Constellation Inter-Satellite Link[J]. Journal of Astronautics, 2014, 35(8): 946–952. |
| [9] |
刘林.
航天器轨道理论[M]. 北京: 国防工业出版社, 2000.
LIU Lin. Orbit Theory of Spacecraft[M]. Beijing: National Defense Industry Press, 2000. |
| [10] |
黄华. 导航卫星广播星历参数模型及拟合算法研究[D]. 南京: 南京大学, 2012. HUANG Hua. Research on the Broadcast Ephemeris Parameters Model and Its Fitting Algorithm[D]. Nanjing: Nanjing University, 2012. |
| [11] | BREITER S, WYTRZYSZCZAK I, MELENDO B. Long-term Predictability of Orbits Around the Geosynchronous Altitude[J]. Advances in Space Research, 2005, 35(7): 1313–1317. DOI:10.1016/j.asr.2005.02.033 |
| [12] | DU Lan, ZHANG Zhongkai, ZHANG Jin, et al. An 18-Element GEO Broadcast Ephemeris Based on Non-singular Elements[J]. GPS Solutions, 2015, 19(1): 49–59. DOI:10.1007/s10291-014-0364-x |
| [13] | IS-GPS-200G (2012) Navstar GPS Space Segment/Navigation User Interface. Global Positioning System Wing, Space and Missile Systems Center[EB/OL]. [2012-07-18]. http://www.navcen.uscg.gov. |
| [14] | IS-GPS-705C (2012) Navstar GPS Space Segment/User Segment L5 Interfaces. Global Positioning System Wing, Space and Missile Systems Center[EB/OL]. [2012-07-18]. http://www.navcen.uscg.gov. |
| [15] |
黄华, 刘林, 周建华, 等.
18参数广播星历分析研究[J]. 飞行器测控学报, 2012, 31(3): 80–84.
HUANG Hua, LIU Lin, ZHOU Jianhua, et al. Research on 18 Elements Broadcast Ephemeris Model[J]. Journal of Spacecraft TT & C Technology, 2012, 31(3): 80–84. |
| [16] |
黄华, 何峰, 刘林.
广播星历参数物理意义分析与相关性研究[J]. 宇航学报, 2014, 35(2): 171–176.
HUANG Hua, HE Feng, LIU Lin. Research on Physical Meaning and Correlation of Broadcast Ephemeris Parameters[J]. Journal of Astronautics, 2014, 35(2): 171–176. |
| [17] | HUGENTOBLER U, PLONER M, SCHILDNECHT T, et al. Determination of Resonant Geopotential Terms Using Optical Observations of Geostationary Satellites[J]. Advances in Space Research, 1999, 23(4): 767–770. DOI:10.1016/S0273-1177(99)00153-2 |
| [18] |
李恒年.
地球静止卫星轨道与共位控制技术[M]. 北京: 国防工业出版社, 2010.
LI Hengnian. Geostationary Satellite Orbital Analysis and Collocation Strategies[M]. Beijing: National Defense Industry Press, 2010. |
| [19] |
陈刘成, 李静, 马瑞, 等.
工程化广播星历参数拟合算法与接口设计[J]. 武汉大学学报(信息科学版), 2011, 36(1): 18–23.
CHEN Liucheng, LI Jing, MA Rui, et al. The Engineering Design for Broadcast Ephemeris Parameters Fitting Arithmetic and Their Interfaces[J]. Geomatics and Information Science of Wuhan University, 2011, 36(1): 18–23. |
| [20] |
黄勇, 胡小工, 王小亚, 等.
中高轨卫星广播星历精度分析[J]. 天文学进展, 2006, 24(1): 81–88.
HUANG Yong, HU Xiaogong, WANG Xiaoya, et al. Precision Analysis of Broadcast Ephemeris for Medium and High Orbit Satellites[J]. Progress in Astronomy, 2006, 24(1): 81–88. |
| [21] |
阮仁桂, 贾小林, 吴显兵, 等.
关于坐标旋转法进行地球静止轨道导航卫星广播星历拟合的探讨[J]. 测绘学报, 2011, 40(S1): 145–150.
RUAN Rengui, JIA Xiaolin, WU Xianbing, et al. Broadcast Ephemeris Parameters Fitting for GEO Satellites Based on Coordinate Transformation[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S1): 145–150. |
| [22] |
张中凯, 杜兰, 刘利, 等.
GEO广播星历参数设计的无奇点根数法[J]. 测绘学报, 2014, 43(5): 452–457.
ZHANG Zhongkai, DU Lan, LIU Li, et al. Parameter Design of GEO Broadcast Ephemeris Based on the Nonsingular Orbital Elements[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(5): 452–457. DOI:10.13485/j.cnki.11-2089.2014.0076 |
| [23] |
常志巧, 郝金明, 张成军.
配置积分方法在GPS卫星轨道确定中的应用[J]. 海洋测绘, 2006, 26(2): 31–33.
CHANG Zhiqiao, HAO Jinming, ZHANG Chengjun. The Application of Collocation Integration Method in the Orbit Determination of GPS Satellites[J]. Hydrographic Surveying and Charting, 2006, 26(2): 31–33. |
| [24] | BEUTLER G, BOCK H, DACH R, et al. Bernese GPS Software Version 5.0[M]. Bern, Switzerland: University of Bern, 2007. |
| [25] |
刘伟平, 郝金明, 李作虎.
由广播星历解算卫星位置、速度及精度分析[J]. 大地测量与地球动力学, 2010, 30(2): 144–147.
LIU Weiping, HAO Jinming, LI Zuohu. Solution Method and Accuracy Analysis of Satellite Position and Velocity from Broadcast Ephemeris[J]. Journal of Geodesy and Geodynamics, 2010, 30(2): 144–147. |
| [26] |
李显, 吴美平, 张开东, 等.
导航卫星速度和加速度的计算方法及精度分析[J]. 测绘学报, 2012, 41(6): 816–824.
LI Xian, WU Meiping, ZHANG Kaidong, et al. Navigation Satellites Velocity and Acceleration Computation:Methods and Accuracy Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 816–824. |
| [27] |
中国卫星导航系统管理办公室. 北斗卫星导航系统空间信号接口控制文件公开服务信号B1C、B2a(测试版)[R]. 北京: 中国卫星导航系统管理办公室, 2017. China Satellite Navigation Office. BeiDou Navigation Satellite System Signal in Space Interface Control Document Open Service Signal B1C and B2a (Beta)[R]. Beijing: China Satellite Navigation Office, 2017. |



