2. 地球空间信息技术协同创新中心, 湖北 武汉 430079
2. Collaborative Innovation Center for Geospatial Technology, Wuhan 430079, China
新一代重力测量卫星GOCE(gravity field and steady-state ocean circulation explorer)以引力梯度测量为主要特征, 实现中高频段重力场信号的有效恢复[1-2]。它的关键载荷是一台高精度的引力梯度仪, 主要由6个加速度计组成, 对称安装在3个互相垂直的坐标轴上, 梯度仪质心与卫星质心重合, 加速度计对构成的梯度仪测量基线长约0.5 m[3]。在理想工作条件下, 由加速度计差分观测值可以确定卫星质心所在位置的地球外部引力梯度[1]。
从上述基本配置可以发现, GOCE卫星与以往的卫星重力任务有着显著的不同。在CHAMP(challenging minisatellite payload)[4]和GRACE(gravity recovery and climate experiment)[5-6]任务中, 不论是采用高低跟踪还是低低跟踪模式, 卫星质心与加速度计质心应该是重合的, 加速度计观测给出的是卫星所受非保守力的合力[7]。对于GOCE卫星, 由于以梯度测量为主, 因此工作模式决定它的加速度计质心不可能放置于卫星质心。但另一方面, GOCE卫星有高精度的高低跟踪数据, 在解算高低重力场方面有着重要优势—轨道数据密集、质量高、拥有无阻尼控制等, 因此对高低跟踪模型研究有很好的促进作用。
在官方发布的GOCE卫星高低跟踪数据处理方法中, 采用的是所谓普通加速度计模式获得卫星的非保守力, 如后文分析, 此种模式不利于研究卫星单个加速度计的特征。本文试图结合加速度计数据研究GOCE卫星的非保守力环境, 并讨论其对数据处理的影响。此外, 引力梯度测量涉及卫星定姿和各种检校问题, 导致梯度数据含有色噪声, 因此引力梯度数据的预处理是整个GOCE任务数据分析中非常关键的部分。本文将按照梯度数据的生成过程, 在加速度计级别上探讨预处理, 既是对加速度计校准成果的推广应用, 也可为后续的梯度数据分析与建模提供有效的先验信息。在GOCE卫星的加速度计质心与卫星质心不重合的情况下, 这是一个新课题。本文利用动力法[8-11]处理GOCE任务中的高低跟踪数据研究GOCE加速度计校准及其非保守力特点, 并试图丰富目前梯度仪的检校手段。
1 单加速度计校准与非保守力的确定本节主要阐述如何从加速度计出发, 确定GOCE卫星的非保守力, 并讨论对当前方法所作的改进。
ESA发布的GOCE任务L1B数据包含几何法精密定轨成果[12], 并且提供了加速度计观测数据、卫星本体坐标系与惯性系之间的姿态矩阵等相关数据。本文选择动力法。其中加速度计校准中目前普遍采用的是比例-偏差模型[7, 13-16]
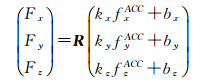 (1)
(1)
式中各分量含义参见参考文献。
GOCE卫星搭载的加速度计质心与卫星质心并不重合, 因此单个加速度计的观测值中还包含了平台旋转相关的惯性力, 与卫星受到的非保守力并不相等。GOCE任务的解决办法是利用对称放置的加速度计对, 组合出所谓的普通模式加速度观测值, 理论上它等于卫星受到的非保守力。但必须指出, 这种测量模式将导致不能采用式(1)给出的模型来校准组合观测值。下面作具体的分析。
暂不考虑坐标框架转换, 式(1)的校准关系可以简写为
 (2)
(2)
GOCE任务的普通模式加速度定义为(ESA, 2008)
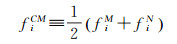 (3)
(3)
式中, fiCM是普通模式加速度
当采用式(2)校准普通模式加速度时, 校准后的结果FiCM为
 (4)
(4)
如果对单个加速度计观测值进行校准后再组合, 注意与平台旋转相关的惯性力是由物理定律规定的系统改正, 在校准后的组合中依然通过对称排列的方式抵消, 则得到下式
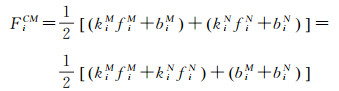 (5)
(5)
式中, 比例系数和偏差系数都引入了上标, 表示该量所属的加速度计编号。
显然, 式(4)只是式(5)的特殊情况, 仅当kiM=kiN时式(4)表示的校准模型才成立。从式(5)可以看出, 在校准普通模式的加速度观测值时, 只能得到加速度计偏差参数的联合影响。换句话说, 组合加速度计观测值的偏差参数是不可分的, 而且利用校准模型(5)在每个坐标轴方向需要两个比例参数和一个偏差参数。而加速度计校准中比例参数是难以准确估计的, 采用轨道数据同时估计两个加速度计的比例参数, 如果没有一定的约束条件, 会出现耦和现象, 比例参数的可靠性没有保障。而且, 采用普通模式的加速度无法生成梯度观测值(无法分离偏差的影响), 因此加速度计的信息无法得到充分利用, 特别是在辅助梯度数据的预处理方面。
本文采用单加速度计校准的方法, 对加速度计比例参数以及重力场模型参数均作为参数估计, 因此可以将普通模式加速度校准中的混叠的比例参数和偏差参数全部分离出来, 获得更丰富的信息。进一步的数据处理方法请参见下节中的方法说明。
2 数据处理及其分析 2.1 动力学方法本文采用动力学方法处理GOCE卫星任务的高低跟踪数据。该方法属于卫星重力学中的经典方法。在GOCE卫星任务的应用中, 需要把加速度计观测到的非保守力通过惯性力改正到卫星质心上[17-18]。虽然已有研究中(文献[18]), 联合GRACE卫星的高低跟踪以及星间距离变率数据可以填补GOCE任务的两极数据空白, 但是瞄准本文的研究目标, 为了回避不同源数据可能带来的影响, 将只采用GOCE任务的观测数据, 使得结论的分析更有针对性。
在单颗GOCE卫星的模式下, 本文选择24 h的积分弧长, 300阶背景场, 并估计完全到60阶次的重力场模型系数, 其他力模型和协议请参见文献[18], 这里着重讨论加速度计校准模型的配置。由于GOCE卫星有沿轨的无阻尼控制系统, 因此卫星飞行方向的非保守力信号非常微弱, 这一点在后面的一系列分析中也可以得到验证, 因此卫星轨道实际上对沿轨向的非保守力不敏感, 自然也带来了加速度计校准参数估计的难度。对沿轨方向, 本文采用固定比例参数(取常数1), 每24 h估计一个偏差参数。对其他两个方向, 依然采用标准的校准公式, 请参见式(2), 比例参数每月估计一个, 偏差参数的估计策略与沿轨方向相同。
2.2 加速度计校准结果在单加速度计模式下, 可以分别利用GOCE卫星的6个加速度计, 获得卫星的非保守力, 利用动力法可以解算重力场模型以及相关的校准参数。主要过程与标准的动力法相同, 但是在卫星力模型中, 惯性力改正需要加速度计质心相对梯度仪质心的偏移矢量[17-18], 本文采用的加速度计质心偏移值取自ESA相关工作组的研究报告[3]。该报告给出了梯度仪的臂长, 根据臂长以及加速度计对相对梯度仪质心对称布置的假设, 可以推出6个加速度计在梯度仪坐标系中的位置矢量。通过每个加速度计校准参数可以初步评价校准的效果。进一步, 可以利用卫星加速度计的校准参数, 联合卫星姿态数据计算卫星的非保守力、引力梯度等, 并通过外部引力位满足的Laplace方程做检核。
本文所有计算都是在GOCE任务发布的L1B数据基础上完成, 并取2009年11月的结果为例进行分析, 其中精密轨道采用的是几何法轨道。轨道、加速度计、姿态、卫星平台角速度和角加速度都归算到相同时刻。动力法需要的卫星初始轨道直接从数据中提取, 速度初值由位置差分获得。在迭代中通过参数估计不断精化。
下面给出6个加速度计的比例参数, 见表 1, 其中, x、y、z表示梯度仪坐标系中的3个坐标轴方向。由于已经说明沿轨方向的信号微弱, 无法估计比例参数, 因此表中x方向的比例参数全部固定为常数。其他两个方向的比例参数均作为参数估计。为了对比, 本文同时采用先验重力场模型对梯度进行了校准[19], 得到的4个主要分量(xx, yy, zz, xz)的比例系数分别为(0.998 9, 1.004 8, 1.003 8, 1.000 2)。可以看出, 本文给出的加速度计比例参数与梯度检校方法给出的结果非常一致。这表明本文提出的利用单加速度计重建非保守力的整个方案是可行的, 即使在两极存在跟踪数据空白的不利条件下, 加速度计校准依然获得了可靠的结果。
| 加速度计编号 | x | y | z |
| 1 | 1.000 0 | 0.991 4 | 0.995 2 |
| 4 | 1.000 0 | 0.991 8 | 0.995 4 |
| 2 | 1.000 0 | 0.992 2 | 0.996 4 |
| 5 | 1.000 0 | 0.992 0 | 0.997 3 |
| 3 | 1.000 0 | 0.991 5 | 0.996 5 |
| 6 | 1.000 0 | 0.992 3 | 0.993 9 |
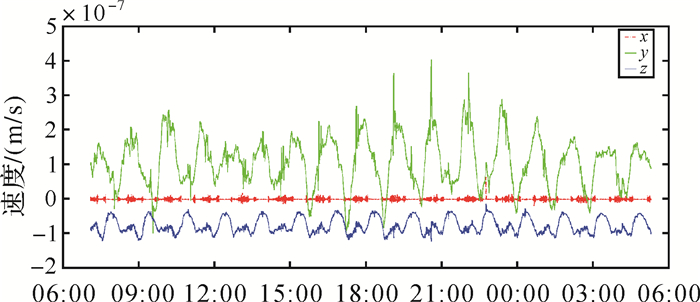
图 1是选择了一个弧段, 由GOCE卫星加速度计校准结果确定非保守力。由于6个加速度计均可以导出卫星受到的非保守力, 因此本文利用6个加速度计获得的非保守力平均作为加速度计校准之后的最终成果, 表达的是卫星质心处受到的非保守力。从该图可以看出, 在卫星的沿轨方向, 由于有无阻尼控制系统, 主要摄动力之一的大气阻力得到了很好的补偿, 信号强度整体上较另外两个方向要弱得多。数值分析表明, 沿轨方向的信号在10-9 ms-2量级(弧段统计结果), 而另外两个方向要更接近两个量级。下面作个对比, 重力卫星GRACE的沿轨方向(主要摄动力之一也是大气阻力)非保守力的量级在10-8 ms-2量级, GOCE卫星的轨道高度约250 km, 该高度的大气密度比500 km高2~3个量级(JB2006[20]、JB2008[21]、NRLMSISE00[22] 3个模型的结果在量级上一致)。而GOCE卫星沿轨方向残余的非保守力较GRACE小一个量级, 这说明无阻尼控制系统有效补偿了沿轨方向的非保守力。
|
| 图 1 加速度计获得的GOCE卫星非保守力时间序列 Fig. 1 Non-gravitational force time series derived by the accelerometers onboard GOCE |
另一个方面, 从重力场建模的角度分析, GOCE卫星沿轨方向的非保守力残余影响对轨道的影响依然处于一个较高水平。在GRACE任务中, 已经知道SuperSTAR加速度计最敏感轴测量精度约为3×10-10 ms-2。换言之, 对于GRACE这类在500 km高度运行的重力卫星, 该量级的非保守力测量误差能影响重力场的确定精度。GOCE卫星轨道高度更低, 因此在利用高低跟踪数据确定重力场模型时仍有必要顾及残余非保守力的影响。
2.3 无阻尼控制对卫星速度计算的影响GOCE卫星的无阻尼控制系统需要实时补偿卫星受到的非保守力(主要是沿轨方向), 这种补偿方式一定会给卫星的运行速度带来一种“脉冲”性质的影响。卫星精密定轨技术中, 几何法是直接利用观测条件解算卫星轨道, 不涉及卫星的力学信息。因此, 在利用几何轨道导出卫星速度时(比如多项式拟合轨道, 对时间求导给出速度), 很难体现补偿非保守力中的这种高频变化。反之, 在动力法中, 无阻尼控制系统提供的外力也属于卫星受到的非保守力中的一种, 通过加速度计校准, 它隐含了这种外力的影响, 因此动力法给出的卫星速度中应该包含有无阻尼控制的影响。分析几何法导出速度与动力法速度两者之间的差异, 应可以比较明显地鉴别这种影响。具体过程为:首先通过几何法精密定轨结果导出卫星速度。其次, 在动力法参数确定完毕后, 顾及卫星非保守力模型, 通过轨道积分导出卫星的速度。图 2即为两套速度之间的差异。很明显, 两种方法导出的速度差异量级较大, 3个分量都在cm/s甚至达到dm/s量级。

|
| 图 2 GOCE卫星轨道导出速度与动力法结果的差异 Fig. 2 Difference between the GOCE velocity derived from position and from the dynamic method |
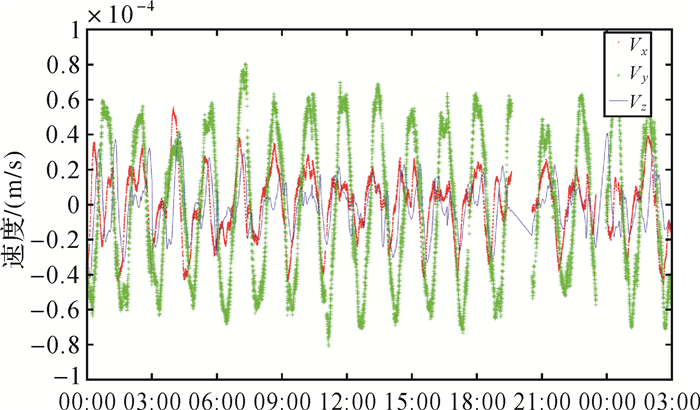
为了进一步分析其原因, 本文采用相似的手段处理GRACE的L1B数据[23]、几何法定轨提供的卫星精密轨道, 得到同类的比较结果, 参见图 3。GRACE卫星的速度差异3个分量在0.1 mm/s量级, 相较GOCE的情况, GRACE卫星任务的同类指标要低将近3个量级。因此, 从精密轨道导出卫星速度的算法中, 显然GOCE受到的影响严重得多。可以认为, GOCE卫星的无阻尼控制模式对卫星速度的确定带来了一定的挑战。在重力场模型解算中, 类似能量法、加速度法等依赖速度、加速度导出量的方法, 建议慎重处理该问题, 在GOCE卫星的速度计算中要充分顾及动力学模型提供的信息。
|
| 图 3 GRACE卫星轨道导出速度与动力法结果的差异 Fig. 3 Difference between the GRACE velocity derived from position and from the dynamic method |
2.4 卫星引力梯度的初步校准
在GOCE任务的重力梯度测量中, 严格来讲, 引力梯度张量并不是直接观测量, 它是基于6个加速度计的观测值, 以及梯度仪相对惯性系的姿态共同导出的。对于梯度仪/卫星的姿态问题, 不在本文的研究范畴内, 暂不讨论, 则梯度数据中的偏差主要来源于加速度计的偏差。反之, 对加速度计的校准一定可以起到对梯度数据的校准作用。为此, 本文利用校准之后的加速度计数据导出引力梯度观测值。若导出值比发布的数据更接近真实的地球重力场梯度信息, 也可以说明单加速度计校准结果的可靠性。为了更加全面地分析这个问题, 本节设计的方案为:首先在单加速度计校准模式下, 卫星重力场模型和加速度计校准参数是同时求解的, 因此卫星重力场模型精度可以作为加速度计校准是否可靠的必要条件。其次, 利用加速度计组合生成新的梯度值, 利用引力位满足的Laplace方程进行检验。
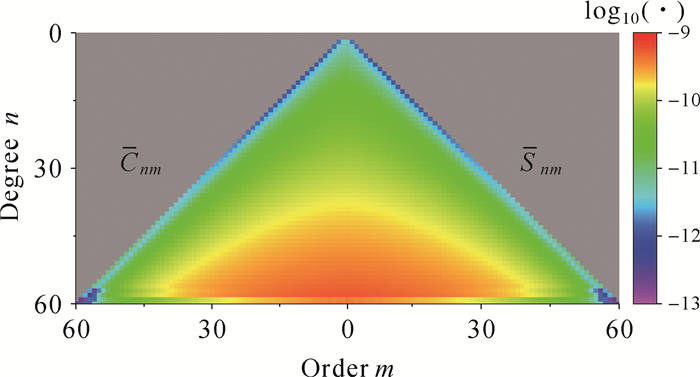
这里首先给出高低跟踪的纯GOCE重力场模型, 参见图 4。本算例中由于对最高估计阶次做了限制(60阶次), 同时GOCE卫星有高采样率的观测数据, 因此高低重力场模型中并没有出现特别显著的极空白效应[24], 但是在整体分布上, 依然是以0次为对称轴, 呈现次数较低的系数精度也较低的特点。与美国公布的GPS水准数据比较, 累积到60阶次的大地水准面精度为0.89 m, 略低于GRACE的同类指标。考虑到GOCE任务没有低低星间跟踪观测, 这种精度指标的略微下降是可以接受的。
|
| 图 4 利用GOCE高低跟踪数据建立的地球重力场模型位系数标准差分布 Fig. 4 Formal error of the earth gravitational model from the high-low SST data of GOCE |
通过上述的一系列检核, 可以认为本文解算的高低跟踪重力场模型及其附属产品质量是可靠的。利用这些数据本节将导出卫星引力梯度数据, 并利用Laplace方程做进一步的检核。
根据GOCE任务的梯度测量原理, 3个对角分量表达如下[12]
 (6)
(6)
式中, Lx、Ly、Lz分别表示梯度参考坐标系下3个坐标轴方向的臂长, 本文采用ESA发布的结果, 分别为0.514 013 5 m、0.499 890 0 m和0.500 201 0 m[3], 上述臂长与GOCE卫星的设计指标0.5 m略有偏移。
地球外部引力位满足Laplace方程
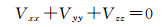 (7)
(7)
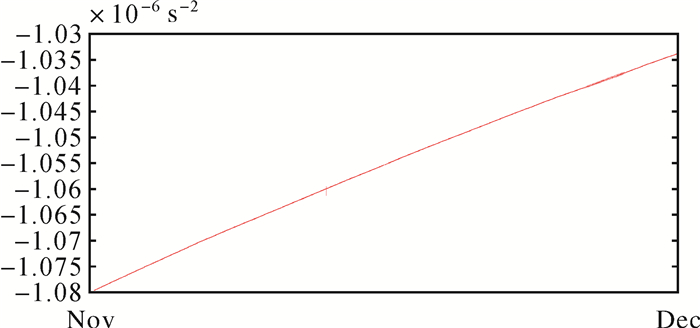
该式可以用于对加速度计观测值进行检核, 结果参见图 5。可以看出, 原始的梯度数据中存在103 E量级的偏差, 并且还有与时间近似呈线性关系的漂移。注意到GOCE卫星的梯度测量指标在mE水平, 上述偏移值是非常大的。
|
| 图 5 GOCE卫星梯度观测值的Laplace方程检验 Fig. 5 Validation on the GOCE gravity gradients by the Laplace's equation |
从梯度测量原理(6)分析, 可以推断这种偏移主要来自加速度计的零偏。GOCE卫星的仿真、实测数据处理研究中已经发现了加速度计偏差参数的漂移[17-18, 25-26], 因此图 5的漂移现象也与加速度计有关。从这个角度也可以发现, 加速度计数据处理以及卫星非保守力分析在GOCE卫星重力数据中有重要价值。利用校准后的加速度计数据做同样的检测, 与理论值偏离的最小值、最大值、平均值以及均方根分别为(-4.491 1, 2.844 5, -0.567 5, 1.394 1)×10-9 s-2, 可以看出, 经过校准之后, 梯度张量的迹减少了3个量级。加速度计校准之后梯度数据中的偏差显著减小。
3 结语本文从确定GOCE卫星非保守力出发, 提出了完全在单加速度计模式下, 只依赖GOCE任务自身的观测数据校准加速度计的思路, 认为该方法可以获得可靠的校准结果, 并通过卫星速度的计算以及重力场模型检核做了进一步的验证。通过引力位满足的Laplace方程以及由加速度计导出的引力位梯度检验, 也显示出加速度计的偏差影响得到了有效的削弱。
上述结果表明, 采用单加速度计模式的方式处理引力梯度测量卫星的轨道跟踪数据有独特的优势, 能有效分离不同加速度计的偏差参数。已有研究表明, 在有效确定了卫星平台姿态的前提下, 加速度计偏置[27]也能获得可靠的重力场建模结果, 联合这两项技术对今后的卫星重力任务实施有一定的参考价值。
最后指出本文研究的几个可能改进方向:①在本文研究的基础上, 若能发展新方法建立6个加速度计同时校准的新模型, 对探讨卫星引力梯度数据处理模型会有更好的促进作用; ②若能获得卫星在轨推进的相关信息, 可以结合星载加速度计给出的非保守力, GOCE卫星的外形、姿态以及表面材料属性, 重建GOCE卫星所受到的大气阻力时间序列, 进而与卫星精密轨道和姿态联合, 有可能对250 km轨道高度中性大气密度模型做出有价值的改进。
致谢: 本论文的数值计算得到了武汉大学超级计算中心的计算支持和帮助。
| [1] | ESA. Gravity Field and Steady-State Ocean Circulation Mission[R]. SP-1233(1), 1999. |
| [2] | DRINKWATER M, HAAGMANS R, MUZI D, et al. The GOCE Gravity Mission: ESA's First Core Explorer[C]//Proceedings of the 3rd International GOCE User Workshop. Frascati, Italy: International GOCE User Workshop, 2007: 1-8. |
| [3] | SIEMES C. GOCE Gradiometer Calibration and Level 1b Data Processing[R]. ESA Working Paper EWP-2384. Noordwijk, Netherlands: ESA, 2012. |
| [4] | REIGBER C, LVHR H, SCHWINTZER P. CHAMP Mission Status[J]. Advances in Space Research, 2002, 30(2): 129–134. DOI:10.1016/S0273-1177(02)00276-4 |
| [5] | GSFC. GRACE: Gravity Recovery and Climate Experiment[R]. FS-2002-1-029-GSFC, 2002. |
| [6] | TAPLEY B D, BETTADPUR S, WATKINS M, et al. The Gravity Recovery and Climate Experiment:Mission Overview and Early Results[J]. Geophysical Research Letters, 2004, 31(9): L09607. |
| [7] | CASE K, KRUIZINGA G, WU S. GRACE Level 1B Data Product User Handbook[R]. JPL D-22027, 2010. https://podaac.jpl.nasa.gov/gravity/grace-documentation |
| [8] | REIGBER C. Gravity Field Recovery From Satellite Tracking Data[M]//SANSÓ F, RUMMEL R. Theory of Satellite Geodesy and Gravity Field Determination. Berlin Heidelberg: Springer, 1989: 197-234. |
| [9] | XU G C. GPS Theory, Algorithms and Applications[M]. Berlin: Springer-Verlag, 2003. |
| [10] | MONTENBRUCK O, GILL E. Satellite Orbits-Models, Methods and Applications[M]. Berlin Heidelberg: Springer, 2000. |
| [11] | KROES R. Precise Relative Positioning of Formation Flying Spacecraft using GPS[D]. Delft: TU Delft, 2006. |
| [12] | ESA. GOCE L1b Products User Handbook[R]. GOCE-GSEG-EOPG-TN-06-137, 2006. |
| [13] | BETTADPUR S. UTCSR Level-2 Processing Standards Document for Level-2 Products Release 0001[R]. GRACE 327-742(CSR-GR-03-03), 2003. |
| [14] | BETTADPUR S. Recommendation for a-Priori Bias and Scale Parameters for Level-1B ACC Data[R]. GRACE TN-02, 2009. |
| [15] | KLINGER B, MAYER-GVRR T. The Role of Accelerometer Data Calibration within GRACE Gravity Field Recovery:Results from ITSG-Grace2016[J]. Advances in Space Research, 2016, 58(9): 1597–1609. DOI:10.1016/j.asr.2016.08.007 |
| [16] |
邹贤才, 李建成, 罗佳, 等.
星载加速度计的动力法校准[J]. 武汉大学学报(信息科学版), 2007, 32(12): 1152–1155.
ZOU Xiancai, LI Jiancheng, LUO Jia, et al. Calibration of Onboard Accelerometer by Dynamic Method[J]. Geomatics and Information Science of Wuhan University, 2007, 32(12): 1152–1155. |
| [17] | VISSER P N A M, VAN DEN IJSSEL J A A. Calibration and Validation of Individual GOCE Accelerometers by Precise Orbit Determination[J]. Journal of Geodesy, 2016, 90(1): 1–13. DOI:10.1007/s00190-015-0850-0 |
| [18] |
邹贤才, 李建成.
单加速度计模式下的GOCE卫星重力场建模方法研究[J]. 地球物理学报, 2016, 59(4): 1260–1266.
ZOU Xiancai, LI Jiancheng. Study on the Earth Gravity Modeling by GOCE in Individual Accelerometer Mode[J]. Chinese Journal of Geophysics, 2016, 59(4): 1260–1266. DOI:10.6038/cjg20160408 |
| [19] |
徐新禹, 赵永奇, 魏辉, 等.
利用先验重力场模型对GOCE卫星重力梯度观测值进行校准分析[J]. 测绘学报, 2015, 44(11): 1196–1201.
XU Xinyu, ZHAO Yongqi, Wei Hui, et al. Calibration and Analysis of SGG Observations of GOCE Based on Prior Gravity Models[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1196–1201. DOI:10.11947/j.AGCS.2015.20140414 |
| [20] | BOWMAN B R, TOBISKA W K, MARCOS F A, et al. The JB2006 Empirical Thermospheric Density Model[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2008, 70(5): 774–793. DOI:10.1016/j.jastp.2007.10.002 |
| [21] | BOWMAN B, TOBISKA W K, MARCOS F, et al. A New Empirical Thermospheric Density Model JB2008 Using New Solar and Geomagnetic Indices[C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit. Honolulu: AIAA, 2008, 37: 367. |
| [22] | PICONE J M, HEDIN A E, DROB D P, et al. NRLMSISE-00 Empirical Model of the Atmosphere:Statistical Comparisons and Scientific Issues[J]. Journal of Geophysical Research:Space Physics, 2002, 107(A12): SIA 15-1–SIA 15-16. DOI:10.1029/2002JA009430 |
| [23] | WU SC, KRUIZINGA G, BERTIGER W. Algorithm Theoretical Basis Document for GRACE Level-1B Data Processing[R]. JPL D-27672, Version 1. 0, California: JPL, 2004. |
| [24] | SNEEUW N, VAN GELDEREN M. The Polar Gap[M]//SANSÓ F, RUMMEL R. Geodetic Boundary Value Problems in View of the One Centimeter Geoid. Berlin, Heidelberg: Springer, 1997, 65: 559-568. |
| [25] | VISSER P N A M. Exploring the Possibilities for Star-Tracker Assisted Calibration of the Six Individual GOCE Accelerometers[J]. Journal of Geodesy, 2008, 82(10): 591–600. DOI:10.1007/s00190-007-0205-6 |
| [26] | VISSER P N A M. GOCE Gradiometer:Estimation of Biases and Scale Factors of All Six Individual Accelerometers by Precise Orbit Determination[J]. Journal of Geodesy, 2009, 83(1): 69–85. DOI:10.1007/s00190-008-0235-8 |
| [27] |
邹贤才. 加速度计偏置下的高低跟踪卫星重力测量模式[C]//第一届中国大地测量和地球物理学学术大会论文集. 北京: 国际大地测量地球物理学联合会, 2014: 1-1. ZOU Xiancai. The SST-HL Satellite Gravimetry Measurement Mode with an Accelerometer Deviating from the Center[C]//The first China Geodetic and Geophysical Academic Conference Proceedings. Beijing: CNC-IUGG, 2014: 1-1. |


