2. 中国科学院遥感与数字地球研究所, 北京 100101;
3. 武汉大学测绘学院, 湖北 武汉 430079
2. Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100101, China;
3. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
三维点云分割的目标是依据点的属性获得空间同质区域的聚类,分割处理是移动设备导航定位、目标提取识别和场景几何建模等应用的重要底层技术[1-2]。然而,由于数据的采样密度非均匀、点云非结构化分布、噪声和外点等影响,完全地自动化分割在计算机视觉、计算机图形学、摄影测量与遥感等研究领域仍然是一项艰巨的任务[3-5]。本文根据原理不同将点云分割算法归为以下4类:
(1) 基于区域增长法(region growing)的分割技术。该方法从种子点出发根据相似性度量和距离度量对邻域点判断是否扩展合并为同一区域[6-7]。区域增长算法相对易于实现,但它对噪声敏感,算法中的增长准则对不同局部区域的细节差异的自适应能力弱,而且种子点选取的不确定性将会影响到分割结果的可靠性。
(2) 基于图(graph-based)的分割算法。这类算法通过将点云模式化为由节点和反映节点关系的边组成的图模型。假设存在一种条件随机场模型,依据极大后验估计准则使用图割算法将图模型的部分连接断开形成独立的区域[8-10]。该方法对前景和背景进行分割,适用于指定的目标提取,或以监督分类方式实现多目标提取。
(3) 基于模型拟合(model-fitting)的分割算法。例如以随机抽样一致性检验(random sample consensus,RANSAC)为依据的参数化几何元素(平面、椭球和圆柱等)拟合算法[11-12],被广泛应用于建筑物立面提取[13-14]。与此类似还有基于霍夫变换(Hough transform)的元素提取技术[15],该类算法提取的几何结构精简紧凑,可视化效果好。但在参数求解时通常使用统一的阈值从而缺乏尺度适应能力,此外一次分割只能提取出一类基本元素,当场景具有复杂多样的结构形态时并不适用。
(4) 以机器学习(machine learning)为基础的分割算法。文献[16]使用支持向量机将几何特征归类,文献[17—18]提出一种以神经网络学习的方法将分割与分类同步结合进行目标识别,文献[19]将点云转化为体素(volume)数据来提取特征再使用AdaBoost进行训练和目标提取。这类算法在训练过程中需要大量的已有标记数据做训练样本,而且分割对象限定为已经训练过的目标物,因此使该算法难以灵活地推广。
前两类算法可以归为自下而上的分割方法,而后两类则是基于模式引导的自上而下的方法,它们的适用性都存在一定的局限。为了提高点云分割算法的抗噪性和对多种类型场景的适用性,解决三维点云特征描述困难的问题,本文针对激光雷达(light detection and ranging, LiDAR)数据的特性,在黎曼几何框架下考虑将体素过分割方法和基于图的方法相结合,设计分层优化的自动分割算法,该算法逻辑清晰易于实现,而且运算速度快,对点云的局部细节具有良好的自适应性。
1 算法设计本文双层优化策略的点云分割算法包括以下3个基本步骤:①通过定义局部坐标系来建立特征提取的参考基准;②以八叉树节点为种子点,结合离散点的特征信息,通过迭代优化聚类实现以超体素为输出的底层分割;③以超体素为节点建立最小生成树图(minimal spanning tree,MST),以MST为对象进行顶层优化聚类实现场景目标分割。
1.1 局部坐标系建立LiDAR点云能反映被观测目标的表面形态特性,与影像重建的点云,如多视立体重建(multi view stereo)相比,LiDAR点云采样均匀且密度高。尽管属于非连续空间采样,但致密的表面点满足建立局部欧氏坐标系的条件,可以用黎曼度量来研究局部可微性质,此时点的邻域关系不再局限于全局坐标系的组织。对点云中的任意一点,以其切平面为基础构建局部欧氏坐标框架,统计邻域内的点集的协方差,由此自适应调整距离度量并提取点特征向量,使特征参数可以考虑到数据局部结构的细节差异,避免了全局统一参数约束,有利于提高算法适用性。
在处理非结构化的LiDAR点云数据时,描述离散点的特征的方式具有多种多样[20-22],各种方法首先都需要建立起空间索引和邻域搜索机制。本文中设p是一个查询点,以Np:{qi|i=1, 2, …, k}表示查询输出的一组邻域点集,其中每个点qi与搜索点p的距离度量满足‖qi, p‖n≤dmax,为此采用近似最邻近查询方法(approximate nearest neighbor,ANN)[23]作为检索结构实现快速的邻域搜索。
点云表面某点处的切平面Π方程可以由点p和对应法向量np表示,其中p表示邻域点集合Np的重心点,即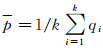
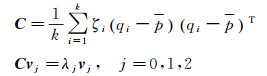 (1)
(1)
式中,ζi表示点qi的权重,等权观测情况下通常设为1;C是一个对称半正定矩阵,也是一个带权的协方差矩阵,它的特征值为实数λj, j=0, 1, 2;而它的3个特征向量vj对应邻域点集合Np的主分量,构成一个空间正交的框架。通过奇异值分解获得矩阵C的特征向量,那么最小特征值λ0对应的特征向量v0在几何意义上就与切平面法向量共线,对其进行归一化即得到单位法向量的估计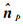
图 1给出一组点云表面局部坐标系构建的示意图,设平面Π为过一点p的切平面,当已知点p的表面法向量估计值时,即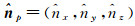
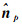

|
| 图 1 局部欧氏坐标系定义示意图 Fig. 1 A diagram of local Euclidean coordinate system |
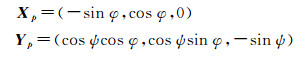 (2)
(2)
式中,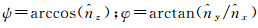
本文将点云分割过程设计分为上下两层递进的组织形式,本节介绍底层优化方法,1.3节内容将介绍顶层优化过程。底层结构的分割效果是利用改化的k均值聚类算法获得过分割的(over-segmented)点云聚类,可以表示为点云体素(voxel)的形式,具体包含以下3步。
(1) 定义相似性度量参数。点云聚类算法通常以法向量、曲率和离散度等属性信息构建特征向量来进行相似性度量,当具有影像数据时,颜色和纹理信息也被包含其中。本文中仅考虑原始LiDAR点云形式的数据,此时底层特征采用法向量和曲率组成的特征向量表示,具体的一点p的特征向量表示形式为fp∈R5:[nx, ny, nz, k1, k2]T,其中k1, k2表示表面位置的两个主曲率值。
对于距离度量而言,本算法不采用全局三维坐标定义的欧氏距离dp, qi,因为全局欧氏距离不顾及点的局部空间走势,不利于细节信息的区分。相反,本文利用局部坐标系统,根据点的曲率改进距离度量,记为dproj。如图 2所示,点p的邻域点qi到p的距离是利用投影点q′i到查询点p的欧氏距离进行计算的,其中ρ为曲率半径。如此,如果某点处的切平面和局部点云拟合越好,则ρ→∞,qi越接近q′i,改进距离dproj越接近于欧氏距离dp, qi;反之,如果曲率越大,切平面与局部点云拟合效果差,则邻域点的距离度量值也将增大。

|
| 图 2 局部欧氏坐标系下的距离度量 Fig. 2 Distance metric in local Euclidean coordinate system |
(2) 聚类中心初始化。对于底层体素分割的另一个关键问题就是分割数目的选取和聚类中心的初始化。本文采用自适应八叉树索引结构来创立聚类中心点集合S:{si|i=1, 2, …, m},与点p类似每一个种子点si也有一组特征fsi∈R5。对于三维数据而言,八叉树可以快速实现邻域点查询,而叶子节点本身即是一类以空间距离做度量的广义上的聚类。算法集成过程中利用了泊松表面重建算法[24]中的自适应八叉树结构做引导,根据经验值以第6、7级节点(与点密度和场景范围相关)作为局部聚类中心效果理想,而节点的宽度dr即作为下一步搜索半径参数。
(3) 聚类搜索阈设计。不同于传统的k均值聚类算法将每个点与所有聚类中心做判断,本算法中原始点只与到自身距离在3倍搜索半径(3×dr)内的聚类中心点做相似性判断。之后运算与k均值聚类相似,利用相似性度量和距离度量的加权距离判别查询点p所属的聚类中心sp。所有点判别结束后,根据聚类结果更新聚类中心sp的位置并进行下一轮迭代聚类,直到聚类中心位置收敛。聚类判别公式为
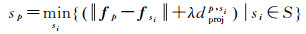 (3)
(3)
式中,
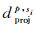
底层优化得到的是过分割的点云体素集合,这类集合表达了点云小尺度的相似性关系,为目标级别的分割提供支撑。顶层优化的数据操作对象不再是独立的点而是体素,具体过程分为以下3步。
(1) 挖掘体素的高级特征,而体素的特征提取目前仍是一项难题。此外,体素的邻接关系的定义不再单纯以距离为依据,因而邻接关系的确定也相对复杂。在底层分割时,每一个体素对应产生了一个聚类中心点,该中心点被用做体素邻域判断的初始条件。所有聚类中心集合形成了一个新的小型点云集合,因此同样利用ANN算法,可以快速的获得聚类中心的邻域中心集合,而这些中心锁定了一组初始的体素的对应关系。此时的ANN算法仅仅利用聚类中心的距离做搜索依据,而体素的固有属性远不止距离信息,因此在初始邻域搜索时利用较大的搜索半径获得一个数量冗余的邻域集合{V′neighbor}。下一步通过高维特征的相似性缩减邻域集合的数目,建立紧凑可靠的体素邻域关系。
一个体素的首要特征是利用其中所有点依据最小二乘法拟合得到的平面法向量Nvoxel。第2类特征是体素所有点集的协方差矩阵的3个特征值[λ0,λ1,λ2]T,它反映了体素的空间分布特性。两类特征组合构成了一个6维的特征向量,据此每个体素在初始邻域{V′neighbor}中进行相似性判别,仅保留属性最接近的k个体素做最终的邻域集合{Vneighbor}。
(2) 当邻域关系确立后,进行拓扑图构建。本文利用Kruskal坐标系[25]建立以体素为节点的MST,实现对体素结构的拓扑关系索引。MST的建立步骤是首先设每一个体素为一个节点e,将其所有邻域节点{Vneighbor}按边的距离权值从小到大排序,循环从权值最小的边开始遍历每条边直至图中所有的节点都在同一个连通分量中,该连通分量所经过的所有路径和节点即构成了一个MST。
(3) 最后从MST中的起点出发,根据边的权值按区域增长法进行聚类判别,当遇到增长终止条件时,自动开始新的区域聚类,从而实现顶层非监督分割聚类。
2 试验与分析 2.1 数据处理与算法实现试验环节采用了室内和室外两组点云数据分别进行处理分析,运算平台为win10 64位系统,处理器为i7-6500U搭配8 GB内存。算法功能采用C++编程实现,利用QT搭建软件界面,OpenGL作为三维绘图引擎,并开发实现八叉树索引和RANSAC几何元素检测等相关功能。
图 3通过室内数据试验展示了处理过程的中间结果。该数据是一组利用Leica ScanStation C10扫描仪获取的卧室点云,共包含45.1万个空间点,扫描距离在1.5 m到3.5 m,采样密度约为9000点/m2。图 3(a)给出原始点云的一个快照;图 3(b)是初始化的过分割聚类中心点,可以发现聚类中心点概括了原始点云的布局;图 3(c)是经过迭代优化后的底层过分割聚类结果,其中不同的体素以随机生成的颜色进行区分标识;图 3(d)展示了以体素为基本节点的MST图构建情况,该图是区域增长法的路径寻优基础。通过建立以超分割体素为节点的MST图,一方面保持了原有数据的几何信息和拓扑信息,另一方面从点云到体素节点极大地减少了数据量,为提高数据处理效率提供了重要的支撑。

|
| 图 3 算法处理流程 Fig. 3 A pipeline of the algorithm |
2.2 试验比较分析
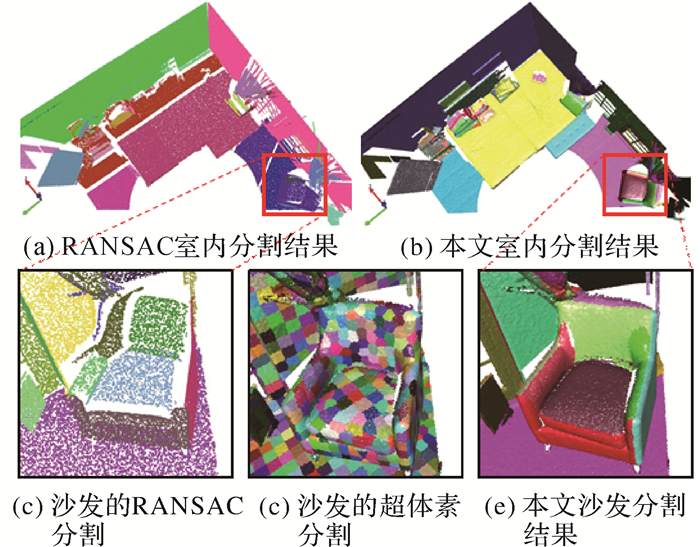
为验证本文算法的先进性,试验中将基于RANSAC的参数化几何元素拟合分割算法[11]与本文双层优化算法进行了比较,其中RANSAC点拟合距离阈值设为0.1 m。两种算法的分割结果如图 4所示,其中图 4(a)、(b)分别表示RANSAC分割结果和本文算法的结果,图 4(c)、(e)是一个沙发的局部放大效果,图 4(d)展示了本文算法的超体素分割的局部效果。由于沙发表面并非规则的几何形状,从图 4(c)、(e)中可以比较发现,RANSAC拟合参数化表面的分割结果不理想,尽管通过设置距离和法向量的拟合残差阈值,可以实现对场景的局部分段分割,但单一模式的平面表达会使分割得到的对象失去原有的细节特性。相反,本文算法利用点云过分割和体素聚类分割两层优化步骤,将扫描点云的局部可微性质保留在体素内部,并在适当的过渡区域断开MST图,实现点云的非监督分类,具有较好的细节保真度。
|
| 图 4 基于RANSAC分割与本文方法结果的比较 Fig. 4 A comparison between the results of RANSAC based method and our results |
两种算法的定量比较统计结果见表 1,包含算法分割耗时、分割数目和拟合残差指标。从表 1中可以得出本文算法比较RANSAC拟合分割算法有优异表现。在效率方面,RANSAC算法需要多次随机采样确定拟合参数,而且每提取一个分割面都需要单独全局拟合计算,计算耗时相对较多;而本文利用超体素作为图节点减少数据量,极大地降低了运算量。另外,RANSAC算法分割的目标局限为参数化的基本几何形状,因此分割数目有限,无法对复杂的场景形状进行有效表达。两种方法的拟合残差接近,这是由于算法本身进行了拟合距离阈值设置,限定了最大的拟合残差,因此具有统一的拟合残差量级。
| 算法 | 耗时/ms | 分割数目 | 拟合残差/m |
| RANSAC算法 | 6019 | 49 | 约0.02 |
| 本文算法 | 5652 | 98 | 约0.02 |
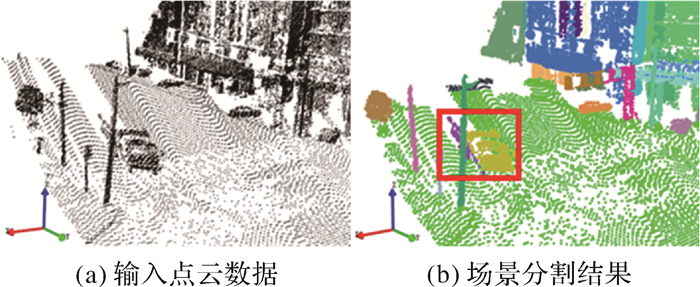
此外,为验证本文算法的广泛适用性,利用车载LiDAR点云数据进行了室外场景分割测试,原始点云和分割结果如图 5所示。算法通过自适应八叉树可以在突变区域提取可靠种子点,根据种子点的邻域点集的局部可微性进行聚类,从而生成有效的超体素,避免丢失场景中的突变地形和地物信息。如图 5(b)所示,路灯和电线杆被正确地分割提取,充分证明了本文算法对多种场景的适用性。本文算法的局限性在于缺乏语义层次的判别,仅从几何层面分析可能将一类目标物分割为几个局部连贯的片段,如图 5(b)图框选区域中将一辆卡车的车头和车身分割成两个区域。
|
| 图 5 车载LiDAR点云分割试验 Fig. 5 An experiment on vehicle borne LiDAR data |
3 结论
本文设计了一种面向LiDAR点云的自动分割算法,首先对底层点云进行迭代均值聚类获得过分割,形成超体素集合。然后,在顶层以体素为节点建立拓扑图模型,利用MST结构极大地简化了图的结构,提高区域增长算法的效率。本文算法不需要限定分割结构是平面或柱面等几何类型,因此适用于多类型目标分割,能够同时兼顾点云的局部细节和全局整体分布情况,适合多类应用场景的推广。下一步的研究工作将提取分割结果的高级特征进行语义层次的判别,实现点云目标识别。
| [1] | RUSU R B, COUSINS S. 3D is Here:Point Cloud Library (PCL)[C]//Proceedings of 2011 IEEE International Conference on Robotics and Automation. Shanghai, IEEE, 2011:1-4. |
| [2] | LI Minglei, NAN Liangliang, SMITH N, et al. Reconstructing Building Mass Models from UAV Images[J]. Computers & Graphics, 2016, 54: 84–93. |
| [3] | ROTTENSTEINER F, SOHN G, GERKE M, et al. Results of the ISPRS Benchmark on Urban Object Detection and 3D Building Reconstruction[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 93: 256–271. DOI:10.1016/j.isprsjprs.2013.10.004 |
| [4] | BERGER M, TAGLIASACCHI A, SEVERSKY L, et al. State of the Art in Surface Reconstruction from Point Clouds[R]. Proceedings of Eurographics 2014:State of the Art Reports. Strasbourg, France:The Eurographics Association, 2014. |
| [5] | VOSSELMAN G, COENEN M, ROTTENSTEINER F. Contextual Segment-based Classification of Airborne Laser Scanner Data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017, 128: 354–371. DOI:10.1016/j.isprsjprs.2017.03.010 |
| [6] | VO A V, TRUONG-HONG L, LAEFER D F, et al. Octree-based Region Growing for Point Cloud Segmentation[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 104: 88–100. DOI:10.1016/j.isprsjprs.2015.01.011 |
| [7] | VIEIRA M, SHIMADA K. Surface Mesh Segmentation and Smooth Surface Extraction through Region Growing[J]. Computer Aided Geometric Design, 2005, 22(8): 771–792. DOI:10.1016/j.cagd.2005.03.006 |
| [8] | GOLOVINSKIY A, FUNKHOUSER T. Min-cut Based Segmentation of Point Clouds[C]//Proceedings of the IEEE 12th International Conference on Computer Vision Workshops. Kyoto, Japan:IEEE, 2009:39-46. DOI:10.1109/ICCVW.2009.5457721 |
| [9] | URAL S, SHAN J. Min-cut Based Segmentation of Airborne LiDAR Point Clouds[C]//International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, XXXIX-B3. Melbourne, Australia:ISPRS, 2012:167-172. |
| [10] | RUSU R B, HOLZBACH A, BLODOW N, et al. Fast Geometric Point Labeling Using Conditional Random Fields[C]//Proceedings of 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems. St. Louis, MO, USA:IEEE, 2009. |
| [11] | SCHNABEL R, WAHL R, KLEIN R. Efficient RANSAC for Point-cloud Shape Detection[J]. Computer Graphics Forum, 2007, 26(2): 214–226. DOI:10.1111/cgf.2007.26.issue-2 |
| [12] |
李卉, 钟成, 黄先锋, 等.
集成激光雷达数据和遥感影像的立交桥自动检测方法[J]. 测绘学报, 2012, 41(3): 428–433.
LI Hui, ZHONG Cheng, HUANG Xianfeng, et al. Automatic Overpass Detection with LiDAR and Remote Sensing Image[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 428–433. |
| [13] |
魏征, 董震, 李清泉, 等.
车载LiDAR点云中建筑物立面位置边界的自动提取[J]. 武汉大学学报(信息科学版), 2012, 37(11): 1311–1315.
WEI Zheng, DONG Zhen, LI Qingquan, et al. Automated Extraction of Building Facade Footprints from Mobile LiDAR Point Clouds[J]. Geomatics and Information Science of Wuhan University, 2012, 37(11): 1311–1315. |
| [14] |
闫利, 谢洪, 胡晓斌, 等.
一种新的点云平面混合分割方法[J]. 武汉大学学报(信息科学版), 2013, 38(5): 517–521.
YAN Li, XIE Hong, HU Xiaobin, et al. A New Hybrid Plane Segmentation Approach of Point Cloud[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 517–521. |
| [15] | VOSSELMAN G, GORTE B G H, SITHOLE G, et al. Recognizing Structure in Laser Scanner Point Clouds[J]. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2004, 46(8): 33–38. |
| [16] | YANG Bisheng, DONG Zhen. A Shape-based Segmentation Method for Mobile Laser Scanning Point Clouds[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 81: 19–30. DOI:10.1016/j.isprsjprs.2013.04.002 |
| [17] | YU Yongtao, LI J, GUAN Haiyan, et al. Learning Hierarchical Features for Automated Extraction of Road Markings from 3-D Mobile LiDAR Point Clouds[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(2): 709–726. DOI:10.1109/JSTARS.2014.2347276 |
| [18] |
张蕊, 李广云, 李明磊, 等.
利用PCA-BP算法进行激光点云分类方法研究[J]. 测绘通报, 2014(7): 23–26.
ZHANG Rui, LI Guangyun, LI Minglei, et al. Classification of LiDAR Point Clouds Based on PCA-BP Algorithm[J]. Bulletin of Surveying and Mapping, 2014(7): 23–26. DOI:10.13474/j.cnki.11-2246.2014.0217 |
| [19] | PANG Guan, NEUMANN U. Training-based Object Recognition in Cluttered 3D Point Clouds[C]//Proceedings of 2013 International Conference on 3D Vision-3DV 2013. Seattle, WA, USA:IEEE, 2013:87-94. |
| [20] | DONG Zhen, YANG Bisheng, LIU Yuan, et al. A Novel Binary Shape Context for 3D Local Surface Description[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017, 130: 431–452. DOI:10.1016/j.isprsjprs.2017.06.012 |
| [21] | HACKEL T, WEGNER J D, SCHINDLER K. Fast Semantic Segmentation of 3D Point Clouds with Strongly Varying Density[J]. ISPRS Annals of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2016, Ⅲ-3: 177–184. |
| [22] | GUO Yulan, BENNAMOUN M, SOHEL F, et al. A Comprehensive Performance Evaluation of 3D Local Feature Descriptors[J]. International Journal of Computer Vision, 2016, 116(1): 66–89. DOI:10.1007/s11263-015-0824-y |
| [23] | ANDONI A, INDYK P. Near-optimal Hashing Algorithms for Approximate Nearest Neighbor in High Dimensions[C]//Proceedings of the 47th Annual IEEE Symposium on Foundations of Computer Science. Berkeley, CA, USA:IEEE, 2006:459-468. |
| [24] | KAZHDAN M, HOPPE H. Screened Poisson Surface Reconstruction[J]. ACM Transactions on Graphics (TOG), 2013, 32(3): 29. |
| [25] | ROBLES-KELLY A, HANCOCK E R. A Riemannian Approach to Graph Embedding[J]. Pattern Recognition, 2007, 40(3): 1042–1056. DOI:10.1016/j.patcog.2006.05.031 |


