电力对现代社会的活动至关重要。为了确保电力的不间断供应,有必要对电力线进行有效地监测和维护。对电网的监测一般包括两个方面:电力线构件和周围物体(如植被)。不断接近电力线生长的树木可能破坏基础设施,甚至导致大面积断电与森林火灾,因此需要对电力线附近的植被做定期监测。而且,暴风雨以及其他自然灾害也可能对电力线造成一定程度的破坏[1]。
传统的人工巡检方式存在劳动力强度大、效率低、复巡周期长等缺点。近年来,诸多学者致力于将遥感技术应用于电力线监测中[1], 其中机载LiDAR以其独特的优势,被日渐广泛地应用于电力巡线中。机载LiDAR在电力方面的研究主要是点云自动分类和电力线构件重建[2-6],其中大部分提取电力线的方法是基于电力线的线性特征。文献[2, 6]利用霍夫变换提取电力线;文献[7]利用多次回波和强度信息分离电力线和植被;文献[8]通过分析首末次回波的高度差和强度信息分离电力线和植被;文献[9]从点云数据中提取21个几何特征并利用随机森林将场景分类为电线、电塔、植被、建筑物和低矮物体;文献[10]在分析点云场景的基础上,提取点云的26个几何特征,同时考虑一定的空间先验信息利用JointBoost实现场景分类。
在分类任务中,引入空间上下文信息进行分类约束已经成为研究人员的一个共识。文献[11—12]以条件随机场为框架,将上下文信息融入到点云分类决策中,使分类精度显著提高。文献[13]提出了一种融合航空影像辅助点云分类的方法,文中用SVM表达观测数据的概率分布,基于马尔可夫随机场实现顾及上下文信息的土地利用分类。文献[14]通过构建图割模型做全局优化,改善初始分类结果。因此,综合MRF模型所描述的空间上下文信息和提取的点云几何结构信息可以改善点云分类精度。
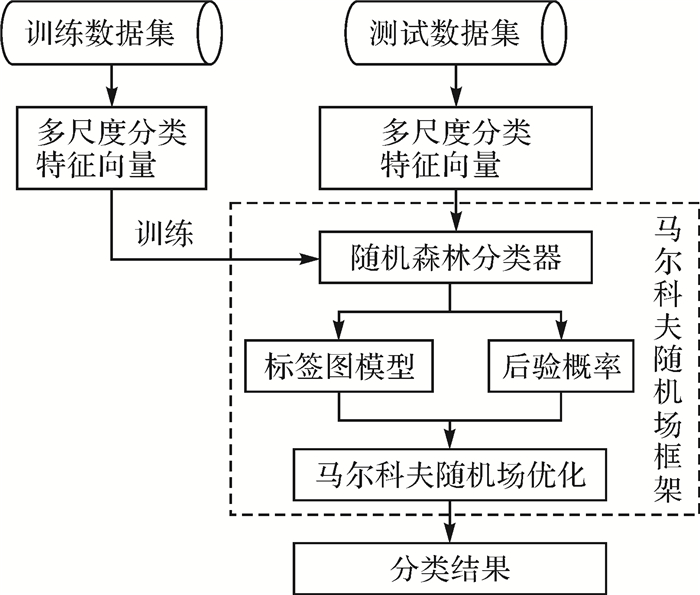
针对电力线场景中地物的连续性,本文提出了一种基于随机森林后验概率的马尔可夫随机场模型,记作MRF_RF模型,用于点云的分类与识别(如图 1所示)。首先结合空间金字塔理论构建多尺度视觉分类特征,以此描述空间点及其邻域的几何形状信息;接着利用随机森林分类器描述观测数据的概率分布,基于马尔可夫随机场模型建立顾及上下文信息的先验概率,构建一个多标记能量函数;最后利用多标记图割技术最小化能量函数完成分类标签优化。
|
| 图 1 马尔可夫随机场分类模型 Fig. 1 MRF classification model |
1 构建多尺度视觉分类特征
在点云视觉分类特征的计算中,通常需要连同三维邻域内的其他点一起统计和分析,因此计算点云的视觉分类特征首先需要考虑邻域的形状和大小[10, 15]。考虑到机载点云密度的变化,本文采用k邻域定义待分类点的邻域,作为计算点特征的支撑区域。
1.1 基于点的单尺度特征构建由于机载LiDAR点云数据具有场景复杂、目标丰富、点密度变化以及存在噪声点等问题,从大量激光雷达点云数据中提取有效信息进行场景分类始终是一个挑战。考虑到电力线场景的点云分布特点,综合文献[16—17]中对点云视觉分类特征的分析,选择点云的绝对高度[17]、基于特征值的特征[11-13, 16-17, 19]和电力线形状描述子作为分类点的视觉分类特征。
1.1.1 绝对高度点云的绝对高度Nh由DSM与DTM[18]的差值表示, 用于消除地形起伏的影响。
1.1.2 基于特征值的特征基于特征值的特征可以用来描述当前点周围小范围内的几何形状特征,被广泛应用于激光雷达点云分类中。假设Cp表示点p的邻域协方差矩阵,则Cp可以通过式(1)进行计算
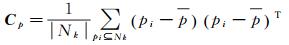 (1)
(1)
式中, 
尽管单条电力线具有很强的线性特征,但是实际场景中往往是两条电力线或者多条电力线并行的结构(即分裂导线)。双线或者多线并行结构在基于点邻域建模提取几何特征时,使得电力线的线性特征不再具有区分性。本文在分析电力线形状分布以及场景特点的基础上,参考ESP特征[20]提取的思路,提出一种描述双线并行电力线形状分布的特征描述子(powerline shape descriptor, PSD)。具体的提取流程如下:
(1) 取当前点p及其k邻域内所有点利用最小二乘拟合平面,并将当前点p及其邻域点沿平面的法线方向投影到拟合平面上。
(2) 从投影点中随机的选择3个点p1、p2、p3,构造三角形Δp1p2p3,如果三角形的任意一条边的边长小于给定阈值(文中设定为电力线的直径),则重新选择3个点。然后定义三角形中的最大角为θ。
(3) 将[60°, 180°]平均分成6个区间,重复步骤(2)MaxIter次,统计最大角θ在每个区间中出现的频率,构建角度频率直方图xPSD。
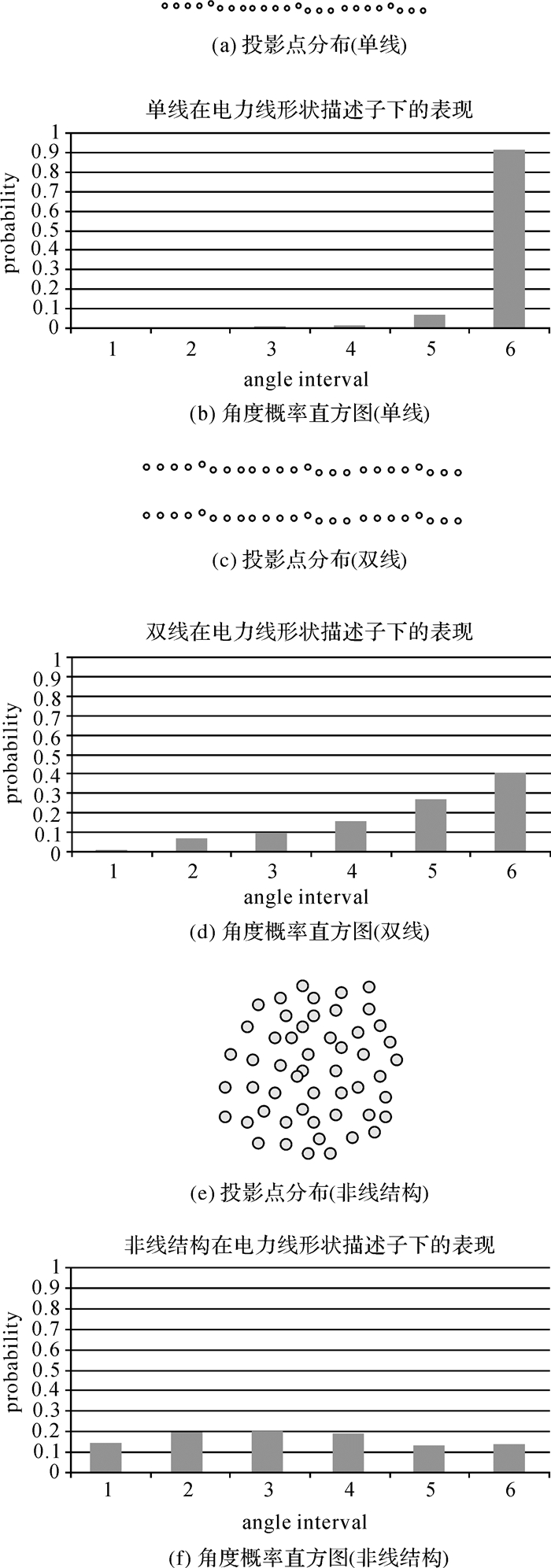
对于单条电力线的情形,当前点p及其邻域点沿平面的法线方向投影到拟合平面上所得到的投影点近似呈一条直线分布(图 2(a)),此时通过随机重复采样选点构造的三角形Δp1p2p3中最大角θ取值在180°附近。因此随机重复采样统计得到的角度频率直方图中第6个区间的概率应该最高且其值接近1,而其他区间的概率接近0,如图 2(b)所示。对于双线平行的情形,当前点p及其邻域点沿平面的法线方向投影到拟合平面上所得到的投影点近似呈两条直线平行分布(图 2(c)),此时通过随机重复采样选点构造的三角形Δp1p2p3中最大角θ是大于90°的,且从第2区间到第6区间概率呈递增趋势,如图 2(d)所示。对于其他非线结构的地物,当前点p及其邻域点沿平面的法线方向投影到拟合平面上所得到的投影点是散乱分布的(图 2(e)),此时通过随机重复采样选点构造的三角形Δp1p2p3中最大角θ取值范围是[60°, 180°]且是等可能的,因此随机重复采样统计得到的角度概率直方图近似为均匀分布,如图 2(f)所示。
|
| 图 2 不同地物构造电力线形状特征示意图 Fig. 2 Schematic diagram of power line shape with different surface features |
1.2 基于单点的多尺度特征构建
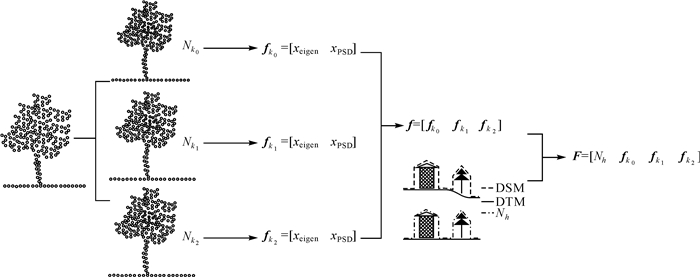
根据文献[19]的结论,k取值对不同地物的分类正确率产生不同的影响。考虑到点云在不同尺度下会表现出不同的纹理特征,本文参考空间金字塔匹配核思想[21],提出构建多尺度的特征向量的策略。具体思路如下:分别取3个不同邻域大小k值(即k=k0, k1, k2)计算当前点的视觉分类特征向量,然后连接成一个长分类特征向量构成当前点的多尺度分类特征向量F=[Nh fk0 fk1 fk2],用于描述电力线三维场景。本文以单木为例说明多尺度特征向量提取流程,如图 3所示。图中,分别取距离当前点最近的Nk0、Nk1、Nk2个点作为支撑区域构建当前点的单尺度特征向量fk0、fk1、fk2,将当前点3个尺度的特征向量fk0、fk1、fk2和绝对高度Nh连接成多尺度特征向量F。试验结果表明,与单尺度特征向量相比,本文构建的多尺度特征向量具有更好的区分性和稳健性。
|
| 图 3 多尺度特征向量提取流程 Fig. 3 The extracting process of multi-scale feature vector |
图 3中,黑色点为当前点,灰色点为当前点邻域Nki(i=0, 1, 2)内的点。基于特征值的特征xeigen=[λ1 λ2 λ3 Aλ Pλ Sλ Lλ]ki,i=0, 1, 2,xPSD为电力线形状描述子,Nh为绝对高度。
2 面向点云分类的MRF模型MRF模型[22]可以表示为一个无向图G=〈V, E〉,其中V表示节点的集合(本文中无向图中的节点与LiDAR点云中点的一一对应),E表示无向边的集合。对于点云数据D, 假定P={p1, p2, …, pN}表示D中N个点的集合,Ω={c1, c2, …, cm}表示m种类别标签的集合(本文中m=3,即植被、电力线和电塔3种地物),F={Fi|i=1, 2, …, N}表示数据D中点的特征向量集合,L={l=(l1, l2, …, lN)|li∈Ω, i=1, 2, …, N}表示数据D所有可能的标签配置。当以F为条件时L满足马尔可夫性:P(lu|{lv}u≠v; F)=P(lu|{lv}v∈N(u); F),其中u、v表示G中的节点,N(u)表示G中节点u的邻域,那么L是关于邻域系统N的一个马尔可夫随机场。因此,在构建面向点云数据的MRF模型之前,需要先定义点的邻域系统。
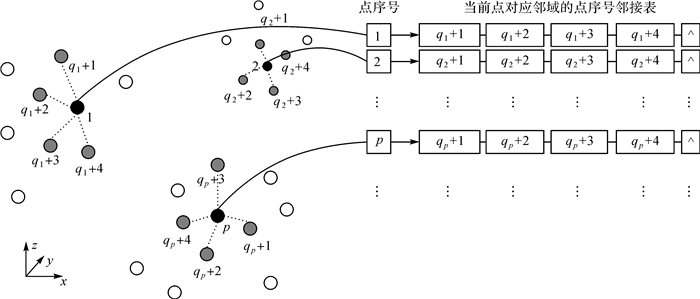
2.1 图模型的构建对于二维的栅格图像而言,可以利用像素的4邻域或者8邻域直观地建模图像像素间的关系。然而机载LiDAR点云数据在三维空间中的分布是不规则,点间也没有必然的拓扑关系。在一个MRF模型中,只有当两个节点是相邻的情况下,它们之间才会有直接的作用关系,而与其他节点无关。基于此,本文以Kd树组织散乱的点云,当前点p与距其最近的4个点连接无向边,构建MRF模型的邻域系统N,如图 4所示。
|
| 图 4 MRF模型的邻域系统N的构建 Fig. 4 The construction of neighborhood system N in MRF model |
图 4中,黑色点表示当前点,灰色点表示距离当前点最近的4个点。
2.2 马尔可夫随机场分类模型在MRF模型中,将点云分类看做是一个标记问题。根据点的视觉特征向量和分块平滑的特性,给任意点p分配一个类别标签ci(1≤i≤m),也就是将每个点映射到标签集Ω中的某个标签上。最优标签L*的确定不仅要满足分块平滑,还要与被观测数据保持一致。
在计算机视觉领域中,寻找最优的标签L*可以被表达为能量最小化问题,按照下式构建一个多标记能量函数
 (2)
(2)
式中,数据项Edata(L)描述了标签L与被观测数据的不一致性;平滑项Esmooth(L)表征了标签L的分块不平滑程度;λ表示平衡数据项和平滑项的比例系数。
诸多研究成果中提出了不同的能量函数表现形式,数据项Edata(L)一般被表示为
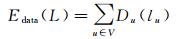 (3)
(3)
式中,Du(lu)度量在给定特征向量Fu的条件下,标签lu与观测数据的一致性。为了尽可能准确地反映每个点的特征信息,本文采用随机森林分类器拟合观测数据特征向量的概率分布,以随机森林分类器的后验概率定量地描述标签lu与观测数据的一致性。考虑到电力线场景中电力线的实际高度,对随机森林分类器的分类过程添加一个强约束,即如果当前点的绝对高度低于一定阈值(本文设置为7 m),则该点不能被分类为电力线点。
平滑项Esmooth(L)的选择至关重要。为了抑制分类过程中可能存在的“椒盐”现象,使得分类结果具有更好的区域性,本文将平滑项Esmooth(L)表示为
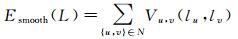 (4)
(4)
式中,N表示邻域系统;Vu, v(lu, lv)=g(u, v)· 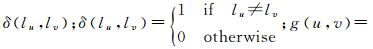
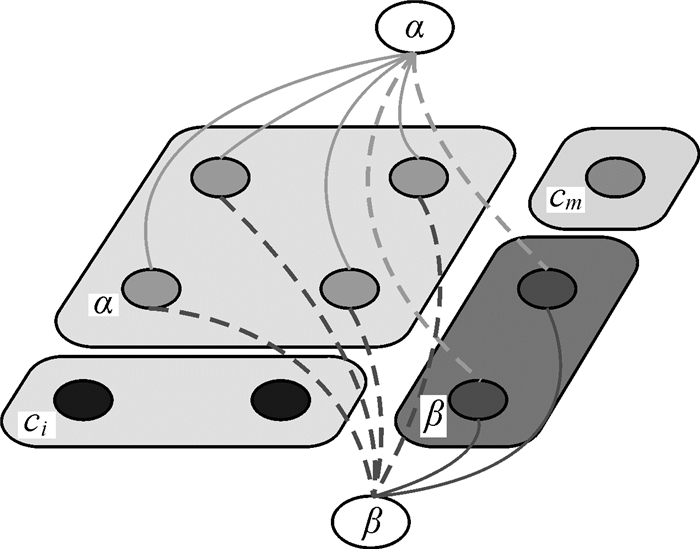
在基于MRF模型的分类问题中,最小化式(2)是一个NP难题。在本文中,式(2)采用多标记图割技术[23]有效地最小化。多标记图割技术是一种对任意有限大小的标签集l(l∈L)近似能量最小化的算法,不仅有效地改善了计算效率,而且可以获得全局最优解,其中α-β swap算法是多标记图割技术中的典型代表,如图 5所示。算法基本流程是:
|
| 图 5 多标记图割中Gαβ原理示意图 Fig. 5 Schematic diagram of Gαβ in multi-label graph cut |
(1) 初始化标签配置L。
(2) 设置标志变量flag=false。
(3) 对于每一对标签α, β(α, β∈Ω, α≠β),通过α-β swap操作调整L′,通过解最小割的方式最小化能量函数E(L′),如果E(L′) < E(L),则令L=L′,flag=true。
(4) 如果flag=true,转步骤(2),否则最优标签配置L*=L。
图 5中,Gαβ中节点集合υ={α}∪{β}∪Vαβ,Vαβ={w|w∈V, lw=α or β}, 无向边的集合Eαβ={euα|u∈Vαβ}∪{euβ|u∈Vαβ}∪{evu|v∈N(u), u, v∈Vαβ},其中,边权重Weuα=Du(α)+ 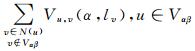
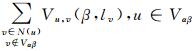
为了验证本文模型的有效性,选取电力行业的LiDAR点云数据作为试验数据。场景1-3为直升机平台的E+AP激光电力巡检系统获取的LiDAR点云数据,点云密度为大约40点/m2,总长约6500 m。场景4为无人机平台的SKY-Lark无人机雷达系统获取的LiDAR点云数据,点云密度为大约80点/m2,总长为约600 m。本文主要将场景分为植被、电塔和电力线,所用训练集和测试集的点云统计如表 1所示。
| 项目 | E+AP激光电力巡检系统 | SKY-Lark无人机雷达系统 | |||||
| 训练区1 | 场景1 | 场景2 | 场景3 | 训练区2 | 场景4 | ||
| 电塔 | 18 585 | 14 258 | 29 656 | 39 687 | 119 701 | 101 398 | |
| 电线 | 65 886 | 34 055 | 62 877 | 76 317 | 229 137 | 142 442 | |
| 植被 | 146 880 | 2 201 831 | 3 959 137 | 4 413 881 | 504 265 | 4 491 236 | |
| 合计 | 231 351 | 2 250 144 | 4 051 670 | 4 529 885 | 853 103 | 4 735 076 | |
本文采用召回率(recall)、精确率(precision)、准确率(overallaccuracy)和F_score对分类结果进行评价。假设原始样本中有两类,其中有P个类别为1的样本,且假设类别1为正例,有N个类别为0的样本,且假设类别0为负例,则
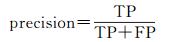 (5)
(5)
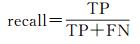 (6)
(6)
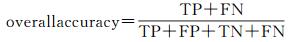 (7)
(7)
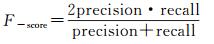 (8)
(8)
式中,TP个类别为1的样本被系统正确判定为类别1;FN个类别为1的样本被系统误判定为类别0;FP个类别为0的样本被系统误判断定为类别1;TN个类别为0的样本被系统正确判为类别0。
3.2 试验与精度分析 3.2.1 最大重复次数MaxIter对分类精度的影响为了验证最大重复次数MaxIter对分类精度的影响,本文以场景1为研究对象做了对比试验,最大重复次数MaxIter分别取值100、250、500、750、1000,其中权重λ设置为0.75,统计得到的分类正确率变化情况,如图 6所示,图中不同灰度的柱状图反映了不同地物的分类F-score值受最大重复次数MaxIter取值的影响,折线图表示了最大重复次数MaxIter的取值对分类总正确率的影响。试验结果表明,随着最大重复次数MaxIter的增加,分类正确率从99.77%逐步提高到99.79%,当MaxIter增加到750时,分类正确率在99.79%处维持稳定状态。在3类地物中,植被和电力线的分类精度受MaxIter取值影响较小,分类F-score值的波动小于0.2%。相反的,电塔的分类精度受MaxIter取值影响最大,分类F-score值的波动大于5%。

|
| 图 6 最大重复次数MaxIter对分类精度的影响 Fig. 6 The effect of maximum iteration number MaxIter on classification accuracy |
3.2.2 不同尺度组合对分类精度的影响
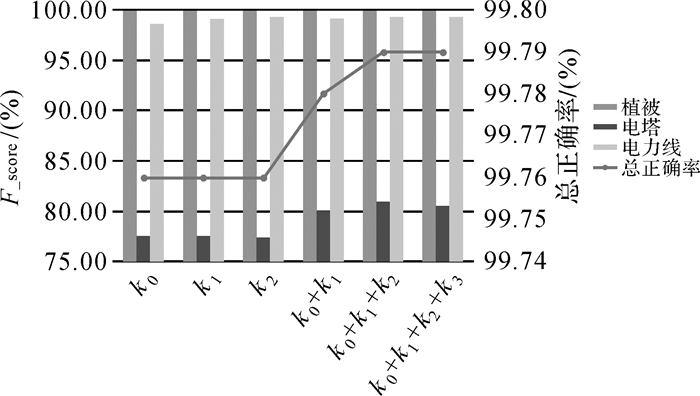
为了验证多尺度特征向量的优势,以场景1为试验对象,将多种不同尺度的组合情况做了对比试验,分别计算k0=30、k1=50、k2=70、k3=90时的特征向量,不同尺度计算的特征向量连接成一个长向量,利用MRF_RF模型对场景1进行分类,统计结果如图 7所示。图中不同灰度的柱状图反映了各类地物的分类F-score值在不同单尺度以及单尺度组合情况下的波动情况,折线图表示了不同单尺度以及单尺度组合情况对分类总正确率的影响。试验结果表明,单尺度特征向量连接成多尺度的长特征向量(如k0+k1、k0+k1+k2、k0+k1+k2+k3)所得到的分类正确率明显好于单一尺度,总正确率从99.76%提高到99.79%。其中,多尺度特征向量对改善电塔分类精度最为显著,在单尺度组合得到多尺度特征向量的不同试验中,电塔的分类F-score值的波动大于3%,而植被和电力线的分类F-score值的波动小于0.5%。然而这种单尺度连接成多尺度特征向量的策略,并不是尺度越多对改善分类精度越有益。从图 7可以看出,在对比试验中3个尺度的组合情况具有最高的分类精度。尽管4个尺度的组合情况在总分类精度上与3个尺度相当,但电塔的分类F-score值开始出现下降趋势。
|
| 图 7 不同尺度组合对分类精度的影响 Fig. 7 The effect of different scale combination on classification accuracy |
3.2.3 不同分类器间的对比
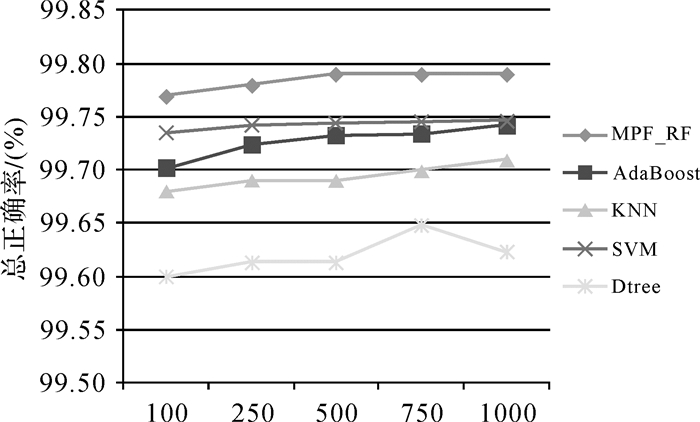
如3.2.1节所述,本文提出的用于描述电力线形状分布的PSD可以改善电力线的分类精度,其中参数MaxIter影响该特征描述子的稳健性。为了说明MaxIter对PSD稳健性的影响,本文以场景1为试验对象,将其应用于其他常规分类器(如AdaBoost、最近邻分类器(KNN)、支持向量机(SVM)、决策树(Dtree))中。试验结果如图 8所示,随着最大重复次数MaxIter的增加,各个分类器的分类总正确率都有不同程度的提高。但是最大重复次数达到750次时,分类总正确率开始趋向稳定状态。
|
| 图 8 最大重复次数MaxIter对不同分类器分类精度的影响 Fig. 8 The effect of maximum iteration number MaxIter on classification accuracy of different classifiers |
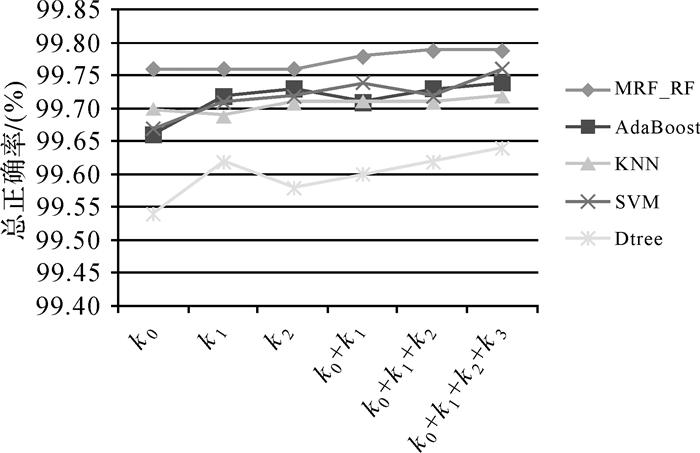
为了进一步验证本文提出的多尺度特征向量的优势,以场景1为试验对象,将单尺度与多尺度特征向量用于不同分类器中。其中,单尺度的试验结果中以尺度k1的分类结果最优,本文将其统计于表 2中,并将多尺度的结果统计于表 3中。对比表 2和表 3可见,尽管多尺度的策略在改善植被分类结果上效果不明显,但是对于电塔和电力线,其分类结果有明显改善,单地物的召回率最大可提高5%以上。图 9显示了不同分类器的分类总正确率受不同尺度组合的影响,多尺度特征向量在一定程度上提高了特征向量的表达能力,改善了分类质量。表 3—6显示了本文MRF_RF模型对比其他分类器的性能。在表 3—6所示的4个场景中,本文模型大多数的数据要优于其他分类器。将MRF_RF模型与其他分类方法对比可得,尽管不同的方法在分类植被方面性能相当,但MRF模型具有更高的总体精度,分类电塔的优势显著。
| (%) | |||||||||
| 项目 | 植被 | 电塔 | 电力线 | 总正确率 | |||||
| 召回率 | 精确率 | 召回率 | 精确率 | 召回率 | 精确率 | ||||
| MRF_RF | 99.99 | 99.79 | 64.70 | 96.86 | 99.25 | 99.02 | 99.76 | ||
| AdaBoost | 99.99 | 99.77 | 62.46 | 93.90 | 98.10 | 98.89 | 99.73 | ||
| KNN | 99.99 | 99.77 | 59.09 | 90.40 | 98.14 | 97.75 | 99.70 | ||
| SVM | 99.99 | 99.76 | 60.16 | 94.97 | 98.67 | 99.04 | 99.72 | ||
| Dtree | 99.86 | 99.82 | 63.60 | 72.12 | 98.61 | 97.42 | 99.62 | ||
| (%) | |||||||||
| 项目 | 植被 | 电塔 | 电力线 | 总正确率 | |||||
| 召回率 | 精确率 | 召回率 | 精确率 | 召回率 | 精确率 | ||||
| MRF_RF | 99.99 | 99.81 | 69.51 | 97.13 | 99.35 | 99.47 | 99.79 | ||
| AdaBoost | 99.99 | 99.80 | 68.14 | 97.44 | 99.36 | 99.32 | 99.73 | ||
| KNN | 99.99 | 99.78 | 60.96 | 90.25 | 97.92 | 97.99 | 99.71 | ||
| SVM | 99.99 | 99.77 | 62.65 | 96.07 | 98.95 | 99.09 | 99.74 | ||
| Dtree | 99.84 | 99.83 | 68.85 | 70.64 | 98.30 | 97.83 | 99.62 | ||
|
| 图 9 不同分类器分类精度受不同尺度组合的影响 Fig. 9 The effect of different scale combination on classification accuracy of different classifiers |
| (%) | |||||||||
| 项目 | 植被 | 电塔 | 电力线 | 总正确率 | |||||
| 召回率 | 精确率 | 召回率 | 精确率 | 召回率 | 精确率 | ||||
| MRF_RF | 99.99 | 99.82 | 75.15 | 96.70 | 98.83 | 99.52 | 99.80 | ||
| AdaBoost | 99.99 | 99.77 | 67.36 | 94.07 | 98.00 | 98.98 | 99.73 | ||
| KNN | 99.96 | 99.79 | 56.88 | 86.31 | 98.21 | 93.38 | 99.61 | ||
| SVM | 99.99 | 99.78 | 63.12 | 94.61 | 98.30 | 96.81 | 99.70 | ||
| Dtree | 99.50 | 99.85 | 73.85 | 51.38 | 98.43 | 97.26 | 99.29 | ||
| (%) | |||||||||
| 项目 | 植被 | 电塔 | 电力线 | 总正确率 | |||||
| 召回率 | 精确率 | 召回率 | 精确率 | 召回率 | 精确率 | ||||
| MRF_RF | 99.99 | 99.79 | 74.33 | 98.10 | 99.43 | 98.82 | 99.76 | ||
| AdaBoost | 99.99 | 99.74 | 67.21 | 95.74 | 98.61 | 98.23 | 99.68 | ||
| KNN | 99.98 | 99.75 | 60.81 | 92.41 | 98.44 | 94.46 | 99.61 | ||
| SVM | 99.99 | 99.74 | 64.29 | 96.65 | 98.94 | 96.39 | 99.66 | ||
| Dtree | 99.76 | 99.83 | 73.47 | 72.36 | 99.04 | 96.4 | 99.52 | ||
| (%) | |||||||||
| 项目 | 植被 | 电塔 | 电力线 | 总正确率 | |||||
| 召回率 | 精确率 | 召回率 | 精确率 | 召回率 | 精确率 | ||||
| MRF_RF | 99.20 | 99.50 | 74.27 | 65.15 | 96.79 | 97.26 | 98.59 | ||
| AdaBoost | 99.99 | 99.50 | 74.27 | 94.35 | 96.79 | 97.36 | 98.26 | ||
| KNN | 99.47 | 99.16 | 57.81 | 49.79 | 72.17 | 91.97 | 97.76 | ||
| SVM | 99.83 | 99.04 | 54.98 | 59.92 | 76.34 | 94.89 | 98.16 | ||
| Dtree | 96.54 | 99.41 | 67.43 | 28.10 | 85.57 | 93.62 | 95.58 | ||
3.2.4 不同分类器的效率对比
为了对比不同分类器所产生的计算时间成本,本文以场景1为研究对象,进行对比试验。表 7列举了不同分类器的运行时间。试验结果表明,Dtree具有最高的效率,但其分类效果明显低于其他方法,分类总正确率低于MRF_RF模型0.17%,电力线和电塔的召回率分别低于MRF_RF模型1.05%和0.66%,电力线和电塔的精确率分别低于MRF_RF模型1.64%和26.49%。与KNN和SVM方法相比,MRF_RF模型不仅在效率上明显高于这两种方法,而且在电力线的分类召回率上分别高出KNN和SVM方法1.43%和0.4%,在电塔的分类召回率上分别高出KNN和SVM方法8.55%和6.86%。尽管MRF_RF模型在效率上略低于AdaBoost方法,但其在总分类正确率上高出AdaBoost方法0.06%,在电塔的分类召回率上高出AdaBoost方法1.37%。
| 分类器 | MRF_RF | AdaBoost | Dtree | KNN | SVM |
| 运行时间 | 37.78 | 16.24 | 0.26 | 105.71 | 128.73 |
4 结束语
针对机载点云数据,本文提出了一种基于随机森林后验概率的马尔可夫随机场模型,用于电力线场景的点云分类。该方法可以有效地分类地物点,同时也为LiDAR电力巡线的数据后处理提供了新思路,大大节省了人力物力。尽管考虑地物之间局部相关性可以改善点云的分类精度,面对复杂的场景以点为单位的点云分类是一种挑战。面向对象的分类方法或者基于对象提取中层以及高层语义信息辅助点云分类将是下一步研究的重点。
| [1] | MATIKAINEN L, LEHTOMÄKI M, AHOKAS E, et al. Remote Sensing Methods for Power Line Corridor Surveys[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2016, 119: 10–31. DOI:10.1016/j.isprsjprs.2016.04.011 |
| [2] |
余洁, 穆超, 冯延明, 等.
机载LiDAR点云数据中电力线的提取方法研究[J]. 武汉大学学报(信息科学版), 2011, 36(11): 1275–1279.
YU Jie, MU Chao, FENG Yanming, et al. Powerlines Extraction Techniques from Airborne LiDAR Data[J]. Geomatics and Information Science of Wuhan University, 2011, 36(11): 1275–1279. |
| [3] |
林祥国, 张继贤.
架空输电线路机载激光雷达点云电力线三维重建[J]. 测绘学报, 2016, 45(3): 347–353.
LIN Xiangguo, ZHANG Jixian. 3D Power Line Reconstruction from Airborne LiDAR Point Cloud of Overhead Electric Power Transmission Corridors[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(3): 347–353. DOI:10.11947/j.AGCS.2016.20150186 |
| [4] |
段敏燕.
机载激光雷达点云电力线三维重建方法研究[J]. 测绘学报, 2016, 45(12): 1495.
DUAN Minyan. 3D Power Line Reconstruction from Airborne LiDAR Point Cloud[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(12): 1495. DOI:10.11947/j.AGCS.2016.20160341 |
| [5] |
赖旭东, 戴大昌, 郑敏, 等.
LiDAR点云数据的电力线3维重建[J]. 遥感学报, 2014, 18(6): 1223–1229.
LAI Xudong, DAI Dachang, ZHENG Min, et al. Powerline Three-dimensional Reconstruction for LiDAR Point Cloud Data[J]. Journal of Remote Sensing, 2014, 18(6): 1223–1229. |
| [6] |
陈驰, 麦晓明, 宋爽, 等.
机载激光点云数据中电力线自动提取方法[J]. 武汉大学学报(信息科学版), 2015, 40(12): 1600–1605.
CHEN Chi, MAI Xiaoming, SONG Shuang, et al. Automatic Power Lines Extraction Method from Airborne LiDAR Point Cloud[J]. Geomatics and Information Science of Wuhan University, 2015, 40(12): 1600–1605. |
| [7] | AXELSSON P. Processing of Laser Scanner Data:Algorithms and Applications[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1999, 54(2-3): 138–147. DOI:10.1016/S0924-2716(99)00008-8 |
| [8] | CLODE S, ROTTENSTEINER F. Classification of Trees and Powerlines from Medium Resolution Airborne Laserscanner Data in Urban Environments[C]//LOVELL B C, MAEDER A J. Proceedings of APRS Workshop on Digital Image Computing 2005(WDIC2005). Brisbane: University of Queensland, 2005, 1: 97-102. http://www.researchgate.net/publication/43459440_Classification_of_trees_and_powerlines_from_medium_resolution_airborne_laserscanner_data_in_urban_environments?ev=prf_high |
| [9] | KIM H B, SOHN G. Point-based Classification of Power Line Corridor Scene Using Random Forests[J]. Photogrammetric Engineering & Remote Sensing, 2013, 79(9): 821–833. |
| [10] | GUO Bo, HUANG Xianfeng, ZHANG Fan, et al. Classification of Airborne Laser Scanning Data Using JointBoost[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 100: 71–83. DOI:10.1016/j.isprsjprs.2014.04.015 |
| [11] | LIM E H, SUTER D. 3D Terrestrial LIDAR Classifications with Super-voxels and Multi-scale Conditional Random Fields[J]. Computer-Aided Design, 2009, 41(10): 701–710. DOI:10.1016/j.cad.2009.02.010 |
| [12] | NIEMEYER J, ROTTENSTEINER F, SOERGEL U, et al. Hierarchical Higher Order Crf for the Classification of Airborne LiDAR Point Clouds in Urban Areas[C]//Proceedings of ISPRS International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Prague, Czech Republic: ISPRS, 2016, XLI-B3: 655-662. http://adsabs.harvard.edu/abs/2016ISPAr41B3..655N |
| [13] | CAO Yang, WEI Hong, ZHAO Huijie, et al. An Effective Approach for Land-cover Classification from Airborne LiDAR Fused with Co-registered Data[J]. International Journal of Remote Sensing, 2012, 33(18): 5927–5953. DOI:10.1080/01431161.2012.676746 |
| [14] | LI Zhuqiang, ZHANG Liqiang, TONG Xiaohua, et al. A Three-step Approach for TLS Point Cloud Classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(9): 5412–5424. DOI:10.1109/TGRS.2016.2564501 |
| [15] | FILIN S, PFEIFER N. Neighborhood Systems for Airborne Laser Data[J]. Photogrammetric Engineering & Remote Sensing, 2005, 71(6): 743–755. |
| [16] | CHEHATA N, GUO L, MALLET C. Airborne LiDAR Feature Selection for Urban Classification Using Random Forests[J]. Laser Scanning, 2009, 38: 207–212. |
| [17] | DITTRICH A, WEINMANN M, HINZ S. Analytical and Numerical Investigations on the Accuracy and Robustness of Geometric Features Extracted from 3D Point Cloud Data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017, 126: 195–208. DOI:10.1016/j.isprsjprs.2017.02.012 |
| [18] | AXELSSON P. DEM Generation from Laser Scanner Data Using Adaptive TIN Models[J]. International Archives of Photogrammetry and Remote Sensing, 2000, 33: 110–117. |
| [19] | KANG Zhizhong, YANG Juntao, ZHONG Ruofei. A Bayesian-network-based Classification Method Integrating Airborne LiDAR Data with Optical Images[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 10(4): 1651–1661. |
| [20] | WOHLKINGER W, VINCZE M. Ensemble of Shape Functions for 3D Object Classification[C]//Proceedings of 2011 IEEE International Conference on Robotics and Biomimetics. Karon Beach, Phuket: IEEE, 2011: 2987-2992. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6181760 |
| [21] | LAZEBNIK S, SCHMID C, PONCE J. Beyond Bags of Features: Spatial Pyramid Matching for Recognizing Natural Scene Categories[C]//Proceedings of Computer Society Conference on Computer Vision and Pattern Recognition. New York, NY: IEEE, 2006: 2169-2178. |
| [22] | GEMAN S, GEMAN D. Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of Images[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1984, PAMI-6(6): 721–741. DOI:10.1109/TPAMI.1984.4767596 |
| [23] | BOYKOV Y, VEKSLER O, ZABIH R. Fast Approximate Energy Minimization via Graph Cuts[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(11): 1222–1239. DOI:10.1109/34.969114 |



