2. 东北林业大学森林作业与环境研究中心, 黑龙江 哈尔滨 150040
2. Center for Forest Operations and Environment, Northeast Forestry University, Harbin 150040, China
针叶林作为森林的主要组成部分,在调节全球气候、维持大气平衡及全球碳循环等方面均发挥着重要的作用。森林冠层描述了林木枝、叶的分布状况,控制着森林与外界的水分、能量及大气交换,对于研究多种森林生物物理活动具有重要意义[1-3]。作为森林冠层结构定量化描述参数,叶面积指数(leaf area index, LAI)定义为单位地表面积上所有叶片表面积的一半[4-6],在森林生长预测[7]、火灾预警[8]及生态过程模拟[9]等方面均发挥着重要的作用。
激光雷达(light detection and ranging,LiDAR)作为一种新型的主动遥感技术,不仅能够获得地物的结构信息,同时也能获得地物的回波强度信息。其中,强度信息作为与地表反射直接相关的信息源,具有结构信息不可比拟的优势,现已广泛应用于多种森林参数的估测研究中,如森林类型分类[10]、树种识别[11]、森林孔隙度估测[12-14]、森林LAI估测[15-16]、森林生物量估测[17]等。
然而,激光雷达强度在获取过程中受多种因素的影响,如传感器与目标物之间的距离、入射角、地物反射率及大气衰减等。近年来,研究人员针对强度影响因素校正进行了不断的尝试并获得了不错的结果。如:文献[12, 18]利用距离对LiDAR点云强度数据进行校正,进而估测了森林LAI,虽获得了不错的估测结果,但却未对强度距离校正前后LAI估测结果差异进行深入研究; 文献[19]同样利用距离对LiDAR点云强度进行校正,从中提取单束激光穿透指数用于估测白桦林LAI,结果经验模型估测精度R2=0.80,MAD=0.11,理论模型估测精度R2=0.77,RMSE=0.16,但同样未对强度校正前后估测结果的差异进行深入研究。与上述研究有所不同,文献[20]对强度校正前后估测结果差异进行了研究,利用距离、入射角及反射率对LiDAR点云强度进行校正,从中提取激光穿透指数用于估测森林LAI,结果发现强度校正后森林LAI的估测精度R2=0.825,RMSE=0.165,结果远高于强度未校正时的估测结果(R2=0.726,RMSE=0.258),但却未对单个因素校正前后的影响进行深入分析。综上分析可知,单因素强度校正森林LAI估测影响结果未知,不能实现强度数据有针对性的校正,会造成多因素综合强度校正效率较低、人力物力浪费,甚至会在一定程度降低估测精度。因此,各影响因素强度校正影响的定量化研究显得尤为重要,对于提高强度校正效率及森林参数估测精度具有重要意义。
先前基于机载LiDAR点云数据森林LAI估测研究多以比尔朗伯定律为基础,通过对点云数据进行分类处理进而计算比值参数,如:激光穿透指数(laser penetration index,LPI),用于替代比尔朗博定律内的森林孔隙度。由比值参数的性质可知,LPI通常是由两类数据经过比值运算得到,而在比值运算的过程中会对数据间的某些差异产生一定程度的影响,因而在反映强度校正前后数据差异时可能存在一定的不足[21]。为了与LPI参数形成对比,本研究同时引入了一个新的变量参数,即冠层总强度(canopy intensity sum,CIS),定义为森林冠层部分所有离散LiDAR点云强度之和[22],由其定义可知,冠层总强度参数只与森林冠层的强度有关,因而,理论上而言能够更加直观地反映强度校正对森林LAI估测的影响。
因此,本研究分别采用距离、入射角及距离和入射角对机载LiDAR点云强度进行校正,从中提取冠层总强度和强度比值两种不同类型的参数变量,用于森林LAI的估测研究,从而实现各影响因素强度校正对不同类型参数估测森林LAI的影响进行量化,以期为未来机载LiDAR强度数据林业应用提供针对性的校正意见与建议。
1 研究区与数据介绍 1.1 研究区概况本研究以长春净月潭国家森林公园(125°21′E,43°52′N)为研究区。该公园位于长春市东南部,地貌为低山丘陵,高程为220~406.5 m,北部高程较高且变化较大,南部则高程较低且变化较小。研究区处于地带类型的过渡区,因而植被组成相对丰富多样,园区内种植了大量的人工林,总面积高达80 km2,森林覆盖率在96%以上。其中,樟子松(pinus sylvestris)作为研究区的主要组成树种,成片分布于研究区内。
1.2 机载LiDAR离散点云数据2012年5月31日对研究区进行机载LiDAR数据采集,研究区总共有9条南北航向的离散点云数据所覆盖,相邻航带之间的重叠度在40%左右。本次LiDAR数据采集所用传感器为Leica ALS70,绝对航高为560 m,激光脉冲波长为1064 nm,扫描角在±20°以内,扫描频率为40.3 Hz,光斑直径为0.28 m。LiDAR数据除包含地物的X、Y、Z坐标数据外,还同时存储了地物的强度、航向及对应的扫描角数据。
1.3 野外数据2014年7月在研究区樟子松林分内随机选取了30块半径为10 m的样方。首先利用天宝GeoXH 6000 GPS和南方NTS 312B全站仪测定样方中心点的坐标、高程及坡度等信息,同时利用三星NV3鱼眼镜头在每个样方的中心点、4个主方向距中心点5 m处各采集一张半球影像。根据野外调查发现,样方内林下植被高度绝大多数在1.5 m以下,为了减少林下植被对半球影像估测结果的影响,在采集半球影像时将鱼眼镜头的高度设定为地面以上1.5 m,同时为了简化后续处理,半球影像拍摄时应指向正北向,且避免太阳直射。之后利用WinSCANOPY 2010软件对采集到的半球影像进行处理,最终取其均值作为样方实测LAI。野外样地基本统计量描述见表 1。
| 因子 | 均值 | 最小值 | 最大值 |
| 树高/m | 16.0 | 12.1 | 19.7 |
| LAI | 2.56 | 2.03 | 3.61 |
| 高程/m | 293 | 244 | 358 |
| 坡度/(°) | 9 | 1 | 30 |
2 研究方法 2.1 机载LiDAR点云数据预处理
原始机载LiDAR数据通常会包含噪声点,因此在进行点云数据处理之前先利用孤立点算法对其进行去噪处理。接着对去除噪后的点云数据进行重叠点移除操作,以消除相邻航带旁向重叠对点云密度造成的影响,并使点云扫描角在±10°以内。之后利用不规则三角网滤波算法实现地面点及非地面点的分类处理,并利用不规则三角网插值算法将得到的地面点插值生成数字高程模型(digital elevation model,DEM),进而完成非地面点的高程归一化。最终将1.5 m以上的非地面点归为植被点,将1.5 m以下的非地面点和地面点统称为地面点。
2.2 LiDAR强度数据校正 2.2.1 雷达方程机载LiDAR系统的工作原理与雷达系统相似,因而LiDAR系统测得的强度数据同样遵循雷达方程,如式(1)所示
 (1)
(1)
式中,Pr为LiDAR传感器接收的强度值;Pt为LiDAR传感器发射的能量值;Dr为传感器光圈的直径;R为传感器到目标物体之间的距离;βt为激光脉冲的发散度;ηsys为LiDAR系统的系统误差;ηatm为大气的衰减系数;σ为被照射物体的后向散射横截面。
由式(1)可知,LiDAR系统记录的强度值受LiDAR传感器设置参数、大气传输及照射物体特性的影响[23]。在假定被照射物体为理想朗伯体反射的时候,传感器接收的能量与cos α成正比,所以被照射物体的后向散射横截面可以表示为cos α的函数,具体如式(2)所示[24-25]
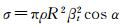 (2)
(2)
式中,ρ为被照射物体的反射率;α为入射角。
实际上,自然界中绝大多数物体均不是理想朗伯体反射,但因物体表面的具体反射特性不易获得,同时也为了简化计算过程,依然采用理想朗伯体反射假设。将式(2)与式(1)进行合并,式(1)可以表达为式(3)
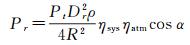 (3)
(3)
因研究区的LiDAR数据均是在一次飞行任务中获得,所以式(3)中的部分参数认为是相同的,如Pt、Dr、ηsys和ηatm,同时因森林冠层真实的反射率数据不可获得,因此忽略反射率的影响,统一将上述参数表示为常数C(文献[25, 27]),式(3)可以简化为式(4)
 (4)
(4)
因而,本研究只对传感器与目标物体间的距离及入射角对LiDAR强度数据产生的影响进行校正研究。
2.2.2 距离校正由式(4)可知,LiDAR传感器接收的强度值与传感器和目标物体间的距离及入射角有关。为了单独研究强度数据距离校正对森林LAI估测产生的影响,在此先假定入射角为常数,因此距离校正公式可简化为式(5)和式(6)
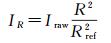 (5)
(5)
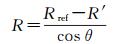 (6)
(6)
式中,IR为校正后的强度数据;Iraw为原始的强度数据,由点云数据直接获得;R为传感器到目标物体之间的距离;Rref为参考距离,取值1500 m;R′为点云数据的高程值,由点云数据直接获得;θ为点云数据的扫描角,由点云数据直接获得。
此距离校正方法现已成功用于多种机载LiDAR强度数据的校正与应用研究中[3, 17, 28]。
2.2.3 入射角校正入射角定义为激光入射方向与物体表面法线之间的夹角。由定义可以看出,入射角不仅与激光的扫描角有关,而且还与激光脉冲接触表面的地形(坡度和坡向)有关。当表面完全水平时,入射角等于扫描角;当物体表面存在坡度时,入射角是扫描角、坡度和坡向共同作用的结果,计算过程见式(7)所示
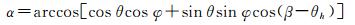 (7)
(7)
式中,α为入射角;φ为坡度,由DEM衍生得到的坡度专题图计算得到;β为坡向,由DEM衍生得到的坡向专题图计算得到;θh为水平投影角,由脉冲及飞行器位置共同计算得到,具体计算过程参见文献[27]。有关公式的详细推导过程参见文献[27]。入射角校正与距离校正相似,即假定传感器与目标物体间的距离为常数,因此校正的强度和入射角的余弦值成反比,如式(8)所示
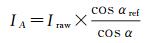 (8)
(8)
式中,IA为入射角校正后的强度;αref为参考入射角,取值0°。
现阶段有关植被LiDAR强度入射角校正所采用的入射角有以下3种:①忽略地形的影响,完全采用扫描角;②考虑地形的影响,采用DEM与扫描角共同衍生得到入射角;③考虑地形及植被表面的影响,采用DEM和扫描角衍生得到地面点入射角,同时利用数字表面模型和扫描角衍生得到植被点的入射角。从理论上讲,第3种入射角强度校正所得结果最为准确,但因森林冠层结构复杂,使得数字表面模型求得的入射角相对较大,会导致植被点云强度过矫正[27, 29]。同时研究表明当扫描角小于15°时,扫描角强度校正对结果的影响不大,甚至可以忽略不计[30-31]。因而,出于简化计算的目的,部分先前研究常采用由DEM和扫描角共同衍生得到的入射角对机载LiDAR点云强度数据进行校正进而估测森林结构参数[20, 32],但却均未考虑由DEM和扫描角共同衍生得到的入射角对森林植被点云强度校正的适用性。为了量化此入射角对森林植被点云强度校正的影响,进而为后续研究提供针对性的校正意见与建议,本研究仅对由DEM和扫描角共同衍生得到的入射角进行研究。
2.2.4 距离和入射角校正为了验证距离及入射角综合强度校正对森林LAI估测的影响,本研究在距离和入射角单独校正的基础上综合考虑二者共同校正的影响,其强度校正过程如式(9)所示
 (9)
(9)
式中,IRA为距离和入射角共同校正后的强度;其余变量所代表的意义同上。
2.3 强度参数提取本文分别选取了两种不同类型的参数用于验证LiDAR强度校正前后对森林LAI估测的影响,其中一种为冠层总强度参数;一种为强度比值参数。
2.3.1 冠层总强度参数提取冠层总强度参数最早由文献[22]从大光斑全波形激光雷达系统中提出,之后由文献[33]引入机载LiDAR离散点云数据森林结构参数估测研究。由CIS定义可知,在机载LiDAR离散点云应用中,冠层总强度参数与多种因素有关,如:样方点云密度和样方面积。为了消除点云密度及面积对CIS计算结果的影响,本研究在计算CIS的过程中充分考虑了样方点云密度及样方坡度的差异,具体计算过程如式(10)所示
 (10)
(10)
式中,CIS为经样方面积和点云密度校正后的冠层总强度和;
为了与冠层总强度参数形成对比,本研究同时采用强度比值参数,即激光穿透指数。LPI在计算的过程中充分考虑了激光在森林冠层内部的传输,现已广泛应用于森林郁闭度及森林叶面积指数的估测研究[1, 34]。有关此变量的详细解释见文献[35],其计算过程如式(11)所示
 (11)
(11)
式中,LPI为由强度数据计算得到的激光穿透指数;∑Iground为样方地面总强度,由样方地面点云原始或校正强度计算得到;∑Ivegetation为样方冠层总强度,由样方植被点云原始或校正强度计算得到。
2.4 森林LAI反演及精度评价为了更加直观地体现点云强度校正对森林LAI估测的影响,本研究采用一元线性回归对森林LAI进行建模,具体如式(12)所示
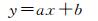 (12)
(12)
式中,y为实测森林LAI;a为拟合系数;x为CIS或-ln(LPI);b为常数项。同时由比尔朗伯定律可知,LAI与-ln(LPI)线性相关,所以在用LPI对森林LAI进行估测时应先对其进行对数变化[20]。
因研究所用样本数量相对较少,为了在有限样本条件下获得较为稳定可靠的森林LAI估测结果,本研究采用留一交叉验证用于森林LAI估测模型的建立及精度评价。其中,模型决定系数(coefficient of determination,R2)和均方根误差(root mean square error,RMSE)用作估测模型精度评价的指标。
3 结果分析与讨论 3.1 基于距离校正强度参数森林LAI估测结果 3.1.1 冠层总强度参数估测结果距离强度校正前后CIS参数森林LAI估测结果如图 1所示。通过对图 1所示森林LAI估测结果进行分析可知,对CIS参数而言,强度距离校正能够提高森林LAI的估测精度。具体如图 1(a)所示,强度距离校正前森林LAI的估测精度R2=0.646,RMSE=0.226,强度经距离校正后森林LAI的估测精度R2=0.714,RMSE=0.203(图 1(b)),相较强度距离校正前R2增加了0.068,RMSE减少了0.023。
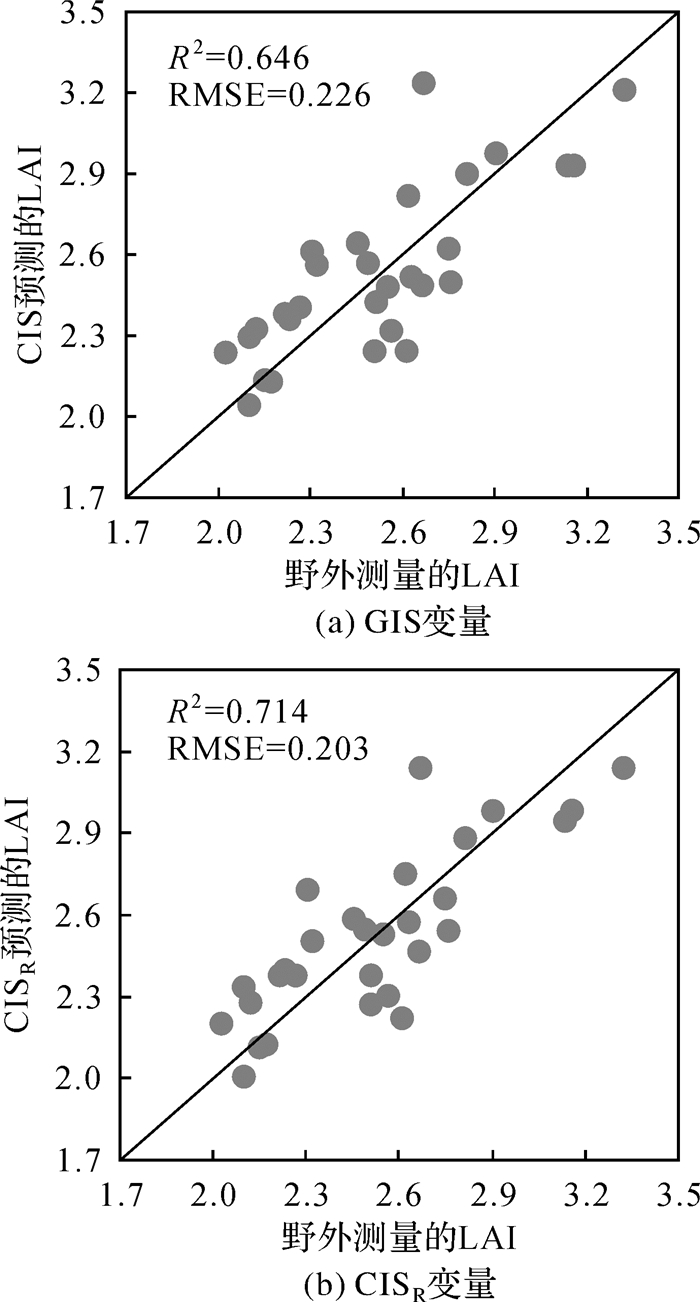
|
| 图 1 野外实测LAI与CIS变量预测LAI关系 Fig. 1 The relationships between the field-measured LAI and CIS predicted LAI |
3.1.2 强度比值参数估测结果
距离强度校正前后LPI参数森林LAI估测结果如图 2所示。通过对图 2所示LPI参数强度校正前后森林LAI估测结果进行对比分析发现,对LPI参数而言,强度经距离校正虽对森林LAI的估测结果有影响,但影响不大。如图 2(a)所示,强度校正前LPI森林LAI估测结果R2=0.794,RMSE=0.172;如图 2(b)所示,强度校正后LPI森林LAI估测结果R2=0.795,RMSE=0.172,相较强度校正前估测精度R2仅增加了0.001,RMSE则保持不变。

|
| 图 2 野外实测LAI与LPI变量预测LAI关系 Fig. 2 The relationships between the field-measured LAI and LPI predicted LAI |
对图 1和图 2所示结果进行综合分析可知,无论是CIS参数还是LPI参数,点云强度距离校正均能提高森林LAI估测精度,只是在增长量上稍有差异,具体为CIS参数估测结果增量高于LPI估测结果增量。结果表明,强度距离校正能够提高森林LAI估测精度,且强度比值参数在一定程度上减弱了强度距离校正对森林LAI估测的影响。这一结果与先前研究在某种意义上具有一致性,先前研究认为传感器与目标之间的距离是所有强度数据影响因素中最为重要的因素,距离强度校正能在一定程度上提高估测结果精度[36]。
3.2 基于入射角校正强度参数森林LAI估测结果 3.2.1 冠层总强度参数估测结果入射角强度校正后CISA参数森林LAI估测结果如图 3所示。对CIS参数而言,强度经入射角校正后森林LAI的反演精度非但没能得到提高,反而出现了一定程度的下降。如图 3所示,强度经入射角校正后的估测精度R2=0.610,RMSE=0.237,相较强度校正前估测结果R2降低了0.036,RMSE增加了0.011。

|
| 图 3 野外实测LAI与CISA预测LAI关系 Fig. 3 The relationships between the field-measured LAI and CISA predicted LAI |
3.2.2 强度比值参数估测结果
入射角强度校正后LPIA参数森林LAI估测结果如图 4所示。对LPI参数而言,入射角强度校正在一种程度上降低了森林LAI的估测精度,但结果差异不明显。如图 4所示,强度经入射角校正森林LAI的估测结果R2=0.793,RMSE=0.173,相较强度校正前森林LAI估测结果而言,R2降低了0.001,RMSE增大了0.001。

|
| 图 4 野外实测LAI与LPIA预测LAI关系 Fig. 4 The relationships between the field-measured LAI and LPIA predicted LAI |
通过对图 3和图 4所示结果进行综合分析可知,无论是CIS参数还是LPI参数,强度经入射角校正对森林LAI估测的影响均为负,且CIS参数估测结果的降低量要大于LPI参数估测结果的降低量。结果表明,由DEM和扫描角计算得到的入射角不适于樟子松冠层点云强度校正,同时强度比值参数在一定程度上减弱了入射角强度校正对森林LAI估测产生的影响。
本研究入射角强度校正影响为负,可以从以下两个方面来解释:
(1) 研究所采用强度校正入射角均是由DEM和扫描角共同衍生得到,而未对森林不同点云强度入射角校正进行差异化处理。众所周知,森林内成片的林木树冠表面会形成一个连续的、类似DEM的表面,称为数字表面模型(digital surface model, DSM),这个DSM与林木的生长状况及林木冠层起伏密切相关。由DEM和扫描角共同衍生得到的入射角适用于森林地面点强度校正,却不适用于森林冠层植被点的强度校正,主要是因为在同一X、Y处,DEM和DSM衍生得到的坡度坡向数据差异相对较大,因而由DSM和扫描角衍生得到的入射角不能等同由DEM和扫描角共同衍生得到的入射角,所以用由DEM和扫描角共同衍生得到的入射角对林木冠层点云强度数据进行校正存在一定的不足。
(2) 研究采用雷达方程校正入射角的影响时,物体表面被假定为理想的朗伯体反射,因此物体反射强度和cos α成一定的比例[24],而现实自然界内的绝大多数物体并不完全遵循朗伯体反射,物体非朗伯体反射部分的存在在一定程度上也会造成校正结果的不准确性。综上所述,在未来林业LiDAR强度校正研究中,应采用更为合适的校正算法对森林不同点云强度数据进行差异化校正,进而提高森林结构参数估测精度。
强度校正对于两种不同类型参数估测结果的影响程度因其性质不同而互有差异。强度经距离和入射角校正对冠层总强度参数的影响相对较大,而对强度比值参数的影响相对较小。如前所述,强度比值参数是由地面总强度和样方总强度经过比值运算得到,比值运算在一定程度上减弱了强度校正对森林LAI估测产生的影响;而冠层总强度参数为强度的简单加和,在一定程度上很好地保留了强度校正的影响。文献[21]曾得出类似结论,认为图像方差之间的比值运算能够消除光学影像中物体和背景之间的对比差异。因此,未来应根据研究目的的不同选用合适的参数变量。
3.3 基于距离和入射角校正强度参数森林LAI估测结果 3.3.1 冠层总强度参数估测结果距离和入射角强度校正CISRA参数森林LAI估测结果如图 5所示。对CIS参数而言,强度经距离和入射角校正能够提高森林LAI的估测精度。如图 5所示,强度经距离和入射角校正后森林LAI的估测精度R2=0.681,RMSE=0.214,较强度校正前森林LAI估测结果R2提高了0.035,RMSE降低了0.012。
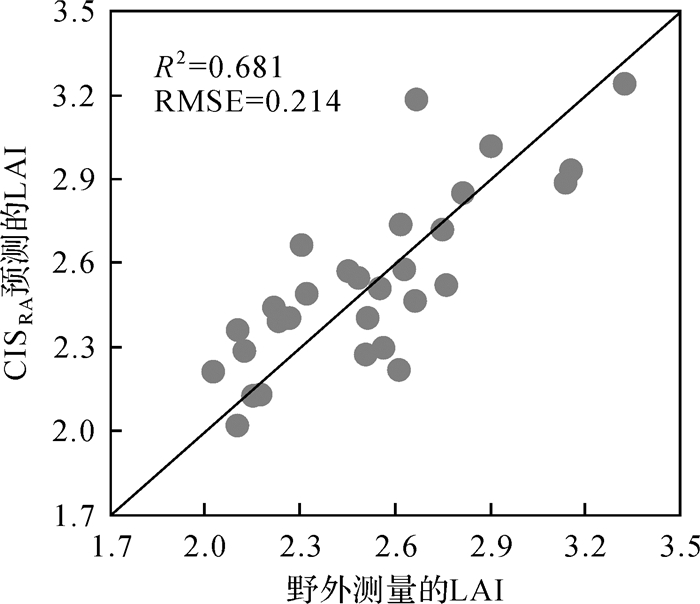
|
| 图 5 野外实测LAI与CISRA预测LAI关系 Fig. 5 The relationships between the field-measured LAI and CISRA predicted LAI |
综合对比分析图 1、图 3和图 5所示结果可知,强度经距离和入射角校正CISRA森林LAI的估测精度低于强度经距离校正的结果,但高于强度经入射角校正的结果。究其原因是主要距离校正对森林LAI的估测为正的影响,入射角校正对森林LAI的估测为负的影响,所以二者综合校正的结果虽为正,但估测精度却低于单独距离校正的估测精度。结果表明:对樟子松而言,强度距离校正森林LAI估测结果最优,入射角的引入非但没能提高结果精度,反而降低了估测精度。
3.3.2 强度比值参数估测结果距离和入射角强度校正LPIRA参数森林LAI估测结果如图 6所示。对LPI参数而言,强度经距离和入射角校正对森林LAI估测精度的影响不大,但整体却表现为负的影响。如图 6所示,强度经距离和入射角校正森林LAI估测结果R2=0.794,RMSE=0.173,较强度校正前森林LAI估测结果仅在RMSE上增大了0.001,R2则保持不变。
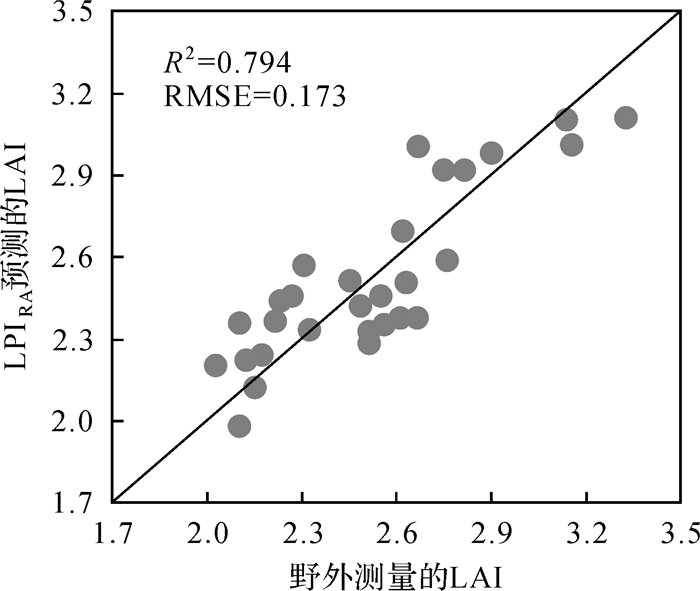
|
| 图 6 野外实测LAI与LPIRA预测LAI关系 Fig. 6 The relationships between the field-measured LAI and LPIRA predicted LAI |
通过对图 2、图 4和图 6所示结果进行综合分析发现,强度经距离和入射角校正LPIRA森林LAI估测结果低于强度距离校正估测结果,却优于强度入射角校正估测结果,总体精度处于二者之间。与此同时,强度经距离、入射角、距离和入射角校正与强度未校正LPI参数森林LAI估测结果差异不大,甚至可以忽略不计。
4 结论本文分别采用距离、入射角及距离和入射角分别对机载LiDAR点云强度数据进行校正,从中提取冠层总强度和强度比值两种不同类型参数,分别用于量化各因素强度校正对樟子松LAI估测的影响,得出以下结论:
(1) 不同因子强度校正对森林LAI估测结果的影响不同。具体而言,距离校正能够提高森林LAI的估测精度,但由DEM和扫描角共同衍生得到的入射角校正非但不能提高森林LAI的估测精度,反而降低了估测精度。相较而言,强度经距离和入射角综合校正虽能提高森林LAI的估测精度,但结果却低于距离单独校正的结果。
(2) 强度校正对森林LAI估测结果影响程度与所用变量参数类型密切相关。对强度比值参数而言,强度校正前后对森林LAI估测结果的影响不大;而对冠层总强度参数而言,强度校正前后森林LAI估测结果的差异较为明显。
本研究所得结论是在地形结构相对平坦,树种结构较为单一区域得出,至于地形复杂区域结论的适用性有待进一步验证。因此,在未来的研究中应逐渐扩大研究范围,以验证上述结论在地形结构相对复杂、林种组成多样区域的适用性。
| [1] | SUMNALL M J, FOX T R, WYNNE R H, et al. Estimating Leaf Area Index at Multiple Heights within the Understory Component of Loblolly Pine Forests from Airborne Discrete-return LiDAR[J]. International Journal of remote Sensing, 2016, 37(1): 78–99. DOI:10.1080/01431161.2015.1117683 |
| [2] | BRÉDA N J J. Ground-based Measurements of Leaf Area Index:A Review of Methods, Instruments and Current Controversies[J]. Journal of Experimental Botany, 2003, 54(392): 2403–2417. DOI:10.1093/jxb/erg263 |
| [3] | GATZIOLIS D. Dynamic Range-Based Intensity Normalization for Airborne, Discrete Return LiDAR Data of Forest Canopies[J]. Photogrammetric Engineering & Remote Sensing, 2011, 77(3): 251–259. |
| [4] | CHEN J M, BLACK T A. Measuring Leaf Area Index of Plant Canopies with Branch Architecture[J]. Agricultural and Forest Meteorology, 1991, 57(1-3): 1–12. DOI:10.1016/0168-1923(91)90074-Z |
| [5] | CHEN J M, PAVLIC G, BROWN L, et al. Derivation and Validation of Canada-wide Coarse-resolution Leaf Area Index Maps Using High-resolution Satellite Imagery and Ground Measurements[J]. Remote Sensing of Environment, 2002, 80(1): 165–184. DOI:10.1016/S0034-4257(01)00300-5 |
| [6] |
尤号田, 邢艳秋, 王铮, 等.
利用LiDAR离散点云估测针叶林叶面积指数[J]. 西北林学院学报, 2014, 29(3): 41–47.
YOU Haotian, XING Yanqiu, WANG Zheng, et al. Estimation of the Leaf Area Index of Coniferous Forests Using LiDAR Discrete Point Cloud[J]. Journal of Northwest Forestry University, 2014, 29(3): 41–47. |
| [7] | WOODGATE W, DISNEY M, ARMSTON J D, et al. An Improved Theoretical Model of Canopy Gap Probability for Leaf Area Index Estimation in Woody Ecosystems[J]. Forest Ecology and Management, 2015, 358: 303–320. DOI:10.1016/j.foreco.2015.09.030 |
| [8] | FINNEY M A. FARSITE: Fire Area Simulator-model Development and Evaluation[R]. RMRS-RP-4, USDA Forest Service, 1998. http://ci.nii.ac.jp/ncid/BA52959634 |
| [9] | MORSDORF F, KÖTZ B, MEIER E, et al. Estimation of LAI and Fractional Cover from Small Footprint Airborne Laser Scanning Data Based on Gap Fraction[J]. Remote Sensing of Environment, 2006, 104(1): 50–61. DOI:10.1016/j.rse.2006.04.019 |
| [10] | WANG Cheng, GLENN N F. Integrating LiDAR Intensity and Elevation Data for Terrain Characterization in A Forested Area[J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(3): 463–466. DOI:10.1109/LGRS.2009.2016986 |
| [11] | KIM S, MCGAUGHEY R J, ANDERSEN H E, et al. Tree Species Differentiation Using Intensity Data Derived from Leaf-on and Leaf-off Airborne Laser Scanner Data[J]. Remote Sensing of Environment, 2009, 113(8): 1575–1586. DOI:10.1016/j.rse.2009.03.017 |
| [12] | HOPKINSON C, CHASMER L. Testing LiDAR Models of Fractional Cover Across Multiple Forest Ecozones[J]. Remote Sensing of Environment, 2009, 113(1): 275–288. DOI:10.1016/j.rse.2008.09.012 |
| [13] | ZHAO Kaiguang, POPESCU S. LiDAR-based Mapping of Leaf Area Index and Its Use for Validating GLOBCARBON Satellite LAI Product in a Temperate Forest of the Southern USA[J]. Remote Sensing of Environment, 2009, 113(8): 1628–1645. DOI:10.1016/j.rse.2009.03.006 |
| [14] |
尤号田, 邢艳秋, 冉慧, 等.
基于LiDAR点云能量信息的樟子松郁闭度反演方法[J]. 北京林业大学学报, 2014, 36(6): 30–35.
YOU Haotian, XING Yanqiu, RAN Hui, et al. Inversion Method for the Crown Density of Mongolian Scotch Pine from Point Cloud Data of Small-footprint LiDAR[J]. Journal of Beijing Forestry University, 2014, 36(6): 30–35. |
| [15] | LOVELL J L, JUPP D L B, CULVENOR D S, et al. Using Airborne and Ground-based Ranging LiDAR to Measure Canopy Structure in Australian Forests[J]. Canadian Journal of Remote Sensing, 2003, 29(5): 607–622. DOI:10.5589/m03-026 |
| [16] | SOLBERG S. Comparing Discrete Echoes Counts and Intensity Sums from ALS for Estimating Forest LAI and Gap Fraction[C]//Proceedings of the SilviLaser 2008: the 8th International Conference on LiDAR Applications in Forest Assessment and Inventory. Edinburgh: Heriot-Watt University, 2008: 301-304. http://www.cabdirect.org/abstracts/20093327973.html |
| [17] | GARCÍA M, RIAÑO D, CHUVIECO E, et al. Estimating Biomass Carbon Stocks for a Mediterranean Forest in Central Spain Using LiDAR Height and Intensity Data[J]. Remote Sensing of Environment, 2010, 114(4): 816–830. DOI:10.1016/j.rse.2009.11.021 |
| [18] | HEISKANEN J, KORHONEN L, HIETANEN J, et al. Use of Airborne LiDAR for Estimating Canopy Gap Fraction and Leaf Area Index of Tropical Montane Forests[J]. International Journal of Remote Sensing, 2015, 36(10): 2569–2583. DOI:10.1080/01431161.2015.1041177 |
| [19] |
邢艳秋, 霍达, 尤号田, 等.
基于机载LiDAR单束激光穿透指数的白桦林LAI估测[J]. 应用生态学报, 2016, 27(11): 3469–3478.
XING Yanqiu, HUO Da, YOU Haotian, et al. Estimation of Birch Forest LAI Based on Single Laser Penetration Index of Airborne LiDAR Data[J]. Chinese Journal of Applied Ecology, 2016, 27(11): 3469–3478. |
| [20] |
骆社周, 王成, 张贵宾, 等.
机载激光雷达森林叶面积指数反演研究[J]. 地球物理学报, 2013, 56(5): 1467–1475.
LUO Shezhou, WANG Cheng, ZHANG Guibin, et al. Forest Leaf Area Index (LAI) Inversion Using Airborne LiDAR Data[J]. Chinese Journal of Geophysics, 2013, 56(5): 1467–1475. DOI:10.6038/cjg20130505 |
| [21] | SONG C. Estimating Tree Crown Size with Spatial Information of High Resolution Optical Remotely Sensed Imagery[J]. International Journal of Remote Sensing, 2007, 28(15): 3305–3322. DOI:10.1080/01431160600993413 |
| [22] | MEANS J E, ACKER S A, HARDING D J, et al. Use of Large-footprint Scanning Airborne LiDAR to Estimate Forest Stand Characteristics in the Western Cascades of Oregon[J]. Remote Sensing of Environment, 1999, 67(3): 298–308. DOI:10.1016/S0034-4257(98)00091-1 |
| [23] | JELALIAN A V. Laser Radar Systems[M]. Boston: Artech House, 1992: 3-10. |
| [24] | JUTZI B, STILLA U. Range Determination with Waveform Recording Laser Systems Using a Wiener Filter[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 61(2): 95–107. DOI:10.1016/j.isprsjprs.2006.09.001 |
| [25] | HÖFLE B, PFEIFER N. Correction of Laser Scanning Intensity Data:Data and Model-driven Approaches[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2007, 62(6): 415–433. DOI:10.1016/j.isprsjprs.2007.05.008 |
| [26] | RONCAT A, BERGAUER G, PFEIFER N. B-spline Deconvolution for Differential Target Cross-section Determination in Full-waveform Laser Scanning Data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(4): 418–428. DOI:10.1016/j.isprsjprs.2011.02.002 |
| [27] | YAN W Y, SHAKER A. Radiometric Correction and Normalization of Airborne LiDAR Intensity Data for Improving Land-cover Classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(12): 7658–7673. DOI:10.1109/TGRS.2014.2316195 |
| [28] | KORPELA I, ØRKA H O, HYYPPÄ J, et al. Range and AGC Normalization in Airborne Discrete-return LiDAR Intensity Data for Forest Canopies[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(4): 369–379. DOI:10.1016/j.isprsjprs.2010.04.003 |
| [29] | KAASALAINEN S, JAAKKOLA A, KAASALAINEN M, et al. Analysis of Incidence Angle and Distance Effects on Terrestrial Laser Scanner Intensity:Search for Correction Methods[J]. Remote Sensing, 2011, 3(10): 2207–2221. |
| [30] | COREN F, STERZAI P. Radiometric Correction in Laser Scanning[J]. International Journal of Remote Sensing, 2006, 27(15): 3097–3104. DOI:10.1080/01431160500217277 |
| [31] | KUKKO A, KAASALAINEN S, LITKEY P. Effect of Incidence Angle on Laser Scanner Intensity and Surface Data[J]. Applied Optics, 2008, 47(7): 986–992. DOI:10.1364/AO.47.000986 |
| [32] | MORSDORF F, FREY O, MEIER E, et al. Assessment of the Influence of Flying Altitude and Scan Angle on Biophysical Vegetation Products Derived from Airborne Laser Scanning[J]. International Journal of Remote Sensing, 2008, 29(5): 1387–1406. DOI:10.1080/01431160701736349 |
| [33] | HALL S A, BURKE I C, BOX D O, et al. Estimating Stand Structure Using Discrete-return LiDAR:An Example from Low Density, Fire Prone Ponderosa Pine Forests[J]. Forest Ecology and Management, 2005, 208(1-3): 189–209. DOI:10.1016/j.foreco.2004.12.001 |
| [34] | JENSEN J L R, HUMES K S, VIERLING L A, et al. Discrete Return LiDAR-based Prediction of Leaf Area Index in Two Conifer Forests[J]. Remote Sensing of Environment, 2008, 112(10): 3947–3957. DOI:10.1016/j.rse.2008.07.001 |
| [35] | PEDUZZI A, WYNNE R H, FOX T R, et al. Estimating Leaf Area Index in Intensively Managed Pine Plantations Using Airborne Laser Scanner Data[J]. Forest Ecology and Management, 2012, 270: 54–65. DOI:10.1016/j.foreco.2011.12.048 |
| [36] | HOPKINSON C. The Influence of Flying Altitude, Beam Divergence, and Pulse Repetition Frequency on Laser Pulse Return Intensity and Canopy Frequency Distribution[J]. Canadian Journal of Remote Sensing, 2007, 33(4): 312–324. DOI:10.5589/m07-029 |



