2. 近地面探测技术重点实验室, 江苏 无锡 214000
2. Science and Technology on Near-Surface Detection Laboratory, Wuxi 214000, China
机载激光测深是一种主动、非接触式的测深技术,相比单波束、多波束等声呐测深技术,具有高效率、高精度、低成本等优点[1]。此外,机载平台能够到达船只无法通行的极浅水域,在浅海测量方面优势明显。机载激光测深系统与传统的陆地激光系统相比,在系统设计上增加了一个蓝绿通道,利用蓝绿激光(532 nm)对水体的较强穿透能力,通过发射和接收蓝绿激光可获取激光在水面、水底的反射回波信号,从而反演水深。
从接收波形中提取水面和水底回波信号的准确位置是机载激光测深的关键,但由于系统发射信号波形、水体后向散射和噪声的影响,原始接收波形中的信号容易发生拉伸、偏移、交叠、减弱等现象,给信号提取带来困难[2]。对于近红外通道下的陆域回波,目前已有一些较为成熟的波形处理方法,如峰值检测、高斯分解和去卷积等[3]。峰值检测对波形具有普适性,但测深波形的噪声较大,直接检测出错率高,精度低;高斯分解法由于测深波形中的水体后向散射成分使水面与水底回波信号相连,在分解时必须对波形整体进行处理,而高斯函数无法精确拟合水体后向散射,使得该方法不适用于处理测深波形;去卷积基于的是信号产生的物理过程,可实现信号的复原,相比上述两种方法更适合应用于测深信号提取[4]。
一些去卷积算法已应用于LiDAR波形数据处理,包括维纳滤波去卷积(Wiener filter deconvolution, WFD)[5]、理查德森-露西去卷积(Richardson-Lucy deconvolution, RLD)[4, 6]、非负最小二乘算法(nonnegative least squares, NNLS)[7-8]、盲源去卷积(blind deconvolution, BD)[9]等。然而,在机载激光测深的研究中,信号提取大多通过系统提供的恒比定时鉴别器(constant fraction discriminator, CFD)或峰值检测实现[10],有关利用去卷积算法处理测深波形数据的研究还不够深入。本文提出一种去卷积信号提取方法应用于测深波形数据的处理,分析对比4种常用去卷积算法处理测深波形数据的性能,并对提出方法的可行性和适用性进行验证。
1 研究方法去卷积信号提取方法包括去卷积和峰值检测两部分。
1.1 去卷积如图 1,接收回波波形wR(t)可看作是系统发射信号波形wT(t)与目标横截面p(t)的卷积
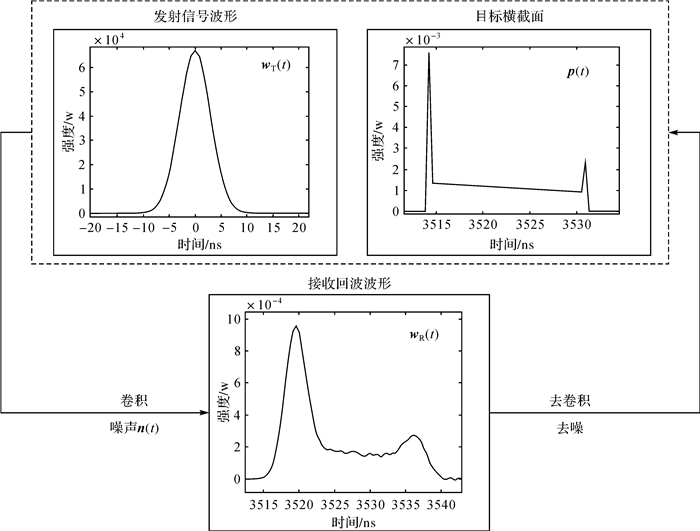
|
| 图 1 去卷积在信号产生过程中的物理意义 Fig. 1 Physical interpretation of deconvolution in signal generation |
 (1)
(1)
式中,“*”表示卷积运算;n(t)为附加噪声项。去卷积则是式(1)的逆向过程,即由接收回波波形反解出目标横截面形状。
激光回波信号的分辨率主要取决于脉宽,窄脉宽意味着高分辨率,长脉宽则意味着低分辨率。反观卷积会使信号变宽,是一个降分辨率、退化的过程,若直接从原始接收回波波形中提取信号,将得到一个不精确、不可靠的结果。去卷积能够从接收回波波形中去除发射信号波形,复原目标横截面形状,提高信号分辨率。但实际上,接收回波波形的产生不单纯是一个卷积的过程,其中还混杂有噪声的影响,因而去卷积算法必须具有一定的抗噪性。
由于机载激光测深系统的发射信号波形或波形参数是已知的,因而可直接应用去卷积。从波形构成上看,蓝绿激光的回波波形主要由水面反射回波、水底反射回波和水体后向散射3部分组成[11],如图 2所示。在利用蓝绿激光进行测深时,只有水面和水底的反射回波信号被视为有效信号,水体后向散射包括水中悬浮物的回波信号都将被视为干扰成分。在纯净水质的条件下,水体后向散射可看作是由连续强度较弱的回波叠加而成,如图 3所示。去卷积后,水体后向散射部分将被分散、弱化,同时水面、水底回波信号将因分辨率的提高而变窄、增强。因此理论上,对测深波形先去卷积后进行峰值检测,能够提高信号检测的成功率与准确性。下面对几种典型的去卷积算法进行介绍。
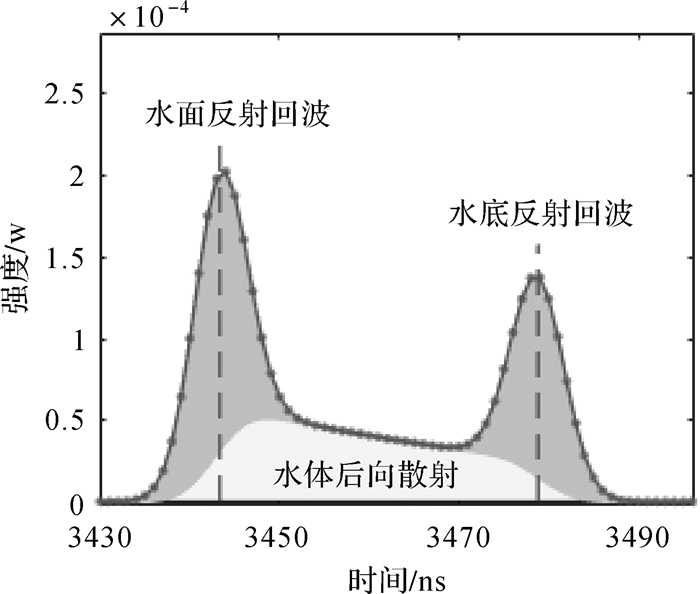
|
| 图 2 蓝绿激光回波波形 Fig. 2 Green LiDAR waveform |

|
| 图 3 水体后向散射构成 Fig. 3 Constitution of the water volume backscatter |
1.1.1 傅里叶去卷积(FTD)
傅里叶去卷积(Fourier transform deconvolution, FTD)是最简单、直接的去卷积算法,它是通过傅里叶变换在频率域中直接进行逆滤波去除发射信号
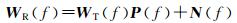 (2)
(2)
式中,WR(f)、WT(f)、P(f)和N(f)分别为wR(t)、wT(t)、p(t)和n(t)的傅里叶变换。若忽略噪声的影响,即可确定目标横截面形状p(t)
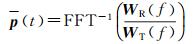 (3)
(3)
式中,FFT-1表示傅里叶逆变换。
FTD计算方便,但当WT(f)接近零时WR(f)的噪声会被无限放大,得到一个病态的解,因此该算法仅适用于无噪声存在的理想波形[12]。
1.1.2 维纳滤波去卷积(WFD)为解决FTD存在的病态问题,WFD通过引入维纳滤波器减少FTD中逆滤波对噪声的敏感性。维纳滤波器在频率域可以表示为[13]
 (4)
(4)
式中,K是一个与噪声相关的常数,需要经过多次试验确定。WFD对目标横截面的频率域估计值为
 (5)
(5)
NNLS是在时间域内计算使波形估计值与实际波形间平方误差最小的非负解
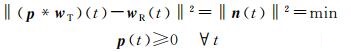 (6)
(6)
NNLS算法实际上是将去卷积转化为矩阵分解问题,从而得到一个严格的凸函数。文献[14]中介绍了求解这一问题唯一解的方法。
1.1.4 理查德森-露西去卷积(RLD)RLD算法最初是一种图像复原算法[15],将LiDAR波形看作一维的图像,可将该算法应用于LiDAR波形处理。RLD通过迭代可在时间域内得到一个逼近极大似然解的结果,它的第i次迭代计算为
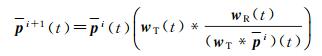 (7)
(7)
式中,pi+1(t)为第i次迭代的目标横截面估计值,当残差||wR(t)-pi+1(t)*wT(t)||小于设定阈值或迭代次数达到上限时迭代终止。
1.1.5 盲源去卷积(BD)BD是一种在点扩散函数(PSF)未知的情况下的图像复原算法,在地震勘探领域有较为广泛的应用。对于LiDAR波形数据处理,BD算法将已知的系统发射波形作为初值,利用极大似然算法迭代估计实际的激光发射波形wT(t),从而复原目标横截面形状p(t)。
1.2 峰值检测去卷积算法仅仅能够增强信号、提高信号分辨率,实现信号提取还需要对去卷积后的波形进行峰值检测。峰值检测方法有许多种,但并非都适用于处理测深波形,如重心检测会因受到水体后向散射成分的影响而产生偏移,因此这里选择适用于测深信号提取的极大值检测和一阶导数检测方法。
1.2.1 极大值检测极大值检测的原理为查找波形wR中的局部极大值点,对于由离散采样点构成的波形数据,极大值点k由式(8)确定[16]
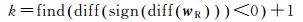 (8)
(8)
式中,diff指差分运算;sign为符号函数;find表示查找数组中满足条件的数据编号。当采样点满足式(8)时,其回波强度在邻域范围内呈先增加后减小趋势,即局部极大值点。检测到的极大值点一般还需要强度和距离等条件约束,由于不同系统、不同测量环境下的波形差异较大,因此设定合理阈值是该方法的关键。
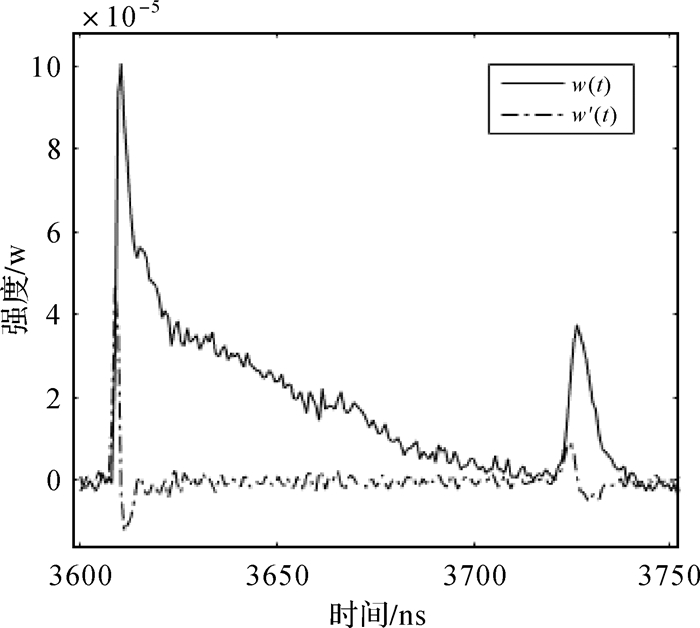
1.2.2 一阶导数检测由于噪声的存在,波形中的轻微抖动也可能出现零交叉点。而当脉冲信号wR(t)强度发生剧变时,对应一阶导数绝对值|w′R(t)|将随之增加[17],如图 4所示。一阶导数检测方法的原理是首先查找一阶导数绝对值的局部极大值,然后在其局部范围内进行极大值检测,从而一定程度上抑制噪声影响。
|
| 图 4 波形与一阶导数关系图 Fig. 4 The relationship between waveform and its derivative |
1.3 性能评定指标
为确定最适用于处理机载激光测深数据的去卷积算法,验证去卷积信号提取方法相较于传统的极大值检测和一阶导数检测方法的优越性,需要利用一系列评定指标进行定量分析。
1.3.1 去卷积算法性能评定指标这里定义了7个评定指标用于对去卷积算法的性能进行分析,具体定义如下:
(1) 目标横截面形状估计值p(t)与真值p(t)的相关系数ρ,用于衡量算法的精度,同时它也是判定算法是否得到正确估计值的重要指标。将原始接收波形wR(t)与p(t)之间的ρ0作为参照,若p(t)的ρ大于ρ0,表明去卷积后的波形相比原始波形更接近于真实的目标横截面形状,即判断p(t)为正确的估计值。ρ的计算公式为
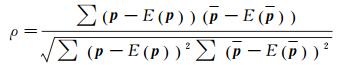 (9)
(9)
式中,E为期望函数。
(2) ρ的标准差(δ),反映了算法的稳健性,定义为
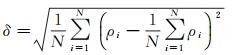 (10)
(10)
式中,N表示试验的波形帧数。
(3) 算法成功率(PS)定义为得到正确估计值的波形帧数在试验总帧数N中所占百分比
 (11)
(11)
式中,NS表示p(t)为正确估计值的波形帧数。
(4) 水面信号偏移量(OS)衡量算法对水面信号位置的影响,单位为采样间隔(仅统计正确估计值)。
(5) 水底信号偏移量(OB)衡量算法对水底信号位置的影响,单位为采样间隔。它与OS共同反映算法对波形产生的形变量(仅统计正确估计值)。
(6) 水底信号强度与水体后向散射平均强度之比(RB/C)。根据前文所述,测深波形中水体后向散射与水面、水底回波是重叠的,RB/C越大表明水底信号更加突出,越容易被检测到。这一指标也需要与原始波形的RB/C0对比,若大于RB/C0表明算法对水底信号具有增强效果(仅统计正确估计值)。
(7) 平均处理每帧波形所需的时间(T),反映算法的处理效率。
1.3.2 信号提取方法性能评定指标选取5个评定指标对信号提取方法的性能进行分析:
(1) 检测率:能够成功检测到水面和水底回波信号且误差在1 m以内的波形占总波形帧数的百分比。此处将误差上限设置为1 m是因为实测数据和模拟数据中信号的半宽约为0.84~1.2 m,当误差在1 m内可以认为检测位置依然位于信号的展宽内。
(2) 误差:信号检测位置相对于真值的均方根误差。
(3) 最小测深:能够成功检测到水面和水底回波信号的波形的最小深度。
(4) 最大测深:能够成功检测到水面和水底回波信号的波形的最大深度。
(5) 运算时间:平均处理每帧波形所需的时间。
2 试验与分析试验数据包括实测数据和模拟数据,分别用于验证方法的有效性和精度。实测数据为中国科学院上海光学精密机械研究所研制的“机载双频激光雷达系统”[18]在南海某地区获取的不同深度水域的波形数据。该系统的测量频率为1 kHz,采样频率为1.25 GHz。测量时飞行高度设置为500 m,速度为250 km/h,扫描角固定为15°,测点密度为0.04~0.33点/m2。模拟数据是由文献[19]提出的激光测深波形模拟工具Water LiDAR(Wa-LiD)生成。Wa-LiD能够生成不同系统参数和测量环境下的波形数据,并准确已知其波形构成和目标横截面形状,如图 5所示。
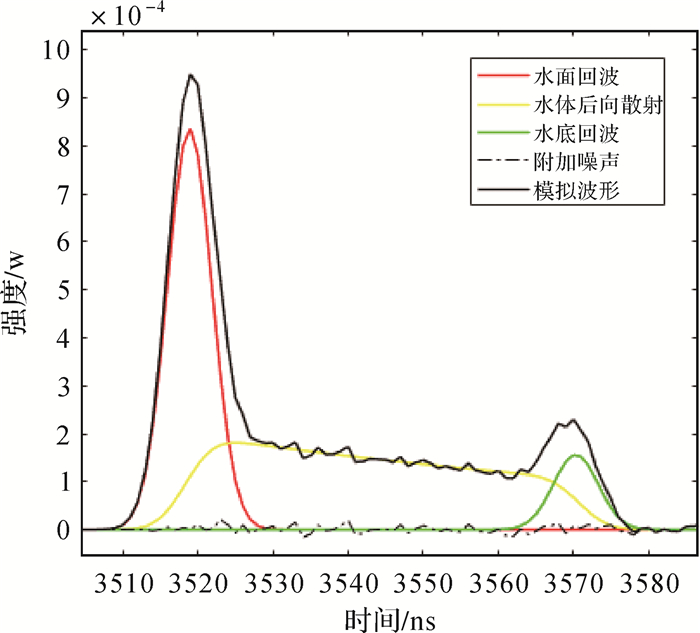
|
| 图 5 模拟回波波形示意图 Fig. 5 Schematic simulated waveform |
2.1 不同去卷积算法的性能对比分析
评定去卷积算法的性能需要已知目标横截面形状的真值,对于实测数据这一信息几乎无法获得,因而利用模拟数据对4种去卷积算法(WFD、NNLS、RLD、BD)进行性能检验,试验部分结果如图 6所示。从图 6可以看出:FTD无法处理有噪声存在的波形;WFD和NNLS得到的结果相似,能够提高有效信号的分辨率,减弱水体后向散射的强度,但仍会受到噪声的影响,存在较为明显的伪信号;BD和RLD的结果相似,都具有较好的抗噪性,但对水底信号的增强效果没有NNLS显著。
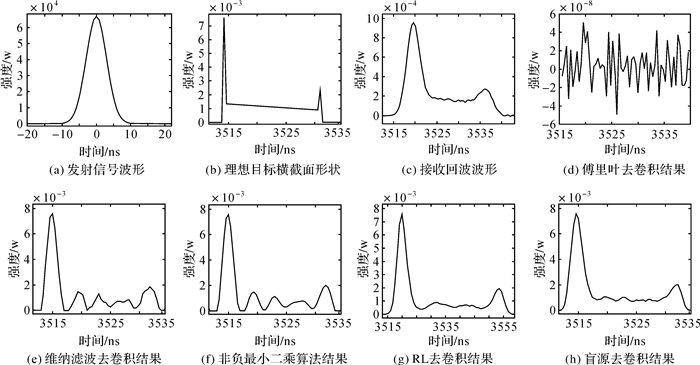
|
| 图 6 模拟数据去卷积结果 Fig. 6 The deconvolution results of simulated data |
前期试验发现,影响算法精度的主要参数包括信噪比(PSNR),采样间隔(interval)和测点水深(Z)。为进一步分析算法对参数的敏感性,试验利用不同参数条件下的模拟波形进行试验,结果见表 1。从表 1中可以看出,在精度上,RLD的精度最高,BD和WFD次之,NNLS精度较低;BD的稳定性最好,受参数影响小,NNLS稳定性较差;RLD的成功率最高,其次是WFD,BD和NNLS;4种算法对信号峰值的位置的影响较小,都控制在1个采样间隔以内,对底部回波信号实现了不同程度的增强,其中NNLS和RLD的效果最为明显,但NNLS在水体后向散射部分存在着大量的伪信号,容易导致错误检测;在效率方面,BD的运算时间最长,其余3种算法差别不大,但实际上WFD和NNLS算法还需要经过多次试验确定合适的参数。
| received | WFD | NNLS | RLD | BD | |
| ρ | 0.439 2 | 0.483 9 | 0.406 3 | 0.501 6 | 0.491 4 |
| δ | — | 0.065 9 | 0.120 1 | 0.065 0 | 0.061 7 |
| PS/(%) | — | 96.0 | 48.8 | 98.5 | 95.2 |
| OS | — | 0.63 | 0.41 | 0.58 | 0.34 |
| OB | — | 0.86 | 0.63 | 0.56 | 0.56 |
| RB/C | 1.07 | 1.80 | 2.89 | 2.06 | 1.74 |
| T/ms | — | 0.50 | 1.84 | 2.55 | 19.54 |
图 7—图 9为ρ随各参数的变化情况,ρ作为评定算法精度的重要指标,分析它与参数PSNR、Interval和Z的关系,可在一定程度上说明算法在不同参数条件下的适应性。从图 7可以看出PSNR对去卷积精度的影响较小,说明4种算法都具有一定的抗噪性;由图 8可以看出NNLS对高频采样的波形处理能力较弱,RLD对不同采样频率的数据适应性最好;图 9中算法精度随水深的增加表现为先降低再升高,在水深约为5 m的位置达到最小值,这是因为在水深较浅或者较深的区域,部分回波信号出现了重叠或被噪声掩盖的现象,波形构成较为简单,表明去卷积算法对越复杂的波形的处理能力越弱。
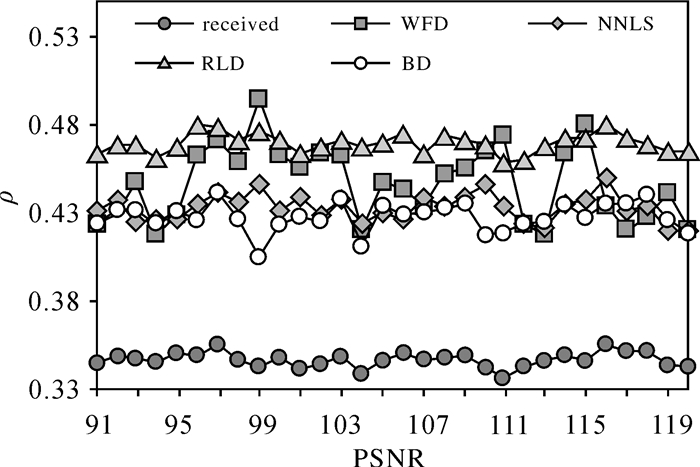
|
| 图 7 相关系数与信噪比的关系 Fig. 7 The ρ changes over PSNR |

|
| 图 8 相关系数与系统采样间隔的关系 Fig. 8 The ρ changes over interval |
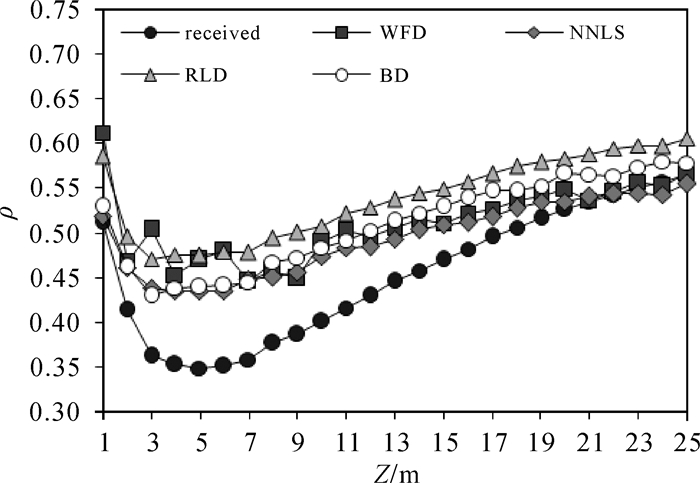
|
| 图 9 相关系数与水深的关系 Fig. 9 The ρ changes over depth |
通过上述的对比分析,对4种去卷积算法的优缺点进行归纳总结:WFD成功率较高,计算效率高,但对水底信号的增强效果不明显;NNLS能够较好的增强水底信号,但算法不稳定,成功率低,在波形复原过程中容易产生大量伪信号;WFD和NNLS都需要经过大量的试验计算经验参数;RLD精度高,成功率高,适用范围广,但计算时间较长;BD稳定性好,对信号峰值产生的偏移量小,精度仅略低于RLD,缺点是计算时间长,对水底信号的增强效果不如RLD;总体上讲,4种去卷积算法中RLD的性能最优。
2.2 去卷积信号提取方法与传统方法的性能对比分析选择性能最优的RLD算法与峰值检测结合进行试验,验证去卷积信号提取方法相对于传统方法的优越性。本文分别采用实测数据和模拟数据对4种方法进行对比,包括极大值检测(方法1)、一阶导数检测(方法2)、RLD+极大值检测(方法3)、RLD+一阶导数检测(方法4),其中方法1和方法2为传统的峰值检测方法,方法3和方法4为去卷积信号提取方法。图 10为波形对应水深为0.8 m和29 m时的试验结果,可以看到在较浅水域,原波形中水面和水底信号发生了重叠,传统方法无法检测,通过去卷积可实现信号的分离;在较深水域,水底信号强度较弱与波形背景噪声接近,去卷积能够将信号增强,增加了探测水底信号的可能性。
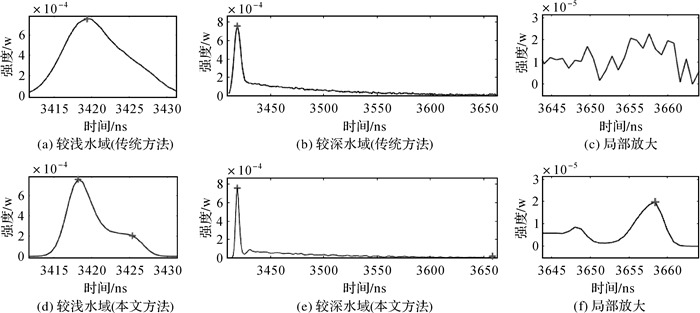
|
| 图 10 去卷积前后检测结果对比 Fig. 10 The comparison of the results in shallow and deep water |
考虑到不同水深下波形形状、特点差异较大,试验将实测数据的波形按深度分为3个区间0~2 m、2~15 m和15~30 m,分别统计4种方法的检测率,结果见图 11,其中实测数据的信号位置真值是由人工解译的方式获取的。对于深度为0~2 m的波形,去卷积信号提取方法的检测率明显高于传统方法,表明去卷积能够处理部分发生信号重叠的波形;对于深度在2~15 m的波形,4种方法都具有较高的检测率,其中方法4的检测率高达95.5%;对于深度在15~30 m的波形,采用极大值检测的方法1和方法3检测率明显降低,这是由于这两种方法检测的是局部极大值点,在水深较深时,水底的回波信号强度较弱,信噪比低,因而检测结果容易受到噪声的干扰,而方法4的检测率高于方法2,证明了去卷积能够在一定程度上增强信号。

|
| 图 11 不同水深下的信号检测率 Fig. 11 The detection rate over different depth |
由于实测数据的真值精度有限,因此试验采用模拟数据对本文方法作进一步的精度分析,结果见表 2。表 2中模拟数据的检测率与实测数据得到的结果基本一致,去卷积信号提取方法相比传统方法具有较高的信号提取精度,但运算时间稍有增加。方法4将RLD与一阶导数检测结合,检测率高达94.45%,能够提取目标水深介于0.75~31.95 m之间的水面、水底回波信号,相比较传统方法,无论是在检测率、精度上,还是在测深范围上都有明显的改善。
| 方法 | 检测率 /(%) |
误差 /m |
最小测深 /m |
最大测深 /m |
运算时间 /ms |
| 方法1 | 54.36 | 0.106 1 | 1.10 | 19.05 | 2.63 |
| 方法2 | 76.70 | 0.108 0 | 1.10 | 31.50 | 2.68 |
| 方法3 | 71.63 | 0.078 2 | 0.80 | 24.75 | 4.42 |
| 方法4 | 94.45 | 0.084 9 | 0.75 | 31.95 | 4.81 |
3 结论
本文全面对比分析了4种常用去卷积算法对测深信号的复原和增强能力,发现RLD算法能够有效提高测深信号的分辨率,精度高,成功率高,适用性强且稳定性好。通过试验证明了去卷积信号提取方法相比传统的极大值检测和一阶导数检测法具有更高的精度和更广的适用范围,对提高机载激光测深系统的测深精度和测深范围具有重要意义。本文下一步的研究方向为:①目前方法的提取结果只能精确到单位采样间隔,精度受限于数据的采样频率,有待进一步改进;②NNLS算法对水底信号的增强效果突出但对噪声过于敏感,若能够增强该算法的抗噪性,有望进一步提升信号的检测能力。
| [1] |
张祖勋, 吴媛.
摄影测量的信息化与智能化[J]. 测绘地理信息, 2015, 40(4): 1–5.
ZHANG Zuxun, WU Yuan. Informatization and Intellectualization of Photogrammetry[J]. Journal of Geomatics, 2015, 40(4): 1–5. |
| [2] |
王越.
机载激光浅海测深技术的现状和发展[J]. 测绘地理信息, 2014, 39(3): 38–42, 67.
WANG Yue. Current Status and Development of Airborne Laser Bathymetry Technology[J]. Journal of Geomatics, 2014, 39(3): 38–42, 67. |
| [3] | MALLET C, BRETAR F. Full-waveform Topographic LiDAR:State-of-the-art[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2009, 64(1): 1–16. DOI:10.1016/j.isprsjprs.2008.09.007 |
| [4] | WANG Chisheng, LI Qingquan, LIU Yanxiong, et al. A Comparison of Waveform Processing Algorithms for Single-wavelength LiDAR Bathymetry[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 101: 22–35. DOI:10.1016/j.isprsjprs.2014.11.005 |
| [5] | JUTZI B, STILLA U. Range Determination with Waveform Recording Laser Systems Using a Wiener Filter[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 61(2): 95–107. DOI:10.1016/j.isprsjprs.2006.09.001 |
| [6] | WU Jiaying, VAN AARDT J A N, MCGLINCHY J, et al. A Robust Signal Preprocessing Chain for Small-footprint Waveform LiDAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(8): 3242–3255. DOI:10.1109/TGRS.2011.2178420 |
| [7] | WU Jiaying, VAN AARDT J A N, ASNER G P. A Comparison of Signal Deconvolution Algorithms Based on Small-footprint LiDAR Waveform Simulation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6): 2402–2414. DOI:10.1109/TGRS.2010.2103080 |
| [8] | NAIK R K, SAHU P K. Least Square Deconvolution of Rayleigh LiDAR System for upper Atmospheric Study[C]//Proceedings of the 10th International Conference on Microwaves, Antenna, Propagation and Remote Sensing. Jodhpur, India: ICMARS, 2014. https://www.researchgate.net/publication/269637933_Least_Square_Deconvolution_of_Rayleigh_LiDAR_System_for_Upper_Atmospheric_Study |
| [9] | NAIK R K, SAHU P K. Comprehensive Study on Deconvolution and Denoising of LiDAR Back-scattered Signal[C]//Proceedings of 2013 International Conference on Microwave and Photonics (ICMAP). Dhanbad, India: IEEE, 2013: 1-6. DOI: 10.1109/ICMAP.2013.6733539. http://ieeexplore.ieee.org/document/6733539/ |
| [10] | FERNANDEZ-DIAZ J C, GLENNIE C L, CARTER W E, et al. Early Results of Simultaneous Terrain and Shallow Water Bathymetry Mapping Using a Single-wavelength Airborne LiDAR Sensor[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(2): 623–635. DOI:10.1109/JSTARS.2013.2265255 |
| [11] | WANG C K, PHILPOT W D. Using Airborne Bathymetric LiDAR to Detect Bottom Type Variation in Shallow Waters[J]. Remote Sensing of Environment, 2007, 106(1): 123–135. DOI:10.1016/j.rse.2006.08.003 |
| [12] | PARK Y J, DHO S W, KONG H J. Deconvolution of Long-pulse LiDAR Signals with Matrix Formulation[J]. Applied Optics, 1997, 36(21): 5158–5161. DOI:10.1364/AO.36.005158 |
| [13] | GONZALEZ R C, WOODS R E, EDDINS S L. Digital Image Processing Using Matlab[M]. New Jersey: Pearson Prentice Hall, 2004. |
| [14] | LAWSON C L, HANSON R J. Solving Least Squares Problems[M]. Englewood Cliffs, NJ: Prentice-Hall, 1974. |
| [15] | BIGGS D S C, ANDREWS M. Acceleration of Iterative Image Restoration Algorithms[J]. Applied Optics, 1997, 36(8): 1766–1775. DOI:10.1364/AO.36.001766 |
| [16] | WAGNER W, ULLRICH A, MELZER T, et al. From Single-pulse to Full-waveform Airborne Laser Scanners: Potential and Practical Challenges[C]//International Archives of Photogrammetry and Remote Sensing. Istanbul, Turkey: IAPRS, 2004: 201-206. https://www.researchgate.net/publication/51997428_From_Singleapulse_to_full-waveform_airborne_Laser_Scanners_Potential_and_practical_challenges |
| [17] |
叶修松. 机载激光水深探测技术基础及数据处理方法研究[D]. 郑州: 信息工程大学, 2010. YE Xiusong. Research on Principle and Data Processing Methods of Airborne Laser Bathymetric Technique[D]. Zhengzhou: Information Engineering University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-90008-1011057276.htm |
| [18] |
胡善江, 贺岩, 臧华国, 等.
新型机载激光测深系统及其飞行实验结果[J]. 中国激光, 2006, 33(9): 1163–1167.
HU Shanjiang, HE Yan, ZANG Huaguo, et al. A New Airborne Laser Bathymetry System and Survey Result[J]. Chinese Journal of Lasers, 2006, 33(9): 1163–1167. |
| [19] | ABDALLAH H, BAGHDADI N, BAILLY J S, et al. Wa-LiD:A New LiDAR Simulator for Waters[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(4): 744–748. DOI:10.1109/LGRS.2011.2180506 |
| [20] | DOUGLASS A R, SCHOEBERL M R, KAWA S R, et al. A Composite View of Ozone Evolution in the 1995-1996 Northern Winter Polar Vortex Developed from Airborne LiDAR and Satellite Observations[J]. Journal of Geophysical Research, 2001, 106(D9): 9879–9895. DOI:10.1029/2000JD900590 |
| [21] | LI Pengcheng, XU Qing, CUI Pingyuan, et al. Stepwise Decomposition of Full-waveform Data Based on Levenberg Marquardt[J]. Studies in Surveying and Mapping Science, 2014, 2: 14–19. |
| [22] | PARK Y J, DHO S W, KONG H J. Deconvolution of Long-pulse LiDAR Signals with Matrix Formulation[J]. Applied Optics, 1997, 36(21): 5158–5161. DOI:10.1364/AO.36.005158 |
| [23] | RONCAT A, BERGAUER G, PFEIFER N. B-Spline Deconvolution for Differential Target Cross-section Determination in Full-waveform Laser Scanning Data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(4): 418–428. DOI:10.1016/j.isprsjprs.2011.02.002 |
| [24] |
李凯, 张永生, 童晓冲, 等.
定角圆锥扫描式机载激光测深系统定位模型与精度评价[J]. 测绘学报, 2016, 45(4): 425–433.
LI Kai, ZHANG Yongsheng, TONG Xiaochong, et al. Positioning Model and Accuracy Evaluation of Conical Scanning Airborne Laser Bathymetry System[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(4): 425–433. DOI:10.11947/j.AGCS.2016.20150161 |
| [25] |
申二华, 张永生, 李凯.
圆扫描式机载激光测深系统检校模型及仿真分析[J]. 测绘学报, 2016, 45(8): 943–951.
SHEN Erhua, ZHANG Yongsheng, LI Kai. The Calibration Model and Simulation Analysis of Circular Scanning Airborne Laser Bathymetry System[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8): 943–951. DOI:10.11947/j.AGCS.2016.20150532 |
| [26] | GUENTHER G C, CUNNINGHAM A G, LAROCQUE P E, et al. Meeting the Accuracy Challenge in Airborne LiDAR Bathymetry[C]//Proceedings of the 20th EARSeL Symposium: Workshop on LiDAR Remote Sensing of Land and Sea. Dresden, Germany: European Association of Remote Sensing Laboratories, 2000: 1-21. http://agris.fao.org/agris-search/search.do?recordID=AV20120133452 |



