2. 中国科学院大学资源与环境学院, 北京 100049;
3. 太原市建筑设计勘测中心, 山西 太原 030000
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Taiyuan Architectural Design Service Office, Taiyuan 030000, China
激光雷达技术,在很多基础经济建设如农林业[1]、水力电力勘察[2]、道路设计[3]及城市规划[4]中已经被普遍使用,而点云滤波分类和特征提取是激光雷达点云数据处理的重要部分,也是后续各类数字产品生产和应用的基础,因此很多学者开展了相关的滤波方法研究,归纳起来可分为以下几类:基于坡度的滤波方法[5-9]、基于数学形态学的滤波算法[10-14]及拟合法[15-20]等。
基于坡度的滤波方法能够较好地保留地形信息,但是坡度阈值的自适应性有待提高;基于数学形态学的滤波算法存在的主要问题是窗口尺寸的人工选取和细节地形的方块效应,拟合法则对拟合半径的依赖性大。在拟合法的基础上,许多学者提出了移动曲面拟合的滤波算法,文献[21]提出了移动曲面拟合滤波算法,该算法简单明了,自适应性强,运算速度快,但是固定的窗口尺寸和阈值大小会影响滤波效果。文献[22]提出的改进移动窗口曲面拟合法可以自适应地调整网格尺寸大小,同时克服滤波过程中高差阈值难以确定的不足,但是该算法使用6个格网中的最低点进行拟合,容易出现方块效应。文献[23]提出的多级移动曲面拟合滤波算法,建立区域格网索引,设置自适应阈值。该方法普适性较好,效率高,解决了粗差点、阈值自动设置等问题,但预处理需要人为设定参数,并且未考虑每个分块的邻域信息。
在综合分析上述算法优点的基础上,本文提出多级移动曲面拟合的自适应阈值点云滤波算法。该算法增加了格网邻域并实现格网大小、邻域大小和阈值的自动设置,有效提高了滤波效率,降低了滤波误差,提高算法的自适应性。
1 算法原理与流程传统移动曲面拟合的滤波算法是利用2×3的移动窗口,通过寻找每个窗口的最低点计算出一个粗略的拟合曲面,然后判断这6个移动窗口中的点与拟合曲面的高程差,将所有高程差超过给定高差阈值的点剔除,得到地面点。传统算法仅用6个点拟合曲面会导致拟合的曲面未更好地考虑周围地形的影响,与真实的地形相差比较大,从而影响滤波效果,而且在滤波过程中,对于不同的地形采用固定窗口尺寸和高差阈值,其滤波效果会更差。
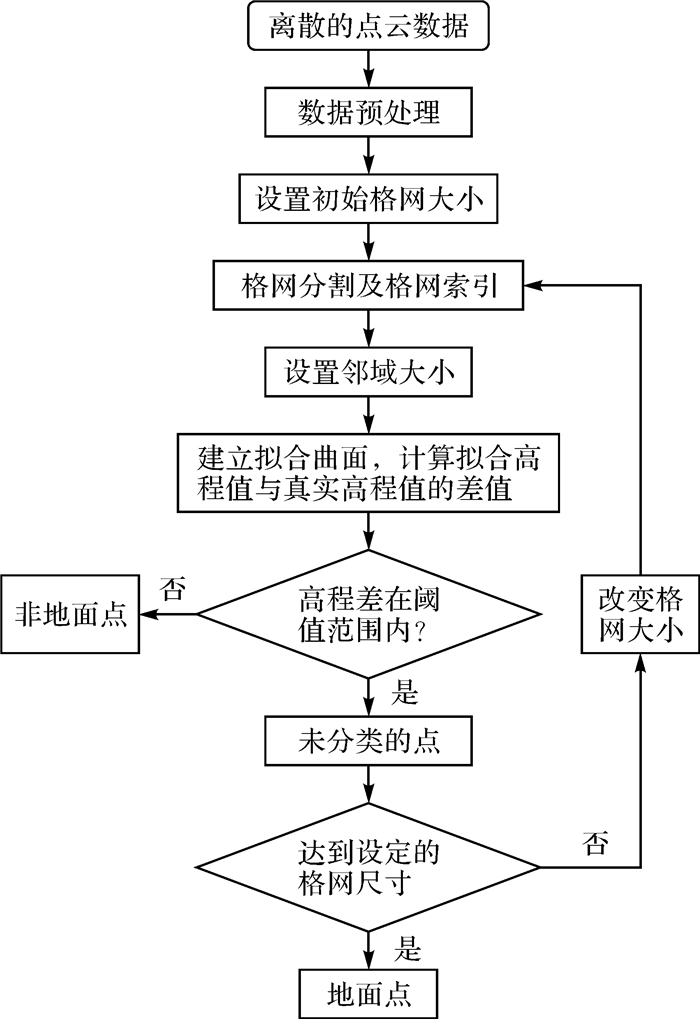
针对上述问题,本文考虑到地形的连续性,增加了窗口邻域,认为每个窗口的拟合曲面均是基于邻域窗口的最低点获得,最小邻域为3×3(点数均大于6)。为了解决格网大小的选取问题,采用网格尺寸按倍数逐级减小的方法,在改变网格尺寸的同时自动设置不同的窗口邻域和高差阈值,具体流程如图 1所示。
|
| 图 1 算法流程 Fig. 1 The flow chart of the algorithm |
1.1 数据预处理
预处理主要是剔除异常点(噪声点),本文通过对点云数据生成频率直方图,设定阈值以去除首尾两端的极大值和极小值,实现去噪的目的。
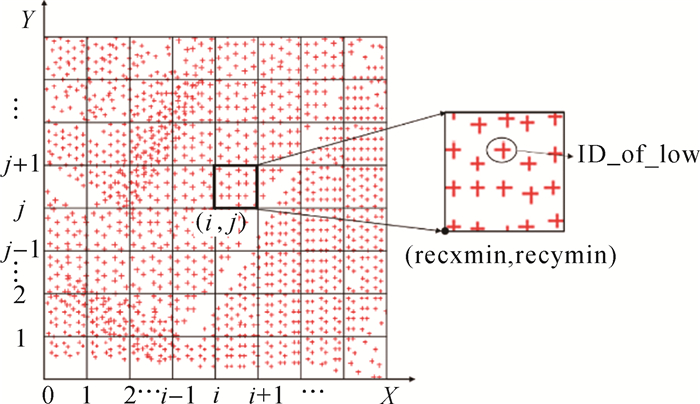
1.2 格网分割及索引点云格网化也称点云分割,即用规则的格网将点云数据全部覆盖,对于不同的地形,采用不同的网格大小,将点云按平面坐标分配到相应格网中,格网的划分及属性如图 2所示。
|
| 图 2 格网划分及属性 Fig. 2 Segmentation process and its attributes |
将点云数据进行编号,按照定义的格网大小划分,为了保证每个格网中的最低点为真实的地面点,首先设置格网大小大于最大建筑物的尺寸以去除具有较大尺寸的地物点,然后按倍数逐级减小格网大小,直到剔除多数地物点,拟合出最佳地形表面为止。其中每个格网有4种不同的属性:
(1) 点集属性。计算每个点对应的格网,并记录点号,从而得到落在每个格网中点的ID及点数。
(2) 最低点ID。用邻域格网中的最低点进行曲面拟合,因此记录每个格网的最低点标号,可以提高计算效率。
(3) 边界坐标。为了保证计算结果的准确性,划分格网时记录格网的边界信息,在拟合曲面时,将所有邻域格网的坐标数据减去邻域格网中左下角坐标。
(4) 标号属性。用二维矩阵的行列号对每个格网进行标号,在后面的计算中根据该标号进行点云资料的快速存储,提高滤波、插值的计算速度。
1.3 建立拟合曲面假设地形表面是一个复杂的空间曲面,该曲面的局部面元可以用二次曲面来逼近,如式(1)所示
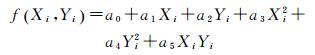 (1)
(1)
真实的地面点得到的拟合曲面反映了地面的起伏,将每个格网中的最低点作为真实地面点,利用每一个格网的邻域窗口中的最低点拟合曲面,然后计算该格网中点的拟合高程值与真实高程值的差值,通过高差阈值进行筛选,每一个格网都用不同的曲面方程来表达,并且该曲面方程具有一定的连续性。该过程的关键是格网邻域大小的自动设置以及拟合曲面参数(a0, a1, a2, a3, a4, a5)的求解。
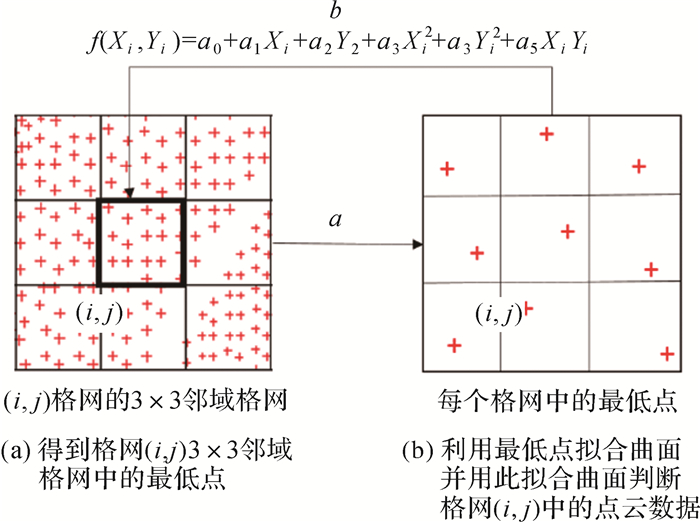
1.3.1 格网邻域大小的设置用于拟合地形表面的二次曲面共有6个参数,许多研究都是基于6个格网中的最低点拟合曲面,然而由于数据分布的不均匀性,有些格网中没有点,因此最低点的个数小于或等于参数的个数,得到的拟合曲面与真实的地形相差较大,滤波效果降低。为了保证拟合曲面的连续性,需要考虑每一个格网周围格网中点云数据的分布特征。为了保证该格网在中间位置,一般设置邻域大小为奇数如3×3、5×5,如图 3所示。邻域3×3即利用9个格网中的最低点拟合一个曲面,用此曲面判断格网(i, j)中的点云数据。
|
| 图 3 邻域格网最低点拟合曲面过程 Fig. 3 The process of fitting surface using the lowest point of neighborhood grids |
本文邻域大小的选择根据地形坡度设置,其中平均坡度阈值(5°,10°)的选取建立在大量试验基础之上。首先计算每个格网对于3×3邻域格网的平均坡度值,即每个格网的最低值和周围8邻域格网最低值的差值与距离比值的平均值,如式(2)所示
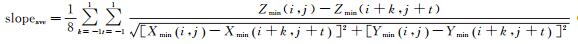 (2)
(2)
式中,Zmin (i, j)是第i行第j列格网的最低点高程值。
如果存在格网的坡度平均值超过0.176(tan10°),则邻域大小设置为3×3,否则计算每个格网对于5×5邻域格网的平均坡度值,如果存在格网的坡度平均值超过0.087(tan5°)则设置格网大小为5×5,否则设置为7×7。
1.3.2 曲面参数的求解本研究利用邻域窗口的方法增加了求解参数的点数,即方程的个数大于待求解参数个数,利用广义逆矩阵及最小二乘法求解曲面方程的参数。
1.4 高差阈值的确定在改变网格尺寸和设置不同的窗口邻域大小时,为了有效地将地面点和非地面点分开,需要设置不同的高差阈值。
根据文献[24]提出的一种假设:大量离散的地面点云数据在自然状态下呈正态分布,而非地面点数据则影响了正态分布的状态。因此,相对于地面点,非地面点为误差点,其标准偏差大于3σ。由此确定总体数据的高差阈值,然而每个格网包含的地物特征不同,不能直接对整块数据选取同样的阈值。考虑到地面点和地物点具有分层现象,因此可以采用谱系聚类的思想对拟合高程差值进行分类,根据不同的分类数,确定高差阈值[25]。然而有些格网中的地面点与地物点分层现象不明显,因此将两种方法进行综合,具体步骤如下:
(1) 总体高差阈值的确定。假设总数据有N个点,计算每个点云与其对应拟合曲面方程的拟合高程差值,并将N个拟合高差数据从小到大顺序排列,设x1 < x2 < … < xN,计算相邻数据间距离li(1≤i≤N-1)和其期望值μl及标准方差σ,则总体阈值为x1+3σ。
(2) 每个格网高差阈值的确定。以其中一个格网为例,假设该格网有n个点,按照与总体高差阈值相同的步骤计算出相邻两个数据间距离,并按照从大到小顺序排列成l1≥l2≥l3≥ …≥ln-1利用类间距离l1,将格网中的全部数据A分为A1和A2两类,两类的直径(同一类中最大数据和最小数据的差)分别为Q1和Q2,两类的中心(同一类中最大数据与最小数据的算术平均数)分别为O1和O2,若这些参数满足下面其中一个条件,则分为以下两类,否则不进行分类:① l1≥max{Q1,Q2},即类间距离相对较大,A1和A2为不同的类别;② l1<max{Q1,Q2},l1>min{Q1,Q2}, 且(O1+O2)/2∈A1或A2,即两类中心的算术平均值落在其中一类之中,说明这一类数据集中于两类中心的算术平均值附近,而另一类则相反,两类数据特征相异。
高差阈值的取值与分类数相关,其取值规定如下,设A中相邻两个数据间距离最大的两个值为l1和l2, 且l1≥l2:①当A不分类时,数据间的分层现象不明显,高差阈值设为总体高差阈值;②当A分成两类,且两类的最大直径为Q*时,当Q*≤l1≤2Q*时,高差阈值取值为l2处的拟合高差值,其他情况下,高差阈值取值为l1处的拟合高差值;
根据每个格网本身的实际情况,在多级滤波的情况下自动设置每个格网的高差阈值,最大可能避免了以往手动设置同一高差阈值而产生的过度滤波或是不完全滤波问题。
2 试验结果及分析 2.1 试验数据及预处理为了验证本算法的精度,试验数据采用ISPRS公开发布的激光雷达数据集。该数据为Optech ALTM系统采集,由8块测试数据组成。这些测试数据包含代表性的地形地物特征,ISPRS提供了8块测试数据的15个样本数据,并且对样本数据进行了手工分类,将激光脚点精确分类为地面点和非地面点。
对样本数据集进行多级滤波,首先根据地物的最大尺寸设置第1次滤波的初始格网大小,之后滤波的格网大小按倍级减小,15个样本集的数据特征、初始格网大小设置见表 1。
| 数据 | 样本 | 地形特征 | 初始格网大小 |
| site 1 | sample 11 | 位于陡坡上的植被和建筑物 | 25 |
| sample 12 | 平地上建筑物及小物体 | 20 | |
| site 2 | sample 21 | 狭窄的桥梁 | 30 |
| sample 22 | 桥梁 | 30 | |
| sample 23 | 复杂建筑物,不连续的地形 | 20 | |
| sample 24 | 陡坡和植被 | 30 | |
| site 3 | sample 31 | 存在低值噪声点 | 30 |
| site 4 | sample 41 | 不连续地形 | 15 |
| sample 42 | 高频率的地形起伏 | 35 | |
| site 5 | sample 51 | 位于斜坡上的植被 | 30 |
| sample 52 | 陡坡 | 10 | |
| sample 53 | 不连续的地形 | 5 | |
| sample 54 | 村庄 | 15 | |
| site 6 | sample 61 | 不连续的陡坡,岸渠 | 5 |
| site 7 | sample 71 | 桥梁 | 15 |
2.2 滤波结果
滤波的前提条件是每个格网的最低点为地面点,然而有的样本数据存在异常点,因此在滤波之前需去除异常点,并将其作为地物点,之后再进行多级滤波。
为了体现多级滤波的处理过程,以sample 12为例,展示每级滤波的结果,其初始格网大小为20,异常点个数为81,共进行3级滤波,每级滤波的地面点和非地面点结果分别如图 4和图 5所示,图 4中白色的标记点为第1类分类错误的点,图 5中白色的标记点为第2类分类错误的点。

|
| 图 4 sample 12滤波后地面点结果 Fig. 4 Ground points of sample 12 after the hierarchical filter |

|
| 图 5 滤波后非地面点结果 Fig. 5 Non-ground points after the hierarchical filter |
从图 4和图 5可以看出,第1次滤波有大量的非地面点被分为地面点,而非地面点基本无地面点,说明第1次滤波窗口尺寸及高差阈值设置大,去除了具有较大尺寸的高大建筑物;第2次滤波地面点中的非地面点明显减少,一些低矮的建筑物及建筑物之间的植被被剔除,而有少部分的地面点被当作非地面点;第3次滤波地面点中的非地面点进一步减少,而一部分地面点被当作非地面点,采用分级滤波可以逐步滤除地物点,保持地面细节信息,达到算法设计的要求。
2.3 滤波结果分析与评价为了对滤波结果进行定量评价,使用ISPRS在2003年提出的滤波误差的评判标准。第1类误差为将地面点分类为非地面点的误差,第2类误差为将非地面点分类为地面点的误差,第3类为总误差即第1类和第2类误差点数占总点数的比例,如表 2所示。其中e和f表示参考数据中地面点和非地面点的个数,g和h分别是滤波后数据中地面点和非地面点的个数,n为扫描数据点总个数,b/e×100%为第1类误差,c/f×100%为第2类误差,(b+c)/n×100%为总误差。
| 参考数据 | 滤波后数据 | 参考数据点 | |
| 地面点 | 非地面点 | ||
| 地面点 | a | b | e=a+b |
| 非地面点 | c | d | f=c+d |
| 滤波后点数 | g=a+c | h=b+d | n=a+b+c+d |
根据滤波误差定义计算15个样本的滤波误差,如表 3所示。结果表明,文中滤波方法对于sample 12、sample 21、sample 42、sample 54、sample 61有相对好的结果,总误差均在4.00%以下,其中sample 61中包含陡坡,说明该方法对于连续的山地区域可以达到较好的滤波效果。而sample 11、sample 23、sample 24、sample 41的滤波结果较差,根据这些样本数据的数据特征可知,sample 11、sample 23、sample 24、sample 41均存在不连续的地形。文中滤波方法是通过拟合地形的曲面方程,判断点云到拟合曲面的距离是否在高差阈值范围内,对于不连续的地形(如sample 11中的梯田)拟合出来的曲面与实际的地形相差会很大,因此滤波效果相对较差。
| (%) | ||||
| 数据 | 样本 | 第1类误差 | 第2类误差 | 总误差 |
| site 1 | sample 11 | 21.52 | 5.95 | 14.87 |
| sample 12 | 3.16 | 3.12 | 3.14 | |
| site 2 | sample 21 | 2.65 | 7.07 | 3.63 |
| sample 22 | 6.76 | 4.07 | 5.92 | |
| sample 23 | 18.39 | 5.60 | 12.34 | |
| sample 24 | 9.02 | 6.62 | 8.36 | |
| site 3 | sample 31 | 4.72 | 4.76 | 4.74 |
| site 4 | sample 41 | 16.33 | 6.57 | 11.44 |
| sample 42 | 8.88 | 0.99 | 3.3 | |
| site 5 | sample 51 | 3.45 | 8.76 | 4.61 |
| sample 52 | 2.30 | 26.94 | 4.89 | |
| sample 53 | 6.23 | 42.77 | 7.71 | |
| sample 54 | 3.11 | 4.58 | 3.9 | |
| site 6 | sample 61 | 1.84 | 6.79 | 2.01 |
| site 7 | sample 71 | 1.56 | 24.98 | 4.21 |
| 平均值 | 7.33 | 10.64 | 6.34 | |
为了进一步分析滤波算法的准确性,将总误差与ISPRS公布的8大经典滤波算法[26-33]进行比较,结果见表 4。从误差平均值结果中可以看出文中滤波方法精确度优于7种滤波算法,其中sample 12和sample 61的效果最好。本文算法在地形连续的城市区域和山地区域可以取得较好的效果。
| (%) | |||||||||
| 样本 | 文献[26] | 文献[27] | 文献[28] | 文献[29] | 文献[30] | 文献[31] | 文献[32] | 文献[33] | 本文方法 |
| sample 11 | 10.76 | 22.4 | 17.35 | 20.49 | 36.96 | 20.80 | 24.02 | 23.25 | 14.87 |
| sample 12 | 3.25 | 8.18 | 4.50 | 8.39 | 16.28 | 6.61 | 6.61 | 10.21 | 3.14 |
| sample 21 | 4.25 | 8.53 | 2.57 | 8.80 | 9.30 | 9.84 | 4.55 | 7.76 | 3.63 |
| sample 22 | 3.63 | 8.93 | 6.71 | 7.54 | 22.28 | 23.78 | 7.51 | 20.86 | 5.92 |
| sample 23 | 4.00 | 12.28 | 8.22 | 9.84 | 27.80 | 23.20 | 10.97 | 22.71 | 12.34 |
| sample 24 | 4.42 | 13.83 | 8.64 | 13.33 | 36.06 | 23.25 | 11.53 | 25.28 | 8.36 |
| sample 31 | 4.78 | 5.34 | 1.80 | 6.39 | 12.92 | 2.14 | 2.21 | 3.15 | 4.74 |
| sample 41 | 13.91 | 8.76 | 10.75 | 11.27 | 17.03 | 12.21 | 9.01 | 23.67 | 11.44 |
| sample 42 | 1.62 | 3.68 | 2.64 | 1.78 | 6.38 | 4.20 | 3.54 | 3.85 | 3.30 |
| sample 51 | 2.72 | 21.31 | 3.71 | 9.31 | 22.81 | 3.01 | 11.45 | 7.02 | 4.61 |
| sample 52 | 3.07 | 57.5 | 19.64 | 12.04 | 45.56 | 9.78 | 23.83 | 27.53 | 4.89 |
| sample 53 | 8.91 | 48.45 | 12.60 | 20.19 | 52.81 | 17.29 | 27.24 | 37.07 | 7.71 |
| sample 54 | 3.23 | 21.26 | 5.47 | 5.68 | 23.89 | 4.96 | 7.63 | 6.33 | 3.90 |
| sample 61 | 2.08 | 35.87 | 6.91 | 2.99 | 21.68 | 18.99 | 13.47 | 21.63 | 2.01 |
| sample 71 | 1.63 | 34.22 | 8.85 | 2.20 | 34.98 | 5.11 | 16.97 | 21.83 | 4.21 |
| 平均值 | 4.82 | 20.73 | 8.02 | 9.35 | 25.78 | 12.34 | 12.04 | 17.48 | 6.34 |
整体来说,文献[26]提出的滤波算法效果比本文方法的效果好,但是其滤波计算量大,需要反复构建三角网并进行高程、角度的计算,速度较慢。其他7种算法的整体效果没有本文滤波效果好,其中文献[28]、文献[27]、文献[30]、文献[32]提出的滤波算法在山地区域滤波效果较差,而本文滤波算法考虑了地形的连续性信息,因此在地形连续的山地区域可以达到较好的滤波效果。文献[28]算法在无地形起伏区域(sample 21、sample 31、sample 42)效果较好,因为该算法多次迭代计算拟合地形高程,充分考虑了地形和地物间的联系。文献[31]、文献[33]滤波算法对地形突变地区滤波难度较大,且其滤波算法阈值的确定需要根据先验知识判断,不同的地形需设置不同的坡度阈值,坡度阈值的自适应性较差,而本文算法是基于自适应阈值的,根据数据本身的特征选取合适的阈值,因此能达到较好的效果。
3 结论本文采用基于多级移动曲面拟合的自适应阈值点云滤波方法在传统滤波算法的基础上增加了窗口邻域,根据区域范围中最大建筑物尺寸设置初始格网大小,并采用多级滤波的方法,在逐级改变网格尺寸的同时, 根据坡度自动设置窗口邻域,根据拟合高差值自适应性设置高差阈值。试验表明本文算法精度高,具有一定的自适应性。与ISPRS公布的8大滤波算法的总误差对比分析,比其中7种滤波算法的效果好。总体来说,本文算法在地形复杂且连续变化的区域能够获得很好的滤波效果,不足之处在于对不连续地形的区域滤波效果有待进一步提高。
| [1] | NIE Sheng, WANG Cheng, ZENG Hongcheng, et al. Above-ground Biomass Estimation Using Airborne Discrete-return and Full-waveform LiDAR Data in A Coniferous Forest[J]. Ecological Indicators, 2017, 78: 221–228. DOI:10.1016/j.ecolind.2017.02.045 |
| [2] |
王平华, 习晓环, 王成, 等.
机载激光雷达数据中电力线的快速提取[J]. 测绘科学, 2017, 42(2): 154–158, 171.
WANG Pinghua, XI Xiaohuan, WANG Cheng, et al. Study on Power Line Fast Extraction Based on Airborne LiDAR Data[J]. Science of Surveying and Mapping, 2017, 42(2): 154–158, 171. |
| [3] |
杨伟, 艾廷华.
运用约束Delaunay三角网从众源轨迹线提取道路边界[J]. 测绘学报, 2017, 46(2): 237–245.
YANG Wei, AI Tinghua. The Extraction of Road Boundary from Crowdsourcing Trajectory Using Constrained Delaunay Triangulation[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(2): 237–245. DOI:10.11947/j.AGCS.2017.20160233 |
| [4] |
李磊, 胡以华, 赵楠翔, 等.
激光三维成像技术应用现状[J]. 激光与光电子学进展, 2009, 46(12): 66–71.
LI Lei, HU Yihua, ZHAO Nanxiang, et al. Application of Three-dimensional Laser Imaging Technology[J]. Laser & Optoelectronics Progress, 2009, 46(12): 66–71. |
| [5] |
宁亚飞, 吴笑天, 张海涛, 等.
基于虚拟三角网与坡度滤波的LIDAR点云数据滤波方法的研究[J]. 工程地球物理学报, 2012, 9(5): 624–627.
NING Yafei, WU Xiaotian, ZHANG Haitao, et al. Research on Filtering LiDAR Point Cloud Data Based on Virtual Triangle Nets and Slope Filtering[J]. Chinese Journal of Engineering Geophysics, 2012, 9(5): 624–627. |
| [6] |
杨洋, 张永生, 邹晓亮, 等.
一种改进的基于坡度变化的机载激光雷达点云滤波方法[J]. 测绘科学, 2008, 33(S1): 12–13, 280.
YANG Yang, ZHANG Yongsheng, ZOU Xiaoliang, et al. An Improved Method of Slope Based Filtering of Airborne LiDAR Point Cloud[J]. Science of Surveying and Mapping, 2008, 33(S1): 12–13, 280. |
| [7] |
唐德瑾, 王楠, 张振华, 等.
一种改进的坡度机载LiDAR数据滤波算法[J]. 测绘信息与工程, 2010, 35(3): 15–16.
TANG Dejin, WANG Nan, ZHANG Zhenhua, et al. An Improved Slope Filtering Algorithm for Airborne LiDAR Data[J]. Journal of Geomatics, 2010, 35(3): 15–16. |
| [8] |
潘中华, 陈性义, 门林杰, 等.
基于两级格网的LiDAR数据组织与改进坡度滤波[J]. 测绘工程, 2011, 20(6): 5–8.
PAN Zhonghua, CHEN Xingyi, MEN Linjie, et al. Data Organization and Improvement of the LiDAR Slope Filter Based on the Two Levels of Grid[J]. Engineering of Surveying and Mapping, 2011, 20(6): 5–8. |
| [9] |
张皓, 贾新梅, 张永生, 等.
基于虚拟网格与改进坡度滤波算法的机载LIDAR数据滤波[J]. 测绘科学技术学报, 2009, 26(3): 224–227, 231.
ZHANG Hao, JIA Xinmei, ZHANG Yongsheng, et al. Filtering of Airborne LiDAR Data Based on Pseudo-grid Concept and Modified Slope Filtering Algorithm[J]. Journal of Geomatics Science and Technology, 2009, 26(3): 224–227, 231. |
| [10] |
赵明波, 何峻, 田军生, 等.
基于改进的渐进多尺度数学形态学的激光雷达数据滤波方法[J]. 光学学报, 2013, 33(3): 0328001.
ZHAO Mingbo, HE Jun, TIAN Junsheng, et al. LiDAR Data Filtering Method Based on Improved Progressive Multi-scale Mathematic Morphology[J]. Acta Optica Sinica, 2013, 33(3): 0328001. |
| [11] | WEIDNER U, FÖRSTNER W. Towards Automatic Building Extraction from High-resolution Digital Elevation Models[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1995, 50(4): 38–49. DOI:10.1016/0924-2716(95)98236-S |
| [12] |
隋立春, 张熠斌, 柳艳, 等.
基于改进的数学形态学算法的LiDAR点云数据滤波[J]. 测绘学报, 2010, 39(4): 390–396.
SUI Lichun, ZHANG Yibin, LIU Yan, et al. Filtering of Airbornee LiDAR Point Cloud Data Based on the Adaptive Mathematical Morphology[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 390–396. |
| [13] |
罗伊萍, 姜挺, 龚志辉, 等.
基于自适应和多尺度数学形态学的点云数据滤波方法[J]. 测绘科学技术学报, 2009, 26(6): 426–429.
LUO Yiping, JIANG Ting, GONG Zhihui, et al. An Adaptive and Multi-scale Mathematic Morphological Filter for Point Cloud Data Filtering[J]. Journal of Geomatics Science and Technology, 2009, 26(6): 426–429. |
| [14] |
罗伊萍, 姜挺, 王鑫, 等.
基于数学形态学的LiDAR数据滤波新方法[J]. 测绘通报, 2011(3): 15–19.
LUO Yiping, JIANG Ting, WANG Xin, et al. A New Filtering Method for LiDAR Data Based on Mathematic Morphological Approach[J]. Bulletin of Surveying and Mapping, 2011(3): 15–19. |
| [15] | SU Wei, SUN Zhongping, ZHONG Ruofei, et al. A New Hierarchical Moving Curve-fitting Algorithm for Filtering LiDAR Data for Automatic DTM Generation[J]. International Journal of Remote Sensing, 2015, 36(14): 3616–3635. DOI:10.1080/01431161.2015.1065356 |
| [16] |
尚大帅, 马东洋, 赵羲, 等.
一种基于移动曲面拟合的机载LIDAR点云数据滤波方法[J]. 测绘技术装备, 2012, 14(2): 23–25, 10.
SHANG Dashuai, MA Dongyang, ZHAO Xi, et al. An Filtering Method Based on Moving Surface Fitting of Airborne LIDAR Point Cloud Data[J]. Geomatics Technology and Equipment, 2012, 14(2): 23–25, 10. |
| [17] |
苏伟, 孙中平, 赵冬玲, 等.
多级移动曲面拟合LIDAR数据滤波算法[J]. 遥感学报, 2009, 13(5): 827–839.
SU Wei, SUN Zhongping, ZHAO Dongling, et al. Hierarchical Moving Curved Fitting Filtering Method Based on LIDAR Data[J]. Journal of Remote Sensing, 2009, 13(5): 827–839. |
| [18] |
张小红.
机载激光雷达测量技术理论与方法[M]. 武汉: 武汉大学出版社, 2007: 9-14.
ZHANG Xiaohong. Theory and Method of Airborne LiDAR Measurement Technology[M]. Wuhan: Wuhan University Press, 2007: 9-14. |
| [19] | NIE Sheng, WANG Cheng, DONG Pinliang, et al. A Revised Progressive TIN Densification for Filtering Airborne LiDAR Data[J]. Measurement, 2017, 104: 70–77. DOI:10.1016/j.measurement.2017.03.007 |
| [20] |
靳克强. 机载激光雷达数据滤波生成DEM技术研究[D]. 郑州: 信息工程大学, 2011. JIN Keqiang. A Study on Data Filtering and DEM Extraction of Airborne LiDAR Point Clouds[D]. Zhengzhou: Information Engineering University, 2011. http://cdmd.cnki.com.cn/article/cdmd-90008-1012325269.htm |
| [21] |
张小红, 刘经南.
机载激光扫描测高数据滤波[J]. 测绘科学, 2004, 29(6): 50–53.
ZHANG Xiaohong, LIU Jingnan. Airborne Laser Scanning Altimetry Data Filtering[J]. Science of Surveying and Mapping, 2004, 29(6): 50–53. |
| [22] |
刁鑫鹏, 吴侃.
改进的移动窗口曲面拟合法点云数据滤波处理[J]. 现代矿业, 2011, 27(6): 59–61.
DIAO Xinpeng, WU Kan. Improved Moving Windows Surface Fitting Method of Point Cloud Data[J]. Modern Mining, 2011, 27(6): 59–61. |
| [23] |
孙崇利, 苏伟, 武红敢, 等.
改进的多级移动曲面拟合激光雷达数据滤波方法[J]. 红外与激光工程, 2013, 42(2): 349–354.
SUN Chongli, SU Wei, WU Honggan, et al. Improved Hierarchical Moving Curved Filtering Method of LiDAR Data[J]. Infrared and Laser Engineering, 2013, 42(2): 349–354. |
| [24] | BARTELS M, WEI Hong. Threshold-free Object and Ground Point Separation in LiDAR Data[J]. Pattern Recognition Letters, 2010, 31(10): 1089–1099. DOI:10.1016/j.patrec.2010.03.007 |
| [25] |
蔡菲娜.
基于聚类分析的数字滤波阈值算法[J]. 数据采集与处理, 2006, 21(2): 234–238.
CAI Feina. Digital Filter Threshold Algorithm Based on Clustering Analysis[J]. Journal of Data Acquisition & Processing, 2006, 21(2): 234–238. |
| [26] | AXELSSON P E. DEM Generation from Laser Scanner Data Using Adaptive TIN Models[J]. International Archives of Photogrammetry and Remote Sensing, 2000, 33: 111–117. |
| [27] | ELMQVIST M. Automatic Ground Modelling Using Laser Radar Data[D]. Linköping, Sweden: Linköping University, 2000. |
| [28] | PFEIFER N, REITER T, BRIESE C, et al. Interpolation of High Quality Ground Models from Laser Scanner Data in Forested Areas[J]. International Archives of Photogrammetry and Remote Sensing, 1999, 32: 31–36. |
| [29] | SOHN G, DOWMAN I. Terrain Surface Reconstruction by the Use of Tetrahedron Model with the MDL Criterion[J]. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2002, 34: 336–344. |
| [30] | BROVELLI M A, CANNATA M, LONGONI U M. Managing and Processing LiDAR Data within GRASS[J]. Proceedings of the Open Source GIS-GRASS Users Conference. Trento, Italy:[s.n.], 2002: 11–13. |
| [31] | ROGGERO M. Airborne Laser Scanning:Clustering in Raw Data[J]. International Archives of Photogrammetry and Remote Sensing, 2001, 34: 227–232. |
| [32] | WACK R, WIMMER A. Digital Terrain Models from Airborne Laser Scanner Data:A Grid Based Approach[J]. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2002, 34: 293–296. |
| [33] | SITHOLE G, VOSSELMAN G. Experimental Comparison of Filter Algorithms for Bare-Earth Extraction from Airborne Laser Scanning Point Clouds[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2004, 59(1-2): 85–101. DOI:10.1016/j.isprsjprs.2004.05.004 |



