2. 昆明理工大学理学院, 云南 昆明 650500
2. School of Science, Kunming University of Science and Technology, Kunming 650500, China
森林是构成极为复杂、组成极为多样的生态系统,其碳储量占全球的86%,对整个地球的生态平衡有着举足轻重的影响。随着人类对自身生存环境的关切不断提升,森林生物量的监测与预估就变得日益重要。目前激光探测技术已经发展的较为成熟,星载激光雷达作为一种主动测量系统,正受到越来越多的关注。卫星平台搭载的高灵敏度探测器通过接收卫星平台激光器发射的激光脉冲在地面目标反射后的回波,计算出卫星到地面目标的距离。结合平台自身的精密定轨和姿态数据,可以获得覆盖全球的高程数据产品[1-3]。
目前,国内外许多学者已经对利用GLAS波形反演植被目标参数开展了大量研究工作。文献[4]阐述了激光雷达系统对森林特征及其冠层结构进行遥感的数学模型。文献[5]阐述了利用GLAS(geoscience laser altimeter system)系统数据反演森林冠层高度的方法。文献[6]将激光雷达数据与地面实测数据融合进行森林冠层遥感的研究。文献[7]将长白山汪清林区的林业测量数据与GLAS在相应地区脚点回波信号的反演结果进行了对比,得到了比较理想的反演结果。文献[8]结合了小兴安岭部分针叶林和阔叶林林业测量数据与GLAS回波信号,验证了利用激光脉冲回波信号反演森林生物量的数学模型。文献[9]同时利用直接反演和统计学模型通过GLAS波形反演山区植被的冠层最大高度,并利用机载LiDAR数据对反演结果进行评估,其研究认为在山区直接反演的方法通常会高估最大冠层高度,而统计学模型的精度较好,但其通用性较差,只适用于特定地区的植被。文献[10]通过Flight三维辐射传输模型建立仿真数据集,通过查询的方式对GLAS波形与数据集进行匹配以获取目标区域植被冠层参数的反演结果,该方法对森林高度的反演误差约为1.5 m,对植被覆盖率的反演误差约为8%。
目前主流的研究工作都基于统计学模型对森林植被目标的参数进行反演,这些研究成果通常没有考虑林下植被产生的影响。而现有的基于回波仿真模型研究也多服务于森林植被目标的参数反演,而对回波波形的生成过程中不同输入变量对结果的影响缺少分析,尤其是林下植被的影响。本文利用薄层模型近似植被地面目标的反射特性,采用几何形状近似植被的树冠形状并采用实测作为森林空间位置和高度分布数据,利用随机过程生成不同高度和覆盖率的林下植被,最后利用辐射传输模型仿真获得该模型的回波波形。
1 基本原理 1.1 星载激光雷达回波波形的基本理论卫星激光测高仪发射激光脉冲在经过菲涅尔衍射后到达地面,并被地面目标反射。反射的激光能量再次经菲涅尔衍射后被星载望远镜系统接收并被聚焦探测器焦点。接收的信号能量可以表示为式(1)[11-12]
 (1)
(1)
式中,η是接收系统和光电探测系统的综合效率;AR是接收系统孔径;Ta是单程大气传输损耗;hv是光子能量;l是星载激光测高仪与地面目标间的距离;β(x, y, z)是地面目标强度反射系数分布函数;a(x, y)表示是入射激光脉冲的空间截面能量分布;z是冠层深度;ψ是由地表起伏和激光脚点水平分布引起的时延,可以表示为
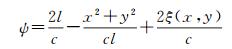 (2)
(2)
式中,ξ(x, y)是(x, y)处的地表高程;c是真空中光速。在针对不同的地面目标时,只需对应的ξ(x, y)函数,即可利用式(1)描述其回波。
1.2 单棵树木的薄层模型激光雷达发射出一个具有一定宽度的脉冲后,通过APD将接收到的激光脉冲能量转换为电压信号。通过对输出电压的采样即获得了对应于某一发射激光脉冲的回波波形。所以回波波形记录的是一个电压随时间变化的离散序列,其垂直空间分辨率由探测器的采样间隔决定[13]。图 1展示了激光脉冲入射到地面目标并发生反射的情形。

|
| 图 1 激光脉冲入射到植被目标发生反射并形成波形过程 Fig. 1 The formation of waveform caused by the plantation's reflection of laser pulse |
为了近似这一过程,对于激光脉冲与地面森林树冠的作用过程,采用离散各向异性辐射传输模型(DART)。该模型对于植物郁闭度不确定的区域,将场景空间分成矩形单元的矩阵,并假设辐射传输被限定在指定的方向上[11],每个矩阵单元包含场景中的不同元素,它们的光学特征由该单元点的散射相位函数决定[14-15]。本文中主要包含叶子、灌木和土壤等元素。
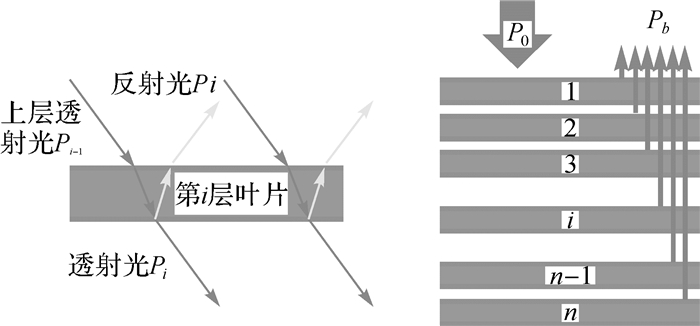
模型首先对树木的冠层形状用某一立体几何形状进行近似,例如圆台、椭球体和圆锥体等[16-17]。由于星载激光雷达的光斑半径通常远大于树木的冠幅,因此在本文的模型中将植被的冠层视为一种等效散射介质。由于激光雷达记录的波形中某一时刻的电压值对应于某一高度处反射能量强度,因此本文更关心树木冠层反射率沿垂直方向的分布,而水平方向在某一高度处的反射率被认为是均匀的。对于反射率率R和透射率T采用了针对阔叶林的PROSPECT模型[18-19]。该模型将叶片视为一个表面粗糙的均匀平板,叶片的反射率和透过率由几何光学理论确定。依据叶片的结构参数N(取值范围1~5),叶绿素Ca+b(取值范围0~100)和水含量Cw(取值范围0~0.05)即可计算出新鲜叶片的反射率R和透过率T。这样,树木的树冠就沿垂直方向被分为若干薄片[18]。其示意图如图 2所示,图中P0表示入射光能量,Pb表示回波能量。
|
| 图 2 叶片薄层模型 Fig. 2 The leaf layer model |
可以利用双向缺口概率(BDGP),来描述激光脉冲在树木冠层中垂直穿透的能量损耗,冠层某一深度处的双向缺口概率可以表示为[5]
 (3)
(3)
式中,z为冠层的深度;Ωi为激光脉冲入射方向;uL(z)是深度为z处的单侧叶区域密度;G(z′, Ωi)是Ross-Nilson G函数,即单位叶面积在z深度Ωi方向上投影面积的平均值。当激光脉冲的入射角和观察角度都较小时,每一个薄片的等效反射率可以表示为
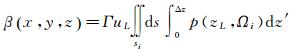 (4)
(4)
式中,Г是树冠的区域散射相位函数,将叶片视作为朗伯体时,Г是常数;Δz为每层的厚度;Si为薄层截树冠所得交线围成的区域面积。
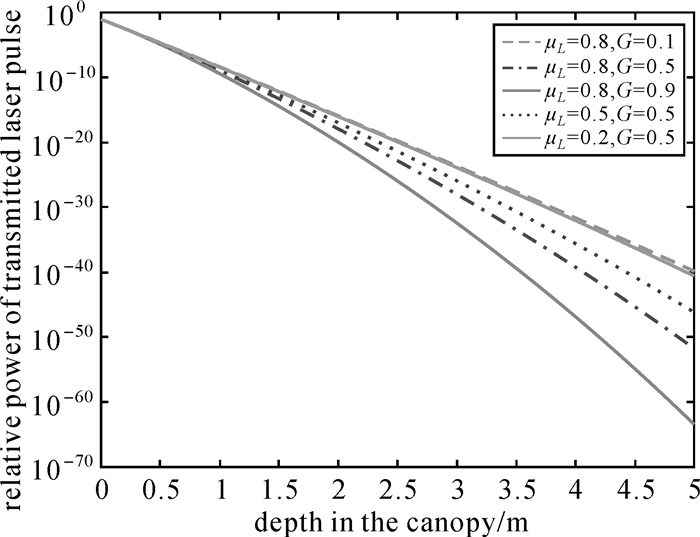
图 3给出了不同叶密度uL和G函数取值的条件下,入射激光脉冲进入树冠不同深度的功率变化曲线(假设入射激光功率为1)。激光脉冲能量进入植被冠层后,功率将急剧衰减。通过计算每层返回的能量,发现在冠层0.5 m深处返回的能量已接近入射能量的10-10数量级,只有树冠表层向下约3~5层的反射能量将对回波产生影响,而更深层的能量则几乎不可能被探测器接收。因此,在真实情况下,树木冠层的表层及浅层叶片对反射的回波波形有主要贡献,而较深处叶片反射的激光脉冲能量对回波波形的贡献可以被忽略。以椭球体形状的树冠为例,ξ(x, y)可以近似表示为
|
| 图 3 叶密度和G函数值对反射脉冲能量的影响 Fig. 3 The variation of relative power influenced by leaf density and G-function |
 (5)
(5)
式中,hbottom为林木的枝下高;hcrown为林木的冠层高度;hground(x, y)为所在坐标的地形高度;w为树木冠幅;x0和y0表示树木中心相对光斑中心的位置坐标。在仿真中hground取值既可以是简单递增斜面,也可以是由DEM给出的复杂地形高程。
1.3 单棵树木的回波波形假设入射激光脉冲的截面分布服从高斯分布,则可以表示为式(6)
 (6)
(6)
式中,θT为激光脉冲的发散角。如果将地面目标的响应视为一个线性系统,则对于任意的输入激光脉冲,其回波信号都可以表示为输入脉冲信号和系统的单位脉冲响应的卷积。将式(1)整理为卷积的形式,即得到对应脉冲的回波信号
 (7)
(7)
式中,h(t)是系统的单位冲激响应,计算公式为
 (8)
(8)
式(7)中,I(t)是发射激光脉冲的波形,假设其为高斯脉冲时,可以表达为
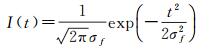 (9)
(9)
将式(2)、式(4)—(6)和式(8)式代入式(7)中即得到单棵树木的回波表达式。
1.4 森林目标的回波波形利用地面林业实测的数据作为输入,确定样方内每一棵树木相对中心的位置及其树高。如图 4所示,图 4(a)是林业实测数据来源地,大兴安岭地区(50.68°N—51.32°N,120.71°E—121.42°E)根河试验区示意图。图 4(b)是某一片样方内森林中树木空间分布示意图,其中小圆圈代表森林中树木的中心位置,大圆代表光斑范围。在此基础上,在每棵林木的位置,利用上一节中推导的模型,即可获得样地范围内植被目标的回波波形。

|
| 图 4 森林树木空间分布 Fig. 4 The spatial distribution of the forest |
2 回波波形的仿真及分析 2.1 采用林业实测数据的仿真波形验证
验证地区选取河南省嵩山境内约3.3×6.8 km2面积区域,高程范围514~1500 m,如图 5所示。地表三维轮廓数据采用河南省遥感测绘院ALS80机载LiDAR设备采集,LiDAR设备采集过程中同时记录对应三维点云位置的反射率信息。卫星激光发射和接收时间波形数据读取GLAS系统GLA01数据包(时间采样间隔均为1 ns),激光能量分布数据读取GLA04 LPA数据包,激光脚点中心位置三维坐标读取GLA14数据包。

|
| 图 5 嵩山地区GLAS脚点与LiDAR点云 Fig. 5 GLAS footprints and airborne LiDAR point cloud on Songshan Forest Park |
由于GLAS系统记录的经纬度和高程坐标基于T/P椭球,首先将GLA14读取所有工作周期的激光脚点三维坐标转换至WGS-84椭球框架,进而转换至高斯三度带投影平面直角坐标系,与机载LiDAR点云进行坐标系统的统一[20]。以GLA14激光脚点三维坐标为中心为圆形,搜索平面方向±70 m方形范围内所有机载LiDAR点云(2倍GLAS光斑直径范围,GLAS光斑直径70 m),共检索出3条轨迹,检索结果如表 1所示。
| 主要参数 | 工作周期 | 工作周期 |
| DOY | 2003-10-21 | 2004-05-23 |
| GLAS period | L2A | L2C |
| track number | 2103_002_9_0_02_1 | 2107_003_0009_0_01_1 |
| UTC start time/ns | 120 095 599.889 | 138 646 972.846 |
| valid footprints | 20 | 37 |
| footprint ellipticity | ≈1.8 | ≈1.8 |
| received energy/fJ | 8.66-14.88 | 0.12-2.57 |
| elevation range/m | 540-854 | 580-1438 |
| slope range/(°) | 1~30 | 2~56 |
| roughness range/m | 4~26 | 4~72 |
为评价GLAS数据质量,同时读取对应激光接收能量,利用LPA阵列数据计算光斑椭圆率;利用LiDAR点云计算当前激光光斑对应位置的地表斜率和粗糙度。
将LiDAR点云提取的数据输入回波仿真模型后生成的仿真波形与对应的GLAS对比的结果如图 6所示。其中左侧曲线为GLAS发射脉冲, 毛刺较多的曲线为GLAS接收波形, 较为平滑的曲线为最佳匹配的仿真波形。

|
| 图 6 GLAS波形与仿真波形对比 Fig. 6 GLAS wave form vs simulated wave form |
模型中根据实际目标森林结构,考虑了二层林的存在和地面灌木覆盖等因素,使得仿真回波更接近真实回波。对应目标区域森林结构的回波,本文建立的植被回波仿真模型模拟的回波波形都与之符合得很好,图 6所示的仿真波形与真实回波的相关系数R2达到0.97以上。
2.2 森林树冠形状对波形的影响由于影响森林回波波形的因素极多,为了避免其他因素对回波波形产生影响,在仿真中去除了地面粗糙度和林下植被。为了使得出的结论更具有普遍性,仿真中树木的空间分布采用服从泊松分布的随机过程生成,树高分布则满足正态分布。仿真输入参数如表 2所示。
| 参数名称 | 参数值 |
| 林木棵数 | 75 |
| 阈值距离/m | 1 |
| 平均树高/m | 13.34 |
| 树高方差 | 0.5 |
| 特征参数 | 0.318 |
| 树冠密度 | 0.8 |
| 空间分布 | 泊松分布 |
| 叶反射率 | 0.55 |
| 土壤反射率 | 0.29 |
| 间隙率 | 0.5 |
| 坡度 | 0° |
| 样地边长/m | 30 |
| 水平间隔/m | 0.1 |
| 纵向间隔/m | 0.1 |
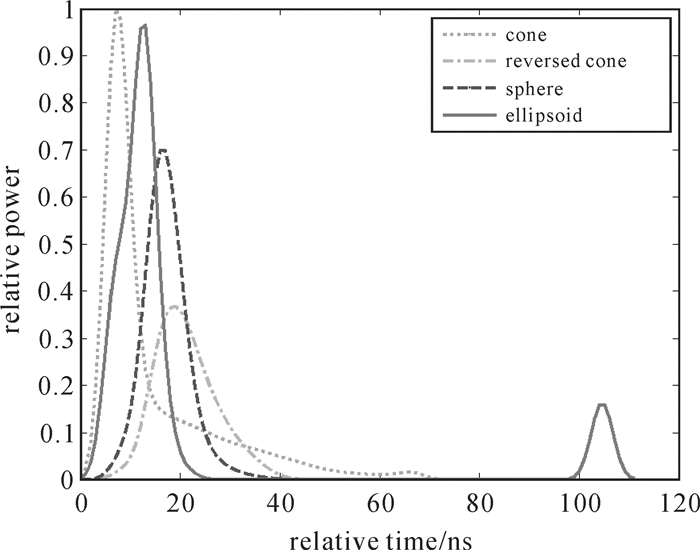
观察图 7可以看出,不同形状的树冠对其接收脉冲回波波形有显著的影响。这种影响主要是由不同形状的树冠具有不同的有效表面积所造成。
|
| 图 7 不同树冠几何形状影响的归一化回波波形 Fig. 7 The variation of waveform influenced by canopy shape |
如图 8所示,分别计算4种几何图形的树冠能被激光脉冲直接照射的表面积。其中h是树冠的长度,其值为树高减枝下高,d为树冠冠幅,其值为南北冠幅和东西冠幅的均值。其有效表面积的计算结果如表 3所示。依据林业数据拟合的结果,h≈5/3d,故有SC>SE>SS>SR。这与仿真结果是一致的。

|
| 图 8 不同几何形状的树冠有效表面积示意图 Fig. 8 The effective area of different canopy shape |
| 树冠几何形状 | 面积计算公式 | 计算结果 |
| 圆锥体 | SC=LR/2 | 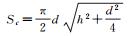 |
| 倒圆锥体 | SR=πR2 | 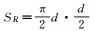 |
| 椭球体 | SE=4/3π(ab+bc+ac)×1/2 |  |
| 球体 | SS=4πR2×1/2 |  |
综上所述,在其他输入参数一致的情况下,在当前的几何图形参数规定下,圆锥体树冠的有效表面积最高,其回波波形的树冠贡献能量最高,而倒圆锥的有效表面积最低。
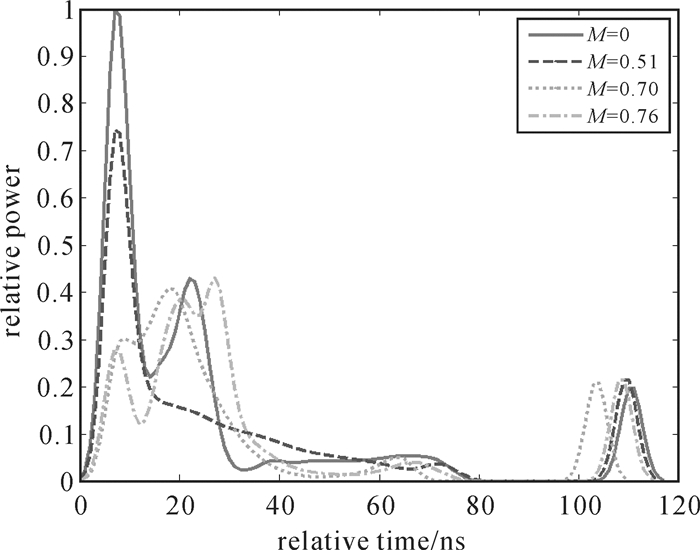
在实际情况下,森林中通常会存在不止一种树种,它们的树冠形状可能也不尽相同,图 9给出了不同混交度森林的回波波形仿真,其中点划线代表由4种形状树冠等比例混交形成的林地,混交度M=0.752,点线代表由圆锥体、椭球体和球体3种形状树冠等比例混交形成的林地,混交度M=0.609,虚线代表圆锥体和倒圆锥体等比例混交形成的林地,混交度M=0.503,实线代表单一圆锥形树冠的林地,混交度M=0。
|
| 图 9 不同混交度的混交林的归一化回波波形 Fig. 9 The variation of waveform influenced by mingling density |
图 9显示,M=0的曲线所对应的树冠贡献能量仍然是最高的。此外,比较图 7和图 9,可以发现当存在多种形状的树冠时,树冠的回波波形将发生展宽,对区分树冠和地面的回波波形产生不利影响。因此,目标区域的混交度,也会对回波波形产生影响。
2.3 森林所处区域对回波波形的影响式(5)中,hground(x, y)是(x, y)处的地表高程,本文主要考虑地形为单调增高的斜面对回波波形的影响,斜面的坡向定义为90°,即斜面法线在水平面上的投影与x轴平行,坡度为θ。此时式hground可以表示为(10)式的形式
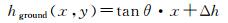 (10)
(10)
式中,Δh是地表粗糙度。在分析坡度时,暂时不考虑地表粗糙度的影响。在保持其他输入参数不变的情况下,选取树冠形状为椭球体,将坡度作为变量,对生长在不同坡度下的林地的回波波形进行仿真,如图 10所示。为了避免曲线过多影响比较,将仿真分为两组进行,前一组坡度为0°~5°的小坡度情况,后一组为10°~20°大坡度的情况。

|
| 图 10 不同坡度影响的归一化回波波形 Fig. 10 The variation of waveform influenced by slope |
观察图 10(a)中的4条曲线,当坡度较小时。波形的展宽和混叠不明显,其中,当坡度为5°时,波形相对于平坦地面的回波波形展宽约为10%,树冠的回波波形与地表的回波波形可以明显地区分。在图 10(b)中,当坡度较大时,可以观察到明显的波形展宽,当坡度达到20°时,波形相对于平坦地面的回波波形展宽超过50%。图 11给出了林木棵数为75棵时,回波整体宽度随坡度变化的曲线。

|
| 图 11 回波整体脉宽随坡度变化曲线 Fig. 11 The pulse width of waveform vs slope |
图 11显示,回波的展宽程度与地表坡度呈线性关系,即随着地表坡度的增加,回波的展宽程度也越大。当坡度大于15°达到约20°时,树冠和地表的回波波峰已经产生混叠,这将大大降低该波形在现有研究基础上的应用价值。
2.4 森林所处区域地表粗糙度对回波波形的影响通常地表粗糙度用h(x, y)+Δh(x, y)的形式来表达,其中h(x, y)表征了该坐标点的高程,而表征了在Δh(x, y)原有斜面基础上地形局部的微小起伏,一般认为服从N(μ, σ2)的正态分布,其均值μ一般取0,而标准差σ表征了微小起伏变化的剧烈程度。如图 11所示,是不同坡度条件下回波波形随地表粗糙度变化的情况,植被的输入参数仍采用表 3中的输入数据,树木冠层形状固定为椭球体。
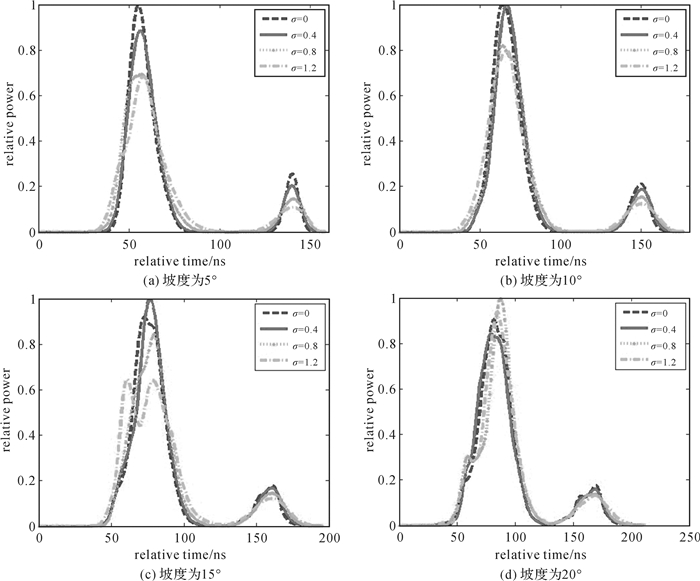
由图 12中虚线、实线、点线和点划线分别代表了地表粗糙度为0 m、0.4 m、0.8 m和1.2 m条件下的回波波形,可以发现随着地表粗糙度的增加,地面回波有明显的展宽,尤其当地形的坡度小于10°时,地表粗糙度带来的地面回波展宽较为显著。同时地表粗糙度也会造成林木回波波形的展宽,但其影响更为复杂,地形的起伏可能使部分林木相对原位置有一定的上升或下降,因此可能带来波形形状的变化。例如图 4(c)中,由于地表粗糙度的增加,林木冠层的回波分裂为两个波峰。这样的影响与坡度增加时有时会导致林木冠层回波出现分裂的情形是相似的。
|
| 图 12 不同坡度下波形随地表粗糙度变化 Fig. 12 The variation of waveform influenced by terrain roughness |
2.5 森林所处区域林下植被对回波波形的影响
本文根据文献[21]中的数据,林下植被的反射率取值为0.207,认为其高度服从N(μ, σ2)的正态分布,其中μ为林下植被的平均高度,σ表征了林下植被间的高度的变化[22-23]。图 12给出了σ=0.5 m时,不同坡度条件下回波波形随林下植被平均高度变化的情况。
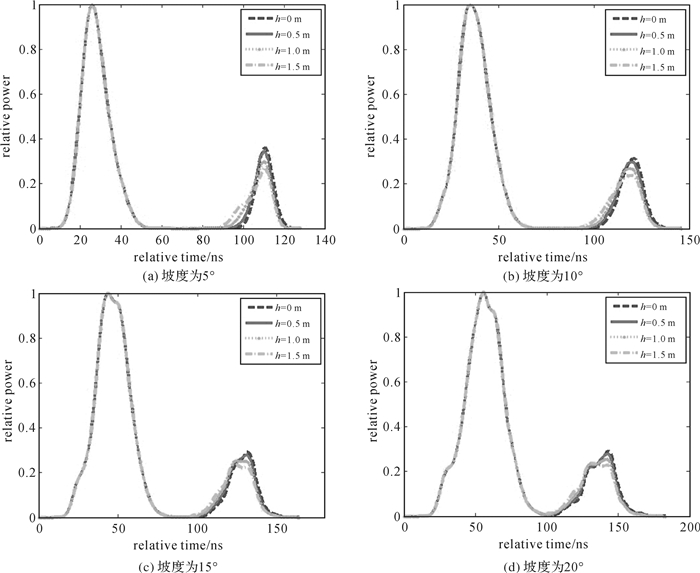
图 13中用虚线、实线、点线和点划线分别表示了林下植被平均高度分别为0 m、0.5 m、1 m和1.5 m时不同坡度下的回波波形。观察波形可以发现,在不考虑多次散射的条件下,林下植被对林木冠层的波形没有影响,但对地面回波有一定的影响。地面回波的前沿发生展宽,观察图 13(d)可以发现,如果林下植被平均高度更高,则甚至有可能在林木冠层回波与地面之间产生新的波峰。图 14中的仿真很好地证实了这一点。图中实线表示林下植被平均高度为3 m时的回波波形,可见地面回波已经分裂为两个波形。
|
| 图 13 不同坡度下回波波形随林下植被平均高度变化 Fig. 13 The variation of waveform influenced by the average height of understory vegetation |

|
| 图 14 林下植被较高时的回波波形 Fig. 14 The waveform of 3 m average height of understory vegetation |
综合上述分析,地表粗糙度和林下植被都会导致地面回波波形的展宽,但地表粗糙度导致的展宽是均匀的,而林下植被将导致地面回波的前沿展宽甚至分裂出新的波峰。此外地表粗糙度对林木冠层回波的影响也较为显著,而林下植被对林木冠层的回波几乎没有影响。
3 结论对于植被目标,星载激光测高仪获取的波形复杂度将远高于海洋和冰盖表面的波形。这些波形中也包含着丰富的细节。本文基于半解析模型建立森林植被目标的回波仿真模型,并以林业实测参数作为输入,与GLAS波形进行对比。在选取合适的输入条件下,仿真波形与真实波形的相关系数R2优于0.91,验证了回波仿真模型的正确性。由于影响回波波形的因素极为复杂,因此充分发挥回波仿真模型定量改变参数的优势,着重分析植被冠层形状、所处区域坡度、地标粗糙度和林下植被各自对回波波形的影响。本文认为,星载激光测高仪针对森林植被目标的波形分析工作中,森林树木冠层形状近似于球体或椭球体的林木的波形更不容易与地面波形产生混叠,其相应的反演工作更易取得更高的精度。而如果目标区域的坡度较大或地表不平整,将导致地面波形更易与植被波形发生混叠,对植被参数的提取产生不利的影响。此外,地表粗糙度和林下植被都将引起地面回波波形的展宽,但前者的展宽是对称的,后者只引起波形的前缘展宽,这一特点可以用于林下植被存在性的分析。星载激光测高仪的数据应用中包含高程的解算,需要提取地面回波的时间重心位置[26-27],本文的结论可以为分析波形时间重心的影响因素提供必要的参考。
| [1] | CHI Hong, SUN Guoqing, HUANG Jinliang, et al. National Forest Aboveground Biomass Mapping from ICESat/GLAS Data and MODIS Imagery in China[J]. Remote Sensing, 2015, 7(5): 5534–5564. |
| [2] | SCHUTZ B E, ZWALLY H J, SHUMAN C A, et al. Overview of the ICESat Mission[J]. Geophysical Research Letters, 2005, 32(21): L21S01. |
| [3] | MA Yue, WANG Mingwei, LI Guoyuan, et al. Waveform Model of a Laser Altimeter for an Elliptical Gaussian Beam[J]. Applied Optics, 2016, 55(8): 1957–1965. DOI:10.1364/AO.55.001957 |
| [4] | LEFSKY M A, COHEN W B, ACKER S A, et al. LiDAR Remote Sensing of the Canopy Structure and Biophysical Properties of Douglas-Fir Western Hemlock Forests[J]. Remote Sensing of Environment, 1999, 70(3): 339–361. DOI:10.1016/S0034-4257(99)00052-8 |
| [5] | NIE Sheng, WANG Cheng, ZENG Hongcheng, et al. A Revised Terrain Correction Method for Forest Canopy Height Estimation Using ICESat/GLAS Data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 108: 183–190. DOI:10.1016/j.isprsjprs.2015.07.008 |
| [6] | SUN G, RANSON K J. Modeling LiDAR Returns from Forest Canopies[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(6): 2617–2626. DOI:10.1109/36.885208 |
| [7] |
邢艳秋, 王立海.
基于ICESat-GLAS完整波形的坡地森林冠层高度反演研究——以吉林长白山林区为例[J]. 武汉大学学报(信息科学版), 2009, 34(6): 696–700.
XING Yanqiu, WANG Lihai. ICESat-GLAS Full Waveform-based Study on Forest Canopy Height Retrieval in Sloped Area:A Case Study of Forests in Changbai Mountains, Jilin[J]. Geomatics and Information Science of Wuhan University, 2009, 34(6): 696–700. |
| [8] |
曲苑婷, 汪垚, 刘观潮, 等.
基于GLAS激光雷达反演森林生物量[J]. 测绘通报, 2014(11): 73–77.
QU Yuanting, WANG Yao, LIU Guanchao. The Inversion of Forest Biomass Based on GLAS Laser Radar[J]. Bulletin of Surveying and Mapping, 2014(11): 73–77. DOI:10.13474/j.cnki.11-2246.2014.0367 |
| [9] | CHEN Qi. Retrieving Vegetation Height of Forests and Woodlands over Mountainous Areas in the Pacific Coast Region Using Satellite Laser Altimetry[J]. Remote Sensing of Environment, 2010, 114(7): 1610–1627. DOI:10.1016/j.rse.2010.02.016 |
| [10] | BYE I J, NORTH P R J, LOS S O, et al. Estimating Forest Canopy Parameters from Satellite Waveform LiDAR by Inversion of the FLIGHT Three-dimensional Radiative Transfer Model[J]. Remote Sensing of Environment, 2017, 188: 177–189. DOI:10.1016/j.rse.2016.10.048 |
| [11] | GARDNER C S. Ranging Performance of Satellite Laser Altimeters[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(5): 1061–1072. DOI:10.1109/36.175341 |
| [12] | GARDNER C S. Target Signatures for Laser Altimeters:An Analysis[J]. Applied Optics, 1982, 21(3): 448–453. DOI:10.1364/AO.21.000448 |
| [13] | DUONG V H, LINDENBERGH R, PFEIFER N, et al. Single and Two Epoch Analysis of ICESat Full Waveform Data over Forested Areas[J]. International Journal of Remote Sensing, 2008, 29(5): 1453–1473. DOI:10.1080/01431160701736372 |
| [14] | KIMES D S. Radiative Transfer in Homogeneous and Heterogeneous Vegetation Canopies[M]//MYNENI R B, ROSS J. Photon-Vegetation Interactions. Berlin: Springer, 1991: 339-388. |
| [15] | GASTELLU-ETCHEGORRY J P, ZAGOLSKI F, ROMIER J. A Simple Anisotropic Reflectance Model for Homogeneous Multilayer Canopies[J]. Remote Sensing of Environment, 1996, 57(1): 22–38. DOI:10.1016/0034-4257(95)00221-9 |
| [16] | GASTELLU-ETCHEGORRY J P, DEMAREZ V, PINEL V, et al. Modeling Radiative Transfer in Heterogeneous 3D Vegetation Canopies[C]//Proceedings of the SPIE Volume 2314, Multispectral and Microwave Sensing of Forestry, Hydrology, and Natural Resources, Satellite Remote Sensing. Rome, Italy: SPIE, 1995, 2314: 131-156. |
| [17] |
吴明钦, 孙玉军, 郭孝玉, 等.
长白落叶松树冠体积和表面积模型[J]. 东北林业大学学报, 2014, 42(5): 1–5.
WU Mingqin, SUN Yujun, GUO Xiaoyu, et al. Predictive Models of Crown Volume and Crown Surface Area for Korean Larch[J]. Journal of Northeast Forestry University, 2014, 42(5): 1–5. |
| [18] | LIU Luxia, PANG Yong, LI Zengyuan, et al. Retrieving Structural Parameters of Individual Tree Through Terrestrial Laser Scanning Data[J]. Journal of Remote Sensing, 2014, 18(2): 365–370. |
| [19] | LAUBHANN D, ECKMULLNER O, STERBA H. Applicability of Non-destructive Substitutes for Leaf Area in Different Stands of Norway Spruce (Picea abies L. Karst.) Focusing on Traditional Forest Crown Measures[J]. Forest Ecology and Management, 2010, 260(9): 1498–1506. DOI:10.1016/j.foreco.2010.07.048 |
| [20] | JACQUEMOUD S, BARET F. PROSPECT:A Model of Leaf Optical Properties Spectra[J]. Remote Sensing of Environment, 1990, 34(2): 75–91. DOI:10.1016/0034-4257(90)90100-Z |
| [21] | ALLEN W A, GAYLE T V, RICHARDSON A J. Plant-canopy Irradiance Specified by the Duntley Equations[J]. Journal of the Optical Society of America, 1970, 60(3): 372–376. DOI:10.1364/JOSA.60.000372 |
| [22] |
岳春宇, 邢坤, 鲍云飞, 等.
以交叉累积剩余熵为准则的星载激光测高仪大光斑波形数据与地形匹配法[J]. 测绘学报, 2017, 46(3): 346–352.
YUE Chunyu, XING Kun, BAO Yunfei, et al. A Matching Method of Space-borne Laser Altimeter Big Footprint Waveform and Terrain Based on Cross Cumulative Residual Entropy[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(3): 346–352. DOI:10.11947/j.AGCS.2017.20160255 |
| [23] | JACQUEMOUD S, BARET F, ANDRIEU B, et al. Extraction of Vegetation Biophysical Parameters by Inversion of the PROSPECT+SAIL Models on Sugar Beet Canopy Reflectance Data. Application to TM and AVIRIS Sensors[J]. Remote Sensing of Environment, 1995, 52(3): 163–172. DOI:10.1016/0034-4257(95)00018-V |
| [24] | MALTAMO M, PACKALÉN P, YU X, et al. Identifying and Quantifying Structural Characteristics of Heterogeneous Boreal Forests Using Laser Scanner Data[J]. Forest Ecology and Management, 2005, 216(1-3): 41–50. DOI:10.1016/j.foreco.2005.05.034 |
| [25] | HOLLAUS M, AUBRECHT C, HÖFLE B, et al. Roughness Mapping on Various Vertical Scales Based on Full-waveform Airborne Laser Scanning Data[J]. Remote Sensing, 2011, 3(3): 503–523. |
| [26] |
唐新明, 谢俊峰, 付兴科, 等.
资源三号02星激光测高仪在轨几何检校与试验验证[J]. 测绘学报, 2017, 46(6): 714–723.
TANG Xinming, XIE Junfeng, FU Xingke, et al. ZY3-02 Laser Altimeter On-orbit Geometrical Calibration and Test[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(6): 714–723. DOI:10.11947/j.AGCS.2017.20160597 |
| [27] |
唐新明, 李国元, 高小明, 等.
卫星激光测高严密几何模型构建及精度初步验证[J]. 测绘学报, 2016, 45(10): 1182–1191.
TANG Xinming, LI Guoyuan, GAO Xiaoming, et al. The Rigorous Geometric Model of Satellite Laser Altimeter and Preliminarily Accuracy Validation[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(10): 1182–1191. DOI:10.11947/j.AGCS.2016.20150357 |



