空间结构是高层次的地图综合知识,空间结构保持是制图综合和多尺度表达的基本要求之一[1-4]。空间分布模式作为一种典型的空间结构知识,反映了地理空间实体的分布规律和内在联系,体现了制图者对客观世界的认知水平。空间模式识别是挖掘地图数据中隐含的高层次空间信息和空间关系的基本工具,在制图综合、空间数据挖掘和空间数据匹配等研究中都有重要的应用[1, 5]。
道路以错综复杂的连接关系构成空间网络,在地图上呈现出特定的、有规律的分布模式,如Stroke、Grid、Star、Ring等[6-10]。近年来,关于道路网典型分布模式的识别逐渐成为研究的热点,已有研究多集中于局部的格网形[8-9, 11-13],少数学者从全局角度研究了环形[10]和放射形[9, 14]。
路网中的环以不同的尺度和层次存在,例如在宏观尺度有包含城市中心的大环路,中观尺度有环形的城市商业中心区,微观尺度有环形交叉口。文献[10]基于Tukey深度和几何矩等指标对道路网眼进行聚合及分组,从而提取包含城市中心的环形模式。由于不同尺度的环形模式在空间结构上的复杂程度不同,该策略对微观的环形交叉口并不适用。
目前,关于道路交叉口识别的方法大致可以分为两类:第一类首先建立典型道路交叉口的模板库,再通过图匹配方法[15]或比对方法[16]进行识别,此类方法对典型对象识别效果较好,但因实际道路网复杂多样,识别的结果会受到模板库描述类型的限制;第二类将道路交叉口识别看成一个分类问题,引入支持向量机[17]或卷积神经网络[18]等方法实现自动识别,识别效果依赖于训练样本。
环形交叉口识别的本质是中心圆环的识别。本文从微观尺度下的环形模式识别出发,将环形交叉口的结构描述为:从道路(线)的角度,环形交叉口由位于中心的圆环(环路)和与其相接的路段(支路)组成;从道路围成的网眼(面)的角度,环形交叉口由位于中心的圆形网眼(中心岛)和与其相接的网眼(分离岛)组成。文献[19]实现了基于面思想的环形交叉口识别,先利用道路网眼周长和圆形度参数筛选中心岛,再提取与其相接的分离岛,二者的组合即为环形交叉口。该方法原理简单,但识别结果存在明显的遗漏和错误,因而应用有限。
针对上述问题,本文采用环形交叉口的道路(线)描述方式,提出一种环形交叉口的几何识别方法:首先利用改进的霍夫变换识别矢量圆环,在此基础上通过均匀度优化和相似度优化识别环路,再根据其他道路与环路的连通性提取支路,最终实现环形交叉口的识别。
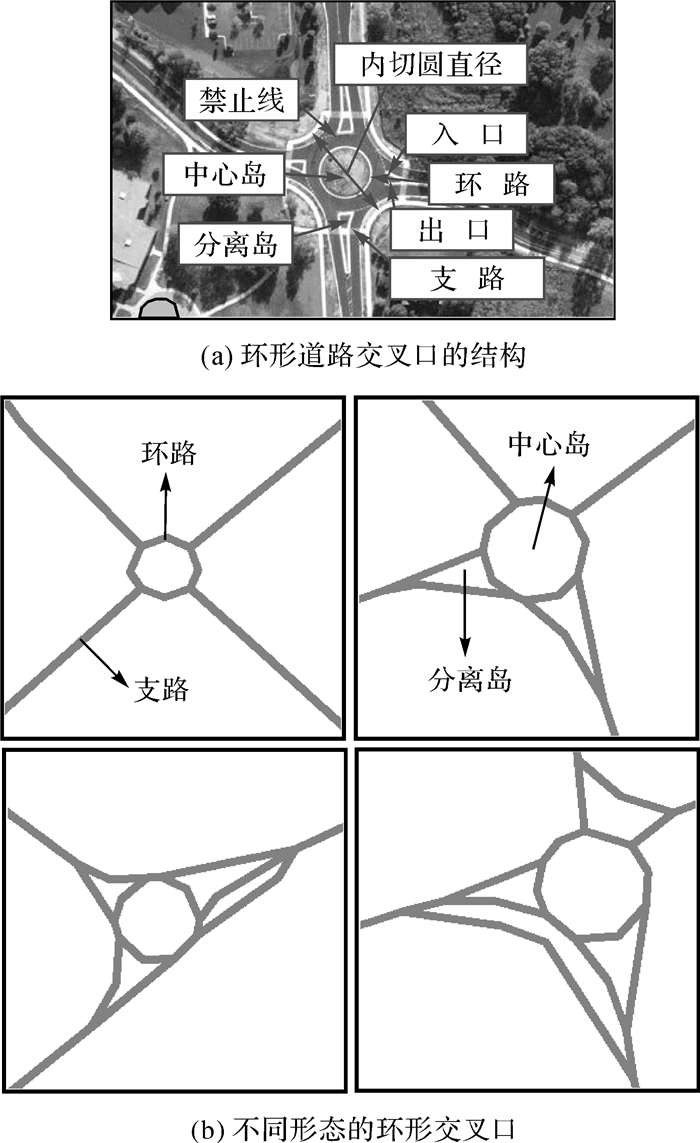
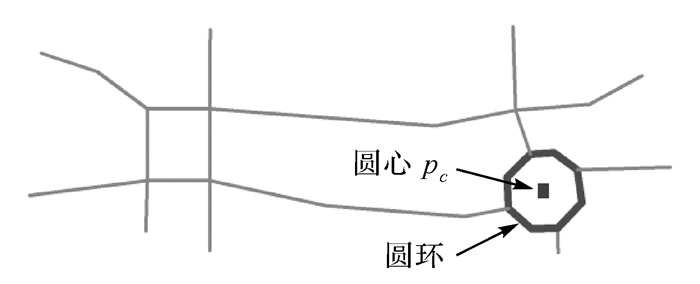
1 环形交叉口结构描述道路交叉口是指两条或两条以上道路的相交处。按照道路相交的几何形状,可将道路交叉口划分为十字形、T形、X形、Y形、多叉形、错位和环形交叉口[20]。其中,环形交叉口作为复杂的交叉口类型,是一种在道路交叉口中间设置中心岛,使车辆绕岛单向行驶的道路结构,其主要部件及名称如图 1(a)所示。
|
| 图 1 环形交叉口 Fig. 1 Examples of roundabouts |
现实中的道路环形交叉口形态繁多、表现形式多样(图 1(b))。可以看出,无论采取哪种描述方式,位于中心的圆环都是环形交叉口的主要特征,其识别问题都是环形交叉口识别的重点。本文基于道路(线)的描述方式,将环形交叉口识别分解为环路识别和支路识别。
2 矢量圆环识别方法矢量圆环识别是环路识别的基础。受霍夫变换检测栅格圆环方法的启发,本文提出一种基于改进霍夫变换的矢量圆环识别方法。
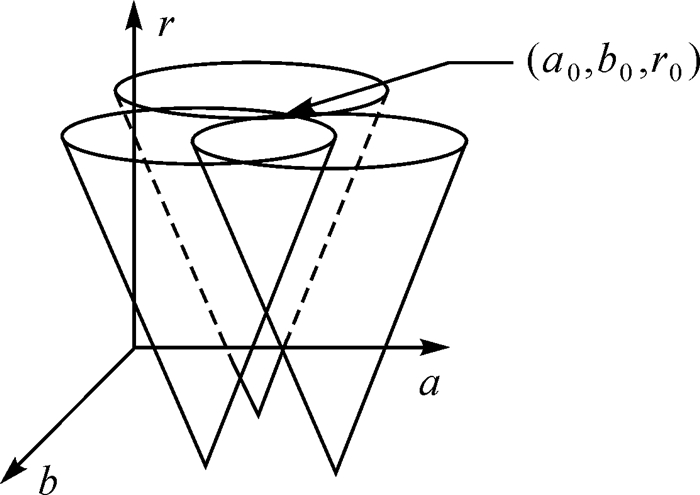
2.1 霍夫变换检测圆的基本思路传统霍夫变换主要针对栅格数据,其本质是对像素位置的计算,即将每个像素点从图形空间转换到参数空间。对单个像素点(a, b)而言,以(a, b, r)为参数的方程(x-a)2+(y-b)2=r2,在参数空间表示的是一个圆锥,那么所有像素点在参数空间上表现为一组圆锥面簇[21-22]。在理想情况下,圆形边界上的像素点在参数空间内对应的圆锥面簇的交点会重合为一点,即为图形空间中的待识别圆形参数(a0, b0, r0)(如图 2所示)。但在实际中会出现待检测圆形状不规则的情况,圆锥面簇的交点不完全重合,此时采用计数法,计算每个交点的重复次数,次数最高的点即为所求点。
|
| 图 2 霍夫变换检测圆的原理 Fig. 2 Principle of detecting circle with Hough transform |
若将霍夫变换用于检测矢量圆环,最直接的方法是将数据栅格化,再求解圆心和半径。但这样不仅会大大增加计算量、丢失道路拓扑信息,还会加剧数据离散程度,导致矢量数据的优势完全丧失,不利于参数空间中的交点定位。与传统栅格化方法相比,线性剖分模型[23-24](linear tessellation model,LTM)能够保持道路网的拓扑结构,准确表达道路网的度量信息。因此先采用线性剖分模型对矢量道路网进行栅格化,再利用圆的几何特征改进现有的霍夫变换实现圆心及圆环的识别。
2.2 道路线性剖分LTM是考虑线性参考特性下进行的一维空间的离散化。采用LTM对道路网数据进行剖分,涉及以下3个概念[23]。
(1) 道路路段:道路数据由一系列节点顺序连接而成,道路路段指相邻节点间的线段。
(2) 路段栅格(linear pixel):对道路路段加密剖分,得到一系列线性细分单元,记为Lixel。
(3) 路段栅格节点(Lxnode):邻接的路段栅格的交点以及路段栅格的端点。
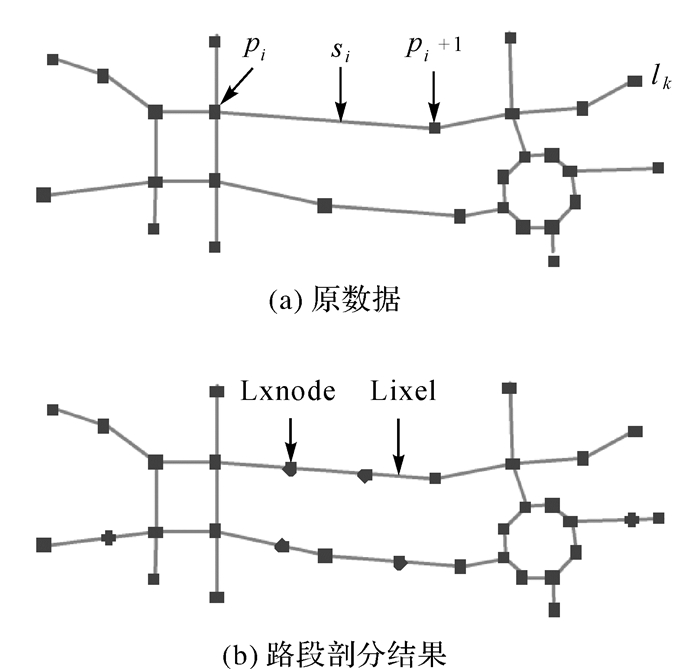
栅格尺寸大小参考文献[12, 24—25]的方法设置为道路路段的平均长度。设组成道路网的线集合为L={l1, l2, …, lk},道路线l={p1, p2, …, pn},路段si=(pi, pi+1),平均路段长度s。剖分方法为:长度大于s的路段以s剖分,长度小于等于s的路段保持不变。因此,剖分后的路段栅格的长度不会完全相等。图 3为路段剖分示意图。
|
| 图 3 路段剖分示意图 Fig. 3 Schematic diagram of road tessellation |
可以看出,Lixel与Lxnode(图 3(b))继承了道路网数据的几何信息和拓扑关系,能够保持道路网原有的形态和分布模式。其中,Lixel是道路网表达的最小划分,将代替栅格数据中的Pixel,作为后续圆环识别的基本单元。
2.3 矢量圆环识别理论上,矢量圆环上任意路段栅格的法向量都指向圆心,本文根据这一性质识别圆心及圆环。
(1) 法向变换。设路段栅格Lixel的端点为pf和pt,中点为pm。以pm为端点,在路段栅格的两侧分别构建长度为d的垂线段VL1=(pv1, pm)和VL2=(pm, pv2)。以VL1的端点pv1为例,该点满足方程
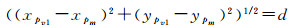 (1)
(1)
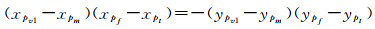 (2)
(2)
式中,端点pv2与pv1关于Lixel对称。将上述由路段栅格描述的道路网转换为对应的中垂线段的过程称为法向变换(normal transform),在法向变换中构建的Lixel的中垂线段NE=(pv1, pv2)称为法向基元(normal element,NE)。
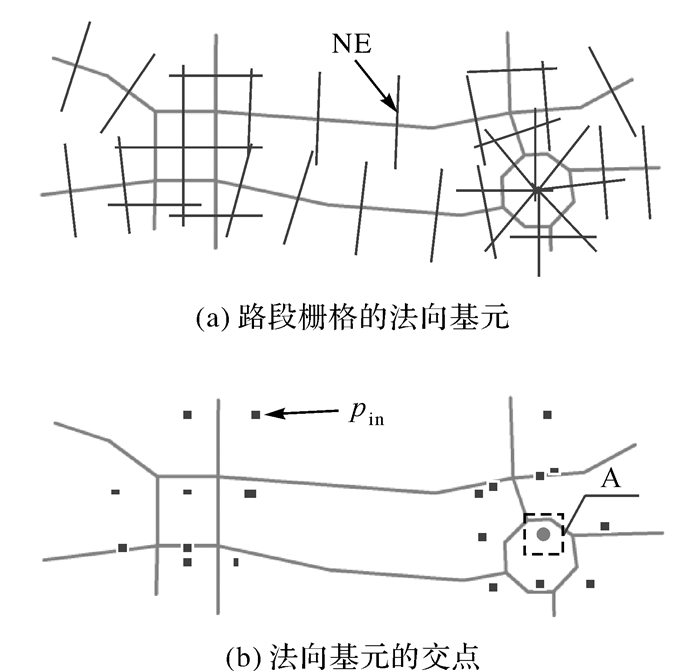
路段栅格经过法向变换得到一系列法向基元(图 4(a))。其中d的取值应大于图中闭合圆环的最小外接矩形的长轴长a的一半,即
|
| 图 4 法向基元交点示意图 Fig. 4 The normal elements and their intersections |
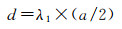 (3)
(3)
式中,λ1为比例系数。要使法向基元能够相交,λ1应大于1;但λ1过大时会产生冗余交点,干扰圆心提取且增大计算量。因此,本文取λ1=1.10。
(2) 圆心及圆环识别。由圆的几何特征可知,待识别圆心位于法向基元上。在理想情况下,法向基元的交点pin会重合于一点,该点即为圆心。但在实际中,矢量圆环可能出现变形,法向基元的交点不会完全重合(如图 4(b)中方框A处)。因此,由交点计数来确定圆心的方法不再适用。但可以确定交点越密集的地方,产生圆心的概率越大,据此采用聚类方法探测交点群中可能会构成圆心的类簇。
探测交点群中的类簇需要注意两点,一是事先无法确定待识别数据中的圆环个数,即类簇数无法预先指定;二是类簇的形状可能是任意的。基于密度聚类的DBSCAN算法能够克服这两点困难,可用于交点群聚类。聚类参数包括搜索半径Eps和最小点数MinPts,设置方法如下。
Eps与圆环直径有关,计算公式为
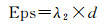 (4)
(4)
式中,λ2(λ2 < 1)为比例系数。λ2越小,Eps越小,类簇的聚集特征越明显。经多次试验分析,当λ2=1/5时,聚类结果较为合理。从构成多边形的边数分析,N边形的法向基元交点个数不超过N(N-1)/2。通常情况下,多边形至少有两组互不平行的边(N=4),才可能被看作一个圆环,即MinPts应大于等于6。但MinPts值不宜过大,否则大部分点将被视为噪声。因此,这里设定MinPts=6。
类簇个数即为可能的圆心个数,类簇包含的交点的坐标平均值即为圆心pc。逆向倒推,每一个圆心都对应一个交点集合,也对应一个路段栅格集合,路段栅格集合所对应的路段集合构成的图形即为目标圆环。图 5表示识别出的圆心及圆环。
|
| 图 5 矢量圆环识别结果 Fig. 5 The recognized ring in vector data |
3 环形交叉口识别方法
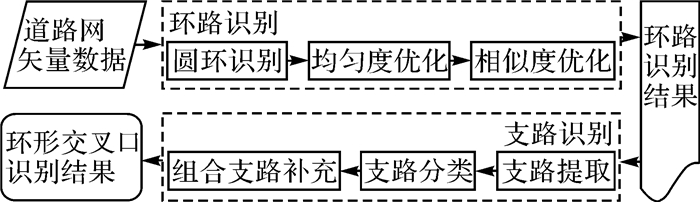
本文将环形交叉口的识别问题分解为环路识别和支路识别两部分,方法流程如图 6所示。
|
| 图 6 环形交叉口识别方法流程 Fig. 6 The recognition method of roundabouts |
3.1 环路识别
人类在进行地图模式识别时,能够排除干扰信息,从杂乱的数据中快速提取“好的”图形,而且对图形的认知具有一定的模糊处理能力。利用计算机进行识别则需要度量图形特征,通过阈值设定筛选出想要的图形。根据格式塔视知觉原理中的闭合原则和简单图形原则,本文通过圆环识别、均匀度优化及相似度优化3个关键步骤实现环路识别。
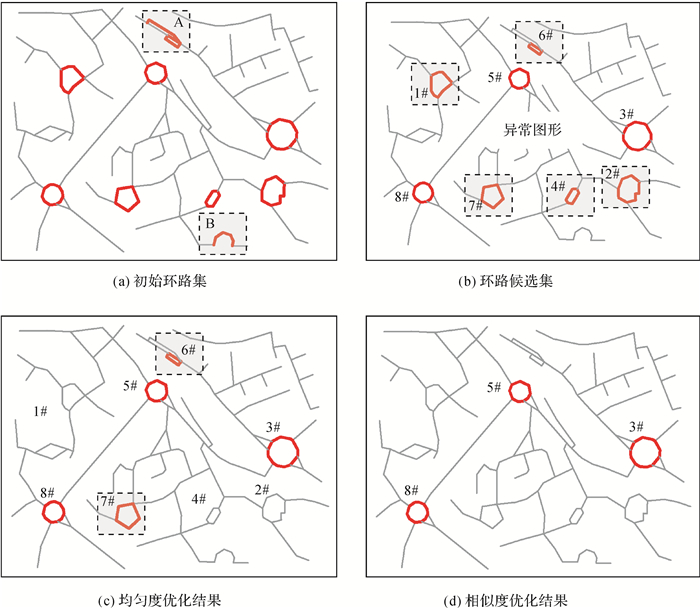
(1) 圆环识别。利用上节所述方法识别道路网中的圆环,得到图 7(a)所示的初始环路集。循环去除环路内的悬空路段(例如方框A及B处),得到图 7(b)所示的环路候选集。
|
| 图 7 环路识别结果 Fig. 7 Recognition results of circulating roads |
由于道路空间结构的多样性,环路候选集中可能存在各种非圆环图形(如图 7(b)中1#、2#、4#、6#、7#等)。为此,本文根据圆环的几何特征设计度量指标对候选环路进行优化。这里给出4个相关概念:
实际环路:圆心pc对应的所有非悬挂路段栅格构成的图形。周长La为路段栅格长度的总和。
实际半径(Ra):圆心pc到实际环路上的路段栅格节点的距离。
模拟半径(Rc):一个实际环路内所有实际半径的长度平均值。
模拟环路:以圆心pc及模拟半径Rc为参数构成的圆环。周长Lc=2πRc。
(2) 均匀度优化。从数据的统计特征分析,一个实际环路对应的所有实际半径Ra的长度值应服从期望为Rc的正态分布。因此,可利用Ra的数值分布特征度量实际环路的形态。Ra的方差越小,分布越均匀,实际环路越接近规则圆环。这里采用实际半径的变异系数(coefficient of variation,CV)
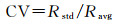 (5)
(5)
度量实际环路的半径均匀性。其中,Ravg和Rstd为一个实际环路中Ra的均值和标准差。在数理统计分析中,当变异系数大于0.15时,则认为该组数据可能不正常。本文也采用这一标准,当Ra的变异系数CV大于0.15时,认为该实际环路变异程度过高,不满足人类对圆环的空间认知,应从环路候选集中剔除。
图 7(c)为均匀度优化结果。1#、2#、4#方框内的变异系数均大于0.15,因此被剔除。但结果中仍然存在“劣质”环路(如6#、7#),因此需对环路的识别结果再次优化。
(3) 相似度优化。从人类对图形构造的空间认知和视知觉感受分析,实际环路与对应的模拟环路越接近,被人类视觉感知为环形交叉口的可能性越大。为此定义周长相似度(similarity of parameter,SP)
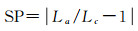 (6)
(6)
来度量实际环路与模拟环路的接近程度。SP的值域是[0, +∞),值越小,环路形状越标准。相似度优化阈值为σ,SP>σ的图形被剔除。经试验分析可知:σ较大时,相似度优化程度低,被保留的环路较多,但可能存在错误识别;随着σ的减小,周长相似度优化限制增强,识别出的环路更接近圆的本质特征,但正确识别的个数也会减少。σ具体设置方法在下文进行讨论。图 7(e)为相似度优化结果。
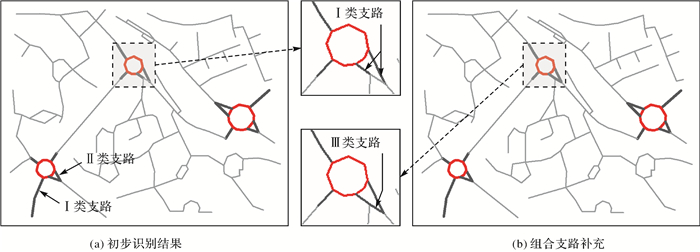
3.2 支路识别支路是环形交叉口的附属结构。参考图 1(b)可发现,环形交叉口的复杂程度在很大程度上是由支路的空间结构决定的。根据支路与中心环路的空间关系,可分为以下3类。
Ⅰ类支路:直接与环路相接,且与其他支路相离。
Ⅱ类支路:直接与环路相接,且只与Ⅰ类支路相接。
Ⅲ类支路:不与环路相接,但两端与Ⅰ类或Ⅱ类支路相接。
其中,Ⅰ类是简单支路,Ⅱ类和Ⅲ类为组合支路。支路的识别主要是对以上3类支路的识别,在环路识别的基础上,通过连通性判别提取环形交叉口的支路(图 8),识别策略如下:
|
| 图 8 支路识别结果 Fig. 8 Recognition results of branches |
(1) 提取与环路直接相连的道路,标记为支路。
(2) 判断每组支路之间的连接性:若相离,则标记为Ⅰ类支路;若与其他支路相接,则标记为Ⅱ类支路(图 8(a))。
(3) 判断其余非环路且非支路类型的道路与Ⅰ类支路的连接度(连接的道路数),将连接度大于等于2的道路标记为Ⅲ类支路(图 8(b))。
3.3 参数设置在上述环形交叉口识别中需要输入两个参数:一是该区域最大环路直径a,可通过查阅区域道路交通资料和数据预览测定两种方式获取;二是周长相似度阈值σ,该值与人类对圆环的空间认知有关,体现了人类对圆环形态变异的接受程度。在实际应用中,可通过大量试验统计的方法确定σ。本文分别从Ordnance Survey和OpenStreetMap开放数据中截取多组道路网数据,统计σ在不同取值下的环路识别结果。召回率R等于算法正确识别个数除以人工判别个数,反映算法对环形交叉口的识别效果;准确率P等于算法正确识别个数除以算法识别总数,表征算法对非环形交叉口的区分效果;F1测度值是召回率和准确率在权重相等时的调和平均值,用于度量某阈值下算法的综合识别效果
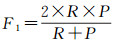 (7)
(7)
限于篇幅,这里直接给出上述统计指标的均值(表 1)。从表 1中可以看出,σ=0.08时,F1最大,即识别效果最优,因此设定σ=0.08。
| σ | 召回率均值/(%) | 准确率均值/(%) | F1测度均值 |
| 0.10 | 100.00 | 97.99 | 0.989 4 |
| 0.09 | 100.00 | 97.99 | 0.989 4 |
| 0.08 | 100.00 | 98.68 | 0.993 2 |
| 0.07 | 98.61 | 99.46 | 0.989 9 |
| 0.06 | 96.26 | 100.00 | 0.980 1 |
| 0.05 | 86.82 | 100.00 | 0.926 3 |
| 0.04 | 72.85 | 100.00 | 0.830 8 |
| 0.03 | 48.93 | 100.00 | 0.624 8 |
| 0.02 | 25.63 | 100.00 | 0.544 1 |
| 0.01 | 1.56 | 100.00 | 0.222 2 |
4 试验与分析
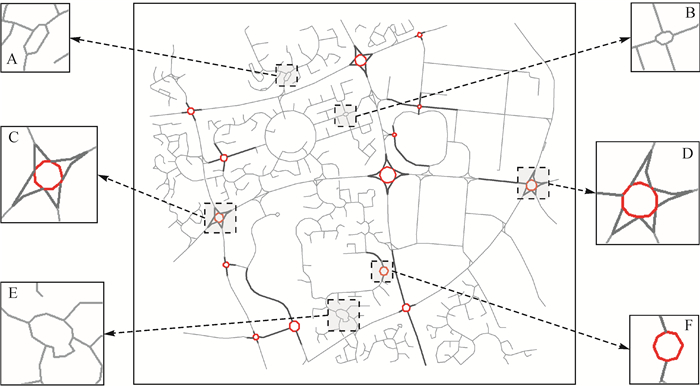
从OpenStreetMap开放数据中截取英国某区域道路网数据进行试验(图 9)。试验区数据包含715条道路,路段平均长度为44.34 m。经数据预览测定a=102.00 m,根据式(3)和式(4)分别计算d=56.10 m,Eps=11.22 m。经人工判别,该区域一共有17个中心带有闭合环路的交叉口。
|
| 图 9 本文方法的试验结果 Fig. 9 Test results of the proposed method |
4.1 试验结果
法向基元的交点聚类结果中包含34个类簇,即初始识别结果中共有34组图形。循环去除非闭合路段,得到21组候选环路,参数计算结果见表 2。然后通过均匀度优化和相似度优化剔除异常图形,剩余14个环路。最后对支路结构进行识别,得到14个环形交叉口。如图 9所示,红色道路表示环路,黑色道路表示支路。
| 序号 | Raver | Rstd | CV | La | Lc | SP |
| 5 | 12.479 | 3.086 | 0.247 | 75.187 | 78.410 | 0.041 |
| 8 | 14.194 | 2.441 | 0.172 | 88.256 | 89.181 | 0.010 |
| 10 | 23.742 | 5.412 | 0.228 | 113.117 | 149.174 | 0.242 |
| 19 | 38.597 | 8.632 | 0.224 | 272.931 | 242.509 | 0.125 |
| 1 | 33.428 | 0.813 | 0.024 | 207.533 | 210.034 | 0.012 |
| 14 | 50.801 | 0.380 | 0.008 | 315.359 | 319.202 | 0.012 |
| 7 | 35.472 | 0.365 | 0.010 | 219.574 | 222.878 | 0.015 |
| 15 | 28.839 | 0.516 | 0.018 | 177.854 | 181.200 | 0.019 |
| 20 | 17.871 | 0.376 | 0.021 | 109.676 | 112.278 | 0.023 |
| 17 | 27.142 | 0.300 | 0.011 | 166.091 | 170.538 | 0.026 |
| 12 | 22.090 | 0.332 | 0.015 | 135.133 | 138.794 | 0.026 |
| 11 | 20.987 | 0.064 | 0.003 | 128.358 | 131.864 | 0.027 |
| 6 | 24.703 | 0.205 | 0.008 | 150.869 | 155.213 | 0.028 |
| 18 | 33.403 | 0.422 | 0.013 | 203.762 | 209.879 | 0.029 |
| 21 | 18.190 | 0.259 | 0.014 | 110.356 | 114.293 | 0.034 |
| 4 | 12.267 | 1.063 | 0.087 | 74.228 | 77.073 | 0.037 |
| 2 | 14.844 | 0.620 | 0.042 | 89.078 | 93.268 | 0.045 |
| 3 | 12.210 | 0.129 | 0.011 | 72.428 | 76.715 | 0.056 |
| 16 | 13.418 | 0.737 | 0.055 | 76.633 | 84.306 | 0.091 |
| 9 | 37.182 | 1.004 | 0.027 | 210.973 | 233.623 | 0.097 |
| 13 | 19.960 | 1.678 | 0.084 | 99.591 | 125.415 | 0.206 |
与人工判别结果相比,本文方法正确识别14个环形交叉口,遗漏3个环形交叉口。主要原因在于有3处环路未能识别(图 9):①A处环路由于法向基元的交点分布不集中,未能加入到环路候选集中;②B处环路由于变异系数偏大(CV=0.172>0.15)被剔除;③E处环路的变异系数(CV=0.224)和周长相似比(SP=0.125)均在阈值范围之外。另外,简单支路(F处)、Y形支路(C处)、混合型支路(D处)等多样化的环形交叉口都得到了正确识别。
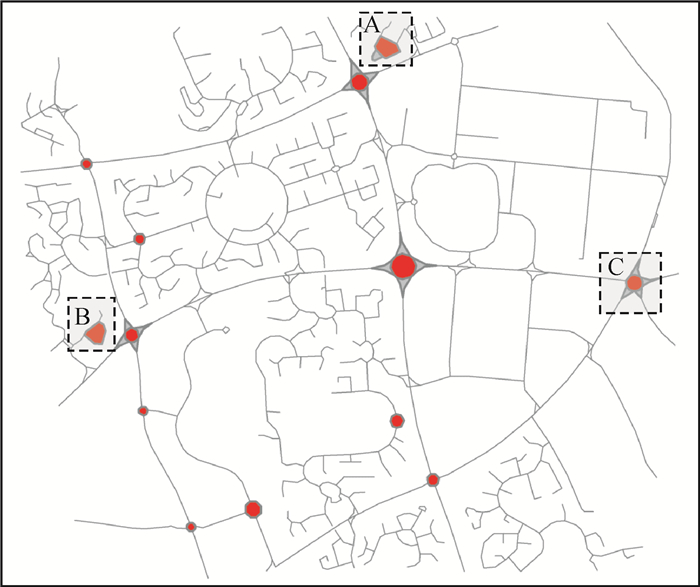
4.2 试验对比以文献[20]作为参考进行了对比试验。识别结果如图 10所示,红色区域为中心岛,灰色区域为分离岛。该方法提取出13个中心岛,其中A、B两处为错误提取,即正确识别11个中心岛;共提取出4个环形交叉口,其中C处丢失简单支路,即正确识别3个环形交叉口。
|
| 图 10 对比方法的试验结果 Fig. 10 Test results of contrast method |
为更加客观地评价两种方法的识别效果,表 3给出了识别结果的定量分析指标值。从表 3可以看出:①在输入参数个数相同的情况下,本文方法识别效果明显优于对比方法:环路的召回率和准确率分别提高了17.64%和15.38%;环形交叉口的召回率和准确率分别提高了64.70%和25.00%。这是由于本文方法能够合理地描述环路特征且对复杂支路结构不敏感。②在正确识别环路的基础上,本文方法可以完全识别出环形交叉口(14/14=100.00%),而对比方法有可能无法识别出环形交叉口的支路,因此无法识别出环形交叉口这一完整的空间结构(3/11=27.27%)。而空间结构的完整性对于多层次地图综合是极其重要的。
| 方法 | 环路/中心岛识别结果 | 环形交叉口识别结果 | |||||||
| 算法识别总数 | 算法正确识别数 | 召回率 /(%) |
准确率 /(%) |
算法识别总数 | 算法正确识别数 | 召回率 /(%) |
准确率 /(%) |
||
| 本文方法 | 14 | 14 | 82.35 | 100.00 | 14 | 14 | 82.35 | 100.00 | |
| 对比方法 | 13 | 11 | 64.71 | 84.62 | 4 | 3 | 17.65 | 75.00 | |
4.3 讨论
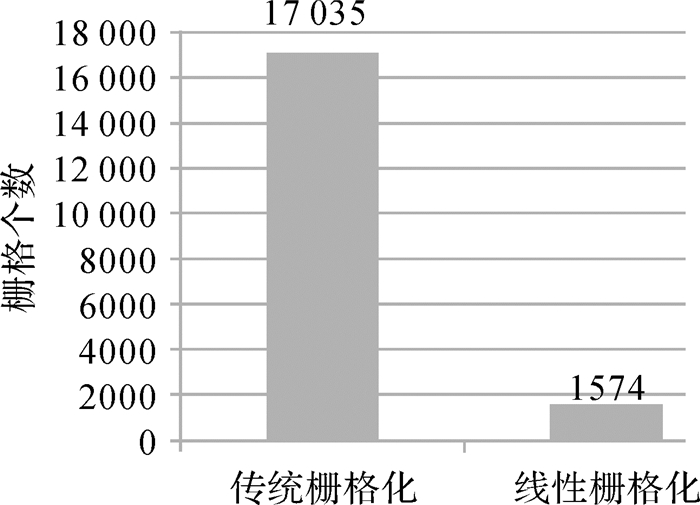
(1) 栅格化对比分析。本文在2.1节中提到,应用霍夫变换识别环形模式的最直接的方法是,按照传统栅格化方法对道路网进行预处理,然后再根据参数方程求解圆心和半径。在设置栅格(像素)尺寸时主要依据路段长度的统计值(平均值、最大值和最小值等)。使用平均值和最大值对道路网进行栅格化会导致大量细节信息的丢失,因此本文采用路段长度最小值作为像素的尺寸。经统计,试验区的路段长度最小值为4.34 m,两种栅格化方法的结果如图 11所示。可以看出,两种方法得到的元素个数大约相差10倍。
|
| 图 11 两种栅格化方法对比 Fig. 11 Contrast of rasterization method |
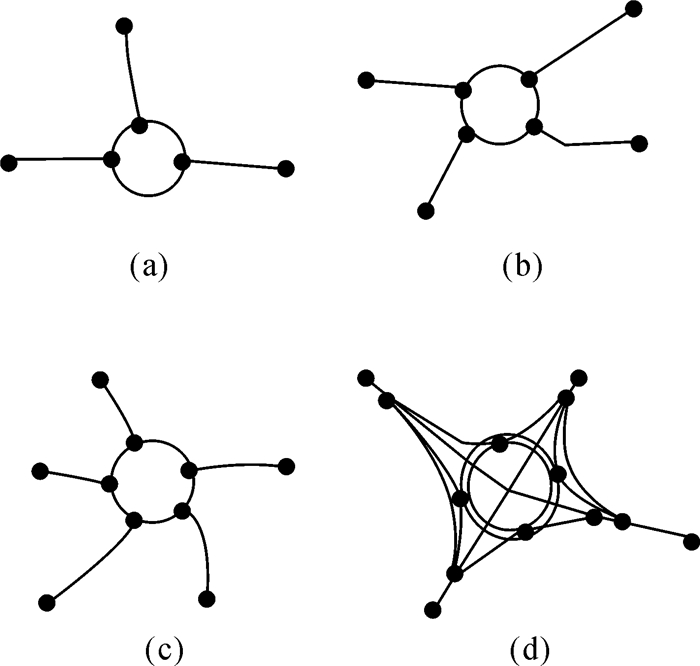
(2) 识别类型对比分析。基于结构描述建立模板库的识别方法存在结构描述不清(对于某一种类型的道路交叉口,可能无法精确描述其空间结构)和结构描述不全(对于现实中的道路交叉口,模板库可能无法包括所有类型)等问题。例如在文献[16]中,环形交叉口的模板有以下4种(图 12),那么该方法识别的环形交叉口就会限制在这4种类型内。实际上,环形交叉口的种类远远多于模板库中所描述的类型。本文方法不受样本类型的限制,可以识别出二支、三支及多支环形交叉口,支路的形式有简单支路、Y形支路及混合型支路。此外,本文方法的识别结果可作为文献[16, 20]等方法的典型案例,丰富其样本库类型。
|
| 图 12 模板库中的环形交叉口 Fig. 12 The roundabout examples in template library |
5 结论
矢量空间数据的分布模式识别是地图综合自动化的关键之一。本文针对道路网中的微观环形模式—环形交叉口识别中存在的问题,提出了一种基于改进霍夫变换的几何识别方法。试验表明:①该方法有效提高了环形交叉口识别的召回率和准确率;②识别的环形交叉口结构更加完整,能够为电子导航、道路网多尺度表达和道路网匹配等研究提供依据。但是,本文方法对于圆形特征不明显的环路(如图 9中的A、B等)还存在漏识别的现象,这是未来研究中需要解决的重点。
| [1] | MACKANESS W, EDWARDS G. The Importance of Modeling Pattern and Structure in Automated Map Generalization[C]//Proceedings of the Joint ISPRS/ICA Workshop on Multi-scale Representations of Spatial Data. Ottawa: [s.n.], 2002. |
| [2] |
王家耀.
地图制图学与地理信息工程学科进展与成就[M]. 北京: 测绘出版社, 2011: 91-120.
WANG Jiayao. Advances in Cartography and Geographic Information Engineering[M]. Beijing: Surveying and Mapping Press, 2011: 91-120. |
| [3] |
武芳, 钱海忠, 邓红艳, 等.
面向地图自动综合的空间信息智能处理[M]. 北京: 科学出版社, 2008: 298-305.
WU Fang, QIAN Haizhong, DENG Hongyan, et al. Intelligent Processing of Spatial Information for Automated Map Generalization[M]. Beijing: Science Press, 2008: 298-305. |
| [4] | GONG Xianyong, WU Fang. A Typification Method for Linear Pattern in Urban Building Generalisation[J]. Geocarto International, 2018, 33(2): 189–207. DOI:10.1080/10106049.2016.1240718 |
| [5] |
武芳, 巩现勇, 杜佳威.
地图制图综合回顾与前望[J]. 测绘学报, 2017, 46(10): 1645–1664.
WU Fang, GONG Xianyong, DU Jiawei. Overview of the Research Progress in Automated Map Generalization[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1645–1664. DOI:10.11947/j.AGCS.2017.20170287 |
| [6] | ZHANG Qingnian. Modeling Structure and Patterns in Road Network Generalization[C]//Proceedings of ICA Workshop on Generalisation and Multiple Representation. Leicester: [s.n.], 2004. |
| [7] | HEINZLE F, ANDERS K H. Characterising Space via Pattern Recognition Techniques: Identifying Patterns in Road Networks[C]//Generalisation of Geographic Information: Cartographic Modelling and Applications.[S.l.]: Elsevier Ltd, 2007: 233-253. |
| [8] | YANG Bisheng, LUAN Xuechen, LI Qingquan. An Adaptive Method for Identifying the Spatial Patterns in Road Networks[J]. Computers, Environment and Urban Systems, 2010, 34(1): 40–48. DOI:10.1016/j.compenvurbsys.2009.10.002 |
| [9] | HEINZLE F, ANDERS K H, SESTER M. Graph Based Approaches for Recognition of Patterns and Implicit Information in Road Networks[C]//Proceedings of the 22nd International Cartographic Conference. La Coruna: [s.n.], 2005: 9-16. |
| [10] | HEINZLE F, ANDERS K H, SESTER M. Pattern Recognition in Road Networks on the Example of Circular Road Detection[C]//Proceedings of the 4th Geographic Information Science. Münster: Springer, 2006: 153-167. |
| [11] | TIAN Jing, SONG Zihan, GAO Fei, et al. Grid Pattern Recognition in Road Networks Using the C4.5 Algorithm[J]. Cartography and Geographic Information Science, 2016, 43(3): 266–282. DOI:10.1080/15230406.2015.1062425 |
| [12] | HE Yakun, AI Tinghua, YU Wenhao, et al. A Linear Tessellation Model to Identify Spatial Pattern in Urban Street Networks[J]. International Journal of Geographical Information Science, 2017, 31(8): 1541–1561. DOI:10.1080/13658816.2017.1298768 |
| [13] |
巩现勇, 武芳, 焦洋洋, 等.
基于关联规则分类的道路网网格模式识别[J]. 测绘科学技术学报, 2013, 30(6): 633–637.
GONG Xianyong, WU Fang, JIAO Yangyang, et al. The Association Rule Based Classification Approach to Grid Pattern Recognition in Road Networks[J]. Journal of Geomatics Science and Technology, 2013, 30(6): 633–637. DOI:10.3969/j.issn.1673-6338.2013.06.020 |
| [14] |
田晶, 张泊宇, 吴荡.
一种矢量道路网辐射模式识别新方法[J]. 武汉大学学报(信息科学版), 2013, 38(18): 1234–1238.
TIAN Jing, ZHANG Boyu, WU Dang. A New Method for Identifying Radial Pattern in Vector Road Networks[J]. Geomatics and Information Science of Wuhan University, 2013, 38(18): 1234–1238. |
| [15] |
徐柱, 蒙艳姿, 李志林, 等.
基于有向属性关系图的典型道路交叉口结构识别方法[J]. 测绘学报, 2011, 40(1): 125–131.
XU Zhu, MENG Yanzi, LI Zhilin, et al. Recognition of Structures of Typical Road Junctions Based on Directed Attributed Relational Graph[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 125–131. |
| [16] |
王骁, 钱海忠, 丁雅莉, 等.
采用拓扑关系与道路分类的立交桥整体识别方法[J]. 测绘科学技术学报, 2013, 30(3): 324–328.
WANG Xiao, QIAN Haizhong, DING Yali, et al. The Integral Identification Method of Cloverleaf Junction Based on Topology and Road Classification[J]. Journal of Geomatics Science and Technology, 2013, 30(3): 324–328. DOI:10.3969/j.issn.1673-6338.2013.03.023 |
| [17] |
马超, 孙群, 陈换新, 等.
利用路段分类识别复杂道路交叉口[J]. 武汉大学学报(信息科学版), 2016, 41(9): 1232–1237.
MA Chao, SUN Qun, CHEN Huanxin, et al. Recognition of Road Junctions Based on Road Classification Method[J]. Geomatics and Information Science of Wuhan University, 2016, 41(9): 1232–1237. DOI:10.13203/j.whugis20160073 |
| [18] |
何海威, 钱海忠, 谢丽敏, 等.
立交桥识别的CNN卷积神经网络法[J]. 测绘学报, 2018, 47(3): 385–395.
HE Haiwei, QIAN Haizhong, XIE Limin, et al. Interchange Recognition Method Based on CNN[J]. Acta Geodaetica et Cartographica Sinica, 2018, 47(3): 385–395. DOI:10.11947/j.AGCS.2018.20170265 |
| [19] | SAVINO S, RUMOR M, ZANON M, et al. Data Enrichment for Road Generalization Through Analysis of Morphology in the Cargen Project[C]//Proceedings of the 13th ICA Workshop on Generalisation and Multiple Representation. Zurich: [s.n.], 2010. |
| [20] |
中华人民共和国住房和城乡建设部. CJJ 152-2010城市道路交叉口设计规程[S].北京: 中国建筑工业出版社, 2010. Ministry of Housing and Urban-Rural Development of the People's Republic of China. CJJ 152-2010 Specification for Design of Intersections on Urban Roads[S]. Beijing: China Architecture and Building Press, 2010. |
| [21] | HOUGH V, PAUL C. Method and Means for Recognizing Complex Patterns: US, 3069654[P]. 1962-12-18. |
| [22] | DUDA R O, HART P E. Use of the Hough Transformation to Detect Lines and Curves in Pictures[J]. Communications of the ACM, 1972, 15(1): 11–15. |
| [23] | XIE Zhixiao, YAN Jun. Kernel Density Estimation of Traffic Accidents in a Network Space[J]. Computers, Environment and Urban Systems, 2008, 32(5): 396–406. DOI:10.1016/j.compenvurbsys.2008.05.001 |
| [24] | AI Tinghua, YU Wenhao, HE Yakun. Generation of Constrained Network Voronoi Diagram Using Linear Tessellation and Expansion Method[J]. Computers, Environment and Urban Systems, 2015(51): 83–96. |
| [25] | SHE Bing, ZHU Xinyan, YE Xinyue, et al. Weighted Network Voronoi Diagrams for Local Spatial Analysis[J]. Computers, Environment and Urban Systems, 2015(52): 70–80. |



