2. 中国科学院大学, 北京 100049;
3. 江苏省地理信息资源开发与利用协同创新中心, 江苏 南京 210023
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023, China
移动通信技术不断发展、定位技术不断进步、移动终端迅速普及,使得实时获取海量、真实的移动对象轨迹数据成为现实,为探索精细时空尺度下人类出行的时空行为模式提供了数据支撑[1-2]。挖掘历史轨迹蕴含的时空模式规律,预测移动对象未来某时刻位置,为城市动力学与群体行为模式分析等研究提供技术支持,也为城市规划与管理、智能交通、公共安全、应急疏散、基于位置的信息服务、个性化商业广告投放等应用提供决策依据。
移动对象轨迹预测根据活动空间可分为路网空间轨迹预测[3]、自由空间轨迹预测[4-5],也可根据预测周期分为短时轨迹预测(如预测移动对象下一时刻所在位置)[5-6]、长时轨迹预测(如预测移动对象下一次旅游城市等)[7-8]。由于移动对象在自由空间下移动行为无路网限制,且轨迹数据的采样间隔较为稀疏,难以准确捕获移动对象运动方向、转向位置等运动特征;同时大规模、长时间、细粒度的自由空间移动对象轨迹数据获取成本较高,使得自由空间下短时稀疏轨迹预测成为轨迹数据挖掘领域研究难点与重点。目前已有研究可分为基于目标移动状态推导方法[6, 9-11],基于频繁模式挖掘方法[12-14]和基于机器学习模型方法[4-5, 8, 15-18]。目标移动状态推导轨迹预测主要依据移动对象位置、速度、移动方向、环境状况等信息建立运动模型,模拟移动对象运动轨迹。如文献[6, 9]提出基于高斯混合模型的轨迹预测方法,通过将轨迹划分为不同高斯过程分量实现位置预测;文献[10]利用卡尔曼滤波对移动轨迹进行平滑和拟合实现位置预测等。频繁模式挖掘轨迹预测主要通过挖掘移动对象历史轨迹,构建模式树和判别函数,通过寻找相似的频繁模式实现轨迹预测,如文献[12]综合考虑移动对象移动时空信息构建T-pattern树,挖掘移动对象运动规律;文献[13]引入停留点语义生成决策树,并设计基于时空语义信息的轨迹相似度计算方法预测移动对象轨迹等。机器学习模型轨迹预测主要对马尔科夫模型[4-5, 15-16, 19]、概率图模型[17]、支持向量机模型[8]、神经网络模型[18]等机器学习模型进行改进,挖掘移动对象历史轨迹中移动对象行为特征,实现移动对象轨迹预测。如文献[5]在隐马尔科夫模型基础上提出自适应参数选择算法,提升轨迹预测在大数据环境下的适应性;文献[20]融合贝叶斯推理与马尔科夫模型,解决轨迹预测中马尔科夫模型冷启动问题等。
虽然国内外研究学者针对轨迹预测问题已取得系列研究成果,但已有预测方法存在以下不足:
首先,移动轨迹点的空间划分多采用确定性格网剖分[19, 21]或聚类[5, 22]方法剖分,将轨迹序列表达为一维空间单元序列[23],通过在空间单元序列中挖掘移动对象出行的频繁模式或将空间序列作为模型输入,实现移动对象轨迹预测。虽然采用这种划分方法可在某种程度上解决空间近似问题,但当轨迹点隶属于且仅隶属于单一空间单元时,空间位置相近轨迹点在被空间划分时可能会落入不同的区域,导致尖锐边界问题。以图 1为例,两条在空间上具有相似模式的轨迹
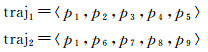
经过空间划分后表现为以下完全不同的两种序列模式
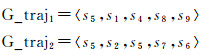
尖锐边界问题可能导致位于格网边界附近的轨迹点被划分入不同格网空间,使得轨迹间相似程度明显降低,从而影响频繁模式识别结果和模型学习能力,降低模型预测准确率。

|
| 图 1 尖锐边界问题示例 Fig. 1 Illustration of sharp boundary limitation |
其次,已有轨迹预测模型大多不关注轨迹历史信息存储,但移动对象未来时刻位置可能同时受到临近轨迹点和历史较远轨迹点影响,造成已有模型对长期依赖信息的学习不足,产生长期依赖问题。假定移动对象行驶在狭窄无岔路口的隧道或地下通道中时,移动对象未来时刻的位置可通过较少的历史轨迹信息即可准确预测,但在城市开放环境中,移动对象未来位置预测方法需要顾及该对象历史轨迹中时空模式,来提高预测精度。如图 2所示,当预测模型能够学习到移动对象到达机场的历史位置信息时,其出行目的地更可能为家或者宾馆(如图中粗实线所示),而当预测模型仅能学习到临近轨迹点(美食城、超市)影响时,由于训练数据中更倾向于下一时刻位置为公司(如图中粗虚线所示),将很可能导致预测错误。
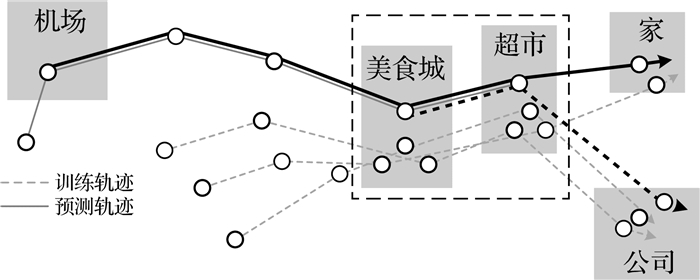
|
| 图 2 长期依赖问题示例 Fig. 2 Illustration of long-term dependencies limitation |
针对上述问题,本文提出基于模糊长短时记忆神经网络(fuzzy-long short term memory network, Fuzzy-LSTM)模型的移动对象轨迹预测算法。该算法通过定义模糊轨迹解决确定性格网剖分导致的尖锐边界问题,对长短时记忆神经网络进行改进使其能够良好适应模糊轨迹输入,综合考虑移动对象历史轨迹邻近性和周期性,基于长期依赖信息的学习过程,实现更加精确的自由空间短时移动对象轨迹预测。
1 基本定义定义1:轨迹 移动对象在地理空间移动,其位置随着时间不断发生变化,离散位置点所构成的有序序列定义为轨迹,表示为

式中,ti表示时间;∀i∈[1, n), ti < ti+1; pi表示移动对象在ti时刻的空间位置。
定义2:子轨迹 子轨迹是指在某条轨迹范围内轨迹点的有序集合,表示为

其中,k表示子轨迹长度;ti表示时间,t1 < tm < ti < tm+k-1 < tn;pi表示移动对象在ti时刻的空间位置。
定义3:格网轨迹 移动对象所在地理空间被固定格网(如正方形、三角形、六边形等)剖分成不同的空间区域,轨迹的单个坐标点pi被映射到所在的空间区域si,原始轨迹traj可被转化后格网区域序列定义为格网轨迹G_traj,表示为
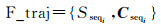
式中,ti表示时间;∀i∈[1, n), ti < ti+1; si表示轨迹点pi映射到格网空间上后对应的格网编号。如图 3所示,轨迹traj={(p1, t1,) (p2, t2), …, (p6, t6)}对应的格网轨迹为G_traj={(s1, t1), (s2, t2), …, (s6, t6)}。
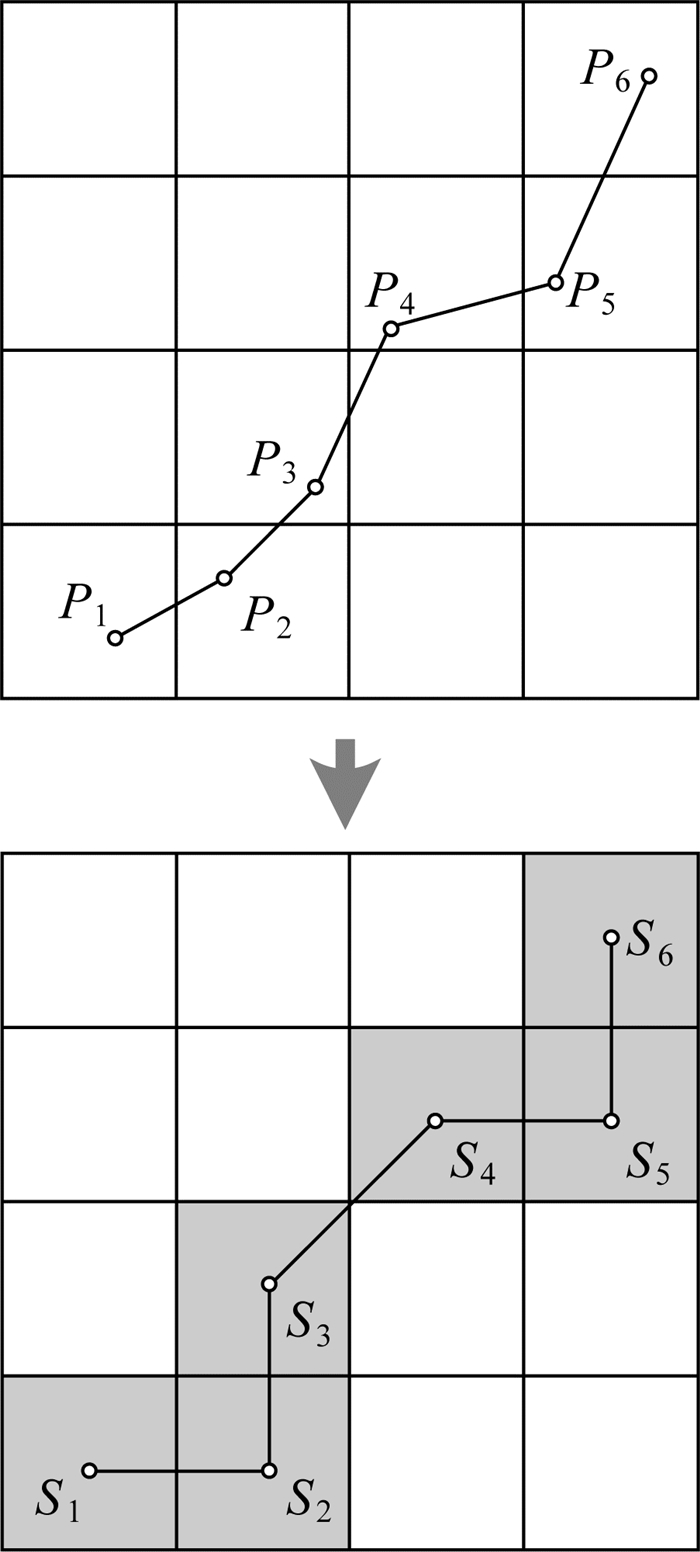
|
| 图 3 格网轨迹示例 Fig. 3 Illustration of grid-based trajectory |
定义4:模糊轨迹点 传统确定性格网轨迹G_traj中,轨迹点pi及所对应的格网空间单元si之间是一一映射关系。借鉴模糊集合理论,单个轨迹点pi可与si的临近空间单元集合建立隶属关系。通过模糊隶属度函数计算,轨迹点pi可以表示为带空间单元标签的模糊轨迹点Cpi=〈Sset, Cset〉,其中,Sset为点pi附近空间单元集合,Cset为点pi到对应空间单元的模糊空间隶属度集合。
定义5:模糊轨迹 模糊轨迹是指由模糊轨迹点有序计算生成的轨迹,由模糊序列集合和序列隶属度集合两部分组成

式中,Sseqi为模糊序列集合,由轨迹内各点所隶属空间单元集合计算笛卡尔积生成; Cseqi为序列隶属度集合,由轨迹内各点所对应隶属空间单元的隶属度的乘积计算生成。以图 4中轨迹traj1={p1, p2}为例,其模糊轨迹为F_traj1=〈{s5s5, s5s2, s5s4, s5s1}, {0.2, 0.25, 0.25, 0.3}〉。

|
| 图 4 模糊轨迹示例 Fig. 4 Illustration of fuzzy trajectory |
2 基于Fuzzy-LSTM模型的轨迹预测方法
基于Fuzzy-LSTM模型的轨迹预测算法流程如图 5所示。算法主要由两部分组成:首先,将输入轨迹进行切分,计算各子轨迹内各点的模糊空间隶属度,生成模糊子轨迹;然后,设计了一种由两组Fuzzy-LSTM神经网络组成的模型结构,用于分别考虑轨迹邻近性和周期性对预测结果产生的影响,并将模糊子轨迹作为模型输入,训练改进后的Fuzzy-LSTM模型,得到轨迹预测模型,实现对移动对象未来位置预测。
2.1 模糊子轨迹生成 2.1.1 模糊轨迹点生成借鉴模糊集合理论思想,将格网划分为明确空间和模糊空间两部分。如图 6所示,每个格网中圆形之内部分定义为明确空间,圆形之外的部分定义为模糊空间。当轨迹点落入明确空间时,该轨迹点完全隶属于其所在格网;而当轨迹点落入模糊空间时,定义该轨迹点隶属于距离其最近的四个格网。当给定一系列格网S={s1, s2, s3, …, sj}和轨迹点pi,可以依据式(1)和式(2)计算其模糊空间隶属度
 (1)
(1)
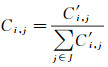 (2)
(2)

|
| 图 5 基于Fuzzy-LSTM模型的移动对象轨迹预测流程 Fig. 5 Architecture of predicting future locations with Fuzzy-LSTM models |
式中,C′i, j为模糊空间隶属度计算中间量;|pi-sj|代表轨迹点pi到格网sj的距离;r为明确空间半径;J为轨迹点邻近格网集合。在分别计算点到各格网的模糊空间隶属度中间量后,对其进行归一化,得到最终模糊轨迹点Cpi。以图中点p1、p2为例,Cp1=〈s5, 1〉,Cp2=〈(s5, s2, s4, s1), 0.2, 0.25, 0.25, 0.3〉。模糊空间隶属度与轨迹点到格网的距离呈反比例关系,轨迹点到格网距离越远,其模糊空间隶属度越低。
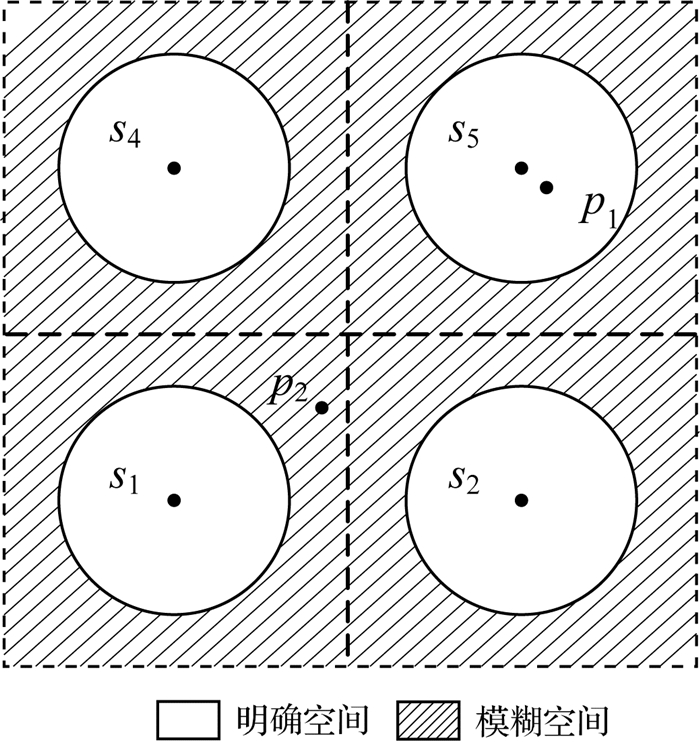
|
| 图 6 模糊空间剖分 Fig. 6 Fuzzy space partition |
在模糊空间剖分中,明确半径r值的选取将对模糊轨迹点生成结果产生一定影响。当r值选取过大时将使得较少点落入模糊空间内,降低模糊轨迹对算法精度的提升程度;当r值选取过小时将降低格网中心附近轨迹点相似度并增加计算复杂度。在应用中,r值多参照轨迹点空间分布依据经验进行设定。参考手机信令数据定位精度及轨迹点空间分布模式,本文格网采用公里格网进行格网划分,并设定明确空间半径r=0.45 km作为默认值完成试验。
2.1.2 模糊子轨迹计算为适应模型输入,需将轨迹切分为固定轨迹点数目的子轨迹,并分别计算子轨迹模糊空间隶属度。对一段子轨迹seqm,其模糊子轨迹可以用模糊子轨迹序列集合Sseqi和对应子轨迹序列隶属度集合Cseqi表示。如图 7所示,模糊子轨迹序列集合Sseqi为子轨迹内各点所隶属空间单元集合计算笛卡尔积获取的序列集合,子轨迹隶属度集合Cseqi由轨迹内各点所对应隶属空间单元的隶属度的乘积计算生成。
2.2 Fuzzy-LSTM模型由于传统LSTM网络神经元结构输入序列为绝对隶属度序列[24],为适应本文提出的模糊轨迹作为输入,需要根据上述模糊轨迹概念对其神经元结构进行改进。其核心思想为将模糊子轨迹序列隶属度作为对应序列权重,与模糊子轨迹序列共同传入Fuzzy-LSTM神经网络,并在完成同一段模糊子轨迹训练后对神经网络权重进行更新。
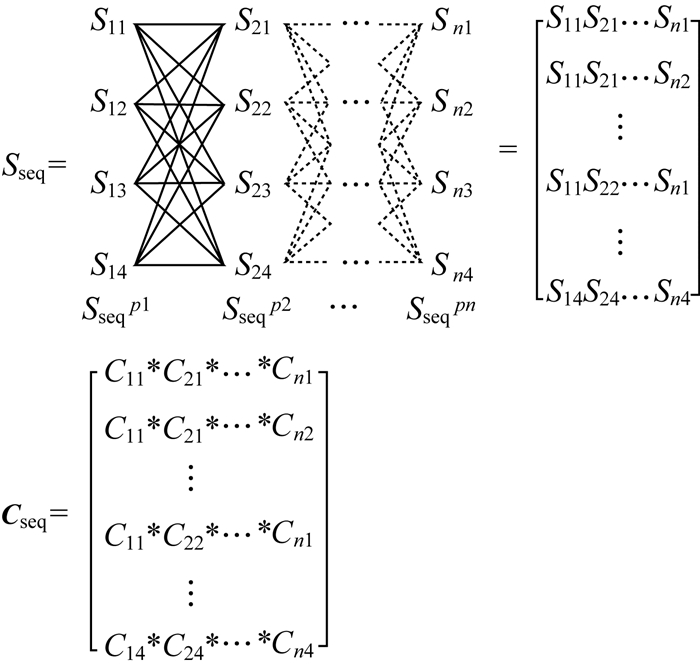
|
| 图 7 模糊子轨迹计算 Fig. 7 Generation of fuzzy sub-trajectories |
Fuzzy-LSTM轨迹预测模型基于移动对象历史轨迹预测移动对象下一位置,其计算过程主要受忘记门层、输入门层、输出门层3部分控制,并由细胞状态记录移动对象历史轨迹信息。当输入新的移动对象位置时,需要遗忘部分旧位置信息。此过程通过忘记门层完成。该门层依次读取模糊子轨迹序列Sseqt、对应子轨迹序列隶属度Cseqt和上一时刻输出ht-1,输出取值范围为[0, 1]的值给细胞状态Ct-1。在轨迹预测问题中,该过程表示当模型接收到新的模糊子轨迹时,需要确定其对原有轨迹信息保留程度。计算过程如式(3)所示
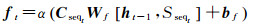 (3)
(3)
式中,ft表示t时刻忘记门层;ht-1表示t-1时刻模型输出值;α表示sigmod函数;Cseqt为t时刻输入的模糊子轨迹序列的空间隶属度;Wf为忘记门层权重矩阵;Sseqt为t时刻输入的模糊子轨迹序列;bf为忘记门层偏执项。
模型随后对新传入位置序列进行处理,主要由输入门层和细胞状态信息完成。当模型接受新位置序列时,需要通过输入门层决定更新值,并利用tanh函数作为激活函数创建细胞状态信息候选值向量。其计算过程如式(4)、式(5)所示
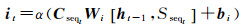 (4)
(4)
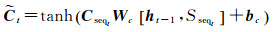 (5)
(5)
式中,it表示t时刻输入门层;tanh表示tanh函数;Wi、Wc为输入门层、细胞状态权重矩阵;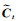
确定模型输入和忘记门层后,模型将更新细胞状态。模型将忘记门层值与原有细胞状态相乘,并与候选值向量和输入向量的乘积求和,确定新的细胞状态。在轨迹预测问题中,该过程表示模型遗忘部分原有轨迹信息并接收新的模糊子轨迹的影响。计算过程如式(6)所示
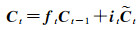 (6)
(6)
式中,Ct表示t时刻细胞状态;Ct-1表示t-1时刻细胞状态。
最后由细胞状态确定模型输出,由输出门层完成。模型先通过sigmod函数作为激活函数确定细胞状态输出,并通过tanh函数处理确定输出结果。计算过程如式(7)、式(8)所示
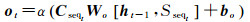 (7)
(7)
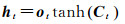 (8)
(8)
式中,ot表示t时刻输出门层;Wo表示输出门层权重矩阵;bo为输出门层偏执项;ht为t时刻模型输出。
2.3 轨迹预测算法 2.3.1 输入数据构建为同时考虑轨迹邻近性和周期性对移动对象下一时刻位置的影响,构建两种子轨迹作为模型输入:邻近性子轨迹和周期性子轨迹。其中,邻近性子轨迹由移动对象刚刚经过的位置组成,用于刻画轨迹邻近性影响;周期性子轨迹由移动对象前几天同一时刻所在位置组成,用于刻画轨迹周期性影响。依据2.1.2节模糊子轨迹生成算法,分别将邻近性子轨迹和周期性子轨迹转换为对应模糊子轨迹,并作为输入数据传输到轨迹预测模型中。
2.3.2 轨迹预测算法结构Fuzzy-LSTM轨迹预测算法结构如图 8所示,模型主要包括两个Fuzzy-LSTM网络,用于分别刻画历史轨迹周期性和邻近性对移动对象下一时刻位置影响。两个Fuzzy-LSTM网络共享相同的网络结构,分别接受周期性模糊子轨迹和邻近性模糊子轨迹作为模型输入,用于分别刻画周期性和邻近性对预测结果的影响。在对模型输出结果依据求和函数进行融合后,采用softmax函数为激活函数的全连接层将模型输出转换为固定维数的位置概率向量,通过损失函数训练Fuzzy-LSTM模型参数确定最终模型。在给定移动对象轨迹trajk和训练好的Fuzzy-LSTM模型后,新的邻近子轨迹和周期子轨迹将会被作为输入传输到训练好的模型中,输出概率最高的位置作为模型预测结果。
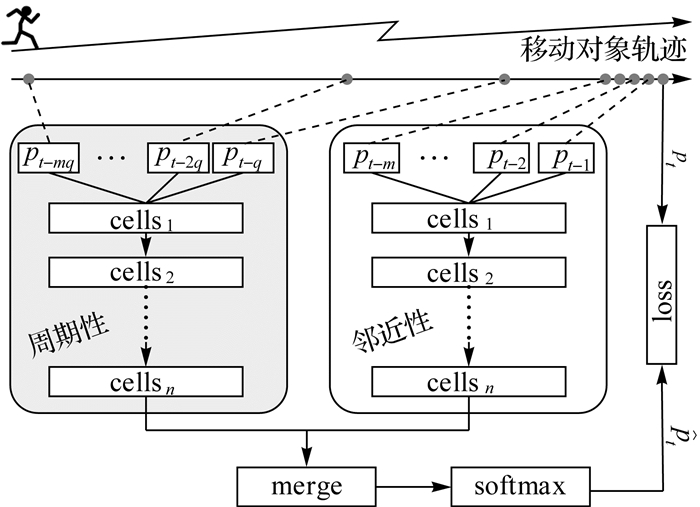
|
| 图 8 Fuzzy-LSTM轨迹预测算法结构 Fig. 8 Fuzzy-LSTM architecture |
3 试验结果与讨论 3.1 试验环境及数据集描述
试验所使用的数据为某市10万移动通讯用户连续15个工作日的手机信令数据,每个用户每天的出行轨迹为一条完整的轨迹停留点记录,共计150万条真实轨迹数据。轨迹点定位精度在市区约100~500 m、郊区约400~1000 m,平均记录时间间隔约20分钟。为便于验证本文提出的预测模型,将轨迹时间粒度统一重构为30 min,数据格式如表 1所示。试验硬件平台为Intel(R) Core(TM) i7-3770, 3.40 GHz CPU, 16 GB内存,操作系统为Windows 7,实现语言为Python。
| 用户编号 | 日期 | 记录时间/t | 经度(x)/°E | 纬度(y)/°N |
| 060F3***** | 1 | 00:00:00 | 121.125 | 31.143 |
| 060F3***** | 1 | 00:30:00 | 121.121 | 31.148 |
| 060F3***** | … | … | … | … |
| 060F3***** | 15 | 23:30:00 | 121.121 | 31.148 |
3.2 预测指标及对比试验
为方便比较不同算法的优劣,算法性能评价指标——预测准确率定义如下:
已知轨迹序列trajk=〈p1, p2, …, pn〉和预测轨迹序列traj′k=〈p′1, p′2, …, p′n〉,预测准确率计算如式(9)、式(10)所示
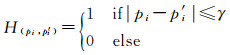 (9)
(9)
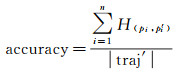 (10)
(10)
式中,|pi-p′i|为真实轨迹点到预测格网中心点的欧氏距离;γ为距离阈值;|traj′|为预测序列的长度。本文中,基于手机信令数据定位精度,选取1 km作为距离阈值。
为了检验本文提出轨迹预测方法的性能,本文实现了经典的NLPMM[4]和朴素LSTM轨迹预测算法Naïve-LSTM。Naïve-LSTM算法为本文算法的基础算法,采用原始LSTM模型进行轨迹预测。该模型能够解决预测中的长期依赖问题,并被广泛应用与时序数据预测领域[25-26]。NLPMM算法为经典的基于马尔科夫模型的轨迹预测算法。该算法综合考虑移动对象个体和群体的行为模式,分别针对移动对象个体和群体轨迹构建马尔科夫模型,并采用线性回归对模型进行融合,从而预测移动对象下一时刻所在位置。该算法在处理如手机信令数据等稀疏轨迹数据时具有良好表现。
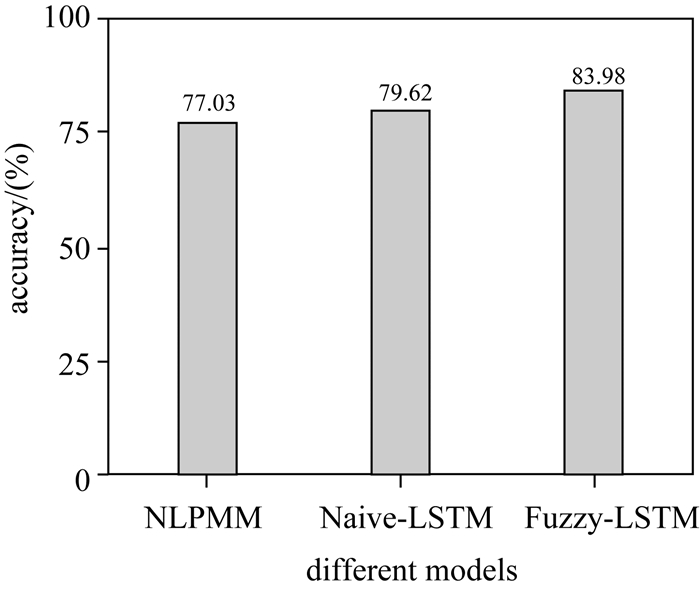
3.3 预测性能对比本文采用预测准确率评价模型预测性能,结果如图 9所示。
|
| 图 9 预测准确率比较 Fig. 9 Comparison of prediction accuracy |
试验结果表明,本文提出的Fuzzy-LSTM算法预测准确率为83.98%,较Naïve-LSTM算法和NLPMM算法分别高出4.36%和6.95%。其中,Fuzzy-LSTM算法和Naïve-LSTM算法预测准确率均高于NLPMM算法,是因为在预测过程中考虑了长期依赖信息,提高了算法的预测性能。同时改进后的Fuzzy-LSTM算法预测准确率优于Naïve-LSTM算法和NLPMM算法,说明考虑模糊空间隶属度和移动对象轨迹周期性影响有利于提高轨迹预测算法性能。
3.4 Fuzzy-LSTM算法预测性能分析本节分别从预测时段、时间粒度和移动对象停留点数3方面分析Fuzzy-LSTM模型性能。
城市居民在不同时间段具有不同的轨迹特征。本文比较了Fuzzy-LSTM预测模型在不同时段的轨迹预测准确率。结果如图 10所示。

|
| 图 10 不同时段预测准确率比较 Fig. 10 Effect of the time slot |
依据统计结果,模型平均预测准确率依次为78.8%(早高峰)、76.19%(晚高峰)、75.84(日间平峰)、91.29%(夜间平峰)。由于白天人群不规律出行较多,预测准确率相对较低;而夜晚轨迹预测准确率较高。
其次,数据时间粒度决定移动对象轨迹被概化的程度,数据时间粒度越大数据采样越稀疏。受限于手机信令数据精度,本文在30 min时间粒度基础上,分别将数据概化为1 h、2 h两种粒度,测试模型预测准确率变化。结果如图 11所示。依据统计结果,Fuzzy-LSTM模型的轨迹预测精度随时间粒度增大而略有下降,时间粒度为1 h、2 h时,较之30 min粒度的轨迹预测准确率分别下降4.83%、12.03%。模型预测准确率降低的原因在于随时间粒度增大,数据源概化程度更高,且模型训练数据量减少,使得模型对移动对象运动特征的学习效果不佳。但本文所提出的Fuzzy-LSTM模型在不同时间粒度下的预测精度均保持最高。

|
| 图 11 不同时间粒度预测准确率比较 Fig. 11 Effect of the temporal granularity |
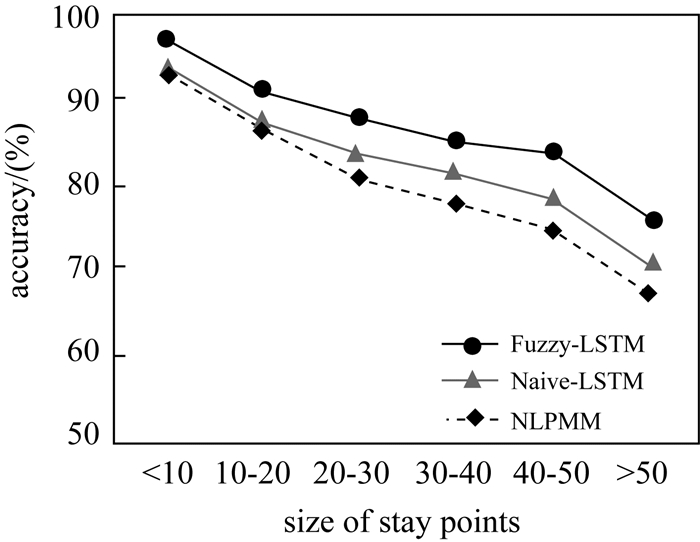
最后,移动对象停留点数目在一定程度上反映了移动对象轨迹的复杂程度。本文分析了不同停留点数目对移动对象轨迹预测准确率的影响,结果如图 12所示。依据统计结果,停留点少于10个的移动对象占总移动对象数6.72%。由于移动对象移动轨迹较为简单,平均预测准确率高达97.36%;62.79%移动对象停留点个数在10~50个之间,平均预测准确率由91.19%降至83.36%;停留点超过50个的移动对象占总数的30.49%。由于轨迹较为复杂,预测准确率有所下降,其平均预测准确率为75.69%。
|
| 图 12 不同停留点数目预测准确率比较 Fig. 12 Effect of the size of stay points |
3.5 讨论
(1) 本文采用的手机信令轨迹数据时间粒度为30 min,采样结果较为稀疏。受数据时间粒度限制,在同一时间间隔内,移动对象可能在匀速移动、加减速运动、静止等多种移动状态之间切换,且由于手机信令数据反映的是人群真实、全面的移动轨迹,移动对象亦可能在网络空间(沿道路街道网出行)或自由空间(如在小区内步行)下移动。因此,本文未考虑速度、方向、加速度等轨迹线特征及城市路网形态等要素,将轨迹预测问题转换为序列生成问题进行建模,从用户历史轨迹中挖掘移动对象出行行为规律及频繁模式,从而解决稀疏轨迹的轨迹预测问题。
(2) 模糊轨迹概念的引入,对提高轨迹预测算法预测精度有很大帮助。但提高程度受到轨迹点空间分布模式及预测区域空间粒度的制约。如轨迹点空间分布较为均匀且预测空间粒度较为精细,使得轨迹点在计算模糊空间隶属度时大多落入明确空间内,将降低算法预测精度提升程度。
(3) 不同尺度和形态的划分单元会对移动对象运动轨迹范围大小、移动事件分辨率、对象群体流动特征等问题产生显著影响[28-29]。当前研究城市内部人类移动模式多将城市空间进行等距离格网划分(如将城市空间划分为500 m(文献[30])、1000 m(文献[31])等不同单元尺度)或泰森多边形[32]划分,研究区域间移动特征。对本文使用研究数据进行统计,由于数据在城市中心区域间隔不足10 m,如采用泰森多边形划分将导致城市中心区域空间划分过于破碎,影响模型学习效率,且受基站服务载荷量及信号强度限制,移动对象并不一定定位于距其最近的基站,因此本文采用等距离格网进行空间划分。同时,参考该数据市区约100~500 m、郊区约400~1000 m的定位精度及前人研究成果,本文采用公里格网进行空间划分。
4 结论与展望针对现有稀疏轨迹预测算法中尖锐边界和长期依赖问题,本文提出一种基于Fuzzy-LSTM模型的移动对象轨迹预测算法。Fuzzy-LSTM模型通过定义模糊空间隶属度解决由空间划分导致的轨迹点的尖锐边界问题,基于长短时记忆神经网络能够学习长期依赖信息的特点,对长短时记忆神经网络模型进行改进,使其能够良好适应模糊序列输入,并同时考虑移动对象运动模式周期性和邻近性对其下一时刻所在位置的影响,实现更加精确移动对象轨迹位置预测。本文使用某市手机信令数据集对Fuzzy-LSTM模型与原始LSTM模型、NLPMM模型进行了比较。结果表明,本文所提出的Fuzzy-LSTM模型30 min内的移动轨迹预测平均精度达到83.98%,较Naïve-LSTM模型和NLPMM模型分别提高了4.36%和6.95%。
本文尚在以下方面存在不足,需在后续工作中进一步研究:①受试验数据时空粒度限制,现有算法预测准确率仅采用半小时及以上时间粒度的数据进行验证,算法短时预测准确率及可靠性需要进一步探究;②现有算法预测时仅考虑移动对象历史轨迹信息,默认移动对象出行行为具有周期性和延续性,未对移动对象当前交通出行方式进行判别,如何将移动对象交通出行方式与现有轨迹预测算法进行有机结合有待解决; ③现有算法综合考虑所有移动对象出行轨迹,下一步将考虑依据轨迹相似性对移动对象聚类并分类别建模,从而进一步提升算法预测精度。
| [1] | ZHENG Yu. Trajectory Data Mining:An Overview[J]. ACM Transactions on Intelligent Systems and Technology (TIST), 2015, 6(3): 29. |
| [2] |
陆锋, 刘康, 陈洁.
大数据时代的人类移动性研究[J]. 地球信息科学学报, 2014, 16(5): 665–672.
LU Feng, LIU Kang, CHEN Jie. Research on Human Mobility in Big Data Era[J]. Journal of Geo-Information Science, 2014, 16(5): 665–672. |
| [3] | FORMENTIN S, BIANCHESSI A G, SAVARESI S M. On the Prediction of Future Vehicle Locations in Free-floating Car Sharing Systems[C]//2015 IEEE Intelligent Vehicles Symposium. Seoul, South Korea: IEEE, 2015: 1006-1011. |
| [4] | CHEN Meng, LIU Yang, YU Xiaohui. NLPMM: A Next Location Predictor with Markov Modeling[C]//Pacific-Asia Conference on Knowledge Discovery and Data Mining. Cham: Springer, 2014: 186-197. |
| [5] | QIAO Shaojie, SHEN Dayong, WANG Xiaoteng, et al. A Self-adaptive Parameter Selection Trajectory Prediction Approach via Hidden Markov Models[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(1): 284–296. DOI:10.1109/TITS.2014.2331758 |
| [6] | WIEST J, HÖFFKEN M, KREβEL U, et al. Probabilistic Trajectory Prediction with Gaussian Mixture Models[C]//2012 IEEE Intelligent Vehicles Symposium. Alcala de Henares, Spain: IEEE, 2012: 141-146. |
| [7] | CHAPUIS B, MORO A, KULKARNI V, et al. Capturing Complex Behaviour for Predicting Distant Future Trajectories[C]//Proceedings of the 5th ACM SIGSPATIAL International Workshop on Mobile Geographic Information Systems. Burlingame, California: ACM, 2016: 64-73. |
| [8] | MUNTEAN C I, NARDINI F M, SILVESTRI F, et al. On Learning Prediction Models for Tourists Paths[J]. ACM Transactions on Intelligent Systems and Technology (TIST), 2015, 7(1): 8. |
| [9] |
乔少杰, 金琨, 韩楠, 等.
一种基于高斯混合模型的轨迹预测算法[J]. 软件学报, 2015, 26(5): 1048–1063.
QIAO Shaojie, JIN Kun, HAN Nan, et al. Trajectory Prediction Algorithm Based on Gaussian Mixture Model[J]. Journal of Software, 2015, 26(5): 1048–1063. |
| [10] | PREVOST C G, DESBIENS A, GAGNON E. Extended Kalman Filter for State Estimation and Trajectory Prediction of a Moving Object Detected by an Unmanned Aerial Vehicle[C]//2007 American Control Conference. New York: IEEE, 2007: 1805-1810. |
| [11] | JEUNG H, LIU Qing, SHEN Hengtao, et al. A Hybrid Prediction Model for Moving Objects[C]//Proceedings of the IEEE 24th International Conference on Data Engineering. Cancun, Mexico: IEEE, 2008: 70-79. |
| [12] | MONREALE A, PINELLI F, TRASARTI R, et al. Wherenext: A Location Predictor on Trajectory Pattern Mining[C]//Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Paris, France: ACM, 2009: 637-646. |
| [13] | YING J J C, LEE W C, TSENG V S. Mining Geographic-Temporal-semantic Patterns in Trajectories for Location Prediction[J]. ACM Transactions on Intelligent Systems and Technology (TIST), 2013, 5(1): 2. |
| [14] | OZER M, KELES I, TOROSLU H, et al. Predicting the Location and Time of Mobile Phone Users by Using Sequential Pattern Mining Techniques[J]. The Computer Journal, 2016, 59(6): 908–922. DOI:10.1093/comjnl/bxv075 |
| [15] | CHEN Meng, LIU Yang, YU Xiaohui. Predicting Next Locations with Object Clustering and Trajectory Clustering[C]//Pacific-Asia Conference on Knowledge Discovery and Data Mining. Cham: Springer, 2015: 344-356. |
| [16] | CHAPUIS B, MORO A, KULKARNI V, et al. Capturing Complex Behaviour for Predicting Distant Future Trajectories[C]//Proceedings of the 5th ACM SIGSPATIAL International Workshop on Mobile Geographic Information Systems. Burlingame, California: ACM, 2016: 64-73. |
| [17] | QIAO Shaojie, TANG Changjie, JIN Huidong, et al. Putmode:Prediction of Uncertain Trajectories in Moving Objects Databases[J]. Applied Intelligence, 2010, 33(3): 370–386. DOI:10.1007/s10489-009-0173-z |
| [18] | SHAH R, ROMIJNDERS R. Applying Deep Learning to Basketball Trajectories[J]. arXiv preprint arXiv: 1608.03793, 2016. |
| [19] | MATHEW W, RAPOSO R, MARTINS B. Predicting Future Locations with Hidden Markov Models[C]//Proceedings of the 2012 ACM Conference on Ubiquitous Computing. Pittsburgh, Pennsylvania: ACM, 2012: 911-918. |
| [20] |
李万高, 赵雪梅, 孙德厂.
基于改进贝叶斯方法的轨迹预测算法研究[J]. 计算机应用, 2013, 33(7): 1960–1963.
LI Wangao, ZHAO Xuemei, SUN Dechang. Prediction of Trajectory Based on Modified Bayesian Inference[J]. Journal of Computer Applications, 2013, 33(7): 1960–1963. DOI:10.11772/j.issn.1001-9081.2013.07.1960 |
| [21] | CHUNG J, PAEK O, LEE J, et al. Temporal Pattern Mining of Moving Objects for Location-based Service[C]//Proceedings of the 13th International Conference on Database and Expert Systems Applications. Berlin/Heidelberg: Springer, 2002: 331-340. |
| [22] |
向隆刚, 邵晓天.
载体轨迹停留信息提取的核密度法及其可视化[J]. 测绘学报, 2016, 45(9): 1122–1131.
XIANG Longgang, SHAO Xiaotian. Visualization and Extraction of Trajectory Stops Based on Kernel-density[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(9): 1122–1131. DOI:10.11947/j.AGCS.2016.20150347 |
| [23] | LI Zhenhui. Spatiotemporal Pattern Mining: Algorithms and Applications[M]//AGGARWAL C, HAN Jiawei. Frequent Pattern Mining. Cham: Springer, 2014: 283-306. |
| [24] | GERS F A, SCHMIDHUBER J, CUMMINS F. Learning to Forget:Continual Prediction with LSTM[J]. Neural Computation, 2000, 12(10): 2451–2471. DOI:10.1162/089976600300015015 |
| [25] | SHI Xingjian, CHEN Zhourong, WANG Hao, et al. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting[C]//Proceedings of the 28th International Conference on Neural Information Processing Systems. Montreal, Canada: MIT Press, 2015: 802-810. |
| [26] | SUTSKEVER I, MARTENS J, HINTON G. Generating Text with Recurrent Neural Networks[C]//Proceedings of the 28th International Conference on Machine Learning (ICML-11). Bellevue, Washington: Omnipress, 2011: 1017-1024. |
| [27] | SONG Chaoming, QU Zehui, BLUMM N, et al. Limits of Predictability in Human Mobility[J]. Science, 2010, 327(5968): 1018–1021. DOI:10.1126/science.1177170 |
| [28] |
鲁仕维, 方志祥, 萧世伦, 等.
城市群体移动模式研究中空间尺度影响的定量分析[J]. 武汉大学学报(信息科学版), 2016, 41(9): 1199–1204.
LU Shiwei, FANG Zhixiang, XIAO Shilun, et al. Quantitative Analysis of the Effects of Spatial Scales on Intra-urban Human Mobility[J]. Geomatics and Information Science of Wuhan University, 2016, 41(9): 1199–1204. |
| [29] | VIEGAS J M, MARTINEZ L M, SILVA E A. Effects of the Modifiable Areal Unit Problem on the Delineation of Traffic Analysis Zones[J]. Environment and Planning B:Planning and Design, 2009, 36(4): 625–643. DOI:10.1068/b34033 |
| [30] | GIANNOTTI F, NANNI M, PEDRESCHI D, et al. Unveiling the Complexity of Human Mobility by Querying and Mining Massive Trajectory Data[J]. The VLDB Journal, 2011, 20(5): 695–719. DOI:10.1007/s00778-011-0244-8 |
| [31] | XU Yang, SHAW S L, ZHAO Ziliang, et al. Another Tale of Two Cities:Understanding Human Activity Space Using Actively Tracked Cellphone Location Data[J]. Annals of the American Association of Geographers, 2016, 106(2). DOI:10.1080/00045608.2015.1120147 |
| [32] | FANG Zhixiang, YANG Xiping, XU Yang, et al. Spatiotemporal Model for Assessing the Stability of Urban Human Convergence and Divergence Patterns[J]. International Journal of Geographical Information Science, 2017: 1–23. DOI:10.1080/13658816.2017.1346256 |



