道路地图数据作为国家基础地理信息的重要组成部分,为智慧城市、LBS位置服务、应急响应等领域提供数据支撑。传统地图数据获取方式包括专业测量、遥感影像等,但传统方法成本高、更新周期长,且无法感知道路网络中的交通规则、交通流语义信息[1],制约其实际应用需求[2]。随着志愿者地理信息的出现,车辆时空轨迹作为其典型代表,蕴含了丰富的道路几何、语义信息,已成为道路数据获取的重要途径[3]。众源轨迹数据的泛在、海量、低成本特征,相比常规方法更适于道路数据采集与更新[1-4]。
当前,运用车辆轨迹提取道路数据、构建道路地图取得了丰硕成果[5],依据模型方法的不同可分为5类,包括聚类方法[6-7]、栅格化方法[8-9]、增量融合方法[10-11]、节点连接方法[12-13]、计算几何与图论方法[14-16]。轨迹聚类方法包括轨迹点、线聚类,如文献[6]运用DBSCAN算法对轨迹点聚类构建道路网络;文献[7]提出TraceBundle算法聚类轨迹线提取道路线。聚类方法多适于低噪音、高精度轨迹,难以处理稀疏采样、高噪音的众源轨迹线。栅格化方法[8-9]将轨迹点(线)转换为二值图像,运用图像形态学方法提取道路中心线,生成路网地图。栅格化方法将所有轨迹点(线)同等对待,使用全局密度参数阈值,无法顾及轨迹在路网空间中的密度、运动特征、噪音的分布差异性,使得提取结果精度、完整度不高[8, 16]。增量融合方法首先初始化空白地图,然后基于地图匹配思想逐次将轨迹线融合构建道路地图,如文献[10]根据轨迹线的空间邻近与方向关系融合提取不同行车方向上的道路线数据;文献[11]提出了符合空间认知规律的轨迹线增量融合生成路网方法。但轨迹数据中的高噪音、GPS漂移等问题对结果精度影响大。节点连接方法将道路网络建模为二维欧氏空间中的图结构,首先探测道路交叉点,然后运用聚类等方法提取道路边,根据节点与边的邻接关系构建完整地图[12-13]。从稀疏采样的轨迹中识别道路交叉点算法复杂,且没有顾及轨迹数据的空间差异性。计算几何与图论方法运用Delaunay三角网[3, 14]、Voronoi图[15]、Morse复型理论[16]等从车辆轨迹点(线)集中提取道路几何数据。但该类方法没有将运动特征与几何模型结合,导致算法对于轨迹密度差异、噪音适应性不强,无法提取不同行车方向道路线,且数据精度有待提高。
综上,运用众源车辆轨迹(采样间隔10~120 s)线构建道路地图仍存在以下问题:①传统方法将所有轨迹点、线作为输入同等对待,没有顾及轨迹数据在路网空间中的差异性,使得道路提取结果精度不高;②已有方法较少融合提取道路几何、语义信息(车行方向、交通流量)构建道路地图,减少了数据内容并制约数据应用。为此,本文在顾及轨迹线集特征差异的前提下,提出了轨迹分割与图层融合的道路地图构建方法。
1 众源轨迹线构建道路地图过程认知分析(1) 众源轨迹线综合过程。运用模型算法对轨迹点(线)集去粗取精,提取道路几何拓扑结构、简化轨迹大数据量,其本质是轨迹综合过程。其与常规地图综合区别为:①众源轨迹的高噪音、GPS定位误差,需用海量轨迹线集以保证道路数据的提取精度,而不是对单根曲线化简;②道路地图构建不仅提取路网拓扑结构,也提取车行方向、交通流量等语义时态信息。故将车行方向、交通流量等语义信息与道路几何数据融合提取是本研究的目标。
(2) 道路数据分层提取过程。道路网等级结构明显,不同等级道路上的车行速度、车行频率、交通流量、轨迹密度差异性显著[17]。道路网地理环境差异大,不同等级道路地表环境不同,使得轨迹丢失、轨迹噪音与误差的严重性不同[18-19]。道路提取应顾及轨迹特征、噪音误差、轨迹密度的差异性,提取过程需具有区分性和层次性。根据轨迹线集特征差异(如速度)选取不同参数条件并分层提取道路数据、构建道路图层是该研究的一个重难点。
(3) 道路图层集成融合过程。将分层提取的多个图层融合为单个完整的道路地图,其本质是空间数据集成融合问题。其与常规数据融合区别为:①融合流程上具有顺序性和层次性,逐次将低精度图层融合到高精度图层中;②融合方式上包括地图增强和地图整合两类[16, 19],且以地图增强为主;③融合方法及内容上不仅考虑道路线几何拓扑特征,还需顾及交通语义信息(方向、交通流量)以提高融合结果精度。顾及道路几何、交通语义特征的多道路图层集成融合是本文的另一个难点。
因此,本文重点关注车辆轨迹特征差异,将轨迹方向与Delaunay三角网集成分层提取道路数据,运用地图融合算法整合多道路图层,建立基于轨迹分割-图层融合(trajectory segmentation- layer fusion, SF)的众源轨迹线构建道路地图方法。
2 轨迹分割与图层融合的众源轨迹线构建道路地图方法分割-融合(SF)方法包括3个关键步骤:①根据车行速度将轨迹线集分割滤选为符合道路等级的3个轨迹线子集;②将轨迹方向与Delaunay三角网融合并根据轨迹线集特征差异选取不同参数阈值、约束条件提取道路线、交通语义数据,构建3个道路图层;③运用地图融合算法将多道路图层数据整合为单个完整道路地图。
2.1 基于速度序列的轨迹线分割滤选算法思想:根据道路设计规范[19]与轨迹特征[20],将每条轨迹线按照轨迹速度分割为高速(大于50 km/h)、中速(20~50 km/h)、慢速(小于20 km/h)3个等级,分别对应主干路、次干路和城市支路,并根据速度、时长阈值对分割后的子轨迹进行滤选。算法步骤为:
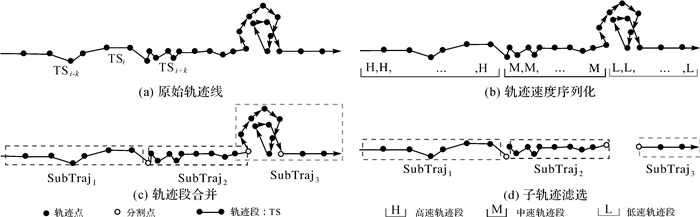
(1) 轨迹段速度序列化。输入1条轨迹线,计算每个轨迹段平均速度TSAv,根据速度分为3个状态,分别用H(高速)、M(中速)、L(慢速)表示,如图 1(b)。考虑到轨迹噪音、红绿灯短时停留情形的影响,对轨迹段TSi采用滑动窗口方法查找TSi时间上前后相邻的k个轨迹段,计算2k+1个轨迹段的平均速度作为TSi的平均速度(本文取k=3)。
|
| 图 1 基于速度序列的轨迹线分割滤选方法 Fig. 1 Trajectory line segmentation and filtering method based on velocity sequence |
(2) 轨迹段合并分割轨迹线。顺序查找同态轨迹段,合并为子轨迹,如图 1(c)。
(3) 子轨迹滤选。设置速度阈值Vmin(Vmin=1.5 m/s)和停留时长Tmin(Tmin=3 min)识别停留子轨迹[21]。时间长度大于Tmin的子轨迹线中的所有轨迹段速度都低于Vmin,则该子轨迹为停留轨迹。停留轨迹噪音高、误差大,影响道路提取精度,故过滤删除,如图 1(d)。
(4) 按照算法步骤对所有轨迹线分割滤选,输出3类轨迹线子集,则算法停止。
2.2 约束Delaunay三角网支持下的道路数据分层提取方法Delaunay三角网作为构建数据集拓扑关系的有效方法,广泛应用于轨迹数据处理[3-4, 14]、地图综合[22]、数据挖掘[23]等领域。本文引入约束Delaunay三角网模型并集成轨迹运动特征探测轨迹点(线)集特征差异,将交通语义信息和道路线几何数据分层提取。
2.2.1 轨迹线插值加密预处理直接对轨迹线集构建约束Delaunay三角网,会破坏三角网最邻近特性[14],故根据轨迹转向角自适应插值加密轨迹线解决该问题。计算每个轨迹段中两轨迹点的转角θ[24], 如果两轨迹点的转角θ都为(45°, 90°],该轨迹段位于道路转弯处,则该轨迹段不加密;反之该轨迹段加密多、加密步长小。自适应加密减少了稀疏采样的众源轨迹在道路转弯处的加密错误。
2.2.2 基于约束条件的Delaunay三角形分类(1) 三角形边长约束。由于车辆轨迹沿路网聚集分布(图 2(a)),加密轨迹线集构建的约束Delaunay三角网中(图 2(b)所示),道路内部区域三角形边长度小,非道路区域边长度大[14]。设定边长阈值,即可区分道路与非道路区域,边长约束阈值计算如下[14, 23]

|
| 图 2 融合几何、语义特征的Delaunay三角形分类 Fig. 2 Delaunay triangles classification based on fusion of geometric and semantic features |
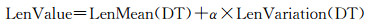 (1)
(1)
式中,LenMean(DT)表示三角网DT的平均边长;LenVariation(DT)为三角网边长变异;α为调节系数,α值越大约束越宽松,反之越严格。如果三角形中任意边长度大于LenValue,则该三角形为非道路区域的无效三角形(如图 2(b)中红色三角形),将其删除。边长约束提取的道路线仍存在两个问题,一是无法将同一道路上不同行车方向的道路线区分开(如图 2(b)所示);二是没有考虑轨迹运动特征、交通规则,这对复杂道路结构的提取精度不高。轨迹方向既表征车辆运动特征,也体现交通规则,有助于复杂道路结构、不同车行方向的道路数据提取,故在Delaunay三角网中加入轨迹方向约束提取道路线。
(2) 轨迹方向约束。对于任意轨迹点Pi,其轨迹方向(车辆运动方向)为向量PiPi+1,i表示时间先后顺序[10, 24]。则轨迹点Pi与其一介邻接点集的轨迹方向关系计算如下
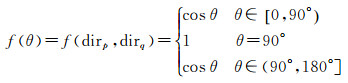 (2)
(2)
式中,f(dirp, dirq)表示轨迹点p、q轨迹方向夹角的余弦值。当0<f(θ)<1时,两轨迹点的行车方向相同,即所在的轨迹段位于同一车行方向。当f(θ)=1时,两轨迹点的行车方向垂直,表示轨迹段位于道路交叉口处[10]。因此,当0<f(θ)≤1,轨迹点p、q组成的三角形边邻接的两个三角形为有效三角形。如图 2(c)中轨迹点p1、p3的轨迹方向夹角为向量p1p2与向量p3p4的夹角,且f(θ)>0,为同一行车方向,则边p1p3邻接的两个三角形为有效三角形。则当f(θ)<0时,两轨迹点的车行方向相反,一是不同道路之间的轨迹方向相反[10],二是同一道路上的轨迹线方向相反(如图 2(a)、2(c))。本文研究目标是提取不同车行方向的道路线,故当f(θ)<0,轨迹点p、q组成的三角形边邻接的两个三角形为无效三角形。如图 2(c)中轨迹点p1、p6的f(θ)<0,为不同行车方向,则边p1p6邻接的两个三角形为无效三角形。如图 2(c)所示,将轨迹方向与三角网融合便于探测、提取不同车行方向的道路线。
2.2.3 不同约束条件下的道路线、交通语义信息提取根据约束条件将Delaunay三角形分为有效、无效两类,删除无效三角形,合并有效三角形,提取道路面域多边形并骨架化提取道路中心线[14],根据三角形邻接关系与轨迹方向统计每条道路中心线所经过的轨迹线数量(交通流量)。顾及3个不同轨迹线集的轨迹密度、数据量、噪音差异性,在道路数据提取过程中选择不同参数值和约束条件,构建高速(主干道)、中速(次干道)、慢速(支路)3个图层。高速轨迹线集行车规范、噪音低,不同行车方向轨迹线区分明显,故对该类轨迹线集加入边长和方向约束。如图 3(a)中B图加入边长(α取值小,约束严格)和方向约束,并根据轨迹车行方向对道路交叉口节点进行后处理(图 3(a)中C、D)。复杂道路交叉口多位于高等级道路处且轨迹线密集,加入边长和方向约束,能更好识别匝道、环形转盘。对比图 3(b)中B、C,图C加入2个约束条件相比图B的提取结果更精确。低速轨迹线集对应城市支路,轨迹数据量少且驾驶行为不规范,如果加入方向约束,则出现较多无效三角形,导致道路提取不完整,故只加入边长约束。如图 3(c)中B图只加入边长约束(α取值大),提取道路单线并记录车行方向属性(单向或双向)。中速轨迹线集是否加入方向约束需根据轨迹数据量来决策,由于轨迹数据量与时间跨度、车行频率、交通流量密切关联,使其难以定量建模,故本文只加入边长约束并通过调节边长阈值来提取道路数据。如图 3(a)中D所示,将提取的道路几何数据与交通语义信息可视化,可分析不同行车方向的交通流量差异及时态变化,有助于交通管理、城市规划决策。

|
| 图 3 不同轨迹线集的道路数据提取策略 Fig. 3 Road data extraction strategy with different trajectory sets |
2.3 多道路图层集成融合方法
算法思想:道路图层用G表示[17, 20],逐次将中、低速图层Gj融合到高速图层Gi中,对Gj中的道路弧段建立缓冲区,从Gi中搜索候选融合道路弧段集,根据候选道路几何拓扑、语义特征采取不同融合策略,整合为单个完整道路地图。算法步骤为:
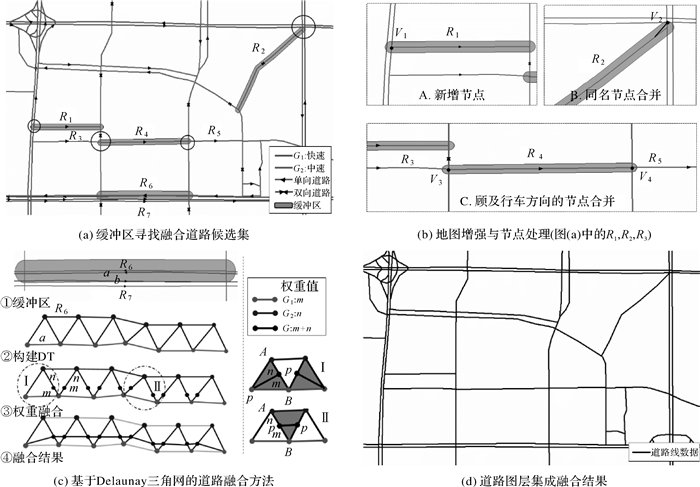
(1) 对低速图层Gj中道路弧段Ri建立w宽度的缓冲区,从高速图层Gi中搜索落入缓冲区长度大于2w的道路弧段作为匹配候选集(如图 4(a))。w取值根据道路等级与GPS定位误差设定[25],本文取值15~25 m;设置道路弧段最大流量[20]flowmax,本文取值25 000。
|
| 图 4 道路地图图层集成融合方法 Fig. 4 The method of road map layer fusion |
(2) 当候选集中没有道路弧段,则直接将Ri增量融合到Gi中,称为地图增强(如图 4(b))。缓冲区内没有其他道路弧段节点,则新增节点并分割原道路弧段,如图 4(b)中V1。缓冲区去内有其他道路节点,找最近节点作为同名节点合并,如图 4(b)中V2;同时需考虑节点合并后相邻两道路弧段的车行方向一致性,如图 4(b)中V3、V4。
(3) 当候选集中有道路弧段,根据道路线几何特征、交通语义来决定是否融合及如何融合生成新道路线,称为地图整合。当候选集中有多条弧段,则将Ri与候选道路弧段集计算Hausddorff距离作相似性度量,选取相似度最高的道路弧段a作为整合对象。判断Ri与a的车行方向和融合后的交通流量值flowmerge,如方向相同且flowmerge≤flowmax,则融合(如图 4(c)中a与R6);反之为不同方向上的道路线,则按算法第2步增量融合到Gi中。
(4) 整合方法:以待融合的两条道路弧段为约束线,构建约束Delaunay三角网,将三角形分Ⅰ(只有1个邻接三角形)、Ⅱ类三角形(有2个邻接三角形),如图 4(c)中②③。根据三角形类型与交通流量权重融合生成新的道路线,并写入图层Gi中(图 4(c)中④)。对于Ⅰ类三角形,新道路线为邻接边的权重分割点与其对应三角形端点的连线;对于Ⅱ类三角形,新道路线为两邻接边的权重分割点的连线(如图 4(c))。权重分割点P由邻接边中A、B两点坐标并集成交通流量权重(A、B点的权重分别为n、m)计算得到
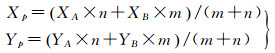 (3)
(3)
(5) 按照步骤,将所有图层的道路弧段融合处理完毕,输出新图层,则算法停止。
3 试验与分析试验数据为北京市12 000辆出租车1天的GPS轨迹,包括车辆ID、时间、经纬度、方向等信息,采样间隔为10~120 s不等。选取北京市朝阳区部分区域作为研究范围,在P4/16G/2G/Win8.1环境下,基于ArcGIS 10.2平台、Python编程语言进行算法试验。
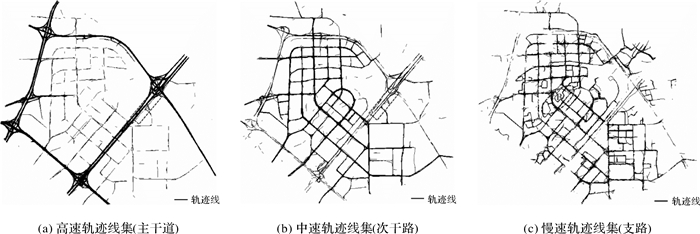
3.1 试验结果分析 3.1.1 轨迹线分割滤选轨迹线子集对原始轨迹数据进行常规(时间错误、越界等)清洗[18],生成轨迹线并速度序列化。按照2.1节中算法分割轨迹线集,根据速度阈值(Vmin=1.5 m/s)、停留时长阈值(Tmin=3 min)过滤停留子轨迹,最后得到高、中、低速3个不同速度等级的轨迹线子集,且轨迹线子集整体上符合主干道、次干道、支路的道路等级结构(如图 5所示)。对比图 5(a)、5(b)中A处,分割滤选算法能将空间邻近道路上的轨迹线集区分开,便于准确识别平行道路、主辅路等道路结构。但车辆运动的复杂性,使得高速轨迹线集中有少量次干道、支路上的轨迹线(如图 5(a)),低速轨迹线集中也有少量的主干道、高速路上的轨迹线(如图 5(c))。众源轨迹的大数据特性可以忽略错误滤选的小数据量轨迹线对道路提取的影响[20]。图 5中3个轨迹线集的数据量、轨迹噪音差异性显著,如图 5(c)中B处的轨迹噪音明显高于图 5(a)(b)中的同区域。这种差异性需要对轨迹线子集选取不同参数值和约束条件来分层提取道路数据。
|
| 图 5 轨迹线分割滤选 Fig. 5 Trajectory lines segmentation and filtering |
3.1.2 轨迹线子集分层构建道路图层
将分割滤选得到的轨迹线子集插值加密并构建约束Delaunay三角网,如图 6所示。按照2.2节中方法,对不同轨迹线集选择不同参数值和约束条件分类Delaunay三角形并提取道路数据(图 6)。对高速轨迹线集加入边长和方向约束条件,并取严格的调节参数阈值(α=0.85)。如图 6(a)中A处,将方向、边长约束条件与Delaunay三角网融合识别同一道路上不同方向的轨迹线集。对中速、低速轨迹集只加入边长约束提取道路单线,中速轨迹线集相比低速轨迹线集数据量大,故中速轨迹线集取严格约束值为α=1.1、低速取宽松约束值为α=2.1。如图 6(a)(b)(c)所示,分类得到的有效Delaunay三角形集能较好地识别车行道路网络。合并有效Delaunay三角形集后,按照2.2节中所述方法[14],将道路几何数据与交通语义信息融合提取,分别构建高、中、低速3个道路图层。如图 6(d)(e)(f)所示,构建的道路数据中包含了道路几何数据和车行方向、交通流量等语义信息。

|
| 图 6 道路几何、交通语义数据分层提取 Fig. 6 Hierarchical extraction of road geometry and traffic semantic data |
3.1.3 多道路图层数据集成融合
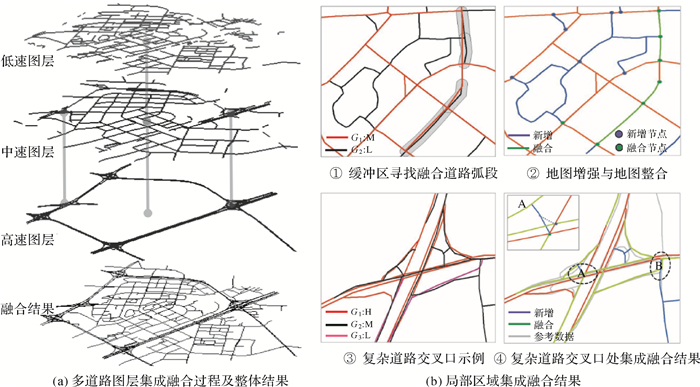
将3.1.2节中提取的3个道路图层融合为单个完整道路地图,即依次将中速、慢速图层融合到高速图层中,融合流程及结果如图 7(a)所示。对低速图层的任意一条道路弧段建立缓冲区(缓冲区中速为25 m,低速15 m),搜索融合道路弧段集(如图 7(a)中①),并考虑道路弧段几何、交通语义特征进行融合。融合方法包括地图增强和地图整合,如图 7(b)所示。对于路网结构简单的区域,该算法融合得到的道路数据精度与完整度高、拓扑正确(如图 7(a)中②)。对于复杂道路结构,如复杂道路交叉口,则会出现节点融合错误、道路边1:n及n:n匹配融合错误。如图 7(b)中④中A处,道路弧段r1应该与v1节点合并,但融合算法采用空间距离最近准则,导致其与v2节点错误合并。图中B处由于出现1:n的匹配情形,导致融合后出现多余的道路边。故对以上两种错误需人工检查并编辑改正。
|
| 图 7 多道路图层数据集成融合 Fig. 7 Multiple road map layer fusion |
3.2 试验结果评价
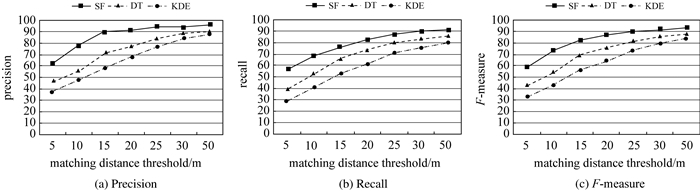
以标准道路矢量数据为参考,将本文方法结果与DT(Delaunay Triangulation)方法[14]、KDE方法[8]的试验结果进行精度对比分析。采用文献[5]中提出的缓冲区方法,对参考道路矢量数据分别建立5 m、10 m、15 m、20 m、25 m、30 m、50 m宽度的缓冲区,统计落入缓冲区内的道路线长度[5, 11, 25]并计算查准率(precision)、查全率(recall)和F值(F-measure)。统计结果如图 8所示,从整体上看,SF方法试验结果的准确率、完整率高于DT方法、KDE方法。SF方法提取的道路线数据在5 m缓冲区的精度相比DT方法、KDE方法有约13%、19%的提高,完整度有约16%、21%的提高。其原因在于DT、KDE方法都选取唯一全局参数提取道路线,导致轨迹数据量少的城市支路难以提取,轨迹数据量大的道路交叉口的结果精度误差大,降低了精度和完整度。SF方法顾及轨迹线集特征差异提取道路数据,提高了结果准确度和完整度。在拓扑正确性方面,KDE方法出现道路线拓扑断开、Z字形不平滑等问题,而SF方法和DT方法则减少该类错误[14]。
|
| 图 8 本文SF方法与DT方法、KDE方法的试验结果精度对比 Fig. 8 Evaluation of accuracy of experimental results of SF method, DT method and KDE method |
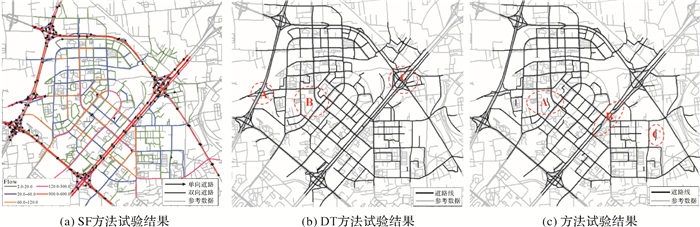
对比分析以上3种方法(图 9所示),SF方法相比DT、KDE方法的优势体现在:
|
| 图 9 不同方法的试验结果对比评价 Fig. 9 Comparative evaluation of experimental results of different methods |
(1) 结果的精度与完整度。DT和KDE方法使用唯一全局参数阈值提取道路线,导致轨迹线高密度区域的不同道路混成一团,无法区分;低密度区域的道路无法完整提取。如图 9(b)中A、C处道路交叉口轨迹线密集,交叉口的匝道、转盘无法准确识别,其结果完整度和精度明显低于图 9(a)同区域。将图 9(b)中B处、图 9(c)中A处(城市支路)与图 9(a)中同区域试验结果对比,SF方法试验结果的完整度高于其他方法。根据轨迹线集特征差异选取参数值和约束条件,避免了DT、KDE方法使用全局参数的缺陷,提高了准确度和完整度。
(2) 复杂道路结构下的轨迹线处理。复杂道路结构(T形、Y形、环形、平行道路)多位于主干道且不同等级道路在空间上邻近,这些区域轨迹线密集且不同道路上的轨迹线集在道路边界处重叠。SF方法运用Delaunay三角网探测轨迹线几何特征差异并融合轨迹方向来识别、提取不同车行方向的道路线数据。如图 9(c)中的B处,由于主干道及其辅路在空间上邻近且轨迹线密集,KDE方法将两条道路错误的识别为一条道路。将图 9(b)、9(c)与图 9(a)对比,DT、KDE方法对复杂道路结构下的轨迹线处理适应性不强,降低了结果的准确度。
(3) 数据内容的丰富性。SF方法将道路几何数据、车行方向、交通流信息融合提取(图 9(a)所示),增加了数据的应用性,如分析高速路上不同车行方向的交通流变化、交通拥堵、潮汐路段等。
4 结论与展望针对车辆轨迹点(线)构建道路地图问题,本文提出了轨迹分割-图层融合的众源车辆轨迹线构建道路地图方法。该方法基于轨迹速度分割滤选符合道路等级结构的轨迹线子集,根据轨迹线子集的特征差异加入边长、方向等约束条件,运用Delaunay三角网分层提取道路几何、语义信息,并通过地图融合算法将不同速度等级的道路图层整合为单个完整、精细的道路地图。运用北京市出租车轨迹数据进行试验,结果表明:该方法顾及轨迹数据的空间差异性,能将道路几何数据、交通语义信息融合提取,提高了道路数据精度及应用范围。
本文仍有较多内容需完善:①多图层道路数据集成过程中的道路节点处理、道路边融合需要更深入研究; ②运用多源时空轨迹提取更精细、完整的道路几何数据与交通语义信息(如转弯规则、转弯时间等)将是后续深入研究的切入点。
| [1] | WANG Jing, WANG Chaoliang, SONG Xianfeng, et al. Automatic Intersection and Traffic Rule Detection by Mining Motor-vehicle GPS Trajectories[J]. Computers, Environment and Urban Systems, 2017(64): 19–29. |
| [2] | LI Jun, QIN Qiming, XIE Chao, et al. Integrated Use of Spatial and Semantic Relationships for Extracting Road Networks from Floating Car Data[J]. International Journal of Applied Earth Observation and Geoinformation, 2012(19): 238–247. |
| [3] | YANG Wei, AI Tinghua, LU Wei. A Method for Extracting Road Boundary Information from Crowdsourcing Vehicle GPS Trajectories[J]. Sensors, 2018, 18(4): 1261. DOI:10.3390/s18041261 |
| [4] |
杨伟, 艾廷华.
运用约束Delaunay三角网从众源轨迹线提取道路边界[J]. 测绘学报, 2017, 46(2): 237–245.
YANG Wei, AI Tinghua. The Extraction of Road Boundary from Crowdsourcing Trajectory Using Constrained Delaunay Triangulation[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(2): 237–245. DOI:10.11947/j.AGCS.2017.20160233 |
| [5] | AHMED M, KARAGIORGOU S, PFOSER D, et al. A Comparison and Evaluation of Map Construction Algorithms Using Vehicle Tracking Data[J]. GeoInformatica, 2015, 19(3): 601–632. DOI:10.1007/s10707-014-0222-6 |
| [6] | QIU Jia, WANG Ruisheng. Road Map Inference:A Segmentation and Grouping Framework[J]. ISPRS International Journal of Geo-Information, 2016, 5(8): 130. DOI:10.3390/ijgi5080130 |
| [7] | KARAGIORGOU S, PFOSER D. On Vehicle Tracking Data-based Road Network Generation[C]//Proceedings of the 20th International Conference on Advances in Geographic Information Systems. Redondo Beach, California: ACM, 2012: 89-98. |
| [8] | LIU Xuemei, BIAGIONI J, ERIKSSON J, et al. Mining Large-scale, Sparse GPS Traces for Map Inference: Comparison of Approaches[C]//Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Beijing, China: ACM, 2012: 669-677. |
| [9] | KUNTZSCH C, SESTER M, BRENNER C. Generative Models for Road Network Reconstruction[J]. International Journal of Geographical Information Science, 2016, 30(5): 1012–1039. DOI:10.1080/13658816.2015.1092151 |
| [10] | CAO Lili, KRUMM J. From GPS Traces to a Routable Road Map[C]//Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. Seattle, Washington: ACM, 2009: 3-12. |
| [11] |
唐炉亮, 刘章, 杨雪, 等.
符合认知规律的时空轨迹融合与路网生成方法[J]. 测绘学报, 2015, 44(11): 1271–1276.
TANG Luliang, LIU Zhang, YANG Xue, et al. A Method of Spatio-temporal Trajectory Fusion and Road Network Generation Based on Cognitive Law[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1271–1276. DOI:10.11947/j.AGCS.2015.20140591 |
| [12] | XIE Xingzhe, BING-YUNGWONG K, AGHAJAN H, et al. Inferring Directed Road Networks from GPS Traces by Track Alignment[J]. ISPRS International Journal of Geo-Information, 2015, 4(4): 2446–2471. DOI:10.3390/ijgi4042446 |
| [13] | WANG Jing, RUI Xiaoping, SONG Xianfeng, et al. A Novel Approach for Generating Routable Road Maps from Vehicle GPS Traces[J]. International Journal of Geographical Information Science, 2015, 29(1): 69–91. DOI:10.1080/13658816.2014.944527 |
| [14] |
杨伟, 艾廷华.
基于众源轨迹数据的道路中心线提取[J]. 地理与地理信息科学, 2016, 32(3): 1–7.
YANG Wei, AI Tinghua. Road Centerline Extraction from Crowdsourcing Trajectory Data[J]. Geography and Geo-Information Science, 2016, 32(3): 1–7. DOI:10.3969/j.issn.1672-0504.2016.03.001 |
| [15] | DAVIES J J, BERESFORD A R, Hopper A. Scalable, Distributed, Real-time Map Generation[J]. IEEE Pervasive Computing, 2006, 5(4): 47–54. DOI:10.1109/MPRV.2006.83 |
| [16] | WANG Suyi, WANG Yusu, LI Yanjie. Efficient Map Reconstruction and Augmentation via Topological Methods[C]//Proceedings of the 23rd SIGSPATIAL International Conference on Advances in Geographic Information Systems. Seattle, Washington: ACM, 2015: 25. |
| [17] | BIAGIONI J, ERIKSSON J. Map Inference in the Face of Noise and Disparity[C]//Proceedings of the 20th International Conference on Advances in Geographic Information Systems. Redondo Beach, California: ACM, 2012: 79-88. |
| [18] | LIU Xuemei, ZHU Yanmin, WANG Yin, et al. Road Recognition Using Coarse-grained Vehicular Traces[J]. Beijing:HP Labs, 2012. |
| [19] |
中华人民共和国住房和城乡建设部. CJJ 37-2012城市道路工程设计规范(2016年版)[S].北京: 中国建筑工业出版社, 2012. Ministry of Housing and Urban-rural Development of the People's Republic of China. Code for Design of Urban Road Engineering[S]. Beijing: China Architecture and Building Press, 2012. |
| [20] | KARAGIORGOU S, PFOSER D, SKOUTAS D. Segmentation-based Road Network Construction[C]//Proceedings of the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. Orlando, Florida: ACM, 2013: 460-463. |
| [21] | PALMA A T, BOGORNY V, KUIJPERS B, et al. A Clustering-based Approach for Discovering Interesting Places in Trajectories[C]//Proceedings of the 2008 ACM Symposium on Applied Computing. Fortaleza, Ceara, Brazil: ACM, 2008: 863-868. |
| [22] | JONES C B, BUNDY G L, WARE M J. Map Generalization with a Triangulated Data Structure[J]. Cartography and Geographic Information Systems, 1995, 22(4): 317–331. |
| [23] | LIU Qiliang, TANG Jianbo, DENG Min, et al. An Iterative Detection and Removal Method for Detecting Spatial Clusters of Different Densities[J]. Transactions in GIS, 2015, 19(1): 82–106. |
| [24] | ZHENG Yu, LI Quannan, CHEN Yukun, et al. Understanding Mobility Based on GPS Data[C]//Proceedings of the 10th International Conference on Ubiquitous Computing. New York: ACM, 2008: 312-321. |
| [25] | LYU Haiyang, SHENG Yehua, GUO Ningning, et al. Geometric Quality Assessment of Trajectory-generated VGI Road Networks Based on the Symmetric Arc Similarity[J]. Transactions in GIS, 2017, 21(5): 984–1009. |


