2. 61618部队, 北京 100094;
3. 平顶山学院, 河南 平顶山 467000;
4. 煤航信息产业有限公司, 陕西 西安 710054
2. 61618 Troops, Beijing 100094, China;
3. Pingdingshan University, Pingdingshan 467000, China;
4. Aerial Photogrammetry and Remote Sensing Bureau, Xi'an 710054, China
由于传感器自身因素和光照、云雾等外部因素的影响,获取的光学影像会在亮度上存在不同程度上的差异,导致影像质量下降,进而影响了影像的进一步处理(如目标判读、影像匀色[1]、影像镶嵌[2]等)及应用。因此研究遥感影像亮度不均校正问题,消除影像内部的亮度差异,具有重要的现实意义和应用价值。
目前常用的影像亮度不均校正的方法可分为3类:统计信息法、数学模型法和频率域滤波法。统计信息法是利用影像的统计信息进行校正。文献[3-4]利用直方图均衡法进行亮度不均校正,虽然计算简单,但是没有考虑像素空间分布,通用性不强。文献[5-6]提出一种基于均值方差的校正方法,可以同时解决亮度不均匀和方差不一致问题,但是容易偏色改变地物性质。数学模型法是根据局部亮度均值,利用数学模型拟合影像内部的亮度分布,然后对不同部分进行不同程度补偿的方法,如文献[7]提出的自适应模板法。由于造成影像亮度分布不均匀的外部因素比较复杂,地物自身分布也不规则,因此采用数学模型方法进行亮度校正时,很难自动选取最适合的模型,而且影像中一些不规则的亮度区域也会导致不能准确地拟合影像的亮度变化。频率域滤波法是最受关注的方法,文献[8]提出基于加性模型的Mask方法,通过高斯低通滤波方法获取光照影像,然后将其从原始影像中减去,达到亮度校正的目的。该方法简单实用,得到了较多学者的关注,并衍生出了很多改进方法[9-10]。文献[11]利用同态滤波法将入射分量与反射分量分离,在削弱低频成分的同时增强高频成分,消除非均匀光照目的。文献[12]提出基于人眼视觉感知理论的Retinex校正方法,将影像经过对数变换后,再利用低通滤波获取光照分量,可以在校正亮度不均的同时避免色彩失真。在此基础上,又发展出了单尺度Retinex[13]和多尺度Retinex算法[14-16]。频率域滤波方法虽然对于阴影、亮斑等特殊区域不敏感,但原始影像与采用低通滤波方式获取背景影像的差值或比值运算可能会造成较多的信息损失,容易引起影像质量的退化,同时滤波器设计和参数选择需要一定的经验和技巧。
随着变分理论[17-18]的发展,文献[19]提出一种基于变分Retinex的影像增强方法,文献[20]将其引入遥感影像处理中,将光照影像估计问题转化为变分模型的最优解问题,为遥感影像亮度不均匀校正问题提供一种新思路。但是只利用一种范数进行约束,不能得到较好的校正结果。文献[21]对边缘信息和非边缘信息采用不同范数约束,但是利用最速下降法求解变分模型,效率较低。
针对上述问题,本文提出一种双范数混合约束的遥感影像亮度不均变分校正方法。首先,结合Retinex算法构造变分能量模型,分别利用L1范数和L2范数[22]对反射图像和光照图像进行约束。然后,利用分裂Bregman方法[23-24]分步迭代求解,交替获得反射图像和光照图像的最佳近似估计。最后,将优化后的光照图像与反射图像重建得到亮度均匀的影像。
1 亮度不均变分校正模型 1.1 Retinex理论Retinex理论,即视网膜大脑皮层理论,是由文献[12]最早提出的关于人类视觉系统如何调节感知到物体颜色和亮度的理论。文献[12]通过大量试验证明,人眼对物体颜色的感知只与视觉系统对物体反射特性的知觉有关,不会因外界光照条件的改变而变化。
根据Retinex理论,一幅影像是由光照影像和反射影像两部分组成,数学模型如下
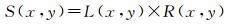 (1)
(1)
式中,(x, y)为像素点坐标;S(x, y)为原始影像;L(x, y)为光照影像;R(x, y)为反射影像。
通常为了简化计算,采用对数变换将式(1)由复杂的乘积运算变为简单的加减运算,即
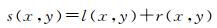 (2)
(2)
式中,s、l、r分别为S、L、R的对数域表示,即s=lgS,l=lgL,r=lgR。
光照影像反映了获取影像时的光照条件,反射影像则对应地物自身的属性。如果能先估计出光照影像,然后将其从原始影像中去除,获得地物的原貌,即可在消除亮度不均的同时保持影像中地物的色彩信息,达到亮度校正的目的。
1.2 变分校正模型Retinex理论的核心思想是将一幅影像分解为光照影像和反射影像,即由一个已知变量求解出两个未知变量,属于数学上的病态反问题,可采用变分正则化的方法求解。文献[20]以求解光照影像为目标,提出基于Retinex算法的变分框架(variational framework retinex, VFR),数学模型如下
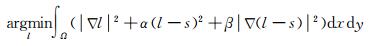 (3)
(3)
也可表示为
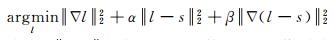 (4)
(4)
式中,‖·‖2表示L2范数;∇为影像梯度;α、β为非负参数。
该模型是基于假设光照影像和反射影像具有空间平滑性提出的,对两者均采用L2范数进行约束,存在一定的不合理性:
(1) 反射影像是由影像中地物本身性质决定的,包含了描述地物内部差异的纹理信息和地物之间的边缘信息,但L2范数保持边缘和细节的能力较差。
(2) 变分模型中未引入反射变量r,反射影像的求解是在计算出光照影像的基础上进行的,得到的结果不一定最优。
基于以上分析,本文将反射分量r加入变分方程并用L1范数对其进行约束,重新构造变分模型如下
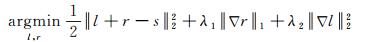 (5)
(5)
式中,‖·‖1为L1范数;λ1、λ2为非负参数;‖l+r-s‖22为保真项,约束l+r与s之间的相似;‖∇r‖1是对反射影像的纹理和细节特征进行约束,通过参数λ1进行权重调整;‖∇l‖22是对光照影像的空间平滑性进行约束,通过参数λ2进行权重调整。
与VFR方法相比,本文方法同时考虑了光照影像和反射影像各自的性质,对两个变量分别采用不同方法进行约束,可以更合理地求解光照影像和反射影像。与VFR方法不同,本文仅将反射影像R的取值范围约束为R≥0,而非[0, 1],即不认为L≥S一定成立。这是由于R的数值较小,迭代计算过程中强制约束R∈[0, 1](r≤0)会损失较多能量,导致获得的反射影像不准确。同时本文的约束条件也更符合实际情况,影像中的高亮区并非全部是高光照的原因,也有地物高反射率的影响。
2 变分模型求解由于本文提出的变分模型中包含两种混合范数,直接求解往往比较困难,本文采用分裂Bregman方法引入辅助变量b1、b2、c1、c2,使L1范数和L2范数约束项不直接相关,得到如下约束优化问题
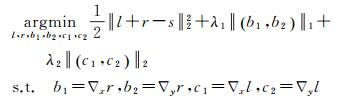 (6)
(6)
式中
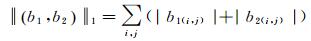 (7)
(7)
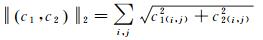 (8)
(8)
添加4个二次惩罚函数项,可将式(6)由约束优化问题转化为无约束问题,如式(9)所示
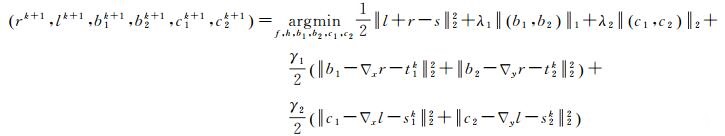 (9)
(9)
式中
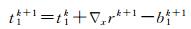 (10)
(10)
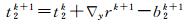 (11)
(11)
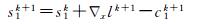 (12)
(12)
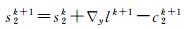 (13)
(13)
为了简化上述最小化问题,本文采用交替迭代方法[25],将变分模型的求解分解为3个子问题:
(1) 反射分量r最优化子问题
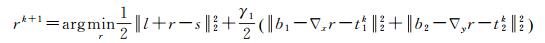 (14)
(14)
对式(4)求导,得
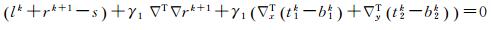 (15)
(15)
整理,得
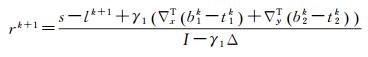 (16)
(16)
式中,∇x表示x方向的梯度;∇y表示y方向的梯度;I表示单位矩阵;Δ表示拉普拉斯算子,Δ=-∇T∇。
(2) 光照分量l最优化子问题
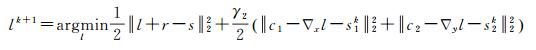 (17)
(17)
对式(17)求导,得
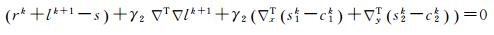 (18)
(18)
整理,得
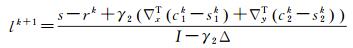 (19)
(19)
(3) 辅助变量最优化子问题
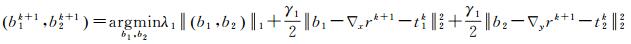 (20)
(20)
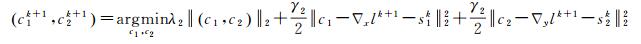 (21)
(21)
通过迭代收缩算法,可以得到式(20)、式(21)的近似解
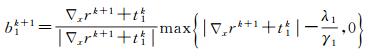 (22)
(22)
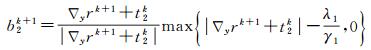 (23)
(23)
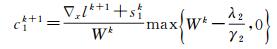 (24)
(24)
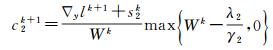 (25)
(25)
式中
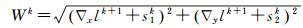 (26)
(26)
当残差‖lk+1-lk‖/‖lk‖小于限差ε时停止迭代,获得最优l和r,再对二者进行指数变换,即可得到光照影像L和反射影像R。理想的校正结果应该是亮度均匀并且亮度、色彩、对比度与原始影像近似,因此,本文作以下增强处理:
(1) 对光照影像进行Gamma校正,即
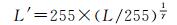 (27)
(27)
(2) 取校正后光照影像L′的均值与反射影像R相乘,即
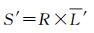 (28)
(28)
式中,L′为L′的均值。
(3) 对S′进行拉伸处理,提高对比度
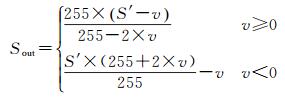 (29)
(29)
式中,v为拉伸参数,取值范围为(-127, 127),经过拉伸后的影像Sout即为亮度校正后的结果影像。
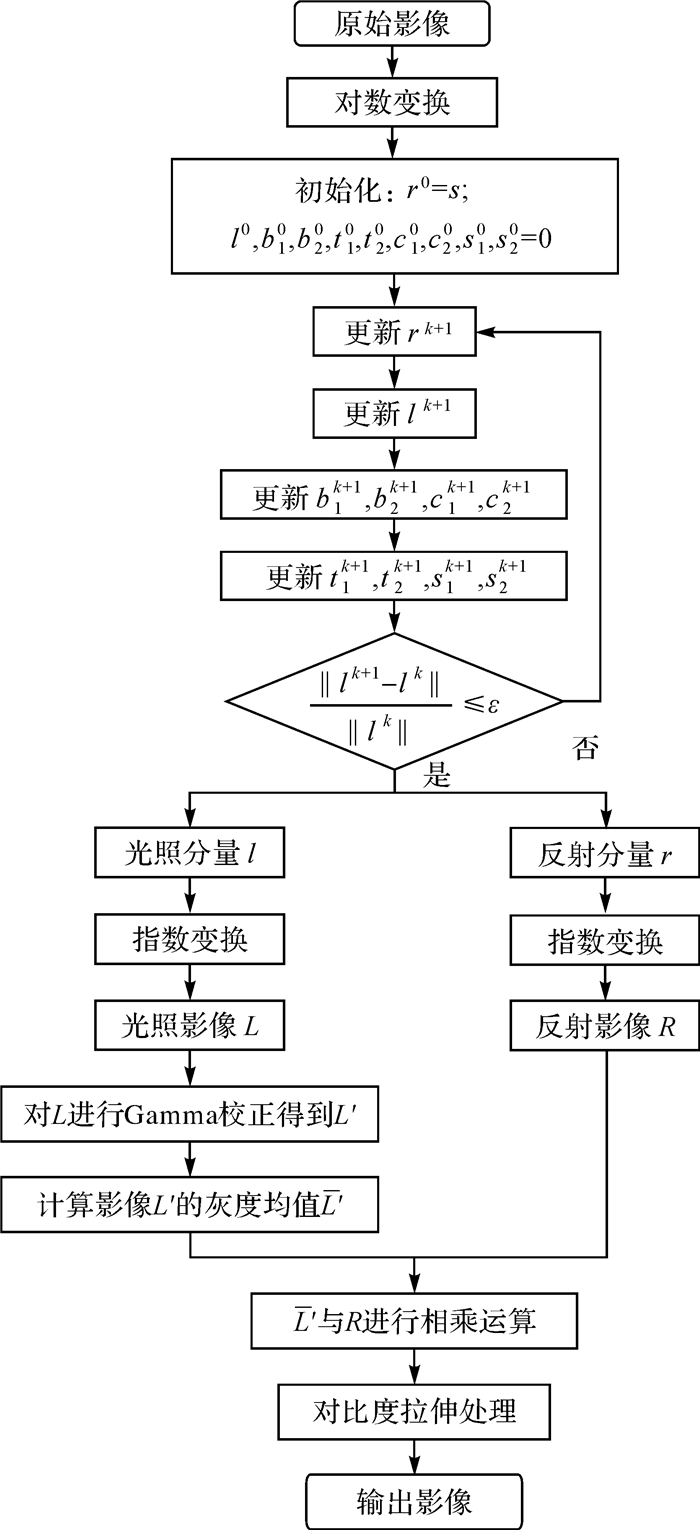
综上所述,本文提出的双范数混合约束的遥感影像亮度不均校正方法流程如图 1所示。处理彩色影像时,本文将影像由RGB色彩模型转换为HSI色彩模型,只对亮度I通道进行处理。
|
| 图 1 本文方法流程 Fig. 1 Flowchart of the proposed method |
3 试验与分析
为了验证本文方法的有效性,利用遥感影像进行以下3组试验并与VFR方法进行比较。试验平台为Intel Core i5 CPU、8GB内存的PC机,编程语言为Matlab。本文方法需要设置4个参数,λ1对结果影响不大,具有稳定性;λ2越小,问题越正定;γ1越小,收敛速度越快,γ2越大,光照影像越平滑。通过试验发现以下参数对不同数据都能取得较好结果:λ1=0.1,λ2=0.0001,γ1=0.0002,γ2=200,在保证校正结果质量的同时收敛速度较快,因此本文试验均采用这组参数。VFR方法的参数设置为α=0.00001,β=0.1[20],文中所有试验均采用同一组参数。
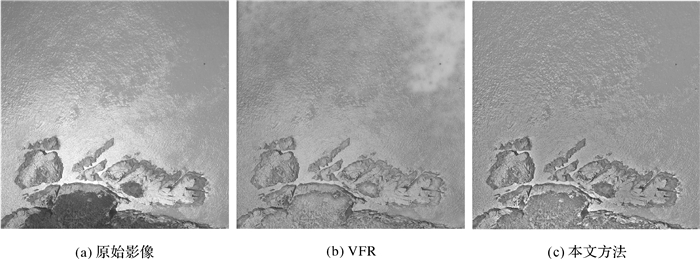
3.1 试验1:亮度均匀性对比试验数据为3幅1024×1024像素的亮度分布不均匀的遥感影像,如图 2(a)、图 3(a)和图 4(a)所示。图 2(a)(影像Ⅰ)和图 3(a)(影像Ⅱ)分别为局部过暗的灰度农村影像和城市彩色影像,图 4(a)(影像Ⅲ)为局部过曝的岛礁影像。分别采用VFR方法和本文方法对3幅影像进行处理,图 2(b)、图 3(b)、图 4(b)为VFR方法的试验结果,图 2(c)、图 3(c)、图 4(c)为本文方法的试验结果。

|
| 图 2 影像Ⅰ的校正结果 Fig. 2 Corrected results of image Ⅰ |

|
| 图 3 影像Ⅱ的校正结果 Fig. 3 Corrected results of image Ⅱ |
|
| 图 4 影像Ⅲ的校正结果 Fig. 4 Corrected results of image Ⅲ |
从目视效果看,VFR方法对影像Ⅰ和影像Ⅱ的校正结果比较理想,整体光照比较均匀。但是,在存在水域亮斑的影像Ⅲ的处理结果即图 4(b)中,右上角出现了局部亮斑。相比而言,本文方法的3幅校正结果亮度分布都比较均匀,目视效果较好。
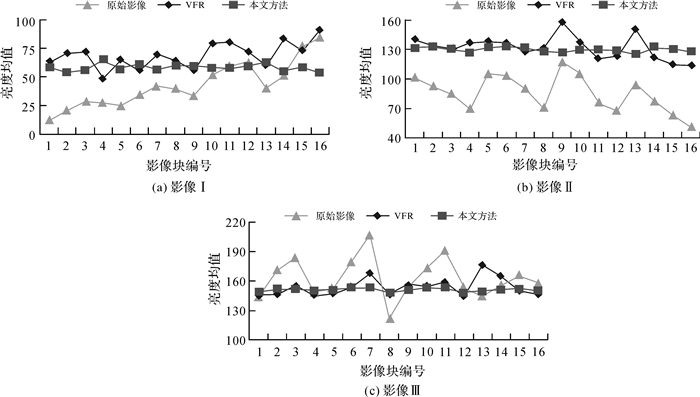
为了进一步比较两种方法校正结果影像亮度的均匀性,将校正影像分成4×4的16个影像块,按照从上至下、从左至右的顺序编号,计算各影像块的亮度均值并绘制亮度分布折线图,如图 5所示。可以看出,而本文方法的校正结果的亮度分布曲线更加平滑,而VFR方法各影像块的亮度均值离散程度相对较大,说明本文方法较VFR方法在亮度均匀性上有明显的优势。
|
| 图 5 校正影像的亮度分布折线图 Fig. 5 Line charts of illumination distribution of corrected images |
3.2 试验2:边缘检测对比
为了对比本文方法与VFR方法保持影像纹理与细节能力的优劣性,本文利用Canny算子对6幅校正影像进行边缘检测。图 6(a)-(c)为VFR方法校正影像的边缘检测结果,图 7(a)-(c)为VFR方法校正影像的边缘检测结果。

|
| 图 6 VFR方法校正影像的边缘检测结果 Fig. 6 Edge detection results of corrected images with VFR method |

|
| 图 7 本文方法校正影像的边缘检测结果 Fig. 7 Edge detection results of corrected images with the proposed method |
对比图 6与图 7可知,本文方法校正影像的边缘检测结果优于VFR方法,道路提取边缘比较完整,如图 7(a)和图 7(b)所示。而VFR方法校正影像中检测的道路边缘不完整,如图 6(a)所示,甚至道路中间出现断裂,如图 6(b)所示。对比图 6(c)和图 7(c)可以看出,VFR方法处理的影像检测的岛礁边缘也不如本文方法准确。这是由于VFR方法仅采用了L2范数对光照影像的光滑性进行约束,而本文综合考虑了光照影像和反射影像的不同性质,采用L1范数和L2范数混合约束,因此保持影像纹理和细节能力要优于VFR方法。
3.3 试验3:定量评价指标对比为了定量评价试验结果,分别统计各校正影像的熵、平均梯度和标准差,3种影像质量评价参数的值越大,说明影像的纹理和细节信息越丰富。其次,统计各影像块亮度均值的标准差,影像块标准差越大,说明各块的亮度均值离散程度越大,影像内部亮度分布越不均匀。最后统计VFR方法和本文方法的处理时间,统计结果如表 1所示。
| 试验数据 | 校正方法 | 熵 | 平均梯度 | 整体标准差 | 影像块标准差 | 耗时/s |
| 影像Ⅰ | 原始影像 | 6.27 | 7.80 | 34.79 | 20.43 | - |
| VFR | 6.98 | 10.23 | 31.64 | 11.37 | 268.18 | |
| 本文方法 | 7.16 | 18.65 | 52.10 | 2.95 | 15.54 | |
| 影像Ⅱ | 原始影像 | 7.43 | 20.04 | 48.37 | 18.71 | - |
| VFR | 7.74 | 28.58 | 57.01 | 11.98 | 263.61 | |
| 本文方法 | 7.83 | 34.31 | 66.18 | 2.41 | 18.08 | |
| 影像Ⅲ | 原始影像 | 7.09 | 15.56 | 37.84 | 21.16 | - |
| VFR | 6.48 | 13.05 | 22.27 | 9.38 | 117.03 | |
| 本文方法 | 6.71 | 18.89 | 27.21 | 2.09 | 16.92 |
由表 1可知,本文方法校正影像的熵、平均梯度和标准差均优于VFR方法,平均梯度和标准差提高了15%以上,说明本文方法校正影像的纹理和细节更丰富。另外,本文方法校正影像的分块均值标准差减小至3以内,约为VFR方法结果的1/4,说明本文方法校正影像内部亮度分布更均匀,与目视效果一致,验证了双范数约束的有效性。在运行速度方面,本文方法和VFR方法均为基于变分模型的迭代求解,VFR方法采用最速下降法求解,而本文方法采用分裂Bregman迭代法进行优化,具有更快的速度,效率提高了7倍以上。
4 结论本文针对遥感影像内部亮度分布不均匀问题,提出一种双范数混合约束的遥感影像亮度不均变分校正方法。试验结果表明,相比于利用单范数约束的VFR方法,本文方法更具优势,可以更好地消除亮度不均匀现象和保持影像的纹理和细节信息;与VFR采用的最速下降法相比,本文采用的分裂Bregman方法效率更高,求解速度提高了7倍以上。然而在试验过程中也发现了本文的局限性,迭代初始值会影响收敛速度。为了提高算法的实用性,后续需要研究多尺度变分方法,利用低分辨率影像的结果作为高分辨率影像迭代的初始值,提高算法收敛速度。
| [1] |
韩杰, 谢勇.
GF-1卫星WFV影像间匀色方法[J]. 测绘学报, 2016, 45(12): 1423–1433.
HAN Jie, XIE Yong. Image Dodging Algorithm for GF-1 Satellite WFV Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(12): 1423–1433. DOI:10.11947/j.AGCS.2016.20160248 |
| [2] |
陈继溢, 许彪, 张力, 等.
采用最优生成树的正射影像镶嵌线快速智能检测[J]. 测绘学报, 2015, 44(10): 1125–1131.
CHEN Jiyi, XU Biao, ZHANG Li, et al. Fast and Intelligent Seamline Detection for Orthoimage Mosaicking Based on Minimum Spanning Tree[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(10): 1125–1131. DOI:10.11947/j.AGCS.2015.20140467 |
| [3] | KIM M, CHUNG M G. Recursively Separated and Weighted Histogram Equalization for Brightness Preservation and Contrast Enhancement[J]. IEEE Transactions on Consumer Electronics, 2008, 54(3): 1389–1397. DOI:10.1109/TCE.2008.4637632 |
| [4] | JENIFER S, PARASURAMAN S, KADIRVELU A. Contrast Enhancement and Brightness Preserving of Digital Mammograms Using Fuzzy Clipped Contrast-limited Adaptive Histogram Equalization Algorithm[J]. Applied Soft Computing, 2016(42): 167–177. |
| [5] | LIU Jun, WANG Xing, CHEN Min, et al. Illumination and Contrast Balancing for Remote Sensing Images[J]. Remote Sensing, 2014, 6(2): 1102–1123. DOI:10.3390/rs6021102 |
| [6] |
朱述龙, 张振, 朱宝山, 等.
遥感影像亮度和反差分布不均匀性校正算法的效果比较[J]. 遥感学报, 2011, 15(1): 111–122.
ZHU Shulong, ZHANG Zhen, ZHU Baoshan, et al. Experimental Comparison Among Five Algorithms of Brightness and Contrast Homogenization[J]. Journal of Remote Sensing, 2011, 15(1): 111–122. |
| [7] |
李治江.彩色影像色调重建的理论与实践[D].武汉: 武汉大学, 2005. LI Zhijiang. Theory and Practice on Tone Reproduction of Color Photos[D]. Wuhan: Wuhan University, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10486-2006031490.htm |
| [8] |
王密, 潘俊.
一种数字航空影像的匀光方法[J]. 中国图象图形学报, 2004, 9(6): 744–748.
WANG Mi, PAN Jun. A Method of Removing the Uneven Illumination for Digital Aerial Image[J]. Journal of Image and Graphics, 2004, 9(6): 744–748. DOI:10.3969/j.issn.1006-8961.2004.06.016 |
| [9] |
张振, 朱宝山, 朱述龙, 等.
小波变换改进的MASK匀光算法[J]. 遥感学报, 2009, 13(6): 1074–1081.
ZHANG Zhen, ZHU Baoshan, ZHU Shulong, et al. Improved MASK Dodging Method Based on Wavelet[J]. Journal of Remote Sensing, 2009, 13(6): 1074–1081. |
| [10] |
袁修孝, 韩宇韬, 方毅.
改进的航摄影像Mask匀光算法[J]. 遥感学报, 2014, 18(3): 630–641.
YUAN Xiuxiao, HAN Yutao, FANG Yi. Improved Mask Dodging Algorithm for Aerial Imagery[J]. Journal of Remote Sensing, 2014, 18(3): 630–641. |
| [11] | FAN Chunian, ZHANG Fuyan. Homomorphic Filtering Based Illumination Normalization Method for Face Recognition[J]. Pattern Recognition Letters, 2011, 32(10): 1468–1479. DOI:10.1016/j.patrec.2011.03.023 |
| [12] | LAND E H, MCCANN J J. Lightness and Retinex Theory[J]. Journal of the Optical Society of America, 1971, 61(1): 1–11. DOI:10.1364/JOSA.61.000001 |
| [13] |
刘海波, 杨杰, 吴正平, 等.
改进的基于雾气理论的视频去雾[J]. 光学精密工程, 2016, 24(7): 1789–1798.
LIU Haibo, YANG Jie, WU Zhengping, et al. Improved Video Defogging Based on Fog Theory[J]. Optics and Precision Engineering, 2016, 24(7): 1789–1798. |
| [14] |
邵振峰, 白云, 周熙然.
改进多尺度Retinex理论的低照度遥感影像增强方法[J]. 武汉大学学报(信息科学版), 2015, 40(1): 32–39.
SHAO Zhenfeng, BAI Yun, ZHOU Xiran. Improved Multi-scale Retinex Image Enhancement of Under Poor Illumination[J]. Geomatics and Information Science of Wuhan University, 2015, 40(1): 32–39. |
| [15] | JIANG Bo, WOODELL G A, JOBSON D J. Novel Multi-scale Retinex with Color Restoration on Graphics Processing Unit[J]. Journal of Real-time Image Processing, 2015, 10(2): 239–253. DOI:10.1007/s11554-014-0399-9 |
| [16] | LIU Changjiang, CHENG I, ZHANG Yi, et al. Enhancement of Low Visibility Aerial Images Using Histogram Truncation and an Explicit Retinex Representation for Balancing Contrast and Color Consistency[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2017(128): 16–26. |
| [17] |
霍丽君, 何斌, 周达标.
遥感图像条带噪声的多尺度变分模型去除[J]. 光学精密工程, 2017, 25(1): 198–207.
HUO Lijun, HE Bin, ZHOU Dabiao. A Destriping Method with Multi-scale Variational Model for Remote Sensing Images[J]. Optics and Precision Engineering, 2017, 25(1): 198–207. |
| [18] |
李赓飞, 李桂菊, 韩广良, 等.
红外成像系统的非均匀性实时校正[J]. 光学精密工程, 2016, 24(11): 2841–2847.
LI Gengfei, LI Guiju, HAN Guangliang, et al. Real-time Non-uniformity Correction of Infrared Imaging System[J]. Optics and Precision Engineering, 2016, 24(11): 2841–2847. |
| [19] | KIMMEL R, ELAD M, SHAKED D, et al. A Variational Framework for Retinex[J]. International Journal of Computer Vision, 2003, 52(1): 7–23. DOI:10.1023/A:1022314423998 |
| [20] |
李慧芳, 沈焕锋, 张良培, 等.
一种基于变分Retinex的遥感影像不均匀性校正方法[J]. 测绘学报, 2010, 39(6): 585–591, 598.
LI Huifang, SHEN Huanfeng, ZHANG Liangpei, et al. An Uneven Illumination Correction Method Based on Variational Retinex for Remote Sensing Image[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(6): 585–591, 598. |
| [21] | LI Huifang, ZHANG Liangpei, SHEN Huafeng. A Perceptually Inspired Variational Method for the Uneven Intensity Correction of Remote Sensing Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(8): 3053–3065. DOI:10.1109/TGRS.2011.2178075 |
| [22] |
孔繁锵, 王丹丹, 沈秋.
L1-L2范数联合约束的鲁棒目标跟踪[J]. 仪器仪表学报, 2016, 37(3): 690–697.
KONG Fanqiang, WANG Dandan, SHEN Qiu. Robust Object Tracking via L1-L2 Norm Simultaneous Constraint[J]. Chinese Journal of Scientific Instrument, 2016, 37(3): 690–697. DOI:10.3969/j.issn.0254-3087.2016.03.028 |
| [23] |
郭从洲, 秦志远.
非凸高阶全变差正则化自然光学图像盲复原[J]. 光学精密工程, 2015, 23(12): 3490–3499.
Guo Congzhou, QIN Zhiyuan. Blind Restoration of Nature Optical Images Based on Non-convex High Order Total Variation Regularization[J]. Optics and Precision Engineering, 2015, 23(12): 3490–3499. |
| [24] | CHEN Chong, XU Guoliang. A New Linearized Split Bregman Iterative Algorithm for Image Reconstruction in Sparse-view X-ray Computed Tomography[J]. Computers & Mathematics with Applications, 2016, 71(8): 1537–1559. |
| [25] |
郭从洲, 时文俊, 秦志远, 等.
空间目标图像的非凸稀疏正则化波后复原[J]. 光学精密工程, 2016, 24(4): 902–912.
GUO Congzhou, SHI Wenjun, QIN Zhiyuan, et al. Non-convex Sparsity Regularization for Wave Back Restoration of Space Object Images[J]. Optics and Precision Engineering, 2016, 24(4): 902–912. |


