海冰占据了全球海洋总面积的5%~8%(文献[1]),是全球气候系统的重要因子,对全球热平衡、大气环流、海洋水循环和温盐平衡起到至关重要的作用[2-3],并作为一种全球性海洋灾害,特别是冬季高纬地区,严重威胁人类的海洋活动,因此海冰监测显得尤为迫切。海冰类型作为海冰重要参数之一,是获取海冰覆盖范围、密集度、冰缘线等其他海冰信息的重要依据,也是海冰监测的重要内容[4]。为此,准确高效地实现海冰分类,具有重要的科学价值和现实应用意义。
合成孔径雷达技术(synthetic aperture radar, SAR)作为主动微波遥感传感器,具有全天时、全天候、不受云雾及日光影响等优点。因而,在过去数十年里SAR技术被越来越多地用于海冰监测[5]。传统方法通常是依据单极化SAR数据的强度(比)、后向散射系数、纹理等特征[6]。由于不同类型海冰的后向散射系数相近,在某些成像条件下甚至难以区分。因此,单纯利用后向散射系数难以实现海冰的准确分类[7-8]。近年来利用灰度共生矩阵或马尔科夫随机场建立的纹理特征模型在单极化SAR海冰分类中取得了较好的结果[9-10]。虽然,这些方法考虑了空间邻域关系,但是纹理特征在不同尺度以及复杂海冰分布场景中的表现不稳定,因此其辨识海冰的作用并不显著。近些年发展起来的全极化SAR技术(简称极化SAR)相对于一般单极化SAR而言,包含更多的极化测度,能够获取更加全面的海冰散射信息。为此,基于极化SAR数据的海冰分类具有极大的研究价值和广阔的应用前景。
常用的极化SAR海冰分类方法可以分为两种。一种是基于统计分布的分类方法[8]。该类方法利用极化SAR数据服从的Wishart分布[11-12]、K分布[13]及G0分布[14]等统计规律,在贝叶斯分类准则下获得对不同类型海冰的统计参数估计,从而实现海冰分类[14-15]。但是这种方法存在统计模型构建复杂,且分类效率低等不足。另一种是基于特征的分类方法。该类方法包括特征提取和特征选择,并结合人工神经网络(artificial neural network,ANN)、支持向量机等机器学习的分类方法。这种方法处理流程简单,采用的分类方法属于非参数分类器,无需获得先验知识,分类效率较高。该类方法的关键在于有效选取特征。目前,常见的特征是H/α/A分解[16-17]特征,它是由相干矩阵特征分解获得反映目标的极化特征参数极化熵H,极化散射角α,各向异性A,根据数据在上述三维参数平面上的分布,进而获得不同类型海冰的更为深层次的散射机制信息。文献[18]利用H/α分解、Freeman分解及极化基变换特征,通过二叉树分类器,对C波段Radarsat-2 SAR海冰数据实现了5类冰水的识别。文献[19]通过提取双、全极化的不同极化特征(包括H/α/A分解),研究其在L、S和X波段的海冰分类性能,并且利用互信息衡量提取特征间的相关性,最后依据ANN实现对4类冰水的分类。文献[20]首次将基于模型的目标分解应用于海冰,对改进Freeman分解分析,对散射机制、同极化比、圆极化相关系数与海冰类型间的关系进行了有益探索,并对C波段全极化海冰数据采用基于统计距离的自动分割算法实现海冰分类[21-22]。虽然上述研究一定程度上利用了SAR的极化信息,并探究特征间的相关性,但这些尝试仍然存在选取的特征对海冰辨识性不高,并且对极化目标分解中最具优势的基于散射模型的目标分解缺乏深入探究。为此,本文将在目标分解理论基础上构建有意义的特征空间进行研究。
本文探究了L波段全极化SAR数据在海冰分类上的应用潜力。首先,经过多视化及滤波等极化处理获得相干矩阵;然后,对相干矩阵进行目标分解,提取对应分解特征参数,构建特征空间,考虑到不同极化分解特征在分类过程中起到不同的作用,对特征相关性分析后进行降维;最后,将其输入BP神经网络分类器中,得到海冰分类结果,并进行精度评价。此外,本文着重对基于模型的目标分解特征在海冰分类上的区分能力进行了深入讨论,并得出相关结论。
1 算法描述 1.1 极化相干矩阵已知全极化SAR单视复数据(single look complex, SLC)X={Xi: i=1, 2, …, M},其中,Xi={xpqi=Ipqi+jQpqi: p, q∈{H, V}};j是虚数单位;p表示天线发射方式;q表示天线接收方式;H表示水平极化;V表示垂直极化;i为像素索引;xpqi表示pq极化方式下第i个像素的复散射系数;Ipqi为xpqi的实部,表示同相分量;Qpqi为xpqi的虚部,表示正交分量;M为像素总数。由X可构建散射矩阵集S={Si:i=1, 2, …, M},其中
 (1)
(1)
对单基站雷达系统,一般认为满足互易性条件,SVHi=SHVi,即Si为复对称矩阵。由S可进一步定义Pauli旋转基下的目标散射矢量集k={ki: i=1, 2, …, M},其中
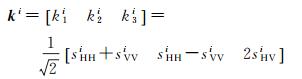 (2)
(2)
作为分布式目标,海冰具有随时间或空间变化而不稳定的特点[14]。为了描述此类目标,在假设其满足平稳性、各向同性及各态历经性等条件下,可以用目标散射矢量k的二阶矩表达,即极化复相干矩阵集T={Ti: i=1, 2, …, M},其中
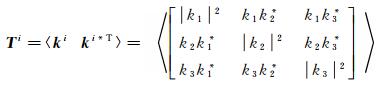 (3)
(3)
式中,*表示共轭操作;〈·〉表示多视处理。多视处理后的极化相干矩阵集T0={T0m: m=1, 2, …, M/N},其中
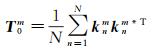 (4)
(4)
式中,N为视数;m表示多视处理后影像中像素索引;方位向分辨率变为原来1/N;距离向分辨率不变。为了消除SAR系统固有的相干斑噪声影响,采用窗口大小为7×7的Refined Lee滤波[23],得到滤波后极化相干矩阵集T1={T1m: m=1, 2, …, M/N},其中
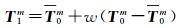 (5)
(5)
式中,
海冰的散射机制一般为表面散射与体散射,海冰随发育年龄、冰厚、SAR系统波长及入射角不同,其散射机理不同[24-25]。基于这个考虑,本文主要提取极化目标分解参数作为特征矢量。极化目标分解将极化矩阵转换为具有物理散射意义的参数组合,是进行后续分类处理等操作的重要预步骤,一般分为基于模型和基于特征值两类目标分解。为了避免单一目标分解在刻画地物散射机理上的局限性,本文经过分析选取了3种不同分解:An分解[26]、Bhattacharya & Frery(B&F)四分量分解[27]、H/α/A分解[16]。
此外,为了充分利用分解信息,还提取了一些衍生极化特征包括直接从相干矩阵提取的具有物理散射信息的3个对角线元素T11、T22和T33,即为Pauli相干分解的3个分解特征,散射总功率span_db,基于H/α/A分解的香农熵[28](Shannon entropy, SE)以及香农熵极化分量(Shannon entropy polarization, SEp),共计15个分解特征。设特征空间F={fd, d=1, 2,…, D},对于fd={fdm, m=1, 2, …, M/N},其中,fd称为提取的第d维特征图像,fdm表示第d维特征图像中第m个像素的特征矢量,D为特征维数。所提取的各特征参数如表 1所示。
| 特征矢量 | 特征参数 | 表达式 | 含义 |
| f1 | T11 | T11∈diag(T) | 相干矩阵对角元素,包含表面散射信息 |
| f2 | oddAn | oddAn=g1(T11, T22, T33, T12) | An分解中表面散射功率 |
| f3 | oddB&F | oddB&F=k1(T11, T22, T33, T12) | B&F分解中表面散射功率 |
| f4 | SE | SE=log(π3e3|T|) | 香农熵,衡量极化程度,包括强度与极化分量之和 |
| f5 | span_db | span_db=10log10(tr(T)) | 散射总功率 |
| f6 | T22 | T22∈diag (T) | 相干矩阵对角元素,包含二次散射信息 |
| f7 | T33 | T33∈diag(T) | 相干矩阵对角元素,包含体散射信息 |
| f8 | volAn | volAn=g2(T33) | An分解中体散射分量功率 |
| f9 | volB&F | volB&F=k2(T11, T22, T33, T12) | B&F分解中体散射分量功率 |
| f10 | SEP | SEP=log(27|T|/tr(T)3) | SE中极化分量,与Barakat极化度相关 |
| f11 | α | 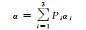
|
H/α/A分解参数,平均极化散射角,识别主要散射机制;Pi为T特征值的伪概率 |
| f12 | H | 
|
极化熵,衡量极化程度;H/α/A分解参数 |
| f13 | doubleAn | doubleAn=g3(T11, T22, T33, T12) | An分解中二次散射功率 |
| f14 | doubleB&F | doubleB&F=k3(T11, T22, T33, T12) | B&F分解中二次散射功率 |
| f15 | A | 
|
各向异性,衡量非主导散射机制的相对大小;H/α/A分解参数,λi为从大到小,第i个特征值 |
1.2.2 特征降维
本文所提取的极化特征存在着一些意义一致的特征,为了筛选出最好的特征,有必要对高相关的特征进行特征降维。本文采用衡量线性相关的简单相关系数r作为特征相关性的度量指标
 (6)
(6)
式中,cov(fu, fv)=E[(fu-E(fu))(fv-E(fv))T];var(fu)=[(fu-E(fu))(fu-E(fu))T];r(fu, fv)表示第fu和fv维特征矢量间的相关系数;cov表示特征矢量fu、fv间的协方差;var表示各特征矢量的方差;E(·)为均值运算符。
根据相关系数分布情况,选取|r|≧0.75作为高相关特征组的判定条件,对高相关特征组进行特征降维。采用主成分分析(principal component analysis, PCA)[29]进行降维:首先,将各维特征归一化,计算各维数据的均值;其次,计算各维特征间的协方差矩阵并对其进行特征分解;再次,将特征向量按对应特征值从大到小排列,取前三列组成矩阵;最后,可得到降维至三维后的数据,即前三主成分,此时保留信息量最多。对于低相关特征则保留不做降维处理。
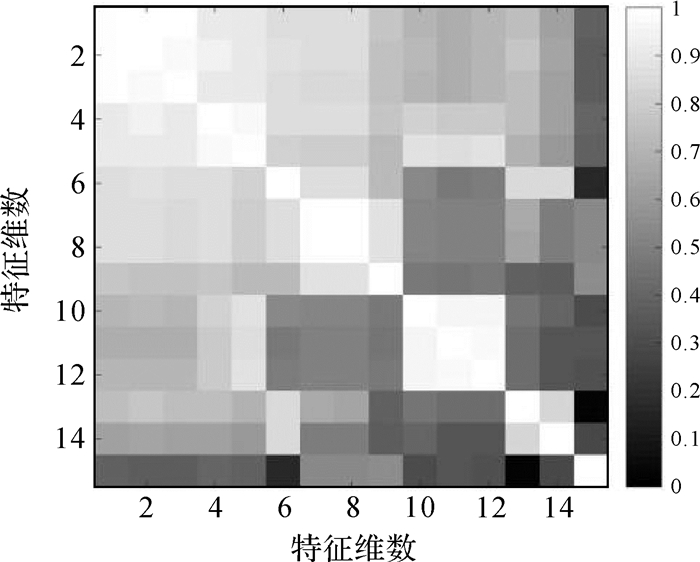
图 1为特征空间中各特征矢量的相关系数图。可以看出,特征空间呈现分块特征,许多特征之间存在较大的相关性,特别是f1-f9维特征即T11、oddB&F、oddAn、SE、span_db、T22、T33、volAn和volB&F间相关性较大,其中f1-f3、f4和f5、f7和f8相关性均高于0.9,这和各特征具有相似的物理意义相吻合。此外f10-f12维特征,f13和f14维特征间相关性也比较明显,f15维特征即各向异性特征与其他特征间的相关性均比较低,所以应该对前9维特征进行PCA降维操作。
|
| 图 1 特征相关系数 Fig. 1 Feature's correlation coefficient |
1.3 BP神经网络分类
BP神经网络分类器[30]是一种非参数的监督分类器,由于单隐含层神经网络可以满足绝大多数遥感应用,因此本文采用单隐含层神经网络结构。首先,设置迭代次数n及正则化系数λ,并随机初始化权重向量Θ(l)
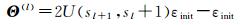 (7)
(7)
式中,sl为第l层所神经元个数;sl+1为第l+1层神经元个数;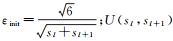
之后执行一次前向传播过程,通过sigmoid激活函数获得每层神经元的输出结果hθ(x(i)),并计算本次传播的损失函数J(θ)
 (8)
(8)
式中,n为神经元个数;y表示期望输出值;等式最右边为正则化项。接着计算本次反向传播时各层权重向量的微分量(即误差值) 
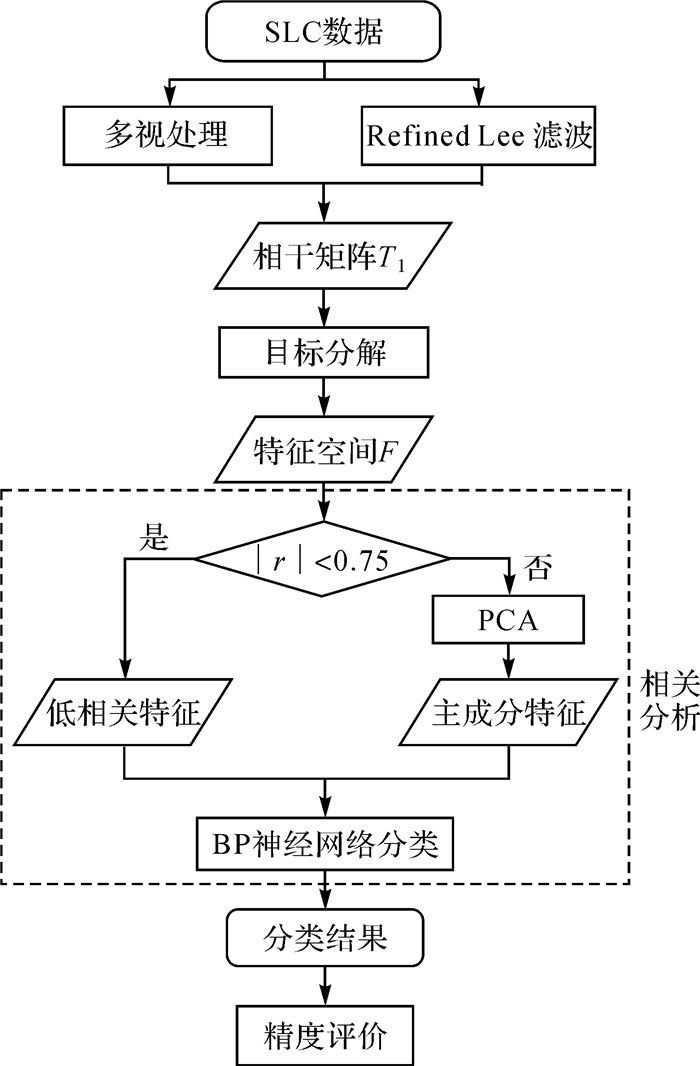
综上所述,本文算法流程为(图 2):
|
| 图 2 算法流程图 Fig. 2 Flowchart of the algorithm |
(1) 对全极化数据进行多视处理生成相干矩阵T0;为抑制相干斑影响,对T0进行Refined Lee滤波T1。
(2) 对极化相干矩阵T1进行极化目标分解,提取分解特征参数,构建特征空间。
(3) 对特征参数相关性分析,计算15维特征参数间的相关系数,判定其相关性;对高相关特征PCA降维。
(4) 设计BP神经网络分类器,将特征矢量作为输入层,实现海冰分类。
(5) 精度评价。
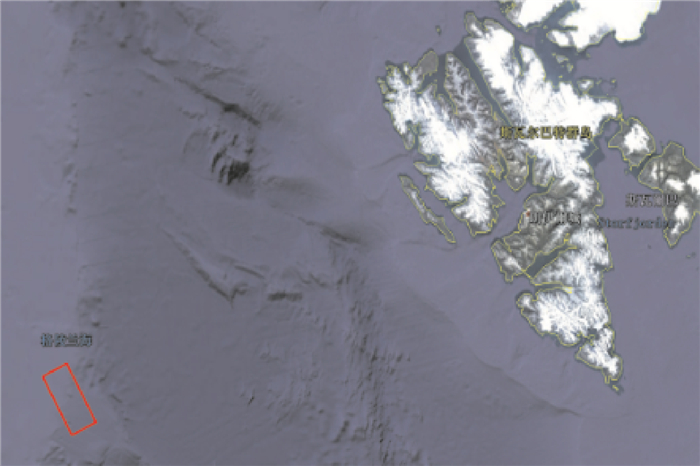
2 试验与讨论 2.1 研究区域本文以格陵兰海中部为研究区域(图 3中红色矩形),研究区域中心地理坐标为05°34′04.8″W,77°21′03.6″N,西距格陵兰岛171 n mile(1 n mile=1.852km),东北距离斯瓦尔巴特群岛首府朗伊尔城273 n mile,处于海冰-海水的过渡地带。格陵兰海属亚极地气候,全年盛行北风和东北风;每年10月至翌年8月为冰期。冬季大部分海面封冻,夏季冰层融化,并且浮冰随西岸的东格陵兰寒流漂流南下,造成航运困难。作为近北极地区高纬海域,是地球变暖的前线,其海冰变化对大西洋乃至全球气候变化有着重要意义。
|
| 图 3 试验区位 Fig. 3 Study area |
2.2 试验数据
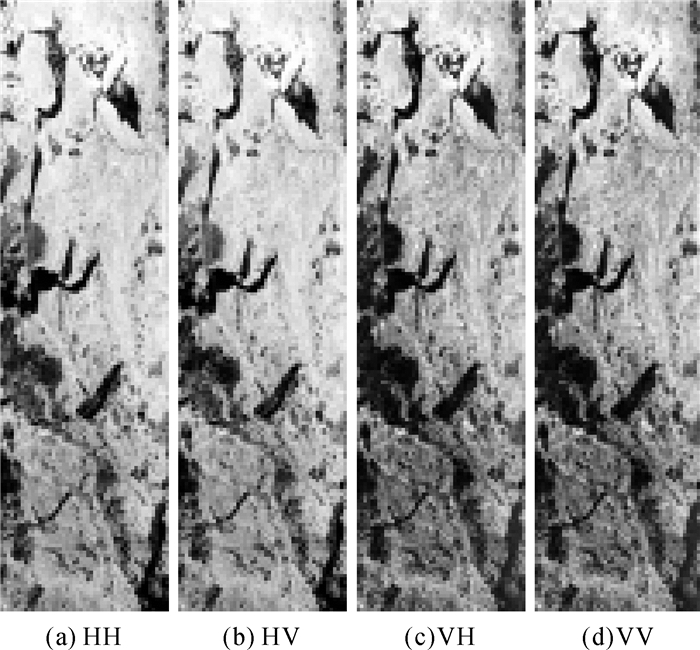
本文采用的试验数据为日本ALOS-1卫星Level 1.1级产品(SLC产品),L波段,包括4个极化方式(HH、HV、VH和VV),成像时间为2010年11月16日,幅宽65×30km,中心入射角为23°53′52.8″,距离向分辨率为23.1m,方位向分辨率为3.6m。对SLC数据进行多视、Refined Lee滤波等处理,由于实际交叉极化测量值(VH和HV)并不相同,在假设满足互易定理条件下,单站交叉极化值采用实际测量值的平均值。如图 4所示,其中图 4(a)-(d)分别为HH、HV、VH和VV极化方式的多视SAR强度影像。
|
| 图 4 全极化图像 Fig. 4 Full-pol images |
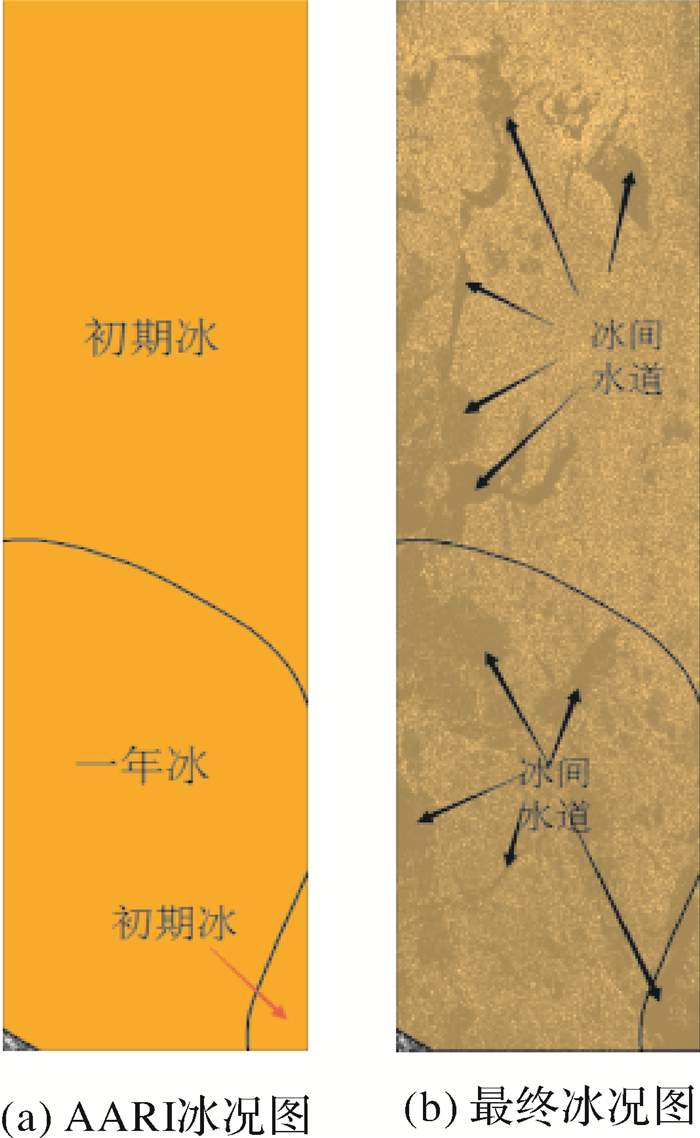
为了对研究区域冰情进行验证,采用俄罗斯Arctic and Antarctic Research Institute(AARI)发布的冰况图为参考数据(图 5(a))。由图 5(a)及专家解译(图 5(b))可知,研究区域内主要存在开放水域(包括冰间水道)、初期冰(厚度0~30cm)、一年冰(厚度30~200cm)3个冰水类型(如图 5(b)所示)。
|
| 图 5 参考数据 Fig. 5 Referenced data |
2.3 试验结果与讨论
采用本文算法及对比算法对研究区域进行分类试验,通过以冰况图为标准对分类结果进行分析以验证本文算法有效性。其中,对比算法分别为基于几何扰动滤波的最大似然分类法(geometry perturbation filter, GPF)[31]、基于Wishart距离的最大似然分类法以及基于径向基函数(radial basis function, RBF)的支持向量机(support vector machine, SVM)分类法。
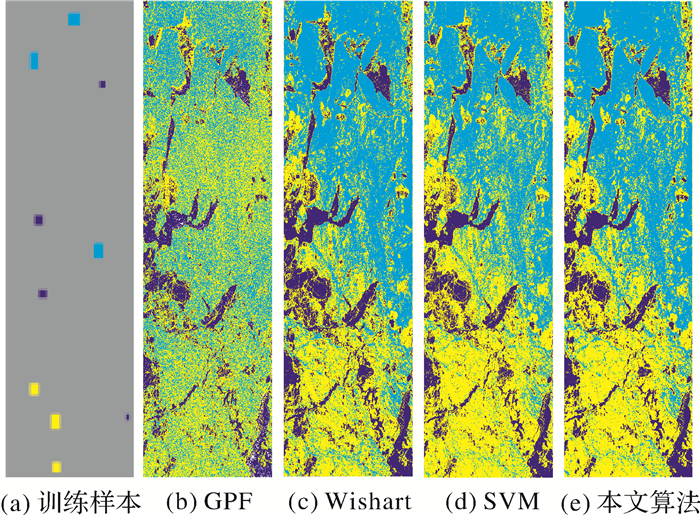
图 6为本文算法及对比算法分类结果。其中,图 6(a)为3类冰水的训练样本,黄色表示一年冰,蓝色表示开放水域,天蓝色表示初期冰,3类训练样本点共计10.2万个,单一类别样本大约3.4万;图 6(b)-(e)分别为GPF、Wishart和SVM 3种对比算法及本文算法的分类结果。
|
| 图 6 分类结果 Fig. 6 Classification result |
以冰况图为标准,对分类结果进行视觉分析可以直观地看出,4种方法对于蓝色的开放水域分类较好,而对于初期冰和一年冰分类效果存在差异,其中使用GPF分类结果明显较差于后3种分类方法;本文算法、Wishart及SVM法整体分类效果相近,局部区域有误分现象,Wishart分类和SVM分类差异主要表现在周围均为一年冰中分布少量初期冰情况,如图 6(c)、6(d)和6(e)中红色椭圆框区域属于一年冰范围,但Wishart分类中出现较多初期冰,而在SVM及本文算法中较少,本文算法与SVM分类结果基本吻合。
由于海冰分布的复杂性,及其易受气候影响的特点,全局的验证数据获取难度较大、精度较差。因此对整幅图验证比较困难,且存在较大误差。为了更好地评价分类精度,同时针对BP网络训练中存在的过拟合问题,本文采用部分样本简单交叉验证方法。方法步骤如下:①从选取的训练数据(见图 6(a))中随机选择一定比例的样本作为训练集,剩余的作为测试集;②对训练集进行训练,得到训练模型及相应训练精度;③将测试集代入训练模型,得到测试集的标签,求出分类正确率;④选择具有最大分类率的模型。样本验证数据采用AARI发布的当天左右冰况图,依据其基本冰型分布,再通过选取各类同质样本得到;精度评价指标采用衡量各类冰型的总精度(overall accuracy, OA)以及衡量分类器总体分类性能的Kappa值。
各算法对各类型海冰的整体分类精度如表 2所示,其中,总体精度(OA)表示样本正确分类个数与样本总个数之比,Kappa系数是分类器性能的一种常用度量,Kappa系数越接近于1,分类性能越优良。由表 2可知,各算法对针对各个时期的冰型分类效果不同。从各个冰型的分类精度来看,4种方法对开放水域的分类精度较高,均达到90%以上,其中最低的为GPF达到91.8%,分类精度最高为SVM,达到98.49%,本文算法也达到97.72%的精度;各类算法对初期冰和一年冰分类精度存在较大差异,GPF对初期冰和一年冰的分类相近,均接近70%,在4种算法中精度最低;本文算法对初期冰分类精度最高,达到97.05%;对一年冰分类精度稍低于SVM算法;Wishart方法对初期冰识别能力较强,达到96.69%,但对一年冰分类精度则低些,为85.96%;SVM对初期冰和一年冰的分类精度较高,在93%左右;本文算法在初期冰分类上比SVM高出5个百分点,一年冰精度与SVM相近。从4种算法的总体精度和Kappa指标来说,本文算法分类精度最高,SVM次之,Wishart再之,GPF法最低,在总体精度及Kappa系数上均不如其他3种方法,不适合海冰分类。
| 冰型 | GPF | Wishart | SVM | 本文 |
| 开放水 | 91.8% | 98.4% | 98.49% | 97.72% |
| 初期冰 | 68.23% | 96.69% | 92.85% | 97.05% |
| 一年冰 | 69.66% | 85.96% | 93.99% | 92.91% |
| OA | 75.16% | 93.85% | 94.46% | 95.72% |
| Kappa | 0.624 | 0.9033 | 0.9138 | 0.9346 |
2.4 极化特征分析
为了具体考察单一特征对开放水域、初期冰及一年冰的区分能力,对各极化特征进行分析和讨论。极化分解特征可分为两种类型:一种是基于模型的目标分解特征,包括各分量具有物理散射含义的相干Pauli分解;另一种是基于相干矩阵特征值的H/α/A分解相关特征。通过分析3类冰水在两类极化特征中的表现,评价其对极化SAR海冰分类能力。
2.4.1 基于模型的目标分解为了分析各目标分解特征对上述3类冰水的区分能力,现从这3类冰水在各特征图像的空间统计特征角度来分析。
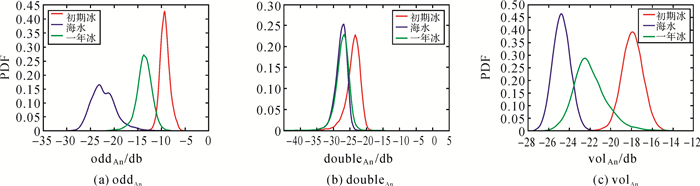
图 7是Pauli分解的3个分量关于3类冰水的概率密度函数(probability density function, PDF)曲线图。可以看出表面散射分量和体散射分量的PDF重叠度较二次散射低,对3类冰水的区分度较好;图 8和图 9分别是An分解和B&F分解分量关于3类冰水的概率密度函数曲线图;与Pauli分解结果类似,但二次散射分量的PDF重叠度更高,不适合海水分类;其中B&F分解的体散射分量范围更广,产生了两个波峰。从图 7、8、9可以看出,海水功率在3种散射中均最低,初期冰最高,一年冰处于两者之间;表面散射分量中海水功率较初期冰和一年冰的差别更大,体散射分量差别次之,二次散射分量差别最小,可以说明表面散射分量对于区分这3种冰水更为明显。

|
| 图 7 Pauli分解分量的PDF Fig. 7 PDF of Pauli decomposition's components |
|
| 图 8 An分解分量的PDF Fig. 8 PDF of An decomposition's components |

|
| 图 9 B&F分解分量的PDF Fig. 9 PDF of B&F decomposition's components |
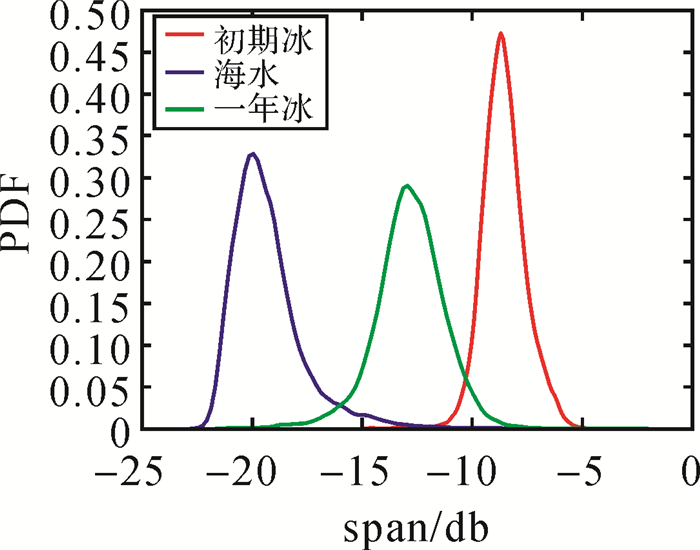
图 10和图 11分别为散射总功率span_db图像以及3类冰水的PDF图。散射总功率是4种极化方式强度之和,能够刻画比单一极化强度更全面的散射信号。可以看出,相较于上述分解特征,总功率特征对区分3类冰更为明显:初期冰散射功率值最高,一年冰次之,开放水域最低。

|
| 图 10 span_db Fig. 10 span_db |
|
| 图 11 span_db的PDF Fig. 11 PDF of span_db |
2.4.2 基于特征值的H/α/A分解
根据H/α/A分解理论,在特征H与α组成的二维平面中,大部分散射机制可被分为8类,对其成图分析可以获得海冰的散射类型分布信息。图 12分别是特征H与α、A与α、H与A二维成图结果,其中红色表示初期冰,蓝色表示海水,绿色表示一年冰。可以看出,蓝色和绿色区分较好,但红色被绿色完全遮挡,说明冰水区别明显,但初期冰与一年冰基本无法区分,因而对于H/α/A分解3个特征较上述分解对冰水区分不是很明显。

|
| 图 12 H/α/A平面图 Fig. 12 H/α/A plane plot |
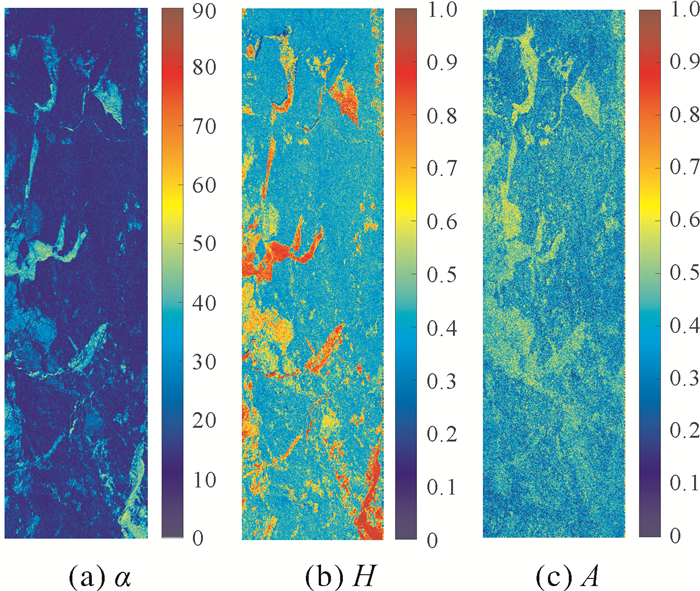
图 13(a)-(c)分别为极化散射角α、极化熵H及各向异性A的海冰图像。α的分布范围在0°~60°之间,整体偏向蓝色,角度较小,趋向于表面散射,海水区域α角相对较大,海冰区域因其表面光滑而α较低;H图像中海水区域呈现红色,说明去极化程度的极化熵较高,海冰区域为蓝绿色,极化熵较低;A反映次级散射机制间的相对大小关系。由图观察可知,冰水区别较小,其中海水区域各向异性相对较大,海冰区则较小。
|
| 图 13 H/α/A分解 Fig. 13 H/α/A decomposition |
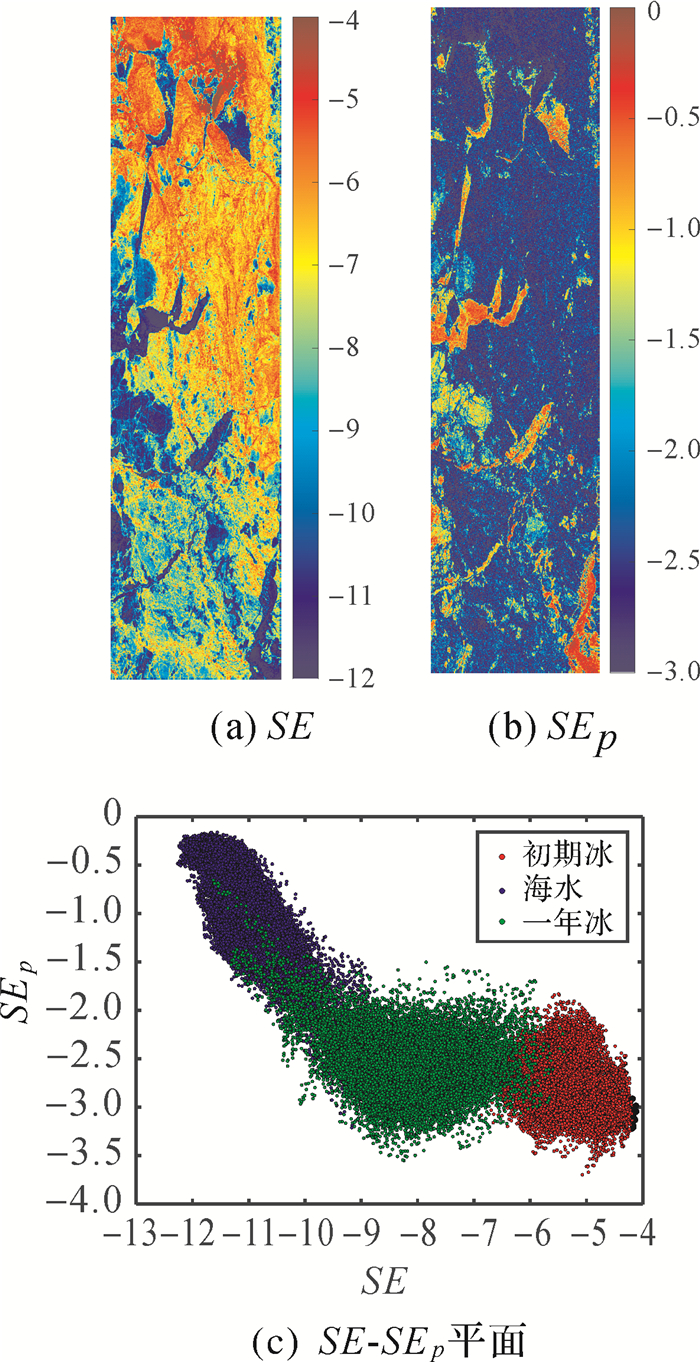
图 14(a)-(c)分别为极化特征香农熵SE,其极化分量SEp,以及3类冰水在SE-SEp平面内数据分布图。可以看出在SE图像中海水的SE较低,初期冰最高,一年冰处于两者之间,区分较为明显;在SEp图像中,海水区域比海冰区的SEp值高,两类冰仅依靠SEp无法区分,反而海水因风速,粗糙性差异明显;将其二维成图可以看出,一年冰作为连接初期冰和海水的中间部分,虽有重叠,但整体区分性较好,适合于冰水的分类。
|
| 图 14 香农熵特征 Fig. 14 Shannon Entropy feature |
2.5 降维分析
本文采用PCA作为高相关特征的降维方法,具有操作简单,易于理解等特点。为了与其他降维方法的降维效果进行对比,现增加局部线性嵌入[32](locally linear embedding, LLE)进行对比分析。
LLE假定在局部邻域内数据点是线性的,由重构成本函数最小化求出最优权值。LLE算法可以归结为3步:首先,寻找每个样本点的k个局部邻域点;接着,由每个样本点的近邻点计算出该样本点的局部重建权值矩阵;最后,由该样本点的局部重建权值矩阵和其近邻点计算出该样本点的输出值。
表 3为采用PCA、LLE对15维及前9维特征降维运行时间以及降维后主分量特征的分类精度对比,LLE参数设置:从训练样本中随机选取10000个特征点,经多次试验,取局部邻域参数k=12,降维至3维。
| 操作 | PCA | LLE | |||
| f1, f2, …, f15 | f1, f2, …, f9 | f1, f2, …, f15 | f1, f2, …, f9 | ||
| 运行时间/s | 0.17 | 0.10 | 41 | 30 | |
| 分类精度/(%) | 95.95 | 95.45 | 79.45 | 81.19 | |
由表 3可以看出,PCA处理算法效率比LLE高,特别是在运行时间上存在明显差异,通过衡量两种不同原理的降维方法的运行性能,本文所构建的特征空间比较适合于基于线性相关的PCA降维,比复杂的非线性降维更优越;局部线性嵌入作为经典的非线性降维方法,尽管能够反映数据的非线性关系并保持高维数据的内在流形结构,但是其计算原理复杂,用于分类效率低,且存在参数调优,因而在实际操作时不如PCA有效。
此外,为了判断降维特征对算法效率的影响,将其进行处理大尺度SAR图像(4608×1248)的运行时间对比。本文算法采用MATLAB编程实现,并在Intel(R) Xeon(R) CPU E5-2609 v2 @ 2.50GHz 8G计算机上运行,运行时间如表 4所示。
| 特征 | f1, f2, …, f15 | PCA15 | f1, f2, …, f9 | PCA9 | f1, f4, f6, f7, f9, f10, f13, f15 | PCA8 |
| 运行时间/s | 24 | 10 | 18 | 11 | 16 | 11 |
| 测试精度/(%) | 92.74 | 86.40 | 91.90 | 87.48 | 92.40 | 86.19 |
通过对各个极化分解特征的具体分析,对其进行不同组合,分别将其作为输入矢量输入到分类器中,考察其分类性能。表 4是输入不同特征矢量时,BP神经网络所具有的不同分类精度:从表 5可以看出,不同输入特征对3类冰水的分类能力差异明显。对单一目标分解来说,基于散射模型的目标分解其分类效果均在88%以上,适合于分类,其中B&F分解分类能力更好,而基于特征分解的H/α/A分解则分类精度较低,在55%左右,且根据试验情况看结果不够稳定,说明在BP神经网络结构训练不够准确,误分情况严重,不适合海冰分类。就单一散射模型看,表面散射特征对3类冰水分类效果的贡献率在3种散射机制中是最大的,体散射次之,二次散射贡献率最低。而对于两个基于特征值的极化特征参数香农熵SE和香农熵极化分量SEp则比较适合这3类冰水的区分。此外,由表 3、4及表 5可以看出,相对于非线性LLE降维算法效果,利用线性的PCA降维对构建的特征空间是直接而有效的,一方面极大地提高了算法运行效率,尽管对分类精度有一定影响,平均下降了6个百分点,但也达到85%以上的分类精度,因而在对精度要求不高、实用情况下,可以采用PCA降维方法。
| % | |||
| 输入特征 | 训练精度 | 测试精度 | |
| 目标分解特征 | Pauli分解 | 93.03 | 88.84 |
| An分解 | 92.93 | 88.61 | |
| B&F分解 | 94.56 | 90.50 | |
| H/A/α分解 | 66.43 | 54.83 | |
| 散射机制特征 | 表面散射特征 (f1, f2, f3) |
94.20 | 90.50 |
| 二次散射特征 (f6, f13, f14) |
67.01 | 75.73 | |
| 体散射特征 (f7, f8, f9) |
84.49 | 79.21 | |
| 降维特征 | f1, f2, …, f15 | 95.51 | 92.74 |
| PCA15 | 95.70 | 86.40 | |
| f1, f2, …, f9 | 92.9 | 91.90 | |
| PCA9 | 95.68 | 87.48 | |
| PCA9+f10, f11…, f15 | 96.04 | 88.73 | |
| f1, f4, f6, f7, f9, f10, f13, f15 | 96.00 | 92.40 | |
| PCA8 | 96.51 | 86.19 | |
| f10, f11…, f15 | 72.52 | 65.48 | |
| PCA6 | 75.20 | 63.79 | |
| 特征分解特征 | f4, f10, f11, f12, f15 | 95.22 | 92.35 |
| f4, f10 | 94.22 | 91.98 | |
| 注:训练精度是指分类器对训练数据的拟合度,测试精度指利用已训练的分类器对测试数据的分类精度;PCA9指对高相关的前9维特征进行PCA,取前三主成分;PCA8指对挑选的各组相关性较低的特征进行PCA(f1, f4, f6, f7, f9, f10, f13, f15);PCA6指对低相关的后6维特征进行PCA,取前三主成分。 | |||
3 结论
本文以格陵兰中部海域为例,采用L波段ALOS PALSAR全极化数据,提取极化目标分解特征参数,构建特征空间,并对相关性大的特征进行PCA降维操作,最后输入到BP神经网络分类器中,得到海冰分类结果。以冰况图解译的海冰类型为标准,对本文算法与对比算法的分类结果进行定性定量分析,可以验证本文算法的有效性。此外,通过对各特征进行进一步分析,可以得出以下结论:基于模型的目标分解对冰水分类能力比H/α/A分解更有效,其中B&F分解的分类精度最高;从散射机理来说,表面散射和体散射是海冰的主要散射机制,二次散射所占贡献较小;散射总功率span_db、香农熵SE及其极化分量SEp对于海冰分类识别是个很好的极化参数;在大尺度海冰分类中,为了提高分类效率,对高维且分类效果较好的特征组应当考虑其相关性,在不致引起较大精度损失前提下,可以进行PCA等降维操作。本文还存在着一些不足,如冰型较少,仅单一频段等,接下来将对更多冰型,特别是多年冰和一年冰的散射机理方面进行深入研究,以及进行多波段极化SAR数据海冰分类性能的比较研究。
| [1] |
杨磊, 常晓涛, 郭金运, 等.
ENVISAT雷达高度计后向散射系数的极区海冰分布特性[J]. 测绘学报, 2013, 42(5): 676–681.
YANG Lei, CHANG Xiaotao, GUO Jinyun, et al. Research on Distribution Characteristics of Polar Sea Ice by ENVISAT Altimetry Backscatter Coefficient[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 676–681. |
| [2] | WALSH J E. The Role of Sea Ice in Climatic Variability:Theories and Evidence[J]. Atmosphere-Ocean, 1983, 21(3): 229–242. DOI:10.1080/07055900.1983.9649166 |
| [3] | TOGGWEILER J R, RUSSELL J L. Ocean Circulation in a Warming Climate[J]. Nature, 2008, 451(7176): 286–288. DOI:10.1038/nature06590 |
| [4] |
沈杨, 郎文辉, 吴杰, 等.
结合MRF与ν-SVM的SAR海冰图像分类[J]. 遥感学报, 2015, 19(5): 844–855.
SHEN Yang, LANG Wenhui, WU Jie, et al. Combining MRF and ν-SVM for SAR Sea Ice Image Classification[J]. Journal of Remote Sensing, 2015, 19(5): 844–855. |
| [5] | ZAKHVATKINA N, KOROSOV A, MUCKENHUBER S, et al. Operational Algorithm for Ice-water Classification on Dual-polarized RADARSAT-2 Images[J]. The Cryosphere, 2017, 11(1): 33–46. DOI:10.5194/tc-11-33-2017 |
| [6] | ZAKHVATKINA N Y, ALEXANDROV V Y, JOHANNESSEN O M, et al. Classification of Sea Ice Types in Envisat Synthetic Aperture Radar Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(5): 2587–2600. DOI:10.1109/TGRS.2012.2212445 |
| [7] | DIERKING W. Mapping of Different Sea Ice Regimes Using Images From Sentinel-1 and ALOS Synthetic Aperture Radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(3): 1045–1058. DOI:10.1109/TGRS.2009.2031806 |
| [8] | SANDVEN S, JOHANNESSEN O M, MILES M W, et al. Barents Sea Seasonal Ice Zone Features and Processes from ERS 1 Synthetic Aperture Radar:Seasonal Ice Zone Experiment 1992[J]. Journal of Geophysical Research:Oceans, 1999, 104(C7): 15843–15857. DOI:10.1029/1998JC900050 |
| [9] | CLAUSI D A, YUE Bing. Comparing Cooccurrence Probabilities and Markov Random Fields for Texture Analysis of SAR Sea Ice Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(1): 215–228. DOI:10.1109/TGRS.2003.817218 |
| [10] | CLAUSI D A. Comparison and Fusion of Co-occurrence, Gabor and MRF Texture Features for Classification of SAR Sea-ice Imagery[J]. Atmosphere-Ocean, 2001, 39(3): 183–194. DOI:10.1080/07055900.2001.9649675 |
| [11] | LEE J S, GRUNES M R, AINSWORTH T L, et al. Unsupervised Classification using Polarimetric Decomposition and the Complex Wishart Classifier[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2249–2258. DOI:10.1109/36.789621 |
| [12] |
郎丰铠, 杨杰, 赵伶俐, 等.
基于Freeman散射熵和各向异性度的极化SAR影像分类算法研究[J]. 测绘学报, 2012, 41(4): 556–562.
LANG Fengkai, YANG Jie, ZHAO Lingli, et al. Polarimetric SAR Data Classification with Freeman Entropy and Anisotropy Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 556–562. |
| [13] | NEZRY E, LOPES A, DUCROT-GAMBART D, et al. Supervised Classification of K-distributed SAR Images of Natural Targets and Probability of Error Estimation[J]. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(5): 1233–1242. DOI:10.1109/36.536539 |
| [14] | DENG Xinping, LOPEZ-MARTINEZ C, CHEN Jinsong, et al. Statistical Modeling of Polarimetric SAR Data:A Survey and Challenges[J]. Remote Sensing, 2017, 9(4): 348. DOI:10.3390/rs9040348 |
| [15] | LEE J S, POTTIER E. Polarimetric Radar Imaging:From Basics to Applications[M]. Boca Raton: CRC Press, 2009. |
| [16] | CLOUDE S R, POTTIER E. An Entropy Based Classification Scheme for Land Applications of Polarimetric SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(1): 68–78. DOI:10.1109/36.551935 |
| [17] | WAKABAYASHI H, MATSUOKA T, NAKAMURA K, et al. Polarimetric Characteristics of Sea Ice in the Sea of Okhotsk Observed by Airborne L-band SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(11): 2412–2425. DOI:10.1109/TGRS.2004.836259 |
| [18] |
张晰, 张杰, 孟俊敏, 等.
基于极化散射特征的极化合成孔径雷达海冰分类方法研究:以渤海海冰分类为例[J]. 海洋学报, 2013, 35(5): 95–101.
ZHANG Xi, ZHANG Jie, MENG Junmin, et al. Polarimetric Scattering Characteristics Based Sea Ice Types Classification by Polarimetric Synthetic Aperture Radar:Taking Sea Ice in the Bohai Sea for Example[J]. Acta Oceanologica Sinica, 2013, 35(5): 95–101. DOI:10.3969/j.issn.0253-4193.2013.05.010 |
| [19] | SINGHA S. Arctic Sea Ice Characterization Using Fully Polarimetric Air-borne and Space-borne Synthetic Aperture Radar[C]//Proceedings of CIRFA Seminar. Tromsö, Norway: CIRFA, 2017. |
| [20] | MOEN M A N, FERRO-FAMIL L, DOULGERIS A P, et al. Polarimetric Decomposition Analysis of Sea Ice Data[C]//Proceedings of POLinSAR 2013 Workshop. Frascati, Italy: [s.n.], 2013. |
| [21] | MOEN M A N, DOULGERIS A P, ANFINSEN S N, et al. Comparison of Automatic Segmentation of Full Polarimetric SAR Sea Ice Images with Manually Drawn Ice Charts[J]. The Cryosphere, 2013, 7(3): 2595–2634. DOI:10.5194/tcd-7-2595-2013 |
| [22] | MOEN M A, ANFINSEN S N, DOULGERIS A P, et al. Assessing Polarimetric SAR Sea-ice Classifications Using Consecutive Day Images[J]. Annals of Glaciology, 2015, 56(69): 285–294. DOI:10.3189/2015AoG69A802 |
| [23] | LEE J S, GRUNES M R, DE GRANDI G. Polarimetric SAR Speckle Filtering and Its Implication for Classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2363–2373. DOI:10.1109/36.789635 |
| [24] | ELTOFT T, DOULGERIS A P, GRAHN J. Model-based Polarimetric Decomposition of Arctic Sea Ice[C]//Proceedings of EUSAR 2014; 10th European Conference on Synthetic Aperture Radar. Berlin, Germany: IEEE, 2014. |
| [25] | ARIENZO A. Physical and Statistical Based Decomposition of Polarimetric Synthetic Aperture Radar Images of Arctic Seaice[D]. Tromso: The Arctic University of Norway, 2015. |
| [26] | AN Wentao, CUI Yi, YANG Jian. Three-component Model-based Decomposition for Polarimetric SAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(6): 2732–2739. DOI:10.1109/TGRS.2010.2041242 |
| [27] | BHATTACHARYA A, MUHURI A, DE S, et al. Modifying the Yamaguchi Four-component Decomposition Scattering Powers Using a Stochastic Distance[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(7): 3497–3506. DOI:10.1109/JSTARS.2015.2420683 |
| [28] | MORIO J, REFREGIER P, GOUDAIL F, et al. Application of Information Theory Measures to Polarimetric and Interferometric SAR Images[C]//Proceedings of Physics in Signal and Image Processing 2007. Mulhounse, France: [s.n.], 2007. |
| [29] | WOLD S, ESBENSEN K, GELADI P. Principal Component Analysis[J]. Chemometrics and Intelligent Laboratory Systems, 1987, 2(1-3): 37–52. DOI:10.1016/0169-7439(87)80084-9 |
| [30] | RUMELHART D E, HINTON G E, WILLIAMS R J. Learning Representations by Back-propagating Errors[J]. Nature, 1986, 323(6088): 533–536. DOI:10.1038/323533a0 |
| [31] | MARINO A, CLOUDE S R, WOODHOUSE I H. Detecting Depolarized Targets Using a New Geometrical Perturbation Filter[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(10): 3787–3799. DOI:10.1109/TGRS.2012.2185703 |
| [32] | ROWEIS S T, SAUL L K. Nonlinear Dimensionality Reduction by Locally Linear Embedding[J]. Science, 2000, 290(5500): 2323–2326. DOI:10.1126/science.290.5500.2323 |


