2. 北京建筑大学测绘与城市空间信息学院, 北京 100044;
3. 武汉大学测绘学院, 湖北 武汉 430079;
4. 山东科技大学 测绘科学与工程学院, 山东 青岛 266590
2. School of Geomatics and Urban Spatial Information, Beijing University of Civil Engineering and Architecture, Beijing 100044, China;
3. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
4. College of Geomatics, Shandong University of Science and Technology, Qingdao 266590, China
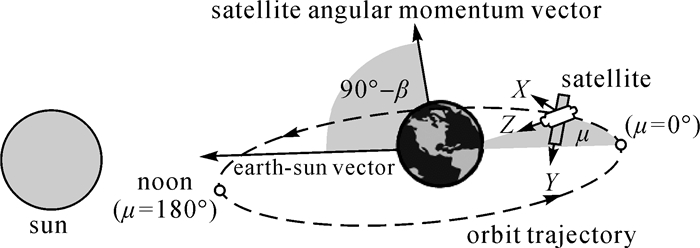
在GNSS精密单点定位(PPP)中,卫星偏航姿态模型主要在两个方面影响高精度定位:①天线相位中心偏差(PCO)及变化(PCV)的改正。②载波相位观测值的天线相位缠绕计算也依赖卫星偏航姿态的确定[1]。如图 1所示,当太阳、地球、卫星处于同一条直线时,GPS、GALILEO卫星姿态将在较短时间内翻转180°,此时卫星硬件能提供的最大偏航角速率不能达到名义偏航角速率,卫星无法维持名义姿态而出现姿态异常时期[2]。此外,当卫星(除IIR卫星)进入地影时,由于光敏感器不能正常工作,卫星名义姿态很难维持而产生地影机动[1]。在卫星姿态处于异常时期, 若采用名义姿态将影响相位缠绕、天线相位中心偏差等误差的计算,严重降低高精度定位的可靠性。
|
| 图 1 卫星姿态异常时期示意图 Fig. 1 Abnormal yaw attitude of satellite |
国内外研究学者针对GNSS卫星姿态异常时期进行了系统性的研究。文献[1-10]提出了GPS卫星姿态改正模型并分析了该模型对卫星钟钟差、定位精度的影响;文献[11-16]分别给出了GLONASS-M、BDS、GALILEO卫星在姿态异常时期的偏航角模型及改正策略。目前,尚未有学者开展多系统卫星姿态异常对定位影响的相关研究,因此,本文基于GPS、GALILEO卫星系统的姿态控制策略,深入研究GPS、GALILEO卫星的子午、子夜、地影机动模型,分析GPS/GALILEO卫星偏航姿态异常时期的载波相位观测值残差变化,比较不同姿态改正策略下GPS/GALILEO动态PPP的定位精度。
1 GPS/GALILEO偏航姿态模型 1.1 GNSS卫星名义姿态模型由于不同类型卫星制造商的星固坐标系定义不同,为保持一致性,IGS(International GNSS Service)定义星固系如下[17]:①Z轴平行于卫星天线信号发射方向并指向地心;②Y轴平行于太阳帆板并垂直于太阳、地球和卫星构成的平面;③X轴垂直于Y轴和Z轴并构成右手坐标系并指向太阳入射方向。为遵循IGS星固系的标准与规范,本文所有GNSS卫星均采用IGS所定义的星固系。
GNSS卫星名义姿态在星固系下3轴单位向量ex、ey、ez可由式(1)确定[17]
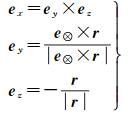 (1)
(1)
式中,e⊗为卫星至太阳方向的单位向量;r为地心指向卫星方向的单位向量;|*|表示向量取模运算符。GNSS卫星偏航角φ定义为沿轨道切线方向与星固系X轴之间的夹角[6]
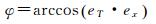 (2)
(2)
式中,eT、ex分别沿轨道切线方向、卫星星固系X轴单位向量;arccos(·)为反余弦函数。根据太阳高度角、轨道角与式(2)的几何关系,名义姿态偏航角可以表示为[4]
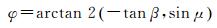 (3)
(3)
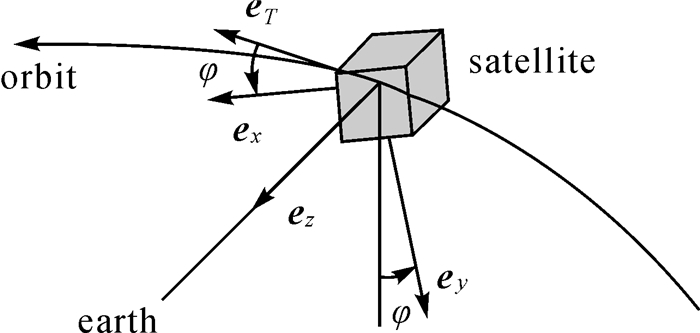
式中,β为太阳高度角;μ为轨道角(以远日点为起点);arctan 2(·)为FORTRAN语言中的反正切函数。对GNSS卫星而言,由于卫星的信号发射方向始终指向地心,因此不存在俯仰角与横滚角,卫星姿态仅用偏航姿态角φ确定[17],如图 2所示,将卫星在轨切线方向eT绕星固系的Z轴旋转φ角度,即可确定星固系X轴的指向,因此,卫星在姿态异常时期,偏航姿态模型的建立主要是确定偏航姿态角φ的变化。
|
| 图 2 载体坐标系X轴与轨道切线方向eT的几何关系 Fig. 2 Geometric relationship between the X axis of the coordinate system and the tangent direction eT of the orbit |
1.2 GPS卫星姿态改正模型
依据GPS卫星在机动时期的不同改正模型,GPS在偏航姿态异常时期可划分为两大类:①仅包含子午机动和子夜机动的BLOCK ⅡR卫星(不受地影影响);②包含子午机动、地影机动的BLOCK ⅡF、BLOCK Ⅱ/ⅡA卫星(该卫星已与2017年1月退役)。相较于BLOCK ⅡA卫星,BLOCK ⅡF卫星进出地影时模型偏航角与名义偏航角的差异不大且恢复期时间较短,即使在太阳高度角较低时,也不会超过5min[5],因此本文采用的GPS卫星姿态改正模型,忽略了ⅡF卫星在进出地影区域时刻偏航角速率加速与减速过程,进入地影时,卫星即以恒定偏航角速率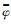
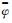
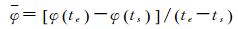 (4)
(4)
式中, te、ts分别为地影机动结束时刻与开始时刻;φ(te)、φ(ts)分别为机动结束时刻和开始时刻的名义偏航角,可由式(3)计算。BLOCK ⅡF卫星在地影区域时,t时刻的模型偏航角φm(t)可由式(5)计算得到
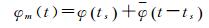 (5)
(5)
BLOCK ⅡF卫星的地影机动不超过54min,除地影机动外,在太阳高度角β较小且在近日点附近时,BLOCK ⅡF卫星姿态会在短时间内发生180°剧烈翻转,由于硬件最大偏航角速率达不到旋转所需要的偏航角速率,从而产生子午机动。在机动时间内,BLOCK ⅡF卫星将以最大偏航角速率旋转,直到模型偏航角等于名义偏航角时机动停止,则t时刻偏航姿态模型为[18]
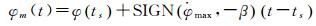 (6)
(6)
式中,ts为子午机动开始时间;φ(ts)为机动开始时的名义偏航角;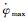
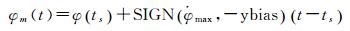 (7)
(7)
由此导致卫星姿态控制方向发生变化,并引起约2min的子午机动延迟,造成约13°的偏航角误差[18]。
BLOCK ⅡR卫星在地影期间能有效维持名义姿态,因此不受地影影响,只存在由于硬件速率限制所产生的子午和子夜机动,姿态改正模型与BLOCK ⅡF子午机动类似[3]。BLOCK ⅡR卫星子午机动(noon)与子夜机动(midnight)期间偏航角可分别由式(8)、式(9)确定[18]
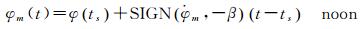 (8)
(8)
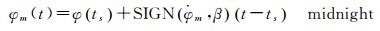 (9)
(9)
与BLOCK ⅡF卫星不同,BLOCK ⅡR卫星没有引进姿态常量偏差ybias,即使太阳高角β较小,也不会出现模型转动方向与名义偏航角转动方向相反的情况[10]。相较于BLOCK ⅡF卫星,BLOCK ⅡR卫星最大偏航角速率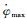
根据欧洲全球导航卫星局(European Global Navigation Satellite Systems Agency)提供的GALILEO姿态控制算法文档表明[19]:GALILEO卫星在地影和子午机动期间采取与GPS卫星不同的姿态控制模式,为保证在姿态异常时期偏航角速率不超过硬件偏航速率的限制(IOV、FOC卫星约为0.203°/s),GALILEO卫星将采用动态动偏(dynamic yaw-steering)的姿态控制策略[17]。对于IOV卫星而言,其名义偏航角φ的计算为[19]
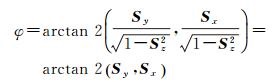 (10)
(10)
式中,Sx、Sy、Sz为太阳单位向量,可根据太阳高度角β与轨道角μ(以近日点为起点)计算[19]
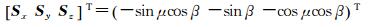 (11)
(11)
可以看出,结合式(11)、式(10)化简后,与式(3)中名义偏航角计算等价。当IOV卫星满足以下条件时进入地影(shadow)或子午机动[18]
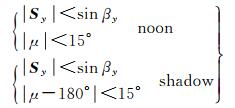 (12)
(12)
式中,βy=2°,根据式(11)中的Sy作等式替换,易得β=2°,即当太阳高度角β < 2°时,IOV卫星将出现偏航姿态异常。在机动时期,IOV卫星将采用动态动偏模式进行姿态控制,使用平滑后的Shy代替等式(10)中的Sy[19]
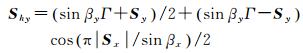 (13)
(13)
式中,Γ为Sy机动开始时正负号(即Sy>0,Γ=1;Sy < 0,Γ=-1),结合式(13)、式(10)易得IOV卫星在机动时的模型偏航角
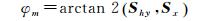 (14)
(14)
从式(13)可以看出,IOV卫星机动模式不同于GPS卫星,当IOV卫星在地影机动或子午机动且μ≈180°或μ≈0°时,太阳单位矢量Sx≈0, Sy≈0,则cos(π|Sx|/sinβx)≈1,Shy≈±sinβy,即式(14)将采用βy=2°计算模型偏航角,确保了偏航角速率不超过硬件限制[19]。IOV卫星地影与子午机动时间约为70min,在开始机动的前15min与机动即将结束的15min,即使在太阳高度角β≈0°时,名义偏航角与模型偏航角差异不超过0°[19]。IOV卫星机动时间较长,在太阳高度角β < 0.07°时,同样应采用机动开始时刻ts的太阳高度角β计算式(13)中的Shy。
与IOV卫星类似,FOC卫星存在地影或子午机动,采用动态动偏模式来控制在姿态异常时期的卫星偏航姿态。FOC卫星t时刻的名义偏航角φ(t)计算公式为[19]
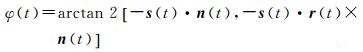 (15)
(15)
式中,r(t)、n(t)、s(t)分别为t时刻惯性系下(J2000)卫星位置、轨道平面、太阳位置的单位向量。当FOC卫星的太阳高度角β较小,且处于近日点与远日点附近时,将产生子午或地影机动,其机动条件为[19]
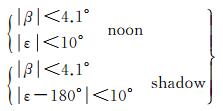 (16)
(16)
式中,ε为太阳-地球-卫星的夹角arccos (r·s),在太阳高度角|β| < 4.1°时,ε近似的等于轨道角μ。FOC卫星在机动期间,t时刻的模型偏航角φm(t)为[19]
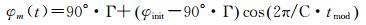 (17)
(17)
式中,tmod为机动所经历的时间tmod=t-ts;φinit为机动干开始时刻ts的名义偏航角;Γ为φinit的正负号(即φinit>0,Γ=1;φinit < 0,Γ=-1);C为常数5656。由式(17)可知,当太阳高度角β≈0°时,模型姿态角需翻转180°且机动时间最长,机动结束时的模型偏航角为φm(te)=φinit-180°,结合式(17)易得cos(2π/C·tmod)≈-1,tmod≈2828,可以看出FOC卫星地影与子午机动所经历的时间不会超过tmod的最大值2828s,约为47min。由于FOC卫星模型偏航姿态的计算与太阳高度角β无关,即使在|β|角较小时,也无需考虑在机动时期太阳高度角正负号的改变。
2 数据测试与分析为研究偏航姿态改正模型在GPS/GALILEO卫星在姿态异常时期对动态PPP定位的影响,本文分别设计了名义姿态(Yaw-Nominal)、模型姿态(Yaw-Modeled)与剔除卫星(Delete)3种不同姿态策略,并选取7个MGEX站的GPS+GALILEO观测数据,结合不同分析中心所提供的精密轨道和钟差产品,对不同姿态模型下动态PPP载波相位观测值残差、PCO改正、相位缠绕以及定位结果等进行了试验与分析。
2.1 GPS卫星不同姿态模型对PPP观测值的影响与分析为研究GPS卫星不同姿态模型对PPP滤波后观测值残差的影响,并顾及地面观测站在卫星姿态异常时期的可见性,本文选取NKLG与JFNG站的GPS+GALILEO观测数据,观测值采样率为30s,截止高度角为7°,电离层采用无电离层组合(Iono-Free-LC)进行消除一阶项延迟,对流层采用Saastamoinen模型与Niell投影函数[20],基于CNES和GFZ分析中心所提供的精密轨道和钟差产品,采用PPP浮点解进行解算[21-22],分别给出各类型卫星在异常时期的偏航角、载波相位观测值残差、相位缠绕与PCO改正值的时间序列图。
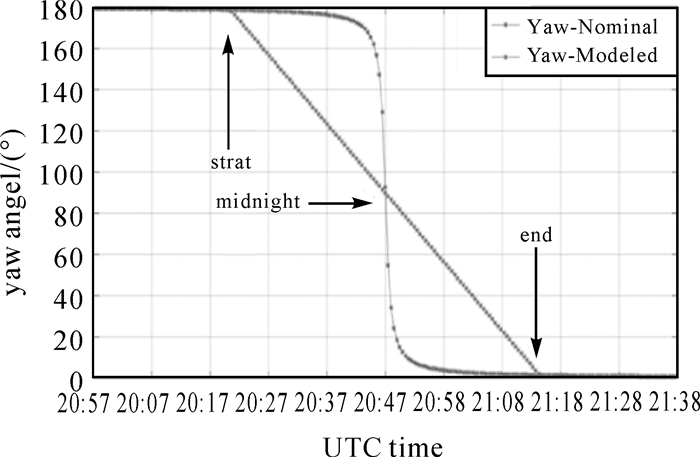
图 3给出了在2016年DOY209 G01(ⅡF)卫星穿过地影区域时期名义偏航角与模型偏航角变化图,太阳高度角β≈-0.32°。从图 3中可知,子夜机动时间约为54min,卫星姿态翻转接近180°,模型偏航角变化是一条直线,这是由于本文模型忽略了偏航角速率加速与减速过程,进入地影区域(strat)就以 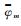
|
| 图 3 G01(IIF)穿过地影区域偏航角变化 Fig. 3 Variation of the yaw angle of G01 (IIF)through the shadow area |
|
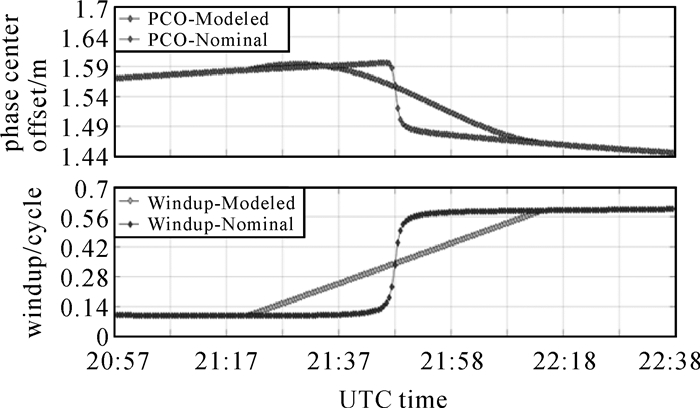
| 图 4 G01(IIF)穿过地影区域相位缠绕与天线改正变化 Fig. 4 Phase wind-up and antenna correction of G01 (IIF)through the shadow area |
|
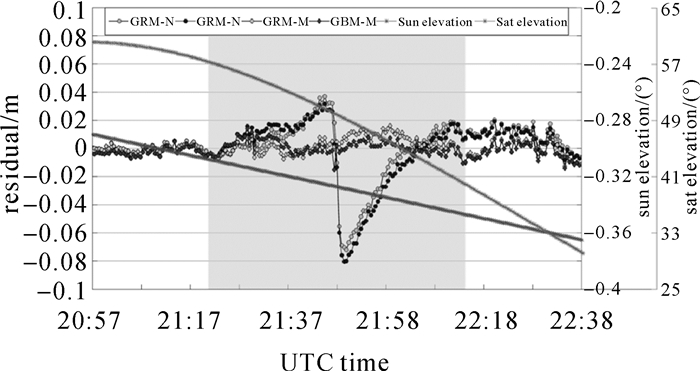
| 图 5 G01(IIF)穿过地影区观测值残差变化 Fig. 5 Residual variation of the observation value of G01 (IIF) through the shadow area |
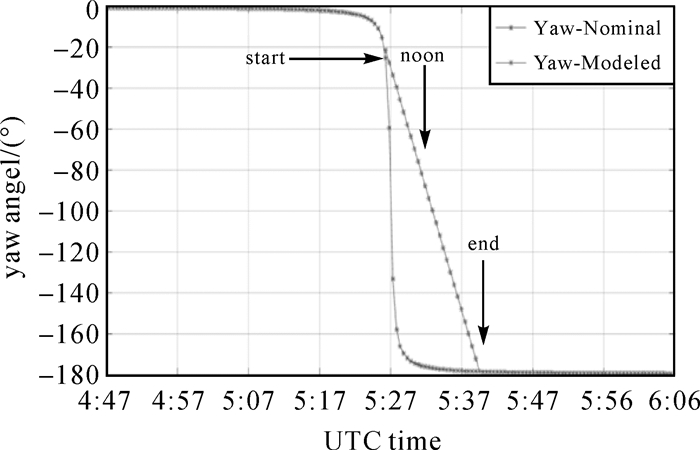
图 6为2016年DOY181 G07(BLOCK ⅡR)卫星子午机动偏航角变化图,太阳高度角β≈0.17°,子午机动时间大约10min,偏航角在短时间内翻转近180°,当硬件本身达不到这个翻转速度,就以最大偏航角速率进行姿态转动(start),直到名义偏航角与模型偏航角相等(end)时结束机动,其中在近日点(noon)两种姿态偏航角差异最大,两者差异高达约110°。
|
| 图 6 G07(IIR)子午机动偏航角变化 Fig. 6 Variation of the yaw angle of G07 (IIR)during noon turn |
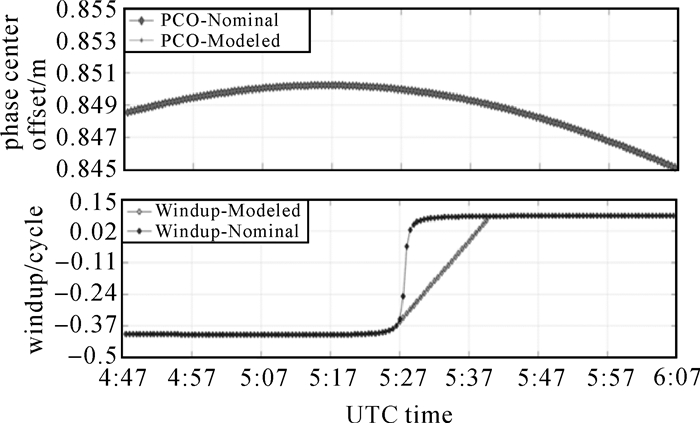
图 7给出了G07卫星子午机动时,名义姿态与模型姿态对PCO、相位缠绕改正的影响,从图 7中可以看出,两种姿态模型对相位缠绕将造成高达0.5周的差异,但对卫星的PCO改正的影响相同,这是由于BLOCK ⅡR的天线相位中心偏差只存在于Z方向,在X、Y方向上的偏差均为0,而GNSS卫星偏航姿态仅与偏航角有关,不存在翻滚与俯仰,因此BLOCK ⅡR卫星的PCO改正不受偏航姿态异常的影响[23, 24]。
|
| 图 7 G07(IIR)子午机动PCO与相位缠绕变化 Fig. 7 Phase wind-up and antenna correction of G07 (IIR) during noon turn |
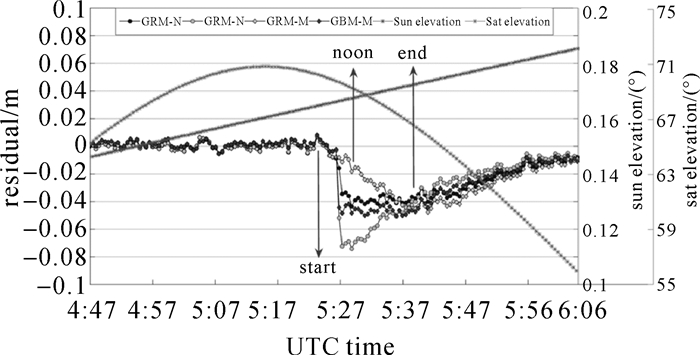
图 8给出相应于图 6中JFNG站G07(BLOCK ⅡR)子午机动观测值残差变化图,太阳高度角β从0.15°增加到0.19°,卫星高度角随时间变化呈现先上升后下降的趋势,从65°变化到约57°。由图 8可以看出,不同分析中心的产品所得到的观测值残差差异较大,使用GFZ、CNES所提供的精密轨道和钟差观测值残差分别高达8、4cm,这可能是由于GFZ、CNES分析中心在G07(BLOCK ⅡR)卫星太阳高度角绝对值|β|较小时,所采用的姿态控制策略存在略微差异。在近日点(noon)附近,采用模型姿态,观测值残差均得到了有效降低,随着名义偏航角与模型偏航角差异的增大,所对应的观测值残差也逐渐增加。
|
| 图 8 G07(IIR)子午机动观测值残差变化 Fig. 8 Residual variation of the observation value of G07 (IIR) during noon turn |
2.2 GALILEO卫星不同姿态模型对PPP观测值的影响与分析
为突出GALILEO卫星采用不同姿态模型对PPP载波相位观测值残差的影响,本文对同一时段机动的GPS卫星进行剔除,选取NKLG站的GPS+GALILEO观测数据,采用CNES、GFZ分析中心所提供的精密轨道和钟差产品,并对IOV、FOC卫星的子午机动偏航角、观测值残差时间序列图进行分析。
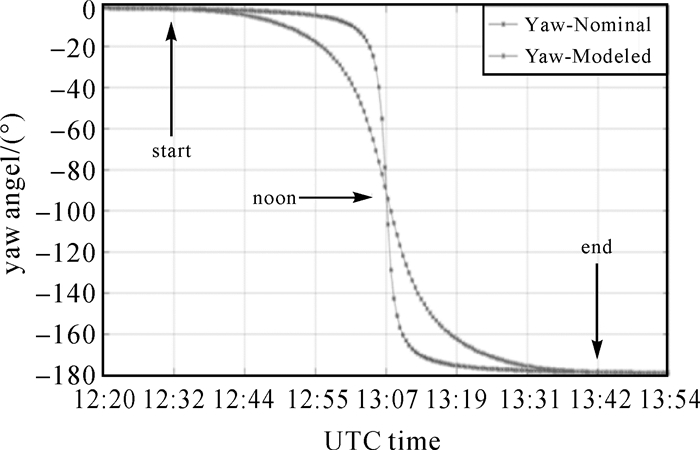
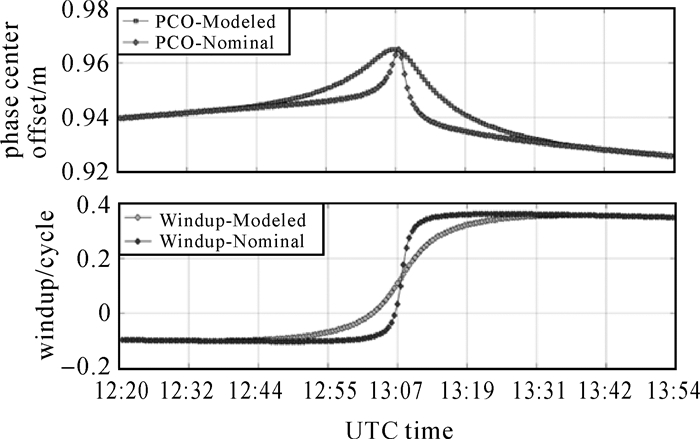
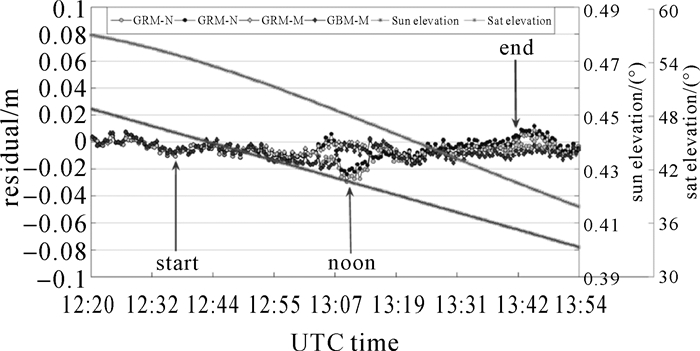
图 9给出了在2016年DOY180d E11(IOV)卫星子午机动名义偏航角与模型偏航角变化图,太阳高度角β≈0.43°。从图 9可知,模型姿态偏航角变化是一条光滑的曲线,IOV卫星机动时间大约1h 10min,姿态翻转近180°。由于IOV卫星采用动态动偏的姿态控制策略,相较GPS卫星,即使在太阳高度角β角接近于0的情况下,名义偏航角与模型偏航角差异不大,最大约为30°。图 10、图 11给出了E11卫星在此期间的PCO改正、相位缠绕与观测值残差变化图,太阳高度角β从0.02°变化到0.19°,卫星高度角从57°变化到约37°。结合图 10和图 11可以看出,在机动开始时名义偏航角与模型偏航角差异不明显,PCO改正、相位缠绕与观测值残差差异较小,接近近日点附近时,两种姿态模型对PCO改正、相位缠绕的影响分别能达到约0.2周、1cm的差异,此外,从图 10可以看出各分析中心名义偏航角观测值残差逐渐增大,且曲线趋势一致,最大能达到3cm。
|
| 图 9 E11(IOV)子午机动偏航角变化 Fig. 9 Variation of the yaw angle of E11(IOV)during noon turn |
|
| 图 10 E11(IOV)子午机动PCO与相位缠绕变化 Fig. 10 Phase wind-up and antenna correction of E11(IOV)during noon turn |
|
| 图 11 E11(IOV)子午机动观测值残差变化 Fig. 11 Residual variation of the observation value of E11(IOV)during noon turn |
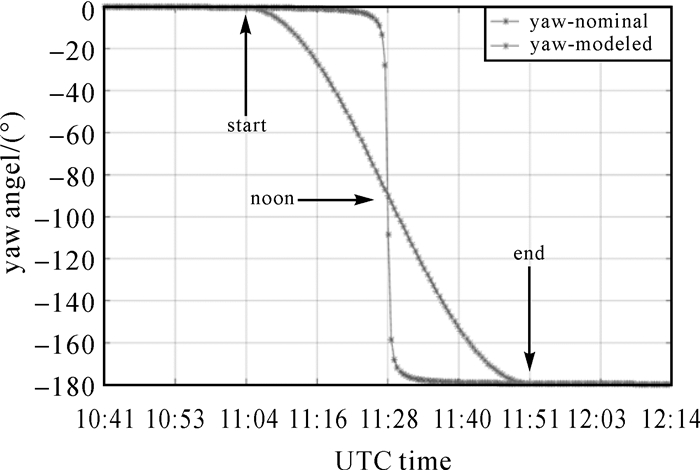
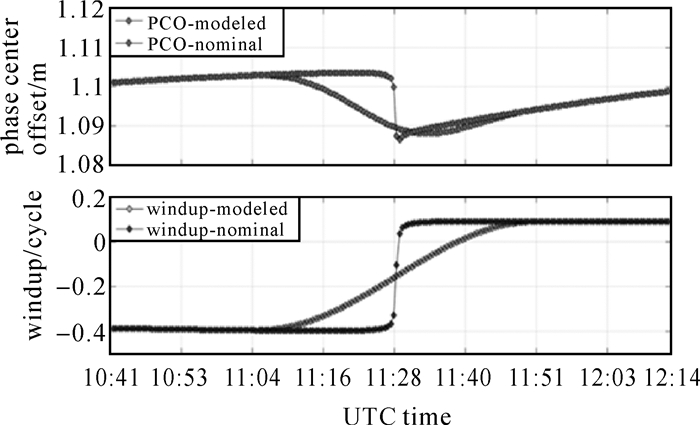
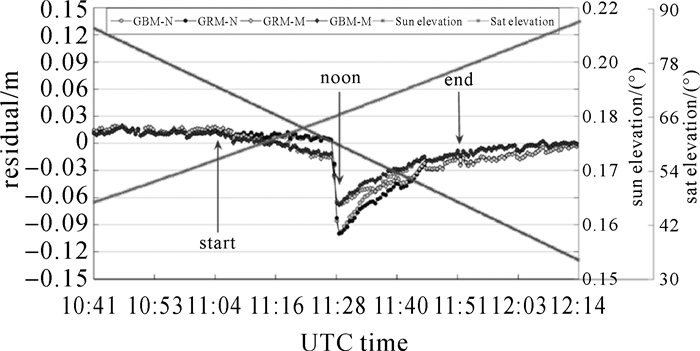
图 12给出2016年DOY210d E24(FOC)卫星子午机动名义偏航角与模型偏航角时间序列图,太阳高度角β≈0.18°,机动时间约40min。相较IOV卫星,机动时间减少,在近日点附近名义偏航角与模型偏航角相差约为为80°。图 13、图 14给出了相应图 12的E24子午机动PCO、相位缠绕与观测值残差时间序列图,太阳高度角β从0.21°变化到0.15°。从图 13可以看出不同姿态模型将对PCO、相位缠绕最高造成分别约0.2周、1cm的差异。由图 14可知,各分析中心观测值残差变化趋势一致,在近日点附近,由于较小的太阳高度角β将导致短时间内卫星姿态急剧翻转,若采用名义姿态计算PCO与相位缠绕,会造成观测值残差的增加,最大能达到10cm,使用模型姿态,观测值残差能降低到6cm。
|
| 图 12 E24(FOC)子午机动偏航角变化 Fig. 12 Variation of the yaw angle of E24(FOC)during noon turn |
|
| 图 13 E24(FOC)子午机动PCO与相位缠绕变化 Fig. 13 Phasewind-up and antenna correction of E24(FOC)during noon turn |
|
| 图 14 E24(FOC)子午机动观测值残差时间序列图 Fig. 14 Residual variation of the observation of E24(FOC)during noon turn |
2.3 GPS/GALILEO卫星不同姿态模型对仿动态PPP定位结果的影响
为验证GPS/GALILEO卫星姿态改正模型在仿动态PPP定位结果的正确性与有效性,本文选取JFNG跟踪站2016年DOY181d(即图 6时间段)的GPS+GALILEO观测数据,并设计名义姿态(Nominal)、模型姿态(Modeled)与卫星剔除(Delete)3种策略对定位结果进行分析,基于CNES分析中心提供的精密轨道与钟差,将SNX文件提供的JFNG站参考坐标作为真值,采用仿动态PPP浮点解进行解算,其中坐标参数与钟差采用单历元估计[21, 25]。
图 15是JNFG跟踪站仿动态PPP在E、N、U 3个方向定位偏差图,从图 15中可以看出, 在虚线Ⅰ、Ⅱ区域GPS、GALILEO卫星都有不同程度的机动。在区域Ⅱ中由于受多颗卫星机动的影响,模型姿态策略较名义姿态策略有较显著的提升,在部分时刻提升幅度能达到约4cm。与剔除卫星策略相比较,模型姿态策略在E、N方向定位结果差异较小,约为2cm。图 16给出了相应图 15的PDOP与卫星数量变化图,由图 16可知,GPS/GALILEO双系统定位可用卫星数量约为13颗左右,PDOP值约为0.8。在区域Ⅰ、Ⅱ中,相较剔除卫星策略,模型姿态策略在卫星分布几何图形强度得到一定程度的改善,进一步确保了定位精确性与可靠性。图 17给出了在机动区域(即Ⅰ、Ⅱ区域)3种策略下的均方根误差(RMS)。从图 17中可以看出,与其他两种策略相比,模型姿态策略的动态PPP均方根误差在水平方向上优于其他两种策略,在U方向上,3种策略相当。
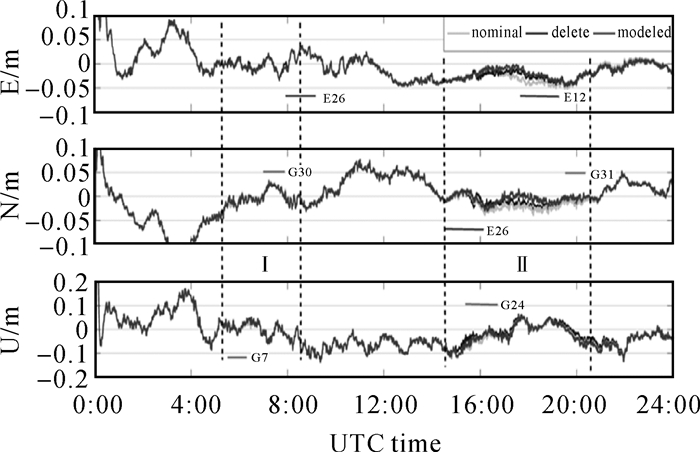
|
| 图 15 动态PPP位置解算示意图(标识有G24等下划线区域表示卫星姿态异常时期) Fig. 15 Positioning error of dynamic PPP(the underlines marked G24, represent abnormal yaw attitude of satellites for a period) |
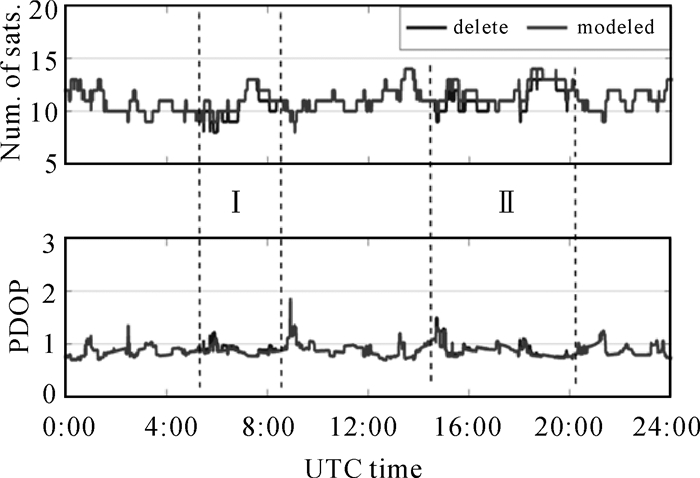
|
| 图 16 卫星数量与PDOP变化图 Fig. 16 The number of satellites and the change diagram of PDOP |
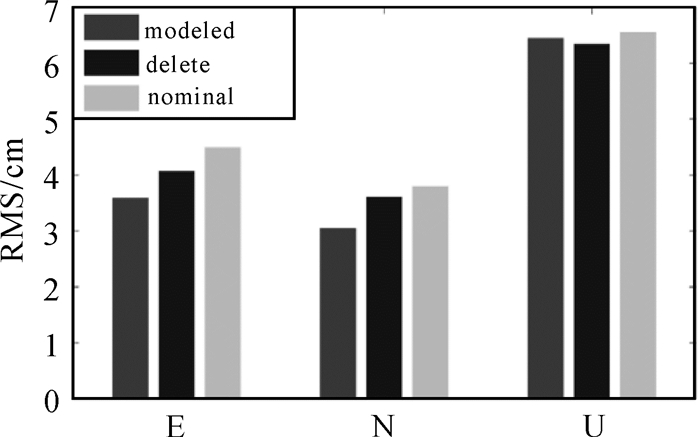
|
| 图 17 卫星姿态异常区域Ⅰ、Ⅱ动态PPP定位结果的RMS Fig. 17 RMS of dynamic PPP positioning results in satellite abnormal area Ⅰ、Ⅱ |
为进一步统计GPS/GALILEO卫星不同改正模型对动态PPP定位结果的影响,本文选取2016年DOY 202-212期间7个MGEX跟踪站GPS+GALILEO观测数据,在卫星偏航姿态异常时期,分别统计了采用模型姿态、剔除卫星策略相较于名义姿态定位精度的提高幅度。图 18给出7个MGEX跟踪站在E、N、U 3个方向的RMS,综合各测站的定位结果可以看出,与名义姿态相比较,模型姿态与剔除卫星策略对定位结果都有一定的提高,并且大部分测站模型姿态策略优于剔除卫星策略。表 1统计了图 18中3个方向的最大提高率、平均提高率以及模型姿态策略相对于剔除卫星策略提高率。从表 1可以看出,与名义姿态相比,模型姿态在E、N、U 3个方向的RMS分别提高了13.3%、15.77%、12.98%,与剔除卫星策略相比,模型姿态在E、N、U 3个方向的RMS可分别提高5.399%、4.430%、5.992%。因此,用户在卫星偏航姿态异常时期应使用姿态模型,避免使用名义姿态而错误地计算PCO与相位缠绕改正,导致定位结果的估值不准确。
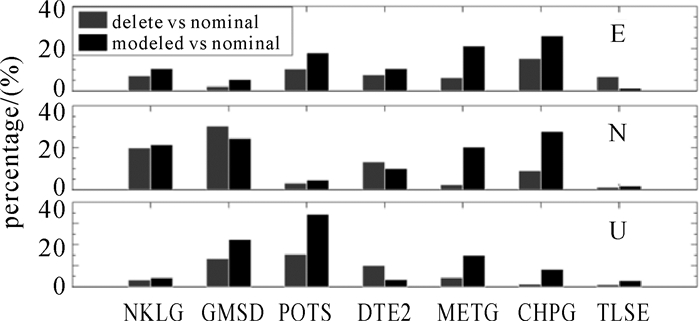
|
| 图 18 卫星姿态异常时期各策略相对名义姿态定位精度提高率 Fig. 18 Improvement rate of positioning precision of each strategy relative tonominal attitude in satellite abnormal area |
| (%) | ||||
| 策略 | 方向 | 最大提高率 | 各方向平均提高率 | 相对提高率 |
| modeled vs nominal | E | 19.21 | 13.30 | 5.399 |
| N | 25.34 | 15.77 | 4.430 | |
| U | 36.43 | 12.98 | 5.992 | |
| delete vs nominal | E | 10.25 | 7.901 | 一 |
| N | 29.12 | 11.34 | 一 | |
| U | 14.95 | 6.988 | 一 | |
3 结论与展望
本文基于不同分析中心所提供的精密轨道和钟差产品,采用不同姿态改正策略,分析了GPS、GALILEO卫星姿态异常时期天线相位中心改正、相位缠绕改正对观测值残差及动态PPP定位结果的影响,得到以下结论:
(1) 在卫星姿态异常时期,GPS、GALILEO卫星采用不同的姿态控制策略,若采用名义姿态计算天线相位中心偏差与相位缠绕误差改正,能对GPS、GALILEO卫星观测值残差分别造成高达8、10cm的影响,采用姿态改正模型可将观测值残差分别降低至2、6cm以内。
(2) 根据JNFG跟踪站的GPS+GALILEO观测数据进行仿动态PPP试验,当多颗卫星处于姿态异常时期,采用模型姿态的定位结果优于名义姿态、卫星剔除策略,部分时刻在E、N方向上的差异可达2~4cm。
(3) 基于7个MGEX跟踪站连续10d的实测数据,针对处于姿态异常时期的卫星,与名义姿态相比,采用模型姿态的仿动态PPP定位结果在E、N、U 3个方向定位精度分别提高了13.3%、15.77%、12.98%,与剔除卫星策略相比,模型姿态在E、N、U 3个方向的定位精度可分别提高5.399%、4.430%、5.992%。
(4) 由于各分析中心在卫星姿态异常时期所基于的策略可能存在差异,导致卫星精密钟差产品吸收一部分由姿态引起的偏差。因此,用户在使用不同分析中心产品时,应明确其异常时期所采用的策略,选取相应的姿态模型进行改正,才能确保定位结果的精确性与可靠性。
| [1] |
戴小蕾.基于平方根信息滤波的GNSS导航卫星实时精密定轨理论与方法[D].武汉: 武汉大学, 2016. DAI Xiaolei. Real-time Precise GNSS Satellite Orbit Determination Using the SRIF Method: Theory and Implementation[D]. Wuhan: Wuhan University, 2016. |
| [2] |
范曹明, 王胜利, 欧吉坤.
GPS/BDS卫星姿态异常对PPP相位缠绕的影响及其改正模型[J]. 测绘学报, 2016, 45(10): 1165–1170.
FAN Caoming, WANG Shengli, OU Jikun. The Impact of Yaw Attitude of Eclipsing GPS/BDS Satellites on Phase Wind-up Solutions for PPP and Its Correction Model[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(10): 1165–1170. DOI:10.11947/j.AGCS.2016.20160126 |
| [3] | KOUBA J. A Simplified Yaw-attitude Model for Eclipsing GPS Satellites[J]. GPS Solutions, 2009, 13(1): 1–12. DOI:10.1007/s10291-008-0092-1 |
| [4] | BAR-SEVER Y E. A New Model for GPS Yaw Attitude[J]. Journal of Geodesy, 1996, 70(11): 714–723. DOI:10.1007/BF00867149 |
| [5] | DILSSNER F, SPRINGER T, ENDERLE W. GPS ⅡF Yaw Attitude Control During Eclipse Season[C]//AGU Fall Meeting Abstracts. Washington, DC: AGU, 2011. |
| [6] | LOU Yidong, ZHENG Fu, GU Shengfeng, et al. The Impact of Non-nominal Yaw Attitudes of GPS Satellites on Kinematic PPP Solutions and Their Mitigation Strategies[J]. Journal of Navigation, 2015, 68(4): 718–734. DOI:10.1017/S0373463315000041 |
| [7] | ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Yaw Attitude of Eclipsing GPS Satellites and Its Impact on Solutions from Precise Point Positioning[J]. Chinese Science Bulletin, 2010, 55(32): 3687–3693. DOI:10.1007/s11434-010-4130-3 |
| [8] | DILSSNER F. GPS ⅡF-1 Satellite Antenna Phase Center and Attitude Modeling[J]. Inside GNSS, 2010, 5(6): 59–64. |
| [9] |
郭靖.姿态、光压和函数模型对导航卫星精密定轨影响的研究[D].武汉: 武汉大学, 2014. GUO Jing. The Impacts of Attitude, Solar Radiation and Function Model on Precise Orbit Determination for GNSS Satellites[D]. Wuhan: Wuhan University, 2014. |
| [10] | KUANG Da, DESAI S, SIBOIS A. Observed Features of GPS Block ⅡF Satellite Yaw Maneuvers and Corresponding Modeling[J]. GPS Solutions, 2017, 21(2): 739–745. DOI:10.1007/s10291-016-0562-9 |
| [11] | DILSSNER F, SPRINGER T, GIENGER G, et al. The GLONASS-M Satellite Yaw-attitude Model[J]. Advances in Space Research, 2011, 47(1): 160–171. DOI:10.1016/j.asr.2010.09.007 |
| [12] | DAI Xiaolei, GE Maorong, LOU Yidong, et al. Estimating the Yaw-attitude of BDS IGSO and MEO Satellites[J]. Journal of Geodesy, 2015, 89(10): 1005–1018. DOI:10.1007/s00190-015-0829-x |
| [13] |
毛悦, 宋小勇, 贾小林, 等.
北斗卫星ECOM光压模型参数选择策略分析[J]. 测绘学报, 2017, 46(11): 1812–1821.
MAO Yue, SONG Xiaoyong, JIA Xiaolin, et al. Analysis about Parameters Selection Strategy of ECOM Solar Radiation Pressure Model for Beidou Satellites[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(11): 1812–1821. DOI:10.11947/j.AGCS.2017.20160485 |
| [14] |
毛悦, 宋小勇, 贾小林, 等.
北斗导航卫星地影状态分析[J]. 测绘学报, 2014, 43(4): 353–359.
MAO Yue, SONG Xiaoyong, JIA Xiaolin, et al. Earth Eclipse Status Analysis of Beidou Navigation Satellite[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4): 353–359. DOI:10.13485/j.cnki.11G2089.2014.0053 |
| [15] | CAO Xinyun, ZHANG Shoujian, KUANG Kaifa, et al. The Impact of Eclipsing GNSS Satellites on the Precise Point Positioning[J]. Remote Sensing, 2018, 10(1): 94. |
| [16] |
叶世榕, 夏凤雨, 赵乐文, 等.
偏航姿态对北斗精密单点定位的影响分析[J]. 测绘学报, 2017, 46(8): 971–977.
YE Shirong, XIA Fengyu, ZHAO Lewen, et al. Impact Analysis of Yaw Attitude on BDS Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(8): 971–977. DOI:10.11947/j.AGCS.2017.20170094 |
| [17] | MONTENBRUCK O, SCHMID R, MERCIER F, et al. GNSS Satellite Geometry and Attitude Models[J]. Advances in Space Research, 2015, 56(6): 1015–1029. DOI:10.1016/j.asr.2015.06.019 |
| [18] | KOUBA J. A Note on the December 2013 Version of the Eclips. f Subroutine[EB/OL].[2013-09-15]. http://acc.igs.org/orbits/eclipsDec-2013note.pdf. |
| [19] | KOUBA J. A Note on the December 2017 Version of the Eclips. f Subroutine[EB/OL].[2017-10-26]. http://acc.igs.org/orbits/May2017-elcipsVersion.pdf. |
| [20] | HERNANDEZ-PAJARES M, JUAN J M, SANZ J, et al. The ESA/UPC GNSS-Lab Tool (gLAB): An advanced multipurpose package for GNSS data processing[C]//20105th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing. Noordwijk, Netherlands: IEEE, 2011: 1-8. |
| [21] | KOUBA J. A Guide to Using International GNSS Service (IGS) Products[J]. Maryland Biological Stream Survey Data Versar Inc, 2009, 4(3): 106. |
| [22] |
任晓东, 张柯柯, 李星星, 等.
BeiDou、Galileo、GLONASS、GPS多系统融合精密单点[J]. 测绘学报, 2015, 44(12): 1307–1313.
REN Xiaodong, ZHANG Keke, LI Xingxing, et al. Precise Point Positioning with Multi-constellation Satellite Systems:BeiDou、Galileo、GLONASS、GPS[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(12): 1307–1313. DOI:10.11947/j.AGCS.2015.20140568 |
| [23] | MONTENBRUCK O, STEIGENBERGER P, PRANGE L, et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)-Achievements, Prospects and Challenges[J]. Advances in Space Research, 2017, 59(7): 1671–1697. DOI:10.1016/j.asr.2017.01.011 |
| [24] | SCHMID R, STEIGENBERGER P, GENDT G, et al. Generation of a Consistent Absolute Phase-center Correction Model for GPS Receiver and Satellite Antennas[J]. Journal of Geodesy, 2007, 81(12): 781–798. DOI:10.1007/s00190-007-0148-y |
| [25] | GUO Fei, LI Xingxing, ZHANG Xiaohong, et al. Assessment of Precise Orbit and Clock Products for Galileo, BeiDou, and QZSS from IGS Multi-GNSS Experiment (MGEX)[J]. GPS Solutions, 2017, 21(1): 279–290. DOI:10.1007/s10291-016-0523-3 |



