2. 信息工程大学地理空间信息学院, 河南 郑州 450001;
3. 国防科技大学, 湖南 长沙 410073
2. Institute of Geospacial Information, Information Engineering University, Zhengzhou 450001, China;
3. National University of Defense Technology, Changsha 410073, China
地球重力场观测数据是地理空间信息的重要组成部分,在地球科学研究、空间基准确定、矿产资源开发、军事应用保障等多个领域具有非常重要的应用价值[1-7]。随着建设海洋强国发展战略的逐步实施和国防发展战略转型的持续推进,我国海洋经济建设和海战场环境建设对海洋重力场信息的保障需求日趋紧迫[8]。为加快推动经济建设和国防建设融合发展,最近一个时期,我国地方涉海部门和军事保障机构都在投入大量人力和物力,用于开展海洋重力场信息的观测、采集装备的研制和观测数据的分析处理工作。作为获取海洋重力场信息的两种主要技术手段,海面和航空(简称海空)重力测量技术体系构建问题一直备受人们的关注,是近期国内外地球重力场研究领域的热点之一[9-15]。当前我们面临的主要挑战是,如何在国家层面制定出合理可行、统一有效,能够体现当今国际先进水平的军民融合海空重力测量技术规程,以便在全国范围内规范海空重力测量的技术要求和实施方法,为加快海洋基础测绘技术标准体系建设,构建军民融合的海洋测绘作业技术体系,建立完善的军民基础测绘数据资源共享机制提供有力的技术支撑。
受管理体制和部门职能分工上的制约,我国海空重力测量技术标准体系建设一直走军民独立发展的道路,军地双方都是根据各自的实际需求制定专门的海空重力测量作业规程或规范。针对海洋资源调查与评价需求,国家海洋管理部门将船载重力测量作业规程纳入了国家推荐标准《海洋调查规范》(第8部分)[16];为满足海洋综合调查测量国家专项建设需要,地方涉海部门组织编写了专项作业标准《地球物理调查技术规程》[17],此后还陆续推出了多个国家专项单要素调查测量作业规程。中国地质调查局正在组织编写行业标准《航空重力测量技术规范》。为满足军事应用需求,军事测绘保障部门也分别组织编写了国家军用标准《海洋重力测量规范》和《航空重力测量作业规范》[18-19]。毫无疑问,上述技术规程的制定和实施,为保障军地双方海空重力测量成果的质量,推动我国海空重力测量标准化进程发挥了重要作用。但必须指出的是,军地双方各自为政的管理模式和发展理念,已经远远不能适应当前国家军民融合深度发展战略大环境的需要,必须以新的视野和新的思维,站在国家的高度统筹谋划我国海洋基础测绘事业的发展。从技术层面上讲,我国现行海空重力测量技术标准存在两个方面的问题需要研究解决:一是军地双方的技术体系不具有可替代性,主要体现为技术指标、质量控制和成果验收等多项要求存在较大的差异,不利于测量数据资源的共享共用;二是军地双方现行技术标准的很多条款已经失去现势性和先进性,因为现行大部分标准的发布时间距今已经接近10年甚至超过10年,相关技术要求不能满足新的应用需求,也无法反映专业技术发展的最新研究成果。针对上述问题,本文以编制能够兼顾军地双方应用实际的海空重力测量技术规程迫切需求为出发点,对军民融合海空重力测量作业规程的关键指标及技术要求进行分析论证和试验评估,旨在推动这个研究领域尽快达成思想和技术上的共识,为下一步启动规程编制工作奠定基础。
1 关键指标分析与论证 1.1 测线布设密度要求测线布设是海空重力测量技术设计的主要内容之一。测线布设密度(通常用测量比例尺参数表示)高低取决于航次测量的目的性,以船载重力测量为例,当海面重力测量与海底地形测量同船作业时,一般要求按照海底地形测量技术规程的规定设计测线密度。但当测量航次是以重力加密精测为主要目的或海底地形测量测线布设密度要求比重力测量更低时,应根据重力测量的目的要求确定测线间距。
测线密度设计原则上应统筹兼顾国家海洋经济和战场环境建设两个方面的需求,但考虑到当前以海洋地质矿产资源调查与评价为主要目标的大尺度重力测量,对测线布设密度的要求一般都比以军事应用为主要目标的要求低一些,故军民融合船载重力测量技术规程宜以军事应用要求为主要依据设计测线密度。对探测分辨率有特殊需求(比如军事应用中的重力匹配导航需求)的局部区域,测线密度设计可依据用户的具体要求作出相应调整,在军民融合作业技术规程中不宜作统一的规定。根据文献[7, 20],海洋重力测量信息在军事上主要有3个方面的应用:一是用于全球高程基准的确定;二是用于潜地战略导弹发射保障;三是用于潜艇惯性导航系统扰动重力补偿及水下匹配导航。前面两个方面的应用要求有超大范围(最好是全球海域)、高分辨率高精度的海洋重力观测数据作保障。根据已有研究成果[15, 20-22],要想将全球高程基准的确定精度控制在cm级、地球外部扰动引力的计算精度(对应于远程飞行器发射保障应用)控制在4 mGal(1 mGal=10-5 m/s2)以内,必须提供至少2'×2'分辨率和优于5 mGal精度的基础数据模型。而要想构建这样的数值模型,在海底地形变化比较平坦的海区,应按照2'的间距(约为4 km)布设海洋重力测线;在海底地形变化比较剧烈的海区,则应按照1'的间距(约为2 km)布设海洋重力测线[20]。此外,测线间距需求还应与沿线(滤波后)重力值的分辨率相匹配。水下潜器匹配导航应用对海洋重力测量数据覆盖范围的要求虽然只是局部性的(因为匹配导航只能在重力场变化比较剧烈的局部海区得以实现),但对重力观测数据分辨率的要求比前面两个方面的应用要求更高,在一些具备匹配导航条件的特定海区(通常称为可匹配区或适配区),海洋重力测线间距应随匹配导航预期精度要求的不同而作出相应的调整。当匹配精度要求优于1 km时,应至少布设间距为500 m~1 km的海洋重力测线[23]。
在海域和地形变化比较平缓的陆部上空开展的航空重力测量,可参照上述船载重力测量的测线布设原则确定测线间距大小;在特大山区开展的航空重力测量,则应适当加密重力测线(比如1 km间距),以满足基础数据模型的计算精度要求。
1.2 测量精度与空间分辨率要求 1.2.1 测量精度要求为讨论问题方便,首先给出本文推荐使用的3个衡量测量精度指标参数的定义[24-25]。
定义1:中误差,也称均方误差,是指各个观测误差(观测值与真值的互差)平方和的平均值的平方根。
定义2:系统误差,也称系统偏差,简称系统差,是指各个观测误差的算术平均值。
定义3:平均误差,是指各个观测误差绝对值的算术平均值。
上述指标参数的具体计算模型将在下文作详细介绍。这里讨论的测量精度和分辨率是指海上重力测量成果的测点精度(因海空重力观测数据都需要作滤波处理,故严格讲应是在一定分辨率下的平均值精度,但为方便起见,下文仍称为测点精度)和沿测线方向上的空间分辨率。由于海上缺乏更高精度的比对基准,测量精度一般采用反映观测值之间离散度的精密度指标即测点中误差M表示。如前所述,用于军事保障的网格基础数据模型精度主要取决于测量分辨率(包括测线密度和沿测线方向分辨率两个因素)和测点精度,前者决定网格基础数据模型的代表误差大小。对于陆地重力测量,因测点精度一般都在几十个微伽(10-8 m/s2)级甚至更高,故陆地重力网格基础数据模型精度主要取决于代表误差大小,测点误差可以忽略不计[6]。对于海洋重力测量,测点精度虽然远不如陆地重力测量,但如果使用新一代海洋重力仪实施海上作业,同时采用严密的数学模型和方法作数据处理,则获取±1~±2 mGal精度的重力测点成果是完全有可能的。从理论上讲,重力测点精度应当是越高越好,最好是高到与代表误差相比可以忽略不计的程度。这里以文献[20]论证获得的数据模型精度指标为例,分析讨论重力测点精度的具体要求。由文献[20]得知,重力场信息特定军事应用保障要求提供优于±5 mGal精度的网格基础数据模型。根据测量误差传播和误差分配估计理论,要想达到与代表误差相比可以忽略不计的目标,必须尽可能将测点重力误差控制在网格基础数据模型总精度指标的1/4以内,即最好不超过±1.5 mGal。目前我国作业部门正在使用的新一代海洋重力仪(包括我国自行研制的重力仪)标称动态测量精度均优于±1 mGal[26],故将海上船载重力测量的测点精度指标规定为优于±1.5 mGal是合理可行的。考虑到航空重力测量环境的高动态性和复杂性,可将航空重力测量的测点精度要求适当放宽到±2.0 mGal。
需要指出的是,将中误差M作为海空重力测量精度唯一的评价指标是不全面的。因为采用传统评价方法的前提假设是:观测误差属于服从正态分布的随机变量(也称偶然误差、随机误差或白噪声)。但实际情况并非完全如此。根据测量平差理论[25],偶然误差具有如下特性:①绝对值较小的误差比绝对值较大的误差出现的可能性较大;②绝对值相等的正误差与负误差出现可能性相等;③偶然误差的算术平均值随着观测次数的无限增加而趋近于零。而由文献[14]得知,源于测量动态环境的特殊性,海洋重力测量从出测前的仪器校准到海上观测作业,再到测量结束后的数据处理各个环节,都不可避免地受到各种系统性和随机性误差源的干扰,观测噪声中必然包含偶然性和系统性误差成分。因此,现实中严格呈现偶然误差特性的测量误差几乎是不存在的(特别是重力观测数据作滤波处理以后形成的重复观测互差值),不同观测误差系列之间的差异性除了体现为拥有不同的中误差参量外,还表现为它们包含了不同比例的误差成分。考虑到系统误差对重力测量信息应用的影响比偶然误差更为显著[3, 15, 21],因此有必要在海空重力测量精度评价指标中增加一个与定义2相对应的系统误差限定参数β,其限差要求可规定为:系统差β不超过0.3 mGal。此量值约为海空重力仪标称动态测量精度的1/4。因重力观测量的真值是未知的,故观测误差一般只能以重力测点观测值互差的形式来表示,此时该项指标要求等价于:测点观测值互差的算术平均值不超过0.6 mGal。这里需要强调的是,无论是船载还是航空重力测量,也无论是正常的海空重力测量作业还是针对重力仪性能所作的动态试验,其系统差β的限定要求都应当是一致的,即不超过0.3 mGal。
除了中误差和系统差限定指标以外,还应增加对观测误差服从正态分布的限制。因为即使不存在系统误差,也无法确保重力观测误差就是服从正态分布的偶然误差。举个极端的例子,观测误差出现正负号相间变化但绝对值保持不变,即它总是在最大值和最小值两者之间交换,此时虽然观测误差的算术平均值为零,但其分布特性显然不满足正态分布的要求。理论上可以通过正态性检验方法来评估观测误差的分布特性[27],但考虑到统计检验方法的计算流程过于复杂和繁琐,不便于推广应用,为简便起见,笔者建议采用与定义3相对应的平均误差θ作为海空重力测量精度的另一个评价指标。当观测误差以重力测点观测值互差的形式表示时,平均误差θ为观测值互差绝对值的平均值除以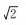
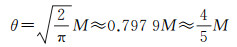 (1)
(1)
相反,如果观测误差不服从正态分布,那么关系式(1)就不再成立。显然,依据中误差M的限定指标可由式(1)确定平均误差θ的限定指标,当要求船载重力测量中误差M不超过±1.5 mGal时,平均误差θ应不超过1.2 mGal;当要求航空重力测量中误差M不超过±2.0 mGal时,平均误差θ应不超过1.6 mGal。
1.2.2 测点分辨率要求由于受测量动态环境噪声的干扰,实践中必须采用低通滤波器对重力观测数据进行滤波处理,以剔除各类观测噪声的影响。因此,海空重力测量沿测线方向上的空间分辨率ρ(半波长λ/2)主要取决于载体航行速度v和数据滤波处理所采用的截止频率f(其倒数称为滤波尺度T)大小,三者之间的关系可表示为[11, 20]
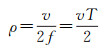 (2)
(2)
由式(2)知,载体航行速度越低、滤波截止频率取得越高,重力测量的空间分辨率就越高。当海面重力测量载体航行速度为15 kn(海里/小时),滤波尺度取为T=200 s时,由式(2)可求得与其相对应的空间分辨率约为ρ=0.77 km;当航空重力测量载体航行速度为200 km/h,滤波尺度取为T=100 s时,可求得与其相对应的空间分辨率约为ρ=2.78 km。显然,也可根据事先确定的测点分辨率指标,反过来约束测量载体航行速度和数据滤波尺度的取值。通常情况下,一般都要求测点分辨率指标高于测线间距大小。
需要补充说明的是,因海空重力测量成果精度与数据滤波尺度的取值密切相关,故测量精度与空间分辨率也有对应的相关关系[11, 14]。当载体运动速度一定时,增大截止频率(即减小滤波尺度)可相应提高重力测量成果的空间分辨率,但截止频率的增大会使得数据滤波的残留噪声增多,从而降低观测数据的精度;减小截止频率有利于消除或减弱观测噪声的影响,提高测量成果评估精度,但会降低观测数据的空间分辨率。对于事先设计好的重力测量分辨率,要想通过改变截止频率达到理想的滤波效果,必须对测量载体航行速度作出必要的调整。相对低的航行速度有利于提高观测数据的空间分辨率,船载重力测量的空间分辨率要远高于航空重力测量,正是源于这个道理。
1.3 海空重力仪性能指标要求 1.3.1 格值标定精度海空重力测量作业规程规定的重力仪技术性能指标一般包括[18-19]:测量范围(量程)、抗干扰能力(动态范围)、动态重复观测精度、零点漂移特性、采样率和工作温度等内容。除上述指标外,还应增加一个关于重力仪格值标定的精度指标要求,因为海空重力仪格值误差对测量结果具有显著影响。地球重力加速度在全球范围内的最大变化幅度超过5000 mGal,从极端情形考虑,要想获取优于±0.25 mGal的重力读数转换精度,海空重力仪格值的标定相对精度必须达到10-5。即使是针对比较常态化的局部区域测量(比如测区纬度跨度不超过10°),考虑到航空重力测量受到的厄特沃什(Eötvös)效应作用量值加上相对应的区域重力场变化幅度总和可能接近2000 mGal, 船载重力测量时的两项数值之和可能接近500 mGal, 也应当要求航空和海洋重力仪格值的标定精度指标分别达到10-4和10-3。
1.3.2 动态重复测量精度关于海空重力仪动态重复观测精度要求,现行技术规程一般都依据仪器生产厂家给出的仪器标称精度设置相对应的限差规定[18, 19],通常的指标要求是动态观测精度优于±1.0 mGal。基于前面讨论测量精度时同样的理由,采用中误差单一参数作为动态重复观测精度评价指标也是不全面的,应当加上与之相匹配的系统差和平均误差参数指标,具体要求可表述为:动态重复观测系统偏差不超过0.3 mGal;平均误差不超过0.8 mGal(取中误差M=±1.0 mGal)。
1.3.3 零点漂移特性关于海空重力仪零点漂移特性要求,我国现行的海空重力测量各类作业规程都有相应的规定和说明[16-19]。比较统一的定性要求是:零点漂移基本呈线性变化。比较一致的定量要求是:月漂移不得超过±3.0 mGal。不难看出,上述规定不够明确,在执行过程中存在一定程度的不确定性[28]:①零点漂移基本呈线性变化这一要求没有明确的量化指标,在执行中无法得到有效控制;②关于如何计算月漂移量问题也没有作出统一的规定,不同方法可能导致计算结果出现较大的差异,因此标准执行结果不具唯一性。针对此问题,笔者建议将重力仪零点漂移指标分解为线性和非线性变化两个部分,对两个部分分别提出具体的量化指标要求。可将相关条款修改为:零点漂移保持线性变化趋势,日漂移不超过0.2 mGal,月漂移不超过4.5 mGal,月漂移非线性变化(扣除重力固体潮)中误差不超过±0.3 mGal,月漂移非线性变化限差不超过0.9 mGal。与现行规定相比,修改意见一方面增加了零点月漂移非线性变化部分的限制要求, 但另一方面也将月漂移总量从3.0 mGal适当放宽到了4.5 mGal。提出这样的修改意见主要基于以下几个方面的考虑:
(1) 现行作业规程的相关规定不够具体和完善。我国现行的海空重力测量作业规范对重力仪零点月漂移总量作出了比较明确和一致的规定,但对月漂移的变化特性只是提出了定性的指标要求,即保持线性变化。显然,这样的要求不具有约束力,也不具备可操作性。因单一限定重力仪零漂总量不能确保作业过程零漂参数变化的稳定性,故现行作业标准的相关规定是不完善的,也是不全面的,必须相应增加零点漂移非线性变化部分的限制要求。
(2) 新规定应与新的应用需求相匹配。如前所述,随着建设海洋强国发展战略的逐步推进,海洋重力测量信息的经济和军事应用价值日趋凸显,但新的应用需求也对海洋重力测量数据质量提出了更高的要求。当前无论是矿产资源勘察还是军事应用保障,几乎都一致要求海洋重力测量精度优于±1.5 mGal, 新型武器系统试验和水下匹配导航对海洋重力测量的精度要求更高[8]。而依据测量误差传播和误差分配估计理论,要想将海上重力测量综合精度提升到±1.5 mGal甚至更高的水平,单一要素对测量结果的影响必须控制在总精度指标的1/4以内,也就是不超过±0.4 mGal或更小。前文将重力仪零点月漂移非线性变化中误差指标限定为±0.3 mGal正是基于这样的新需求,因为零点漂移线性部分可以通过适当的数学模型进行改正,非线性部分才是影响测量精度的直接因素。
(3) 新型海空重力测量装备能够满足新的应用需求。进入21世纪以来,随着重力传感器结构设计的持续改进和精密元器件制作工艺的不断完善,海空重力测量装备技术取得了重大进展,其一是国内外厂家陆续推出了不同型号的新一代海空重力仪;其二是这些新型重力仪的技术性能都得到了较大提升[14, 26]。目前在国际市场上发布的各型海空重力仪动态测量标称精度都优于±1 mGal,我国正在研制的多型海空重力仪技术指标也标称优于±1 mGal。根据笔者对几种新型海洋重力仪所作的测试分析结果及部分仪器生产厂家提供的测试分析报告,目前国内作业单位正在使用的海空重力仪基本上都能清晰监测到地球重力固体潮的变化信息,剔除重力固体潮后的零点月漂移非线性变化中误差都能控制在±0.1~±0.3 mGal之间[28]。由地球动力学得知,重力固体潮在全球范围内的变化幅度不超过0.3 mGal,海空重力仪具备监测重力固体潮变化信息的能力这一事实说明,新型海空重力仪的测量稳定性已经达到一个比较高的水平,能够满足文中提出的“零点月漂移非线性变化中误差不超过±0.3 mGal”的限定要求。
(4) 新型海空重力仪改进结构设计,要求作业规程作相应的改变。从理论上讲,只要能确保海空重力仪零点漂移在任何内外部条件下都严格保持线性变化,那么零点月漂移总量可以不加以限制。但这种理想化的情形在实际应用中是无法实现的:①因为仪器内部元器件制作工艺及老化问题不能确保零点漂移变化规律持久保持不变;②不能确保由陆上静态试验获取的零点漂移变化规律与海上动态作业时段完全保持一致。因此,从这个意义上讲,月漂移总量越小对保证重力测量数据的可靠性越有利。我国现行作业规程之所以都一致将零点月漂移量限定为3.0 mGal,主要源于:在过去较长一个时期内,国内作业单位大多都在使用以零长弹簧作为传感器的摆杆型海空重力仪,具有较好的长期稳定性是零长弹簧传感器的显著特点,根据仪器生产厂家提供的测试结果和国内外用户多年的作业实践,这类仪器的零点月漂移量能够控制在3.0 mGal以内。而当前在国际市场上陆续推出的各类新型海空重力仪(包括捷联惯导重力仪),虽然在动态测量精度和作业效率等方面都有较大提升,但由于新型仪器大多都改变了原有的结构设计,更多采用了非传统的零长弹簧传感器,受此影响,这类仪器的长期稳定性反而会有所下降[14, 26]。根据目前掌握的试验和应用数据分析结果,各类新型仪器的零点月漂移量基本能够控制在4.5 mGal以内。基于上述综合分析和判断,为了较好地平衡新型仪器使用需求与测量成果质量保障之间的关系,在增加零点月漂移非线性变化限差要求基础上,将月漂移总量从原来规定的3.0 mGal适当放宽但仍限定在4.5 mGal以内是合理可行的。
2 关键指标验证与评估需要指出的是,明确指标要求只是发挥技术规程指导性作用的一个方面,对技术指标提出具体的验证和评估要求,也是作业规程非常重要的组成部分。
2.1 海空重力仪性能指标检验 2.1.1 零点漂移指标海空重力仪零点漂移指标验证通常也称仪器静态试验,是开展海空重力测量作业前期的一项非常重要的准备工作。新重力仪投入使用之前或旧重力仪经重大检修后,都应进行不少于2个月的静态试验,正常复用的重力仪在年度工作开始前,应进行不少于1个月的静态试验,以验证重力仪的零点漂移特性是否满足前面提出的技术指标要求。零点漂移指标测试流程和评估方法如下[28]:
(1) 按照仪器操作规程连续观测记录重力仪读数,获取时间系列观测量g0(t),t为观测时间。
(2) 使用与海上作业数据处理相同的方法对原始观测量g0(t)进行滤波处理,以消除观测场地环境干扰对重力读数的影响。
(3) 从经过数字滤波后的观测量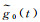
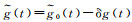
(4) 对剩余观测量作线性拟合处理,即确定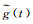
(5) 从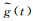
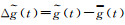
(6) 求非线性变化中误差:M=
将依据上述流程求得的月漂移量Δg0、非线性变化最大偏差
当具备实验室动态测试条件时,新重力仪投入使用之前或旧重力仪经重大检修后,都应当在实验室完成动态重复观测精度检验,正常复用的重力仪也应当每隔1至2年开展一次动态重复测量精度检验工作。当不具备实验室动态测试条件时,动态重复观测精度验证工作可结合重力仪海空试验进行,也可结合海空实际测量作业同时进行。考虑到动态重复观测精度不完全等同于海空实际作业的测量精度(因为后者比前者更能体现测量环境时空变化对重力测量成果的影响),故此项检验工作只要求在东西和南北方向上各布设1条长度不少于20 km(航空重力测量时设为50 km)的重复测线。完成重复线测量后,比较两条重复测线在相同测点处的重力观测值,可分别求得重复测线观测重力的系统差β、平均误差θ和中误差M(均应为平差前计算结果,下同)。根据前面提出的指标要求,系统差β应不超过0.3 mGal,平均误差θ不超过0.8 mGal,中误差M不超过±1.0 mGal。当计算值不满足上述要求时,应分析其原因,并提出相应处理意见。如出现较大偏差,则应将仪器返厂进行检测和维修。
2.1.3 格值标定精度指标海空重力仪格值标定精度检验可通过实验室的倾斜变化法和质量改变法来完成,也可采用基于野外标准重力基线场的基线法对格值进行重新标定[3]。当不具备实验室和野外基线场测试条件时,格值标定精度验证工作可结合前面介绍的动态重复观测精度检验流程同时进行。但考虑到格值标定误差影响规律的特殊性,此项检验工作要求:在东西和南北方向上各布设1条长度不少于20 km(航空重力测量时设为50 km)、航向相反的重复测线,船载重力测量时尽可能高速航行(最好高于15 kn),以凸显由于航向相反引起的厄特沃什效应对重复测线观测量影响的差异性。同样,完成重复线测量后,可求得重复测线观测的系统差β,当东西和南北方向重复测线的系统差均不超过0.3 mGal时,即说明海空重力仪原格值的标定精度满足规定指标要求,原格值可继续使用。当南北方向重复测线的系统差较小(比如不超过0.2 mGal),而东西方向重复测线出现比较明显的系统差(比如超过了0.4 mGal)时,基本上可以判断是由格值标定误差引起的系统性影响,因为在高精度GNSS导航定位保障条件下,其他误差源对海空重力测量成果的系统性影响应当已被削弱到较低的水平。此时,可利用东西方向两条正反向重复测线比对数据,依据式(3)计算重力仪原格值的修正量
 (3)
(3)
式中,ΔC代表格值修正量;si1和si2分别代表东西方向两条正反向重复测线在第i个相同测点处的重力仪读数;δgi12代表重复测线在第i个相同测点处的重力不符值;n为重复测线测点总数。将原格值加上修正量作为新的格值参数使用,即可达到消除海空重力测量成果系统性偏差的目的。关于利用重复测线校正海空重力仪格值及试验验证的详细情况拟另文讨论。
2.2 海空重力测量精度指标检验 2.2.1 海空试验测量精度海空重力测量精度指标检验可通过重力仪海空试验和海空作业两种方式来完成。新重力仪投入使用之前或旧重力仪经重大检修后,都应当按要求选择有代表性的区域开展海上或空中测量试验,以验证重力仪的实际测量精度是否满足前面提出的技术指标要求。试验区应尽量选择在海底或陆地地形具有一定起伏度的宽阔海区或陆区,宜按5 km的间距沿东西和南北方向各布设6条相互正交的主测线和检查测线,并按相关要求完成所有测线的重力测量。经数据处理后可求取主、检测线交叉点重力不符值,进而分别计算得到与不符值系列相对应的系统差β、平均误差θ和中误差M,但有效交叉点不符值个数不得少于30个。根据前面提出的指标要求,船载重力测量的系统差β应不超过0.3 mGal,平均误差θ不超过1.2 mGal,中误差M不超过±1.5 mGal;航空重力测量的系统差β应不超过0.3 mGal,平均误差θ不超过1.6 mGal,中误差M不超过±2.0 mGal。当计算值不满足上述要求时,应分析其原因,并提出具体处理意见,必要时应重新开展相关试验。
2.2.2 海空作业测量精度通过海空试验测量精度验证的新重力仪(包括经返厂检修后的重力仪)和正常复用的重力仪,均可利用年度航次测量内部测线组成的检核条件开展实际测量精度指标检验。尽管正常作业时一般要求主测线应尽量垂直于区域地质主要构造线或海底地形走向线的方向,且检查测线的数量要远远少于主测线,但仍要求单一航次主、检测线的有效交叉点个数不得少于30个。故利用海空测量作业内部检核条件进行重力仪测量精度指标检验的计算流程和要求与前面介绍的海空试验方法几乎完全相同,这里不再重复。
需要补充说明的是,除了上述内部符合检验方法外,还可采用两种外部符合方法对海空重力仪的实际测量精度进行检验:①采用两台或多台重力仪同船或同机观测的方法,通过对比不同仪器在同一时刻的观测结果,即可获取参试重力仪测量精度的评估信息;②在事先建设好的海上或空中重力标准场中进行测量和比对测试,同样可获得被检测重力仪的精度评估信息。上述检验方法采用的具体评估计算模型见后面的3.4小节。
3 关键数学模型分析与改进除了关键指标需要细化、明确和验证以外,随着新技术的发展和应用需求的提升,我国现行海空重力测量技术规程规定采用的一些关键数学模型也应当作相应的改进,下面就此作出必要的说明,并给出具体的改进模型。
3.1 船载重力测量测点归算模型海空重力测量测点成果最终都应当按要求统一归算到同一基准面上,以方便后端用户的综合利用。我国现行的船载重力测量技术规程对此项要求一直不够明确,相关规定不够统一。现行国家军用标准要求将船载重力测量成果统一归算到平均海面,其采用的归算模型为[18]
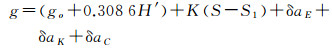 (4)
(4)
式中,g为测点绝对重力值;go为基点绝对重力值;H'为重力仪弹性系统重心至平均海面的高度(前者在后者上方为正);K为重力仪格值;S为测点处重力仪读数;S1为出测前归算至基点处的重力仪读数;δaE为厄特沃什改正值;δaK为零点漂移改正值;δaC为吃水变化改正值。上述归算模型存在两个问题:①没有单独分离出测点重力空间改正项,体现不出不同空间基准面之间的传递关系,概念上不够清晰;②该模型只将测点成果归算到平均海面,而不是应用更为广泛的全球统一基准面——大地水准面。为此,笔者建议将测点归算模型修改为
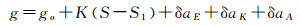 (5)
(5)
式中,δaA代表重力空间改正项;其他符号意义同前。δaA的计算公式为
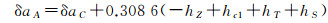 (6)
(6)
式中,hZ为重力仪传感器重心到甲板面的高度(前者在后者下方为正);hc1为出测前测量船左右舷甲板面到瞬时海面高度的平均值(前者在后者上方为正,下同);hT为瞬时海面到平均海面的高度,即潮汐高度,可通过潮汐预报方法计算获得[30];hS为平均海面到海洋大地水准面的高度,即海面地形,可利用球谐展开式或数值模型计算获得[4, 31]。
3.2 航空重力测量厄特沃什改正模型厄特沃什改正是海空重力测量最重要的改正项之一。在航空重力测量研究领域,由于各方面的原因,国内外学者在不同的应用时期采用了不同形式的厄特沃什改正公式,导致该项改正的计算模型在使用上一直存在着不一致和不规范的问题[14, 32-33],我国现行的航空重力测量作业标准仍在采用近似的厄特沃什改正公式,同时存在比较明显的引用错误[19]。因此,有必要尽快对其进行更正,统一采用如式(7)所示的严密的厄特沃什改正计算模型[11, 32]
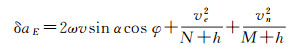 (7)
(7)
式中,δaE为厄特弗斯改正数;ω为地球自转角速度;v为载体运动速度;α为载体运动方位角;φ为测点大地纬度;R为地球平均半径;ve为v的东向分量,vn为v的北向分量;h为测点相对于地球椭球面的大地高;N和M分别为地球椭球卯酉圈和子午圈曲率半径,其计算式分别为
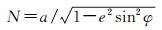 (8)
(8)
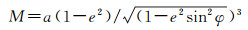 (9)
(9)
式中,a代表地球椭球长半轴;e为椭球第一偏心率,e2=2f-f2;f为椭球扁率;其他符号含义同前。
3.3 海空重力测量平台倾斜改正模型传统上,海空重力测量平台倾斜改正通常被称为水平加速度改正,也是平台式海空重力测量最重要的改正项之一。实际上,作业过程中测量平台发生倾斜一方面会导致各类干扰水平加速度在重力传感器垂向敏感轴上产生附加的投影分量,另一方面又会使得重力传感器只敏感到测点加速度在垂向敏感轴上的投影分量,从而产生偏差。可见,只要发生平台倾斜(比如由重力传感器安装误差引起),即使不存在水平加速度干扰,重力观测量仍然会产生一定的偏差,故必须进行相应的重力改正[11, 14, 34]。关于此项改正,我国现行的作业规程存在两个方面的问题:①海洋重力测量作业规程不要求做平台倾斜改正计算[16-18];②航空重力测量作业规程采用的是近似的平台倾斜改正模型[19]。出现问题①的原因是,人们一直认为船载重力测量的平台倾斜改正值较小,不足以影响海洋重力测量成果的精度。但实际分析计算结果表明,稳定平台倾斜对船载重力观测量的影响最大可超过0.5 mGal。显然,这么大的影响量值对当今高精度海洋重力测量要求已经不能忽略,必须加以顾及。
我国现行航空重力测量作业规范采用的平台倾斜改正(规范中称为水平加速度改正)模型为[19]
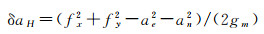 (10)
(10)
式中,δaH为平台倾斜重力改正数;fx和fy分别为稳定平台两个水平轴敏感到的横向和纵向水平加速度;gm为重力仪测得的重力加速度;ae和an分别代表由高精度定位系统确定的运动载体东向和北向水平加速度。实际上,式(10)只是平台倾斜改正的近似公式,因为在水平方向上,该式忽略了地球扰动重力和由载体运动引起的科里奥利(Coriolis)加速度两类干扰水平加速度的影响。严密的平台倾斜重力改正模型为[35]
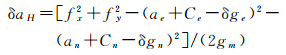 (11)
(11)
式中,δge和δgn分别为扰动重力加速度的东向和北向分量,可直接采用国际上最新发布的超高阶地球位模型进行计算, 计算模型参见文献[3, 6];Ce和Cn分别为科里奥利加速度的东向和北向分量,其计算式为[11, 14]
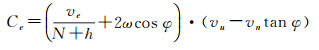 (12)
(12)
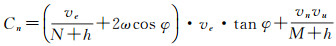 (13)
(13)
式中,ve、vn和vu分别代表飞机飞行速度的东向、北向和径向(向上为正)分量,其他符号意义同前。实际数值计算对比分析结果表明,航空重力测量平台倾斜改正严密模型和近似模型的互差最大可达1 mGal,故新的作业规程应统一要求采用严密的改正模型[35]。
3.4 海空重力测量精度评估模型 3.4.1 内符合精度计算模型依据主、检测线交叉点重力不符值或两条重复测线观测重力互差值进行内符合精度评估的计算公式为
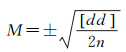 (14)
(14)
式中,M代表测点重力观测内符合中误差;d为主、检测线交叉点重力不符值或重复测线观测重力互差值;n为测线交叉点或重复点个数。与其相对应的测点重力系统差计算公式为
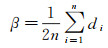 (15)
(15)
式中,β代表测点重力观测系统差,与其相对应的平均误差计算公式为
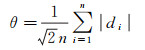 (16)
(16)
式中,θ代表测点重力观测平均误差。式(16)的推导过程如下:
设重力重复观测互差值d对应的中误差为Md,平均误差为θd,其计算式分别为
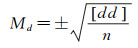 (17)
(17)
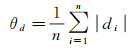 (18)
(18)
则由式(1)得
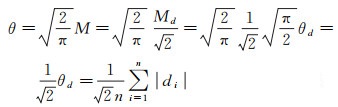 (19)
(19)
可见式(16)得证。
当重复测线数目多于2条时,其相对应的内符合精度计算公式为[36]
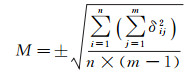 (20)
(20)
式中,M代表多条重复测线测点重力观测内符合中误差;δij为第j条重复测线上的第i个测点重力异常观测值Δgij与该点各重复测线观测的平均值Δgi之差;n为重复线上重复测点个数;m为重复测线数目。δij的计算公式为
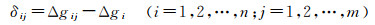 (21)
(21)
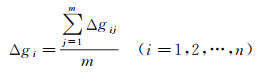 (22)
(22)
当重复测线数目m=2时,式(20)与式(14)取得一致。考虑到式(20)计算结果只能反映重复测线测量结果的整体离散化程度,不能真实反映不同测线测量结果相互之间的偏离情况,而这一偏离参数指标对于客观评定海空重力仪的稳定性是至关重要的。因此,在实际应用中,即使实施了多条(m>2)重复测线测量,建议仍采用两条重复测线的相关计算公式评估内符合精度,即对多条重复测线进行两两组合,按照式(14)—(16)作互比计算,并以其中的最大中误差、最大系统差和最大平均误差作为重复测线的精度评估组合参数。
3.4.2 外符合精度计算模型当作为比对基准的重力值比待检核的观测值精度高出一倍以上时,采用式(23)计算外符合精度
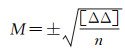 (23)
(23)
式中,M代表测点重力观测外符合中误差;Δ为重力观测值与基准值之差;n为比对点数。与其相对应的系统差计算公式为
 (24)
(24)
式中,β代表重力观测相对于基准值的系统差。与其相对应的平均误差计算公式为
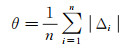 (25)
(25)
式中,θ代表重力观测相对于基准值的平均误差。
当作为比对基准的重力值与待检核的观测值精度处于同一个水平时,应采用与内符合相同的计算模型评估外符合精度。
4 结语作业规程是统一海空重力测量工作流程和技术要求最重要的指导性文件之一,是开展海空重力测量作业的重要依据。本文针对我国现行海空重力测量规范或标准涉及的一些重要技术指标,仍存在要求不够明确、规定不够统一、执行不够规范、缺乏现势性等问题,开展了海空重力测量测线布设密度、测量精度、空间分辨率、海空重力仪稳定性与可靠性等关键性指标分析和论证,提出了相关技术指标的验证和评估方法,同时对涉及船载重力测量测点归算、航空重力测量厄特沃什改正、测量平台倾斜改正及海空重力测量精度评估等关键性数学模型进行了分析和讨论,提出了相应的改进意见和使用建议,为统一军地双方测量作业体系技术要求,提高海空重力测量成果质量,推动测量数据资源共享共用,提供了必要的技术支撑。
| [1] | DEHLINGER P. Marine Gravity[M]. New York: Elservier Scientific Publishing Company, 1978. |
| [2] | TORGE W. Gravimetry[M]. Berlin: Walter de Gruyter, 1989. |
| [3] |
黄谟涛, 翟国君, 管铮, 等.
海洋重力场测定及其应用[M]. 北京: 测绘出版社, 2005.
HUANG Motao, ZHAI Guojun, GUAN Zheng, et al. Determination and Application of Marine Gravity Field[M]. Beijing: Surveying and Mapping Press, 2005. |
| [4] |
李建成, 陈俊勇, 宁津生, 等.
地球重力场逼近理论与中国2000似大地水准面的确定[M]. 武汉: 武汉大学出版社, 2003.
LI Jiancheng, CHEN Junyong, NING Jinsheng, et al. Theory of the Earth's Gravity Field Approximation and Determination of China Quasi-geoid 2000[M]. Wuhan: Wuhan University Press, 2003. |
| [5] |
宁津生, 刘经南, 陈俊勇, 等.
现代大地测量理论与技术[M]. 武汉: 武汉大学出版社, 2006.
NING Jinsheng, LIU Jingnan, CHEN Junyong, et al. Theory and Technology of Modern Geodesy[M]. Wuhan: Wuhan University Press, 2006. |
| [6] |
陆仲连, 吴晓平, 丁行斌, 等.
弹道导弹重力学[M]. 北京: 八一出版社, 1993.
LU Zhonglian, WU Xiaoping, DING Xingbin, et al. Gravimetry in Ballistic Missile[M]. Beijing: Bayi Press, 1993. |
| [7] |
黄谟涛, 翟国君, 欧阳永忠, 等.
海洋磁场重力场信息军事应用研究现状与展望[J]. 海洋测绘, 2011, 31(1): 71–76.
HUANG Motao, ZHAI Guojun, OUYANG Yongzhong, et al. Prospects and Development in the Military Applications of Marine Gravity and Magnetic Information[J]. Hydrographic Surveying and Charting, 2011, 31(1): 71–76. DOI:10.3969/j.issn.1671-3044.2011.01.020 |
| [8] |
刘敏, 黄谟涛, 欧阳永忠, 等.
海空重力测量及应用技术研究进展与展望(一):目的意义与技术体系[J]. 海洋测绘, 2017, 37(2): 1–5.
LIU Min, HUANG Motao, OUYANG Yongzhong, et al. Development and Prospect of Air-sea Gravity Survey and Its Applications, PartⅠ:Objective, Significance and Technical System[J]. Hydrographic Surveying and Charting, 2017, 37(2): 1–5. DOI:10.3969/j.issn.1671-3044.2017.02.001 |
| [9] | OLESEN A V. Improved Airborne Scalar Gravimetry for Regional Gravity Field Mapping and Geoid Determination[D]. Copenhagen: University of Copenhagen, 2002. |
| [10] | ALBERTS B. Regional Gravity Field Modeling Using Airborne Gravimetry Data[C]//Publications on Geodesy 70. Delft: Netherlands Geodetic Commission, 2009. |
| [11] |
孙中苗.航空重力测量理论、方法及应用研究[D].郑州: 信息工程大学, 2004. SUN Zhongmiao. Theory, Methods and Applications of Airborne Gravimetry[D]. Zhengzhou: Information Engineering University, 2004. |
| [12] |
张开东.基于SINS/DGPS的航空重力测量方法研究[D].长沙: 国防科学技术大学, 2007. ZHANG Kaidong. Research on the Methods of Airborne Gravimetry Based on SINS/DGPS[D]. Changsha: National University of Defense Technology, 2007. |
| [13] |
邓凯亮.海域多源重力数据的处理、融合及应用研究[D].大连: 海军大连舰艇学院, 2011. DENG Kailiang. Research on the Procession, Combination and Application of the Multi-source Gravity Data on the Sea[D]. Dalian: Dalian Naval Academy, 2011. |
| [14] |
欧阳永忠.海空重力测量数据处理关键技术研究[D].武汉: 武汉大学, 2013. OUYANG Yongzhong. On Key Technologies of Data Processing for Air-sea Gravity Surveys[D]. Wuhan: Wuhan University, 2013. |
| [15] |
陈欣.海域重力测量数据的精化处理研究[D].大连: 海军大连舰艇学院, 2016. CHEN Xin. Research on Refined Procession of Marine Gravity Measurement Data[D]. Dalian: Dalian Naval Academy, 2016. |
| [16] |
GB/T 12763.8-2007海洋调查规范第8部分: 海洋地质地球物理调查[S].北京: 中国标准出版社, 2007. GB/T 12763.8-2007 Specifications for Oceanographic Survey-Part 8: Marine Geology and Geophysics Survey[S]. Beijing: China Standard Press, 2007. |
| [17] |
国家海洋局908专项办公室.地球物理调查技术规程[S].北京: 海洋出版社, 2005. 908 Special Project Office of National Bureau of Oceanography. Specifications for Geophysics Survey[S]. Beijing: Oceanographic Press, 2005. |
| [18] |
GJB 890A-2008海洋重力测量规范[S].北京: 总装备部军标出版发行部, 2008. GJB 890A-2008 Specification for Marine Gravity Survey[S]. Beijing: Military Standard Press of the Headquarters of General Equipment, 2008. |
| [19] |
GJB 6561-2008航空重力测量作业规范[S].北京: 总装备部军标出版发行部, 2008. GJB 6561-2008 Rules for Operations of Airborne Gravimetry[S]. Beijing: Military Standard Press of the Headquarters of General Equipment, 2008. |
| [20] |
黄谟涛, 刘敏, 欧阳永忠, 等.
重力场对飞行器制导的影响及海洋重力测线布设[J]. 测绘学报, 2016, 45(11): 1261–1269.
HUANG Motao, LIU Min, OUYANG Yongzhong, et al. Effect of External Disturbing Gravity Field on Spacecraft Guidance and Surveying Line Layout for Marine Gravity Survey[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(11): 1261–1269. DOI:10.11947/j.AGCS.2016.20160175 |
| [21] |
章传银, 党亚民, 晁定波, 等.
似大地水准面的误差分析与抑制技术[J]. 测绘科学, 2006, 31(6): 26–29.
ZHANG Chuanyin, DANG Yamin, CHAO Dingbo, et al. Error Analysis and Prevention Technique of Quasi-geoid[J]. Science of Surveying and Mapping, 2006, 31(6): 26–29. DOI:10.3771/j.issn.1009-2307.2006.06.005 |
| [22] |
李建成.
最新中国陆地数字高程基准模型:重力似大地水准面CNGG2011[J]. 测绘学报, 2012, 41(5): 651–660, 669.
LI Jiancheng. The Recent Chinese Terrestrial Digital Height Datum Model:Gravimetric Quasi-geoid CNGG2011[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 651–660, 669. |
| [23] |
李姗姗.水下重力辅助惯性导航的理论与方法研究[D].郑州: 信息工程大学, 2010. LI Shanshan. Research on the Theory and Method of Underwater Gravity-aided Inertial Navigation[D]. Zhengzhou: Information Engineering University, 2010. |
| [24] |
《数学手册》编写组.
数学手册[M]. 北京: 高等教育出版社, 1979.
Writing Group of 《Mathematical Directory》. Mathematical Directory[M]. Beijing: Higher Education Press, 1979. |
| [25] |
於宗俦, 鲁林成.
测量平差基础[M]. 北京: 测绘出版社, 1983.
YU Zongchou, LU Lincheng. Foundation of Measurement Adjustment[M]. Beijing: Surveying and Mapping Press, 1983. |
| [26] |
刘敏, 黄谟涛, 欧阳永忠, 等.
海空重力测量及应用技术研究进展与展望(二):传感器与测量规划设计技术[J]. 海洋测绘, 2017, 37(3): 1–11.
LIU Min, HUANG Motao, OUYANG Yongzhong, et al. Development and Prospect of Air-sea Gravity Survey and Its Applications, PartⅡ:Sensor, Plan and Design of Survey[J]. Hydrographic Surveying and Charting, 2017, 37(3): 1–11. DOI:10.3969/j.issn.1671-3044.2017.03.001 |
| [27] |
李庆海, 陶本藻.
概率统计原理和在测量中的应用[M]. 北京: 测绘出版社, 1982.
LI Qinghai, TAO Benzao. Introduction to Probability and Statistics and Its Applications in Surveys[M]. Beijing: Surveying and Mapping Press, 1982. |
| [28] |
黄谟涛, 刘敏, 孙岚, 等.
海洋重力仪稳定性测试与零点漂移问题[J]. 海洋测绘, 2014, 34(6): 1–7.
HUANG Motao, LIU Min, SUN Lan, et al. Test and Evaluation of the Stability for Marine Gravimeter and Its Zero Drift[J]. Hydrographic Surveying and Charting, 2014, 34(6): 1–7. DOI:10.3969/j.issn.1671-3044.2014.06.001 |
| [29] |
许厚泽.
精密重力测量的潮汐改正[J]. 测绘学报, 1984, 13(2): 88–93.
XU Houze. Tide Corrections of Precisegravity Measurments[J]. Acta Geodaetica et Cartographica Sinica, 1984, 13(2): 88–93. DOI:10.3321/j.issn:1001-1595.1984.02.002 |
| [30] |
暴景阳, 许军.
卫星测高数据的潮汐提取与建模应用[M]. 北京: 测绘出版社, 2013.
BAO Jingyang, XU Jun. Tide Analysis from Altimeter Data and the Establishment and Application of Tide Model[M]. Beijing: Surveying and Mapping Press, 2013. |
| [31] |
管泽霖, 管铮, 翟国君.
海面地形与高程基准[M]. 北京: 测绘出版社, 1996.
GUAN Zelin, GUAN Zheng, ZHAI Guojun. Sea Surface Topography and Height Datum[M]. Beijing: Surveying and Mapping Press, 1996. |
| [32] |
黄谟涛, 宁津生, 欧阳永忠, 等.
航空重力测量厄特弗斯改正公式注记[J]. 测绘学报, 2015, 44(1): 6–12.
HUANG Motao, NING Jinsheng, OUYANG Yongzhong, et al. Comments on the Formulae of Eötvös Corrections for Airborne Gravimetry[J]. Acta Geodaetica et Cartogra-phica Sinica, 2015, 44(1): 6–12. DOI:10.11947/j.AGCS.2015.20130330 |
| [33] |
刘敏, 黄谟涛, 欧阳永忠, 等.
海空重力测量及应用技术研究进展与展望(三):数据处理与精度评估技术[J]. 海洋测绘, 2017, 37(4): 1–10.
LIU Min, HUANG Motao, OUYANG Yongzhong, et al. Development and Prospect of Air-sea Gravity Survey and Its Applications, Part Ⅲ:Data Processing and Precision Evaluation[J]. Hydrographic Surveying and Charting, 2017, 37(4): 1–10. DOI:10.3969/j.issn.1671-3044.2017.04.001 |
| [34] |
黄谟涛, 宁津生, 欧阳永忠, 等.
海空重力测量平台倾斜改正模型等价性证明与验证[J]. 武汉大学学报(信息科学版), 2016, 41(6): 738–744.
HUANG Motao, NING Jinsheng, OUYANG Yongzhong, et al. Test and Equivalent Verification of Gravity Correction Models for Platform Tilt in Sea-borne and Air-borne Gravimetry[J]. Geomatics and Information Science of Wuhan University, 2016, 41(6): 738–744. |
| [35] |
刘敏, 黄谟涛, 马越原, 等.
海空重力测量平台倾斜改正修正模型[J]. 武汉大学学报(信息科学版), 2018, 43(4): 586–591.
LIU Min, HUANG Motao, MA Yueyuan, et al. A Modified Correction Model for Platform Tilt in Air-sea-borne Gravimetry[J]. Geomatics and Information Science of Wuhan University, 2018, 43(4): 586–591. |
| [36] |
黄谟涛, 欧阳永忠, 翟国君, 等.
海面与航空重力测量重复测线精度评估公式注记[J]. 武汉大学学报(信息科学版), 2013, 38(10): 1175–1177.
HUANG Motao, OUYANG Yongzhong, ZHAI Guojun, et al. Comment on the Formulas of Accuracy Evaluation for Multi-line Overlapping Measurements in Ship-borne and Airborne Gravity Survey[J]. Geomatics and Information Science of Wuhan University, 2013, 38(10): 1175–1177. |



