2. 信息工程大学地理空间信息学院, 河南 郑州 450001;
3. 三亚城市职业学院, 海南 三亚 572000
2. School of Geospatial Information, Information Engineering University, Zhengzhou 450001, China;
3. Sanya City Vocational College, Sanya 572000, China
伴随着经济的快速发展,道路的建设发展一直保持在一个较高的水平上,尤其是城市道路网成为建设发展的重点。发达的城市道路网(简称道路网)具备强大的通行能力,极大促进了城市经济社会的发展,加之数据采集手段的日益多样化、准确度日益提高,对道路网数据的快速更新带来极大的挑战。现阶段数据采集与处理技术难以满足海量变化数据更新需求,而且数据来源的多样化会给数据融合带来巨大的挑战,准确及时更新道路网的变化信息成为研究的重点。作为更新的关键技术,匹配技术成为解决该问题的主要途径,是目前研究的难点。在多源道路网数据中,同名道路的特征表达存在显著差异,尤其在几何特征表达方面,传统上通过几何特征相似性进行同名道路识别[1-4],但结果的可靠性较差。同名道路空间结构特征的表达具有相对的稳定性,可作为同名道路选取的重要约束性条件。传统数据组织结构不利于对数据进行分析和处理,建立具有丰富空间结构特征的数据模型是非常必要的[5-10]。现在大部分算法对道路网空间结构特征在匹配中发挥的作用重视程度不够,仅有部分文章关注到这一问题。/1/2通过对道路弧段的重新组织,将对道路弧段的匹配转化为对道路stroke的匹配,从而形成一种新的道路网空间结构特征表达模型,利用渐进式的匹配策略,设计匹配算法。上述算法存在的普遍问题是在匹配过程中道路网空间结构特征发挥的作用有限,主要依靠多次的迭代和优化提高匹配质量。本文深入挖掘道路网的空间结构特征,将整个道路网作为一个面域,利用具有稳定空间结构特征的骨干道路将整个道路网剖分为由若干面域组成的集合,然后依据骨干道路的等级信息建立不同面域间的层次关系,使得道路网中的所有道路不仅具有空间特征信息,而且具有空间分布信息,极大地缩小了潜在匹配对象的搜索范围。
1 基于“stroke”原理的城市道路网层次化表达 1.1 “stroke”的基本概念及道路等级划分 1.1.1 “stroke”的基本概念Thomson等最早提出了stroke概念[20-21]。stroke概念的提出主要是为了解决传统数据模型在数据分析和处理时的一些固有缺陷:①传统数据模型在表达线状要素整体性时存在缺陷;②传统数据模型在表达地理现象连续分布特征时存在缺陷。将视觉感受上具有相同方向的线元素通过首尾相连构成一个具有良好整体性和连续性的stroke,作为道路数据特征表达的基本对象单元,被广泛应用于道路网的自动综合和结构分析中。
1.1.2 道路等级划分道路按照通行能力或用途差异划分为不同等级。在道路网数据中,一般将道路等级信息作为属性信息进行标记,但实际上大部分道路的属性信息不完整,所以一般利用道路的几何或拓扑特征进行道路等级评价[22-24]。道路的长度和宽度是常用的几何特征指标,度、紧密度和中介度是常用的拓扑特征指标。在实际上往往只采用有限的几个指标进行评价,面对不同类型的数据,指标使用的优先级并不固定,需结合道路数据的类型特点进行分析和评估,选取最合适的指标组合进行道路等级的评价。
1.2 城市道路网面域剖分模型 1.2.1 基本思路本文以道路网眼作为表达道路网空间结构特征的基本单元。首先提取道路网中各层次的道路网眼,但由于本文对道路网的结构化是面向匹配的,所以对目标数据和参考数据道路网眼的层次化分割需同步进行,即对目标数据中的道路网眼进行分割时,参考数据中的同名道路网眼也要分割,且必须保证道路网眼分割后,存在同名道路网眼。这样可以确保组成道路网眼的骨干道路优先匹配,然后对网眼内道路匹配时可大幅度提高匹配的质量和效率。在实际中,由于多源道路网数据在特征表达方面的差异以及道路stroke生成算法不能完全保证提取结果符合人的认知习惯,基于此,本文将这种面向道路网匹配的,建立在道路网眼层次化分割原理基础上的不完全分割称为层次化面域剖分。
1.2.2 方法模型(1) 最大封闭区域提取。道路网一般会在所在区域形成一个最大的封闭区域,提取这个封闭区域是进行面域层化剖分的第一步。组成这个最大封闭区域的道路是道路网最外围的道路。
(2) 分别判断目标数据和参考数据的封闭面域内所有道路的首末点是否同时与对应的面域边界道路接触。若接触且道路不封闭,就将该条道路作为候选剖分道路;反之,则不作为候选剖分道路。
(3) 对候选剖分道路进行重要性等级评价。
(4) 选取候选剖分道路集中重要性等级最高的道路对目标数据的封闭面域进行剖分,同时利用距离指标搜索在参考数据中候选剖分道路集中与其最近的剖分道路,计算两者之间对应的拟剖分面域的中心点之间的距离和剖分道路的首末点之间的距离是否小于阈值,若成立,则选取这组同名剖分道路作为剖分道路对封闭面域进行剖分,若不成立,则继续步骤(4),直到封闭面域内不存在同名的剖分道路。
(5) 将不能再剖分的面域作为基本剖分面域进行存储。
2 基于层次化面域剖分模型的城市道路网匹配方法 2.1 基本思路道路网匹配的目的是识别出目标数据集和参考数据集中的同名道路。同名道路不仅具有高度的特征相似性,而且其所在的局部道路网络结构也具有一定的相似性,道路网具有鲜明的层次化特征,同一层次间的道路也应具有一定的相似性。基于此,本文利用道路网结构层次化的特点,建立由“整体-局部-对象本身”的道路网层次化表达模型,在同名道路选取中发挥结构性约束的作用,有效提高匹配的质量和效率。
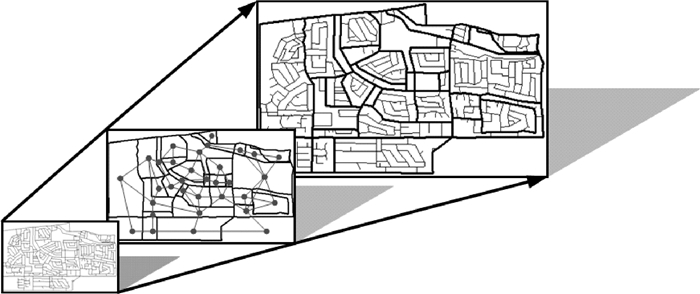
基于层次化面域剖分模型的城市道路网匹配方法,首先是对目标数据和参考数据进行面向匹配的面域剖分处理,使骨干道路实现匹配,同时,将道路网作为一个面要素进行剖分,可建立目标面域和参考面域之间的同名匹配关系和不同层次剖分面域间的层次隶属关系,实现了层次化模型基本架构的搭建;然后以基本面域为研究对象,基于道路重要性等级和与面域边界的连通关系,对面域内道路进行层次性划分。具体过程在2.2节中阐述。通过上述处理,基本建立了由“整体-局部-对象本身”的道路网层次化表达模型(如图 1所示),基于该模型本文提出城市道路网匹配模型,由高等级道路到低等级道路逐级进行匹配。
|
| 图 1 道路网层次化表达模型示意 Fig. 1 A hierarchical model of road network |
2.2 基本面域单元道路的层次性分类表达
本文将包括面域边界在内的道路按照道路重要性等级和与面域边界的连通关系划分为4类:
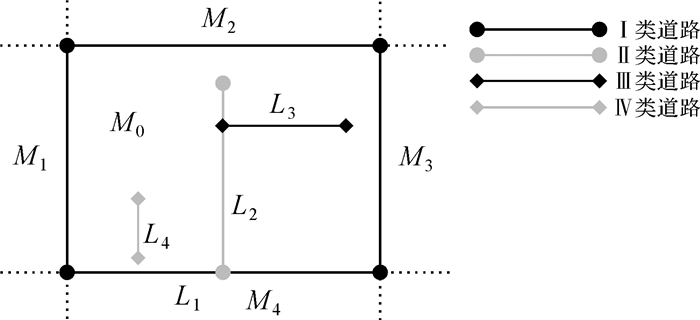
Ⅰ类道路是指基本面域内等级最高的道路,是指基本面域的边界道路(图 2中L1),此类道路是构成道路网整体空间分布的骨干道路,具有较高几何位置精度和完整的拓扑结构信息。由于面域剖分是面向匹配,所以Ⅰ类道路具有与之精确匹配的同名道路,是进行面域内其他道路匹配的重要约束性条件。
|
| 图 2 基本面域内道路类型示例 Fig. 2 Road types for basic area |
Ⅱ类道路是基本面域内的次等级道路(图 2中L2),此类道路一般与Ⅰ类道路至少有一个交点,与Ⅰ类道路具有连通性,是优先匹配的道路。
Ⅲ类道路是指仅与Ⅱ类道路至少有一个交点的道路(图 2中L3),且与Ⅱ类道路具有连通性。
Ⅳ类道路是指与上述几种类型道路均没有连通关系的道路(图 2中L4),一般是独立道路,等级最低。
对基本面域内道路的分类完善了模型的层次性划分,构建起道路网层次性表达模型,在“横向”和“纵向”上建立了层次关联关系。“横向”是指道路网的层次性划分是面向匹配过程的,对目标数据中的任一条道路,当明确本身的层次后,匹配对象选取数量大幅度减少,提高了匹配的效率和准确性。“纵向”是指任一条道路都具有明确的层次隶属关系,且每个层次之间都是包含与被包含的关系,对匹配先后顺序的指向性更为明确,当出现错误的匹配结果时,对结果的修正也更为高效。
2.3 匹配模型 2.3.1 匹配模型的基本思想上节将基本面域内的道路进行了层次化分类,建立了基本面域道路的层次化模型。同一层次之间的道路准确匹配的前提是道路本身的特征相似度与邻近道路的特征相似保持高度一致。基于这个原则,假设每条道路的特征相似性与邻近道路特征相似性具有一致性,然后通过邻近道路的实际相似性验证该假设,如果两者在一定条件下同时成立,证明该匹配结果可信。
2.3.2 匹配过程步骤1:设同一层次中,目标数据道路集A={a1, a2, …, am},参考数据道路集B=b{1, b2, …, bn},任意选择集合A中一条道路ai(i∈(0, m)),选择集合B中与ai的相似度最大的一条道路bj(j∈(0, n))作为潜在的匹配道路,将其作为种子道路。
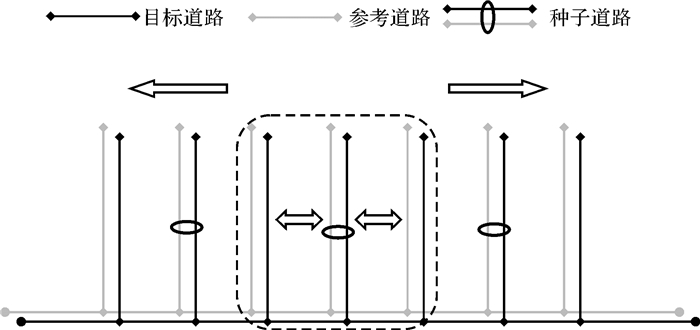
步骤2:在集合A中选取与ai在空间位置上相邻的道路ai-1与ai+1,与ai组成目标局部道路网络G={ai, ai-1, ai+1},在集合B中选取与bj在空间位置上相邻的道路bj-1与bj+1,与bj组成参考局部道路网络V={bj, bj-1, bj+1}(如图 3所示)。
|
| 图 3 道路网络选取示意 Fig. 3 The example of road network selection |
步骤3:若道路ai和bj是同名道路。(G, V)中的道路两两之间的特征相似性具有高度一致性。若上述假设成立(图 4(a)),转到步骤4;若上述假设不成立,转到步骤5。

|
| 图 4 匹配过程示例 Fig. 4 The example of matching |
步骤4:集合G与V中的道路两两之间互为同名道路,转到步骤6。
步骤5:删除集合V中相似性不一致的道路bj-1(bj+1),选取该道路邻近方向上的道路bj-2(bj+2)加入集合V(图 4(b)),转到步骤7。
步骤6:选取集合G和V中边界元素的相邻道路ai'和bj'作为新的种子道路,继续上述步骤2的处理,直到该层次所有道路匹配结束。
步骤7:若集合G与V中的道路两两之间的特征相似性具有高度一致性(图 4(b)),转到步骤4;反之(图 4(c)),转到步骤6。
2.3.3 特征一致性评价模型 2.3.3.1 相似性评价指标选取同名道路之间最为显著的特征差异是位置差异,本文将距离作为表达同名道路之间位置差异的指标,当存在多个(n≥2)相似度大小接近的候选匹配对象时,本文采用道路连通度和形状相似度两个指标作进一步判断,选择相似度最大的道路作为匹配道路。
2.3.3.2 模型构建在匹配过程中,对道路相似性的计算分为两个部分:种子道路选取和相似度一致性评价。其中,种子道路选取是指选取相似度最高的同名匹配道路,将其作为局部道路网络的特征道路;相似度一致性评价是指对同名局部道路网络特征一致性的判断。特征一致性评价模型由上述两部分组成,如式(1)所示
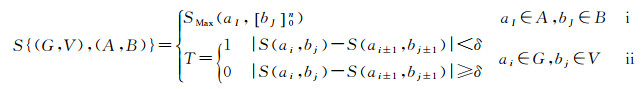 (1)
(1)
式中,S{(G, V), (A, B)}表示局部道路网络(G, V)的总相似度。模型分为两部分:式(1-ⅰ)是种子道路选取模型,式(1-ⅱ)表示相似度一致性评价模型。
种子道路选取模型SMax(aI, [bJ]0n),是指选取同一层次的目标道路与匹配对象间相似度最大的道路,作为种子道路。其中
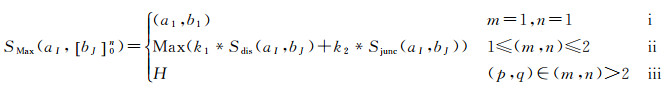 (2)
(2)
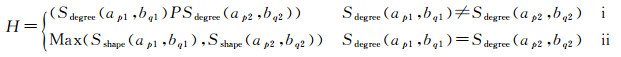 (3)
(3)
模型SMax(aI, [bJ]0n)是一个选择判断过程:
(1) 当m=1, n=1,说明数据集A和B中只有(a1, b1)一组道路,(a1, b1)自动成为种子道路。
(2) 当1≤(m, n)≤2时,说明数据集中至多存在两组道路,这时SMax(aI, [bJ]0n)=Max(k1·Sdis(aI, bJ)+k2·Sjunc(aI, bJ)),k1和k2分别为弧段距离[25]和节点距离指标的权重系数,由于对弧段和节点均采用距离指标度量相似性,所以本文设定k1=k2,选取相似度最大的一组道路作为种子道路。
(3) 当(p, q)∈(m, n)>2时,说明数据集中存在多于两组道路,首先利用式(2-ⅱ)选取相似度大小位于前两位的两组道路,然后判断两组道路的连通度,如式(3)所示,当Sdegree(ap1, bq1)≠Sdegree(ap2, bq2)时,说明只有一组道路的连通度一致(式(6)),选取连通度相同一组道路作为种子道路,反之则计算两组道路的形状相似度,选取Sshape(ap, bq)值最大的一组道路作为种子道路。
通过上述过程选取了特征相似性最高的种子道路。
式(1-ⅱ)所示为相似度一致性评价模型,在选取种子道路后,构建了由种子道路和相邻道路组成的局部道路网络(G, V),相似度一致性评价模型就是用于评价局部道路网络(G, V)中,两两道路之间的特征相似性是否具有一致性。|S(ai, bj)-S(ai±1, bj±1)|表示同名种子道路与同名相邻道路之间相似度的差异,其中δ为上述两者之间的极限差值(通过多次试验获得),当|S(ai, bj)-S(ai±1, bj±1)|<δ时,表示相邻道路之间的特征相似性具有高度一致性,即道路ai±1和bj±1是一同名道路,反之,则不是。
上述公式中
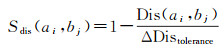 (4)
(4)
式中,Dis(ai, bj)为道路ai和bj弧段距离值,采用/1/2中提出的距离度量方法计算Dis(ai, bj)的值,采用ΔDistolerance为弧段距离阈值,当Dis(ai, bj)>ΔDistolerance时,道路ai和bj不是同名道路,反之可用式(5)进一步判断
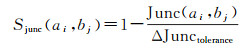 (5)
(5)
式中,Junc(ai, bj)为道路ai和bj节点的欧氏距离;ΔJunctolerance为距离阈值。Junc(ai, bj)>ΔJunctolerance时,道路ai和bj不是同名道路,反之可用式(6)进一步判断
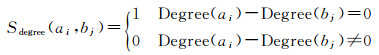 (6)
(6)
式中,Degree(ai)-Degree(bj)为道路ai和bj连通度的差值,Degree(ai)、Degree(bj)分别表示道路ai和bj的连通度,通过计算与目标道路相交的道路的数量可获得Degree(ai)、Degree(bj)的值,当Degree(ai)-Degree(bj)=0时,即Sdegree(ai, bj)=1,道路ai和bj是同名道路,反之可用式(7)进一步判断
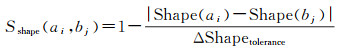 (7)
(7)
式中,|Shape(ai)-Shape(bj)|为道路ai和bj形状相似度的差值,Shape(ai)、Shape(bj)分别表示道路ai和bj的形状相似度,采用Arkin提出一种的形状描述方法[25]计算Shape(ai)、Shape(bj)的值,ΔShapetolerance为弧段形状阈值,当|Shape(ai)-Shape(bj)|>ΔShapetolerance时,道路ai和bj不是同名道路,反之可进行进一步判断。
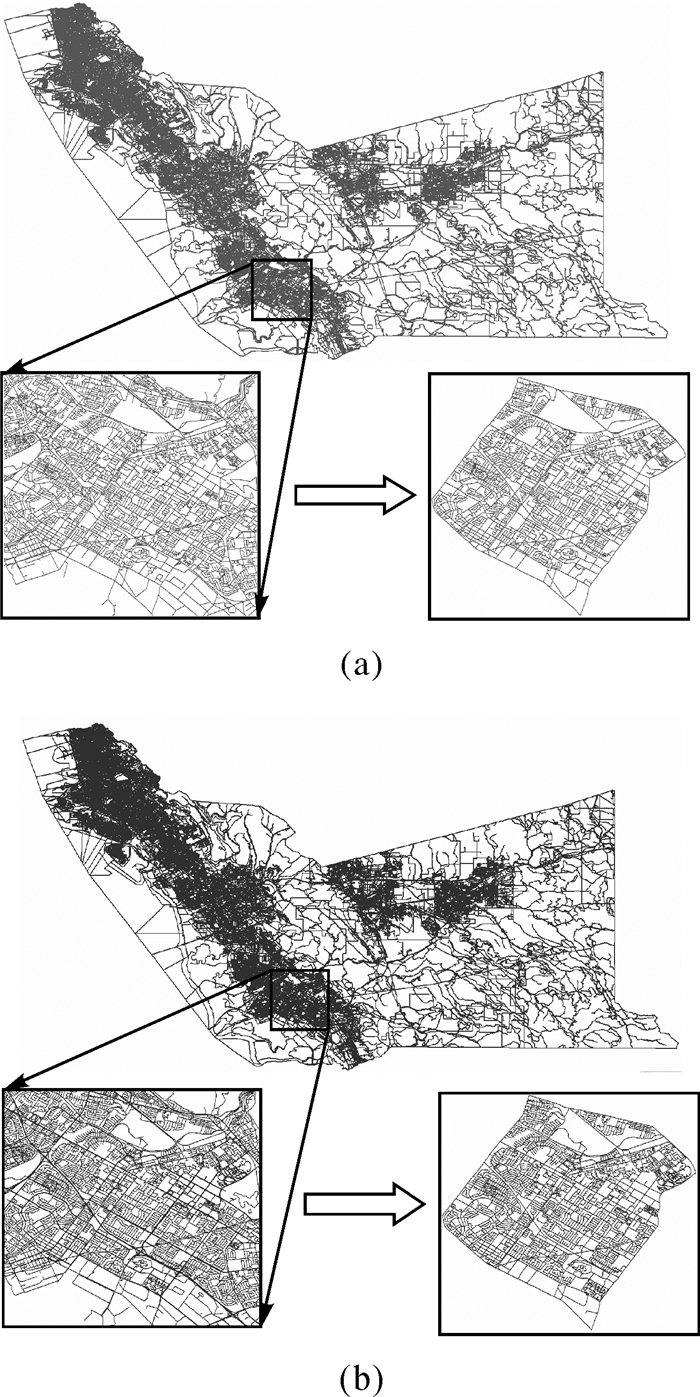
3 试验分析 3.1 面域剖分 3.1.1 数据预处理本文选取某地区的两幅比例尺为1: 1万的不同时间的道路网数据进行了匹配试验,其中目标数据(图 5(a))为2007年的数据,参考数据(图 5(b))为2012年的数据。两幅道路数据既包括城市道路数据也包括乡村道路数据,本文截取了部分典型特征的城市道路网数据(矩形区域)进行匹配试验,并在试验之前对数据进行了预处理。图 6为两幅试验数据的叠加后的显示效果,从图上可以看出,两数据集并不完全重叠,不同区域内同名道路的空间位置和形态特征存在明显差异,而且参考数据中存在一部分新增道路。试验数据经过整饰和拓扑关系处理后包含的弧段与节点信息见表 1。
|
| 图 5 试验数据 Fig. 5 Experimental data |

|
| 图 6 试验数据叠加显示效果 Fig. 6 Overlay display of experimental data |
| 数据 | 匹配数据源 | 截取数据 | 预处理后数据 | |||||
| 弧段数量 | 节点数据 | 弧段数量 | 节点数据 | 弧段数量 | 节点数据 | |||
| 目标数据 | 62 607 | 58 963 | 5328 | 4852 | 3378 | 3205 | ||
| 参考数据 | 98 438 | 99 624 | 7864 | 7913 | 3854 | 4135 | ||
试验数据中同名道路之间存在着一定的差异,主要是位置精度误差,而且呈现分布不均的特点,有些区域误差比较大,而有些区域误差较小,总体上,在不同的“街区”内,同名道路之间的位置差异和形态特征差异变化较为一致,反之,不同“街区”之间则存在明显不同。
3.1.2 高等级道路选取从原始数据的属性信息分析,两幅图由于出自不同的技术部门,道路的属性信息存在不一致性,无法直接利用属性信息提取stroke,而数据的几何以及拓扑结构比较完整,位置精度较高,比较适合利用道路的几何和拓扑特征提取stroke。本文的另外的一篇论文对不同指标的选取效果进行了对比分析,其中,道路紧密度和道路长度对于城市道路网的选取结果更加符合人的认知习惯,所以本文采用上述两个指标作为道路重要性等级评价的约束性条件,其中长度指标的优先级高于紧密度,设定关联弧段间的偏向角阈值为45°。
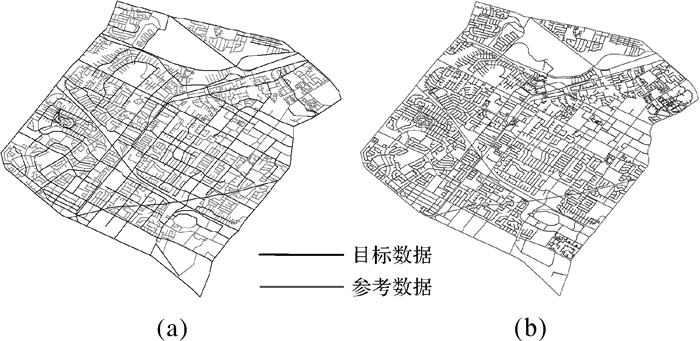
在提取道路stroke之前首先对数据进行拓扑处理,去除道路数据中的伪节点。对拓扑处理后的道路网数据提取道路stroke,表 2是提取stroke前后相关数据的统计。提取道路stroke后,以长度和道路紧密度作为道路等级评价指标进行排序。选取重要性排名前10%的道路(stroke)作为高等级道路(图 7)。由图 7可见,目标数据按照10%的选取标准,提取了75条道路stroke,参考数据提取了93条道路stroke。选取结果基本符合人对道路的空间认知,经叠加计算,两幅数据的叠合率为83%(以目标数据为基准),较好地保持了道路网整体的结构形态特征,可以利用选取结果进行层次化的面域剖分。
| 数据 | 原始数据 | 拓扑处理后 | Stroke构建后 | ||||
| 弧段数量 | 节点数量 | 弧段数量 | 节点数量 | Stroke数量 | |||
| 目标数据 | 3627 | 7254 | 3378 | 3205 | 750 | ||
| 参考数据 | 4551 | 9102 | 3854 | 4135 | 930 | ||
|
| 图 7 高等级道路提取结果 Fig. 7 Extraction result of high grade road |
3.1.3 层次化面域剖分
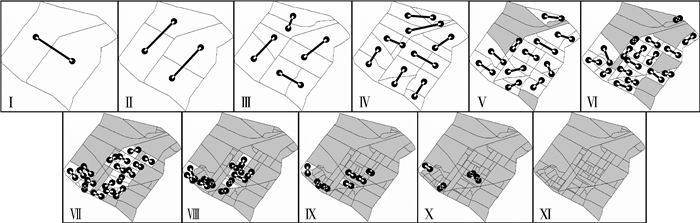
提取道路stroke后,基于1.2.2节中的面域剖分方法,对道路网进行了剖分。图 8为展示了整个剖分过程,图中黑色短线表示当前的剖分结果,经过11次剖分,道路网构成的最大封闭面域被剖分成84个基本面域(见表 3),每次剖分后的面域数量如表 3所示。在剖分初始阶段,每次剖分后,面域内包含大量的可剖分道路,而且由于该道路等级较高,参考数据和目标数据之间道路的特征相似度较高,符合面域剖分的基本条件,进而可以实现连续的剖分。当剖分等级大于Ⅳ时,面域的数量结束了指数增长的趋势,出现了不可继续剖分的基本面域,且其数量出现了快速增长,可剖分面域数量快速下降,在整个道路网中,不同区域的道路呈现不同的空间分布特征,如图 9所示,V1、V2、V3等区域的道路的连通性较差,同时存在形状不规则的弯曲道路,在进行面域剖分判断时,特征相似度较低,难以实现高质量的剖分,所以相较于其他区域更容易提前结束剖分,成为基本面域。特别指出的是目标数据和参考书的面域剖分是同步进行的,根据剖分的基本条件,当剖分结束后,目标数据中每个基本面域在参考数据中都有与之对应的同名面域,相应的构成面域边界的道路互为同名道路。图 9为参考数据和目标数据剖分结果的叠合效果,通过目视检验,构成基本面域的道路均为同名道路。
|
| 图 8 层次化面域剖分结果 Fig. 8 Results of hierarchical area partitioning |
| 剖分等级 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ | Ⅶ | Ⅷ | Ⅸ | Ⅹ | Ⅺ |
| 可继续剖分面域 | 2 | 4 | 8 | 16 | 22 | 34 | 34 | 24 | 14 | 8 | 0 |
| 形成基本面域 | 0 | 0 | 0 | 0 | 5 | 10 | 27 | 49 | 66 | 76 | 84 |
| 总计 | 2 | 4 | 8 | 16 | 27 | 44 | 61 | 71 | 80 | 84 | 84 |

|
| 图 9 剖分面域叠合 Fig. 9 Overlap of partition area |
3.2 面域内道路层次划分
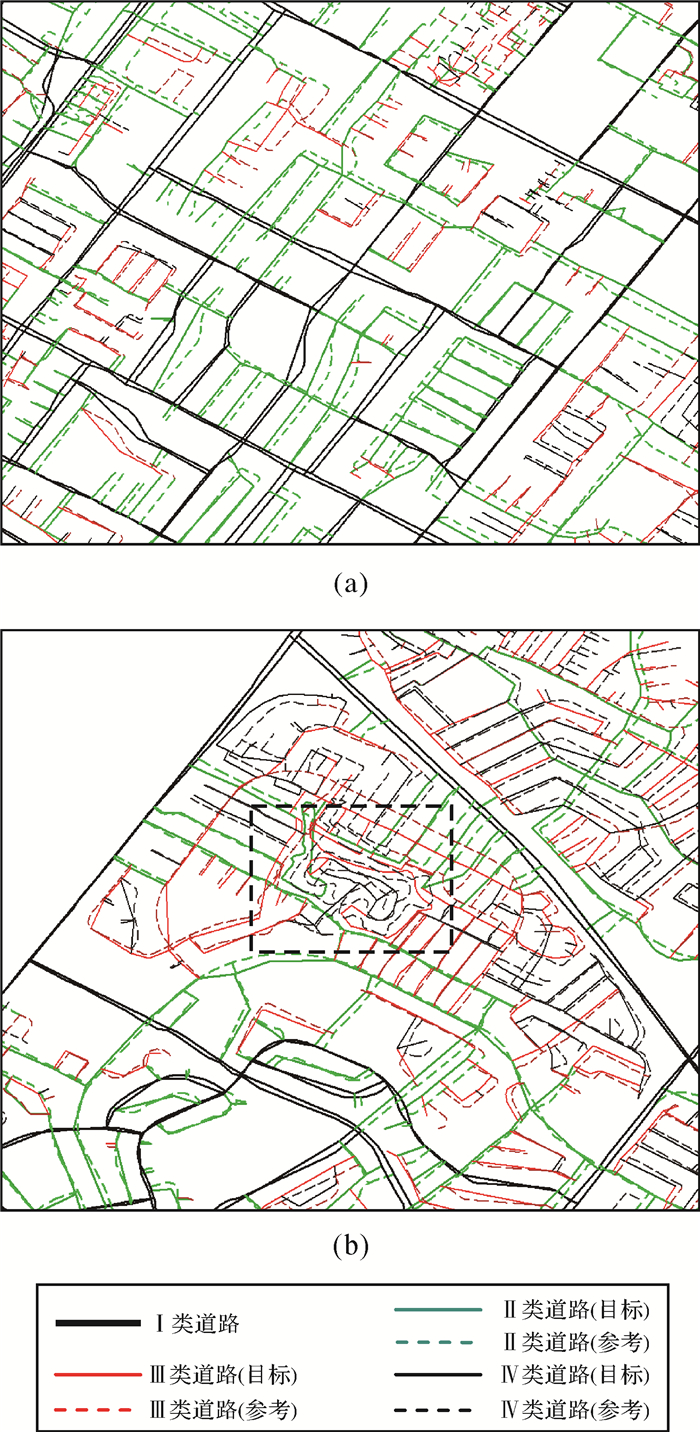
在完成面域剖分后,将基本面域内道路进行层次性划分,结果如图 10所示。图中黑色标识道路围成的区域是基本面域,是Ⅰ类道路;绿色实线标识道路和绿色虚线标识道路分别是目标面域内和参考面域内的Ⅱ类道路;红色实线标识道路与红色虚线标识道路分别是目标面域内和参考面域内的Ⅲ类道路;基本面域内剩余的道路为Ⅳ类道路,分别用黑色细实线和黑色细虚线进行标识。通过对基本面域内道路层次性的划分,实现了道路网数据由基本面域向单个道路对象表达的进一步延伸,在匹配时,潜在的匹配对象一般集中于同一层次的道路,少量道路集中于邻近层次的道路,这样的划分结果大幅减少了同名道路的搜索次数,提高了匹配的效率。本文对基本面域内道路的划分结果大部分与人的认知结果一致,只有如图 10(b)虚线矩形区域内所示,存在少部分道路划分结果不理想的情况,可通过扩大搜索范围或进行人工交互的方式进行纠正,提高匹配的准确度。
|
| 图 10 基本面域内道路层次划分效果 Fig. 10 Results of hierarchically divided for basic area |
面域内道路层次划分的结果见表 4,在层次划分前,试验数据中道路对象的数量是原始数据构建stroke的数量,通过层次划分,目标数据与参考数据的道路对象的数量分别为1478和1765,这是由于层次化面域剖分将部分道路stroke分解为若干道路对象,虽然增加了道路对象的数量,但这些道路对象均具有明确的层次属性,是道路匹配重要的约束性条件。
| 层次划分前 | 层次划分后 | |
| 目标数据 | 730 | 1478 |
| 参考数据 | 950 | 1765 |
3.3 道路匹配
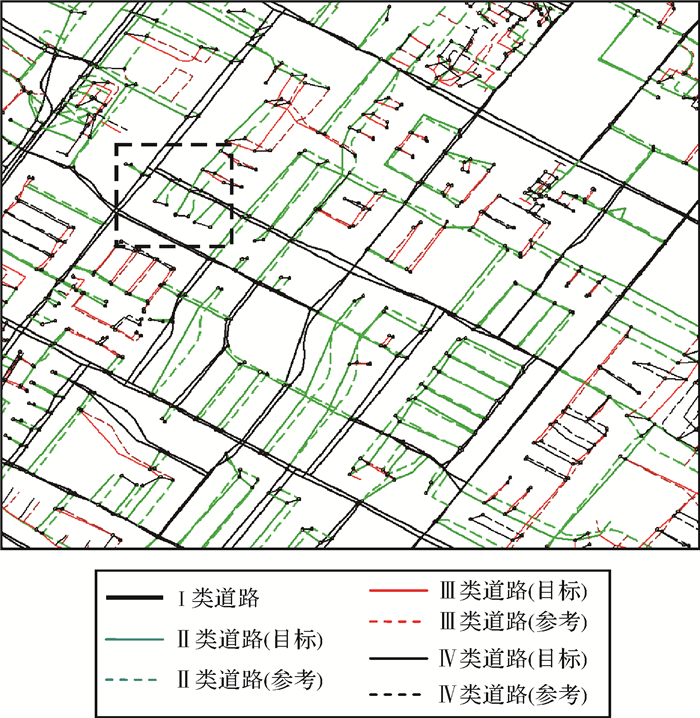
通过对面域内道路的层次性划分,重要性等级最高的Ⅰ类道路已实现匹配,经过人工检查,准确率为100%,所以对面域内道路的匹配主要是针对Ⅱ、Ⅲ、Ⅳ类道路,匹配结果如图 11—图 13所示。由于试验数据量较大,本文截取局部区域的匹配结果进行说明,试验中相邻道路之间相似度的差异值δ设定0.5(经多次试验获得)。
|
| 图 11 规则区域匹配效果 Fig. 11 Results of matching for rule area |
|
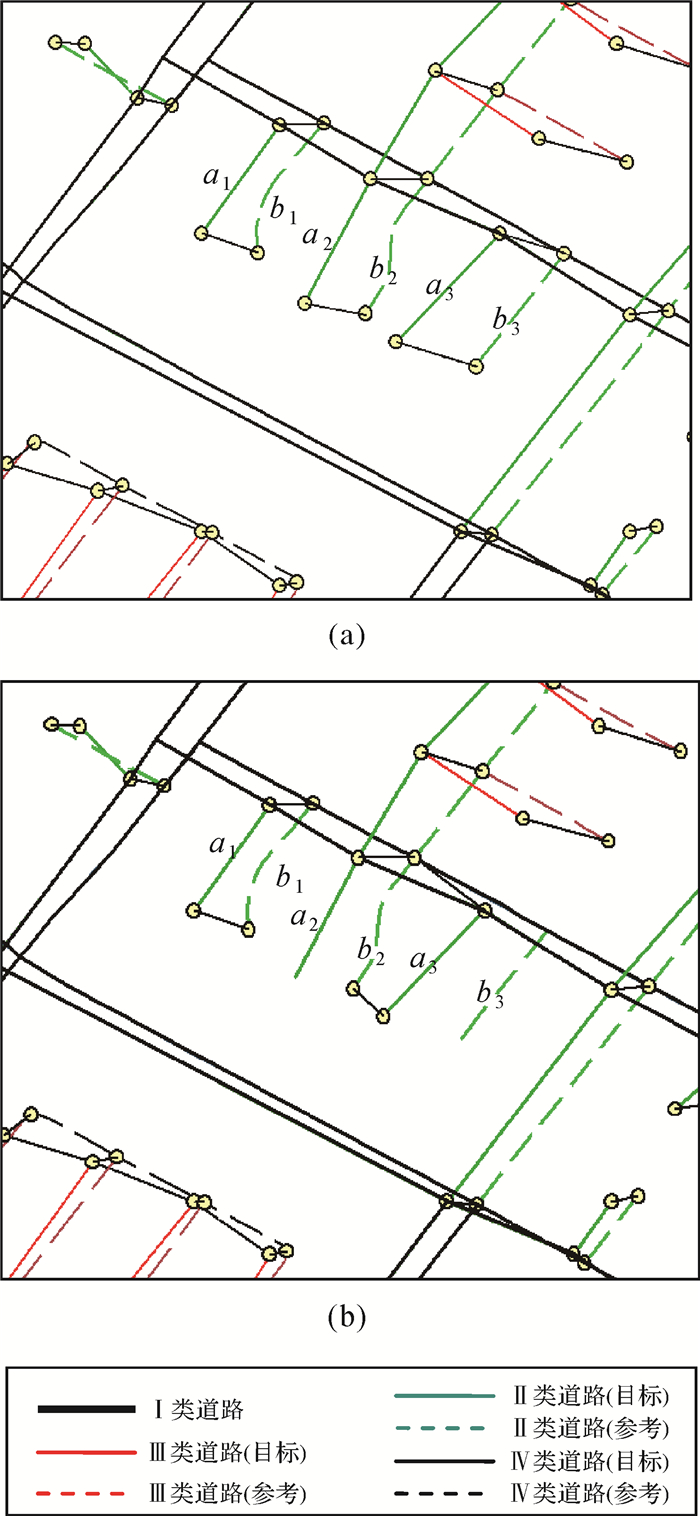
| 图 12 局部对比 Fig. 12 Comparison of the part |

|
| 图 13 不规则区域匹配效果 Fig. 13 Results of matching for rule area |
图 11是道路比较规则区域的匹配结果图。图中将同名道路的首末节点分别用浅棕色填充的黑色圆环标识,并将同名节点用黑色线段相连,同名节点之间的道路即为同名道路。如图可见,规则道路之间的匹配结果比较理想,经人工检核,大部分匹配结果与人工判断相一致。同时,在道路层次性划分的前提下,本文利用多指标约束匹配模型对同一数据进行了匹配处理,选取了与本文方法的匹配结果不一致的区域(图 11中的虚线矩形区域)进行了对比分析,结果如图 12所示。
图 12中匹配结果存在不一致的道路属于局部道路网络,G={a1, a2, a3}和V={b1, b2, b3},属于Ⅱ类道路。在采用本文方法的匹配结果中(图 12(a)),道路a1和b1、a2和b2、a3和b3分别为同名道路,匹配结果与人工判断结果一致,采用多指标约束匹配模型的匹配结果为道路a1和b1、道路a3和b2为同名道路,a2没有匹配对象,显而易见,a3和b2不是同名道路,而道路a2的同名道路是b2,a3和b3是同名道路。文中的多指标约束匹配模型采用了距离和长度2个约束性指标,但由于道路a3与b2的计算距离值要略小于道路a3与b3的计算距离值,易造成错误的匹配结果,由此可知,同名道路之间的特征表达存在着很大的不确定性,有的同名道路与非同名道路之间的特征差异很小,难以准确度量,甚至非同名道路之间的特征相似度要高于同名道路,仅利用相似性评价指标的约束作用难以处理上述情况,但从空间结构分布上看,局部道路网络G={a1, a2, a3}和V={b1, b2, b3}的特征表达具有高度的一致性,所以本文提出的城市道路网匹配模型,在利用空间结构特征的相似性进行匹配时相较于常规的匹配时模型具有一定的优势。
图 13是不规则区域的匹配结果,图中存在部分形状特征复杂的道路(如图 13中虚线矩形区域所示),同名道路存在较大的特征差异,且与邻近道路的拓扑关系复杂,难以表达。由于道路层次划分结果不理想,少数同名道路之间甚至分属于不同的道路类型,所以匹配结果不理想,只有部分长度较短、道路弯曲特征不明显的道路实现匹配。但该区域大部分道路均能准确匹配,上述问题仅少量存在,且在人工检查中辨识度较高,可以快速地实现纠正。
3.4 匹配结果统计分析本文算法的匹配统计结果见表 5。匹配率为94.36%,匹配正确率达到91.23%,匹配质量较好。从试验结果来看,该算法在解决具有典型城市特征的道路匹配问题时,能达到较好的匹配效果,尤其是规则区域的匹配准确率接近100%,但处理不规则道路时效果不佳,目前需要人工检查纠正,下一步可以针对不规则道路的匹配问题开展深入研究,进一步提高算法的可用性。
| 匹配结果类型 | 匹配结果 |
| 匹配数/个 | 1395 |
| 未匹配/个 | 83 |
| 正确匹配/个 | 1273 |
| 错误匹配/个 | 122 |
| 匹配率/(%) | 94.36 |
| 准确率/(%) | 91.23 |
| 召回率/(%) | 86.13 |
4 结论
本文提出了一种基于层次化面域剖分模型的城市道路网匹配方法。该方法首先对道路网进行层次化面域剖分,然后对面域内道路层次划分,组成了“整体-局部-对象本身”的道路网层次化表达模型,最后在此基础上提出了城市道路网匹配模型,并采用城市道路网数据进行了匹配试验,取得了较好的匹配效果。但仍存在需进一步改进的方面:
(1) 本文对城市道路网的层次性特征进行了结构化的表达,同时完成了对组成基本面域高等级道路的精确匹配,提高了匹配的质量和效率,但面对复杂道路网时,算法的可用性需进一步提高。
(2) 本文方法可有效解决相邻道路几何和拓扑结构特征相似而出现的误匹配问题。但对于一些结构复杂,特征差异较大的同名道路处理效果不理想,需借助人工方法进行纠正。
| [1] | DAVIS M. JCS Conflation Suite Technical Report[EB/OL]. http://www.vividsolutions.com/JCS/main.htmh, 2003. |
| [2] | LI Linna, GOODCHILD M F. An Optimisation Model for Linear Feature Matching in Geographical Data Conflation[J]. International Journal of Image and Data Fusion, 2011, 2(4): 309–328. DOI:10.1080/19479832.2011.577458 |
| [3] | TONG Xiaohua, LIANG Dan, JIN Yanmin. A Linear Road Object Matching Method for Conflation Based on Optimization and Logistic Regression[J]. International Journal of Geographical Information Science, 2014, 28(4): 824–846. |
| [4] |
陈玉敏, 龚健雅, 史文中.
多尺度道路网的距离匹配算法研究[J]. 测绘学报, 2007, 36(1): 84–90.
CHEN Yumin, GONG Jianya, SHI Wenzhong. A Distance-based Matching Algorithm for Multi-scale Road Networks[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 84–90. DOI:10.3321/j.issn:1001-1595.2007.01.015 |
| [5] | ZHANG Qingnian. Modeling Structure and Patterns in Road Network Generalization[C]//Proceedings of ICA Workshop on Generalization and Multiple Representation. Leicester: [s.n.], 2004: 21. |
| [6] | HEINZLE F, ANDERS K H, SESTER M. Pattern Recognition in Road Networks on the Example of Circular Road Detection[M]//RAUBAL M, MILLER H J, FRANK A U, et al. Geographic Information Science. Berlin, Heidelberg: Springer, 2006: 153-167. |
| [7] | HEINZLE F, ANDERS K H. Characterising Space via Pattern Recognition Techniques: Identifying Patterns in Road Networks[M]//MACKANESS W A, RUAS A, SARJAKOSKI L T. Generalisation of Geographic Information: Cartographic Modelling and Applications International Cartographic Association. Amsterdam: Elsevier Science, 2007: 233-253. |
| [8] |
徐柱, 蒙艳姿, 李志林, 等.
基于有向属性关系图的典型道路交叉口结构识别方法[J]. 测绘学报, 2011, 40(1): 125–131.
XU Zhu, MENG Yanzi, LI Zhilin, et al. Recognition of Structures of Typical Road Junctions Based on Directed Attributed Relational Graph[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 125–131. |
| [9] |
田晶, 艾廷华, 丁绍军.
基于C4.5算法的道路网网格模式识别[J]. 测绘学报, 2012, 41(1): 121–126.
TIAN Jing, AI Tinghua, DING Shaojun. Grid Pattern Recognition in Road Networks Based on C4.5 Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 121–126. |
| [10] |
翟仁健, 武芳, 黄博华, 等.
城市道路网面域层次结构特征的识别与表达[J]. 测绘科学技术学报, 2014, 31(4): 413–418.
ZHAI Renjian, WU Fang, HUANG Bohua, et al. A Method for Recognition and Representation of Areal Hierarchy of Urban Road Networks[J]. Journal of Geomatics Science and Technology, 2014, 31(4): 413–418. DOI:10.3969/j.issn.1673-6338.2014.04.018 |
| [11] | ZHANG Meng, MENG Liqiu. Delimited Stroke Oriented Algorithm-working Principle and Implementation for the Matching of Road Networks[J]. Geographic Information Sciences, 2008, 14(1): 44–53. |
| [12] |
刘海龙, 钱海忠, 王骁, 等.
采用层次分析法的道路网整体匹配方法[J]. 武汉大学学报(信息科学版), 2015, 40(5): 644–651.
LIU Hailong, QIAN Haizhong, WANG Xiao, et al. Road Networks Global Matching Method Using Analytical Hierarchy Process[J]. Geomatics and Information Science of Wuhan University, 2015, 40(5): 644–651. |
| [13] |
陈军, 胡云岗, 赵仁亮, 等.
道路数据缩编更新的自动综合方法研究[J]. 武汉大学学报(信息科学版), 2007, 32(11): 1022–1027.
CHEN Jun, HU Yungang, ZHAO Renliang, et al. Road Data Updating Based on Map Generalization[J]. Geomatics and Information Science of Wuhan University, 2007, 32(11): 1022–1027. |
| [14] |
巩现勇, 武芳, 姬存伟, 等.
道路网匹配的蚁群算法求解模型[J]. 武汉大学学报(信息科学版), 2014, 39(2): 191–195.
GONG Xianyong, WU Fang, JI Cunwei, et al. Ant Colony Optimization Approach to Road Network Matching[J]. Geomatics and Information Science of Wuhan University, 2014, 39(2): 191–195. |
| [15] |
田晶, 何青松, 颜芬.
道路网Stroke生成问题的形式化表达与新算法[J]. 武汉大学学报(信息科学版), 2007, 39(5): 556–560.
TIAN Jing, HE Qingsong, YAN Fen. Formalization and New Algorithm of stroke Generation in Road Networks[J]. Geomatics and Information Science of Wuhan University, 2007, 39(5): 556–560. |
| [16] |
张朋东, 石岩, 邓敏, 等.
基于拓扑强度的城市道路网络层次表达[J]. 武汉大学学报(信息科学版), 2016, 41(2): 178–183, 213.
ZHANG Pengdong, SHI Yan, DENG Min, et al. Hierarchical Representation of Urban Road Network Based on Topological Intensity[J]. Geomatics and Information Science of Wuhan University, 2016, 41(2): 178–183, 213. |
| [17] |
杨林, 万波, 王润, 等.
一种基于层次路划结构关系约束的矢量道路网自动匹配方法[J]. 武汉大学学报(信息科学版), 2015, 40(12): 1661–1668.
YANG Lin, WAN Bo, WANG Run, et al. Matching Road Network Based on the Structural Relationship Constraint of Hierarchical Strokes[J]. Geomatics and Information Science of Wuhan University, 2015, 40(12): 1661–1668. |
| [18] |
栾学晨, 杨必胜.
城市复杂道路网的Stroke生成方法[J]. 地理与地理信息科学, 2009, 25(1): 49–52.
LUAN Xuechen, YANG Bisheng. Generating Strokes from City Road Networks[J]. Geography and Geo-Information Science, 2009, 25(1): 49–52. |
| [19] |
赵彬彬, 邓敏, 李光强, 等.
基于城市形态学原理的面状地物层次索引方法[J]. 测绘学报, 2010, 39(4): 435–440.
ZHAO Binbin, DENG Min, LI Guangqiang, et al. A New Hierarchical Spatial Index for Area Entities Based on Urban Morphology[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 435–440. |
| [20] | THOMSON R C, RICHARDSON D E. The "Good Continuation" Principle of Perceptual Organization Applied to the Generalization of Road Networks[C]//Proceedings of the 19th International Cartographic Conference. Ottawa, Canada: ICA/ACI, 1999: 1215-1223. |
| [21] | THOMSON R C. The "Stroke" Concept in Geographic Network Generalization and Analysis[C]//Proceedings of the 12th International Symposium on Spatial Data Handling. Vienna, Austria: Springer, 2006: 681-697. |
| [22] | JIANG Bin, CLARAMUNT C. Topological Analysis of Urban Street Networks[J]. Environment and Planning B:Planning and Design, 2004, 31(1): 151–162. DOI:10.1068/b306 |
| [23] |
李清泉, 曾喆, 杨必胜, 等.
城市道路网络的中介中心性分析[J]. 武汉大学学报(信息科学版), 2010, 35(1): 37–41.
LI Qingquan, ZENG Zhe, YANG Bisheng, et al. Betweenness Centrality Analysis for Urban Road Networks[J]. Geomatics and Information Science of Wuhan University, 2010, 35(1): 37–41. |
| [24] |
叶彭姚, 陈小鸿.
基于道路骨架性的城市道路等级划分方法[J]. 同济大学学报(自然科学版), 2011, 39(6): 853–856, 878.
YE Pengyao, CHEW Xiaohong. Urban Road Hierarchy Based on Road Arteriality[J]. Journal of Tongji University (Natural Science), 2011, 39(6): 853–856, 878. DOI:10.3969/j.issn.0253-374x.2011.06.012 |
| [25] |
黄博华, 武芳, 许俊奎, 等.
一种面向同名线要素的距离度量方法[J]. 武汉大学学报(信息科学版), 2017, 42(3): 395–401.
HUANG Bohua, WU Fang, XU Junkui, et al. A Method of Distance Measurement for Corresponding Linear Feature[J]. Geomatics and Information Science of Wuhan University, 2017, 42(3): 395–401. |
| [26] | ARKIN E M, CHEW L P, HUTTENLOCHER D P, et al. An Efficiently Computable Metric for Comparing Polygonal Shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(3): 209–216. DOI:10.1109/34.75509 |


