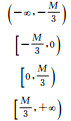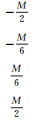2. 江苏省地理环境演化国家重点实验室培育建设点, 江苏 南京 210023;
3. 江苏省地理信息资源开发与利用协同创新中心, 江苏 南京 210023
2. State Key Laboratory Cultivation Base of Geographical Environment Evolution(Jiangsu Province), Nanjing 210023, China;
3. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023, China
矢量地理数据具有空间特征明显、精度高、组织结构多样的特点,其中小数据量的矢量地理数据例如矢量切片、区域采样点、矿井分布、军事敏感区等,在数据共享和分发中面临着盗版、侵权和泄密等安全问题,迫切需要有效的技术手段进行安全保护和版权鉴定。数字水印技术将版权信息与数据紧密结合,能够有效实现矢量地理数据的版权保护、追踪溯源和安全管理。目前矢量地理数据水印算法已取得较多研究成果,根据嵌入域的不同可分为空间域、频率域及几何域的水印算法。空间域水印算法运用量化、坐标映射等方法,直接对矢量数据坐标嵌入水印,实现较强的抵抗增删攻击的能力[1-5];频率域水印算法将水印嵌入至坐标变换域系数中,例如离散傅里叶变换、离散余弦变换等,提升了算法抗噪声、平移等攻击的能力[6-12];基于几何域的水印算法将水印嵌入至地理数据几何特征中,包括角度、距离、弧长等,能够对旋转、缩放、平移等几何攻击具有更好的抵抗性[13-18]。
综合来看,现有的矢量地理数据水印算法研究侧重于稳健性的提升,但对水印容量方面研究较少,大多数水印算法对每个节点嵌入的水印容量不超过2 bit[1-18]。但在实际中,小数据量的矢量地理数据往往只有100个节点左右,而水印信息长度可超过1000位。例如,一幅32×32像素的二值版权图像的信息量为1024 bit。因此,高水印容量的需求与载体小数据量的特性矛盾明显,现有的水印算法难以对小数据量数据进行有效的水印嵌入和检测。
本文针对水印算法容量较低的问题,提出一种适用于小数据量的矢量地理数据水印算法。在水印生成阶段,通过压缩感知并构建量化表,减小水印信息的长度和冗余;水印嵌入时,增加量化区间数量以提高单位节点嵌入的水印容量,对节点形成的夹角进行多段量化调制,从而既保证对增删攻击和几何攻击具有一定的稳健性,也能够提高小数据量数据中嵌入的水印容量。
1 水印信息的稀疏采样和量化水印算法的主要步骤包括水印信息生成、嵌入和检测。其中水印信息生成方法包括有意义版权图像的获取、水印信息的置乱或者加密等[4, 19-20]。加密或者置乱的方法能够提高水印算法的安全性,但不能显著地压缩水印信息。因此为提高水印嵌入容量,需要对二值版权图像进行压缩,降低图像的冗余性。
压缩感知作为一种信号处理的新兴方法,能够以较低的采样率测量信号并稳健重构信号[21-22]。它的原理是当数据在特定域φ中稀疏表示时,用与φ不相关的矩阵对数据进行欠采样,获得测量结果的同时实现数据压缩;恢复和重构信号时,虽然欠定方程组理论上没有确定解,但根据原始信号在φ中稀疏的性质,通过优化算法或者贪婪算法能够重构原始信号,并在一定程度上抵抗噪声、信号丢失的攻击[23]。因此,在水印信息生成中运用压缩感知方法,能够在压缩水印信息的同时增加水印信息重构过程中的稳健性。同时,测量矩阵作为密钥也可以保证水印的安全性[24]。
运用压缩感知对二值图像水印信息进行测量时,测量结果的数值范围往往超过(-1, +1),并含浮点型数值,直接转换为二值水印信息反而会大幅增加水印信息长度。为实现水印信息的压缩和准确重构,本文提出了压缩感知和量化机制相结合的水印信息生成算法,对压缩感知的测量值进行量化调制,有效压缩水印信息量并保证其恢复的准确性。
基于压缩感知和量化机制的水印信息生成步骤为:
(1) 获取大小为L×L的二值版权图像W。
(2) 对二值版权图像W进行分块,分块大小为N×N,对各块进行小波分解,实现图像的稀疏化表达。
(3) 设采样率为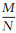
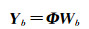 (1)
(1)
式中,Yb为图像各分块的测量结果。
(4) 对测量结果Yb进行取整量化,为计算方便,建立量化表将测量结果映射为量化值,量化表如表 1所示。
根据映射后的结果生成水印信息WM,长度为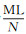
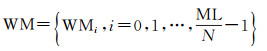
式中,WMi∈{-2, -1, 1, 2}。
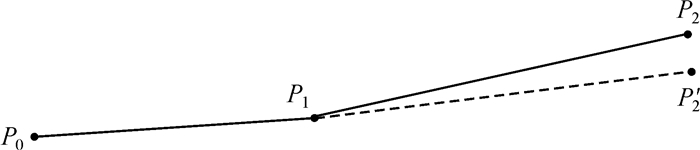
2 角度多段量化规则角度能够在旋转、平移和缩放等几何变换中保持不变,具有抵抗几何攻击的能力,因此水印算法选择在相邻节点形成的夹角中进行水印嵌入。考虑到矢量地理数据的点、线、面的数据组织结构,水印算法对点数据进行水印嵌入时,可嵌角度依据点坐标(x, y)大小排序生成,对于线数据、面数据直接使用相邻线段的角度即可。设可嵌角度∠P0P1P2由点P0(x0, y0)、P1(x1, y1)和P2(x2, y2)构成,对可嵌角度∠P0P1P2量化调制后,P0、P1点保持不变,P2点调制至P2',量化调制的过程如图 1所示。
|
| 图 1 可嵌角度调制过程 Fig. 1 The process of quantization modulation on angle |
为提高算法可嵌入的水印容量,本文提出了角度多段量化规则。根据表 1,水印信息量化值有4种,为保证水印的稳健重构,在角度的量化嵌入过程中,多段量化区间的数目也设定为4。根据表 1水印生成的测量结果量化表,对测量结果即水印信息WMi,与量化区间索引WMi'建立映射关系
 (2)
(2)
对于角度α,设多段量化区间的单位角度为θ,嵌入水印信息WMi时,首先计算角度α对应的量化区间索引值R为
 (3)
(3)
式中,
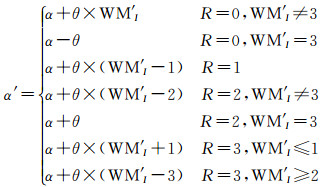 (4)
(4)
式中,α'为嵌入水印后的角度值,从而实现角度的多段量化调制。
3 水印算法 3.1 误差控制策略水印算法对相邻节点形成的夹角嵌入水印时,需要考虑到夹角调制过程对节点坐标的精度影响。根据式(4),起始夹角最大调制幅度为3θ,顺序地对多个节点的原始夹角进行调制,会导致后序角度调制幅度不断累积并远大于3θ,从而影响矢量地理数据的可用性。因此水印嵌入时,对节点的夹角进行动态更新。在夹角∠PkPk+1Pk+2嵌入水印后,节点Pk+2更新为Pk+2',下一水印嵌入角度根据Pk+2'更新为∠Pk+1Pk+2'Pk+3。理论上所有可嵌角度的调制幅度不超过3θ,从而严格控制了节点坐标在嵌入水印后的误差。
3.2 水印嵌入水印嵌入算法在水印信息稀疏采样和量化基础上,运用角度多段量化机制、动态更新方式对矢量地理数据的夹角嵌入水印,具体嵌入步骤为:
(1) 根据基于压缩感知和量化表的水印信息生成方法,生成水印信息WM,保存水印信息生成过程中的测量矩阵Φ,作为水印检测的密钥。
(2) 依据第2节中可嵌角度的选取规则,读取矢量地理数据并获取所有可嵌角度,记为∠PkPk+1Pk+2(0≤k<N2, N2为可嵌角度的个数)。
(3) 从第一个可嵌角度∠PkPk+1Pk+2开始,根据三点的坐标计算对应的角度αk。
(4) 建立水印同步机制。选择MD5消息摘要算法作为散列函数Hash,由于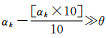
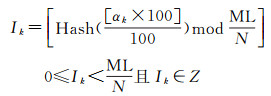 (5)
(5)
(5) 计算多段量化区间索引。根据式(2)和式(3),分别计算αk和WMIk对应的量化区间索引值R和WMIk'。
(6) 根据式(4),将角度αk量化调制为αk',并计算嵌入水印后Pk+2'的坐标(x2', y2')
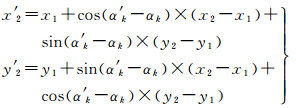 (6)
(6)
更新Pk+2坐标值为Pk+2'(x2', y2'),完成对∠PkPk+1Pk+2的水印嵌入。考虑到矢量地理数据的坐标数值范围,θ可取10-6以满足矢量地理数据的精度要求。
(7) 根据嵌入水印的点坐标Pk+2'(x2', y2'),计算下一可嵌角度∠Pk+1Pk+2'Pk+3并嵌入水印;重复上述水印嵌入过程,对所有可嵌角度实现水印嵌入。
3.3 水印检测水印检测是水印嵌入的逆过程,水印检测时根据角度所在的量化区间判断水印值,对检测出的水印值进行压缩感知重构,从而恢复原始水印。水印检测步骤为:
(1) 读取待检测的矢量地理数据,判断点、线、面的数据类型和待检测的角度,记为∠Pk'Pk+1'Pk+2'(0≤k<N3, N3为待检测角度的个数)。
(2) 从第一个待检测角度∠Pk'Pk+1'Pk+2'开始,计算对应的角度αk'。
(3) 基于水印同步机制,根据式(5)得到αk'映射的水印位Ik'。
(4) 计算角度αk'对应的量化区间索引WMIk'
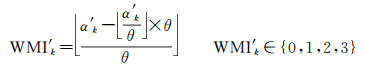 (7)
(7)
则水印值WMIk'为
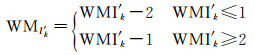 (8)
(8)
(5) 遍历所有待检测角度,得到水印检测结果,即为水印压缩感知的测量值WM'=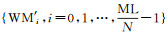
(6) 基于密钥Φ,运用正交匹配追踪法重构版权图像[25],完成水印检测。
4 试验与分析水印算法的有效性从数据可用性、水印容量和稳健性3个方面进行试验验证。试验数据如图 2所示,图 2(a)和(b)各为小数据量的点数据和线数据,图 2(c)为普通数据量的面数据,所含有的节点个数分别为100个、126个和2000个,比例尺分别为1: 2000、1: 5000和1: 10 000。
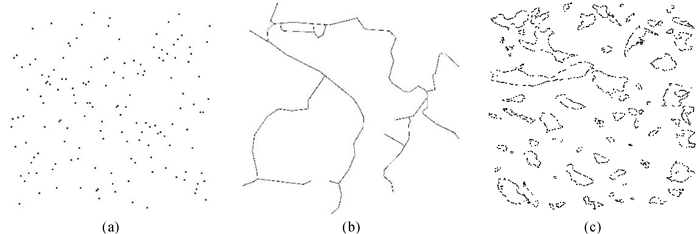
|
| 图 2 试验数据 Fig. 2 Experimental data |
水印信息为32×32像素的二值版权图像,如图 3所示。

|
| 图 3 二值版权图像 Fig. 3 Binary copyright image |
水印信息生成中分块大小N=8,采样率设为75%,即M=6,运用本文提出的水印算法对试验数据嵌入并检测水印。选择相关系数NC作为客观评价指标,设检测出的水印信息为Wi',原始水印信息为Wi,则相关系数NC计算公式为
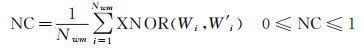 (9)
(9)
式中,Nwm为水印长度;XNOR为异或运算。当NC=1时,表示水印检测完全正确,当NC=0时,表示完全未检测出水印。
在未攻击的情形下对水印进行检测,水印检测结果如表 2所示。
| 试验数据 | 数据(a) | 数据(b) | 数据(c) |
| 节点个数 | 100 | 126 | 2000 |
| 水印检测图像 | 
|
||
| NC | 0.564 8 | 0.819 5 | 1 |
从表 2中可以看出,对于含有100个和126个节点的小数据量数据(a)和数据(b),检测结果与原始水印存在部分像素差异,但是图像内容可辩,能够明确反映出版权标识,且NC均高于0.5;对于含2000个节点的数据(c),无论是视觉上还是NC值都表明检测出的水印图像与原始水印完全一致。上述试验结果表明,提出的水印算法能够对小数据量的数据嵌入较为完整的水印信息,也适用于较大数据量数据的水印嵌入和检测。
4.1 数据可用性为验证水印算法对矢量地理数据精度和可用性的影响,统计试验数据在水印嵌入后的误差,统计结果如表 3所示。
| 试验数据 | 误差大小/m | 数据点个数 | 所占百分比/(%) |
| (a) | 0 | 46 | 46.0 |
| <0.01 | 54 | 54.0 | |
| ≥0.01 | 0 | 0 | |
| (b) | 0 | 57 | 45.2 |
| <0.01 | 69 | 54.8 | |
| ≥0.01 | 0 | 0 | |
| (c) | 0 | 966 | 48.3 |
| <0.01 | 1034 | 51.7 | |
| ≥0.01 | 0 | 0 |
从表 3可知,嵌入水印后坐标误差均能够控制在0.01 m之内,满足不同比例尺下矢量地理数据精度要求,这是因为在水印嵌入时,角度动态更新方法和较小的参数θ严格控制了数据误差,避免角度调制过程引起坐标数值的大幅变化。因此本文提出的水印算法能够保证矢量地理数据的可用性。
4.2 水印容量为验证水印算法的嵌入容量,对不同数据量的数据嵌入和检测水印,验证检测结果的正确性并计算单个节点嵌入的水印容量。
首先对试验数据(a)和(b)进行不同程度的增删点预处理,生成不同数据量的数据,嵌入的水印信息统一为图 3所示的二值版权图像,水印信息量为1024 bit。对比试验算法为稳健性较好的/1/2(算法1)和/1/2(算法2),分别从主观视觉和客观指标方面评价水印检测的结果。在计算嵌入容量时,式(9)中未检测到的水印位XNOR计算结果为0。小数据量数据(a)和(b)的水印检测结果如表 4和表 5所示。
| 预处理后节点个数 | 本文算法 | 算法1 | 算法2 |
| 95 | 
|
||
| 0.550 4 | 0.105 5 | 0.069 6 | |
| 100 | 
|
||
| 0.564 8 | 0.115 0 | 0.074 8 | |
| 110 | 
|
||
| 0.593 2 | 0.132 2 | 0.094 3 | |
| 200 | 
|
||
| 1 | 0.243 1 | 0.151 4 | |
| 预处理后节点个数 | 本文算法 | 算法1 | 算法2 |
| 100 | 
|
||
| 0.571 8 | 0.112 9 | 0.074 5 | |
| 110 | 
|
||
| 0.630 7 | 0.150 1 | 0.112 6 | |
| 126 | 
|
||
| 0.819 5 | 0.211 6 | 0.148 2 | |
| 300 | 
|
||
| 1 | 0.372 8 | 0.267 8 | |
在小数据量数据试验基础上,根据嵌入的总水印容量和节点个数,计算单个节点嵌入的水印容量。取上述试验的平均值作为衡量水印算法容量的指标,结果如表 6所示。
| 容量指标 | 本文算法 | 算法1 | 算法2 |
| 单个节点水印容量 | 7.35 | 1.97 | 0.74 |
由表 4和表 5可知,对于相同数据量的试验数据,本文水印算法的检测结果无论是视觉上还是相关系数NC,均优于对比算法;并且数据量越小,检测结果的差异性也越明显。极限情况下对仅含100个节点的矢量地理数据,本文的算法仍然能成功嵌入水印并检测,检测结果视觉可辩,版权归属明确,且相关系数NC保持在较高的水平;相同条件下算法1和算法2难以完整地嵌入水印,版权信息辨识度低,无法鉴定小数据量的版权归属。从表 6的结果可以看出,本文水印算法的单个节点水印容量高于对比算法,每个节点能够承载的水印位数得到较大提升。因此,试验证明本文提出的水印算法有效地提高了水印容量,能够满足小数据量矢量地理数据版权保护的需求。
4.3 稳健性为验证水印算法抵抗各类攻击的能力,分别对普通数据量的数据(c)和小数据量数据(b)进行稳健性试验,嵌入水印并对矢量地理数据进行增删攻击和几何攻击,对比水印检测结果的NC值,从而评价本文算法和算法1、算法2的稳健性。根据表 4和表 5的试验结果可设置经验阈值T=0.5,即NC<0.5时版权归属难以分辨,此时试验结果记为“×”,表明水印未成功检测。基于普通数据量数据(c)的稳健性试验结果如表 7所示。
| 攻击类型 | 攻击强度 | 本文算法NC | 算法1NC | 算法2NC |
| 数据增点 | 增加20% | 1 | 1 | 1 |
| 增加50% | 0.987 8 | 0.979 2 | 0.974 1 | |
| 增加80% | 0.960 0 | 0.921 6 | 0.861 3 | |
| 数据删点 | 删除30% | 1 | 1 | 1 |
| 删除50% | 1 | 0.876 1 | 0.736 3 | |
| 删除70% | 0.940 4 | 0.683 5 | ||
| 数据平移 | 平移500 m | 1 | 1 | 1 |
| 平移5000 m | 1 | 1 | 1 | |
| 数据旋转 | 旋转30° | 1 | 1 | 1 |
| 旋转120° | 1 | 1 | 1 | |
| 数据缩放 | 缩放1.5倍 | 1 | 1 | 1 |
| 缩放2.5倍 | 1 | 1 | 1 | |
| 节点排序 | 置乱50% | 1 | 1 | 1 |
| 置乱100% | 1 | 1 | 1 |
由表 7可知,对于普通数据量的数据,本文算法和对比算法都能完全抵抗几何攻击;但本文算法由于水印容量高,因此在抵抗增删攻击方面具有更好的稳健性。对于节点排序攻击,线数据和面数据的拓扑关系未改变,点数据经坐标排序后的顺序也未改变,因而水印算法能完全抵抗节点排序攻击。
基于小数据量数据(b)的稳健性试验结果如表 8所示。
| 攻击类型 | 攻击强度 | 本文算法NC | 算法1NC | 算法2NC |
| 数据增点 | 增加10% | 0.970 7 | × | × |
| 增加20% | 0.848 9 | × | × | |
| 增加30% | 0.756 8 | × | × | |
| 数据删点 | 删除10% | 0.627 9 | × | × |
| 删除20% | 0.573 8 | × | × | |
| 删除30% | × | × | × | |
| 数据平移 | 平移500 m | 1 | × | × |
| 平移5000 m | 1 | × | × | |
| 数据旋转 | 旋转30° | 1 | × | × |
| 旋转120° | 1 | × | × | |
| 数据缩放 | 缩放1.5倍 | 1 | × | × |
| 缩放2.5倍 | 1 | × | × | |
| 节点排序 | 置乱50% | 1 | × | × |
| 置乱100% | 1 | × | × |
由表 8可知,对于小数据量的数据,算法1和算法2的水印容量较低,无法完整地嵌入二值版权图像水印信息,更难以抵抗任意程度的增删、平移、旋转等攻击。而本文提出的水印算法由于使用了压缩感知、角度多段量化等机制,提高了水印嵌入容量,能够完全抵抗平移、旋转、缩放等几何攻击和节点排序攻击,也能较好地抵抗增删攻击。因此,本文的水印算法不仅能对小数据量数据嵌入水印,同时保证了良好的稳健性。
5 结论针对小数据量矢量地理数据的版权保护需求,本文提出了一种高水印容量的水印算法。水印生成阶段,运用压缩感知进行测量并量化测量结果,在保证水印信息稳健重构的基础上实现了水印信息的压缩;水印嵌入阶段,提出角度的多段量化规则,进一步提升了单个节点能承载的水印容量,也提高了算法的稳健性。试验结果表明,提出的水印算法能够在小数据量的矢量数据中嵌入和检测水印,检测结果版权意义明确,单个节点嵌入的水印容量高于现有的水印算法,同时算法对增点、删点、缩放、旋转、裁切、排序等攻击也具有很好的稳健性。本文研究有效地解决了矢量数据的小数据量与水印容量的矛盾,实现了小数据量矢量地理数据的水印嵌入和检测,对矢量地理数据的版权保护具有重要的理论和应用价值。
| [1] |
王超, 王伟, 王泉, 等.
一种空间域矢量地图数据盲水印算法[J]. 武汉大学学报(信息科学版), 2009, 34(2): 163–165.
WANG Chao, WANG Wei, WANG Quan, et al. A Watermarking Algorithm for Vector Maps in Spatial Domain[J]. Geomatics and Information Science of Wuhan University, 2009, 34(2): 163–165. |
| [2] |
杨成松, 朱长青, 陶大欣.
基于坐标映射的矢量地理数据全盲水印算法[J]. 中国图象图形学报, 2010, 15(4): 684–688.
YANG Chengsong, ZHU Changqing, TAO Daxin. A Blind Watermarking Algorithm for Vector Geo-spatial Data Based on Coordinate Mapping[J]. Journal of Image and Graphics, 2010, 15(4): 684–688. |
| [3] |
孙鸿睿.矢量地图无损数字水印技术和算法研究[D].长沙: 中南大学, 2013. SUN Hongrui. Study on Lossless Digital Watermarking Technology and Algorithm for Vector Map[D]. Changsha: Central South University, 2013. |
| [4] | YAN Haowen, ZHANG Liming, YANG Weifang. A Normalization-based Watermarking Scheme for 2D Vector Map Data[J]. Earth Science Informatics, 2017, 10(4): 471–481. DOI:10.1007/s12145-017-0310-x |
| [5] | WANG Yingying, YANG Chengsong, ZHU Changqing. A Multiple Watermarking Algorithm for Vector Geographic Data Based on Coordinate Mapping and Domain Subdivision[J]. Multimedia Tools and Applications, 2017. DOI:10.1007/s11042-017-5358-6 |
| [6] | SOLACHIDIS V, PITAS I. Watermarking Polygonal Lines Using Fourier Descriptors[J]. IEEE Computer Graphics and Applications, 2004, 24(3): 44–51. |
| [7] | IM D H, LEE H Y, RYU S J, et al. Vector Watermarking Robust to Both Global and Local Geometrical Distortions[J]. IEEE Signal Processing Letters, 2008(15): 789–792. |
| [8] |
于涛.基于离散余弦变换的矢量地图水印算法研究[D].哈尔滨: 哈尔滨工程大学, 2009. YU Tao. Research on Vector Map Watermarking Algorithm Based on DCT[D]. Harbin: Harbin Engineering University, 2009. |
| [9] |
许德合, 朱长青, 王奇胜.
利用QIM的DFT矢量空间数据盲水印模型[J]. 武汉大学学报(信息科学版), 2010, 35(9): 1100–1103.
XU Dehe, ZHU Changqing, WANG Qisheng. Blind Watermarking Model of Vector Spatial Data Based on DFT of QIM[J]. Geomatics and Information Science of Wuhan University, 2010, 35(9): 1100–1103. |
| [10] | WANG Chuanjian, ZHANG Li, LIANG Bin, et al. Watermarking Vector Maps Based on Minimum Encasing Rectangle[C]//Proceedings of the 2011 Fourth International Conference on Intelligent Computation Technology and Automation. Shenzhen, China: IEEE, 2011: 1243-1246. |
| [11] | NEYMAN S N, PRADNYANA I N P, SITOHANG B. A New Copyright Protection for Vector Map Using FFT-based Watermarking[J]. Telkomnika, 2014, 12(2): 367–378. DOI:10.12928/telkomnika.v12i2 |
| [12] |
张黎明, 闫浩文, 齐建勋, 等.
基于DFT的可控误差矢量空间数据盲水印算法[J]. 武汉大学学报(信息科学版), 2015, 40(7): 990–994.
ZHANG Liming, YAN Haowen, QI Jianxun, et al. A Blind Watermarking Algorithm for Copyright Protection of Vector Geospatial Data Under Controllable Errors Based on DFT[J]. Geomatics and Information Science of Wuhan University, 2015, 40(7): 990–994. |
| [13] |
杨成松, 朱长青.
基于常函数的抗几何变换的矢量地理数据水印算法[J]. 测绘学报, 2011, 40(2): 256–261.
YANG Chengsong, ZHU Changqing. Robust Watermarking Algorithm for Geometrical Transform for Vector Geo-spatial Data Based on Invariant Function[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 256–261. |
| [14] | WANG Chuanjian, PENG Zhiyong, PENG Yuwei, et al. Watermakering Geographical Data on Spatial Topological Relations[J]. Multimedia Tools and Applications, 2012, 57(1): 67–89. DOI:10.1007/s11042-010-0536-9 |
| [15] |
张驰, 李安波, 闾国年, 等.
以夹角调制的矢量地图可逆水印算法[J]. 地球信息科学学报, 2013, 15(2): 180–186.
ZHANG Chi, LI Anbo, LÜ Guonian, et al. A Reversible Watermarking Algrithm for Vector Map Based on Angle Modulating[J]. Journal of Geo-Information Science, 2013, 15(2): 180–186. |
| [16] | LEE S H, HUO Xiaojiao, KWON K R. Vector Watermarking Method for Digital Map Protection Using Arc Length Distribution[J]. IEICE Transactions on Information and Systems, 2014, E97-D(1): 34–42. DOI:10.1587/transinf.E97.D.34 |
| [17] | ABUBAHIA A, COCEA M. Partition Clustering for GIS Map Data Protection[C]//Proceedings of the 26th IEEE International Conference on Tools with Artificial Intelligence. Limassol, Cyprus: IEEE, 2014: 830-837. |
| [18] | PENG Zhiyong, YUE Mingliang, WU Xia, et al. Blind Watermarking Scheme for Polylines in Vector Geo-spatial Data[J]. Multimedia Tools and Applications, 2015, 74(24): 11721–11739. DOI:10.1007/s11042-014-2259-9 |
| [19] |
曹刘娟, 门朝光, 孙建国.
基于空间特征的二维矢量地图可逆水印算法原理[J]. 测绘学报, 2010, 39(4): 422–427, 434.
CAO Liujuan, MEN Chaoguang, SUN Jianguo. Space Feature-based Reversible Watermarking Theory for 2D-Vector Maps[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 422–427, 434. |
| [20] |
杨辉, 侯翔.
一种抗等角投影变换矢量地图数据水印机制[J]. 测绘科学技术学报, 2014, 31(5): 524–528.
YANG Hui, HOU Xiang. A Watermarking Scheme Against Equal-angle Projection for Vector Map Data[J]. Journal of Geomatics Science and Technology, 2014, 31(5): 524–528. DOI:10.3969/j.issn.1673-6338.2014.05.018 |
| [21] | DONOHO D L. Compressed Sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306. DOI:10.1109/TIT.2006.871582 |
| [22] |
戴琼海, 付长军, 季向阳.
压缩感知研究[J]. 计算机学报, 2011, 34(3): 425–434.
DAI Qionghai, FU Changjun, JI Xiangyang. Research on Compressed Sensing[J]. Chinese Journal of Computers, 2011, 34(3): 425–434. |
| [23] | CANDES E J, TAO T. Near-optimal Signal Recovery from Random Projections:Universal Encoding Strategies?[J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406–5425. DOI:10.1109/TIT.2006.885507 |
| [24] | MAYIAMI M R, SEYFE B, BAFGHI H G. Perfect Secrecy via Compressed Sensing[C]//Proceedings of 2013 Iran Workshop on Communication and Information Theory. Tehran, Iran: IEEE, 2013: 1-5. |
| [25] | TROPP J A, GILBERT A C. Signal Recovery from Random Measurements Via Orthogonal Matching Pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655–4666. DOI:10.1109/TIT.2007.909108 |