2. 河南省城建学院, 河南 平顶山 467036
2. Henan University of Urban Construction, Pingdingshan 467036, China
静止轨道遥感卫星与地球处于相对静止状态,可以实现对地面目标的持续观测,同时具备动态目标探测能力和动态目标指示潜力,特别是近年来三轴稳定型静止轨道遥感卫星的发展,对进一步提升静止轨道上持续观测的时间和空间分辨率都具有重要的意义[1-4]。当前,静止轨道遥感卫星已经成为国家的基础性、战略性资源,美、欧、日、印、韩等国均投入了大量资源进行研发。美国、日本于2016年11月分别将新一代三轴稳定的静止轨道气象卫星GOES-R[5]和“葵花9号”[6]发射升空;我国于2015年12月和2016年12月分别发射了具有自主产权的三轴稳定型静止轨道遥感卫星“高分四号”[7]和“风云四号”气象卫星[8];欧洲下一代地球静止轨道气象卫星MTG-Ⅰ系列成像卫星01星计划于2021年发射升空[9];印度也于2016年9月发射了一颗先进的气象卫星INSAT-3DR[10]。
遥感卫星在轨运行时,受到内部系统和外部环境因素的影响,会导致遥感仪器扫描镜指向发生变化,使遥感图像产生几何失真,即指向偏差[11-13]。静止轨道遥感卫星属于高轨卫星,运行在距离地球3.6万千米的地球静止轨道上,卫星的微小偏差在地面上会产生较大的地面误差[14],该问题成为所有静止轨道遥感卫星不可规避的问题[15]。为保证观测结果的准确性和可靠性,需要对卫星的指向偏差进行修正。目前,国内外多采用地标匹配的方法来获取地标偏移量,并由地标偏移量确定导航调整量,以实现对遥感卫星姿态的纠正[16-20]。其中存在的问题在于现有的算法大多针对的是自旋稳定式静止轨道遥感卫星和极轨卫星获取的数据,这些数据的空间分辨率普遍偏低,只能得到像元级的匹配结果,适用于整体刚性图像的指向计算,其粗差剔除方法仅针对误差分布均匀的情况,而且上述两类卫星均不受热形变的影响,不需要每次都进行指向计算,只需要在间隔较长的时间进行一个系统差计算即可。而最近一两年发射的三轴稳定型高分辨率静止轨道遥感卫星对于地标匹配能力提出了更高的要求,一方面要求地标匹配能够精度更高,稳健性更强;另一方面为了达到更高定位精度,还需要具备局部刚性图像的指向计算能力,特别是扫描成像的地球圆盘数据。除此之外,静止轨道遥感卫星在拍摄地球圆盘的过程中,由于不同圆盘区域受到云层、光照或者地标位置区影像特征、地标本身几何形态等问题的影响,导致不同地标会产生匹配质量的差异,如果直接使用这些地标匹配结果,将会给指向计算带来较大的偏差,因此需要在指向偏差计算中考虑观测量的粗差剔除、不等权处理等问题,保证算法的稳健性,使其能够适应一天内多种类型成像条件下的图像计算问题。本文围绕三轴稳定型静止轨道遥感卫星拍摄地球圆盘时的指向确定,针对现有方法存在的问题以及新型传感器的成像特点,提出了一套基于地标匹配的指向计算方法,并已经在我国相关卫星数据的在线处理中得到应用。
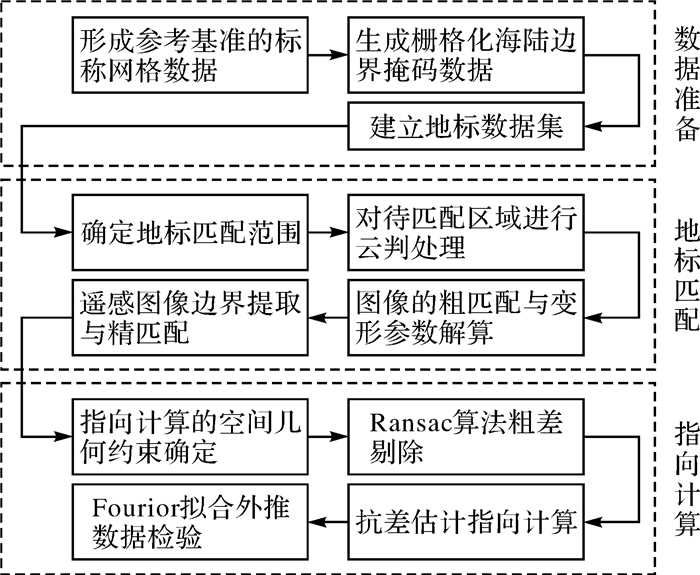
1 静止轨道遥感卫星指向确定的地标匹配方法 1.1 基本思路实现三轴稳定型静止轨道遥感卫星的指向偏差计算,主要是利用地球表面固定、明显的地标进行匹配,由于静止轨道遥感卫星的分辨率普遍在百米量级(例如:美国GOES-R最高分辨率为星下点500 m[5]),而一般性的地标物中,能较均匀地覆盖整个地球圆盘并且能够被大多数可见光、红外波段观测到的地标物只有海陆分界线,因此静止轨道遥感图像的地标参照应选择地球圆盘上相对固定的海陆分界线上的特征区域。结合以上分析,静止轨道遥感卫星指向确定的地标匹配方法主要包括:数据准备、地标匹配及指向计算3个部分。具体为:
(1) 数据准备:按照静止轨道遥感卫星成像方式的不同,制作与成像方式类似的地标模板数据,其中涉及地标数据的选择、成像投影网格的计算、地标数据的投影与重采样、根据地标形态和分布形成地标特征区域和地标库。
(2) 地标匹配:根据实时获取的静止轨道遥感数据,对整个圆盘区域分布的地标特征区域进行云筛选,选择无云或者少云的区域作为待匹配区,利用海陆模板形成的地标区域和遥感图像处理后得到的边界信息进行匹配处理,选取合适的整体特征(梯度和)完成粗匹配,并得到像平面的几何变形参数,在此基础上,针对局部特征点的复合特征(灰度相关、形态相关、矩相关)完成最小二乘精匹配。
(3) 指向计算:将地标匹配的结果用于指向偏差角的计算,利用粗差剔除和抗差估计的方法,得到指向角计算结果,并针对昼夜各半的特殊圆盘数据进行多波段合成处理等工作。
总体技术路线如图 1所示。
|
| 图 1 总体技术路线流程 Fig. 1 Flowchart on general technical roadmap |
1.2 地标数据准备
按照三轴稳定型静止轨道遥感卫星的成像规律,拍摄地球表面的区域数据主要有两种方式:一是画幅式成像,即采用面阵CCD对某区域进行一次性成像,这种情况往往面阵较大,成像投影方式采用的是面阵中心投影的方法,例如高分四号的对地成像[4, 21];二是扫描镜成像,为了快速获取大面积的遥感数据,特别是地球完整圆盘数据,常采用线阵扫描成像方式,利用东西、南北两个方向的快速扫描与步进完成大幅面区域的覆盖[22],这种成像方式常采用的是规范化地球静止投影(normalized geostationary projection,NGP)[23]。因此,在地标数据准备的第1步,需要根据卫星的成像特点,选择恰当的投影方式,并在特定的投影方式下,形成作为参考基准的标称网格数据。
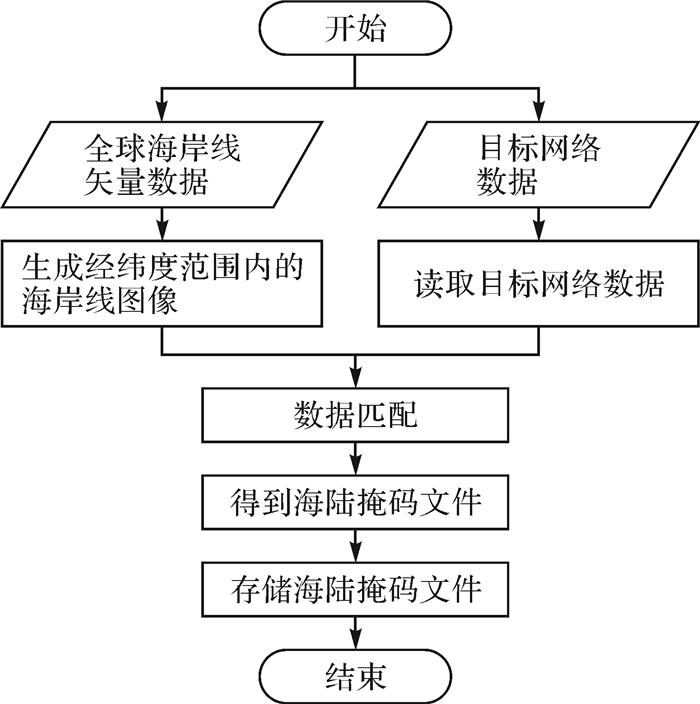
第2步,根据矢量的海陆边界数据,结合成像投影,生成栅格化的海陆边界掩码数据。海陆掩码需要结合全球海岸线矢量数据和标称网格数据计算获得。其基本流程如图 2所示。
|
| 图 2 海陆掩码文件生成流程 Fig. 2 Flowchart on the generation of sea-land mask file |
第3步,建立地标数据集。自动由海陆边界模板生成地标控制点,以地标控制点为中心的一定大小的区域就是地标,所有地标构成地标数据集。该部分的技术难点在于地标控制点检测算法以及地标的分布等问题。检测海陆边界模板中的地标控制点,地标控制点一般选取海陆边界上的角点、“检”型连接点或者其他高曲率点。
1.3 图像地标匹配本节重点讨论图像与地标的匹配问题,具体的步骤如下。
1.3.1 匹配范围的确定首先是匹配初值的问题,目前三轴稳定型静止轨道遥感卫星,利用星上传感器测量数据进行直接定位会带来大约数十公里的偏差,也就是说,折算成特定分辨率的图像(以500 m分辨率为例),通过定位计算得到的图像上像素的几何位置与该像素的理想几何位置(标称网格位置)之间会有十几个到几十个像元的差异,那么可以以该误差的上限作为匹配初值,设定搜索的半径R。
1.3.2 对待匹配区域进行云判处理卫星观测的遥感数据中有大量的云覆盖于地表信息之上,对后续的海陆边缘检测及地标匹配带来影响,因此必须进行云检测,对云覆盖区域不进行地标匹配处理。在处理过程中,引入了最小交叉熵的概念,采用基于最小交叉熵的云区域检测方法[24],获取一幅二值的云掩膜图像M(x, y)。
1.3.3 图像的粗匹配与变形参数解算在静止轨道遥感数据和地标的匹配过程中,由于图像和地标数据一个是灰度图,一个是黑白栅格图,二者的相似度较低,直接进行灰度特征相关很难达到可靠的相关结果,因此需要寻找其他的测度。对于地标数据,图像上与其最相似的实际上就是灰度的梯度信息,也就是图像上的边界。
需要说明的是,静止轨道遥感图像f(x, y)常见的方式是采用单中心小面阵拼接的方式,使用局部较大区域进行匹配存在几何上的形变,该形变直接影响匹配的精度与可靠性。另外,即使在地标数据和图像数据保持同样投影的过程中,仍然存在较小的空间几何变换关系导致差异的产生,因此在匹配的过程中需要同步解算像面几何形变与空间的变换,才能使地标和图像可靠地匹配上。在匹配测度上,采用梯度信息最大为目标,与大部分匹配以图像与基础,地标为目标进行匹配相反,该方法以地标D(x, y)为基础,图像为目标进行匹配,其根本原因是最终需要在图像上形成梯度。该方法的步骤包括:
(1) 以静止轨道完整幅面遥感图像数据为基础,计算粗匹配变换参数。将地标D(x, y)进行几何变换F(D),得到与地标(海陆掩码为1的位置)格网坐标(x, y)对应的(x', y'),(x', y')是经过变换的图像像平面坐标,再将该位置转换成像素坐标(i', j'),通过Robert梯度算子计算图像梯度,由于(i', j')不一定是整数坐标,需要内插出梯度▽(i', j'),目标函数为
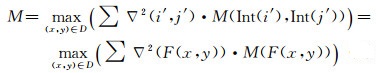 (1)
(1)
需要说明的是,(i', j')如果对应的图像是有云区域,需要使用云掩膜M(x, y)处理,D对应的区域是选择的待匹配无云地标区域的全集。
(2) 给出几何变换F的变换形式。由于该问题是以地标D(x,y)为基础,图像为目标的匹配,因此可以建立一个虚拟成像的几何过程,即从地标格网到真实图像的虚拟投影。下面给出的是基本思路:
令地标格网D(x, y)虚拟出射向量: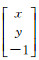
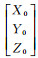
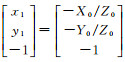
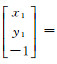
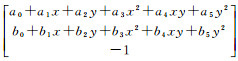
纠正后格网坐标通过若干次旋转后,综合旋转矩阵是R,由式(2)
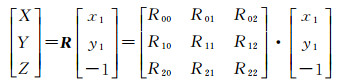 (2)
(2)
得到真实像空间坐标系下的坐标。其中,综合旋转矩阵R是遥感图像定位过程中,从真实像空间到卫星本体坐标系综合旋转矩阵R'的逆矩阵(R')-1,在每次成像过程中是已知量。
令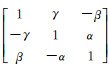
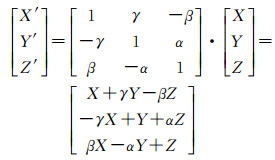 (3)
(3)
式中,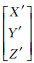
真实像平面坐标系下的坐标为: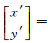
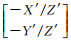
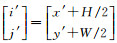
(3) 对式(1)进行优化,采用LM算法(Levenberg-Marquard)[25]进行最大值的求解与计算,求解参数[α β γ a0 a1 a2 a3 a4 a5 b0 b1 b2 b3 b4 b5]'(共15个参数)和综合旋转矩阵R。其中,初值α0=β0=γ0=0,[a0 1 a2 a3 a4 a5 b0 b1 b2 b3 b4 b5]'=[0 1 0 0 0 0 0 0 0 1 0 0 0]'。
该过程的核心是计算待求解变量的偏导数问题,首先需要将[x' y']T与[X Y Z]T建立等式关系,由式(3)得到式(4)
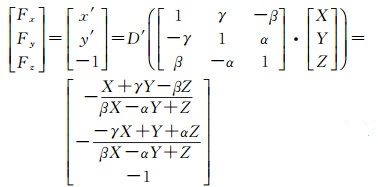 (4)
(4)
式中,D'(·)运算表示从真实的像空间坐标系到真实像平面坐标系的转换,再对式(4)进行线性化,过程略。利用LM算法进行迭代优化,其中初值
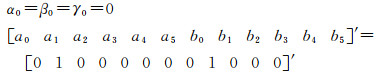
(4) 根据整体匹配的结果以及计算出的几何变换参数,将每一个地标的网格坐标(x, y)代入式(3)可以得到对应的图像坐标(i', i'),形成粗匹配的匹配对。
1.3.4 遥感图像边界提取与精匹配遥感图像中存在各种地物的纹理特征,边界特征不明显,无法直接与地标模板进行直接匹配,因此,需要对遥感图像进行边缘提取。对灰度图像的边缘提取较常采用梯度算子,运算效率高且适用于全圆盘大范围的遥感图像,但梯度算子容易出现漏检边缘,即间断的地方。还有方法采用边界跟踪来提取边缘,但得到的边界点就会在角点附近出现大段缺失,因而丢失许多有用的边界信息[26]。结合两种方法,研究中采用图像相加的方式,将两种方法处理得到的边界图进行叠加,从而得到一幅效果更加良好的边界图。
在边界图像和粗匹配的基础上,本文设计了遥感图像与地标的精匹配方法,精匹配的思路采用最小二乘匹配,以梯度与海陆地标相似性及梯度方向的相关性作为匹配测度。下面给出精确匹配的步骤:
(1) 针对选择的多块地标特征区域的海陆掩码图像,采用高斯模糊的方式,将海陆掩码的0-1图像进行模糊处理,得到0~1之间的浮点数组成的浮点矩阵。
该步骤是最小二乘方法精匹配能够收敛的关键性问题之一,因为海陆掩码图像本身是0-1图像,像素之间的数值并不连续,而遥感图像梯度所形成的图像是连续变化的,两者进行相关得到的相关系数也是一个不连续的曲面,而最小二乘图像相关的关键是相关函数是连续的,不连续的相关函数将直接影响到最小二乘算法的收敛程度。采用高斯模糊的方式将0-1图像转变成相对连续的浮点图像,可以保证相关函数的连续性,使得最小二乘精匹配可以收敛。
(2) 由于遥感图像在作边缘检测的过程中,容易受到各种噪声和地物变化的影响,采用单一的测度存在可靠性较低的情况,因此为了增加匹配的可靠性,本项研究引入了多重判据匹配的思路,其目的是希望利用多个测度得到一致性的结果,这样匹配结果的可靠性大大增强。除了灰度相关系数(适合图像灰度分布特征)匹配方法外,此处还引入Zernike矩差异测度[27](适合图像统计的匹配测度)和误差椭圆之差[28](适合形态的匹配测度)作为匹配测度,其目的是由于这种测度与相关系数测度有所不同,并且地标特征点与边缘图像点的误差椭圆应该是接近的,因此选择这3种测度作为匹配测度。
考虑到相关系数测度的优良特性,本文将其作为主要的测度,其他两个测度作为一种有力的补充,在相关系数测度得到的结果可靠性不高的情况下寻找更为可靠的结果。相关系数测度结果的可靠性依据相关系数值来确定,需要给定相关系数一个最大阈值Tmax和一个最小阈值Tmin,对任意点的匹配过程如下:
步骤1:在给定大小窗口下计算相关系数γ;
步骤2:对γ进行判断,若γ≥Tmax,则认为匹配结果可靠,接受该结果;若γ≤Tmin,则认为匹配结果错误,将其舍弃;若Tmin<γ<Tmax,认为匹配结果的可靠性值得怀疑,转入步骤3;
步骤3:加入Zernike矩差异与误差椭圆之差两个测度,并将三者的结果进行比较,如果三者结果一致,则接受它;如果三者结果不一致,则逐渐扩大目标窗口并重复步骤1—步骤3;
步骤4:如果到目标窗口扩大终止仍得不到可接受的结果,则将其标示为可疑点,进入下一步的匹配。
设计这样的匹配过程,是因为采用多重判据匹配会带来时间的消耗,而对于那些相关系数较大或较小的点,无需进一步判断和计算,仅需要对那些相关系数处于中间的点进行多重判据匹配,这样在提高匹配成功率的基础上有效地控制了计算效率。
1.4 指向偏差计算方法经过上述地标匹配工作,将得到一系列均匀分布在图像上的地标匹配点对,使用这些点对可以直接解算光轴的指向偏差。文献[17]中给出了风云二号卫星的指向计算方法,在上一代自旋稳定的平台上,对地指向精度较高,利用地标指向修正并不是一项经常性的工作,常采用人工检查地标匹配点后再计算。而新一代三轴稳定的静止遥感卫星由于指向精度受到更多因素影响[29],这项处理变得更加频繁。由于静止轨道遥感图像的匹配本质上是图像与矢量边界的匹配,受到图像中线状地物的影响较大,特别是受到复杂的云迹、薄云等现象的影响,而这些云极难被云检测算法准确定位,因此地标匹配很难保证严格的准确性。另外,由于图像和地标格网本身并不是简单的平移旋转关系,还存在空间的变换,因此直接使用简单的地标偏差统计方法进行剔除(例如2σ的方式)很难得到理想的效果。
本文工作的试验表明,由于地标匹配精度受图像中复杂云场景的变化影响,无法做到一天内每次观察都能稳定给出高质量的匹配结果,可能出现许多不同等级误差的匹配点,而图像匹配中常使用的RANSAC方法[30]剔除匹配误差的方式,在直接使用效果并不理想。为了得到稳健的指向偏差计算方法,本文结合RANSAC方法、抗差估计[31]与拟合外推方法,设计了下面的思路:
(1) 选择合适的坐标系统(例如:卫星本体系),根据地标匹配结果中的第i个图像点Pi的像空间坐标计算出射光线,转换到卫星本体系中,得到理想的单位化光线指向Ll={x1, yi, zi};将该时刻与图像点对应的格网点Pi'的大地坐标取出,转换到该时刻的卫星本体系中,得到实际的单位化光线指向Ll'={xi', yi', zi'},实际光线和理想光线间的差异就是光线的指向偏差角(α,β,γ),使用3(γ)1(α)2(β)转轴的旋转矩阵表示,可以写成式(5)的形式
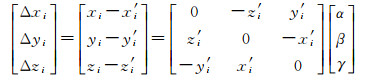 (5)
(5)
(2) 使用Ransac算法对匹配点对的粗差进行第1次剔除,其中约束的几何模式采用式(5)的方程。根据几何关系与试验给出设定参数:适用于模型的最小数据集数据个数为4个,判定新的数据是否适用于数据集模型的标准是代入后偏差(均方差)小于数据集残差的2倍(2σ),新的数据适用于数据集模型的数据数目占总匹配数目的60%,迭代次数设定为100次。
(3) 由于海陆模板与静止轨道图像匹配的复杂性,会出现许多不同等级误差的匹配点,针对该问题本文在第2层次误差处理的过程中,采用将粗差归入随机模型的粗差定位法[32](基于选权迭代的抗差估计方法),试验表明,使用IGGIII方案[33-35]给出的等价权函数,如式(6),可以达到较好的粗差剔除效果
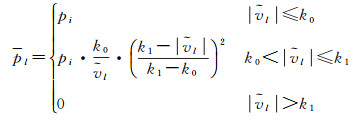 (6)
(6)
式中,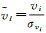
在使用选权迭代方法进行指向计算的过程中,实际上也同步完成了匹配误差点的剔除工作,通过迭代若干次后的权矩阵,设定阈值来判断需要剔除的地标匹配结果。在试验中,迭代的次数选择20次,由于一组匹配点对应3个方程,即3个权值P1、P2、P3,设置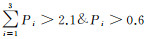
(4) 第3层次的工作是为了保证长时间多次指向计算的结果的稳定,避免出现由于地标匹配误差而导致的指向计算不稳定的现象。在该过程中,考虑到指向偏差变化与轨道位置、温差变化的物理因素相关,变化本身具有一定周期特性,因此采用Fourior拟合的方式对指向偏差角的三轴(α,β,γ)分别进行拟合处理,拟合的数据来自本次解算之前的若干次数据,然后外推本次的三轴,再与直接解算的结果进行对比,设置一定阈值,大于阈值范围认为本次计算失败,反之则成功,并将本次解算三轴的结果存入数据库中,为下一次解算结果的验证提供依据。
在实现中,以轨道周期(24H)为基频,进行1、2、4、8、16、32倍频共6阶傅里叶函数的拟合,如式(7),其中共需要解算a0—a6,b1—b6,c0—c6,d1—d6,e0—e6,f1—f6,ω共40个参数,因此至少需要之前14次观测的结果,才能拟合外推本次的结果。方程式(7)是非线性的方程,本文采用LM算法进行优化,得到拟合参数
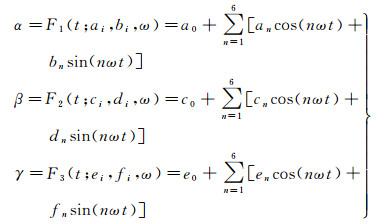 (7)
(7)
试验以某静止轨道遥感卫星数据为例来验证算法。试验选择该卫星多波段扫描辐射计获取的第2波段(500 m分辨率,550 nm波段)数据进行试验处理,选择某日4幅不同时段(UTC时间)的全圆盘成像数据为例,如图 3所示。

|
| 图 3 一天内不同时段的全圆盘数据(UTC时间) Fig. 3 Full-disc data in different time periods within one day (UTC) |
主要完成下面两个方面的试验:
(1) 标称数据及标称模板生成:针对该卫星多波段扫描辐射计的成像扫描方式和定点位置,生成全球标称格网数据,利用全球海陆矢量边界数据,生成地标模板数据。
(2) 地标匹配与指向计算:通过获取的4幅全圆盘数据,开展地标匹配试验,并利用地标匹配结果解算指向偏差,最后利用解算后的指向偏差,对影像进行重新纠正并重采,检查与标准地标数据的偏差。
2.1 标称数据及标称模板生成试验采用适合于该型卫星成像规律的标称格网数据(NPG投影的一种),其成像规律是利用南北、东西两个方向的扫描镜的机械扫描来实现地面区域的覆盖,而标称格网的计算核心是其入射光线的计算,式(8)给出了入射光线的形式
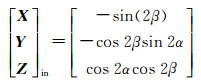 (8)
(8)
式中,α是南北镜转角;β是东西镜转角。
以卫星定点位置104.7°E为例,结合式(8)的光线方程,形成标称格网的数据(格网点对应的地面点大地坐标),其经纬度范围为:纬度-81.253 585°S—81.253 585°N,经度23.421 845°E—174.021 845°W,尺寸21 984×21 984(500 m分辨率),该格网为地标模板生成提供空间参考基础。
试验中所用的矢量海岸线数据是GSHHG数据(Version 2.3.1,2014),GSHHG数据包括世界海岸线、河流、湖泊、岛屿、冰冻圈等水文要素内容[36]。GSHHG数据坐标系为WGS-84坐标系,矢量节点的坐标为大地经纬度坐标,数据包括5种精度的数据,分别以f、h、i、l、c表示,其含义为:全分辨率(full resolution)、高分辨率(high resolution)、中分辨率(intermediate resolution)、低分辨率(low resolution)、粗分辨率(rude resolution)。
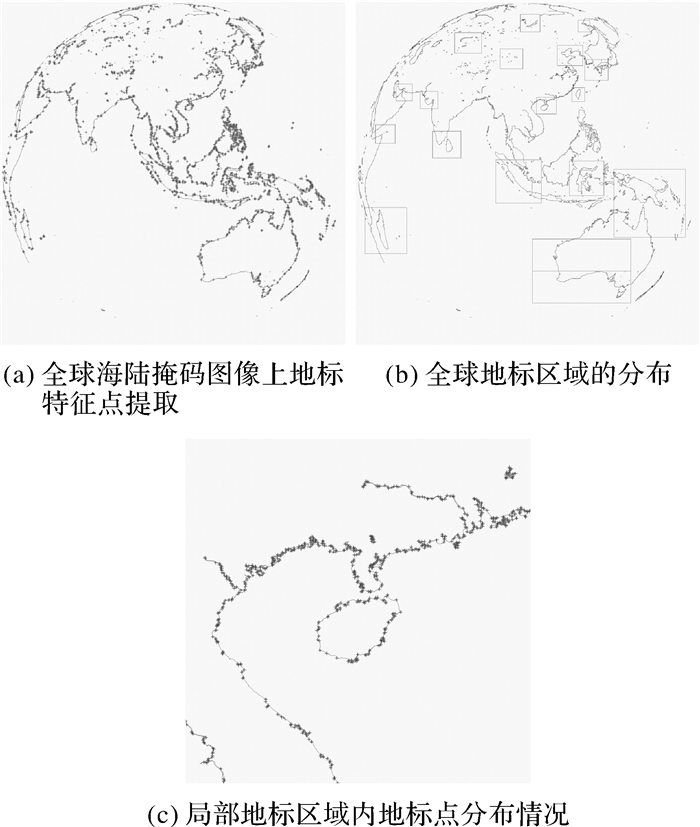
在数据相关说明中并没有对具体5种数据的具体比例尺及精度进行说明,以该卫星的多波段扫描辐射计为例,其中包括:500 m、1 km、2 km、4 km 4种不同的分辨率,在生成标称格网时,同时也生成对应4种分辨率的格网。对不同分辨率标称格网对应的海陆边界模板采用不同精度的矢量海岸线数据,其中500 m、1000 m分辨率的海陆边界用f精度数据,2000 m分辨率的海陆边界采用h精度数据,4000 m、8000 m分辨率的海陆边界采用i精度数据。同时各精度数据只应用观测范围内几大洲的海岸线,以及面积较大的湖泊、岛屿的数据用于地标生成。图 4是通过重采样方法计算的不同分辨率标称格网下的海陆掩码图像数据,这些数据是地标匹配的数据基础。图 5是500 m标称格海陆掩码图像上的特征提取结果(“+”),并根据全圆盘范围内的海岸线分布以及常年的云层分布特点,形成了全球多块不同的地标区域。

|
| 图 4 不同分辨率标称格数据形成的海陆掩码图像 Fig. 4 Sea-land mask images based on the nominal grid with a varying resolution |
|
| 图 5 500 m标称格海陆掩码图像上的特征提取结果与地标区分布 Fig. 5 Results of characteristic extraction and distribution of landmark regions in the sea-land mask image based on the nominal grid with the resolution of 500 m |
2.2 地标匹配与指向计算
采用地标匹配的方法,进行静止轨道遥感数据与地标区域的匹配,得到相关的匹配结果。以图 3(c)中的数据为例,主要经过下面几个步骤:
(1) 图像的粗匹配与变形参数解算。进行图像按区域的整体匹配与变形参数解算,得到图 6的结果,其中图 6(a)中是不解算变形参数,直接按照式(1)进行匹配的结果,可以发现图中下半部分的海陆边界基本匹配较好,但是“○”标注的湖泊,发生了偏差;(b)中是匹配过程中,直接解算变形参数的方式,可以发现无论是下半部海陆边界还是湖泊,都匹配得很好。

|
| 图 6 图像的粗匹配与变形参数解算过程中的对比(局部:青藏高原) Fig. 6 Rough image matching and comparison in the calculation of deformation parameters (local:tibet plateau) |
在粗匹配的基础上,完成了地标精确匹配的过程,精匹配是按照图 5(b)的全球地标区域进行匹配的,全球范围内共18块区域,图 7是其中两块区域的精确匹配的结果。

|
| 图 7 不同区域、海陆掩码地标数据与图像之间的精确匹配 Fig. 7 Precise matching between sea-land mask landmark data and images in different regions |
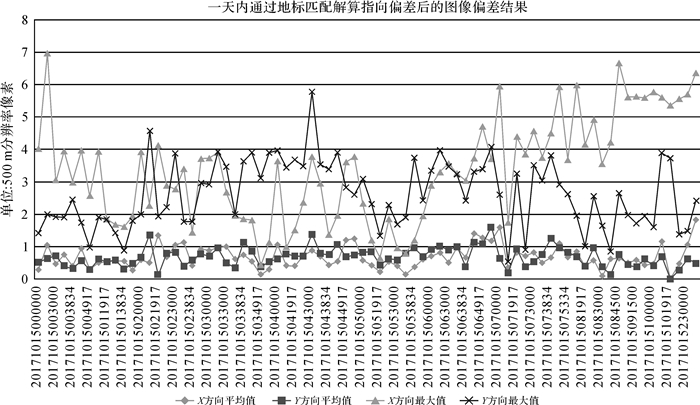
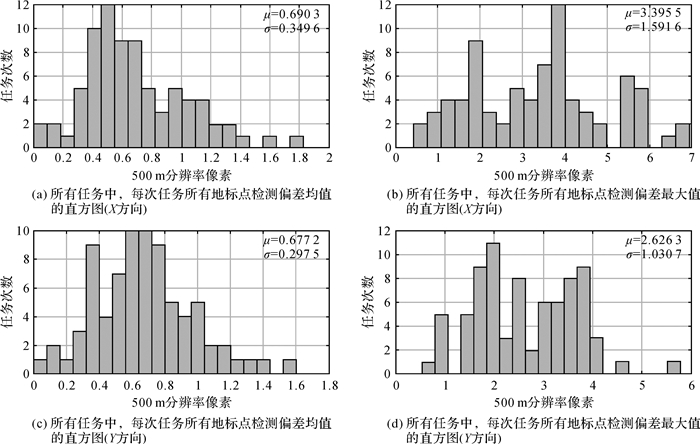
图 8是局部区域利用地标纠正指向后的图像结果与纠正前的图像定位结果的对比;图 9是一天内不同时次(横坐标是UTC时间)图像(78次)利用地标进行纠正后再进行检测的结果,一天内有78次数据观测任务,每次都需要批量进行地标处理与纠正,由于数据变化的周期是以天为单位进行变化的,因此分析一天内的纠正情况是合理的,统计的内容包括不同时次的平均偏差和最大偏差(每一个时次观测图像都会有若干个地标匹配点对),其中一天内平均偏差的均值:X方向0.690 325 874像元,Y方向0.677 241 358个像元;一天内最大偏差的均值X方向3.395 537 354个像元,Y方向2.626 338 072个像元;图 10是一天内利用地标进行图像纠正得到的指向偏差的统计分析结果,是在图 9的基础上,对所有任务中,每次任务所有地标点检测偏差均值的直方图(X/Y方向)和偏差最大值的直方图(X/Y方向)。

|
| 图 8 利用地标纠正指向后的图像结果与纠正前的图像结果对比 Fig. 8 Comparisons of image results before/after pointing error correction through landmark matching |
|
| 图 9 一天内利用地标进行图像纠正得到的指向偏差结果对比 Fig. 9 Comparison of pointing error results after image rectification through landmark matching within one day |
|
| 图 10 一天内利用地标进行图像纠正得到的指向偏差的统计分析结果 Fig. 10 Pointing error statistical analysis results after image rectification through landmark matching within one day |
需要说明的是,图 8(a)和(b)是没有经过地标指向纠正的原始图像,通过地标匹配(1.3.3节、1.3.4节),并经过选权迭代的指向偏差计算(1.4节),一方面对匹配地标的进行粗差剔除,另一方面同步得到指向偏差的三轴关系(如式(5)中的指向偏差角(α, β, γ));图 8(c)和(d)是在指向角的基础上,再将图像逐点按照指向角进行空间相似变换(利用式(5)),完成图像的重采样工作后,再与标准地标数据进行套合,得到的对比结果。另外,图 9中一天内偏差的统计,是对每一次任务都完成上述的地标匹配与指向计算,形成外推模式(式(7)),每一次任务使用前面多次指向角拟合后外推的指向角再进行纠正,然后本次任务再进行本次地标匹配并得到本次指向角,加入到指向角序列中,为下一次任务外推服务,其中本次地标匹配的结果即为本次的偏差统计量,整个流程是一个完整迭代的过程。图 10展示的是偏差的分布情况,从中可以看出,一天内的每一次任务的偏差均值/最大值基本呈现正态分布的特征,其中,均值表现出更好的正态特性,最大值相对更加发散,具体的统计值(均值/均方差)如图 10所示。
从上述试验可以看出,本文提出的基于地标匹配的指向偏差计算方法,能够较好地对静止轨道遥感数据进行纠正,纠正后平均差异在0.6个像元左右,每次最大误差平均在3个像元左右。通过对一天内78次全球圆盘观测的试验结果进行分析发现,本文提出的算法能够较稳定地保证图像的纠正精度,算法整体的稳定度较好,但由于静止轨道遥感数据的全圆盘图像是采用拼图方式完成,受到机械控制精度等各方面因素的影响,很难保证图像内部的严格几何关系,因此在匹配过程中会出现全图中不同区域受到同一组全局指向偏差纠正后,纠正的精度存在差异的情况;一天内太阳光照变化也会给图像匹配精度和指向偏差计算的效果带来影响,这两部分都将是后序工作需要继续改进的内容。
3 结论本文围绕三轴稳定型静止轨道遥感卫星的指向偏差计算问题开展了研究,利用分布在地球表面的海陆边界数据作为匹配模板与地标,研究了一套精度较高且能够稳健运行的地标匹配方法,重点突破了静止地标数据的制作、图像与地标的高精度匹配及基于粗差剔除的指向计算等方法。试验表明,该方法在解决静止轨道遥感图像指向偏差方面具有较好效果,并已经在我国相关卫星数据的在线处理中得到应用。该方法目前还存在不少问题,主要集中在图像与地标匹配的效率上,目前的全圆盘地标匹配算法的效率在几分钟到十几分钟之间(业务系统中),匹配精度的稳定性还不能完全适应全天24 h的各时段、各类型数据,仍然有待提升。下一步工作中,由于静止轨道遥感卫星的时间分辨率(从十几分钟变成几分钟)、空间分辨率(数百米变成数十米)越来越高,对地标匹配的效率也要求越来越高,需要进一步突破精度更高、更加稳健、效率更快(准实时)的匹配与指向计算方法,且能够适应更加复杂的图像场景。
| [1] | SHUSTER M D, OH S D. Three-axis Attitude Determination from Vector Observations[J]. Journal of Guidance Control and Dynamics, 1981, 4(1): 70–77. DOI:10.2514/3.19717 |
| [2] | AMINOU D M, LAMARRE D, STARK H, et al. Meteosat Third Generation (MTG) Status of Space Segment Definition[C]//Proceedings of Sensor, Systems, and Next-generation Satellite XⅢ. Berlin: SPIE, 2009, 7474(1): 50-73. |
| [3] | MURPHY D. EUMETSAT Geostationary Meteorological Satellite Programs[M]//PELTON J N, MADRY S, CAMACHO-LARA S. Handbook of Satellite Applications. New York: Springer, 2013: 991-1019. |
| [4] |
王密, 程宇峰, 常学立, 等.
高分四号静止轨道卫星高精度在轨几何定标[J]. 测绘学报, 2017, 46(1): 53–61.
WANG Mi, CHENG Yufeng, CHANG Xueli, et al. High Accuracy On-orbit Geometric Calibration of Geosationary Satellite GF4[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(1): 53–61. DOI:10.11947/j.AGCS.2017.20160300 |
| [5] | SULLIVAN P C, KRIMCHANSKY A, WALSH T J. An Overview of the Design and Development of the Geostationary Operational Environmental Satellite R-Series (GOES-R) Space Segment[C]//Proceedings of 2017 EUMETSAT Meteorological Satellite Conference. Rome: NASA Goddard Space Flight Center, 2017. |
| [6] | BESSHO K, DATE K, HAYASHI M, et al. An Introduction to Himawari-8/9-Japan's New-generation Geostationary Meteorological Satellites[J]. Journal of the Meteorological Society of Japan. Ser. Ⅱ, 2016, 94(2): 151–183. DOI:10.2151/jmsj.2016-009 |
| [7] | ROTH R M, ZEH A. Long Cyclic Codes Over GF(4) and GF(8) Better than BCH Codes in the High-rate Region[J]. IEEE Transactions on Information Theory, 2017, 63(1): 150–158. DOI:10.1109/TIT.2016.2627078 |
| [8] | YANG Jun, ZHANG Zhiqing, WEI Caiying, et al. Introducing the New Generation of Chinese Geostationary Weather Satellites, Fengyun-4[J]. Bulletin of the American Meteorological Society, 2017, 98(8): 1637–1658. DOI:10.1175/BAMS-D-16-0065.1 |
| [9] | EUMETSAT. Meteosat Third Generation (MTG) Will See the Launch of Six New Geostationary (Imaging and Sounding) Satellites from 2021 Onwards[EB/OL]. (2017-10-15)[2018-01-20]. https://www.eumetsat.int/website/home/Satellites/FutureSatellites/MeteosatThirdGeneration/index.html. |
| [10] | BEULAH R, PUNITHAVALLI M. Prediction of Sugarcane Diseases Using Data Mining Techniques[C]//Proceedings of 2016 IEEE International Conference on Advances in Computer Applications. Coimbatore: IEEE Press, 2016: 393-396. |
| [11] | BARRY J D, MECHERLE G S. Beam Pointing Error As a Significant Design Parameter for Satellite-borne, Free-space Optical Communication Systems[J]. Optical Engineering, 1985, 24(6): 1049–1054. |
| [12] | NUTH C, KÄÄB A. Co-registration and Bias Corrections of Satellite Elevation Data Sets for Quantifying Glacier Thickness Change[J]. The Cryosphere, 2011, 5(1): 271–290. DOI:10.5194/tc-5-271-2011 |
| [13] |
张占睦, 芮杰.
遥感技术基础[M]. 北京: 科学出版社, 2007.
ZHANG Zhanmu, RUI Jie. Fundamental of Remote Sensing Technology[M]. Beijing: Science Press, 2007. |
| [14] |
林栋, 秦志远, 童晓冲, 等.
静止轨道卫星的对地观测高程修正方法[J]. 武汉大学学报(信息科学版), 2017, 42(6): 851–856.
LIN Dong, QIN Zhiyuan, TONG Xiaochong, et al. Elevation Correction Method for Earth Observation of Geosationary Satellites[J]. Geomatics and Information Science of Wuhan University, 2017, 42(6): 851–856. |
| [15] |
常学立.静止轨道高分辨率面阵相机几何处理关键技术研究[D].武汉: 武汉大学, 2015. CHANG Xueli. Research on Key Technologies of Geometric Processing for High-resolution Area-array Camera of Sationary Orbit Satellite[D]. Wuhan: Wuhan University, 2015. |
| [16] |
杨磊, 杨忠东.
极轨气象卫星自动地标导航方法[J]. 应用气象学报, 2009, 20(3): 329–336.
YANG Lei, YANG Zhongdong. The Automated Landmark Navigation of the Polar Meteorological Satellite[J]. Journal of Applied Meteorological Science, 2009, 20(3): 329–336. DOI:10.3969/j.issn.1001-7313.2009.03.009 |
| [17] |
杨磊, 冯小虎, 郭强, 等.
风云二号气象卫星图像自动几何精校正[J]. 计算机工程与应用, 2011, 47(3): 202–206.
YANG Lei, FENG Xiaohu, GUO Qiang, et al. Automatic Geometric Precision Correction of Fengyun-2 Meteorological Satellite Imagery[J]. Computer Engineering and Applications, 2011, 47(3): 202–206. DOI:10.3778/j.issn.1002-8331.2011.03.060 |
| [18] | BUZSÁKI G. Theta Rhythm of Navigation:Link Between Path Integration and Landmark Navigation, Episodic and Semantic Memory[J]. Hippocampus, 2005, 15(7): 827–840. DOI:10.1002/(ISSN)1098-1063 |
| [19] | YANG Lei, FENG Xiaohu, LV Ke, et al. Automated Landmark Matching of FY-2 Visible Imagery with Its Applications to the On-obit Image Navigation Performance Analysis and Improvements[J]. Chinese Journal of Electromics, 2014, 23(3): 649–654. |
| [20] | EUGENIO F, MARQUÉS F. Automatic Satellite Image Georeferencing Using a Contour-matching Approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(12): 2869–2880. DOI:10.1109/TGRS.2003.817226 |
| [21] |
徐文, 龙小祥, 李庆鹏, 等.
"高分四号"卫星影像辐射与几何精度评价[J]. 航天返回与遥感, 2016, 37(4): 16–25.
XU Wen, LONG Xiaoxiang, LI Qingpeng, et al. Image Radiometric and Geometric Accuracy Evaluation of GF-4 Satellite[J]. Spacecraft Recovery and Remote Sensing, 2016, 37(4): 16–25. DOI:10.3969/j.issn.1009-8518.2016.04.003 |
| [22] |
胡炳亭, 徐涛, 江世臣, 等.
多通道扫描成像辐射计热设计[J]. 红外技术, 2011, 33(3): 141–146.
HU Bingting, XU Tao, JIANG Shichen, et al. Thermal Control Design of Multi Channel Scanning Imagery Radiometer[J]. Infrared Technology, 2011, 33(3): 141–146. DOI:10.3969/j.issn.1001-8891.2011.03.004 |
| [23] | EUMETSAT. LRIT/HRIT Global Specification[R]. Darmstadt: Coordination Group for Meteorological Satellites, 2013. |
| [24] |
徐慧.遥感图像中的云区域检测及去除方法研究[D].合肥: 安徽大学, 2011. XU Hui. Research on Cloud Detection and Removal of Remote Sensing Image[D]. Hefei: Anhui University, 2011. |
| [25] |
耿则勋, 张保明, 范大昭.
数字摄影测量学[M]. 北京: 测绘出版社, 2010.
GENG Zexun, ZHANG Baoming, FAN Dazhao. Digital Photogrammetry[M]. Beijing: Surveying and Mapping Press, 2010. |
| [26] |
田军委, 王沁, 赵鹏, 等.
特定边界跟踪中角点检测研究[J]. 应用光学, 2014, 35(6): 991–995.
TIAN Junwei, WANG Qin, ZHAO Peng, et al. Corner Point Detection in Interested Boundary Tracking[J]. Journal of Applied Optics, 2014, 35(6): 991–995. |
| [27] | KHOTANZAD A, HONG Y H. Invariant Image Recognition by Zernike Moments[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 12(5): 489–497. |
| [28] | BROWN M E, TRUJILLO C, RABINOWITZ D. Discovery of A Candidate Inner Oort Cloud Planetoid[J]. The Astrophysical Journal, 2004, 617(1): 645–649. DOI:10.1086/apj.2004.617.issue-1 |
| [29] |
皮英冬, 杨博, 李欣.
基于有理多项式模型的GF4卫星区域影像平差处理方法及精度验证[J]. 测绘学报, 2016, 45(12): 1448–1454.
PI Yingdong, YANG Bo, LI Xin. Block-adjustment and Accuracy Validation for GF4 Patch-images Based on RFM[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(12): 1448–1454. DOI:10.11947/j.AGCS.20160262 |
| [30] | YANG Shaowen, WANG C C, CHANG Chunhua. RANSAC Matching: Simultaneous Registration and Segmentation[C]//Proceedings of 2010 IEEE International Conference on Robotics and Automation. Anchorage: IEEE Press, 2010: 1905-1912. |
| [31] | JENKINSON M, SMITH S. A Global Optimisation Method for Robust Affine Registration of Brain Images[J]. Medical Image Analysis, 2001, 5(2): 143–156. DOI:10.1016/S1361-8415(01)00036-6 |
| [32] |
陈西强, 黄张裕.
抗差估计的选权迭代法分析与比较[J]. 测绘工程, 2010, 19(4): 8–11, 15.
CHEN Xiqiang, HUANG Zhangyu. Analysis and Comparison of the Selecting Weight Iteration Method in Resistance Robust Estimation[J]. Engineering of Surveying and Mapping, 2010, 19(4): 8–11, 15. DOI:10.3969/j.issn.1006-7949.2010.04.003 |
| [33] |
王冰, 李积捷, 王春瑛, 等.
基于改进IGGⅢ和快速分解法的电力系统状态估计算法[J]. 继电器, 2008, 36(11): 1–4, 41.
WANG Bing, LI Jijie, WANG Chunying, et al. State Estimation Algorithm Based on the Improved Method of IGGⅢ and Fast Decoupled Arithmetic[J]. Relay, 2008, 36(11): 1–4, 41. |
| [34] |
隋立芬, 宋力杰, 柴洪洲.
误差理论与测量平差基础[M]. 北京: 测绘出版社, 2010.
SUI Lifen, SONG Lijie, CHAI Hongzhou. Error Theory and Foundation of Surveying Adjustment[M]. Beijing: Surveying and Mapping Press, 2010. |
| [35] | MANSOUR Y, VAAHEDI E, CHANG A Y, et al. BC Hydro's On-line Transient Stability Assessment (TSA) Model Development, Analysis and Post-processing[J]. IEEE Transactions on Power Systems, 1995, 10(1): 241–253. DOI:10.1109/59.373947 |
| [36] | WESSEL P, SMITH W H F. A Global Self-consistent, Hierarchical, High-resolution Geography Database[R]. Honolulu: GSHHG, 2017. |



