2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
干涉合成孔径雷达(interferometric SAR, InSAR)利用交轨向双天线或重复轨迹飞行对地面同一区域进行成像,由于观测目标到双天线存在波程差,从而可利用干涉形成的相位图反演地面高程信息。InSAR技术将合成孔径雷达技术和干涉测量相结合,具有测绘范围广、测量精度高,能够全天时、全天候工作等优点,在地形测绘方面具有良好的应用前景。
在实际干涉SAR系统中,由于系统采样延时误差、通道间相位误差、基线矢量测量误差等因素的存在,使得三维重建几何模型中的参数取值不准确,需要通过干涉参数定标来校准各参数,以提高平面定位和高程反演的精度[1-2]。文献[3—5]给出了单控制点或无控制点SAR图像定位方法,针对的是单天线SAR系统定标,通过单个控制点对雷达斜距或系统采样延时进行标定,然后根据SAR成像几何模型对图像中每个像素点进行定位。对于机载双天线InSAR而言,不仅需要对雷达斜距进行标定,更为重要的是基线矢量、相位偏置等干涉参数测量误差引起高程精度的下降。干涉参数定标是InSAR高程测量精度的保证,是干涉SAR地形测图流程的关键环节。
干涉参数定标方法从单景定标发展到多景大区域联合定标。文献[6—10]利用平坦地形干涉相位频率或外部DEM估计基线参数,这种方法要求成像场景中存在平坦地形或已知场景地形信息。文献[11—14]针对初始相位偏置参数估计问题,提出基于外源粗精度DEM或交叉轨数据的相位偏置估计方法;这两种针对基线和初始相位偏置两种干涉参数单独进行估计的方法,均需要外部信息才能实现对干涉参数的估计,且依赖于外部数据的精度,主要研究对象还是单景干涉图像对。文献[15—16]通过事先布放的大量控制点信息来解算干涉参数,这是最为直接和精度最高的干涉参数定标方法,但缺点是需要大量的控制点,在实际工程中难以实现。针对大区域干涉参数定标的难题,国内外学者们相继提出利用相邻图像对重叠部分连接点信息来降低控制点数量,文献[17—21]详细阐述了将重叠区域同名点信息构建到干涉定标方程中,实现稀疏控制点InSAR区域网平差算法。为了解决同名点信息质量问题,文献[22—23]研究了赋予各同名点不同权值,从而进一步提高区域网平差算法精度。文献[24—26]在稀疏控制点加上同名点联合平差的思想框架里,从InSAR构像模型出发,进一步完善了干涉参数联合定标方程。
基于稀疏控制点和同名点连接的区域网联合干涉参数定标方法,理论上能够有效实现控制点稀疏分布,但是由于干涉参数定标方程的病态性[19],要求增加较多GCP(ground control points)来减小干涉参数间的耦合性引起的高程误差。然而,与摄影测量遥感不同的是,为了能够在雷达图像中定位识别,地面控制点为角反射器,在InSAR作业前需要外业人员现场布放,这给外定标工作带来巨大的工作量,特别是在山区、沙漠等人难以到达的区域。为了进一步降低控制点数量,本文提出一种联合对飞数据的单控制点干涉SAR定标算法。
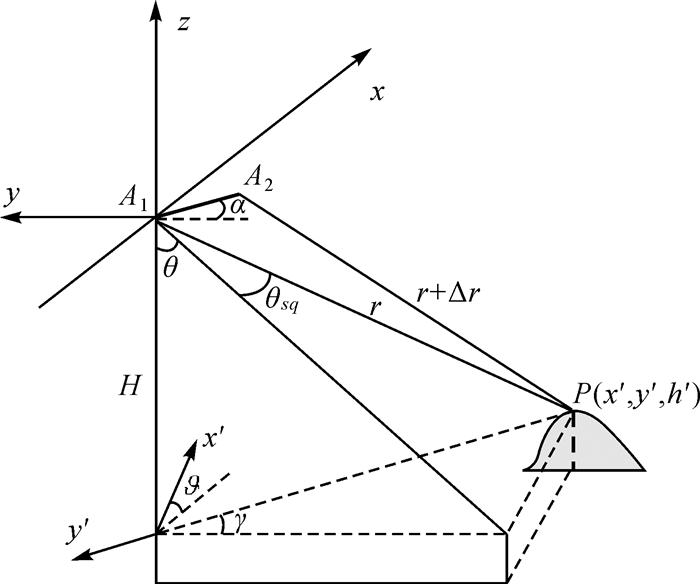
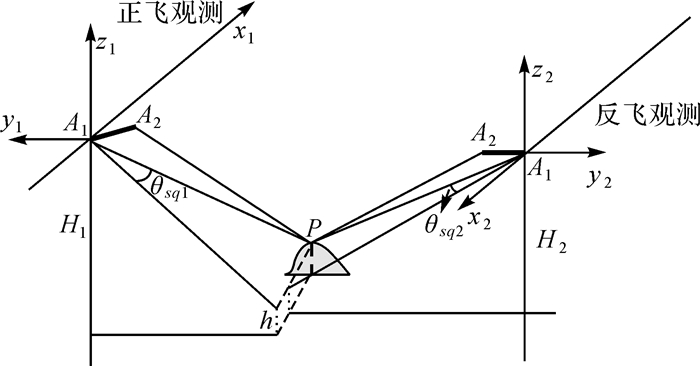
1 InSAR三维定位建模干涉SAR三维重建几何关系如图 1所示,A1、A2是双天线相位中心。以主天线相位中心为坐标原点建立SAR成像坐标系A1-xyz,x轴指向平台飞行方向,z轴朝下,y轴与xz构成右手系。设平台高度为H,成像区域中任意一目标点P高程为h,主天线A1相对目标P点的雷达斜距为r,副天线A2对应的雷达斜距为r+Δr。副天线相位中心A2的坐标为(Bx, By, Bz),Bx是由于SAR斜视观测(姿态扰动)引起的顺轨基线,由于干涉高程测量对顺轨基线不敏感[2],这里直接忽略,令Bx=0,By和Bz是基线矢量在交轨平面上投影对应的水平基线和垂直基线,即
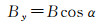 (1)
(1)
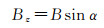 (2)
(2)
|
| 图 1 InSAR三维定位基本原理 Fig. 1 Principle of InSAR three-dimensional location |
式中,基线长度B=|A1A2|,α是A1A2矢量与水平面夹角,即基线倾角。干涉合成孔径雷达通过视角差异引起的干涉相位来反演目标高程信息,由图 1中三维重建几何关系,目标高程可表示为
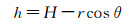 (3)
(3)
可见雷达主天线相对目标P下视角θ包含了目标高程信息,而双天线接收到信号的干涉相位差φ能够真实反映入射角的变化
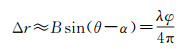 (4)
(4)
式中,λ是SAR发射信号波长,干涉相位差可通过双天线得到的复图像对共轭相乘来计算。式(3)、式(4)为InSAR高程测量的基本公式,表明高程测量与干涉相位、基线长度、基线倾角、平台高度和SAR斜距5个特征参数测量有关,这5个参数的测量误差均会引起高程测量性能的退化。
再来考虑目标P点图像平面几何位置。如图 1所示,InSAR在对地成像时,通过距离方程、多普勒方程和干涉相位方程描述InSAR基本测量值与地面目标位置之间的关系。干涉相位信息包含了第三维高程信息,平面位置信息可通过距离多普勒成像方程来计算
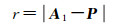 (5)
(5)
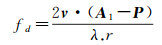 (6)
(6)
式中,fd=2|v|sin θsq/λ是方位多普勒频率;v是速度矢量;A1(x0, y0, H)是主天线相位中心空间三维位置;P(x', y', h)是待解算目标点三维空间位置。首先来定义地理空间直角坐标系x'y'z',x'轴、y'轴分别指向地理东向和北向,z'轴和InSAR成像坐标系z轴重合。将成像坐标系xyz绕z轴逆时针旋转角度ϑ(InSAR成像参考航迹地理方位角),并将坐标原点移至地理坐标系原点,就可得到空间直角坐标系x'y'z'。根据图 1空间成像几何及式(5)、式(6),化简可得图像空间P点在地理空间直角坐标系中坐标
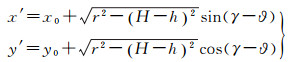 (7)
(7)
式中,γ是SAR成像斜视角在水平面上的投影,可由斜视角和雷达斜距计算得到
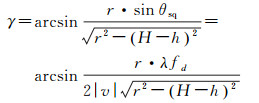 (8)
(8)
分析式(7)、式(8)得知,InSAR平面定位与SAR位置、雷达斜距、多普勒频率、目标高程和地理方位角有关。而SAR位置可由高精度定位定姿系统事先测量已知。多普勒频率和地理方位角虽然也可由POS系统提供的姿态信息进行计算,由式(7)可知,平面定位误差对这两个角度敏感度与斜距成正比,因此需要对二角度进行精确的估计。
至此,式(3)—式(8)描述了InSAR测量几何中目标点P(x', y', h)空间三维定位模型。总的说来,影响三维定位精度的因素包括平台高度、雷达斜距r、基线长度B、基线倾角α、干涉相位φ、多普勒频率和参考航迹地理方位角ϑ。平台高度参数的测量精度由高精度POS测量来保障;雷达斜距由系统初始采样延迟(电缆延迟、大气延迟等)误差引起;基线参数、多普勒频率和参考航迹地理方位角均受平台姿态变换影响随时间发生变化。
2 单控制点InSAR参数定标算法 2.1 三维定标方程降维为了降低三维定标方程的自由度,对干涉测量的特征参数的独立性和相关性进行系统的分析。SAR图像各像素点三维定位是通过雷达天线相位中心绝对定位基准通过成像几何传递来实现,因此平台高度H完全由POS高度向测量精度决定。雷达斜距误差主要由系统初始采样延迟(电缆延迟、大气延迟等)误差引起,初始采样延迟误差在环境稳定雷达系统安装方式固定情况下是稳定的,因此可以利用1个控制点三维空间位置计算其与平台之间的实际距离来校正
 (9)
(9)
式中,(xgcp, ygcp, zgcp)是地面控制点三维位置;(xr, yr, zr)是雷达主天线相位中心三维位置;ri是地面控制点在SAR图像中对应的实际斜距值。
由式(7)、式(8)可知,多普勒频率的估计精度可等效为斜视角在水平面上的投影角γ,而γ与参考航迹地理方位角γ的差进一步对平面定位精度产生影响,因此可将两者之差γ-ϑ作为一个特征参数同时解算,从而可降低控制点数量。因此,在平面定位方程(7)和式(8)中,首先利用一个控制点斜距误差校正之后,平面位置只与高程和γ-ϑ有关
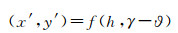 (10)
(10)
高度误差由POS系统保障,利用一个控制点的空间三维位置信息(x', y', h)可分别对雷达斜距和参考航迹地理方位角进行独立的校正。然而,剩下的3个特征参数(基线长度、基线倾角和初始相位偏置)存在相互耦合,难以独立地分离出来。由于雷达天线相位中心是一种等效的逻辑中心,不在天线的几何中心,基线长度不能在地面直接测量获得;基线倾角测量虽然可以通过POS姿态测量获得,但POS测量坐标系与成像坐标系存在固定的安装误差,因此也需要通过外定标的方式校准;干涉相位是通过复图像对经过配准、滤波和相位展开后获得,但由于三角函数的缠绕特性,经过相位解缠后的干涉相位φunw不是绝对相位,仍然存在一个初始相位偏置φ0
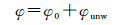 (11)
(11)
干涉相位测量误差除了图像信噪比引起的随机相位误差之外,还存在雷达系统初始相位漂移引起的固定误差,因此需要通过外定标的手段进行校准。由高程反演式(3)、式(4)可知,初始相位偏置估计与基线长度和基线倾角相耦合,难以独立的分离出来。因此,7个自由度的InSAR干涉参数定标方程可以降低到3个未知参数,需要地面至少有3个控制点才能解算出耦合的3个特征参数。
为了更进一步降低定标方程的维度,减少控制点数量,本文提出增加一条对飞航线对目标区域重复观测,如图 2所示。假设第1轨观测称为正飞,从相反方向对同一块区域观测称为反飞。主要思想是两次观测拥有相同目标点(同名点),就可以依赖图像中更多的分布式目标点建立大量的定标方程,利用增加的反飞航线获得额外的观测信息,从而降低对控制点数量的要求。
|
| 图 2 InSAR对飞观测 Fig. 2 InSAR observing in two converse flights |
2.2 对飞数据同名点定标
由2.1节三维定标方程中,平台高度、雷达斜距、多普勒频率和参考航迹地理方位角4个参数的测量误差可以成功从InSAR三维定标方程中分离出来,利用一个控制点即可完成这4个参数测量误差的校正。根据图 1干涉SAR高程反演基本原理,目标高程与基线参数和干涉相位的函数关系可写成
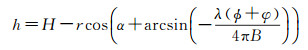 (12)
(12)
式(12)中包含基线长度、基线倾角和初始相位偏置3个未知数,理论上至少需要3个控制点,这是前面提到的每个条带至少包含3个控制点才能完成干涉参数定标解算的理论来源。本文提出通过对同一成像区域在反方向增加一条反飞航线,利用增加的对飞与正飞干涉图像对间的内在联系,建立新的参数定标方程,从而减少控制点数量。
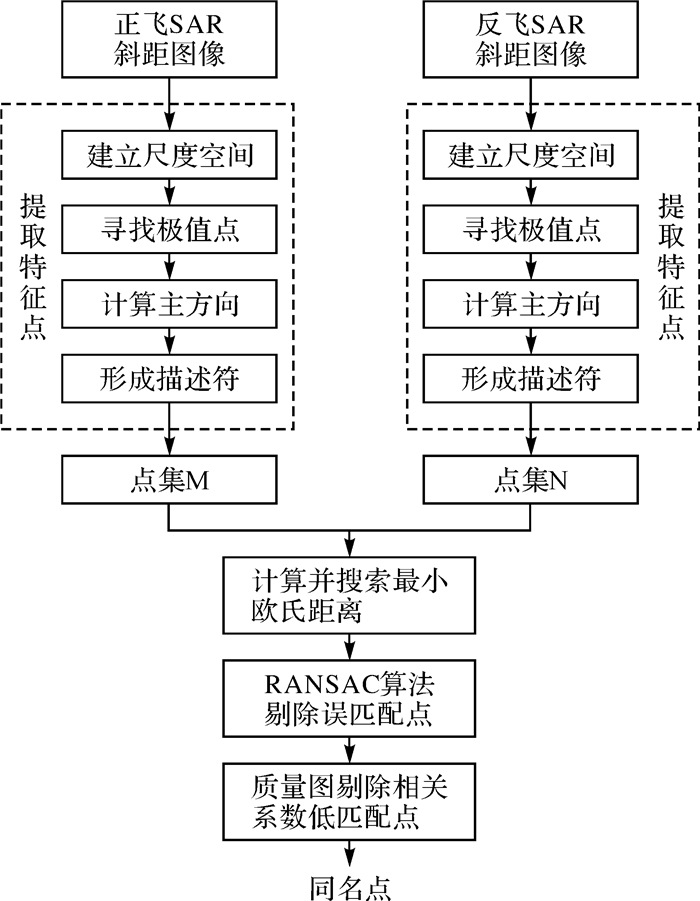
2.2.1 基于SIFT的同名点提取流程首先需要通过SAR图像匹配建立起正反飞干涉图像对间联系,必须对两组干涉图像对进行匹配处理。由于两组数据为不同方向和角度获取的同一区域影像,且存在地物类型差异及SAR侧视成像几何,不能实现图像中每个像素点完全匹配。本文考虑采用尺度不变特征变换(scale-invariant feature transform,SIFT)算法对正反两幅数据中提取一定数量的同名点,SIFT算法提取的特征对图像尺度变化、旋转、仿射变换、噪声污染、明亮度变化及视角变化具有良好的不变性。SIFT方法是一种提取图像局部特征的有效算法,它能够在尺度空间内寻找到一些极值点,对图像的亮度、平移、旋转、尺度变化具有较强的适应性,利用特征点周围图像提取该特征点的特征描述符,从而可以在特征描述符之间进行匹配。因此虽然二次SAR图像获取存在较大的角度差异,但是SIFT算法目前能够很好地适应SAR图像同名点提取应用[27-28]。同名点提取算法处理流程如图 3所示,主要包含构建尺度空间、计算主方向和描述符、计算最小欧氏距离、随机抽样一致性算法(RANSAC)剔除误匹配点、基于质量图的低相干区同名点剔除。同名点提取完成后得到两幅图像中同一目标点的图像空间坐标信息。
|
| 图 3 基于SIFT算法的SAR图像同名点提取流程 Fig. 3 Tie-points extraction flowchart based on SIFT |
2.2.2 同名点定标方程
在完成同名点信息提取后,然后针对两组干涉复图像对分别经过配准、滤波和相位解缠处理,得到两组干涉数据解缠后的干涉相位矩阵ϕ1、ϕ2。根据提取的同名点在各自图像空间中坐标信息,在解缠后的干涉相位中提取相应的干涉相位值,建立同名点约束方程
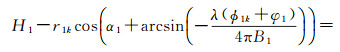
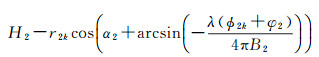 (13)
(13)
式中,k=1, 2, …, N,且N是同名点数量;ϕ1k、ϕ2k是第k个同名点在两组干涉数据中的解缠后相位;H1、H2是正飞和反飞航迹下平台高度;r1k、r2k分别是第k个同名点对应的斜距;B1、α1、φ1、B2、α2、φ2分别是正反飞条带基线长度、基线倾角和初始相位偏置值,是待求解的6个未知参数。分析式(13)可知,理论上只要找到6个二次干涉图像对间的同名点,不需要任何无控制点的情况下可解算出6个未知的干涉定标参数。然而,干涉参数的反演精度受入射角、基线参数、干涉相位噪声等因素的影响。定性的分析可知,两组方程特征参数差异越大方程越稳健,而实际中平台高度、雷达斜距、基线长度和基线倾角4个参数受平台飞行和设备安装条件的限制往往难以做到较大的差异,因此只剩下可以通过干涉相位差异来提升定标方程的稳健性。
干涉相位值的差异与地形起伏程度和入射角差异关系密切。本文设计通过对向飞行实现入射角差异最大化,但是入射角受雷达波束宽度的限制不可能无限大,因此只剩下地形起伏程度来增大两次观测间的干涉相位差异。为了定量化的解释此问题,引入定标矩阵条件数的概念来定量化地说明地形起伏对于联合对飞数据定标方程稳健性问题。矩阵条件数等于F的范数与F逆矩阵范数的乘积。矩阵条件数决定了对应的线性方程组的数值解的好坏和可信程度。条件数越小,则考虑的线性方程组的数值解的精度越高。高程反演敏感度矩阵F的条件数可以表示为
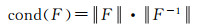 (14)
(14)
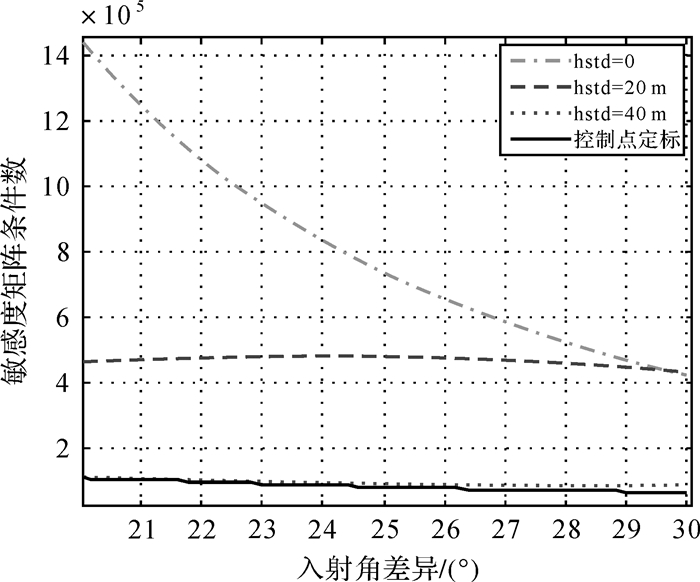
仿真了X波段2 m基线机载双天线干涉SAR情况下,在高程起伏标准差分别在0 m、20 m、40 m条件下联合对飞数据的定标方程矩阵条件数与完全利用控制点定标情况下的矩阵条件数对比情况。由图 4可知,随着地形起伏程度和入射角差异的增大,矩阵条件数变小,方程更为稳健,这与前面定性分析的结论是一致的。同时在地形起伏标准差达到40 m时,矩阵条件数已逐渐逼近到完全依赖控制点的干涉参数定标矩阵条件数变化曲线。
|
| 图 4 定标方程矩阵条件数随地形起伏变化 Fig. 4 Calibration matrix condition number under different terrain conditions |
地形起伏越大,干涉定标方程越稳健。然而地形起伏越大,地表高程对基线参数估计影响越大,当用于定标的同名点存在匹配误差时,将会引起干涉参数的反演精度下降。因此,在地形起伏较大区域对同名点匹配精度提出了更高的要求。实际中同名点选取应综合考虑平地和山区,使其兼顾稳健性和精度的要求。在实际InSAR地形测图应用中,无法保证所有的区域均有较大的地形起伏,因而笔者提出单控制点干涉参数定标方法,利用控制点绝对位置信息,降低算法对地形起伏的要求,从而提高算法地形适应性能。
2.3 联合对飞数据的单控制点参数定标完全依赖同名点定标方程解算干涉参数在地形平坦区域性能无法保障,因此引入一个单控制点定标方程,来提高算法的适应性。假设控制点对应的高程为hgcp,在正反两组解缠后的干涉相位图中相位值为ϕ1gcp和ϕ2gcp,该单控制点可在两组干涉数据中分别建立一个定标方程,如式(15)所示
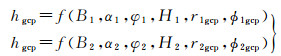 (15)
(15)
式中,f(·)是干涉SAR高程反演模型,可参考式(12)。控制点具有外部的绝对的高程信息,因此每个方程解算是相对稳健的。根据2.2.2节,还可以构建N组同名点定标方程
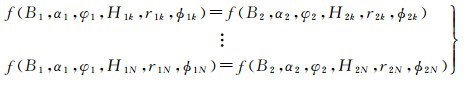 (16)
(16)
同名点约束方程中,由于没有绝对的高程信息参考,但是两组干涉参数间仍然存在相互耦合,特别是地形平坦的区域。虽然正反对飞入射角的差异能够一定程度上缓解这个问题,但是仍然存在一定的误差耦合。基于此,将式(15)和式(16)联立起来,方程稳健性将得到很大的提升。因此,干涉参数定标的问题就归结为N+2个方程组(联立式(15)、式(16))解6个未知数的数学问题。由于该方程组是超定的非线性方程组无解析解,拟采用最优化函数的方法进行求解。最优化函数能够获取全局最优解,避免方程组取得局部最优解,从而降低干涉参数的定标精度。联立控制点定标方程式(15)和同名点定标式(16),构建如下的最优化函数
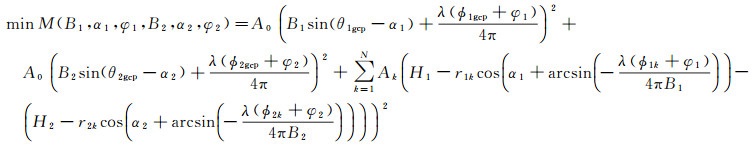 (17)
(17)
式中, θ1gcp、θ2gcp是该单个控制点相对雷达入射角,可通过控制点高程值计算。A0、Ak分别是控制点方程和同名点方程不同的权值,受InSAR相位噪声和同名点匹配精度影响,一般A0>Ak。使得最优化函数M达到最小值的干涉参数(B1, α1, φ1, B2, α2, φ2)即为方程组的解,为最终的干涉参数定标结果。由于同名点为非人工布设的定标点,其信噪比直接决定了干涉参数定标精度。评价同名点相位噪声质量通常采用干涉相关系数来表征,因此针对每个同名点对最优化函数的贡献进行了加权处理,加权系数与该点的相干系数值相关
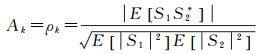 (18)
(18)
式中,S1和S2是干涉图像对的单视复图像。
式(17)是解定标方程构建的最优化函数,即找到一组干涉定标参数,使得在全局范围内最优化函数达到最小值。在求解此最优化问题时,最优化理论中包括最速下降法、牛顿法、共轭梯度法、遗传算法、模拟退火算法等。采用经典的最速下降法进行求解定标方程,求解步骤如下:
(1) 给定迭代初值B10, α10, φ10, B20, α20, φ20,设定终止误差ε,ε依据精度要求而设定。
(2) 求梯度向量模的值‖ΔM(B1i, α1i, φ1i, B2i, α2i, φ2i)‖,若该值小于ε,则停止计算,输出B1i, α1i, φ1i, B2i, α2i, φ2i作为联合定标结果,否则转下一步。其中,Δ表示向量微分算子;ΔM(·)表示函数M(·)的梯度向量;向量维数等于函数自变量的数目。
(3) 构造负梯度方向q(i)=-ΔM(B1i, α1i, φ1i, B2i, α2i, φ2i)作为搜索方向。
(4) 确定最优搜索步长ηi,并令(B1i+1, α1i+1, φ1i+1, B2i+1, α2i+1, φ2i+1)=(B1i, α1i, φ1i, B2i, α2i, φ2i)+ηiq(i),置i=i+1,转步骤(2)。
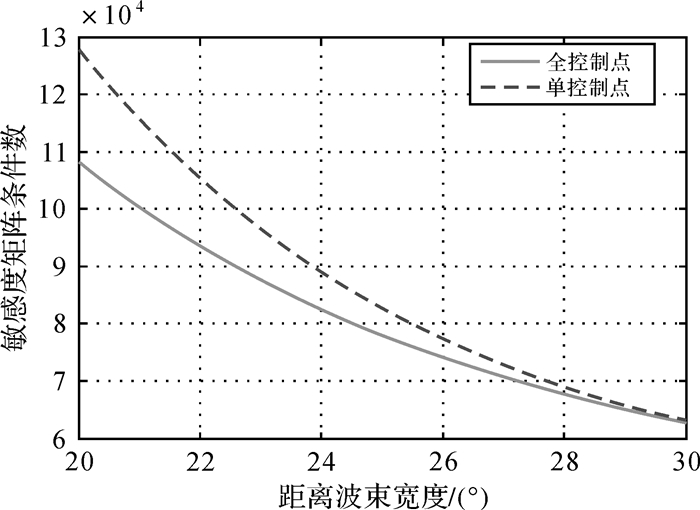
为了验证添加一个控制点能够提高定标方程组的稳健性,这里给出了联立单控制点和对飞定标方程的矩阵条件数仿真结果,如图 5所示,在使用了地形起伏程度在0 m情况下,单控制点定标在入射角差异为30°时已经逼近于全控制点定标的结果,可见引入单个控制点可以大大降低本文方法对地形起伏程度的依赖。
|
| 图 5 单控制点定标敏感度矩阵条件数 Fig. 5 Calibration matrix condition number using single corner reflector |
3 机载实际数据试验验证
采用中国科学院电子学研究所研制的机载干涉合成孔径雷达系统在某机场开展的飞行试验来进行实际数据验证。该InSAR系统工作在X波段,具备全极化干涉数据获取能力,最高分辨率0.5 m,搭载奖状Ⅱ型机载平台,如图 6所示。双天线水平安装在机腹下小型吊舱中,物理基线长度达2.2 m,系统设计高程测量精度满足1: 10 000比例尺地形测图精度要求。

|
| 图 6 机载InSAR系统及飞行平台 Fig. 6 Airborne InSAR system and flying platform |
采用的一组对飞干涉数据获取于2013年,对飞两组数据为一个架次飞行试验中获取,两条设计航线观测同一块成像区域,平台飞行相对地面高度3000 m,雷达中心下视角45°,测绘幅宽3 km。图 7是对飞两次观测获取的主天线SAR斜距影像。平台东往西飞行时,双天线SAR工作在乒乓收发模式,有效基线约2.2 m;西往东飞时,双天线SAR工作在一发双收模式,有效基线减半。成像区域中布放了5个地面控制点,GCP1—GCP5分布如图 7(a)所示。控制点布放范围主要集中在波束中心附近区域,没有完全覆盖整个测绘带,因而这里仅将控制点覆盖区域(图 7中虚线方框)作为精度验证的有效区域。该成像区域地形较为平坦,高程落差绝大部分小于5 m。针对平面定位定标和干涉参数定标实验结果分别进行分析。其中干涉参数定标分别针对多控制点、对飞无控制点和对飞单控制点3种定标方案的定标结果进行比较。

|
| 图 7 InSAR对飞获取的两景影像 Fig. 7 Two images of InSAR in two converse flights |
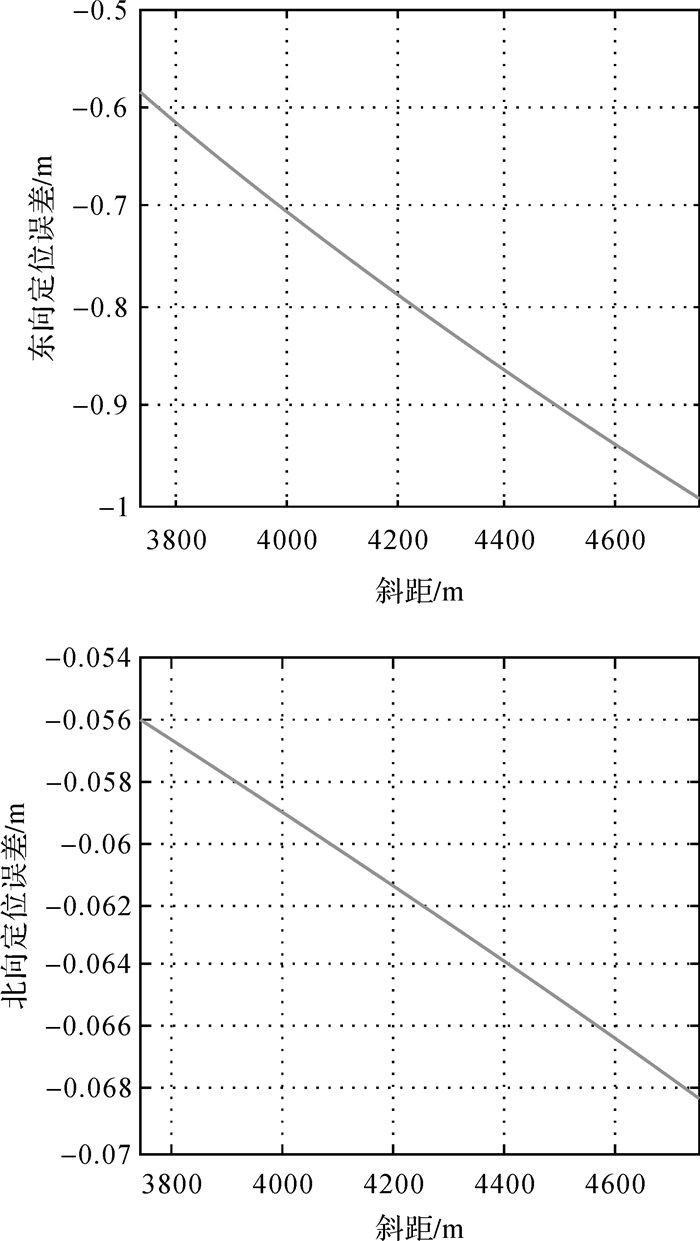
首先分析平面位置定标精度(如表 1所示),由于高度测量误差直接由POS系统决定,一般其测量精度优于0.1 m,误差量较小。雷达初始斜距误差受通道信号传输延迟、大气传输等因素的影响,在机载大气环境相对稳定情况下,主要由通道信号传输过程中引起的时间延迟决定,因此在安装方式固定情况下是相对稳定值。结合POS数据及地面控制点信息,计算得到斜距误差约为42.1 m。下面来看γ-ϑ参数定标情况,正飞角度误差估计值0.015°,引起的平面定位误差如图 8所示,东西向引起最大1 m的平面定位误差,而南北向由于位于距离向,因此对方位角的估计误差不是很敏感。可见,微小的角度差γ-ϑ估计误差会引起较大的平面定位误差,而传统基于InSAR成像模型干涉定标方法[17-21]只考虑了干涉高程反演参数的校正,忽略了多普勒中心频率和参考航迹地理方位角参数的校正,因此必然导致平面定位精度的下降。
| 特征参数 | 正飞 | 误差校正值 | 反飞 | 误差校正值 |
| 高度/m | 3 410.7 | 0 | 3 414.2 | 0 |
| 初始斜距/m | 3 510.3 | 42.1 | 3 464.9 | 42.1 |
| γ-ϑ/(°) | 179.353 | 0.015 | -0.291 | 0.022 |
|
| 图 8 传统方法平面位置未校正误差 Fig. 8 Planar location error using Conditional method |
再对高程测量特征参数反演精度进行分析。这里针对多控制点定标、对飞无控制点定标和对飞单控制点定标3种方案进行了比较。多控制点定标表示利用场景中的5个控制点对正飞InSAR数据进行干涉参数定标;对飞无控制点定标指的是完全利用对飞数据中同名点定标方程对干涉参数进行反演,在地形平坦的试验区理论性能将不高;对飞单控制点定标是本文提出的干涉参数定标算法,相比于对飞无控制点定标方案能够适应平坦区域的干涉参数定标解算。首先对两组对飞的干涉图像进行同名点提取,同名点提取结果分布如图 9所示,同名点主要集中在波束中心区域,完全覆盖了控制点区域,且在距离向形成一定的分布。经过RANSAC剔除误匹配点后共产生335组同名点,再根据干涉图像对的质量图信息剔除相干性差的点(相位误差大),仍然能够提取到大量的同名点信息(82组)。可见即使是两次获取的图像不同方向获取,由于基于SIFT的同名点提取具备尺度、旋转不变性,提取正确度和精度都较高。

|
| 图 9 同名点提取结果 Fig. 9 Tie-points extraction results |
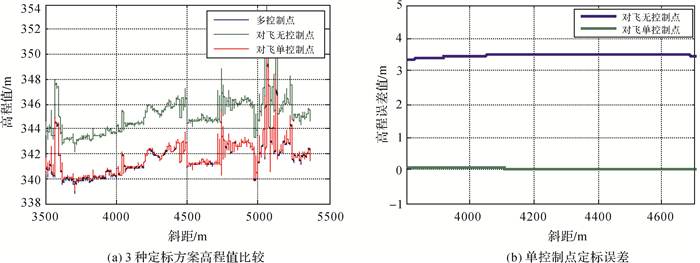
根据提取的同名点信息,联合控制点和同名点联合定标方程,利用构建的最优化函数(式(17))求解干涉参数。3种定标方案输出的高程误差分析情况如图 10所示。图 10(a)中传统的多控制点定标结果与本文提出的对飞单控制点定标算法的高程反演值吻合较好,而对飞无控制点高程反演曲线在高度向存在一个较大的常数误差,这也证明了在地形平坦区域完全依赖同名点间联系,是难以获得高精度的干涉参数定标结果。以传统的多控制点定标结果作为真值,分析另外2种方案的定标误差,如图 10(b)所示。对飞单控制点方法趋近于0,已经很好地逼近多控制点的定标结果。以正飞航线干涉测量为例,干涉参数定标结果及高程误差统计情况如表 2。本文提出的定标方案与传统多控制点干涉参数反演结果有较大的差异,基线长度估计值差异2 mm,基线倾角估计值差异0.05°,而初始相位偏置更在1 rad附近。这主要是由于3个干涉参数误差是相互耦合的,干涉参数反演的结果不是其真实值,而是在高程误差最小情况下的最优值。从表 2中高程误差的统计结果可看出,平坦场景情况下对飞无控制点定标方案存在高程误差均值为3.39 m,高程误差标准差为0.14 m,无法满足该InSAR系统指标设计要求。由于无绝对参考控制点条件下对飞定标方法,无同名连接点高程真值,即使定标方程两侧出现同样常数误差,定标方程仍然成立,这是对飞无控制点定标方法产生较大的常数误差主要原因。因此,本文提出单控制点定标,该定标方案高程误差均值和标准差均在0.05 m附近,比该机载InSAR系统精度设计指标低1个量级,因此是能够满足高精度的InSAR地形测绘应用需求的。
|
| 图 10 3种定标方案高程解算值比较 Fig. 10 DEM comparison of three calibration methods |
| 误差 | 正飞多控制点 | 对飞无控制点 | 对飞单控制点 |
| 基线长度/m | 2.192 4 | 2.198 5 | 2.194 4 |
| 基线倾角/(°) | 2.961 | 2.995 | 2.911 |
| 初始相位偏置/rad | 695.134 | 697.135 | 696.229 |
| 高程误差均值/m | 0 | 3.39 | 0.053 |
| 高程误差标准差/m | 0 | 0.14 | 0.050 |
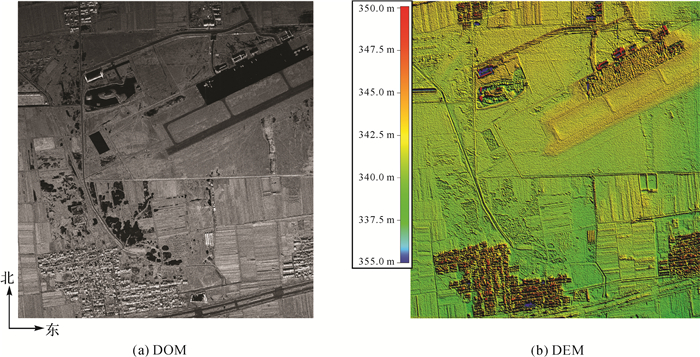
经过平面定位、高程反演和地理编码处理后,图 11给出了单控制点定标后经过处理获取的场景区域数字正射影像图(DOM)和数字高程模型(DEM)图。更进一步的,利用没有参与定标的剩余4个控制点对高程精度进行检查,高程误差值分别为-0.048 m、-0.01 m、0.047 m和0.052 m。综上所述,本文提出的方法与传统多控制点的定标结果差异小于0.05 m,比标称的InSAR系统干涉高程测量精度(0.5 m)低一个数量级,能够满足该机载InSAR系统地形测图精度要求。
|
| 图 11 单控制点DOM和DEM反演结果 Fig. 11 DOM and DEM results using single corner reflector |
4 结论
本文提出了一种联合对飞数据的单控制点干涉SAR参数定标算法,在构建InSAR平面和高程三维定标模型的基础上,提出了单个控制点加对飞数据同名点约束的最优化联合定标方程。以某机场区域X波段2.2 m基线机载InSAR获取的实际数据进行验证,结果表明,本文提出的定标算法与传统多控制点干涉定标高程差异小于0.05 m,比该机载InSAR测图系统设计精度低一个量级,较好地逼近传统的多控制点干涉定标精度。
| [1] | MADSEN S N, ZEBKER H A, MARTIN J. Topographic Mapping Using Radar Interferometry:Processing Techniques[J]. IEEE Transactions on Geoscience and Remote Sensing, 1993, 31(1): 246–256. DOI:10.1109/36.210464 |
| [2] | SUN Zhongchang, GUO Huadong, LI Xinwu, et al. DEM Generation and Error Analysis Using the First Chinese Airborne Dual-antenna Interferometric SAR Data[J]. International Journal of Remote Sensing, 2011, 32(23): 8485–8504. DOI:10.1080/01431161.2010.542197 |
| [3] |
张红敏, 靳国旺, 徐青, 等.
基于DEM和图像仿真的单幅SAR图像无控制定位[J]. 测绘科学技术学报, 2013, 30(3): 274–278.
ZHANG Hongmin, JIN Guowang, XU Qing, et al. Positioning with Single SAR Image Based on DEM without Ground Control Point[J]. Journal of Geomatics and Technology, 2013, 30(3): 274–278. DOI:10.3969/j.issn.1673-6338.2013.03.013 |
| [4] |
张红敏, 靳国旺, 徐青, 等.
利用单个地面控制点的SAR图像高精度立体定位[J]. 雷达学报, 2014, 3(1): 85–91.
ZHANG Hongmin, JIN Guowang, XU Qing, et al. Accurate Positioning with Stereo SAR Images and One Ground Control Point[J]. Journal of Radars, 2014, 3(1): 85–91. |
| [5] |
潘志刚, 潘卓, 曹舸.
机载SAR图像无控制点直接定位方法[J]. 中国科学院大学学报, 2015, 32(4): 536–541.
PAN Zhigang, PAN Zhuo, CAO Ge. A Direct Location Method for Air-borne SAR Image without Ground Control Point[J]. Journal of University of Chinese Academy of Sciences, 2015, 32(4): 536–541. |
| [6] | SINGH K, STUSSI N, KEONG K L, et al. Baseline Estimation in Interferometric SAR[C]//Proceedings of 1997 IEEE International Geoscience and Remote Sensing Symposium. Remote Sensing-A Scientific Vision for Sustainable Development. Singapore: IEEE, 1997: 454-456. |
| [7] |
徐华平, 朱玲凤, 刘向华, 等.
一种基于干涉条纹频率的星载InSAR基线估计新方法[J]. 电子学报, 2011, 39(9): 2212–2216.
XU Huaping, ZHU Lingfeng, LIU Xianghua, et al. A Novel Baseline Estimation Approach of Spaceborne InSAR Based on Interferometric Fringe Frequency[J]. ACTA Electronica Sinica, 2011, 39(9): 2212–2216. |
| [8] |
韦海军, 朱炬波, 梁甸农.
基于粗精度DEM的复杂地形InSAR基线估计方法[J]. 国防科技大学学报, 2010, 32(1): 74–78, 89.
WEI Haijun, ZHU Jubo, LIANG Diannong. An Accurate Baseline Estimate Method for Rugged Terrain Utilize Rough DEM[J]. Journal of National University of Defense Technology, 2010, 32(1): 74–78, 89. DOI:10.3969/j.issn.1001-2486.2010.01.014 |
| [9] |
靳国旺, 吴一戎, 向茂生, 等.
基于区域网平差的InSAR基线估计方法[J]. 测绘学报, 2011, 40(5): 616–622, 627.
JIN Guowang, WU Yirong, XIANG Maosheng, et al. Baseline Estimation Algorithm of InSAR with Block Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(5): 616–622, 627. |
| [10] |
云烨, 曾琪明, 焦健, 等.
基于参考DEM的机载InSAR定标方法[J]. 测绘学报, 2014, 43(1): 74–82.
YUN Ye, ZENG Qiming, JIAO Jian, et al. Calibration of Airborne Interferometric SAR Data Based on Reference DEM[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(1): 74–82. DOI:10.13485/j.cnki.11-2089.2014.0011 |
| [11] | MURA J C, PINHEIRO M, ROSA R, et al. A Phase-offset Estimation Method for InSAR DEM Generation Based on Phase-offset Functions[J]. Remote Sensing, 2012, 4(3): 745–761. DOI:10.3390/rs4030745 |
| [12] | PERNA S, ESPOSITO C, BERARDINO P, et al. Phase Offset Calculation for Airborne InSAR DEM Generation Without Corner Reflectors[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(5): 2713–2726. DOI:10.1109/TGRS.2014.2363937 |
| [13] | ESPOSITO C, PAUCIULLO A, BERARDINO P, et al. A Simple Solution for the Phase Offset Estimation of Airborne SAR Interferograms without Using Corner Reflectors[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(3): 379–383. DOI:10.1109/LGRS.2016.2644110 |
| [14] | GATTI G, TEBALDINI S, D'ALESSANDRO M M, et al. ALGAE:A Fast Algebraic Estimation of Interferogram Phase Offsets in Space-varying Geometries[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6): 2343–2353. DOI:10.1109/TGRS.2010.2091278 |
| [15] | MALLORQUI J J, BARA M, BROQUETAS A. Calibration Requirements for Airborne SAR Interferometry[C]//Proceedings Volume 4173, SAR Image Analysis, Modeling, and Techniques Ⅲ. Barcelona, Spain: SPIE, 2000: 267-278. |
| [16] |
张薇, 向茂生, 吴一戎.
基于三维重建模型的机载双天线干涉SAR外定标方法及实现[J]. 遥感技术与应用, 2009, 24(1): 82–87.
ZHANG Wei, XIANG Maosheng, WU Yirong. Realization of Outside Calibration Method Based on the Sensitivity Equation for Dual-antenna Airborne Interferometric SAR[J]. Remote Sensing Technology and Application, 2009, 24(1): 82–87. |
| [17] | GONZALEZ J H, BACHMANN M, KRIEGER G, et al. Development of the TanDEM-X Calibration Concept:Analysis of Systematic Errors[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(2): 716–726. DOI:10.1109/TGRS.2009.2034980 |
| [18] | WESSEL B, GRUBER A, WENDLEDER A, et al. Production Chain Towards First Calibrated and Mosaicked TanDEM-X DEMs[C]//Proceedings of 2011 IEEE International Geoscience and Remote Sensing Symposium. Vancouver: IEEE, 2011: 2432-2435. |
| [19] |
胡继伟, 洪峻, 明峰, 等.
一种适用于大区域稀疏控制点下的机载InSAR定标方法[J]. 电子与信息学报, 2011, 33(8): 1792–1797.
HU Jiwei, HONG Jun, MING Feng, et al. A Calibration Method for Airborne InSAR Applied to Large Areas with Sparse GCPs[J]. Journal of Electronics & Information Technology, 2011, 33(8): 1792–1797. |
| [20] | LI Yiwei, XIANG Maosheng, LÜ Xiaojie, et al. Joint Interferometric Calibration Based on Block Adjustment for an Airborne Dual-antenna InSAR System[J]. International Journal of Remote Sensing, 2014, 35(17): 6444–6468. DOI:10.1080/01431161.2014.954060 |
| [21] |
王萌萌, 黄国满, 花奋奋, 等.
机载双天线InSAR联合定标算法[J]. 测绘学报, 2014, 43(12): 1259–1265.
WANG Mengmeng, HUANG Guoman, HUA Fenfen, et al. Joint Calibration Method of Airborne Dual-antenna Interferometric SAR[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1259–1265. DOI:10.13485/j.cnki.11-2089.2014.0139 |
| [22] |
毛永飞, 向茂生.
基于加权最优化模型的机载InSAR联合定标算法[J]. 电子与信息学报, 2011, 33(12): 2819–2824.
MAO Yongfei, XIANG Maosheng. Joint Calibration of Airborne Interferometric SAR Data Using Weighted Optimization Method[J]. Journal of Electronics & Information Technology, 2011, 33(12): 2819–2824. |
| [23] |
熊新, 靳国旺, 张红敏, 等.
方差分量估计在机载InSAR区域网平差中的应用[J]. 测绘学报, 2016, 45(5): 592–600.
XIONG Xin, JIN Guowang, ZHANG Hongmin, et al. Application of Variance Components Estimation in Airborne InSAR Block Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(5): 592–600. DOI:10.11947/j.AGCS.2016.20150415 |
| [24] |
毛永飞, 汪小洁, 向茂生.
机载干涉SAR区域网三维定位算法[J]. 雷达学报, 2013, 2(1): 60–67.
MAO Yongfei, WANG Xiaojie, XIANG Maosheng. Joint Three-dimensional Location Algorithm for Airborne Interferometric SAR System[J]. Journal of Radars, 2013, 2(1): 60–67. |
| [25] |
岳昔娟, 韩春明, 窦长勇, 等.
机载InSAR区域网平差数学模型研究[J]. 武汉大学学报(信息科学版), 2015, 40(1): 59–63.
YUE Xijuan, HAN Chunming, DOU Changyong, et al. Mathematical Model of Airborne InSAR Block Adjustment[J]. Geomatics and Information Science of Wuhan University, 2015, 40(1): 59–63. |
| [26] |
陈乾福, 黄国满, 杨书成, 等.
利用三维重建模型的机载InSAR区域网平差方法[J]. 武汉大学学报(信息科学版), 2017, 42(2): 157–162.
CHEN Qianfu, HUANG Guoman, YANG Shucheng, et al. A Method for Block Adjustment with Airborne InSAR by Aid of Three Dimensional Reconstruction Model[J]. Geomatics and Information Science of Wuhan University, 2017, 42(2): 157–162. |
| [27] |
王山虎, 尤红建, 付琨.
基于大尺度双边SIFT的SAR图像同名点自动提取方法[J]. 电子与信息学报, 2012, 34(2): 287–293.
WANG Shanhu, YOU Hongjian, FU Kun. An Automatic Method for Finding Matches in SAR Images Based on Coarser Scale Bilateral Filtering SIFT[J]. Journal of Electronics & Information Technology, 2012, 34(2): 287–293. |
| [28] |
姜丽敏, 陈曙暄, 向茂生.
面向InSAR稀疏控制点测图的同名点提取方法[J]. 电子与信息学报, 2011, 33(12): 2837–2845.
JIANG Limin, CHEN Shuxuan, XIANG Maosheng. A Method of Homologue Points Extraction for InSAR Mapping with Sparse Control Points[J]. Journal of Electronics & Information Technology, 2011, 33(12): 2837–2845. |


