2. 信息工程大学数据与目标工程学院, 河南 郑州 450052;
3. 信息工程大学作战指挥系, 河南 郑州 450052
2. Data and Object Engineering Institute, Information Engineering University, Zhengzhou 450052, China;
3. Combat Command Department, Information Engineering University, Zhengzhou 450052, China
三线阵CCD相机是目前主流的测绘相机,在测绘生产效率和三维量测精度上具有明显优势,在航空航天遥感方面获得广泛应用,展示出卓越的立体测绘和地形测图性能。在星载三线阵CCD相机研究及应用方面,我国具有代表性的有“天绘一号”和“资源三号”三线阵立体测绘卫星。针对这二者的几何处理和标定技术的研究已比较成熟,其数据产品在国内外均获得肯定和认可[1-4]。但目前国内关于机载三线阵CCD相机的研制及几何标定技术的研究还相对滞后。国内普遍使用的机载三线阵CCD相机还是ADS40/80/100系列。关于ADS数据的几何处理,Leica公司在ORIMA软件中定制了空中三角测量模块[5-7];美国BAE Systems公司的SOCET SET和法国ISTAR公司的Pixel Factory软件也都开发了支持ADS影像的空三和测图模块[8-9]。同时,国内外多位学者针对ADS相机及类似传感器的几何定标定位技术进行了深入研究。文献[10-11]针对日本TLS三线阵相机进行了平差试验;文献[12-13]提出了利用常规光束法区域网平差结果比对POS系统直接测定的外方位角元素,从而检校机载POS系统视准轴误差的方法,又提出了通过POS辅助自检校光束法区域网平差来消除定位测姿系统误差的方法;文献[14-16]利用ADS40影像对机载三线阵影像的光束法平差技术进行了研究;文献[17]对ADS40系统几何检校的原理与方法进行了系统研究,并取得了比较理想的检定效果;文献[18]对ADS40影像进行了自检校光束法平差试验,定位精度改善极为明显;文献[19-21]对ADS40传感器的自检校定标技术进行了深入研究,设计了相适应的相机误差模型和自检校联合平差模型,通过试验表明其定标效果非常理想。
这些研究成果为我国开展机载三线阵CCD相机的研制和几何处理工作积累了宝贵的经验。GFXJ是在我国高分辨率对地观测系统重大专项支持下自行研制的首台机载大视场三线阵CCD相机。课题组在相关单位的支持下,对国内首台自主产权机载大视场三线阵CCD相机的相机标定、空三平差等处理技术展开了深入研究。GFXJ相机采用三线阵推扫方式成像,在航摄过程中可同时从前视、下视、后视3个不同角度对地面目标进行推扫成像,提供3个视角的全色影像与4个波段的多光谱(R、G、B、NIR)影像。每条电荷耦合元件(charge-coupled device,CCD)线阵列达到32 756个像元,且为整条CCD而非多片拼接,是目前像元最多的单条线阵CCD。像元大小为5 μm,相机焦距达到130 mm。与ADS系列相机相比,该相机焦距更长,CCD更宽,覆盖范围更广。为了提高影像定位精度,满足1:1000比例尺地形图测制的要求,需要对影像实施区域网平差,进行空中三角测量处理。为进一步提高该测绘相机的无控直接定位精度水平和降低空中三角测量处理中对地面控制点的依赖,需要对三线阵CCD相机立体测绘中的固有系统误差源进行标定处理。其中,降低机载三线阵CCD相机立体测绘精度,引起影像几何变形的系统误差源主要有两部分:一部分是GNSS天线中心的偏心矢量和IMU视轴偏心角[12, 22],另一部分是相机镜头、CCD等畸变误差[17-21]。
在目前国内对自主研制机载三线阵CCD相机没有先期几何处理和标定研究经验的背景下,本文针对GFXJ相机的GNSS偏心矢量和IMU视轴偏心角展开标定研究。首先,建立了GFXJ相机的GNSS偏心矢量模型和IMU视轴偏心角模型,并提出了相应的标定模型;然后,设计了循环两步法GNSS偏心矢量和IMU视轴偏心角标定方案;最后,采用多架次航空飞行数据进行试验验证。通过对多组标定结果进行对比研究,得出GFXJ相机GNSS偏心矢量和IMU视轴偏心角的标定数值,并以之为基础,再次进行无控直接定位和空中三角测量处理以评估验证标定效果。
试验证实本文建立的GNSS偏心矢量和IMU视轴偏心角模型是正确可靠的,利用本文提出的循环两步法标定方案可获得稳定可靠的GNSS偏心矢量和IMU视轴偏心角标定值。利用标定结果,可有效去除GFXJ相机GNSS和IMU观测值中的系统误差,显著提升GFXJ相机的无控直接定位精度,并有效降低空中三角测量处理对地面控制点的依赖程度。试验证实对国产机载三线阵CCD相机,项目组自主研发的软件可达到Orima软件对ADS相机的标定效果。
1 GFXJ相机的GNSS偏心矢量标定GNSS/IMU组合系统中,GNSS相对动态定位确定的是机载GNSS天线相位中心的空间位置,而摄影测量所需要的却是摄影物镜后节点(透视中心)的空间坐标。实际作业中,为了不遮挡GNSS信号,机载GNSS天线一般被安放在飞机顶部,导致GNSS天线相位中心与透视中心之间存在较大的空间偏移。该偏移值在实际飞行之前,可以地面实测获取初值,但是由于飞行过程中,气流、飞行运动等各种因素的影响,实际值与初始量测值会出现一定的偏差,因此必须建立二者之间的数学关系才能将GNSS定位数据转化为摄影测量定位所需的外方位元素。
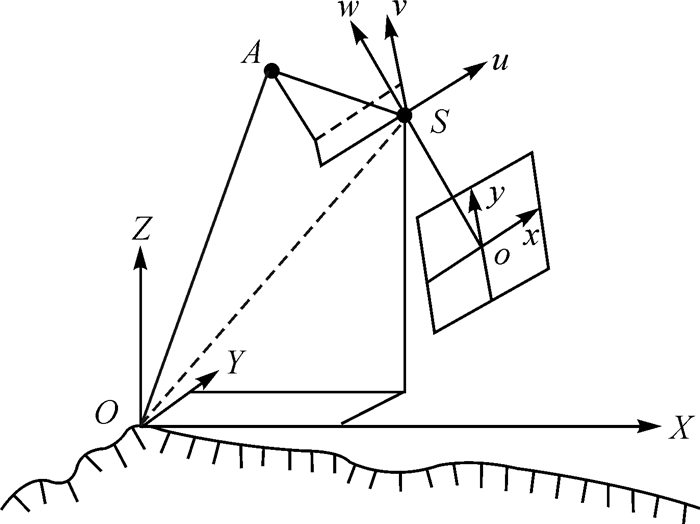
GNSS天线相对于透视中心S的偏心矢量如图 1所示。其中A为机载GNSS天线,S为透视中心,O-XYZ为地辅坐标系,GNSS天线相位中心的坐标为(XA,YA,ZA),相机透视中心坐标为(XS,YS,ZS);S-xyz为像空间坐标系,GNSS天线在其中的坐标为(u,v,w),这也是需要进行标定的GNSS偏心矢量。根据成像关系,建立GNSS偏心矢量的几何模型如下[20-22]
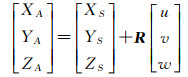 (1)
(1)
|
| 图 1 GNSS天线相对于透视中心S的偏心矢量 Fig. 1 GNSS lever arms to optical imaging center S |
式中,R为像片姿态角(ω, φ, κ)确定的旋转矩阵[16],本文采用OPK角度系统。
模型(1)是非线性方程组,其中(XA,YA,ZA)为GNSS的实际观测量,(u,v,w)为未知数,若已知(u,v,w)的初始值,可将式(1)线性化为
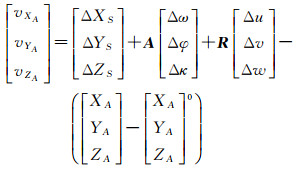 (2)
(2)
式中,(ΔXS, ΔYS, ΔZS, Δω, Δφ, Δκ)为像片外方位元素的改正数;(Δu,Δv,Δw)为GNSS天线偏心矢量改正数;A为未知数(Δω, Δφ, Δκ)的系数矩阵;(XA, YA, ZA)为GNSS测定的天线相位中心坐标;(XA, YA, ZA)0为由各近似值按式(1)计算出的天线相位中心坐标近似值。
针对GPS辅助的面阵框幅式Wild-RC20相机定位处理,文献[22]给出了模型(2)的GPS坐标观测方程。对于GNSS/IMU辅助的机载线阵CCD数据的定位处理,该模型同样适用,但GFXJ相机情况更为复杂。随着技术的发展,现在机载相机不仅具备GNSS系统的辅助,同时还有IMU惯导系统的支持。除了需要考虑GNSS偏心矢量,还要考虑IMU视轴偏心角的标定。而且对于线阵CCD图像,各扫描行的外方位元素各不相同,每一扫描行的外方位元素是相对独立的,与面阵框幅式Wild-RC20相机[22]相比,未知外方位元素个数急剧增多,外方位元素之间的相关性大大增强,给区域网平差的稳定性和可靠性带来挑战。在模型(2)中,外方位元素的改正数(ΔXS, ΔYS, ΔZS, Δω, Δφ, Δκ)和GNSS天线偏心矢量改正数(Δu,Δv,Δw)一起答解,这种求解模型称为GNSS天线偏心矢量标定的整体化模型。虽然有研究[18]认为,整体化模型比两步法模型在理论上更为严密,但是并没有文献对两者进行具体深入的分析研究和比较。本项目组通过大量试验分析证实,即使整体化模型的答解精度与两步法模型相当,但是鉴于机载三线阵CCD相机外方位元素复杂性等因素,整体化模型答解获得的GNSS偏心矢量标定值并不稳定,其原因是在每次答解中整体化模型只是将地面定位残差在外方位元素和GNSS偏心矢量之间进行最优配赋,并不能获得GNSS偏心矢量的稳定标定真值。为了深入研究,本文提出和建立GNSS天线偏心矢量的具体标定模型如下
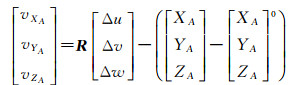 (3)
(3)
模型(3)中,各参数的具体意义不变,外方位元素由区域网平差求解获得,在GNSS天线偏心矢量的标定过程中认为是已知固定值,(Δu,Δv,Δw)是待标定的未知数——GNSS偏心矢量。如果在飞行前,GNSS偏心矢量已准确量测并在GNSS观测数据处理中已经考虑,则标定值(Δu,Δv,Δw)是GNSS偏心矢量实验室标定值与实际飞行值之间的差异。地形图测图的比例尺越高,则飞行时各种条件变化引起的差异越不能忽略。
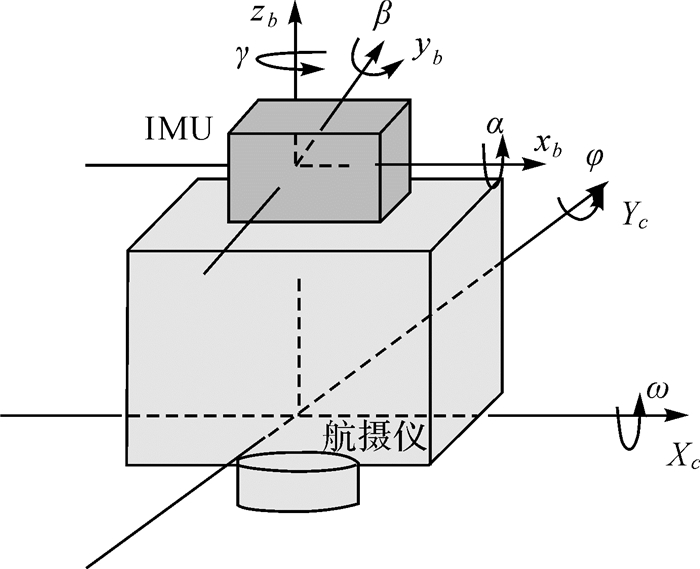
2 GFXJ相机的IMU视轴偏心角标定从GNSS/IMU组合定位定姿的基本原理可知,GNSS/IMU提供的是IMU在局部水平坐标系中的位置、姿态、速度和加速度等信息,但摄影测量定位需要的却是航摄仪在物方坐标系中的位置和姿态。实际应用中IMU都是与航摄仪刚性连接,并尽可能使相应轴线保持平行。二者之间的相对关系如图 2所示,其中下标b代表IMU,c代表航摄仪。由于系统安装的原因,IMU和航摄仪的相应轴线严格平行几乎是不可能的,相应轴线之间总会存在一个角度差,称为IMU视轴偏心角,也称为视准轴误差。
|
| 图 2 IMU与航摄仪之间的相对几何关系 Fig. 2 Relative geometric relationship between IMU and camera |
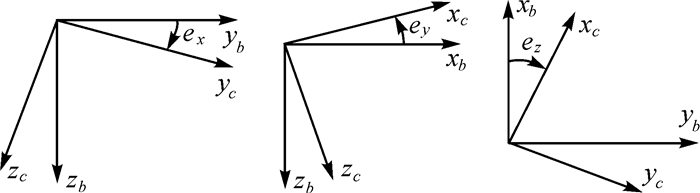
IMU视轴偏心角一般情况下数值较小(<3°),特殊安装情况下可能为±π/2或其他角度。偏心角可分解为3个方向的角度偏差,分别为ex、ey、ez,如图 3所示。由于IMU轴线是不可视的,有时由于安装在相机内部的IMU本身也是不可视的,因此偏心角很难采用地面测量手段直接量测,必须通过标定技术间接求解。偏心角严重影响了航空遥感直接对地目标定位的精度,在实际应用中必须检定。
|
| 图 3 IMU与航摄仪之间的视轴偏心角 Fig. 3 Boresight misalignments between IMU and camera |
设GNSS/IMU直接测量的姿态角为(α, β, γ),其构成的旋转矩阵为Rbm

航摄像片的外方位角元素为(ω, φ, κ),其构成的旋转矩阵为Rcm
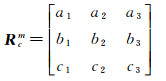
偏心角(ex, ey, ez)构成的旋转矩阵为Rcb

由于视轴偏心角的存在,3个旋转矩阵之间满足如下的数学关系
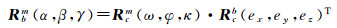 (4)
(4)
本文采用OPK角度系统,由OPK角度系统的定义[12, 16],可反算(α, β, γ),建立GNSS/IMU姿态角的观测方程
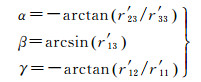 (5)
(5)
观测方程(5)中,方程左边(α, β, γ)是GNSS/IMU姿态角的观测值,右边r′23等数值是由模型(4)得到的计算值,所以方程右边是GNSS/IMU姿态角的计算值。如果视轴偏心角ex、ey、ez为0,或者ex、ey、ez具有准确值,方程(5)中等式关系成立;如果ex、ey、ez没有准确标定,则方程(5)等式关系不成立。方程(5)是IMU视轴偏心角标定的理论基础。
如果飞行时间过长,时间变化对IMU姿态角产生影响,则GNSS/IMU姿态角的观测方程还需要考虑漂移模型
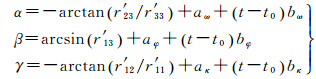 (6)
(6)
将GNSS/IMU姿态角观测方程(6)线性化,得到IMU视轴偏心角的标定模型如下
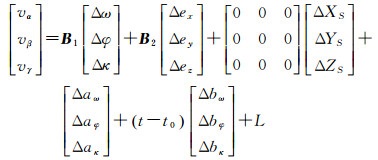 (7)
(7)
式中,(ΔXS, ΔYS, ΔZS, Δω, Δφ, Δκ)为像片外方位元素的改正数;(Δex, Δey, Δez)为IMU视轴偏心角改正数;B1为未知数(Δω, Δφ, Δκ)的系数矩阵;B2为未知数(Δex, Δey, Δez)的系数矩阵。因为IMU视轴偏心角模型中没有涉及外方位线元素,所以外方位线元素的系数矩阵为零矩阵;L为常数项矩阵,其数值为对应项姿态角的测量值(α, β, γ)减去由方程(5)得到的姿态角计算值。
在IMU视轴偏心角的标定过程中,外方位元素假设为常量,提出针对GFXJ相机的具体标定模型如下
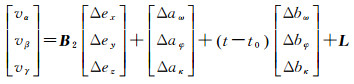 (8)
(8)
如果IMU测量值不随时间漂移,或者航线较短,可以不考虑模型(8)中右边的后两项。
3 GFXJ相机的GNSS偏心矢量和IMU视轴偏心角循环两步法标定方案综合第1节和第2节提出的标定模型,设计针对GFXJ相机GNSS偏心矢量和IMU视轴偏心角的循环两步法标定方案如下:
(1) 对于GFXJ影像建立以每条扫描行为中心的严格成像模型,将GNSS/IMU观测数据转换到UTM地图投影坐标系下(也可以采用局部地面辅助坐标系或地心空间直角坐标系)。
(2) 对GFXJ影像数据实施基于GPU加速处理的多航线影像匹配,提取大量连接点数据。
(3) 利用控制点数据和影像匹配获得的连接点数据,构建多航线的平差区域网。采用定向片模型[5],建立GFXJ影像的大规模平差区域网,进行空中三角测量处理。镜头畸变和CCD变形的综合影响表现为前/下/后视CCD上每一探元的实际几何位置会偏离实验室标定值。以每条扫描行的GNSS/IMU观测值为初值,获得定向片的外方位元素值、每条扫描行的外方位元素改正数(ΔXS, ΔYS, ΔZS, Δω, Δφ, Δκ)和前/下/后视CCD每一探元几何位置的标定值。
(4) 固定步骤(3)获得外方位元素值不变,以每个定向片为采样数据,采用模型(3)和模型(8)进行GNSS偏心矢量和IMU视轴偏心角标定,获得标定数值(Δu,Δv,Δw)和(Δex, Δey, Δez)。
(5) 利用标定数值(Δu,Δv,Δw)和(Δex, Δey, Δez),对外方位元素值进行更新,更新模型如下
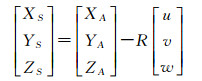 (9)
(9)
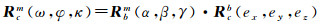 (10)
(10)
(6) 以更新后的外方位元素值为基础,再次进行步骤(3)中的区域网平差,以及步骤(4)和步骤(5)的计算,迭代循环步骤(3)-步骤(5),直至外方位元素的改正数(ΔXS, ΔYS, ΔZS, Δω, Δφ, Δκ)和GNSS偏心矢量以及IMU视轴偏心角的改正数(Δu,Δv,Δw)和(Δex, Δey, Δez)趋于稳定,前后两次迭代改正数之差小于阈值,则迭代结束,跳出循环。获得改正后的GNSS/IMU观测值、GNSS偏心矢量和IMU视轴偏心角标定值、以及前/下/后视CCD探元位置的标定文件。
4 试验数据介绍试验采用GFXJ相机在2017年5月23日和5月25日在河南登封嵩山遥感综合实验场区域飞行获取的两组数据进行区域网平差和标定试验。嵩山遥感综合实验场选址在河南登封嵩山地区,是国家级遥感定标实验场[23-24]。该地区主要地貌类别齐全,涵盖平原、丘陵地、山地等,地形起伏较大,海拔高度为100~1500 m。实验场包括航空定标实验场,摄影测量与遥感综合实验场和航天定标实验场3部分,其中航空定标实验场主要用于各种航空相机或传感器的检定,面积约8 km×8 km,控制点采用埋石方式分级布设了214个永久性高精度控制点(图 4), 平面精度优于2 mm,高程精度优于1 cm,也是本次试验的航摄区域。

|
| 图 4 控制点埋石 Fig. 4 Stationary solid GCP |
图 5所示为嵩山遥感实验场覆盖区域、两次飞行的试验区域和控制点分布图,两次试验飞行高度均为2000 m。其中实线框表示2017年5月23日飞行获取的4条十字交叉航线数据,影像覆盖区域内分布70个控制点, 其中21个控制点位于多条航线重叠范围内(下文简称为试验数据A),虚线框表示2017年5月25日飞行获取的两条往返航线数据,分布54个控制点,5个控制点位于多条航线重叠范围内(简称为试验数据B)。

|
| 图 5 嵩山摄影测量与遥感定标综合实验场及飞行数据和控制点分布 Fig. 5 Songshan RS calibration testfield and GCP distribution |
控制点像点坐标采用人工量测,精度约在0.3个像元左右。试验数据A的4条航线采用SIFT特征匹配算法,利用GPU加速计算和RANSAC匹配粗差点剔除策略,实施多航线间交互式分块影像匹配,共提取63 088个特征连接点。根据GFXJ相机前/下/后三视CCD影像上同名像点应交于地面同一点的理论依据,对63 088个特征连接点再次进行粗差点剔除和筛选处理,最后保留14 157个点进行区域网平差和标定处理。试验数据B两条航线经SIFT特征匹配后共提取21 389个特征连接点,进行粗差点剔除和筛选处理,最后保留8802个点进行区域网平差和标定处理。
5 试验结果和分析试验分为3部分内容:①对试验数据A进行区域网平差和GNSS偏心矢量和IMU视轴偏心角标定试验;②对试验数据B进行区域网平差和GNSS偏心矢量和IMU视轴偏心角标定试验;③利用GNSS偏心矢量和IMU视轴偏心角标定值,对试验数据A和试验数据B再次进行区域网平差试验。
5.1 试验数据A的区域网平差和GNSS偏心矢量和IMU视轴偏心角标定试验对试验数据A进行了4组试验:①直接定位试验,利用GNSS/IMU测量值和前/下/后视CCD探元位置的实验室测量值为初值,进行直接定位,检查相机的初始定位精度,并分析误差来源;②区域网平差和GNSS/IMU标定试验,进行循环两步法标定,获得前/下/后视CCD每一探元几何位置的标定值、GNSS偏心矢量和IMU视轴偏心角,以及得到区域网平差和标定处理后的定位精度;③第2次直接定位试验,利用前/下/后视CCD探元位置标定值和GNSS/IMU测量值作为外方位元素,进行直接定位,检验区域网平差后相机直接定位的精度水平;④第3次直接定位试验,利用GNSS偏心矢量和IMU视轴偏心角标定值对GNSS/IMU测量值进行改正,获得GNSS/IMU改正值。利用GNSS/IMU改正值和前/下/后视CCD探元位置标定值,进行直接定位试验,验证GNNS偏心矢量和IMU视轴偏心角标定后的定位精度水平。
试验数据A试验结果见表 1。表 1第2行列出了直接定位试验结果,第3行列出了区域网平差和标定后的定位精度,第4行给出了第2次直接定位精度,第5行给出了第3次直接定位精度。第2列、第3列和第4列分别统计了各组试验在X、Y和Z 3个方向的定位精度指标。表 1中第2、4和5行统计的是全部控制点的精度指标,第2行统计的是采用50个控制点参与平差和标定后,剩余20个检查点的精度。
| m | ||||||||||||||
| 试验内容 数据来源和组合方式 | X方位定位精度 | Y方位定位精度 | Z方位定位精度 | |||||||||||
| 最大值 | 最小值 | 均值 | 中误差 | 最大值 | 最小值 | 均值 | 中误差 | 最大值 | 最小值 | 均值 | 中误差 | |||
| 直接定位 | 6.340 | -4.739 | 1.402 | 3.897 | 5.073 | -4.980 | 1.438 | 3.654 | -2.803 | -8.932 | -6.930 | 6.487 | ||
| 区域网平差和标定 | 0.643 | -0.503 | -0.018 | 0.224 | 0.408 | -0.586 | -0.015 | 0.234 | 1.392 | -1.767 | 0.076 | 0.579 | ||
| 第2次直接定位 | 4.763 | -4.003 | 1.409 | 3.311 | 4.475 | -3.833 | 1.264 | 3.211 | 2.788 | -1.721 | 0.301 | 0.992 | ||
| 第3次直接定位 | 0.560 | -0.856 | -0.002 | 0.320 | 0.740 | -0.744 | 0.001 | 0.302 | 1.513 | -1.545 | -0.116 | 0.664 | ||
从表 1第2行可以看出采用GFXJ相机的原始参数和GNSS/IMU测量值,影像直接定位精度存在较大的系统误差。从表 1第3行可以看出经过区域网平差和标定处理后,相机镜头和CCD变形、GNSS偏心矢量和IMU视轴偏心角引起的定位误差得到了有效消除。从第2次直接定位试验结果可以看出,利用前/下/后视CCD探元位置标定值可有效改善镜头畸变、CCD旋转、缩放等几何变形引起的定位误差,尤其高程定位误差改善尤为显著,但是平面精度改善效果不显著。第3次直接定位结果表明,利用前/下/后视CCD探元位置标定值和GNSS/IMU改正值进行直接定位,X、Y和Z 3个方向的定位精度都得了显著改善,精度水平接近区域网平差和标定后的定位精度,这证实GNSS偏心矢量和IMU视轴偏心角是影响GFXJ相机几何定位精度的一个主要误差来源,在机载三线阵CCD相机几何标定中必须考虑。
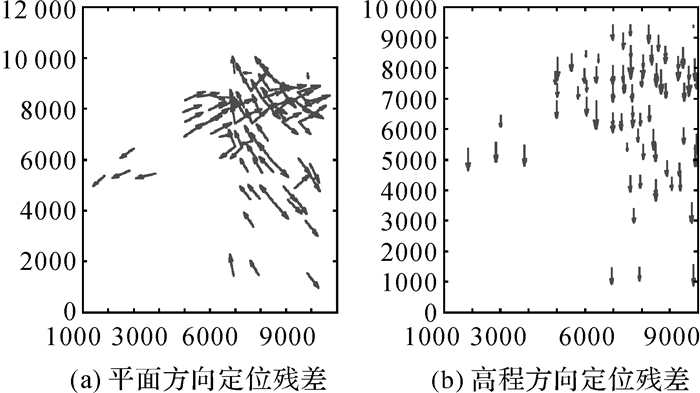
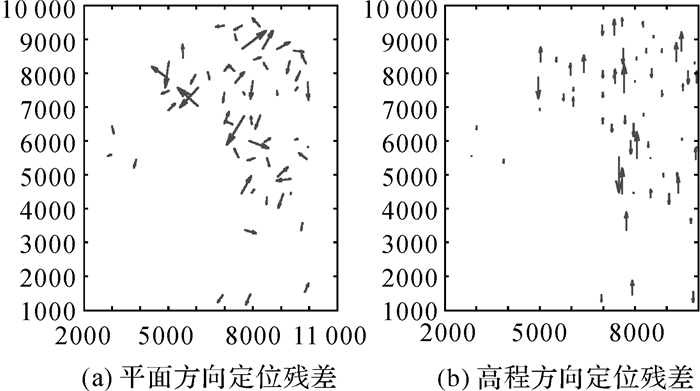
将表 1中的试验结果绘图显示,图 6显示了试验数据A直接几何定位后,70个控制点的定位残差分布,图 6(a)显示了平面方向(X、Y方向)的残差分布,图 6(b)显示了高程方向的残差分布。图 7列出了区域网平差和标定后70个控制点的残差分布,图 8和图 9分别列出了第2次和第3次直接定位的残差分布。其中图 6-图 9显示的残差坐标采用的是局部坐标系。
|
| 图 6 试验数据A直接定位的几何残差 Fig. 6 Geometric residuals distribution of dataset A after direct geometric positioning |
|
| 图 7 试验数据A区域网平差和标定后的几何残差 Fig. 7 Geometric residuals distribution of dataset A after bundle block adjustment and calibration |
|
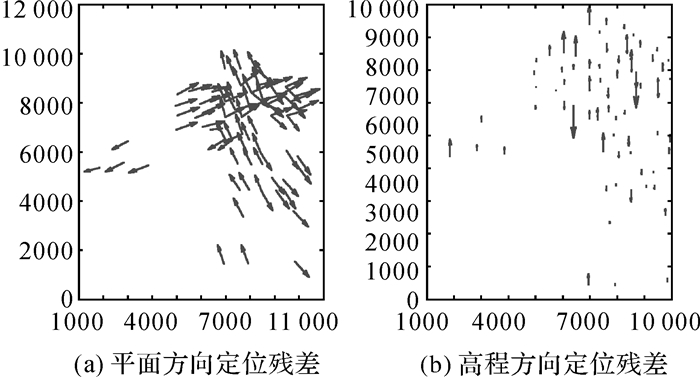
| 图 8 试验数据A第2次直接定位后的几何残差 Fig. 8 Geometric residuals distribution of dataset A after the second geometric direct positioning |
|
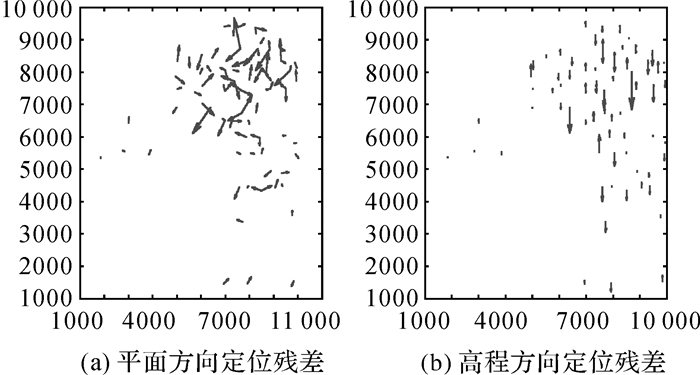
| 图 9 试验数据A第3次直接定位后的几何残差 Fig. 9 Geometric residuals distribution of dataset A after the third geometric direct positioning |
从图 6中可以看出,采用前/下/后视CCD探元位置实验室测量值和GNSS/IMU测量值直接定位,试验结果存在明显的系统误差,不同航线的平面残差具有明显方向性,高程残差变化非常一致。图 7显示经过区域网平差和标定处理后,GNSS偏心矢量、IMU视轴偏心角、镜头畸变和CCD变形等引起的系统误差得到有效消除,控制点上的残余误差不再表现出系统性,剩余误差应主要为偶然误差。利用标定后的镜头畸变和CCD变形参数,对前/下/后视CCD上每一个探元的几何位置进行标定,得到前/下/后视CCD探元位置标定值,并和GNSS/IMU测量值一起进行第2次直接定位,图 8显示高程精度明显改善,但是平面精度改善并不明显。利用GNSS偏心矢量和IMU视轴偏心角标定值对GNSS/IMU改正值进行改正,利用前/下/后视CCD探元位置标定值和GNSS/IMU改正值进行第3次直接定位,图 9显示平面和高程精度都得到显著改善,精度接近区域网平差和标定后的几何定位精度水平。从表 1和图 6-9中,可以得到初步结论:①GNSS偏心矢量和IMU视轴偏心角、镜头畸变和CCD变形是造成GFXJ相机几何定位精度下降的两个最主要误差源;②GNSS偏心矢量和IMU视轴偏心角主要影响GFXJ相机的平面定位精度;③镜头畸变和CCD几何变形主要影响GFXJ相机的高程定位精度。
5.2 试验数据B的区域网平差和GNSS偏心矢量和IMU视轴偏心角标定试验对试验数据B,同样进行了4组试验:直接定位试验、区域网平差和GNSS/IMU标定试验、第2次直接定位试验和第3次直接定位试验,结果见表 2。表 2中第2行、第4行和第5行统计的是全部控制点的精度指标,第2行统计的是采用40个控制点参与区域网平差和标定后,剩余14个检查点的精度。
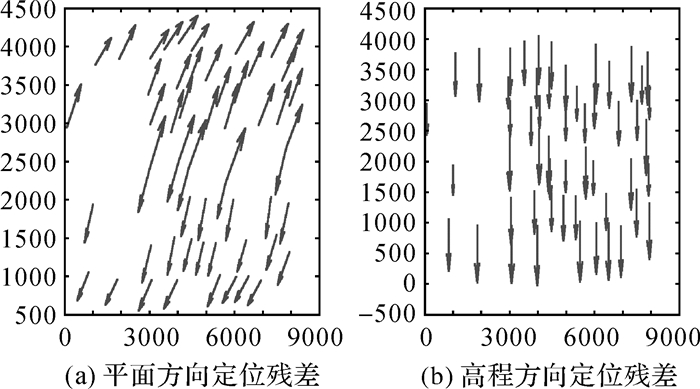
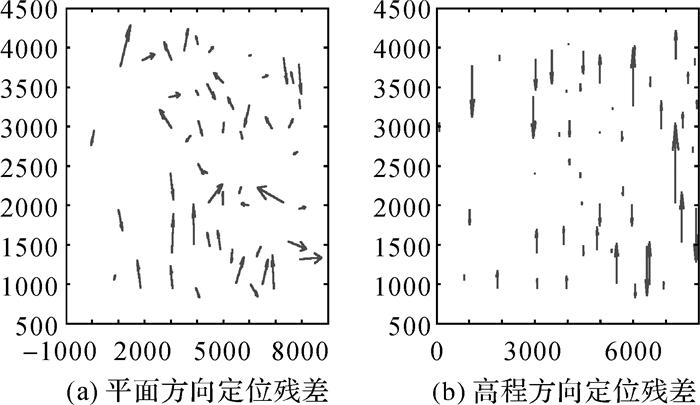
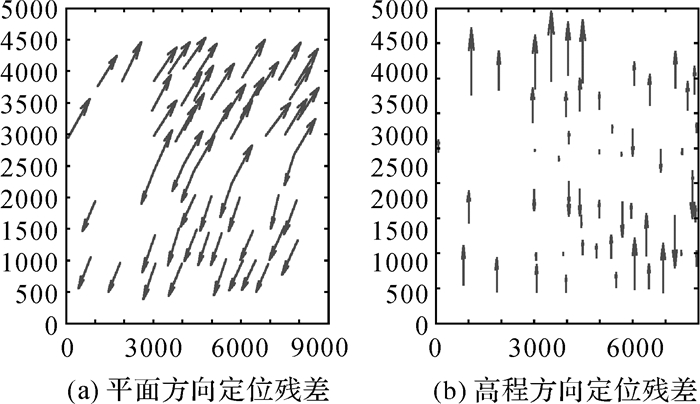
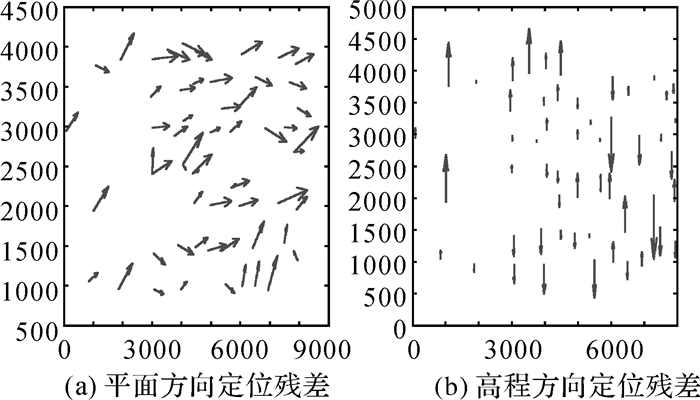
对表 2也进行绘图分析,图 10显示了试验数据B直接几何定位后,54个控制点的定位残差分布,图 11列出了区域网平差和标定后54个控制点的残差分布,图 12和图 13分别列出了第2次和第3次直接定位的残差分布。其中图 10-13显示的残差坐标采用局部坐标系。对表 2和图 10-图 13进行分析可以得出与试验数据A相似的结论:区域网平差和标定处理可以有效消除机载三线阵GFXJ相机的系统误差,提高影像的定位精度。镜头畸变、CCD旋转、缩放等变形主要影响相机的高程定位精度,部分影响平面定位精度;GNSS偏心矢量和IMU视轴偏心角不仅影响相机的高程精度,还影响相机的平面定位,是相机标定处理中必须考虑的一项重要误差源。
| m | ||||||||||||||
| 试验内容 数据来源和组合方式 | X方位定位精度 | Y方位定位精度 | Z方位定位精度 | |||||||||||
| 最大值 | 最小值 | 均值 | 中误差 | 最大值 | 最小值 | 均值 | 中误差 | 最大值 | 最小值 | 均值 | 中误差 | |||
| 直接定位 | 4.625 | -3.186 | 0.880 | 3.256 | 4.634 | -4.020 | 0.369 | 3.344 | -3.777 | -7.806 | -6.386 | 6.218 | ||
| 区域网平差和标定 | 0.531 | -0.654 | 0.024 | 0.189 | 0.345 | -0.246 | 0.037 | 0.146 | 1.305 7 | -0.877 | 0.046 | 0.420 | ||
| 第2次直接定位 | 3.560 | -2.292 | 0.882 | 2.675 | 2.807 | -2.529 | 0.278 | 2.394 | 2.331 | -1.727 | 0.449 | 1.061 | ||
| 第3次直接定位 | 0.836 | -0.167 | 0.187 | 0.428 | 0.587 | -0.225 | 0.143 | 0.253 | 1.137 | -1.529 | -0.019 | 0.551 | ||
|
| 图 10 试验数据B直接定位的几何残差 Fig. 10 Geometric residuals distribution of dataset B after geometric direct positioning |
|
| 图 11 试验数据B区域网平差和标定后的几何残差 Fig. 11 Geometric residuals distribution of dataset B after bundle block adjustment and calibration |
|
| 图 12 试验数据B第2次直接定位后的几何残差 Fig. 12 Geometric residuals distribution of dataset B after the second geometric direct positioning |
|
| 图 13 试验数据B第3次直接定位后的几何残差 Fig. 13 Geometric residuals distribution of dataset B after the third geometric direct positioning |
5.3 试验数据A和试验数据B的再次区域网平差
5.1节和5.2节中利用对应试验数据的GNSS偏心矢量和IMU视轴偏心角标定值改正GNSS/IMU观测值,具有一定局限性。为了证实标定值的通用性,对试验数据A和试验数据B的标定结果进行对比分析。试验数据A标定获取的GNSS偏心矢量和IMU视轴偏心角见表 3第2行,试验数据B标定获取的GNSS偏心矢量和IMU视轴偏心角见表 3第3行,两者的均值和差值见第4行和第5行。由于在飞行前已经实际测量过GNSS偏心矢量的初值,所以GNSS/IMU观测值中已经考虑了GNSS偏心矢量,这里的GNSS偏心矢量标定值是在飞机飞行过程中,由于各种因素引起的GNSS偏心矢量实际值相对于实验室标定值的变化量。如果初值为0,则标定的是GNSS偏心矢量的实际数值。由于IMU轴线是不可视的,安装在相机内部的IMU本身也是不可视的,所以视轴偏心角无法采用地面测量手段直接量测,初值为0,标定值是IMU视轴偏心角的实际数值。GNSS偏心矢量(u,v,w)单位是m,IMU视轴偏心角(ex, ey, ez)单位是度。
| 试验数据 | u/m | v/m | w/m | ex/(°) | ey/(°) | ez/(°) |
| 试验数据A | 0.008 934 454 33 | 0.007 232 732 39 | -0.028 659 779 41 | -0.080 022 701 87 | -0.053 075 547 49 | -0.016 461 199 89 |
| 试验数据B | 0.006 185 773 2 | 0.004 649 604 61 | -0.003 878 048 95 | -0.072 276 851 80 | -0.077 858 618 04 | -0.018 734 542 98 |
| 平均值 | 0.007 560 113 7 | 0.005 941 168 5 | -0.016 268 914 18 | -0.076 149 776 83 | -0.065 467 082 76 | -0.017 597 871 43 |
| 差值 | 0.002 748 681 13 | 0.002 583 127 78 | -0.024 781 730 46 | -0.007 745 850 07 | 0.024 783 070 55 | 0.002 273 343 09 |
从表 3可以看出,试验数据A和试验数据B的GNSS偏心矢量标定值和IMU视轴偏心角的标定数值是基本一致的,其中3个GNSS偏心矢量标定值差异更小,表明GNSS偏心矢量标定值和IMU视轴偏心角的标定结果比较稳定。
为验证GNSS偏心矢量和IMU视轴偏心角标定值的适用性,利用表 3中第4行GNSS偏心矢量和IMU视轴偏心角标定平均值对试验数据A和试验数据B的GNSS/IMU测量值进行改正,得到试验数据A和试验数据B的GNSS/IMU改正值。同时对两组数据对应的前/下/后视CCD探元位置标定值进行计算,取每一探元的位置平均值作为标定值,得到前/下/后视CCD探元位置标定文件。采用GNSS/IMU改正值和CCD探元位置标定文件,对试验数据A和试验数据B进行直接定位试验,结果见表 4。
| m | ||||||||||||||
| 试验内容 | X方位定位精度 | Y方位定位精度 | Z方位定位精度 | |||||||||||
| 最大值 | 最小值 | 均值 | 中误差 | 最大值 | 最小值 | 均值 | 中误差 | 最大值 | 最小值 | 均值 | 中误差 | |||
| 试验数据A | 0.712 | -0.957 | -0.015 | 0.367 | 0.839 | -0.943 | 0.032 | 0.467 | 1.613 | -1.557 | -0.136 | 0.765 | ||
| 试验数据B | 0.903 | -0.206 | 0.205 | 0.513 | 0.624 | -0.406 | 0.189 | 0.392 | 1.567 | -1.722 | -0.092 | 0.732 | ||
将表 4与表 1、表 2中的试验结果进行对比分析可以看出,利用GNSS偏心矢量和IMU视轴偏心角平均标定值和CCD探元位置标定文件对试验数据A和B进行直接定位,直接定位的精度仍然有很大提高。这说明通过两组试验获得的GNSS偏心矢量和IMU视轴偏心角平均标定值是稳定的,具有很好的适用性,利用这两者的标定值对GNSS/IMU测量值进行改正,可以显著提高GFXJ相机的直接定位精度。
以试验数据A的GNSS/IMU改正值和前/下/后视CCD探元位置标定文件为基础,利用少量控制点对试验数据A再次进行区域网平差。表 5列出了采用不同数量的控制点,试验数据A再次区域网平差后的定位精度,统计精度是检查点的定位精度。
| m | ||||||||||||||
| GCP 数目 | X方位定位精度 | Y方位定位精度 | Z方位定位精度 | |||||||||||
| 最大值 | 最小值 | 均值 | 中误差 | 最大值 | 最小值 | 均值 | 中误差 | 最大值 | 最小值 | 均值 | 中误差 | |||
| 3 | 0.672 | -0.827 | -0.010 | 0.337 | 0.789 | -0.953 | 0.027 | 0.432 | 1.526 | -1.425 | -0.121 | 0.689 | ||
| 5 | 0.654 | -0.669 | -0.008 | 0.301 | 0.618 | -0.678 | 0.008 | 0.348 | 1.423 | -1.520 | 0.080 | 0.632 | ||
| 7 | 0.642 | -0.513 | -0.008 | 0.256 | 0.423 | -0.552 | 0.008 | 0.247 | 1.396 | -1.489 | 0.078 | 0.598 | ||
| 9 | 0.643 | -0.512 | -0.007 | 0.223 | 0.411 | -0.523 | 0.007 | 0.234 | 1.385 | -1.490 | 0.070 | 0.587 | ||
| 11 | 0.641 | -0.511 | -0.007 | 0.221 | 0.401 | -0.521 | 0.007 | 0.223 | 1.390 | -1.467 | 0.069 | 0.581 | ||
以试验数据B的GNSS/IMU改正值和前/下/后视CCD探元位置标定文件为基础,利用少量控制点对试验数据B再次进行区域网平差。表 6列出了采用不同数量的控制点,试验数据B再次区域网平差后的定位精度,统计精度是检查点的定位精度。
| m | ||||||||||||||
| GCP 数目 | X方位定位精度 | Y方位定位精度 | Z方位定位精度 | |||||||||||
| 最大值 | 最小值 | 均值 | 中误差 | 最大值 | 最小值 | 均值 | 中误差 | 最大值 | 最小值 | 均值 | 中误差 | |||
| 3 | 0.901 | -0.189 | 0.185 | 0.478 | 0.609 | -0.386 | 0.181 | 0.347 | 1.426 | -1.567 | -0.068 | 0.652 | ||
| 5 | 0.680 | -0.167 | 0.112 | 0.389 | 0.467 | -0.312 | 0.121 | 0.264 | 1.320 | -1.212 | -0.045 | 0.517 | ||
| 7 | 0.668 | -0.152 | 0.078 | 0.292 | 0.361 | -0.289 | 0.082 | 0.173 | 1.239 | -0.921 | 0.042 | 0.469 | ||
| 9 | 0.589 | -0.149 | 0.032 | 0.230 | 0.356 | -0.223 | 0.032 | 0.151 | 1.238 | -0.822 | 0.040 | 0.422 | ||
| 11 | 0.529 | -0.145 | 0.022 | 0.209 | 0.343 | -0.214 | 0.033 | 0.143 | 1.235 | -0.815 | 0.041 | 0.418 | ||
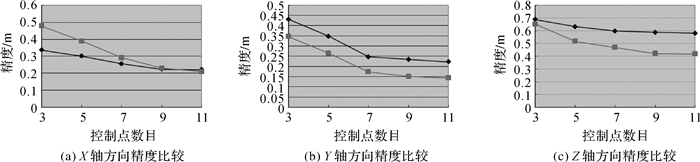
将表 5和表 6中的试验结果,绘图显示在图 14,菱形节点标识线代表试验数据A的试验结果,方形节点标识线代表试验数据B的试验结果。图 14(a)显示了试验数据A和B在X方向,中误差误差随着控制点数目增多的精度变化,图 14(b)显示了Y方向的定位精度变化,图 14(c)显示了Z方向的定位精度变化。
|
| 图 14 试验数据A和B再次区域网平差精度比较 Fig. 14 Accuracy comparison for reblock adjustment for dataset A and B |
从图 14中可以看出,在GNSS/IMU改正值和前/下/后视CCD探元位置标定文件的基础上,采用少量控制点就能显著提高GFXJ相机的直接定位精度。随着控制点数目的增多,定位精度基本趋于稳定。该试验区域为丘陵地、山地相间类型,其中丘陵地占60%~70%,其余为山地。参考国家测绘局颁布的《数字航空摄影测量空中三角测量规范》[25](表 7),以丘陵地貌为标准进行分析。从表 5和表 6可以看出(以11个控制点为例),对比规范要求,数据A和数据B平面精度均可满足1:1000地形图测图的空中三角测量精度要求(0.5 m),高程精度还达不到1:1000地形图测图的空中三角测量精度要求(0.4 m),其中数据A(0.581 m)有一定差距,数据B(0.418 m)非常接近。
| m | |||||||||
| 成图比例尺 | 平面位置中误差 | 高程中误差 | |||||||
| 平地 | 丘陵地 | 山地 | 高山地 | 平地 | 丘陵地 | 山地 | 高山地 | ||
| 1:1000 | 0.5 | 0.5 | 0.7 | 0.7 | 0.28 (0.15) | 0.4 | 0.6 | 1.2 | |
| 1:2000 | 1.0 | 1.0 | 1.4 | 1.4 | 0.28 (0.15) | 0.4 | 1.0 | 1.5 | |
| 1:5000 | 1.75 | 1.75 | 2.5 | 2.5 | 0.3 | 1.0 | 2.0 | 2.5 | |
6 总结
本文的创新点是首创性地对国内自主研制的机载三线阵CCD相机的GNSS偏心矢量和IMU视轴偏心角标定技术进行了探索和研究,建立了具体的标定模型,提出了详细的标定方案。针对GFXJ的具体成像特点,分析、建立了GFXJ相机的GNSS偏心矢量标定模型和IMU视轴偏心角标定模型,并结合实际研究工作,提出了具体可行的GNSS偏心矢量和IMU视轴偏心角循环两步法标定方案。试验结果证实,本文提出的标定模型对于国产GFXJ相机是正确有效的,GNSS偏心矢量和IMU视轴偏心角的标定数值可以作为合格可靠的标定结果提供给后续用户使用,同时本文提出的标定方法和研究成果对于国产其他航测相机的几何标定研究具有一定的参考价值。
通过系列试验研究和分析,得出以下几点结论:①在未经区域网平差和标定处理前,GFXJ的直接定位误差存在明显的系统性,有必要采用区域网平差和标定技术对系统误差进行处理;②GNSS偏心矢量和IMU视轴偏心角引起的变形误差表现出明显的系统性,是不可忽视的几何变形误差源之一,必须予以标定;③GNSS偏心矢量和IMU视轴偏心角引起的误差主要影响平面方面的几何定位精度,对高程定位精度也有影响,相机镜头畸变和CCD变形等几何参数的综合影响主要影响高程定位精度,对平面定位精度影响次之;④本文提出的循环二步法标定方案是可靠可行的,针对不同组试验数据采用该标定方案获得的GNSS偏心矢量和IMU视轴偏心角标定值数值稳定,变化一致,具有很好的可参考性,可提供给该相机的其他飞行数据处理使用;⑤国产GFXJ相机是国内首台机载三线阵CCD相机,通过多次飞行试验验证该相机具备很好的立体测绘性能。采用本文方法,经GNSS/IMU测量值改正和前/下/后视CCD探元位置标定后,以此为基础,利用少量控制点进行区域网平差,即可显著提高GFXJ影像的立体定位精度。在2000 m飞行高度上,平面定位精度可满足1:1000地形图测图的空中三角测量精度要求,高程精度也比较接近指标。目前该款相机仍在校飞阶段,定型后几何性能有望进一步提高。后期针对不同地形区域还会进行标定试飞和应用试飞,通过更多的实际标定测试,本文提出的标定模型和方案可以得到进一步验证和完善。
| [1] |
王任享, 胡莘, 王新义, 等.
"天绘一号"卫星工程建设与应用[J]. 遥感学报, 2012, 16(S1): 2–5.
WANG Renxiang, HU Xin, WANG Xinyi, et al. The Construction and Application of Mapping Satellite-1 Engineering[J]. Journal of Remote Sensing, 2012, 16(S1): 2–5. DOI:10.11834/jrs.20120001 |
| [2] |
王任享, 胡莘, 王建荣.
天绘一号无地面控制点摄影测量[J]. 测绘学报, 2013, 42(1): 1–5.
WANG Renxiang, HU Xin, WANG Jianrong. Photogrammetry of Mapping Satellite-1 Without Ground Control Points[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 1–5. |
| [3] |
王密, 杨博, 李德仁, 等.
资源三号全国无控制整体区域网平差关键技术及应用[J]. 武汉大学学报(信息科学版), 2017, 42(4): 427–433.
WANG Mi, YANG Bo, LI Deren, et al. Technologies and Applications of Block Adjustment Without Control for ZY-3 Images Covering China[J]. Geomatics and Information Science of Wuhan University, 2017, 42(4): 427–433. |
| [4] | TANG Xinming, ZHOU Ping, ZHANG Guo, et al. Verification of ZY-3 Satellite Imagery Geometric Accuracy Without Ground Control Points[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(10): 2100–2104. DOI:10.1109/LGRS.2015.2450251 |
| [5] | SANDAU R, BRAUNECKER B, DRIESCHER H, et al. ADS40 Calibration and Verification Process[C]//Proceedings of the 6th Conference on "Optical 3D Measurement Techniques". Zurich: [s.n.], 2003. |
| [6] | HINSKEN L, MILLER S, TEMPELMANN U, et al. Triangulation of LH Systems' ADS40 Imagery Using ORIMA GPS/IMU[J]. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2002, 34: 156–162. |
| [7] | SANDAU R, BRAUNECKER B, DRIESCHER H, et al. Design Principles of the LH Systems ADS40 Airborne Digital Sensor[C]//International Archives of Photogrammetry and Remote Sensing. Amsterdam: ISPRS, 2000: 258-265. |
| [8] | KOCAMAN S, ZHANG L, GRUEN A. Self-calibrating Triangulation of Airborne Linear Array CCD Cameras[C]//Euro COW 2006 International Calibration and Orientation Workshop. Castelldefels: [s.n.], 2006. |
| [9] | BIGNONE F. Processing of Stereo Scanner: From Stereo Plotter to Pixel Factory[C]//Photogrammetric Week 2003. Stuttgart, Germany: [s.n.], 2003. |
| [10] | Gruen A, Zhang Li. Sensor Modeling for Aerial Triangulation with Three-line-scanner (TLS) Imagery[C]//International Archives of Photogrammetry and Remote Sensing. Xi'an: IAPRS, 2002. |
| [11] | POLI D. General Model for Airborne and Spaceborne Linear Array Sensors[C]//International Archives of Photogrammetry and Remote Sensing. Denver: IAPRS, 2012: 177-182. |
| [12] |
袁修孝, 杨芬, 赵青, 等.
机载POS系统视准轴误差检校[J]. 武汉大学学报(信息科学版), 2006, 31(12): 1039–1043.
YUAN Xiuxiao, YANG Fen, ZHAO Qing, et al. Boresight Misalignment Calibration of Integrated DGPS/IMU System[J]. Geomatics and Information Science of Wuhan University, 2006, 31(12): 1039–1043. |
| [13] |
袁修孝.
一种补偿POS定位测姿系统误差的新方法[J]. 自然科学进展, 2008, 18(8): 925–934.
YUAN Xiuxiao. A New Method Compensating POS Positionng and Attitude Measurement Systematic Error[J]. Progress in Natural Science, 2008, 18(8): 925–934. |
| [14] |
李德仁, 赵双明, 陆宇红, 等.
机载三线阵传感器影像区域网联合平差[J]. 测绘学报, 2007, 36(3): 245–250.
LI Deren, ZHAO Shuangming, LU Yuhong, et al. Combined Block Adjustment for Airborne Three-line CCD Scanner Images[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 245–250. DOI:10.3321/j.issn:1001-1595.2007.03.001 |
| [15] |
赵双明, 李德仁.
ADS40机载数字传感器平差数学模型及其试验[J]. 测绘学报, 2006, 35(4): 342–346.
ZHAO Shuangming, LI Deren. Experimentation of Adjustment Math Model for ADS40 Sensor[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(4): 342–346. DOI:10.3321/j.issn:1001-1595.2006.04.009 |
| [16] |
刘军. GPS/IMU辅助机载线阵CCD影像定位技术研究[D].郑州: 信息工程大学, 2007. LIU Jun. A Study on the Positioning Theory of Airborne Line CCD Imagery Supported by GPS/IMU[D]. Zheng zhou: Information Engineering University, 2007. |
| [17] |
涂辛茹, 许妙忠, 刘丽.
机载三线阵传感器ADS40的几何检校[J]. 测绘学报, 2011, 40(1): 78–83.
TU Xinru, XU Miaozhong, LIU Li. The Geometric Calibration of Airborne Three-line-scanner ADS40[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 78–83. |
| [18] |
王冬红.机载数字传感器几何标定的模型与算法研究[D].郑州: 信息工程大学, 2011. WANG Donghong. A Study on the Mathematic Model and Algorithm of the Geometric Calibration of Airborne Digital Sensor[D]. Zhengzhou: Information Engineering University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-90008-1012325172.htm |
| [19] |
王涛, 张永生, 张艳, 等.
基于自检校的机载线阵CCD传感器几何标定[J]. 测绘学报, 2012, 41(3): 393–400.
WANG Tao, ZHANG Yongsheng, ZHANG Yan, et al. Airborne Linear CCD Sensor Geometric Calibration Based on Self-calibration[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 393–400. |
| [20] |
王涛.线阵CCD传感器实验场几何定标的理论与方法研究[D].郑州: 信息工程大学, 2012. WANG Tao. Study on Theories and Methods of Linear CCD Sensor Geometric Calibration Based on Field[D]. Zhengzhou: Information Engineering University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-90005-1013161424.htm |
| [21] |
王涛, 张艳, 潘申林, 等.
机载三线阵CCD影像自检校光束法区域网平差[J]. 武汉大学学报(信息科学版), 2012, 37(9): 1073–1077.
WANG Tao, ZHANG Yan, PAN Shenlin, et al. Airborne Three-line-scanner CCD Imagery Self-calibration Block Adjustment[J]. Geomatics and Information Science of Wuhan University, 2012, 37(9): 1073–1077. |
| [22] |
袁修孝.
GPS辅助空中三角测量原理及应用[M]. 北京: 测绘出版社, 2001.
YUAN Xiuxiao. GPS-aided Aerial Block Adjustment Principle and Application[M]. Beijing: Surveying and Mapping Publishing House, 2001. |
| [23] |
许妙忠, 尹粟, 李振涛.航空几何定标场建设技术研究[C]//Aisa GIS 2010 International Conference. Taiwan, China: [s.n.], 2010 XU Miaozhong, YIN Su, LI Zhentao. Aerial Geomatic Calibratation Building Technology Research[C]//Aisa GIS 2010 International Conference. Taiwan, China: [s.n.], 2010. |
| [24] |
张永生.
高分辨率遥感测绘嵩山实验场的设计与实现——兼论航空航天遥感定位精度与可靠性的基地化验证方法[J]. 测绘科学技术学报, 2012, 29(2): 79–82.
ZHANG Yongsheng. Design and Implementation of Songshan Test Field for High Resolution Remote Sensing and Mapping[J]. Journal of Geomatics Science and Technology, 2012, 29(2): 79–82. DOI:10.3969/j.issn.1673-6338.2012.02.001 |
| [25] |
国家测绘局. GB/T 23236-2009数字航空摄影测量空中三角测量规范[S].北京: 中国标准出版社, 2009. State Bureau of Surveying and Mapping. GB/T 23236-2009 Specifications for Aerotriangulation of Digital Aerophotogrammetry[S]. Beijing: China Standards Press, 2009. |


