2. 重庆大学光电技术与系统教育部重点实验室, 重庆 400044;
3. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079;
4. 中国兵器工业集团北方信息控制研究院集团有限公司, 江苏 南京 211153;
5. 武汉大学测绘学院, 湖北 武汉 430079
2. Key Laboratory of Optoelectronic Technology and Systems of the Ministry of Education of China, Chongqing University, Chongqing 400044, China;
3. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
4. North Information Control Research Academy Group Co. Ltd., Nanjing 211153, China;
5. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
自20世纪末文献[1]首次提出精密单点定位技术(precise point positioning,PPP),PPP技术便成为GNSS领域中的一大研究热点。PPP技术无需地面基准站,具有更大的作业覆盖范围,可直接获得国际地球参考框架(ITRF)下的高精度测站坐标,是继RTK和网络RTK技术后出现的又一次技术革命。但在实际运用中,PPP往往会因障碍物的遮挡、接收机的运动、到达接收机处卫星信号的信噪比低、接收机或卫星的故障等原因而发生周跳[2]。若连续跟踪卫星少于5颗,则PPP在定位处理中需要数十分钟才能重新收敛到分米至厘米级定位精度[3]。因此,精确地探测与修复周跳有利于提高PPP重收敛速度,是PPP实际工程应用中的关键技术问题。
近年来,国内外不少学者针对周跳探测与识别问题提出了很多解决方案。这些方案能被归纳为以下4类:非差模型、双差模型、三频模型及外部器件辅助模型[4]。由于双差模型[5]主要针对DGPS,不适用于PPP;三频模型[6-8]以传输三频信号的卫星和接收三频信号的接收机为条件,并非现今工程运用中的主流;因此,非差模型和外部器件辅助模型成为国内外不少学者解决PPP周跳探测与修复的切入点。
在非差模型方面,文献[9]提出的TurboEdit方法首次融合了GF组合和MW组合去探测和修复周跳,并成功运用于GIPSY[10]、Bernese[11]等商业软件中;之后,文献[12-13]针对电离层快速变化的情况,提出了改进的TurboEdit方法。此外,文献[14]针对历元间差分模型,将周跳量引入方程作为参数估计,以实现实时PPP周跳瞬时校正;文献[15]通过预报的电离层延迟信息以实现PPP宽巷模糊度的快速固定;文献[16]运用MW组合和GF组合,提出了一种适用于实时PPP周跳探测与修复的策略;文献[17]则通过预测电离层延迟变化,提出了WL-L3-LX分级方法处理周跳。文献[18-19]将相对伪距而言精度较高的多普勒观测值用于周跳探测。以上这些方法,大都结合了MW组合。MW组合通过使用伪距和载波相位观测值,能有效探测出大周跳,但由于码伪距噪声及多路径误差的影响而不能有效探测出小周跳。
在外部器件辅助模型方面,借鉴于DGPS/INS组合中惯导信息被用于辅助GPS信号周跳探测与修复的思路[20-22],INS辅助PPP探测周跳成为了近几年一些学者的研究热点。其中,文献[23]首次发现,利用INS辅助PPP的宽巷与超宽巷相位组合,可实现周跳的探测与识别;文献[24]基于PPP/INS紧密组合模型,运用INS辅助PPP的无电离层组合与电离层残差组合联合求解,以实现周跳的探测与修复;文献[25]也运用INS辅助PPP去加快模糊度的收敛过程。
本文以PPP/INS组合为基础,利用INS短时高精度的位置信息,取代传统MW方法中伪距观测量,消除周跳探测中的几何位置关系,并通过星间差、相邻历元差、电离层延迟变化模型等方法,建立起INS辅助PPP的宽巷探测模型;通过与无几何距离(GF)组合方法相结合,实现对PPP双频等周周跳和特殊周跳(5/4、9/7等)的高精度探测。为了简化,本文所采用的双频组合为f1/f2,本方法也适用于f1/f3和f2/f3双频组合观测值的周跳探测。
1 PPP/INS组合模型对于PPP原始相位观测方程,当使用精密星历和精密钟差产品消除其卫星轨道误差和卫星钟差,并将其他系统误差如天线相位中心偏差、相位缠绕、相对论效应、固体潮、大洋负荷改正,以及地球自转等,采用模型改正后,相位观测方程可以写为
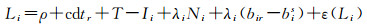 (1)
(1)
式中,Li表示原始相位观测值(单位为m);ρ表示自卫星信号发射时刻到信号到达接收机时刻接收机与卫星间的几何距离;c表示光速;dtr表示接收机钟差;T表示对流层延迟;Ii表示电离层延迟;λi和Ni分别表示波长和模糊度;(bir-bis)表示相位小数偏差;ε表示相位观测噪声及多路径误差;下标i表示频率。
在实际定位计算中,人们往往采用双频无电离层组合模型。该模型消除了电离层延迟低阶项,将接收机三维坐标、接收机钟差、对流层延迟和无电离层组合模糊度作为待估参数,并视相位小数偏差由模糊度吸收。无电离层组合模型可表示为
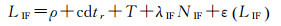 (2)
(2)
式中,下标IF表示无电离层组合。
PPP与INS紧密组合,由一个主滤波器对来自GPS接收机的原始测量数据和由INS估算的导航解进行融合。INS运用陀螺和加表测量数据进行捷联惯导计算,得到位置、速度、姿态等导航估算值,并结合精密星历与钟差产品,预测GPS伪距、载波和多普勒观测量;GPS利用误差模型与精密星历、钟差产品,校正伪距、载波和多普勒原始观测量,并将校正量与INS预测观测量之差作为卡尔曼滤波器的输入;经卡尔曼滤波融合处理,得到组合系统的误差状态估计并反馈至INS,一方面校正INS导航解并输出组合系统导航信息,另一方面补偿惯导传感器误差;此外,INS定位估算值也被用于辅助PPP进行周跳探测与修复,以增强组合系统的质量控制,如图 1所示。综合考虑系统性能和可观测性因素,建立包括15维INS误差状态和GPS误差状态的状态向量
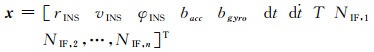 (3)
(3)

|
| 图 1 PPP/INS紧密组合模型框图 Fig. 1 Architecture of cascade SINS/GPS deeply integrated system |
式中,误差状态按顺序分别为INS位置误差、INS速度误差、INS失准角、加速度计零偏、陀螺零偏、接收机钟差、钟差变化率、天顶对流层湿延迟及无电离层组合模糊度。滤波器观测量则为INS估计的相位、伪距、多普勒与GPS观测值之差
 (4)
(4)
需要注意的是,伪距观测误差较大,因此只在初始化阶段使用。
2 周跳探测模型 2.1 INS辅助PPP的宽巷探测模型利用宽巷易于探测的特点,本文运用INS辅助PPP进行宽巷周跳探测(WL-INS)。其基本原理为:利用INS和精密星历提供的接收机与卫星高精度位置信息,消除宽巷中的站星几何位置关系;通过星间差和历元间差分别消除接收机钟差、对流层延迟误差、电离层延迟误差和模糊度等参数,形成仅包含周跳参数且具有较高精度的检测量。由式(1),宽巷组合测量方程可写为
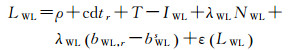 (5)
(5)
式中,下标WL表示宽巷组合。
首先,利用INS定位结果和IGS精密星历,估计星站几何位置ρINS,建立包括INS位置信息的宽巷组合观测量LWL-INS
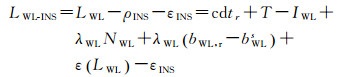 (6)
(6)
其次,选择合适的参考卫星进行星间差分,消除接收机钟差和接收机端宽巷相位小数偏差
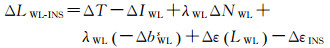 (7)
(7)
式中,Δ表示星间差。
最后,对连续的历元观测量作历元差分,消除模糊度。由于24 h内卫星端宽巷相位小数偏差非常稳定[26],故历元间差分便将卫星端宽巷相位小数偏差消除;对流层延迟干分量采用模型估计,湿分量固定为PPP最新估计结果,由于短期内对流层延迟具有较强的时间相关性[15],因此对流层延迟残差可以被忽略。影响周跳探测的一个重要因素是未模型化的电离层延迟,当电离层中的电离子含量平滑变化时,历元间差分可以消除电离层延迟[15];但当电离层变化较快及GPS信号长时间中断的情况时,历元间差分便无法消除电离层延迟,此时采用相对电离层模型的方法,将短时间内电离层延迟近似成线性变化[27],在无周跳或周跳修复成功的条件下,通过电离层残差组合获取滑动窗口内电离层变化δIi,进而预报当前历元时刻的电离层信息。由此可得双差相位宽巷组合观测方程
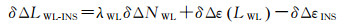 (8)
(8)
 (9)
(9)
式中,δ表示历元间差;δΔNWL为宽巷周跳;δΔε(LWL)为双差相位宽巷误差;δΔεINS为双差后的INS误差;δΔLWL-INS即为周跳探测的检测量DVWL-INS(decision variable, DV)。
2.2 无几何距离组合探测模型根据式(1)可得无几何距离组合(phase geometry free, GF组合)的载波相位观测值LGF
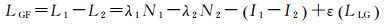 (10)
(10)
将前后两历元GF组合的载波相位观测值作差
 (11)
(11)
式(11)也被称为电离层残差。在一般情况下,电离层残差方法探测精度较高,但它对残余电离层误差敏感,即当电离层快速变化或GPS信号长时间中断的情况下时,其探测精度往往大大降低。此时同样采用相对电离层模型去估计下一历元时刻相位无几何距离组合估算值L′GF,以此削弱电离层变化带来的影响,其中电离层残差可写为
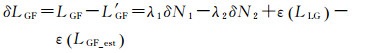 (12)
(12)
式中,δLGF即为检测量DVGF。
3 精度分析 3.1 WL-INS探测模型精度分析假定所有误差满足高斯分布,由误差传播律可得
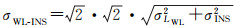 (13)
(13)
式中,σWL-INS表示INS辅助宽巷周跳检测量中误差;σINS表示惯导中误差;σLWL表示相位宽巷组合中误差
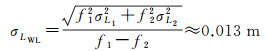 (14)
(14)
式中,f表示载波频率;σ表示载波相位观测值误差。
为实现单历元对最小1周的周跳探测,INS辅助宽巷周跳探测阈值TWL-INS应为宽巷波长的一半,本文取0.5 m作为WL-INS周跳探测阈值。当检测量DVWL-INS大于周跳探测阈值时,即认为此时发生了周跳。以3倍中误差为标准,INS辅助宽巷周跳检测量中误差应满足
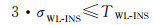 (15)
(15)
结合式(13)和式(14),可知惯导中误差σINS≤0.082 3 m。即当惯导单独定位精度在0.08 m以内时,惯导可有效辅助PPP宽巷周跳探测。
根据惯导误差传播方程[28-29],惯导独立导航期间位置中误差为
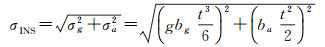 (16)
(16)
式中,σg为陀螺引起的位置中误差;σa为加速度计引起的位置中误差;g表示重力加速度;bg表示陀螺零偏;ba表示加速度计零偏;t为惯导独立导航时长。
以典型战术级IMU(陀螺零偏0.3(°)/h,加速度计零偏100 μg)为例,0.1 s、1 s和10 s独立导航时间内,惯导位置误差分别为5×10-6 m、5×10-4m和0.05 m,完全满足WL-INS周跳探测模型对惯导精度要求,且在短时间内,惯导误差远小于相位宽巷误差。因此,INS辅助PPP宽巷模型对周跳非常敏感,它不仅可以探测出小周跳,而且能在短时间内恢复很高精度的整数周跳,从而实现PPP快速重新初始化。但由于INS辅助PPP的宽巷探测周跳方法无法确定各个频率上的周跳,也无法探测双频等周周跳,因此本文将其与探测精度较高的GF组合方法相结合。
3.2 GF组合探测模型精度分析由误差传播律,GF组合载波相位观测值中误差为
 (17)
(17)
考虑到受残余大气层延迟误差、多路径误差和电离层模型误差等影响[19],一般取σGF=0.01~0.02 m。以3倍中误差为标准,取GF组合周跳检测量阈值TGF为0.05 m。当检测量DVGF大于周跳探测阈值时,即认为此时发生了周跳。
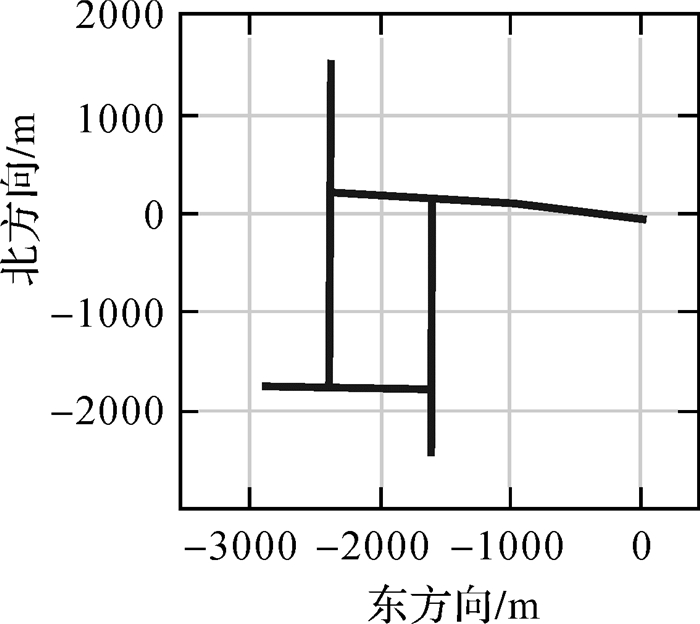
4 试验测试与分析本文试验采用的跑车数据采集于2013年7月2日,地点为北京郊外一段空旷地区,卫星观测条件较好,主要设备包括基站、流动站GNSS测地级接收机,以及某型国产光纤IMU。基站和流动站接收机采样率均为10 Hz,IMU采样率为200 Hz,陀螺零偏0.3°/h,加速度计零偏100 μg,总数据时长约为1.5 h,跑车平面轨迹如图 2所示。本文使用流动站GPS和IMU数据实施PPP/INS组合及周跳探测试验;使用基站数据作双差处理(星间差、站间差),固定流动站L1、L2模糊度,获得对应的宽巷周跳并作为INS辅助PPP周跳探测参考值。在整个测量过程中,PRN03号卫星仰角均在70°以上,且未发生周跳,故被选作为参考卫星。
|
| 图 2 跑车平面轨迹 Fig. 2 Plane trajectory of the car |
4.1 模拟周跳试验
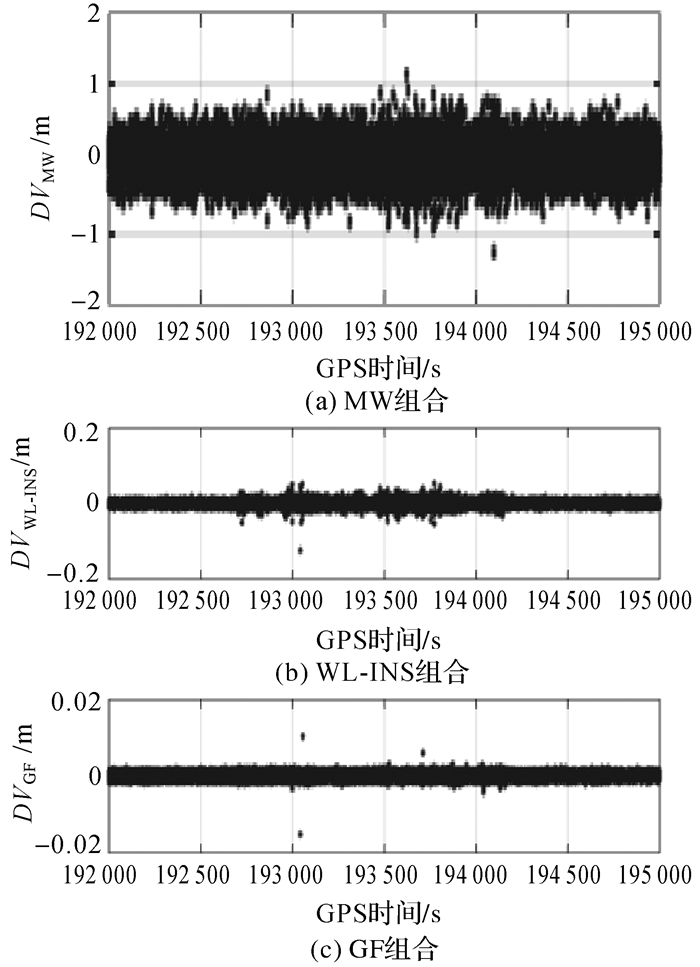
MW组合、WL-INS组合和GF组合检测量DV及其统计量分别如图 3和表 1所示。其中MW组合由于引入了观测误差较大的测距码观测量,其探测精度较低,周跳检测量数值范围达±100 cm,标准差为15.3 cm;INS辅助宽巷组合采用了较测距码精度要高INS位置信息,其检测量精度得到大幅度提高,基本在±2 cm以内,检测量标准差为0.61 cm;GF组合由于仅使用相位观测量,其探测精度最高,基本保持在±0.2 cm以内。在整个测试周期内,PRN23号卫星的周跳检测量均未发现明显变化,表明该颗卫星没有发生周跳。
|
| 图 3 PRN23号卫星各组合检测量变化 Fig. 3 DVs for PRN23 |
| m | ||
| PRN23号卫星 | 平均值 | 标准差 |
| DVMW | 0.000 001 76 | 0.153 0 |
| DVWL-INS | 0.000 202 28 | 0.006 1 |
| DVGF | 0.000 058 77 | 0.000 7 |
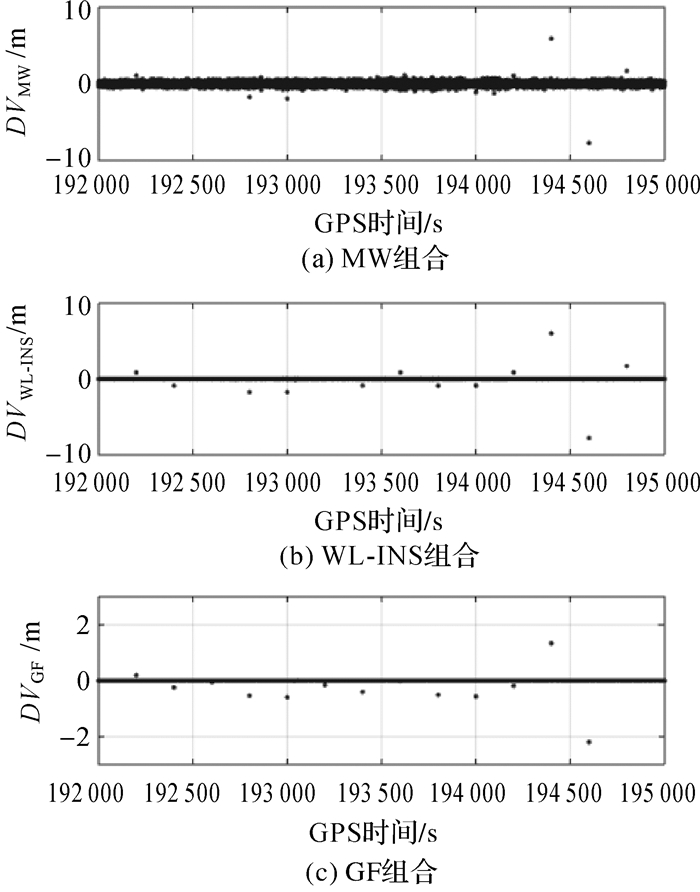
对上述PRN23号卫星人为引入等时间间隔(即200 s)的14组周跳,使用MW组合、WL-INS组合和GF组合方法分别进行周跳探测,模拟周跳数值及检测量变化分别如表 2和图 4所示。其中MW组合周跳检测量噪声为
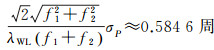 [12]
[12]
|
| 图 4 加入模拟周跳后PRN23号卫星各检测量变化 Fig. 4 DVs for PRN23 with simulated cycle slips |
| GPS时间 /s | L1上 | L2上 | MW | WL-INS | GF | ||||||
| 引入周跳数 | 引入周跳数 | m | 周 | m | 周 | m | |||||
| 192 200 | 1 | 0 | 1.071 50* | 1.243* | 0.863 36 | 1.002 | 0.190 27 | ||||
| 192 400 | 0 | 1 | -0.477 95* | -0.554* | -0.857 08 | -0.994 | -0.242 76 | ||||
| 192 600 | 1 | 1 | 0.135 13* | 0.157* | -0.000 18* | 0.000* | -0.054 76 | ||||
| 192 800 | 1 | 3 | -1.732 55 | -2.009 | -1.727 27 | -2.004 | -0.542 81 | ||||
| 193 000 | 2 | 4 | -1.970 12 | -2.286 | -1.722 32 | -1.998 | -0.595 43 | ||||
| 193 200 | 3 | 3 | 0.164 82* | 0.191* | 0.004 54* | 0.005* | -0.161 37 | ||||
| 193 400 | 3 | 4 | -0.530 27* | -0.615* | -0.853 04 | -0.990 | -0.405 73 | ||||
| 193 600 | 5 | 4 | 0.586 92* | 0.681* | 0.869 82 | 1.010 | -0.025 01* | ||||
| 193 800 | 5 | 6 | -0.483 36* | -0.561* | -0.865 57 | -1.004 | -0.512 96 | ||||
| 194 000 | 6 | 7 | -1.115 26* | -1.294* | -0.860 62 | -0.998 | -0.567 47 | ||||
| 194 200 | 8 | 7 | 1.046 95* | 1.215* | 0.874 80 | 1.015 | -0.185 88 | ||||
| 194 400 | 7 | 0 | 5.906 12 | 6.852 | 6.036 52 | 7.003 | 1.332 9 | ||||
| 194 600 | 0 | 9 | -7.728 76 | -8.966 | -7.756 17 | -8.998 | -2.198 23 | ||||
| 194 800 | 9 | 7 | 1.671 30 | 1.934 | 1.722 34 | 1.998 | 0.003 76* | ||||
| 注:*号标记为未探测出周跳处。 | |||||||||||
式中,σP表示码误差噪声中误差。以3倍中误差为标准,MW组合周跳检测量阈值TMW取为1.5 m。由表 2和图 4可知:
(1) MW组合方法因采用了随机误差较大的码数据,对小周跳不太灵敏,宽巷小周跳(如0/1、3/4、5/4、5/6等)和双频等周周跳(如1/1、3/3等)淹没在系统噪声中,且部分检测量(如2/4、7/0等)的小数周部分数值过大,不利于后续修复周跳。
(2) WL-INS组合方法探测精度较高,对宽巷小周跳非常敏感,且检测量的整数性明显较MW组合要好,有利于后续修复周跳以及快速恢复模糊度,但WL-INS方法无法探测双频等周周跳(如1/1、3/3等)。
(3) GF组合方法探测精度较高,能探测出绝大多数大小周跳以及双频等周周跳,但对于特殊组合周跳(如5/4、9/7等)则无法有效探测。
因此,综合WL-INS组合和GF组合方法,可以实现此两种方法的优势互补,进而成为一种探测精度高的周跳探测方法。
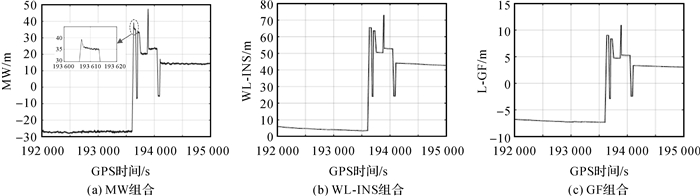
4.2 实测周跳试验以PRN07号卫星为例,图 5为PRN07号卫星的MW组合、WL-INS和GF组合观测量的变化图。
|
| 图 5 PRN07号卫星各组合观测值变化图 Fig. 5 Observed values for PRN07 |
从原始数据分析和图形变化可以发现:在测试期间,PRN07号卫星信号一共发生了8处数据中断(中断时长详见表 3)。在卫星连续观测区间内,WL-INS组合和GF组合观测量连续变化且波动较小,但因受电离层等延迟影响,出现趋势化漂移现象;相比之下,MW组合观测量无漂移现象,但受码随机误差影响,数值波动比较大;当信号中断并重新捕获后,MW组合、WL-INS组合和GF组合观测量均发生跳变,但WL-INS组合和GF组合观测量在跳变后仍然保持平稳,而MW组合观测量则出现明显的“毛刺”现象,说明接收机在重新捕获信号后短时间内有明显观测偏差。
| GPS时间 /s | 中断时长 /s | MW | WL-INS | GF /m | 宽巷周跳参考值 /周 | |||
| m | 周 | m | 周 | |||||
| 193632.8 | 28.8 | 66.342 21 | 76.972 | 62.062 91 | 72.007 | 16.392 29 | 72 | |
| 193684.8 | 18.2 | -41.872 93 | -48.582 | -41.425 77 | -48.063 | -11.891 22 | -48 | |
| 193704.0 | 5.8 | 40.682 62 | 47.201 | 39.654 98 | 46.009 | 11.253 03 | 46 | |
| 193756.4 | 23.4 | -12.277 60 | -14.245 | -13.085 69 | -15.182 | -3.637 93 | -15 | |
| 193887.6 | 13.0 | 27.306 72 | 31.682 | 22.551 78 | 26.165 | 6.198 71 | 未固定 | |
| 193893.6 | 3.2 | -17.965 54 | -20.844 | -19.803 74 | -22.977 | -5.616 25 | 3 | |
| 194067.2 | 18.8 | -29.215 84 | -33.897 | -28.561 93 | -33.138 | -7.712 26 | -33 | |
| 194104.2 | 10.6 | 22.517 01 | 26.125 | 19.797 34 | 22.969 | 5.766 44 | 23 | |
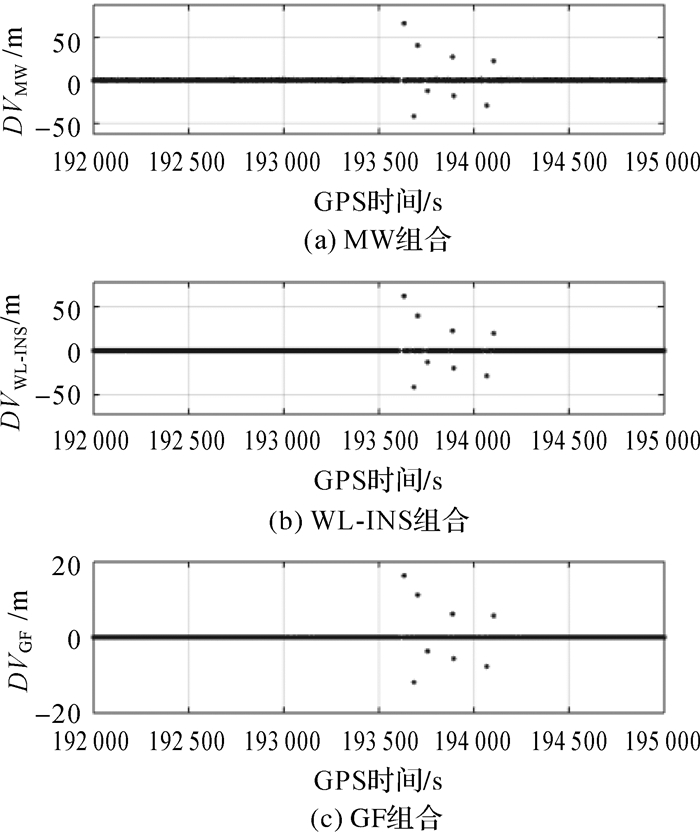
图 6为MW组合、WL-INS组合与GF组合3种周跳检测量随时间的变化。表 3则给出了各检测量数值、相应宽巷周跳数,以及宽巷周跳参考值。由于实际发生的周跳较大,上述方法均能有效探测出周跳。将WL-INS与MW组合方法所探测出的宽巷周跳数与宽巷周跳参考值作对比,可以发现:
|
| 图 6 PRN07号卫星的各组合检测量 Fig. 6 DVs for PRN07 |
(1) MW组合方法未能成功求解所有实际周跳,这是由于当接收机信号中断并重新捕获后,短期内码观测误差较大,需要经过一段时间收敛到稳定状态,导致MW观测量出现如图 5(a)所示“毛刺”现象。此时若运用MW方法进行处理,它将无法避免“毛刺”的影响,求解周跳错误。
(2) WL-INS组合方法不受初始捕获阶段较大观测误差的影响,对所有的实际周跳均能成功求解出,且取整精度较高。
需要说明的是,在运用双差方法固定模糊度的过程中,193 887.6 s与193 893.6 s两个历元时刻PRN07号卫星均发生周跳。由于时间间隔短,导致前者模糊度无法被固定,而后者模糊度实现了固定,此时检测出193 893.6 s的宽巷周跳为两者周跳之和。此外,本文中所采用的陀螺零偏为0.3(°)/h,加速度计零偏为100 μg,由式(16)可得,惯导辅助PPP周跳探测的有效时间约为13 s。
5 结论本文针对PPP/INS组合中载波相位周跳探测问题,提出了一种INS辅助PPP周跳探测的新策略。将INS高精度位置信息引入到宽巷组合中,消除其中的站星几何位置关系,并综合运用星间差分、历元间差分的方法,实现INS辅助的宽巷组合周跳探测方法。通过模拟周跳与实测数据表明,WL-INS方法克服了传统MW方法受码误差、多路径等因素影响的不足,能识别各种宽巷小周跳;针对WL-INS方法无法探测等周周跳的问题,提出综合运用GF组合和WL-INS组合方法,弥补各自的探测盲点,实现高精度周跳探测的目的。此外,WL-INS方法仅利用周跳前后两个历元的观测值进行处理,可实现实时单历元周跳探测。
惯导累积误差是影响WL-INS方法探测精度的主要因素之一,在PPP连续定位条件下,即使部分卫星出现信号中断,惯导受GPS连续校正,惯导累积误差影响可以被忽略;在GPS信号全部中断条件下,惯导单独进行定位,其误差会随时间显著增加,导致WL-INS方法探测精度降低,但由于宽巷波长比较长,在惯导辅助PPP周跳探测的有效时间内,WL-INS辅助周跳方法仍然有效。
| [1] | ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research:Solid Earth, 1997, 102(B3): 5005–5017. DOI:10.1029/96JB03860 |
| [2] |
李征航, 张小红.
卫星导航定位新技术及高精度数据处理方法[M]. 武汉: 武汉大学出版社, 2009.
LI Zhenghang, ZHANG Xiaohong. New Techniques and Precise Data Processing Methods of Satellite Navigation and Positioning[M]. Wuhan: Wuhan University Press, 2009. |
| [3] | BISNATH S, GAO Y. Current State of Precise Point Positioning and Future Prospects and Limitations[M]//SIDERIS M G. Observing Our Changing Earth. Berlin Heidelberg: Springer, 2009: 615-623. |
| [4] | CHEN Dezhong, YE Shirong, ZHOU Wei, et al. A Double-differenced Cycle Slip Detection and Repair Method for GNSS CORS Network[J]. GPS Solutions, 2016, 20(3): 439–450. DOI:10.1007/s10291-015-0452-6 |
| [5] |
韩厚增, 王坚, 李增科.
GPS/INS紧组合的INS辅助周跳探测与修复[J]. 测绘学报, 2015, 44(8): 848–857.
HAN Houzeng, WANG Jian, LI Zengke. Inertial Aided Kinematic GPS Cycle Slip Detection and Correction for GPS/INS Tightly Coupled System[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(8): 848–857. DOI:10.11947/j.AGCS.2015.20140350 |
| [6] |
黄令勇, 翟国君, 欧阳永忠, 等.
三频GNSS电离层周跳处理[J]. 测绘学报, 2015, 44(7): 717–725.
HUANG Lingyong, ZHAI Guojun, OUYANG Yongzhong, et al. Ionospheric Cycle Slip Processing in Triple-frequency GNSS[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 717–725. DOI:10.11947/j.AGCS.2015.20140348 |
| [7] |
李金龙, 杨元喜, 徐君毅, 等.
基于伪距相位组合实时探测与修复GNSS三频非差观测数据周跳[J]. 测绘学报, 2011, 40(6): 717–722.
LI Jinlong, YANG Yuanxi, XU Junyi, et al. Real-time Cycle-slip Detection and Repair Based on Code-phase Combinations for GNSS Triple-frequency Undifferenced Observations[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 717–722. |
| [8] |
黄令勇, 翟国君, 欧阳永忠, 等.
削弱电离层影响的三频TurboEdit周跳处理方法[J]. 测绘学报, 2015, 44(8): 840–847, 883.
HUANG Lingyong, ZHAI Guojun, OUYANG Yongzhong, et al. Triple-frequency TurboEdit Cycle-slip Processing Method of Weakening Ionospheric Activity[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(8): 840–847, 883. DOI:10.11947/j.AGCS.2015.20140380 |
| [9] | BLEWITT G. An Automatic Editing Algorithm for GPS Data[J]. Geophysical Research Letters, 1990, 17(3): 199–202. DOI:10.1029/GL017i003p00199 |
| [10] | LICHTEN S M, BAR-SEVER Y E, BERTIGER E I, et al. GIPSY-OASIS Ⅱ: A High Precision GPS Data Processing System and General Orbit Analysis Tool, Technology 2006[C]//NASA Technology Transfer Conference, Chicago, IL, 24-26 October 1995. Chicago, IL: NASA, 1995. |
| [11] |
郑作亚.
Bernese GPS4.2版本数据处理软件的介绍与探讨[J]. 中国科学院上海天文台年刊, 2003(24): 143–149.
ZHENG Zuoya. The Introduction and Discussion on Bernese GPS Software Version 4.2[J]. Annals of Shanghai Observatory Academia Sinica, 2003(24): 143–149. |
| [12] | LIU Zhizhao. A New Automated Cycle Slip Detection and Repair Method for a Single Dual-frequency GPS Receiver[J]. Journal of Geodesy, 2011, 85(3): 171–183. DOI:10.1007/s00190-010-0426-y |
| [13] | CAI Changsheng, LIU Zhihzao, XIA Pengfei, et al. Cycle Slip Detection and Repair for Undifferenced GPS Observations Under High Ionospheric Activity[J]. GPS Solutions, 2013, 17(2): 247–260. DOI:10.1007/s10291-012-0275-7 |
| [14] | BANVILLE S, LANGLEY R B. Improving Real-time Kinematic PPP with Instantaneous Cycle-slip Correction[C]//Proceedings of ION GNSS. Savannah, GA: [s.n.], 2009: 2470-2478. |
| [15] | GENG Jianghui, MENG Xiaolin, DODSON A H, et al. Rapid Re-convergences to Ambiguity-fixed Solutions in Precise Point Positioning[J]. Journal of Geodesy, 2010, 84(12): 705–714. DOI:10.1007/s00190-010-0404-4 |
| [16] |
易重海, 朱建军, 陈永奇, 等.
实时精密单点定位中周跳探测与修复的算法研究[J]. 武汉大学学报(信息科学版), 2011, 36(11): 1314–1319.
YI Zhonghai, ZHU Jianjun, CHEN Yongqi, et al. Cycle-slip Detection and Correction Algorithm for Real-time PPP[J]. Geomatics and Information Science of Wuhan University, 2011, 36(11): 1314–1319. |
| [17] | ZHANG Xiaohong, LI Xingxing. Instantaneous Re-initialization in Real-time Kinematic PPP with Cycle Slip Fixing[J]. GPS Solutions, 2012, 16(3): 315–327. DOI:10.1007/s10291-011-0233-9 |
| [18] |
丁文武, 欧吉坤.
增加Doppler观测值实现实时动态PPP快速重新初始化[J]. 宇航学报, 2013, 34(6): 795–800.
DING Wenwu, OU Jikun. Instantaneous Re-initialization of Real Time Kinematic PPP by Adding Doppler Observation[J]. Journal of Astronautics, 2013, 34(6): 795–800. DOI:10.3873/j.issn.1000-1328.2013.06.008 |
| [19] |
柴艳菊, 阳仁贵, 张宝成.
动态PPP定位中周跳自动探测与处理策略[J]. 地球物理学报, 2014, 57(5): 1433–1439.
CHAI Yanju, YANG Rengui, ZHANG Baocheng. Cycle-slip Automatic Detection and Processing Strategy for Dynamic PPP[J]. Chinese Journal of Geophysics, 2014, 57(5): 1433–1439. |
| [20] | ALTMAYER C. Enhancing the Integrity of Integrated GPS/INS Systems by Cycle Slip Detection and Correction[C]//Proceedings of the IEEE Intelligent Vehicles Symposium, Dearborn, MI, USA, 3-5 October 2000. Dearborn, MI, USA: IEEE, 2000. |
| [21] | LEE H K, WANG Jinling, RIZOS C. Effective Cycle Slip Detection and Identification for High Precision GPS/INS Integrated Systems[J]. The Journal of Navigation, 2003, 56(3): 475–486. DOI:10.1017/S0373463303002443 |
| [22] | COLOMBO O, BHAPKAR U. Inertial-aided Cycle-slip Detection/Correction for Precise, Long-baseline Kinematic GPS[C]//Proceedings of the ION GPS. Nashville, TN, USA: [s.n.], 1999: 1915-1922. |
| [23] | DU Shuang, GAO Yang. Inertial Aided Cycle Slip Detection and Identification for Integrated PPP GPS and INS[J]. Sensors, 2012, 12(11): 14344–14362. DOI:10.3390/s121114344 |
| [24] |
刘帅, 孙付平, 张伦东, 等.
INS辅助周跳修复以实现精密单点定位瞬时重新收敛[J]. 中国惯性技术学报, 2015, 23(5): 607–614.
LIU Shuai, SUN Fuping, ZHANG Lundong, et al. Instantaneous Re-convergence of Precise Point Positioning by Using INS-aided Cycle-slip Correction[J]. Journal of Chinese Inertial Technology, 2015, 23(5): 607–614. |
| [25] | LI Zengke, GAO Jingxiang, WANG Jian, et al. PPP/INS Tightly Coupled Navigation Using Adaptive Federated Filter[J]. GPS Solutions, 2017, 21(1): 137–148. DOI:10.1007/s10291-015-0511-z |
| [26] | GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS Carrier-phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations[J]. Journal of Geodesy, 2008, 82(7): 389–399. DOI:10.1007/s00190-007-0187-4 |
| [27] | DAI L, WANG J, RIZOS C, et al. Predicting Atmospheric Biases for Real-time Ambiguity Resolution in GPS/GLONASS Reference Station Networks[J]. Journal of Geodesy, 2003, 76(11-12): 617–628. DOI:10.1007/s00190-002-0286-1 |
| [28] | CHIANG K W, DUONG T T, LIAO J K. The Performance Analysis of A Real-time Integrated INS/GPS Vehicle Navigation System with Abnormal GPS Measurement Elimination[J]. Sensors, 2013, 13(8): 10599–10622. DOI:10.3390/s130810599 |
| [29] | TITTERTON D H, WESTON J L. Strapdown Inertial Navigation Technology[M]. 2nd ed. Reston, VA, USA: American Institute of Aeronautics and Astronautics, 2004. |


