2. 信息工程大学地理空间信息学院, 河南 郑州 450001
2. Institute of Geographical Spatial Information, Information Engineering University, Zhengzhou 450001, China
视觉定位是目前移动机器人自主导航研究的一个热点[1-5],其关键技术是视觉同时定位和地图构建(visual simultaneous localization and mapping,V-SLAM),图优化V-SLAM是其中一个重要研究方向[6-8]。图优化V-SLAM把自主导航过程建模为因子图中的推理问题。在因子图模型中,路标点位置和机器人位姿是变量节点,而空间测量值是作为变量节点之间约束的观测节点。该推理问题的目标是得到该因子图联合概率的最大似然估计,也就是机器人轨迹和地图点之间的几何一致性估计[9]。该最大似然估计问题可转化为非线性最小二乘问题,通过数值算法求解[10-11]。
经典的V-SLAM算法大都假定环境静止[12-15],但最新的移动机器人应用场景往往是周围人群或者设备不断移动的动态环境[16-17]。V-SLAM通过提取场景特征点进行数据处理,若场景中存在动态物体,提取的特征点不断移动,则选定的路标点集合不再属于刚体,那么计算机视觉多像几何约束方程不再成立,进而导致定位错误,且会造成构建的地图扭曲。
关于动态场景V-SLAM的研究,主要有两种思路。一种是把目标识别和跟踪技术融入视觉动态定位过程[18-19],称为视觉前端“预滤波”。文献[18]提出了一种解决动态场景SLAM的贝叶斯模型框架,设计了一种目标识别、跟踪及数据融合算法对目标进行运动建模。在这种方法中,目标识别和跟踪技术主要用于视觉前端(front-end),把运动目标作为干扰背景剔除。
另外一种思路是采用抗差技术处理前端“外点”问题[20-22],主要方法为建立稳健目标函数或者抗差观测表达式。动态方差膨胀(dynamic covariance scaling,DCS)方法[20]使用抗差核函数调整路标点观测量高斯分布的马氏误差(Mahalanobis error)。文献[21]使用混合高斯分布替代单峰高斯分布以增强潜在因子的影响。可切换约束(switchable constraints)方法[22]在优化过程中把切换变量作为与约束相关联的信息矩阵的缩放因子,可自然改变SLAM问题的拓扑结构。这类方法仍然假定数据关联错误主要源于错误的“闭环”,而忽视了环境动态的影响。除非在潜在因子中进行明确建模,这些方法无法处理动态场景中的运动路标点。也有学者通过在后端图优化框架中定义“运动指数”来处理视觉前端的“外点”和动态因素。文献[23]在图优化模型中加入了潜在指示变量来推断路标点是否运动。采用期望最大化(expectation maximization,EM)算法迭代推断潜在路标点指示变量,并估计SLAM最优解。然而,这类基于EM算法的解决方案缺少抗差函数方法的稳健性,且基于单观测量的指示变量仅对该观测量建模,而不能反映与多观测量相关联的路标点的运动性。
本文提出了一种适用于移动机器人视觉动态定位的稳健高斯混合模型,致力于解决动态场景中运动路标点带来的状态估计不一致问题,以提高图优化V-SLAM算法在动态场景中的适用性。
1 传统图优化视觉动态定位模型 1.1 视觉动态定位的最大后验概率问题建模移动机器人视觉动态定位可建模为一个最大后验概率估计(maximum-a-posteriori,MAP)问题[24]。
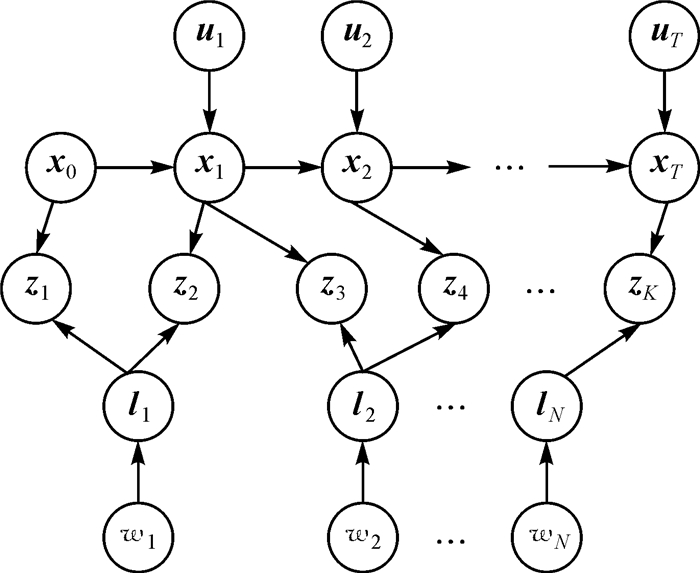
如图 1所示,机器人状态(在地图坐标系中随时间变化的位置和姿态)表示为X={xi, i=0, 1, …, T},在地图坐标系中的路标点位置表示为L={lj, j=1, 2, …, N},控制运动的输入量表示为U={ui, i=1, 2, …, T},路标点在机器人坐标系下的观测量表示为Z={zk, k=1, 2, …, K}。
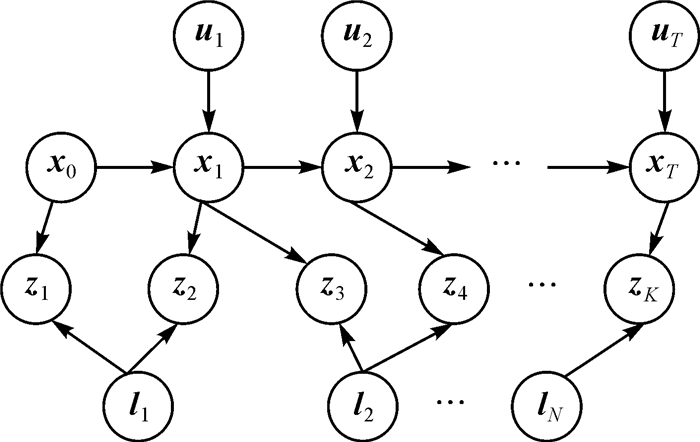
|
| 图 1 传统图优化视觉定位模型示意 Fig. 1 Traditional graph-based vision-based localization model formulation |
假设每次观测相互独立,且运动模型为马尔科夫过程,则所有变量和观测量的联合概率[23]可表示为
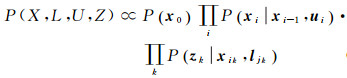 (1)
(1)
式中,P(x0)表示初始状态的先验概率(一般设为常量);P(xi|xi-1, ui)表示机器人运动模型,由控制输入ui参数化;P(zk|xik, ljk)表示路标点测量模型。
运动模型可写为
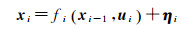 (2)
(2)
式中,fi(·)是已知函数(运动模型);ηi表示运动过程噪声。
测量模型可写为
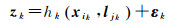 (3)
(3)
式中,hk(·)为已知函数(视觉测量模型);εk表示测量噪声。
1.2 视觉动态定位的非线性优化问题建模在MAP估计问题中,给定运动控制输入U和路标测量值Z,通过计算使得后验概率P(X, L, U, Z)最大的变量(X*, L*)来估计机器人位姿X和路标点三维坐标L,也就是最小化该对数似然函数
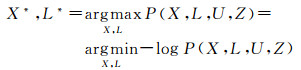 (4)
(4)
当过程噪声及测量噪声服从高斯分布时,即ηi~N(0, Γi),εk~N(0, Σk)。式(4)转化为如式(5)所示非线性最小二乘优化问题
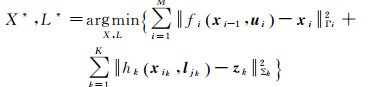 (5)
(5)
式中,符号||·||Σ表示协方差为Σ的Mahalanobis范数。
2 视觉动态定位的稳健高斯混合模型 2.1 模型建立如图 2所示,与传统图优化视觉定位模型不同,这里为每个路标点标记了运动指示性参数,W={wj, j=1, 2, …, N},文中称为“运动指数”。在每个时刻k,观测量zk与机器人位姿xik、路标点ljk及指示变量wjk相对应。其中ik把机器人位姿和测量值关联起来,jk把路标点与测量值关联起来。
|
| 图 2 视觉定位的稳健高斯混合模型示意 Fig. 2 Robust Gaussian mixture model for vision-based Kinematical localization |
考虑到动态场景,使用运动指数W对每一个路标点的运动性进行建模,以表示其运动的可能性,使得观测量更稳健。通过W,与动态路标点相关联的“不好”的观测量会在视觉定位过程中作为“外点”去除掉。这里给出所有变量和观测量的联合概率
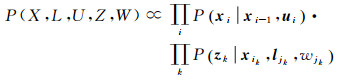 (6)
(6)
给定观测量Z,控制量U和当前运动指数W,机器人状态X和路标点L的最大似然估计可写为
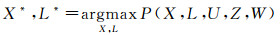 (7)
(7)
与传统图优化视觉定位模型不同,式(6)中第二部分加入了运动指数,另外,这里在观测量误差项中加入抗差函数vk,那么zk的条件概率可表示为增强的高斯分布
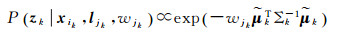 (8)
(8)
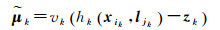 (9)
(9)
式中,wjk表示在k时刻与观测量zk相关联的路标点ljk为静态的可能性;vk表示与每一个路标观测量相关的抗差函数,用来约束该观测量的“粗差”。当wjk或vk趋于0时,等价于把高斯分布的方差设置为无穷大,使得该分布退化为均匀分布,导致该分布表示的约束对图优化过程无影响。
2.2 模型求解式(8)中“运动指数”不可直接被观测到,属于隐性变量,故所描述模型为高斯混合分布模型。这里使用EM算法求解增强的目标函数,估计路标点“运动指数”,并解算机器人位姿和地图点。
2.2.1 估计运动指数(M-step)文献[23]指出,隐性变量wk必须通过对同一路标点的多次观测才能进行估计。在M-step(最大化步骤)需要选取最优的w,使得联合似然最大化。借鉴文献[23],首先令所有wk=0(假设所有路标点都是运动的),可最大化该似然函数(为1);然后引入拉格朗日算子来“惩罚”“设置过多运动路标点”这个假设,也可把拉格朗日算子理解为潜在路标点运动性的先验知识。引入拉格朗日算子的对数似然目标函数为
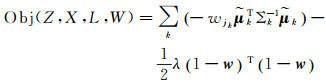 (10)
(10)
式中,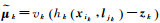
该对数似然目标函数对W求导,令导数为零,可使得该目标函数最大化
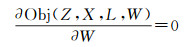 (11)
(11)
对每一个wl,有
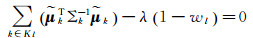 (12)
(12)
式中,Kl表示路标点l的一系列观测量;λ为设定的常量,来权衡“惩罚”目标函数,λ越大,认为原假设“所有路标点都是运动的”越不可靠。
2.2.2 增强的图优化目标函数求解(E-step)在E-step(期望步骤)中,需要使用已经在M-step估计出的潜在隐性变量“运动指数”,求解机器人位姿以及路标点三维坐标。直接使用M-step估计的运动指数变量,采用图优化方法进行求解。这里直接使用文献[24]中提出的标准图优化方法,求解加入路标点运动指数和稳健观测函数的增强目标函数。该问题可写为如下优化问题
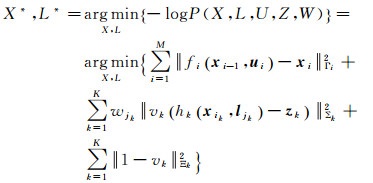 (13)
(13)
式中,符号||·||Σ表示协方差为Σ的Mahalanobis范数;目标函数式(13)中fi(xi-1, ui)-xi||2Γi表示过程约束项,第2部分表示观测约束项,||1-vk||2Ξk表示文献[22]提出的转换先验项。这里参考文献[20],对每一个观测量应用DCS核函数vk
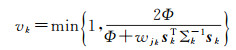 (14)
(14)
式中,sk=hk(xik, ljk)-zk,表示k时刻观测量的原始预测误差。DCS核函数为目标函数(13)限定了一个由Φ确定的上界。通过对所有观测确定上界Φ,核函数vk在图优化过程每次迭代中动态缩放所有观测节点的信息矩阵(权重),并且把“外点”方差替换为较大的值以削弱其对目标函数的贡献。本文参考文献[20]的建议,取Φ=1。
该优化问题可转化为一个标准最小二乘问题,具体推导如下:
把目标函数中过程约束项进行一阶泰勒展开
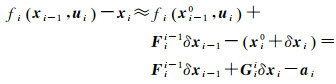 (15)
(15)
式中,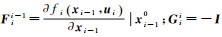
对目标函数中测量约束项一阶泰勒展开,得
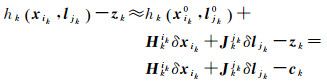 (16)
(16)
式中,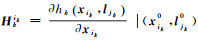
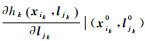
因此,该优化问题可写为
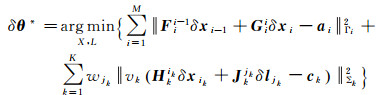 (17)
(17)
重写Mahalanobis范数,考虑到
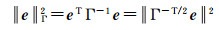 (18)
(18)
故,式(17)可写为
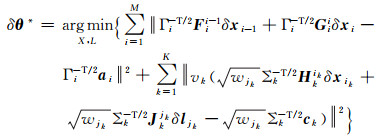 (19)
(19)
把矩阵F、G、H、J连接起来组成系数方阵A,δx、δl组成待估计向量δθ,a、c组成残差向量b,则转化为标准最小二乘问题
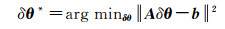 (20)
(20)
E-step和M-step循环迭代进行,直到达到收敛条件,输出机器人位姿和路标点坐标。
3 试验与分析为测试本文算法,分别用仿真数据和真实数据进行试验。
3.1 仿真试验使用的仿真数据是由佐治亚理工大学随iSAM[10]发布的Vicotoria_park数据集和Citytrees10000数据集,该仿真数据集被广泛应用于基于路标点的SLAM算法对比。其中,Vicotoria_park数据集包含6969个机器人位姿,6968个里程计测量值,151个路标点及3640个路标点测量值;Citytrees10000数据集包含10 000个机器人位姿,9999个里程计测量值,100个路标点及4443个路标点测量值。图 3为两组数据集初始化情况,其中“*”表示机器人在各时刻的位姿,“+”号表示场景内的路标点位置。
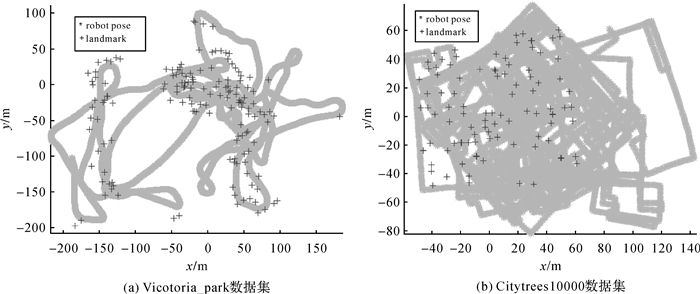
|
| 图 3 两组数据集初始化机器人位姿和路标点 Fig. 3 Robot poses and landmarks initialization of 2 datasets |
为测试本文算法对动态路标点的稳健性,分别对两组数据中特定的路标点进行“破坏”。针对Vicotoria_park数据集,选取“249”号路标点,让其北向匀速运动,最终位置偏离初始位置约10 m;针对Citytrees10000数据集,选取“50”号路标点,让其西向匀速运动,最终位置偏离初始位置约20 m。之所以选择这两个特殊的路标点,是因为这两个路标点与机器人位姿之间的关联相对较多(分别为171个和84个)。一般认为对同一路标点的观测越多,那么该路标点的运动对最终优化结果的影响越大。
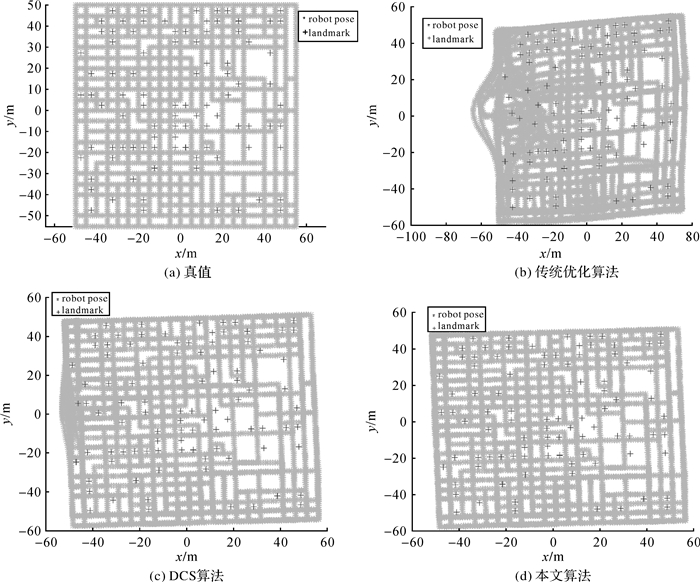
本文对比了传统优化算法、DCS算法[20]和本文算法对两组数据集的优化结果,如图 4和图 5所示。由解算结果可看出:
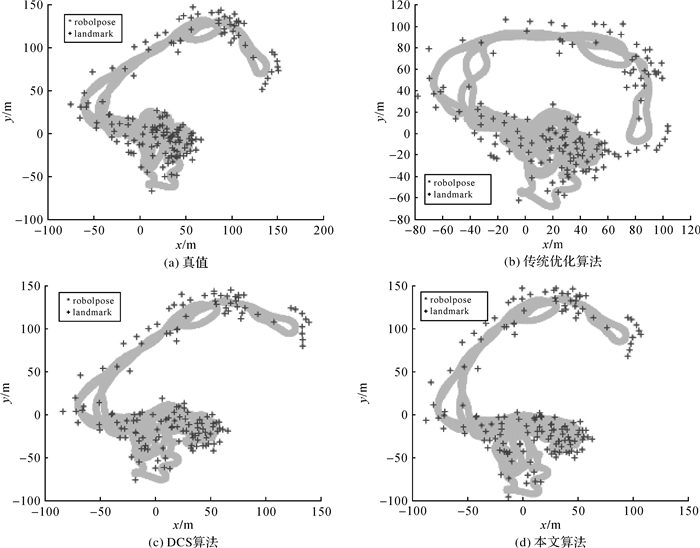
|
| 图 4 Vicotoria_Park数据集机器人位姿和路标点算法优化结果 Fig. 4 Optimization results of robot poses and landmarks in Vicotoria_Park dataset |
|
| 图 5 Citytrees 10000数据集机器人位姿和路标点算法优化结果 Fig. 5 Optimization results of robot poses and landmarks in Citytrees10000 dataset |
(1) 由于动态路标点的存在,破坏了整个图优化的约束关系,传统优化算法已经失效。
(2) DCS算法能削弱部分影响,但效果不显著。因为DCS算法属于抗差估计核函数模型,不区分路标点是否运动。动态路标点造成的前后观测不一致使得全局约束的子集可能收敛至局部最优值,但其余观测会扭曲整个解算结果。
(3) 本文算法可有效缓解动态路标点的影响,解算结果与真值基本吻合。值得注意的是,Vicotoria_park数据集解算结果劣于Citytrees10000数据集。这主要是因为,Vicotoria_park中动态路标点“249”的观测更多(171个,从位姿节点“248”至位姿节点“7091”都有观测,甚至存在环路),因此对最终优化结果影响更大。不过通常移动机器人视觉动态定位过程中,对路标点的观测往往集中在某一特定短时间段内,因此本文算法可处理实际移动机器人行进中的动态路标点问题。
3.2 真实数据试验为进一步验证算法有效性,选用真实数据进行试验。试验数据为德国卡尔斯鲁厄理工学院提供的KITTI Odometry数据集[25]。KITTI Odometry数据集包含Flea2 Firewire相机采集的高质量立体图像序列及OXTS RT 3000 IMU/GPS测量系统采集的地理数据(作为真值)。KITTI给出了22组车载测量数据,内容涵盖城市街道、乡村、高速路等复杂场景,包括运动车辆、行人等各种动态目标。由于只有00~10数据给出了载体位置姿态真值,因此为客观对比算法优劣,这里选取00~10数据进行试验,以下分别记为KITTI00~KITTI10。
3.2.1 精度评价指标文中有两种精度评定指标:绝对误差与相对误差。其中,绝对误差为算法解算结果与真值的绝对定位差异,定义如下
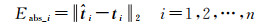 (21)
(21)
式中,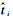
相对误差采用KITTI数据集的精度评价指标[25],它计算固定运动距离下所有相对位姿误差的平均值,定义如下
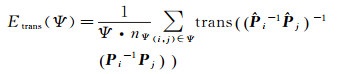 (22)
(22)
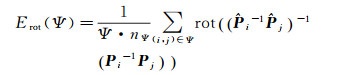 (23)
(23)
式中,Ψ表示特定运动距离;(i, j)∈Ψ表示所有满足特定运动距离Ψ的所有初始帧i和结束帧j;
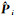
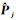
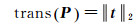 (24)
(24)
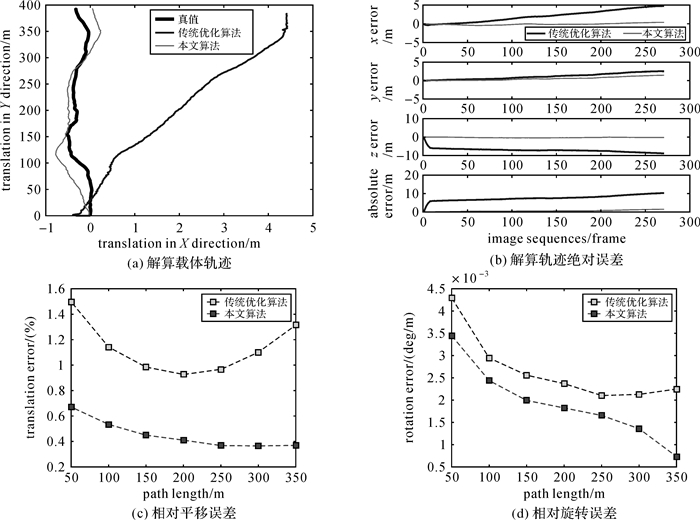
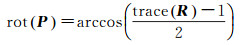 (25)
(25)
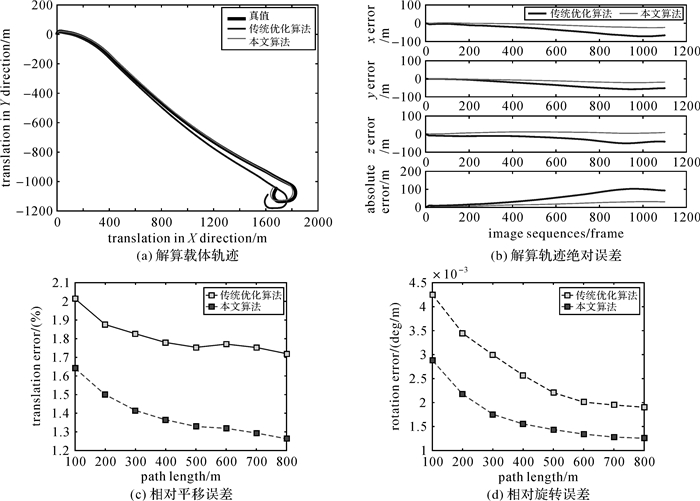
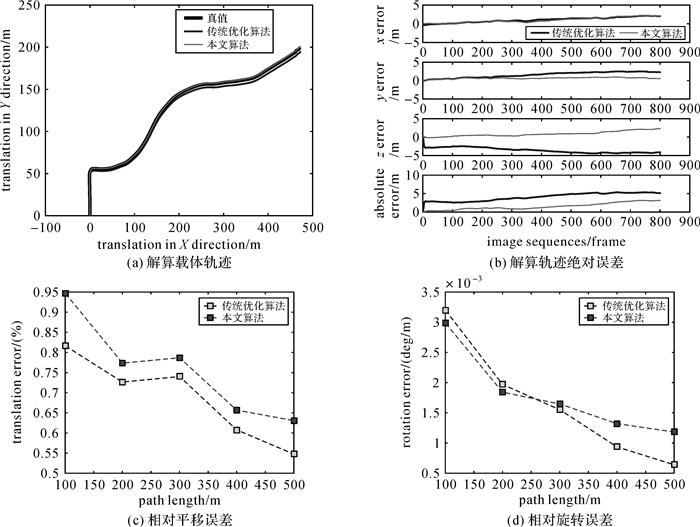
由于DCS算法跟踪过程不够稳健,导致多条序列导航过程中跟踪失败,因此这里只给出了传统优化算法和本文算法的试验结果对比。表 1为KITTI00~KITTI10共计11组试验的误差统计结果,加粗字体表示结果较优。篇幅所限,图 6-图 9分别给出了具有代表性的KITTI01、KITTI03、KITTI04和KITTI07的解算结果:载体轨迹、解算轨迹的X、Y、Z及绝对点位误差和相对平均误差。
| 序号 | 传统优化算法 | 本文算法 | |||||||||||
| 绝对定位误差/m | 相对误差 | 绝对定位误差/m | 相对误差 | ||||||||||
| mean | median | RMSE | Etrans /(%) | Erot /(deg/m) | mean | median | RMSE | Etrans /(%) | Erot /(deg/m) | ||||
| 00 | 7.453 | 7.659 | 7.750 | 0.962 | 0.003 5 | 8.816 | 9.288 | 9.305 | 0.894 6 | 0.003 3 | |||
| 01 | 52.699 | 47.095 | 62.484 | 1.793 4 | 0.002 7 | 17.759 | 16.927 | 20.307 | 1.376 9 | 0.001 7 | |||
| 02 | 15.204 | 12.818 | 16.237 | 0.837 | 0.003 0 | 9.491 | 6.367 | 12.176 | 0.820 | 0.003 1 | |||
| 03 | 4.090 | 4.192 | 4.218 | 0.668 | 0.001 7 | 1.539 | 1.181 | 1.779 | 0.737 | 0.001 8 | |||
| 04 | 7.641 | 7.513 | 7.770 | 1.090 | 0.002 7 | 0.689 | 0.635 | 0.784 | 0.435 | 0.001 9 | |||
| 05 | 3.068 | 3.300 | 3.564 | 0.555 | 0.002 4 | 3.234 | 3.401 | 3.760 | 0.602 | 0.002 4 | |||
| 06 | 2.744 | 2.644 | 2.948 | 0.702 | 0.002 2 | 3.051 | 2.672 | 3.371 | 0.774 | 0.002 3 | |||
| 07 | 2.660 | 2.680 | 3.201 | 0.888 | 0.004 2 | 2.983 | 2.897 | 3.659 | 0.984 | 0.004 7 | |||
| 08 | 11.110 | 11.224 | 11.372 | 1.157 4 | 0.003 7 | 10.153 | 10.552 | 10.427 | 1.004 8 | 0.003 0 | |||
| 09 | 6.450 | 6.713 | 7.397 | 0.902 | 0.003 0 | 5.502 | 5.177 | 6.501 | 0.857 | 0.002 3 | |||
| 10 | 4.942 | 3.936 | 6.039 | 0.678 | 0.002 6 | 4.218 | 3.487 | 5.078 | 0.581 | 0.002 0 | |||
|
| 图 6 KITTI01数据试验结果 Fig. 6 Experimental results of KITTI01 dataset |
|
| 图 7 KITTI03数据试验结果 Fig. 7 Experimental results of KITTI03 dataset |
|
| 图 8 KITTI04数据试验结果 Fig. 8 Experimental results of KITTI04 dataset |
|
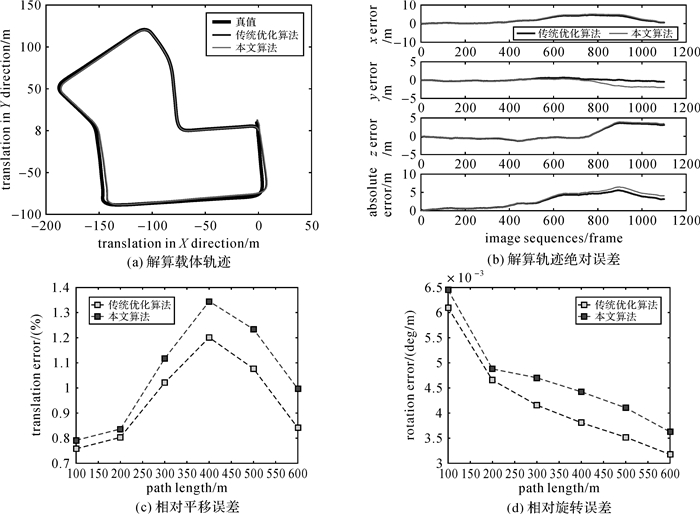
| 图 9 KITTI07数据试验结果 Fig. 9 Experimental results of KITTI07 dataset |
KITTI01和KITTI04的试验结果可看出:本文算法精度明显优于传统优化算法。由于强动态场景中多处出现大量动态目标(车辆、行人),传统优化算法不能保证解算过程中动态路标点的正确识别与过滤,使得解算结果与真值出现较大偏差,如图 6和图 8所示。而本文算法可大大削弱动态路标点的影响,验证了算法设计的正确性及对动态场景的有效性。
KITTI00、KITTI02和KITTI05-KITTI10的试验结果可看出:本文算法与传统优化算法精度相差不大,这是由于数据场景中动态目标较少,且少量动态路标点在解算过程中被当作“外点”剔除掉了,因此不会影响整体优化结果。某些情况下(KITTI00,KITTI05-KITTI07数据中),如图 9所示,传统优化算法精度要优于本文算法,这是由于静态场景或弱动态场景中动态目标较少(或基本没有),而本文算法则把优化函数中静态路标点的权重降低了,因此会影响最终优化结果。
KITTI03的结果比较特殊,绝对定位误差本文算法优于传统优化算法(图 7(a)和图 7(b)所示),而相对误差传统优化算法优于本文算法,但基本上相差不大(图 7(c)和图 7(d)所示)。这是由于开始解算阶段数据中存在动态目标(车辆)的干扰,导致起始优化结果出现较大偏差,进而影响了后续所有的定位结果,因此使得本文算法绝对定位误差优于传统优化算法。而后续解算过程中动态目标干扰较小,因此统计相对误差时,两种算法精度相当。
综上,在强动态场景中,本文算法优于传统优化算法;在静态或弱动态场景中,本文算法与传统优化算法精度相当,说明了本文算法对动态场景中动态路标点的稳健性,验证了算法设计的有效性和正确性。
表 2为算法运算时间统计,可看出单帧运算时间约为70 ms,可满足移动机器人实时自主定位的需求。
| s | ||
| 单帧运算时间 | 传统优化算法 | 本文优化算法 |
| 平均数 | 0.072 450 8 | 0.073 667 23 |
| 中位数 | 0.076 872 3 | 0.084 322 6 |
4 结论
在移动机器人视觉动态定位研究中,针对动态环境中传统图优化视觉定位算法精度低甚至失效的问题,提出了一种顾及动态路标点的稳健高斯混合模型。通过EM算法估计该高斯混合模型中的路标点“运动指数”和相机位姿及路标点坐标。仿真试验和真实数据试验验证了算法在强动态场景中的有效性和正确性,且该方法具有良好的可扩展性,可应用于目前任一图优化SLAM框架内,以提高算法对动态环境的适应性。
值得注意的是,模型求解时,参数λ的取值为预先设置的经验值,具有主观性;且惩罚函数模型的选取具有多样性。关于如何选取合适的参数值和惩罚函数模型及参数值对算法的敏感性研究是下一步工作的主要内容。
另外,在实际应用中,视觉场景复杂多变,光照明暗、快速旋转运动及遮挡情况极易造成视觉动态定位失败,而惯性传感器具有其特殊优势(位姿输出稳定,工作频率高,短时精度可靠),因此下一步也将开展惯性传感器与视觉传感器的融合方法研究,以进一步提高移动机器人自主导航应用的稳健性。
| [1] | PERSSON M, PICCINI T, FELSBERG M, et al. Robust Stereo Visual Odometry from Monocular Techniques[C]//Proceedings of 2015 IEEE Intelligent Vehicles Symposium. Seoul: IEEE, 2015: 686-691. |
| [2] |
黄楠楠, 刘贵喜, 张音哲, 等.
无人机视觉导航算法[J]. 红外与激光工程, 2016, 45(7): 269–277.
HUANG Nannan, LIU Guixi, ZHANG Yinzhe, et al. Unmanned Aerial Vehicle Vision Navigation Algorithm[J]. Infrared and Laser Engineering, 2016, 45(7): 269–277. |
| [3] | WU Meiqing, LAM S K, SRIKANTHAN T. A Framework for Fast and Robust Visual Odometry[J]. IEEE Transactions on Intelligent Transportation Systems, 2017, 18(12): 3433–3448. DOI:10.1109/TITS.2017.2685433 |
| [4] | QU Xiaozhi, SOHEILIAN B, PAPARODITIS N. Landmark Based Localization in Urban Environment[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2018, 140: 90–103. DOI:10.1016/j.isprsjprs.2017.09.010 |
| [5] |
陈锐志, 陈亮.
基于智能手机的室内定位技术的发展现状和挑战[J]. 测绘学报, 2017, 46(10): 1316–1326.
CHEN Ruizhi, CHEN Liang. Indoor Positioning with Smartphones:The State-of-the-art and the Challenges[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1316–1326. DOI:10.11947/j.AGCS.2017.20170383 |
| [6] | STRASDAT H, DAVISON A J, MONTIEL J M M, et al. Double Window Optimisation for Constant Time Visual SLAM[C]//Proceedings of 2011 International Conference on Computer Vision. Barcelona, Spain: IEEE, 2011: 2352-2359. |
| [7] | MUR-ARTAL, MONTIEL J M M, TARDÓS J D. ORB-SLAM:A Versatile and Accurate Monocular SLAM System[J]. IEEE Transactions on Robotics, 2015, 31(5): 1147–1163. DOI:10.1109/TRO.2015.2463671 |
| [8] | CADENA C, CARLONE L, CARRILLO H, et al. Past, Present, and Future of Simultaneous Localization and Mapping:Toward the Robust-perception Age[J]. IEEE Transactions on Robotics, 2016, 32(6): 1309–1332. DOI:10.1109/TRO.2016.2624754 |
| [9] | CARLONE L, KIRA Z, BEALL C, et al. Eliminating Conditionally Independent Sets in Factor Graphs: A Unifying Perspective Based on Smart Factors[C]//Proceedings of 2014 IEEE International Conference on Robotics and Automation. Hong Kong, China: IEEE, 2014: 4290-4297. |
| [10] | KAESS M, JOHANNSSON H, ROBERTS R, et al. iSAM2: Incremental Smoothing and Mapping with Fluid Relinearization and Incremental Variable Reordering[C]//Proceedings of 2011 IEEE International Conference on Robotics and Automation. Shanghai, China: IEEE, 2011: 3281-3288. |
| [11] | KVMMERLE R, GRISETTI G, STRASDAT H, et al. G2o: A General Framework for Graph Optimization[C]//Proceedings of 2011 IEEE International Conference on Robotics and Automation. Shanghai, China: IEEE, 2011: 3607-3613. |
| [12] | SONG Shiyu, CHANDRAKER M, GUEST C C. Parallel, Real-time Monocular Visual Odometry[C]//Proceedings of 2013 IEEE International Conference on Robotics and Automation. Karlsruhe, Germany: IEEE, 2013: 4698-4705. |
| [13] | ENGEL J, STVCKLER J, CREMERS D. Large-scale Direct SLAM with Stereo Cameras[C]//Proceedings of 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems. Hamburg: IEEE, 2015. |
| [14] |
刘浩敏, 章国锋, 鲍虎军.
基于单目视觉的同时定位与地图构建方法综述[J]. 计算机辅助设计与图形学学报, 2016, 28(6): 855–868.
LIU Haomin, ZHANG Guofeng, BAO Hujun. A Survey of Monocular Simultaneous Localization and Mapping[J]. Journal of Computer-aided Design and Computer Graphics, 2016, 28(6): 855–868. DOI:10.3969/j.issn.1003-9775.2016.06.001 |
| [15] |
曹天扬, 蔡浩原, 方东明, 等.
结合图像内容匹配的机器人视觉导航定位与全局地图构建系统[J]. 光学精密工程, 2017, 25(8): 2221–2232.
CAO Tianyang, CAI Haoyuan, FANG Dongming, et al. Robot Vision System for Keyframe Global Map Establishment and Robot Localization Based on Graphic Content Matching[J]. Optics and Precision Engineering, 2017, 25(8): 2221–2232. |
| [16] | PERERA S, PASQUAL A. Towards Realtime Handheld Mono SLAM in Dynamic Environments[C]//Proceedings of the 7th International Symposium on Advances in Visual Computing. Las Vegas, NV: Springer, 2011: 313-324. |
| [17] | TAN Wei, LIU Haomin, DONG Zilong, et al. Robust Monocular SLAM in Dynamic Environments[C]//Proceedings of 2013 IEEE International Symposium on Mixed and Augmented Reality. Adelaide, SA, Australia: IEEE, 2013: 209-218. |
| [18] | WANG C C, THORPE C, THRUN S. Online Simultaneous Localization and Mapping with Detection and Tracking of Moving Objects: Theory and Results from a Ground Vehicle in Crowded Urban Areas[C]//Proceedings of 2003 IEEE International Conference on Robotics and Automation. Taipei, Taiwan, China: IEEE, 2003: 842-849. |
| [19] | HOCHDORFER S, NEUMANN H, SCHLEGEL C. Landmark Rating and Selection for SLAM in Dynamic Environments[C]//Proceedings of the 13th International Conference on Intelligent Autonomous Systems 13. Cham: Springer, 2014: 401-414. |
| [20] | AGARWAL P, TIPALDI G D, SPINELLO L, et al. Robust Map Optimization Using Dynamic Covariance Scaling[C]//Proceedings of 2013 IEEE International Conference on Robotics and Automation. Karlsruhe, Germany: IEEE, 2013: 62-69. |
| [21] | OLSON E, AGARWAL P. Inference on Networks of Mixtures for Robust Robot Mapping[J]. The International Journal of Robotics Research, 2013, 32(7): 826–840. DOI:10.1177/0278364913479413 |
| [22] | SVNDERHAUF N, PROTZEL P. Switchable Constraints for Robust Pose Graph SLAM[C]//Proceedings of 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems. Vilamoura, Portugal: IEEE, 2012: 1879-1884. |
| [23] | ROGERS J G, TREVOR A J B, NIETO-GRANDA C, et al. SLAM with Expectation Maximization for Moveable Object Tracking[C]//Proceedings of 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems. Taipei, Taiwan, China: IEEE, 2010: 2077-2082. |
| [24] | KAESS M, RANGANATHAN A, DELLAERT F. iSAM:Incremental Smoothing and Mapping[J]. IEEE Transactions on Robotics, 2008, 24(6): 1365–1378. DOI:10.1109/TRO.2008.2006706 |
| [25] | GEIGER A, LENZ P, URTASUN R. Are We Ready for Autonomous Driving? The KITTI Vision Benchmark Suite[C]//Proceedings of 2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence, RI: IEEE, 2012: 3354-3361. |



