2. 武汉大学海洋研究院, 湖北 武汉 430078;
3. 武汉大学动力与机械学院自动化系, 湖北 武汉 430072;
4. 辽宁省海域和海岛使用动态监视监测中心, 辽宁 沈阳 110000
2. Marine Research Institute, Wuhan University, Wuhan 430078, China;
3. School of Power and Mechanical Engineering, Wuhan Universality, Wuhan 430072, China;
4. The Sea and Islands Use Dynamic Monitoring Center, Shenyang 110000, China
声速剖面(sound velocity profile, SVP)是水下测距、测深等基础要素测量中声线跟踪必不可少的参数。借助实测SVP,根据折射定律,可跟踪计算波束的传播距离及波束脚印的水深[1-12]。SVP测量时深度间隔设置越小,越能准确反映声速分布,声线追踪精度也越高。由于声线跟踪采用分层计算和逐层累加思想[13],高密度SVP常会导致声线追踪耗时随层数显著增加,尤其对于深海多波束测深[14]。此外,一些设备如EM710、EM122等在声线跟踪时限制了SVP序列长度[15-16],增加了计算繁琐度,简化SVP和提高声线跟踪效率成为必然。
人工法是一种SVP简化方法。通过人工挑选特征声速,形成新的SVP,实现SVP简化。人工法具有操作简单和易于实现特点,但简化过于依赖于人工经验,易遗漏SVP中的特征点,声线跟踪精度不能保证。等效声速剖面法也是一种SVP简化方法。通过寻找一个与原始SVP面积差为零的SVP作为等效SVP实现声线跟踪,在深度变化不大区域可取得较高的精度和计算效率,但当地形变化比较大时,声线跟踪所得深度误差较大,甚至难以满足精度需求。文献[17-21]先后给出了多种等效声速模型或改进方法,在试验中取得了较好的效果。等效声速虽极大地简化了SVP和缩短了声线跟踪耗时,但因抛弃了原始SVP结构,导致无法掌控声线的中间经由路径,在水深变化较大水域声线跟踪效果不佳。此外,该方法因未顾及水体环境中测量误差的复杂性和多源性,易掩盖其他非声速剖面造成的误差[14]。文献[22]提出了一个包含3层的SVP简化模型,用于解决由于声速剖面不准确造成的多波束相邻条带测深结果不一致问题,并取得了很好的应用效果,但会存在与上面方法相同的问题,即未充分顾及声速剖面的中间变化,在地形变化较大的水域声线跟踪误差相对较大。Douglas-Peucker(D-P)法是一种全局化的经典线要素简化算法,常用于制图系统。该算法以垂直距离为简化指标,可以保证声速剖面的形状特点。但由于仅顾及了几何相似性,忽视了声线跟踪的物理机制,因此存在SVP简化率在声速变化剧烈情况下不稳定的问题。此外D-P算法最开始是用来解决在两个维度具有相同单位的折线简化,因此距离阈值对于SVP来说没有实际物理意义[23]。MOV(maximum offset of sound velocity)法是D-P法的改进,不同于D-P法中以距离为简化阈值,而通过计算声速维度上的最大偏移量为阈值实施简化,比D-P算法更为合理。文献[24]通过试验比较了D-P算法和MOV算法的性能,研究了不同阈值下的深度偏差,结果显示MOV方法整体上优于D-P法,并从理论上分析了原因,但并未给出阈值的确定方法,同时指出未来可以通过使简化后的SVP与原始SVP面积差小于给定的值来简化声速剖面。文献[14, 25]研究了MOV方法阈值的自动选择问题,分析了简化率与阈值之间的关系,指出针对一个特定的SVP进行精简,其阈值存在一个区间[T1,T2],T1和T2就是SVP精简率梯度发生突变的位置,并通过精度评定模块和以一定步长搜索来实现阈值确定,最终实现SVP简化,但是阈值区间和计算步长的合理确定需要进一步探讨[24]。
据此,本文提出了一种基于面积差约束的SVP自适应简化方法,确保SVP基本空间变化结构和计算精度情况下,实现自适应于设计精度的SVP简化以及声线高精度、高效追踪。
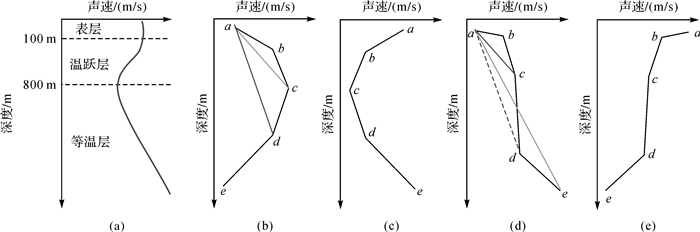
1 声速剖面特点及简化原则典型海区SVP沿深度变化有一定规律性。如图 1(a)所示,水表层和温跃层变化较大,而等温层声速成线性变化。SVP简化的目的在于满足声线跟踪精度下尽可能减少SVP上声速的个数(层数),进而提高声线跟踪效率。由声线跟踪理论知,声波在海底测深点位置计算与声波经历各水层的声速密切相关,不恰当的SVP简化会导致声线跟踪精度不能满足要求。根据SVP变化特点(如图 1(b)—(e)所示),下面给出SVP简化的原则:
|
| 图 1 SVP及其变化特点 Fig. 1 Sound velocity profile |
(1) 确保波束在海底测深点位置计算的精度。
(2) 保留代表性强的声速采样点,保留SVP的基本结构。
(3) 声速变化相对稳定的等温层可视为一个水层。
2 面积差与声线跟踪精度的关系模型文献[17]推导了两个SVP存在面积差εS时,声线跟踪修正与入射角α0和εS的关系
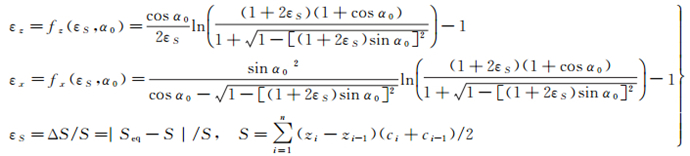 (1)
(1)
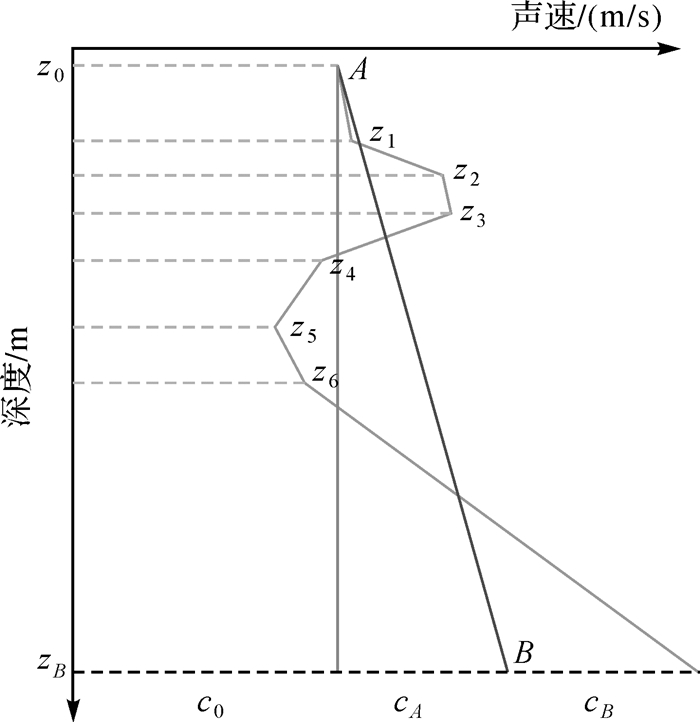
式中,εz和εx分别为深度和水平位移相对误差,是初始入射角α0和相对面积差εS函数;S和Seq分别代表原SVP和等效SVP与纵轴(深度)包围的面积。各符号的意义如图 2所示。
|
| 图 2 原始SVP及其等效SVP Fig. 2 SVP and its equivalent SVP |
由式(1)和图 2可知,相同α0时,若原SVP和另一个SVP的面积差εs为零,则声线跟踪后二者所得波束在海底的测深点坐标(0, y, z)相同,则该SVP称为原SVP的等效SVP。这为简化SVP提供了思路,即如果能寻找到原有SVP的等效SVP,也即实现了对原有SVP的简化。等效SVP具有多样性,最简单的为图 2所示的常梯度geq声速剖面AB。则有
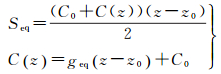 (2)
(2)
式中,C(z)为关于深度z的声速函数;geq为等效声速剖面的常梯度;其他变量与图 2中变量意义相同。
由于Seq与原SVP面积S0相同,依式(2)则可得常梯度等效SVP的梯度geq
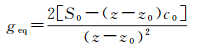 (3)
(3)
定义以上为常梯度等效SVP简化法。该方法将整个水体视为一个水层,不顾及声线中间传播,只能确保与SVP深度相同的海底测深点坐标跟踪精度。
简化是在原SVP上对声速点的取舍。基于等效SVP思想,若去除某声速后的SVP与原SVP包围的面积相同,则可以去除;否则不予去除。不可避免的是简化SVP与原SVP存在面积差ΔS。若ΔS造成的声线跟踪点位相对误差小于限差,则该简化是合理的,否则不合理。声线跟踪点的相对误差为
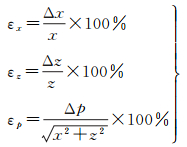 (4)
(4)
式中,εx、εz和εp分别为水平、垂直和点位相对误差;x、z表示波束脚印在换能器坐标系下的横、纵向传播距离;简化SVP产生的声线跟踪误差分布为Δx、Δz;点位误差为Δp。
若能根据式(4)计算每次简化后SVP声线跟踪精度ε,则可根据设定的声线跟踪限差判断该简化是否恰当。ε需在完成声线跟踪计算后才能得到,过程繁琐且耗时。由图 2知,每次简化,简化SVP和原始SVP间的面积差容易得到。又由式(1)知,相对坐标误差ε与SVP面积差ΔS存在较强的相关性,若能够将ε表示为ΔS函数,则对于判断是否对SVP中声速去除,实施SVP简化将非常有益。下面推导这一模型。
若对某一深度层的SVP简化,根据式(3),可分别得到原始和简化后的SVP的等效SVP的梯度geq和g。以等效SVP的梯度geq为参考,则二者在深度z产生的面积差ΔS为
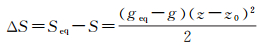 (5)
(5)
则可得
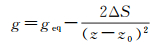 (6)
(6)
式中,g为简化后SVP的等效SVP梯度。
式(6)表明,借助简化SVP和实际SVP的面积差ΔS,可计算出简化SVP的常梯度g。根据式(4),简化SVP声线跟踪的相对误差为
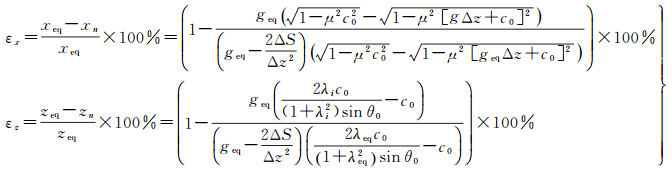 (7)
(7)
式中
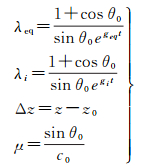
式中,g和geq分别为原始和简化SVP的等效SVP梯度;(0, x, z)和(0, x, z)eq分别为借助原始和简化的SVP声线跟踪得到的测深点坐标,以前者为参考得到的相对误差为εx、εz。
式(7)表明,εx、εz是初始声速C0、初始入射角θ0、面积差ΔS和传播时间t函数。对于一个声速剖面段,由于C0和θ0已知,若对该段SVP简化,简化形成的新SVP均会与实际SVP产生面积差ΔS。将ΔS代入式(7)可计算由此简化带来的声线跟踪误差。根据设定限差ε0,判断该次简化是否恰当。因此,式(7)实则是给出了如下SVP采样点保留原则
 (8)
(8)
式中,ε0为设定的声线跟踪相对误差;ε为由式(7)计算的简化后SVP点位相对误差。如果ε超限,则该点不能去除;否则,可以去除。
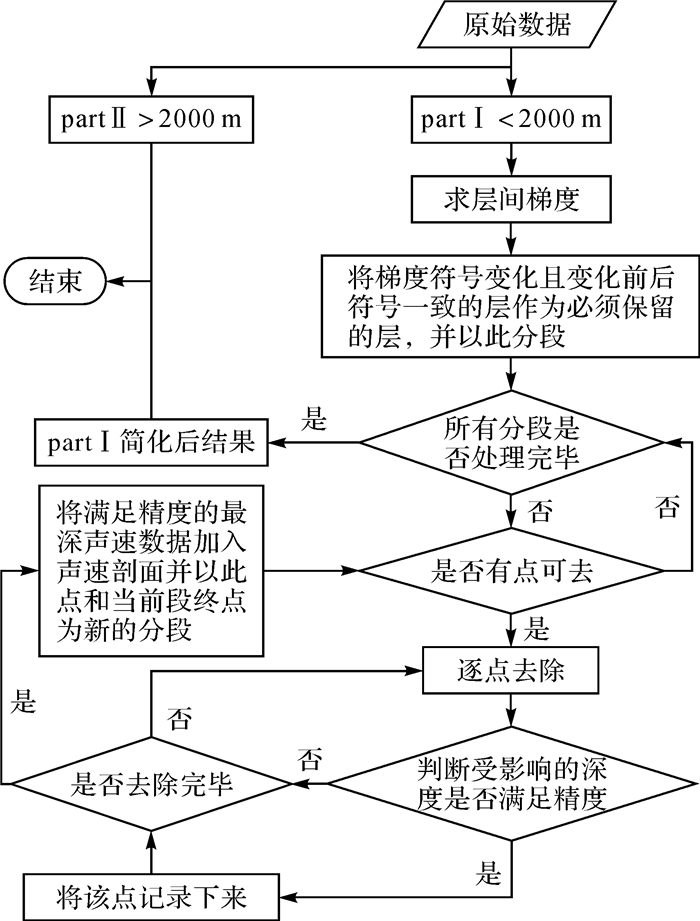
3 SVP简化过程由于SVP不可能是简单的凸曲线或者是凹曲线,所以去掉一个采样点,新产生的SVP和原SVP的面积差可能增大也可能减小(图 1)。为了取得最大简化率的同时确保不同深度下的声线跟踪精度,当一个采样点根据式(8)需要保留时,不应该立刻保留,而是需先将该点记录下来,继续下一个采样点的移除,并根据简化原则判断移除该点产生的面积差变化引起的该处声线跟踪误差是否小于给定的精度阈值ε0。若是,则记录该点,继续开展后面采样点的移除和判断;若不是,同样继续采样点移除和判断。重复上述点移除与判断过程,直到该段处理完毕,最后的记录才是该段需要保留的点。将保留点与该段的下端点形成新段,重复上述过程,直到所有分段处理完毕。图 3给出了完整的简化过程。
|
| 图 3 SVP简化流程 Fig. 3 Flowchart of SVP simplification |
4 试验及分析
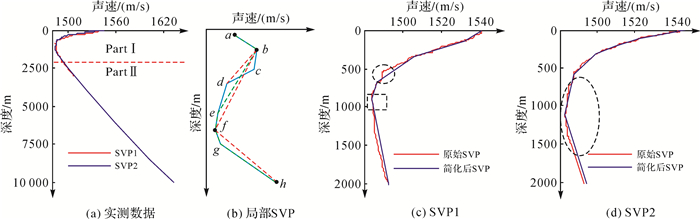
为检验给出的简化算法的有效性,利用2016年7月在关岛与印尼间(6.53°N, 149.73°E)海区多波束测深过程中实测的两个SVP数据(图 4(a))开展试验。声速采用SBE 911plus CTD测量(采样率24 Hz;电导率量程0~7 S/m,精度±0.000 3 S/m;温度量程-5~+35℃, 精度±0.001℃;压力量程0~15 000 psia, 精度±0.015%水深)。深水多波束EM122(操作频率12 kHz,测深范围20~11 000 m,幅宽6倍深度,范围采样率3.03 kHz,每ping波束432个)实施测深。试验水域水深变化2372~9568 m,声速变化1482~1631 m/s。考虑表层和温跃层声速变化较大而等温层声速主要受压力影响呈小的正梯度变化,将整个SVP分为浅于和深于2000 m两部分(part Ⅰ和part Ⅱ,如图 4(a)所示)。partⅠ由凸曲线、凹曲线以及近似直线部分组成,具有一定的代表性,而partⅡ基本为一条直线。
|
| 图 4 实测SVP及其简化 Fig. 4 Actual SVP and its simplification |
设定声线跟踪精度0.1%开展SVP简化。进行简化前首先对声速剖面进行平滑处理,去除异常数据。抽取一段SVP(图 4(b)),说明SVP简化过程:
(1) 计算每个声速点到表层声速点间SVP的等效常梯度SVP的梯度geq。
(2) a点和h点为端点需保留。b点和f点分布为声速梯度从正到负进而再变化为正的拐点,因此将图 4(b)所示SVP分为3段a—b、b—c—d—e—f和f—g—h。
(3) a—b段无可移除采样点需要直接保留。对于b—c—d—e—f段,先去掉c,此时新产生的SVP与原始SVP的面积差为三角形bcd所对应的面积,此时声线追踪结果受影响的点为b点深度以下的测深点,而d点以下所有深度对应的SVP面积差为定值,因此d点对应的相对偏差最大,只需计算c点和d点处的SVP等效梯度gc,利用式(7)计算由此产生的声线跟踪误差εx、εz,由式(8)判断精度是否满足要求。如果c点和d点的精度都满足精度要求,则该点保留,否则不保留。若c需保留,将c记录。继续去掉d点,重复上述过程,直到完成当前段所有采样点取舍判断。取最深点作为保留点,如e点,然后判断保留点是否已到达本段下端点;若没有,则将保留点和当前段下端点组成新的分段继续上述过程,否则进行下一段处理,最终简化为b—e—f。类似的,对f—g—h段简化,发现去掉任何声速点均会导致超限。最后,整个SVP简化为a—b—e—f—g—h。
对两SVP简化,图 4(c)和图 4(d)显示了part Ⅰ的简化结果。表 1统计参数表明简化率均达到了98%,极大地简化了原SVP。
| 声速剖面 | 原始点数 | 简化后点数 | 简化率/(%) |
| SVP1 | 400 | 9 | 97.8 |
| SVP2 | 649 | 15 | 97.7 |
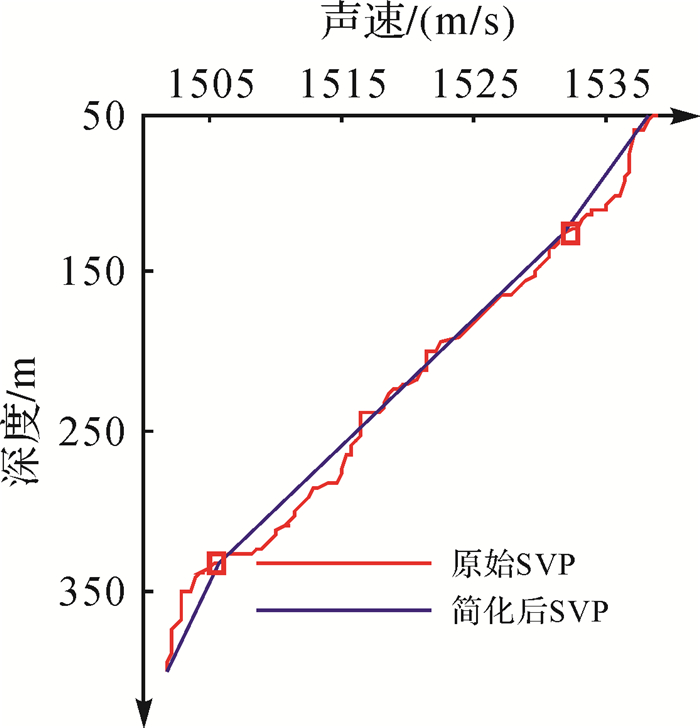
本文方法基于面积差约束简化SVP,声速变化大的不一定保留,梯度变化的拐点以及SVP的基本结构会得到保留。将图 4(d)原始SVP中一段和对应的利用本文方法简化后的SVP段放大如图 5所示。可以看出,本文方法保留了两个点,使得原始SVP均匀地分布在简化SVP两侧,简化后的SVP趋势与简化之前的一致性较好,面积差较小。分析图 4(d)中的其他段,可得出类似结论。
|
| 图 5 使用本文方法简化SVP2中部分结果 Fig. 5 A segment of SVP2 simplified by the proposed method |
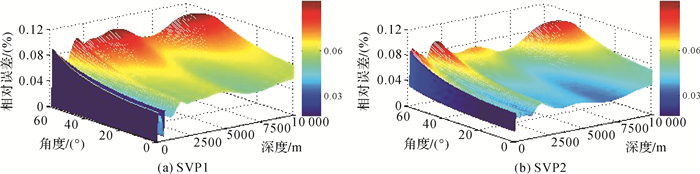
为评价使用简化后的SVP进行声线跟踪的精度,利用简化的SVP在波束入射角0~60°、不同深度下开展声线跟踪。以原始SVP声线跟踪结果为参考,将简化后SVP声线跟踪结果与之比较,声线跟踪精度随入射角和深度变化如图 6所示。
|
| 图 6 简化SVP产生的相对误差 Fig. 6 Relative errors produced by the simplified SVP |
从图 6可看出,当水深小于2000 m时,使用简化SVP进行声线跟踪的误差变化较为剧烈,在不同深度下,相对误差随波束入射角的增大而增大。对不同深度下声线跟踪的误差统计如表 2所示。可以看出,最大相对误差控制在0.1%以内,与算法预期结果相符。
| 声速剖面 | 相对误差 | 绝对最大偏差/m | 平均偏差/m | 中误差/m | max ε/(%) | max εp/(%) |
| SVP1 | εx | -18.94 | -3.98 | 3.97 | -0.10 | 0.10 |
| εz | -15.03 | -1.14 | 2.79 | 0.10 | ||
| SVP2 | εx | -16.61 | -3.21 | 3.32 | -0.10 | 0.10 |
| εz | -12.90 | -0.89 | 2.32 | 0.10 |
以上结果与本文SVP简化方法的简化原理密切相关,通过建立面积差与声线跟踪百分比误差的关系,在简化过程中对面积差进行约束,因此可以取得与原始SVP在变化趋势上的一致,虽然会忽略一些特征点,但可以保证较高的简化率以及声线跟踪的精度。
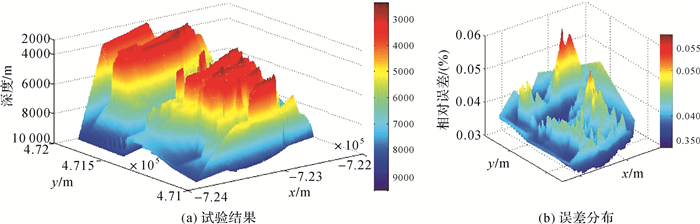
将本文方法简化所得SVP用于调查水域多波束测深数据处理,所用数据的总Ping数为5696,每Ping432个波束,数据处理程序采用所在课题组自研软件,算法为层内常声速声线跟踪算法,通过植入代码记录声线跟踪模块执行的开始和结束时刻计时。计算平台处理器型号为Intel(R) Core9(TM) i7 6700HQ。试验水域水深变化较大,可较好地评估本文方法简化SVP的性能。以原始SVP声线跟踪得到的海底地形为参考,简化SVP所得海底地图(图 7(a))与之比较,点位的相对误差分布如图 7(b)所示,精度统计如表 3所示。可以看出,相对误差全部控制在0.1%以内。利用原始SVP和简化后SVP开展声线跟踪的耗时分别为434.112 s和12.432 s,显著提高了测深数据处理的效率。
|
| 图 7 基于简化SVP跟踪获得的海底地形及其偏差分布 Fig. 7 Seabed topography and its errors obtained by simplified SVP |
| 相对误差 | 绝对最大偏差/m | 平均偏差/m | 中误差/m | max ε/(%) |
| εx | 5.83 | 1.41 | 0.97 | 0.096 |
| εz | 5.31 | 2.03 | 0.86 | 0.044 |
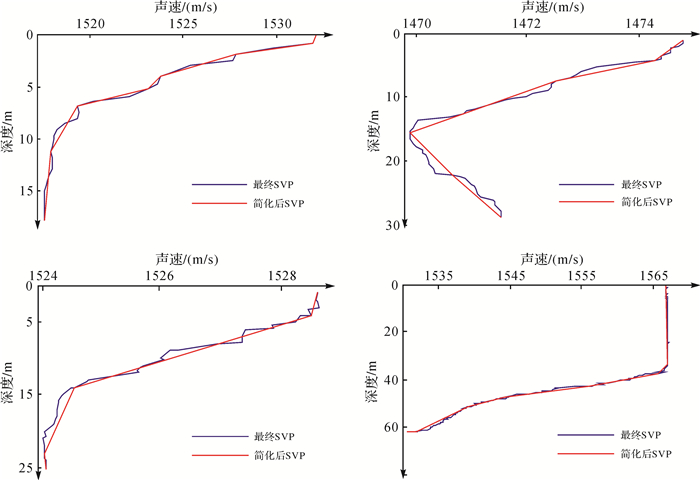
为进一步验证算法的普适性,在浅水区选择4根不同深度(18、30、25和60 m)、变化较复杂(先显著负梯度再缓慢负梯度变化、先显著负梯度再显著正梯度变化、先缓慢正梯度负梯度再缓慢负梯度变化、先缓慢正梯度再显著负梯度变化)具有代表性的SVP开展试验,试验结果如图 8所示。可以看出,试验取得了几乎与深海试验相同的结论,表明本文方法同样适用于浅水复杂SVP的简化。就简化率而言,60 m的SVP从原始声速448个简化到8个,30 m的SVP声速从原来的57个简化到6个,25 m的从原始49个到简化后5个,18 m的SVP从原始的33个简化到8个,均取得了不同程度上的简化。
|
| 图 8 不同变化形态下的浅水SVP简化 Fig. 8 Results of the simplification of shallow water SVPs |
5 结论
针对声速剖面(SVP)数据冗余及多波束声线跟踪带来的计算低效率问题,本文给出了一种基于面积差约束的SVP简化方法。该方法给出了面积差与声线跟踪误差的关系,较好地保留了SVP基本结构,取得了较高的SVP简化率,显著提高了多波束测深数据处理的效率。整个简化过程不需要人工干预,实现了SVP简化的自动化。
| [1] |
齐娜, 田坦.
多波束条带测深中的声线跟踪技术[J]. 哈尔滨工程大学学报, 2003, 24(3): 245–248.
QI Na, TIAN Tan. Ray Tracing in Multi-beam Swath Bathymetry[J]. Journal of Harbin Engineering University, 2003, 24(3): 245–248. DOI:10.3969/j.issn.1006-7043.2003.03.003 |
| [2] |
魏玉阔.多波束测深假象消除与动态空间归位技术[D].哈尔滨: 哈尔滨工程大学, 2011. WEI Yukuo. Technique of Bathymetric Artifact Elimination and Seafloor Footprint Positioning for Multibeam Bathymetry[D]. Harbin: Harbin Engineering University, 2011. http://cdmd.cnki.com.cn/article/cdmd-10217-1012264994.htm |
| [3] |
朱小辰, 刘雁春, 肖付民, 等.
海道测量多波束声速改正精确模型研究[J]. 海洋测绘, 2011, 31(1): 1–3, 8.
ZHU Xiaochen, LIU Yanchun, XIAO Fumin, et al. Rigorous Model of Multibeam Echosounding System Sounding Velocity Correction[J]. Hydrographic Surveying and Charting, 2011, 31(1): 1–3, 8. DOI:10.3969/j.issn.1671-3044.2011.01.001 |
| [4] |
陆秀平, 边少锋, 黄谟涛, 等.
常梯度声线跟踪中平均声速的改进算法[J]. 武汉大学学报(信息科学版), 2012, 37(5): 590–593.
LU Xiuping, BIAN Shaofeng, HUANG Motao, et al. An Improved Method for Calculating Average Sound Speed in Constant Gradient Sound Ray Tracing Technology[J]. Geomatics and Information Science of Wuhan University, 2012, 37(5): 590–593. |
| [5] |
张居成, 郑翠娥, 孙大军.
用于声线跟踪定位的自适应分层方法[J]. 哈尔滨工程大学学报, 2013, 34(12): 1497–1501.
ZHANG Jucheng, ZHENG Cui'e, SUN Dajun. A Self-adapting Division Method for Ray-tracing Positioning[J]. Journal of Harbin Engineering University, 2013, 34(12): 1497–1501. |
| [6] |
李圣雪.水下声学定位中声速改正方法研究[D].青岛: 中国石油大学(华东), 2015. LI Shengxue. Research on the Method of Sound Speed Correction in Underwater Acoustic Positioning[D]. Qingdao: China University of Petroleum (East China), 2015. http://cdmd.cnki.com.cn/Article/CDMD-10425-1017809037.htm |
| [7] |
何林帮, 赵建虎, 张红梅, 等.
顾及姿态角的多波束声线精确跟踪方法[J]. 哈尔滨工程大学学报, 2015, 36(1): 46–50.
HE Linbang, ZHAO Jianhu, ZHANG Hongmei, et al. A Precise Multibeam Sound Ray Tracking Method Taking into Account the Attitude Angle[J]. Journal of Harbin Engineering University, 2015, 36(1): 46–50. |
| [8] |
辛明真, 阳凡林, 闫循鹏, 等.
一种等效声速梯度的迭代计算方法[J]. 海洋测绘, 2015, 35(5): 28–31, 42.
XIN Mingzhen, YANG Fanlin, YAN Xunpeng, et al. An Equivalent Sound Velocity Profile Iterative Algorithm[J]. Hydrographic Surveying and Charting, 2015, 35(5): 28–31, 42. DOI:10.3969/j.issn.1671-3044.2015.05.007 |
| [9] |
孙强, 李明叁, 王洪燕, 等.
多波束测深系统声线跟踪方法对比分析[J]. 海洋测绘, 2015, 35(2): 48–51.
SUN Qiang, LI Mingsan, WANG Hongyan, et al. Comparison and Analysis of Ray-tracking Methods for Multibeam Sounding System[J]. Hydrographic Surveying and Charting, 2015, 35(2): 48–51. DOI:10.3969/j.issn.1671-3044.2015.02.013 |
| [10] |
李圣雪, 王振杰, 聂志喜, 等.
一种适用于深海长基线定位的自适应分层声线跟踪法[J]. 海洋通报, 2015, 34(5): 491–498.
LI Shengxue, WANG Zhenjie, NIE Zhixi, et al. A Self-adapting Division Ray-tracing Method in the Long Baseline Acoustic Positioning[J]. Marine Science Bulletin, 2015, 34(5): 491–498. |
| [11] |
王振杰, 李圣雪, 聂志喜, 等.
水声定位中一种大入射角声线跟踪方法[J]. 武汉大学学报(信息科学版), 2016, 41(10): 1404–1408.
WANG Zhenjie, LI Shengxue, NIE Zhixi, et al. A Large Incidence Angle Ray-tracing Method for Underwater Acoustic Positioning[J]. Geomatics and Information Science of Wuhan University, 2016, 41(10): 1404–1408. |
| [12] |
杨保国.超短基线系统安装校准技术研究[D].哈尔滨: 哈尔滨工程大学, 2013. YANG Baoguo. Research of the Install-calibration for USBL[D]. Harbin: Harbin Engineering University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10217-1014133969.htm |
| [13] |
赵建虎.
现代海洋测绘-上册[M]. 武汉: 武汉大学出版社, 2007: 90-96.
ZHAO Jianhu. Modern Marine Surveying and Charting[M]. Wuhan: Wuhan University Press, 2007: 90-96. |
| [14] |
赵荻能, 吴自银, 周洁琼, 等.
声速剖面精简运算的改进D-P算法及其评估[J]. 测绘学报, 2014, 43(7): 681–689.
ZHAO Dineng, WU Ziyin, ZHOU Jieqiong, et al. A Method for Streamlining and Assessing Sound Velocity Profiles Based on Improved D-P Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(7): 681–689. DOI:10.13485/j.cnki.11-2089.2014.0132 |
| [15] | L3 Communicatons. SEA BEAM 2100 Multibeam Bathymetric Survey Mapping System, External Interface Specification[EB/OL].[1999-08-15]. http://www.mbari.org/data/mbsystem/formatdoc/SB2100ExternalInterface.pdf. |
| [16] | Kongsberg Maritime AS. EM Series Multibeam Echo Sounders Datagram Formats, Revision[EB/OL].[2010-01-20]. http://www.ldeo.columbia.edu/res/pi/MBSystem/formatdoc/EM_Datagram_Formats_RevP.pdf. |
| [17] | GENG Xueyi, ZIELINSKI A. Precise Multibeam Acoustic Bathymetry[J]. Marine Geodesy, 1999, 22(3): 157–167. DOI:10.1080/014904199273434 |
| [18] | KAMMERER E L L M. A New Method for the Removal of Refraction Artifacts in Multibeam Echosounder Systems[D]. Saint John: University of New Brunswick, 2000. |
| [19] | YANG Fanlin, LI Jiabiao, WU Ziyin, et al. A Post-processing Method for the Removal of Refraction Artifacts in Multibeam Bathymetry Data[J]. Marine Geodesy, 2007, 30(3): 235–247. DOI:10.1080/01490410701438380 |
| [20] |
赵建虎, 刘经南.
精密多波束测深系统位置修正方法研究[J]. 武汉大学学报(信息科学版), 2002, 27(5): 473–477.
ZHAO Jianhu, LIU Jingnan. Development of Method in Precise Multibeam Acoustic Bathymetry[J]. Geomatics and Information Science of Wuhan University, 2002, 27(5): 473–477. |
| [21] |
丁继胜, 周兴华, 唐秋华, 等.
基于等效声速剖面法的多波束测深系统声线折射改正技术[J]. 海洋测绘, 2004, 24(6): 27–29.
DING Jisheng, ZHOU Xinghua, TANG Qiuhua, et al. Ray-tracking of Multibeam Echosounder System Based on Equivalent Sound Velocity Profile Method[J]. Hydrographic Surveying and Charting, 2004, 24(6): 27–29. DOI:10.3969/j.issn.1671-3044.2004.06.008 |
| [22] | YANG Fanlin, LI Jiabiao, WU Ziyin, et al. A Post-processing Method for the Removal of Refraction Artifacts in Multibeam Bathymetry Data[J]. Marine Geodesy, 2007, 30(3): 235–247. DOI:10.1080/01490410701438380 |
| [23] | DOUGLAS D H, PEUCKER T K. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature[J]. The International Journal for Geographic Information and Geovisualization, 1973, 10(2): 112–122. DOI:10.3138/FM57-6770-U75U-7727 |
| [24] | JONATHAN B, STEVE S, ARNOLD F, et al. Streamlining Sound Speed Profile Pre-processing: Case Studies and Field Trials[C]//Proceedings of US Hydrographic Conference. Florida: [s.n.], 2011: 25-28. |
| [25] | ZHAO Dineng, WU Ziyin, ZHOU Jieqiong, et al. A New Method of Automatic SVP Optimization Based on MOV Algorithm[J]. Marine Geodesy, 2015, 38(3): 225–240. DOI:10.1080/01490419.2015.1006798 |



