近年来,随着我国海洋强国战略的提出,水下潜航器(underwater vehicle, UV)在军事和民用领域都得到了快速的发展[1-3]。特别是在军事上,基于安全性和隐蔽性的考虑,往往要求UV具有执行长时间、远距离水下任务的能力。在这种情况下,UV通常采用技术成熟且短时定位精度高的惯性导航系统(inertial navigation system,INS)来提供位置服务,但由于其难以解决误差随时间累积的问题,很难满足当前UV长时间的高精度导航需求[4-5]。因此,采用自主性强、隐蔽性好且定位精度与航程无关的水下地形匹配算法辅助INS进行导航是解决这一问题的重要手段[6-9]。
目前,国内外针对水下地形匹配算法已经开展了大量的研究工作[9-13]。其中,比较经典的算法有TERCOM(terrain contour matching)算法[14-15]和ICCP(iterative closet contour point)算法[9-13],这两种算法具有原理简单、匹配效率高等优点。但由于这类算法在匹配定位时仅使用了UV下方地形剖面线的起伏信息(本文称此类算法为线匹配算法),导致对原始地形的描述不够丰富,所以在地形相似性高的区域易出现误匹配的现象[9-10]。为此,文献[9]提出了一种基于Hu矩的水下地形二维特征匹配算法,该算法利用了多波束测深系统(multi-beam bathymetric system, MBS)所测得的更丰富的地形信息,因而可以获得稳健性更好的匹配结果(本文称此类算法为面匹配算法)。但是,由于Hu矩的7个不变量是从低阶中心矩扩展而来的[16-17],对目标细节的辨识能力差,导致该算法在应用于水下地形匹配定位时对地形局部信息的利用不够充分,从而导致该算法的定位精度比较低。
为此,本文在借鉴面匹配思想的基础上,提出一种线面组合的水下地形匹配算法,以期提高水下地形匹配辅助系统的整体精度。
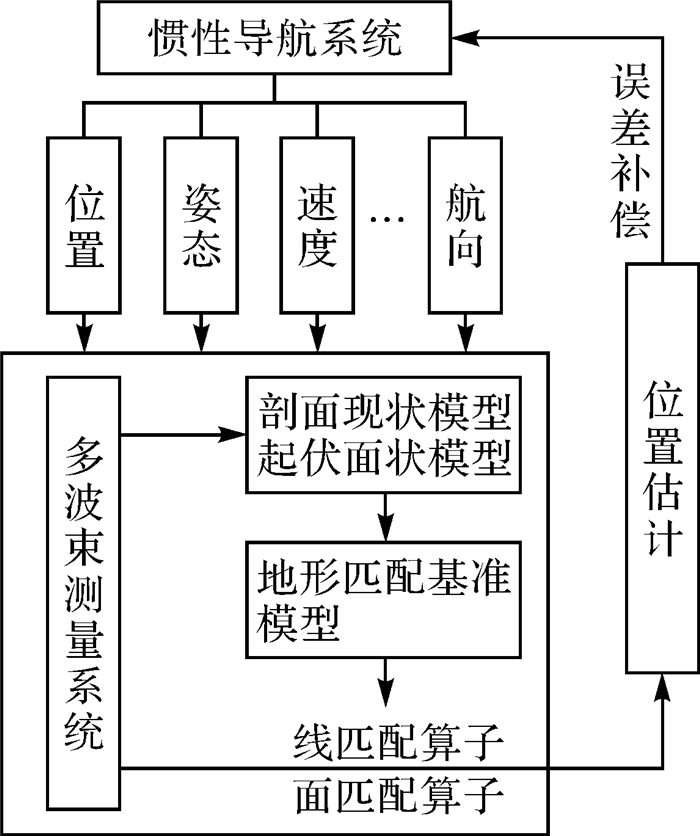
1 线面组合水下地形匹配算法 1.1 算法的基本思路本文所提组合算法的基本思路(图 1)为:首先,基于现有的水深数据处理方法[18-20],根据MBS测得的水深信息构建局部地形的剖面线状模型和水平起伏面状模型;其次,利用改进的线匹配算法进行初次匹配定位以缩小INS的位置和航向误差;再次,构建一种基于几何相似性的面匹配算子,并利用该算子对INS的位置误差进行估计;最后,判断INS的误差估计是否小于其理论值σ[10],若小于则以该位置误差对INS进行补偿,否则需要重新进行匹配定位。
|
| 图 1 算法的基本思路示意 Fig. 1 Schematic diagram of the algorithm |
1.2 线匹配算法 1.2.1 相似性度量方法
MAD(mean absolute difference)算法是经典TERCOM算法中一种常用的相似性度量方法,其公式为[10]
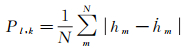 (1)
(1)
式中,N表示参与匹配运算的水深点个数;hm表示实测水深值;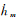
分析式(1)可知,该算子采用实测水深与待匹配水深绝对差的平均值来表达实测地形与待匹配地形的相似程度,这一思想在实测水深系统误差较小的情况下是比较合理的。但考虑到安全、隐蔽的需求,UV在地形匹配定位时往往不能与外界通信,难以获得所在位置精确的潮高数据,实时测水深中不可避免地存在系统误差(研究表明潮汐和余水位等因素产生的实时测量水深系统误差可达米级[21-23]),同时,文献[24]的研究结果表明:系统误差的存在将会影响匹配算子对地形相似性的判别能力。
为此,本文对MAD算子进行改进,采用实测水深距平与待匹配水深距平绝对差的平均值来表达实测地形与待匹配地形的相似性
 (2)
(2)
式中,h′m和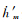
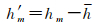 (3)
(3)
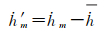 (4)
(4)
式中,h和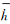
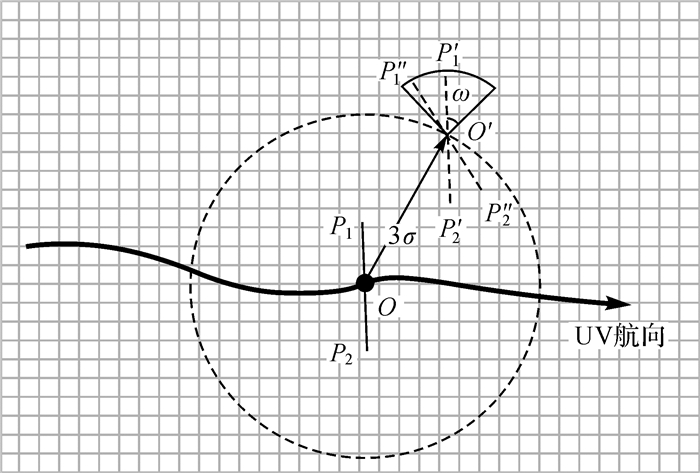
如图 2所示,为线匹配算法匹配搜索区示意图。其中黑色曲线表示根据INS计算的UV航行轨迹线,O点表示根据INS计算的UV位置,O′点表示UV实际位置的估计,线段P1-P2表示UV航行到O点时MBS测得的条带中心水深点连成的水平位置线,σ表示INS的系统误差限[10],ω表示INS的航向误差限。
|
| 图 2 匹配搜索区示意图 Fig. 2 Schematic diagram of the searching area |
由于INS存在位置误差和航向误差,线段P1-P2实际位置可能有所偏移,图 2中虚线P″1-P″2为其中的可能位置之一。
为了获得UV的实际位置,经典的TERCOM算法以实测水深位置线P1-P2为参照,采用遍历的方法在以INS指示位置为中心,3σ为半径的区域内(如图 2中虚线圆所示)进行平移搜索[10],这种搜索策略虽然简单,但是没有顾及航向误差的影响,因此算法的精度受航向误差影响较大。
为此,本文对搜索策略进行了改进,其基本思路为:
(1) 在搜索过程中,对P1-P2的每个平移变换位置进行旋转变换。
(2) 在第i次平移变换中,选取与实测水深相似性最高的待匹配水深序列,将该水深序列对应的水平位置线段P″i, 1-P″i, 2与线段P1-P2的夹角作为航向修正角ωi。
(3) 计算前n次平移变换中,各航向修正角的均值为ωn,若第n+1次航向修正角ωn+1满足|ωn+1-ωn| < (1-k)ωn,且线段P″i, 1-P″i, 2重心与线段P1-P2重心的水平距离σn+1小于INS误差限σ,则认为匹配成功,停止搜索;若不满足,则继续搜索直至满足,或者完成对整个匹配区的搜索。其中,k表示匹配搜索的置信度阈值,为了提高定位精度本文取k为99%。
1.2.3 匹配结果的检验在匹配区的搜索过程中,若在第n+1次旋转变换就已经达到了1.2.2节的搜索停止条件,则认为ωn+1为INS的航向误差,σn+1为INS的位置误差;若在完成对整个搜索区的搜索后,仍不满足停止条件,则选取与实测水深相似性最佳的待匹配水深对应的线段P″i, 1-P″i, 2作为最佳匹配。此时,若满足线段P″i, 1-P″i, 2重心与将线段P1-P2重心的水平距离σi小于σ,则将P″i, 1-P″i, 2与线P1-P2的夹角作为INS的航向误差估计,将σi作为INS的位置误差估计,反之则认为匹配失败,需要重新进行匹配定位。
1.3 面匹配算法 1.3.1 待匹配地形的选取由于MBS的正横波束角通常远小于纵向波束角[8],因此单Ping测量的地形数据只能获得较窄的地形条带。鉴于此,本文首先以一定时间段内测得的水深数据来构建实时测量地形模型,然后以实测地形模型的水平投影面为参照在地形基准图中选取待匹配地形。
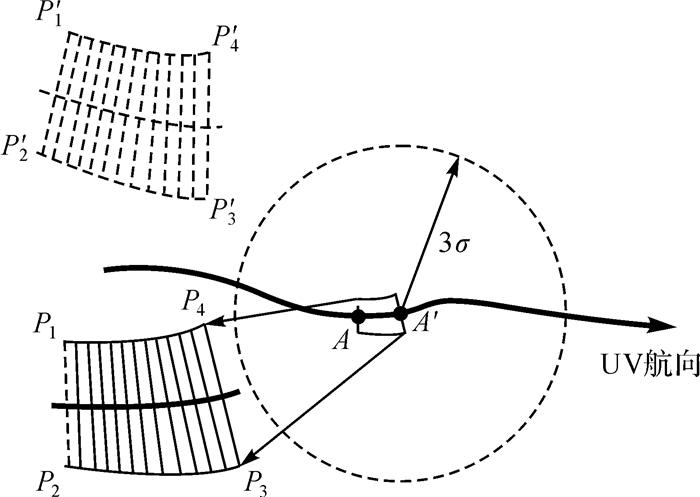
如图 3所示,为待匹配地形面的选取示意图。具体方法为:首先,在水深测量过程中,采用现有的误差改正手段对实测水深进行实时修正[18-20],并选取每一Ping中央波束的水深点组成地形剖面线模型;其次,计算各地形剖面线模型的地形标准差σi,并记录其中的最大值σi, max;再次,计算UV正下方水深值的标准差σunder,并判断σunder与σi, max的关系:当满足σunder≥σi, max时结束采样,并以各地形剖面线构成实测地形模型;最后,以地形剖面线模型的水平投影(如图 3中的线段簇所示)表达局部地形模型的水平投影面P1、P2、P3、P4。
|
| 图 3 待匹配地形面的选取示意图 Fig. 3 Schematic diagram of the selection of terrain |
在获得实测局部地形的水平投影面后,首先根据1.2节线匹配算法提供的航向修正角ωn+1对地形水平投影面P1、P2、P3、P4进行旋转;然后,借鉴文献[10],以旋转后的地形水平投影面为参照,以3σ为最大幅度(σ为INS系统误差限[10]),在基准图中进行采样即可获得待匹配地形(其水平投影面如图 3中P′1、P′2、P′3、P′4所示)。
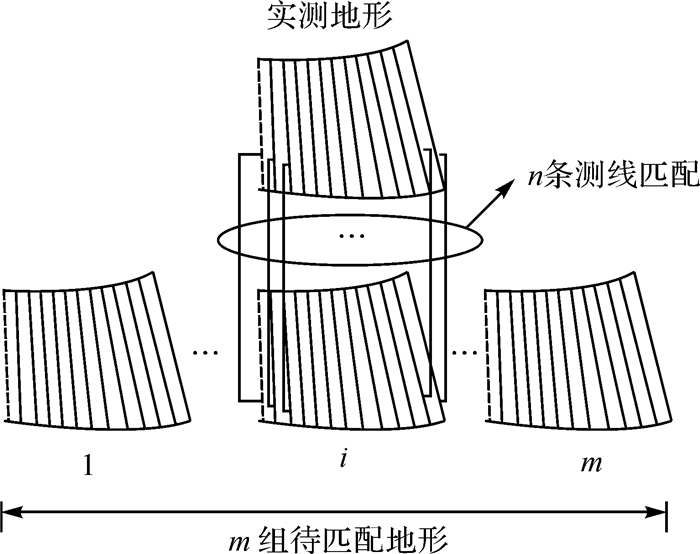
1.3.2 面匹配算子图 4为本文WSS面匹配算子(whole surface similarity)的原理示意图。其基本原理为:首先,计算实测地形剖面与待匹配地形剖面的几何相似性,得到m组n个相似性指标Φi={Ωi, 1, Ωi, 2, …,Ωi, n}, i∈[1, m],其中, Ωi, j表示实测地形与第i个待匹配地形面之间第j条地形剖面的相似性,该相似性描述了实测地形面与待匹配地形面沿UV正横的局部相似性;然后,计算各相似性指标Φi的归一化标准差Pi[19],Pi描述了实测地形面与待匹配地形面沿UV正横的局部相似性在UV纵向上的分布情况,体现了实测地形与待匹配地形之间在UV正横和纵向上的整体相似性,因此可将其作为最优匹配的判别算子。
|
| 图 4 WSS算子的原理示意图 Fig. 4 Schematic diagram of the principle of the algorithm WSS |
计算指标Ωi, j的公式为
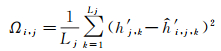 (5)
(5)
式中,h′j, k表示实测地形面中第j条剖面的第k个水深距平值,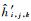
此时,WSS算子的公式为
 (6)
(6)
式中,n表示地形面被划分为n个地形剖面;Ωi表示Ωi, j的平均值。由式(5)和式(6)可知,Ρi的值越小,两地形面之间的相似性越强。
1.4 线面匹配算法的组合策略线面匹配算法的组合策略为:首先,根据文中的线匹配算法计算INS的航向误差ωn+1和定位误差σn+1;其次,以ωn+1和σn+1对INS进行初步校正;再次,根据面匹配算子选取与实测地形相似性最好的待匹配地形面(如图 4中的地形面i所示)作为最优匹配地形面,计算两个面之间的水平位置之差
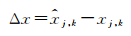 (7)
(7)
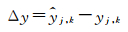 (8)
(8)
式中,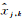
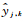
最后,判断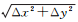
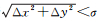
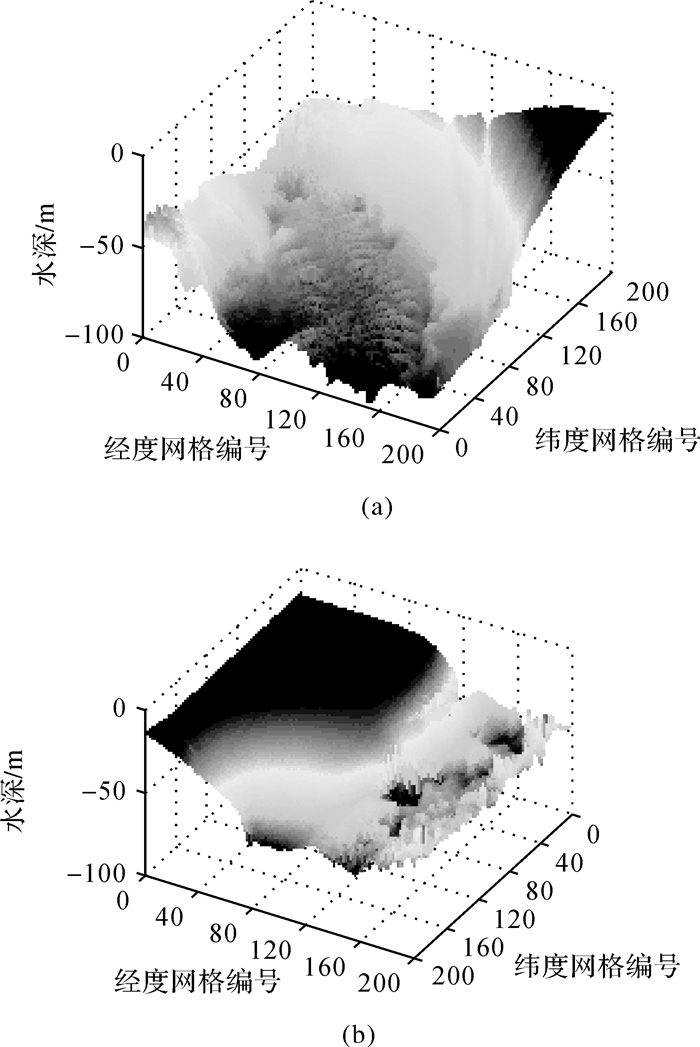
图 5为试验区海底地形的三维显示效果图,其中,图 5(a)表示的海区(本文称为一号海区)最大水深约99.1 m,最小水深约13.5 m,水深标准差约17.0 m,整个海区的地形较为复杂;图 5(b)表示的海区(本文称为二号海区)最大水深约69.4 m,最小水深约14.5 m,水深标准差约为10.3 m,海区的局部地形较为复杂。
|
| 图 5 试验区海底三维示意图 Fig. 5 3D chart of the experimental sea bed |
参照文献[9, 25]对两片海区的水深数据进行处理,采用双线性插值算法构建两组格网距离为40 m×40 m的规则格网模型作为地形匹配基准图。
2.1 定位精度分析参考文献[9, 10, 26],匹配试验的基本参数设置为:INS的初始位置误差为450 m,一号海区UV经向和纬向航速分别为5 m/s和2 m/s,经向和纬向速度误差分别为0.7 m/s和0.5 m/s,经向和纬向加速度均为0.2 m/s2;二号海区UV经向和纬向航速分别为7 m/s和-5 m/s,经向和纬向速度误差分别为0.7 m/s和0.5 m/s,经向和纬向加速度分别为-0.2 m/s2;UV经向和纬向的加速度存在振幅为0.05 m/s2的随机误差,陀螺漂移为0.001°/h,加速度计零偏为0.001 mg[20];航行过程中UV的横摇角、纵摇角和艏摇角度分别在2°以内随机变化;实测水深由构建规则格网模型的原始多波束水深附加振幅为水深值20 dB的随机噪声和1 m的系统误差而得到。
在以上参数设置的基础上,分别采用基于Hu矩的匹配定位算法和本文算法在两个海区进行水下地形匹配定位试验,匹配任务每隔12 s进行一次匹配定位以补偿INS的位置误差。
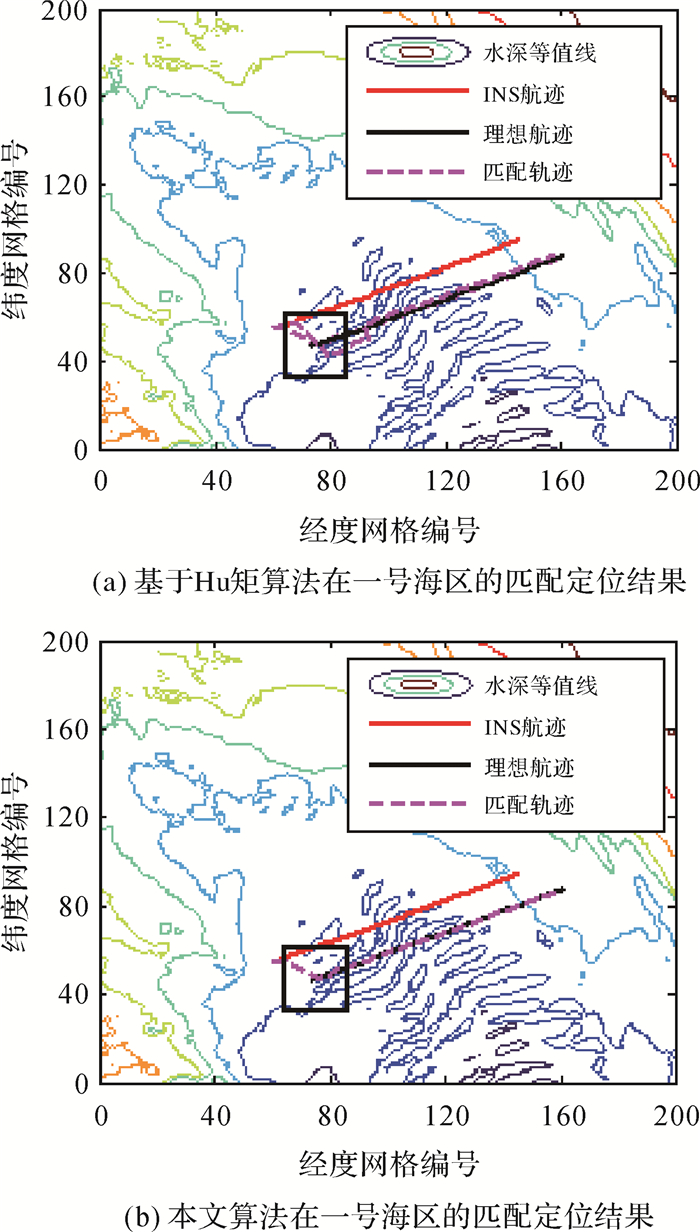
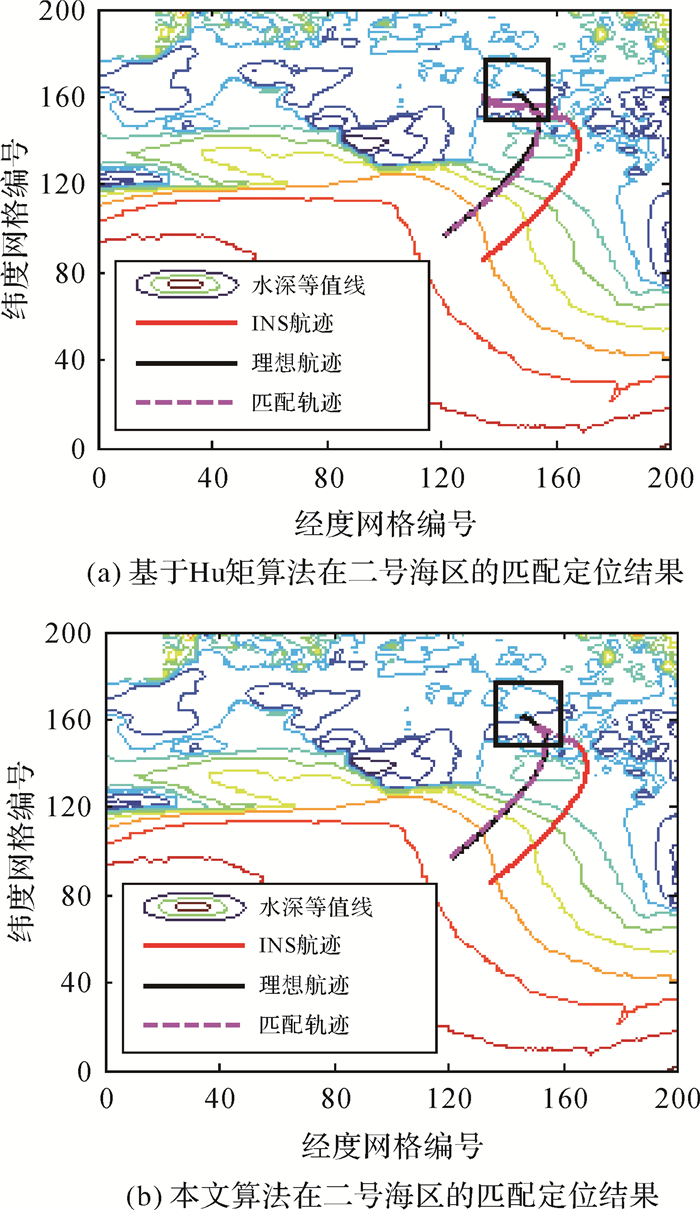
图 6和图 7为两种算法分别在一号海区和二号海区中进行匹配定位的代表性试验结果;其中,在一号海区中UV始终航行于地形较为复杂的区域,航迹起始位置的局部地形标准差为2.04 m(如图 6中黑色矩形所示区域),在二号海区中UV由地形复杂区域航行至地形简单区域,航迹起始位置的局部地形标准差为0.91 m(如图 7中黑色矩形所示);图中黑色实线曲线表示UV的理想航迹[16](根据UV初始位置、速度和加速度计算而来),红色曲线表示根据含误差的UV位置、速度、加速度等参数计算的INS航迹,粉色虚曲线表示根据地形匹配定位修正后的INS航迹。其中,图 6(a)和图 7(a)为基于Hu矩算法的试验结果,图 6(b)和图 7(b)为本文算法的试验结果。
|
| 图 6 一号海区中两种算法的定位精度对比 Fig. 6 Precision comparison of two algorithm in experimental area 1 |
|
| 图 7 二号海区中两种算法的精度对比 Fig. 7 Precision comparison of two algorithms in experimental area 2 |
由图 6(a)和图 7(a)可以看出,粉色虚曲线和黑色曲线在个别位置相差仍然较大,这表明采用基于Hu矩的地形匹配算法作为辅助导航算法时,存在局部地形定位精度较低的情况,这正是由于Hu矩对地形细节辨识能力差导致的;由图 7(b)和图 8(b)可以看出,粉色曲线和黑色曲线基本重合,这表明采用本文所提算法作为辅助导航算法时,其定位精度要优于基于Hu矩的地形匹配算法,这是由于本文所提面匹配算子一方面以实测水深距平与待匹配水深距平的均方差作为相似性度量方法,能够精细表达出实测地形剖面与待匹配地形剖面起伏形态的差异;另一方面该算子兼顾了实测地形面和待匹配地形面沿UV正横和纵向的差异,对地形信息的利用更加充分。
|
| 图 8 具有代表性的10组试验平均定位精度 Fig. 8 Mean location precision of 10 typical experiments |
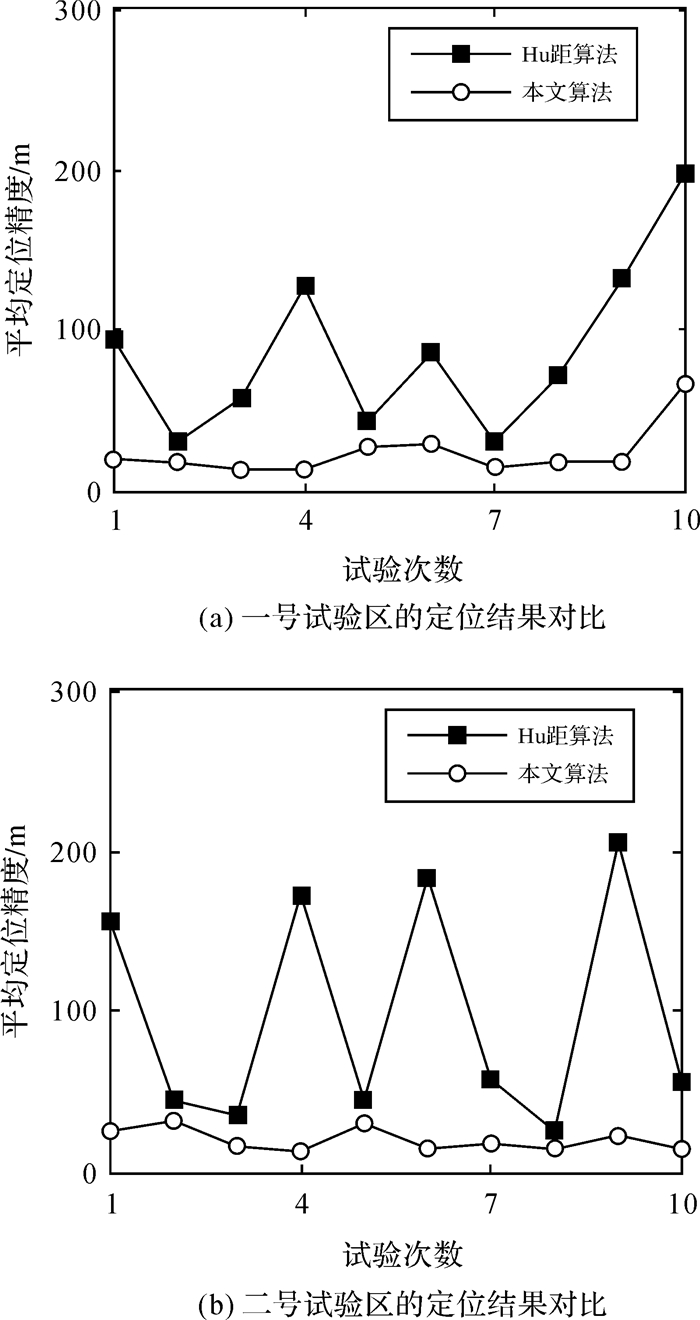
为进一步定量分析本文所提组合算法的匹配定位性能,通过改变UV的初始位置,分别以Hu矩算法和本文算法在两个海区中开展了100次匹配定位试验,分别对两种算法的定位结果进行个例分析和统计分析。图 8为其中10组具有代表性的试验个例,图 9为两种算法定位精度的核密度分布对比图,表 1为两种算法定位关键参数的量化对比结果。其中,图 8中折线

|
| 图 9 两种算法定位精度的核密度分布对比 Fig. 9 Mean location precision of 10 typical experiments |
| m | ||
| 统计参数 | 匹配算法 | |
| Hu距算法 | 本文算法 | |
| 中位数 | 31.93 | 18.06 |
| 平均值 | 89.03 | 24.45 |
| 标准差 | 122.97 | 40.88 |
| 上四分位数 | 16.36 | 9.48 |
| 下四分位数 | 79.01 | 28.29 |
从图 8可以看出,基于Hu矩的地形匹配定位算法,其平均定位精度均在200 m以内,最高平均定位精度为30.1 m,最低平均定位精度为198.8 m,约为规则格网模型网格间距(40 m)的5倍,且各次试验的平均定位精度变化较大(标准差为53.21 m),这一结论与文献[9]一致;与之相比,本文算法的平均定位精度均在50 m以内,其最高平均定位精度为12.7 m,最低平均定位精度为66.4 m,且各次定位试验的精度变化较小(标准差为15.9 m)。这说明,本文算法的平均定位精度及其可靠性要优于对比算法。
由图 9可以看出,相比基于Hu矩算法的核密度分布存在两个峰值(0~100 m的峰值及图 9中黑色矩形所示的峰值),本文所提算法的核密度分布仅为一个峰值;与此同时,本文所提算法定位精度核密度的分布更为集中(分布于0~50 m范围内)。由表 1分析可知,本文所提算法的中位数、平均值、标准差及四分位数均小于对比算法,这一结论与图 9的结果一致。
以上结果表明,相比于基于Hu矩算法,本文所提算法匹配定位精度的分布更为集中,可靠性更好。分析其原因,是由于Hu矩计算的7个不变矩没有顾及局部地形特征在方向性的差异,本文所提面匹配算子以实时测量地形与待匹配地形之间沿正交方向(UV航行方向和UV航行正横方向)上的相似性作为判别依据,顾及了地形特征在方向性的差异,从而使得算法在识别地形相似性上更为准确。
2.2 稳健性分析 2.2.1 地形稳健性分析为了分析本文所提组合算法的稳健性,本文进一步在两个海区中各选取了10个具有不同地形标准差的区域作为试验区,通过改变INS的初始位置在两个海区中分别进行匹配定位试验。
如表 2所示,为两种算法定位精度标准差的统计结果。由表 2可知,在各次试验中,基于Hu矩的地形匹配定位算法,在一号海区中匹配定位精度标准差的最大值为151.71 m,最小值为16.95 m,平均值为72.51 m;在二号海区中匹配定位精度标准差的最大值为183.72 m,最小值为14.03 m,平均值为98.49 m。与之相比,本文算法定位精度的标准差在各次试验中的变化要远小于基于Hu矩的对比算法,在一号海区中匹配定位精度标准差的最大值为98.00 m,最小值为7.91 m,平均值为24.45 m;在二号海区中匹配定位精度标准差的最大值为26.99 m,最小值为6.81 m,平均值为14.48 m。这说明,基于Hu矩算法虽然在个别地形中具有较好的地形稳健性,但在多数地形中的地形稳健性仍然较差。与之相比,本文所提算法在不同地形标准差情况下定位精度的变化更小,算法具有更好的地形稳健性。分析其原因,是由于本文算法既考虑了实测水深剖面和待匹配地形剖面沿UV正横的相似性,又兼顾了这一相似性在UV纵向上的分布,从而给相似性指标赋予了方向性,使得本文所提组合算法在选取实测地形的最优匹配上更具优势。
| m | |||||||
| 试验区编号 | 一号海区 | 二号海区 | |||||
| 地形标准差 | Hu矩 | 本文算法 | 地形标准差 | Hu矩 | 本文算法 | ||
| 1 | 2.22 | 84.13 | 13.51 | 0.6 | 168.83 | 11.83 | |
| 2 | 1.19 | 17.27 | 8.85 | 0.89 | 45.86 | 16.09 | |
| 3 | 0.68 | 46.57 | 9.54 | 1.04 | 29.23 | 16.05 | |
| 4 | 1.38 | 77.77 | 7.91 | 1.08 | 159.01 | 6.81 | |
| 5 | 2.81 | 30.52 | 29.67 | 1.21 | 37.68 | 26.99 | |
| 6 | 2.54 | 104.89 | 38.11 | 1.27 | 174.63 | 11.09 | |
| 7 | 2.55 | 16.95 | 10.26 | 1.38 | 119.99 | 9.44 | |
| 8 | 1.86 | 64.93 | 17.33 | 1.66 | 14.03 | 12.71 | |
| 9 | 1.99 | 151.71 | 11.3 | 1.72 | 183.72 | 19.49 | |
| 10 | 2.52 | 130.38 | 98.0 | 2.94 | 51.96 | 14.25 | |
2.2.2 抗旋转稳健性分析
正如文献[9]中所考虑的一样,由于INS的陀螺漂移和加速度计误差,UV的航向误差会随时间累积,从而导致实测地形与待匹配地形之间存在任意旋转关系。因此,本文在2.1节试验设置的基础上,分别在一号海区和二号海区中随机选择50个匹配初始位置,在保证匹配搜索区落在试验海区范围内的情况下给INS随机增加0~20°的初始航向误差,分别在两个海区中进行50组匹配定位试验。
如图 10所示,为50组匹配试验中定位精度与航向误差构成的箱形图。由图 10可知,INS的航向误差在0~20°变化时,Hu矩算法仍能获得50~100 m的平均定位的精度,这一结论与文献[9]基本一致,但是其定位精度最高为20 m左右,最低为170 m左右,定位精度的变化幅度较大;与之相比,本文所提组合算法的平均定位精度可达20 m,最低精度也在35 m以内,这说明随着航向误差的增加,本文算法的定位精度没有明显的变化。这一试验结果说明:由于本文算法先采用线匹配算法对INS的航向误差和位置误差进行初步校正,再采用对地形细节识别能力更强的面匹配算法进行精匹配,兼顾了线、面匹配算法分别在降低航向误差和提高定位精度上的优势,使得本文算法相比基于Hu矩的地形匹配算法具有更好的抗旋转稳健性。
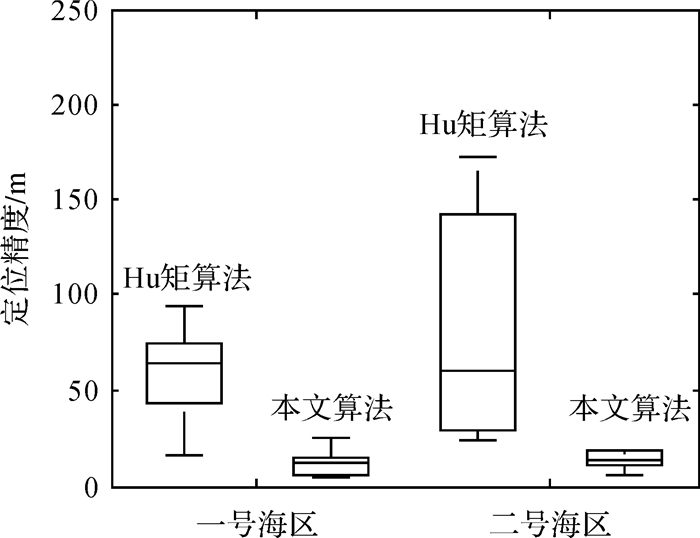
|
| 图 10 定位精度随航向误差变化的箱形图 Fig. 10 Box chart of location precision along with INS course error |
3 结论
通过分析、计算及试验比对,得出如下结论:
(1) 在相同的INS和水深测量误差条件下,相比基于Hu矩的水下地形匹配定位算法,本文所提线面组合的匹配定位算法具有更高的定位精度和可靠性。
(2) 本文所提组合算法首先以线匹配算法对航向误差进行初步校正,然后以面匹配算法对UV进行精确定位,使组合算法具有更好的地形稳健性和抗旋转稳健性。
当然,由于组合算法中的线匹配算法采用遍历搜索的方式来修正INS的航向误差,必然导致匹配效率有所降低;此外,结合其他具体地形可导航性评价方法对本文所提算法的适用性进行分析也是必要的。限于文章篇幅,本文并没有对这些问题展开讨论,这有待于在以后的研究中进一步完善。
| [1] | LI Ye, MA Teng, CHEN Pengyun, et al. Autonomous Underwater Vehicle Optimal Path Planning Method for Seabed Terrain Matching Navigation[J]. Ocean Engineering, 2017(133): 107–115. |
| [2] |
严浙平, 王璐.
UUV水下定位方法的研究现状与进展[J]. 哈尔滨工程大学学报, 2017, 38(7): 989–1000.
YAN Zheping, WANG Lu. Research Status and Progress of UUV Underwater Localization[J]. Journal of Harbin Engineering University, 2017, 38(7): 989–1000. |
| [3] |
张涛, 石宏飞, 陈立平, 等.
基于UKF的SINS/LBL水下AUV紧组合定位技术[J]. 中国惯性技术学报, 2016, 24(5): 638–642.
ZHANG Tao, SHI Hongfei, CHEN Liping, et al. An Underwater Positioning Technology Based on Tightly Coupled SINS/LBL for AUV[J]. Journal of Chinese Inertial Technology, 2016, 24(5): 638–642. |
| [4] |
李翔, 华一新, 张宏, 等.
粗精匹配结合的矢量道路辅助惯性导航算法[J]. 测绘学报, 2017, 46(8): 1034–1046.
LI Xiang, HUA Yixin, ZHANG Hong, et al. Positioning Correction Algorithm of Vector Road Aided Inertial Navigation Based on the Rough/Fine Matching Method[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(8): 1034–1046. DOI:10.11947/j.AGCS.2017.20160469 |
| [5] | MELO J, MATOS A. Survey on Advances on Terrain Based Navigation for Autonomous Underwater Vehicles[J]. Ocean Engineering, 2017(139): 250–264. |
| [6] | AATRE V K. Sonars and ASW Sensors[J]. IETE Technical Review, 1993, 10(2): 81–91. DOI:10.1080/02564602.1993.11437302 |
| [7] | ROEY B Y. Anti-submarine Warfare Search Models[D]. Monterey, California: Naval Postgraduate School, 2016. |
| [8] | JALVING B, MANDT M, HAGEN O K, et al. Terrain Referenced Navigation of AUVs and Submarines Using Multibeam Echo Sounders[R].OSLO: Norwegian Defence Research Establishment, 2004. |
| [9] |
徐晓苏, 岳增阳, 张涛, 等.
基于Hu矩的水下地形二维特征匹配辅助导航方法[J]. 中国惯性技术学报, 2015, 23(3): 363–368.
XU Xiaosu, YUE Zengyang, ZHANG Tao, et al. Method on Underwater Assisted Navigation System Using Two-dimensional Terrain Feature Matching Based on Hu Moments[J]. Journal of Chinese Inertial Technology, 2015, 23(3): 363–368. |
| [10] |
程传奇, 郝向阳, 张振杰, 等.
鲁棒性地形匹配/惯性组合导航算法[J]. 中国惯性技术学报, 2016, 24(2): 202–207.
CHENG Chuanqi, HAO Xiangyang, ZHANG Zhenjie, et al. Robust Integrated Navigation Algorithm of Terrain Aided Navigation/INS[J]. Journal of Chinese Inertial Technology, 2016, 24(2): 202–207. |
| [11] | TEIXEIRA F C, QUINTAS J, MAURYA P, et al. Robust Particle Filter Formulations with Application to Terrain-aided Navigation[J]. International Journal of Adaptive Control and Signal Processing, 2017, 31(4): 608–651. DOI:10.1002/acs.2692 |
| [12] | CHEN Pengyun, LI Ye, SU Yumin, et al. Review of AUV Underwater Terrain Matching Navigation[J]. Journal of Navigation, 2015, 68(6): 1155–1172. DOI:10.1017/S0373463315000429 |
| [13] | ZHOU Ling, CHENG Xianghong, ZHU Yixian, et al. An Effective Terrain Aided Navigation for Low-cost Autonomous Underwater Vehicles[J]. Sensors, 2017, 17(4): 680. DOI:10.3390/s17040680 |
| [14] | SHUAI Xiang, WU Shaochun, LUO Naibin. The Dynamic TERCOM Algorithm of Underwater Positioning Based on Terrain Entropy[J]. Applied Mechanics and Materials, 2014, 644-650: 1774–1777. DOI:10.4028/www.scientific.net/AMM.644-650 |
| [15] | ZHAO Long, GAO Nan, HUANG Baoqi, et al. A Novel Terrain-aided Navigation Algorithm Combined with the TERCOM Algorithm and Particle Filter[J]. IEEE Sensors Journal, 2015, 15(2): 1124–1131. DOI:10.1109/JSEN.2014.2360916 |
| [16] |
徐晓苏, 吴剑飞, 徐胜保, 等.
基于仿射修正技术的水下地形ICCP匹配算法[J]. 中国惯性技术学报, 2014, 22(3): 362–367.
XU Xiaosu, WU Jianfei, XU Shengbao, et al. ICCP Algorithm for Underwater Terrain Matching Navigation Based on Affine Correction[J]. Journal of Chinese Inertial Technology, 2014, 22(3): 362–367. |
| [17] | LIANG Chenhua, CHANG Qing. Weighted Modified Hu Moment in Human Behavior Recognition[J]. Advanced Materials Research, 2013, 765-767: 2603–2607. DOI:10.4028/www.scientific.net/AMR.765-767 |
| [18] |
孙文川, 暴景阳, 金绍华, 等.
一种多波束换能器横摇角度偏差二次校准方法[J]. 武汉大学学报(信息科学版), 2016, 41(11): 1440–1444.
SUN Wenchuan, BAO Jingyang, JIN Shaohua, et al. A Re-calibration Method for Roll Bias of Multi-beam Sounding System[J]. Geomatics and Information Science of Wuhan University, 2016, 41(11): 1440–1444. |
| [19] |
王乐洋, 陈汉清.
多波束测深数据处理的抗差最小二乘配置迭代解法[J]. 测绘学报, 2017, 46(5): 658–660.
WANG Leyang, CHEN Hanqing. Multi-beam Bathymetry Data Processing Using Iterative Algorithm of Robust Least Squares Collocation[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(5): 658–660. DOI:10.11947/j.AGCS.2017.20160491 |
| [20] | LUCIEER V, HUANG Zhi, SIWABESSY J. Analyzing Uncertainty in Multibeam Bathymetric Data and the Impact on Derived Seafloor Attributes[J]. Marine Geodesy, 2016, 39(1): 32–52. DOI:10.1080/01490419.2015.1121173 |
| [21] | MILLS G B. International Hydrographic Survey Standards[J]. International Hydrographic Review, 1998, 75(2): 161–165. |
| [22] |
团文征, 李建成, 裴氏坚贞.
越南海防市近岸海洋水位变化特征分析[J]. 武汉大学学报(信息科学版), 2015, 40(4): 552–557.
VAN CHINH D, LI Jiancheng, BUI THI KIEN TRINH. Analysis on Sea Level Variability Along the Coast of Haiphong Vietnam[J]. Geomatics and Information Science of Wuhan University, 2015, 40(4): 552–557. |
| [23] |
暴景阳, 许军, 于彩霞.
海洋空间信息基准技术进展与发展方向[J]. 测绘学报, 2017, 46(10): 1778–1785.
BAO Jingyang, XU Jun, YU Caixia. Technical Progress and Development Directions of Oceanic Spatial Information Datum[J]. Acta Geodaetical et Cartographica Sinica, 2017, 46(10): 1778–1785. DOI:10.11947/j.AGCS.2017.20170371 |
| [24] |
刘现鹏, 张立华, 贾帅东, 等.
基于自适应格网数字水深模型的水下地形匹配定位算法[J]. 中国惯性技术学报, 2017, 25(4): 488–494.
LIU Xianpeng, ZHANG Lihua, JIA Shuaidong, et al. Underwater Terrain Matching Algorithm Based on Adaptive Grid Digital Depth Model[J]. Journal of Chinese Inertial Technology, 2017, 25(4): 488–494. |
| [25] |
贾帅东, 张立华, 宋国大, 等.
基于区域平均垂直不确定度的自适应网格水深建模方法[J]. 测绘学报, 2012, 41(3): 454–460.
JIA Shuaidong, ZHANG Lihua, SONG Guoda, et al. A Method for Constructing an Adaptive Grid Digital Depth Model Based on Mean Vertical Uncertainty of Area[J]. Acta Geodaetical et Cartographica Sinica, 2012, 41(3): 454–460. |
| [26] |
王巍.
惯性技术研究现状及发展趋势[J]. 自动化学报, 2013, 39(6): 723–729.
WANG Wei. Status and Development Trend of Inertial Technology[J]. Acta Automatica Sinica, 2013, 39(6): 723–729. |



