2. 城市空间信息工程北京市重点实验室, 北京 100044
2. Beijing Key Laboratory of Urban Spatial Information Engineering, Beijing 100044, China
从卫星立体影像获取精确数字表面模型的关键在于影像间的密集匹配,通常按照匹配优化策略的不同主要分为局部和全局匹配算法两种[1]。局部匹配算法通过计算像素的最小匹配代价获取最佳匹配点,其特点是速度快,但在重复纹理或低纹理区域的匹配效果较差,因此不能满足生成高精度数字表面模型的需求。全局匹配算法[2-3]匹配效果较好,但由于算法本身的计算复杂度较高、计算时间较长,因此很难应用到大像幅的遥感影像匹配。文献[4-5]提出的半全局匹配算法在匹配效果和计算效率方面有较好的平衡,而且比较容易实现并行加速,因此被广泛应用于近景[6]、航空[7]和卫星[8-10]影像匹配中。
目前,将半全局匹配算法应用于卫星影像匹配的思路主要有两种:基于物方的OSGM匹配(object-based semi-global matching)和基于像方的SGM匹配。文献[11-12]提出的OSGM匹配算法在物方空间上计算代价矩阵,然后进行代价积聚和最优视差选择得到最终的匹配结果,这种方法省去了核线影像生成的步骤,可以直接应用于多视影像的匹配中。基于像方的SGM匹配算法[13]在影像面上计算代价矩阵,属于严格的逐像素匹配算法。文献[10]利用卫星影像数据对OSGM和SGM算法的匹配效果进行了对比分析,结果表明基于像方SGM算法获取的DSM精度要高于OSGM,且SGM算法可以利用左右视差一致性检查剔除误匹配,因此生成的DSM粗差较少,此外,SGM算法的惩罚系数P2可以根据影像灰度信息自适应调整,也有效地提高了DSM精度。
由于卫星影像的幅宽较大,直接应用SGM算法存在一定的困难。文献[14-15]提出利用影像分块约束视差搜索范围,基于SGM算法逐块获取匹配结果;文献[16]将已有的DEM高程信息反算至核线影像,限制SGM算法的视差空间大小。这两种方法在一定程度上解决了大像幅影像匹配时的难点问题,然而算法本身的计算效率并不高,且每个像素都需要在相同的视差搜索范围内计算匹配代价,造成了误匹配概率的增大。文献[7, 17]提出的tSGM算法在金字塔影像上逐层进行半全局匹配,利用上层匹配结果动态限定每个像素的视差搜索范围,大大地减少了算法的内存开销和计算时间,同时提高了匹配准确度。文献[18]将tSGM算法应用于卫星立体影像匹配取得了较好的结果,但当影像重复纹理信息较多时,tSGM算法在核线范围内获取的顶层匹配结果会受到一定的影响,且会逐层传递到下一层匹配结果上。另外,tSGM算法通过搜索窗口内最大、最小视差来确定视差搜索范围,视差图边缘像素的搜索范围可能超出视差预设最大值,导致计算内存增加,视差边缘处误匹配的概率也会增大。在视差后处理阶段,tSGM算法采用传统的中值滤波算法不能将噪声同细节区别出来,因此视差图的边缘和尖角会受到破坏,导致图像细节模糊。文献[19]利用改进的导向中值滤波替代传统的中值滤波算法有效保护了视差图的边缘信息,其不足之处在于滤波过程中阈值的设置不具备较好的普适性。
针对上述问题,本文提出一种基于改进半全局匹配的高分辨率遥感影像DSM生成方法。该方法利用影像分块策略约束半全局匹配时的初始视差搜索范围,对核线影像块建立金字塔后逐层进行半全局匹配,并引入顾及影像纹理信息的视差图膨胀、腐蚀算法和加权中值滤波算法保护视差图边缘信息,同时减少匹配过程中的内存开销和计算时间。利用WorldView3和资源三号立体影像匹配结果验证了本文方法的有效性。
1 改进半全局匹配的高分辨率遥感影像DSM提取流程本文基于改进半全局匹配的高分遥感影像DSM生成方法主要包括:影像精确定向、核线影像生成、影像密集匹配和前方交会生成DSM 4个部分,流程如图 1所示。

|
| 图 1 高分辨率遥感影像DSM生成流程 Fig. 1 Flowchart of DSM generation from high resolution satellite imagery |
1.1 连接点几何约束下的影像精确定向
高分辨率遥感卫星影像通常采用有理函数模型来描述像点与地面点之间的对应关系,由于卫星影像的RPC模型存在一定的系统误差,需要对有理函数模型进行系统误差补偿。文献[20]采用像方系统误差补偿方法获得了较好的定向结果,其实质是通过对原始的有理函数模型增加补偿项,消除像点坐标上的系统误差,从而提高基于有理函数模型的目标定位精度,其基本原理为
 (1)
(1)
式中,(Δr, Δc)为像点坐标(r, c)的改正值;(Xn, Yn, Zn)为像点对应的地面点坐标;pi(i=1, 2, 3, 4)为关于Xn、Yn、Zn的三阶有理多项式。本文首先获取影像间匹配点,得到立体影像间相对几何约束关系后对定向模型进行系统误差补偿,几何约束关系定义为影像面上的仿射变换
 (2)
(2)
式中,(e0, e1, e2, f0, f1, f2)是仿射变换系统误差补偿参数。在式(1)和式(2)的基础上,采用文献[21]中的方法对每个连接点建立误差方程,然后采用直接列改化法方程的策略消除一类连接点地面坐标未知数,再基于传统光束法平差求解即可得到精确的定向模型。
1.2 核线影像生成为了提高影像匹配的精度并减少匹配时间,在立体影像匹配前需要对影像进行核线校正,将二维匹配搜索降低为一维搜索。通常情况下,高分遥感影像的核线类似于双曲线,但在局部范围内可以近似看作直线[22]。鉴于此,本文利用立体像对的连接点计算得到影像间的仿射变换模型,在模型的基础上对原始影像进行分块处理,对于左影像块利用仿射变换关系可找到相应的右影像块,分块完成后利用文献[23]中的投影轨迹法生成核线影像对,以保证相邻核线影像块生成的视差图之间不产生空隙,块与块之间保证一定的重叠。通过对影像进行分块,一方面可以减小核线影像的误差,另一方面,通过将视差搜索限定在一个较小的区间,可以减小重复纹理区域因视差搜索范围过大造成的误匹配。
1.3 影像密集匹配原始的SGM算法[4]通过建立全局能量函数,使能量函数达到最小时获取潜在的最优视差。能量函数为
 (3)
(3)
全局能量函数E(D)由数据项和平滑项组成。式(3)右侧第1项为数据项,表示所有像素点的匹配代价之和,C(p, Dp)表示左影像像素p视差为Dp时与右影像点的匹配代价[24]。第2项为平滑项,其目的是对像点p临近视差差值等于1的像素q增加惩罚数P1。这使得相邻像素点的视差尽可能的一致,其中T[·]为一个判断函数,当判断条件为真时返回1,否则为0。第3项为平滑项,对像素点p临近视差差值大于1的像素点q给予更大的惩罚数P2。通常P2随影像梯度的变化而改变,P2不能过大,否则视差边缘会被过度平滑。
SGM算法首先计算左影像上每个像素在视差搜索范围内的匹配代价,组成代价矩阵。代价矩阵维度为r×c×(dmax-dmin),其中r为影像行数,c为影像列数,dmax、dmin表示视差搜索的上下界。计算完代价矩阵后,对代价矩阵上的每个点考虑从多个方向(8或者16方向)进行积聚,如图 2所示。

|
| 图 2 视差空间上代价积聚过程 Fig. 2 Aggregation of costs in disparity space |
对像素点p,其在r方向上的积聚函数为
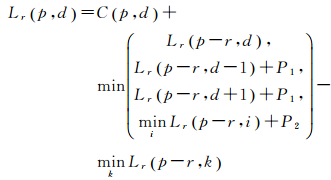 (4)
(4)
式中,右侧第1项表示像素点p视差为d时的匹配代价;第2项表示像素p在r方向上的前一个像素代价积聚的最小值(包含惩罚系数);最后一项减去积聚方向上的最小代价值保证了Lr(p, d) < Cmax(p, d)+P2,这一项对最优路径的选择没有影响。通过将不同方向上的代价积聚值进行求和后即可得到最终的代价积聚值,代价积聚求和公式为
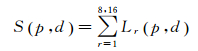 (5)
(5)
完成代价矩阵的积聚后,在视差搜索范围内利用胜者为王(winner take all,WTA)算法获取积聚值最小位置即为当前像素的最优视差,最优视差选择的公式见式(6),D为最终的视差图
 (6)
(6)
对于大像幅的高分遥感影像而言,将整条核线作为视差搜索范围时应用半全局匹配算法存在较大的困难。一方面代价矩阵计算和代价积聚过程所需的内存开销较大,计算时间也相对较长;另一方面,由于每个像素都在整条核线上计算匹配代价,当影像中存在较多低纹理或重复纹理信息时,会造成误匹配概率的增大。
文献[7]提出tSGM算法,通过在金字塔影像上逐层进行半全局匹配,利用本层匹配结果限制下一层匹配时的视差搜索边界,从而动态限定每个像素的视差搜索范围。tSGM算法确定像素的视差搜索范围时,首先在视差像素D(x)周围窗口中搜索视差最大值dmax、最小值dmin,然后判断最大、最小视差差值是否超出最大预设搜索范围R。如果dmax-dmin < R,此时上边界范围设置为tmax=dmax-D(x)+2,下边界范围设置为tmin=D(x)-dmin+2,如果超出最大预设范围,此时将视差搜索范围定义为式(7)
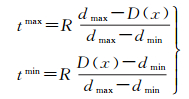 (7)
(7)
确定了本层影像的视差搜索边界后,将视差上下边界放大一倍作为下一层核线影像匹配时的视差搜索范围,然后逐层进行半全局匹配得到最终的匹配结果。
这种搜索窗口内视差最大、最小值直接确定视差边界的方法存在一定的不足。首先,在视差变化较大的区域(地物边缘处),由于像素周围窗口中最大、最小的视差值存在较大的变化,因此会造成视差边缘处的像素误匹配概率的增大;其次,视差边缘处的搜索范围较大时,会影响代价矩阵整体的内存开销,导致计算时间增加。
本文提出一种顾及影像纹理信息的视差图膨胀、腐蚀算法约束视差搜索范围。其基本原理是在获取窗口中视差最大、最小值的同时,记录最大、最小视差值对应核线影像上的像素灰度,依据灰度变化量与视差值的变化量存在正相关的关系,将视差上下边界搜索范围定义为
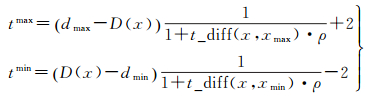 (8)
(8)
式中,dmax、dmin分别为视差像素D(x)膨胀、腐蚀后的视差值,其计算公式为
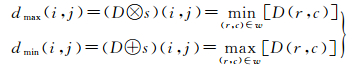 (9)
(9)
式中,ρ表示弱化因子(本文取0.2),其作用是减弱灰度差对搜索边界的影响;t_diff(x, xmax)、t_diff(x, xmin)分别为当前像素x与最大、最小视差值对应像素灰度差的绝对值,计算公式为
 (10)
(10)
式中,D为视差图像素值;s为结构元素;D⊗s为视差图腐蚀操作;D⊕s为视差图膨胀操作;dmax(i, j)、dmin(i, j)分别为膨胀、腐蚀后视差图上索引为(i, j)的视差值;w为结构元素对应的窗口大小。
将纹理信息纳入视差搜索范围的判定中,可以进一步缩小视差搜索范围,尤其是在视差变化较大的区域,能够将视差搜索范围限定在一个较为合理的区间内,修改后的视差搜索范围定义为
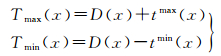 (11)
(11)
式中,Tmax(x)、Tmin(x)分别为视差上下边界。需要说明的是,当搜索窗口内存在多个最大或者最小的视差像素时,此时计算最大的视差tmax作为视差上边界搜索范围,最小的视差tmin作为视差下边界搜索范围。
图 3为tSGM和顾及影像纹理信息的视差图膨胀腐蚀算法获取的视差上下边界。可以看出,在视差变化较大的像素处,顾及纹理信息的膨胀、腐蚀算法得到的视差上下搜索边界范围更小,最大范围小于20个像素(见图 3中虚线框1),而tSGM算法的最大视差搜索范围基本达到了60个像素(见图 3中虚线框2),说明顾及影像纹理信息的视差图膨胀腐蚀算法能够更好地确定像素的视差搜索范围。

|
| 图 3 tSGM和本文方法的视差搜索范围对比 Fig. 3 Contrast of tSGM and the proposed method of parallax search |
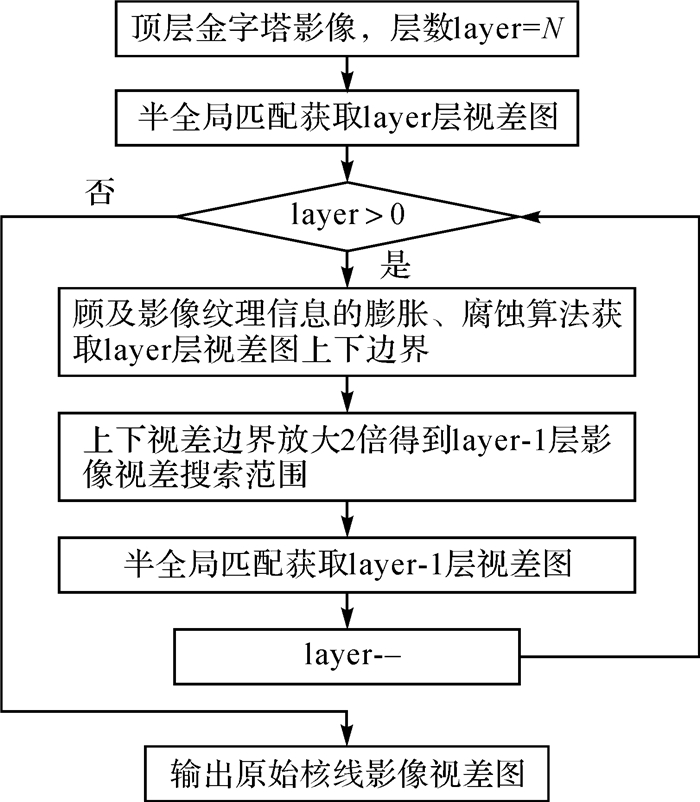
结合顾及影像纹理信息的视差图膨胀腐蚀算法,本文提出一种改进的半全局算法。首先利用影像分块策略约束初始视差搜索范围,减小影像重复纹理信息造成的误匹配,然后对核线影像块建立金字塔,在金字塔影像上逐层进行半全局匹配,匹配过程中引入顾及影像纹理信息的视差图膨胀、腐蚀算法约束每一层影像的视差搜索范围,逐层得到最终匹配结果,改进的半全局匹配算法流程如图 4所示。
|
| 图 4 改进的半全局匹配算法流程 Fig. 4 Flowchart of modified semi-global matching |
在顶层金字塔核线影像上进行半全局匹配时,初始视差搜索范围根据影像缩放比例进行设置(例如原始视差搜索范围为128,对影像块构建两层金字塔后初始视差搜索范围为32),设置了初始视差搜索范围后,采用9×7窗口的Census变换[25]作为代价函数计算代价矩阵,然后从16个方向对代价矩阵进行代价积聚,最后选取像素的最优视差形成初始视差图。
为了确定layer-1层影像的视差搜索范围,首先利用顾及影像纹理信息的视差图膨胀、腐蚀算法对layer层视差图进行膨胀操作得到视差上界搜索范围tmax,腐蚀后得到视差下界搜索范围tmin,膨胀腐蚀的窗口大小为7×7,然后对视差搜索边界放大一倍后作为layer-1层影像的视差搜索上下界。例如对layer层视差值为d的像素p,其在第layer-1层影像上的视差搜索范围为[Tmin(p), Tmax(p)],其中Tmin(p)=2(d-tmin(p)),Tmax(p)=2(d+tmax(p))。需要说明的是,对于layer层视差图上的无效像素,将其膨胀后的视差值减去32作为视差搜索下边界范围。
利用上述方法确定layer-1层的视差搜索边界后,在视差搜索范围内计算动态代价矩阵,然后从8个方向对代价矩阵进行积聚。积聚过程中由于当前像素和临近像素的视差搜索区可能仅有部分重叠或者没有重叠,可能导致Lr(p-r, d+k)不存在,因此将代价积聚公式修改为
 (12)
(12)
积聚完成后在代价积聚矩阵上选择最优视差即可得到本层视差图。
上述匹配过程得到的每一层视差图可能含有匹配粗差,因此每一层影像匹配结束时需要交换左右影像获取视差图,剔除左右视差差值大于1的像素,最后对视差图进行滤波后得到最终的视差结果。对视差图滤波处理时,本文对文献[19]中的导向中值滤波算法进行改进,不采用固定阈值判断邻域范围内有效像素,而是在计算邻域范围内的视差中值时,将像素的灰度差值信息视为权值(灰度差越大则对应的视差像素权值就越小),采用加权中值滤波保护视差图细节信息。加权中值滤波算法的原理为
 (13)
(13)
式中,dis为视差像素;(r, c)为当前像素位置;med代表中值运算;◇为复制算子;W(r, c)是以(r, c)为中心的滤波窗口区域。计算当前像素的滤波结果时,首先计算核线影像上当前像素与3×3邻域窗口内像素灰度差的绝对值diff(i, j)=|grey(r, c)-grey(i, j)|,根据差值大小为视差图窗口内第(i, j)像素分配权值wij=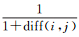
图 5显示了改进的半全局匹配算法和tSGM算法获取的视差图。可以看出,相比于tSGM算法,本文方法更好地保护了视差图的边缘和尖角(如椭圆1、2所示),且有效像素数要多于tSGM算法(如椭圆3所示)。

|
| 图 5 tSGM和本文方法计算的视差图 Fig. 5 Disparity maps computed by SGM and the proposed method |
表 1为相同硬件测试环境下3种算法的匹配时间统计结果(3种算法的代价矩阵计算、代价积聚和最优视差选择过程进行了并行加速[26])。从匹配效率上看,本文匹配算法效率要高于tSGM和SGM算法。需要说明的是,试验时仅对影像建立了两层金字塔,当金字塔层数增多时本文方法和tSGM算法计算时间相差不大。
| 影像分辨率652×665 | 初始视差搜索范围/pixel | 代价矩阵计算用时/s | 8个路径代价积聚用时/s | 最优视差选择用时/s | 总时间/s |
| 本文算法 | 32 | 0.14 | 0.93 | 0.085 | 1.15 |
| tSGM算法 | 326 | 0.26 | 2.51 | 0.087 | 2.86 |
| SGM算法 | 652 | 0.61 | 3.59 | 0.11 | 4.31 |
采用改进的半全局匹配算法获取视差图后,利用核线影像与原始影像之间的对应关系,逐像素地将视差图计算出的同名像点反算至原始影像,再基于前方交会原理[27]即可获取物方密集点云。
2 试验与分析试验选取的第1组数据为阿曼首都马斯喀特地区的WorldView 3下视与后视立体像对,影像分辨率为0.4 m,获取时间为2014年10月,影像像幅大小为12 984×12 928,立体影像的基高比为0.725 8。由于缺少该区域精确的DSM作为基准参考,因此将本文算法和商业软件ENVI5.4的SGM密集匹配模块以及ERDAS2016的Tridicon SGM模块进行相对精度和计算效率的对比分析。立体影像和本文方法生成的DSM如图 6所示。

|
| 图 6 WorldView 3全色立体像对和DSM Fig. 6 Panchromatic stereo images of WorldView-3 and DSM |
第2组数据为法国圣马克西姆地区的资源三号前视与后视立体影像,影像分辨率为3.5 m,获取时间为2014年8月,像幅大小为16 306×16 384。该数据配套了同地区航空影像获取的高精度DSM,分辨率为10 m,可作为绝对高程参考数据评价本文方法生成的DSM高程精度。资源三号立体影像和本文方法生成的DSM如图 7所示(本文方法生成的DSM在水域和影像无效值区域进行了掩膜处理)。

|
| 图 7 ZY-3全色立体像对和DSM Fig. 7 Panchromatic stereo images of ZY-3 and DSM |
基于Win10 64位系统采用VC++2013开发了密集匹配算法,并使用OpenMP对算法的金字塔影像构建、顾及纹理信息的视差图膨胀、腐蚀算法、代价矩阵计算、代价积聚、最优视差选择、视差一致性检查和加权中值滤波过程进行了并行加速。试验使用的硬件平台为华硕PU403UF笔记本,处理器为Intel i7-6500U、主频2.5 GBHz,内存8 GB。
2.1 连接点几何约束的RPC区域网平差为验证本文基于连接点几何约束的区域网平差方法的有效性,在WorldView 3立体影像四角选取4个控制点,同时利用SIFT特征提取算子获取21对同名像点,采用区域网平差方法求解系统误差补偿参数,然后利用补偿的有理函数模型将同名点交会出的地面点反投影至左右影像,统计像点反投影误差的最大值、平均值和标准差(表 2)。
| pixel | |||||
| 误差 | 左影像 | 右影像 | |||
| 行方向 | 列方向 | 行方向 | 列方向 | ||
| 最大误差 | 0.350 6 | 0.653 4 | 0.356 7 | 0.690 3 | |
| 平均误差 | 0.169 3 | 0.337 9 | 0.176 1 | 0.347 4 | |
| 标准差 | 0.102 5 | 0.169 0 | 0.100 7 | 0.180 3 | |
从表 2的试验结果可以看出,经过连接点几何约束的RFM区域网平差后,像点坐标的反投影误差在行方向上标准差仅为0.1个像素,列方向上最大为0.18个像素,达到了亚像素级精度,可以满足生成核线影像的要求。
2.2 核线影像生成为验证本文方法生成核线影像的精度,在WorldView 3影像上选取地形高差较大的城区和高差较小的平地区域的核线影像,利用SIFT算子提取核线影像上同名像点,并采用最小二乘匹配精化后得到精确的同名点坐标。通过比较同名像点的y视差差值作为误差结果,对误差进行统计分析,剔除不符合正态分布的粗差点后计算中误差作为核线影像精度评价指标。表 3为上下视差的精度评价结果。
| pixel | |||
| 试验区 | 最大绝对值误差 | 平均绝对值误差 | 标准差 |
| 平坦地区 | 0.637 1 | 0.282 0 | 0.182 5 |
| 城区 | 0.734 3 | 0.297 3 | 0.309 1 |
从表 3可以看出,本文方法在城区和平坦地区生成的核线影像上下视差标准差在0.3个像素左右,可以满足核线影像的要求。
2.3 DSM生成及精度分析 2.3.1 WorldView 3生成的DSM精度对比分析本文对核线影像块构建两层金字塔后进行密集匹配。为保证ENVI5.4的SGM密集匹配模块、ERDAS2016的Tridicon SGM模块和本文匹配方法对CPU具有相同的利用率,将本文密集匹配算法设置为4线程并行加速(Envi和ERDAS的密集匹配模块默认为4线程并行),Envi和ERDAS的匹配参数按默认的设置。最后,将3种方法生成的密集点云统一栅格化为1 m分辨率的DSM后进行对比分析。图 8、9为平坦地区和城区的DSM对比结果。需要说明的是,本文方法生成的DSM在影像水域和无效值区域进行了掩膜处理。

|
| 图 8 平坦地区DSM对比分析 Fig. 8 Comparison of DSM in planer area |

|
| 图 9 城区DSM对比分析 Fig. 9 Comparison of DSM in city area |
从图 8平坦地区的对比结果可以看出,本文方法和ERDAS生成的DSM均能保持完整地表形态,而Envi生成的DSM在屋顶上存在缺失现象,造成房屋不完整(图 8中椭圆区域1)。从DSM的平滑性可以看出,ERDAS生成的DSM平滑性最好,本文方法结果介于ERDAS和Envi之间,Envi生成的DSM在屋顶和路面上存在较多的噪声(图 8中椭圆区域1、2)。这主要是由于屋顶和路面属于重复纹理区域,在这些区域的像素匹配代价较为相似,匹配错误率较高。比较图 9城区的DSM可以看出,3种方法生成的DSM在水域均存在较多噪声,原因和屋顶与路面类似。从图 9中建筑物的DSM可以看出,由于采用顾及纹理信息的视差图膨胀腐蚀算法和加权中值滤波算法,本文方法生成的DSM能够更好地保持建筑物的边缘信息(图 9中椭圆区域1、2、3)。在建筑物遮挡的阴影区域,本文方法存在匹配缺失现象(图中椭圆区域1、2),这种现象在ENVI和ERDAS生成的DSM上并不明显。将ENVI和ERDAS生成的DSM与正射影像图叠加后发现,DSM上建筑物区域的边界范围扩大,猜测可能是ENVI和ERDAS的密集匹配算法对建筑物阴影区域的DSM进行了填充处理。
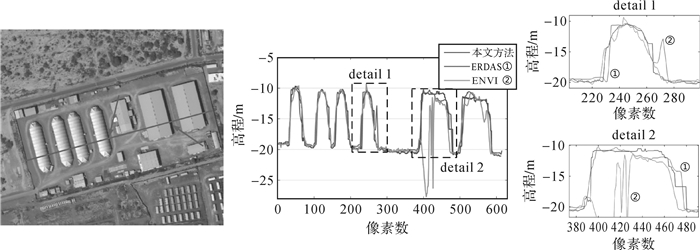
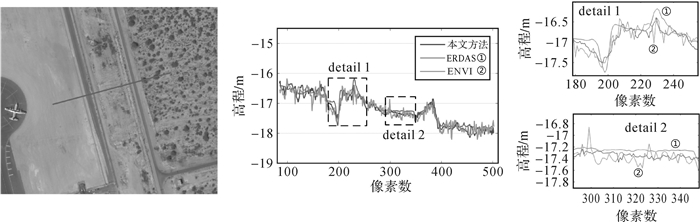
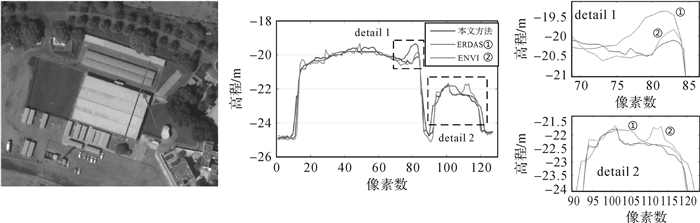
为评价本文方法生成的DSM在垂直方向上的匹配效果,选取典型地物的高程断面进行3种方法的对比分析。图 10为连续的房屋断面,可通过4个连续的弧形屋顶和两个斜坡屋顶轮廓反映DSM的垂直精度;图 11为平坦路面的断面,从断面曲线的趋势和平滑性可以间接反映DSM的垂直精度;图 12为弧形棚房断面,可以根据屋顶断面曲线轮廓反映DSM垂直精度。
|
| 图 10 3种方法获取的连续房屋断面和局部细节图 Fig. 10 The profiles of continuous house section as well as superposition of details derived from three methods |
|
| 图 11 3种方法获取的路面断面和局部细节图 Fig. 11 The profiles of pavement section as well as superposition of details derived from three methods |
|
| 图 12 3种方法获取的棚房断面叠加和局部细节图 Fig. 12 The profiles of shed building section as well as superposition of details derived from three methods |
从图 10弧形屋顶和斜坡屋顶的整体断面曲线可以看出,本文方法和ERDAS生成的DSM能够较好地反映屋顶的整体轮廓,而Envi结果在斜坡屋顶上存在较多的误匹配导致屋顶形态丢失,detail 1和detail 2为弧形屋顶和斜坡屋顶的局部放大区域。从局部细节可以看出,ENVI生成的DSM平滑性不佳,且有一定的粗差产生,ERDAS在房屋遮挡的阴影区域和屋顶边缘处(图 10中箭头指向处)效果不好,本文方法在这些区域均表现出了较好的匹配结果。这主要是由于本文方法采用顾及纹理信息的视差图膨胀、腐蚀算法更好地确定了这些区域的视差搜索范围,使得误匹配率降低,而且在视差图后处理时利用加权中值滤波算法,较好地保持了屋顶的边缘信息。从图 11路面断面曲线的整体平滑度可以看出,本文方法获取的DSM断面曲线平滑度要优于Envi,ERDAS的平滑效果最好,但从局部细节可以看出,ERDAS的断面曲线整体趋势存在一定的偏差,可能是由于ERDAS对DSM进行了过渡平滑处理的缘故。比较图 12棚房的断面曲线可以看出,3种算法均能较好地反映出屋顶的整体轮廓,从detail 1和detail 2房屋边缘的局部细节可以看出,本文方法较好地保护了房屋的边缘信息,在DSM的整体效果和局部效果上都具有较好的结果。
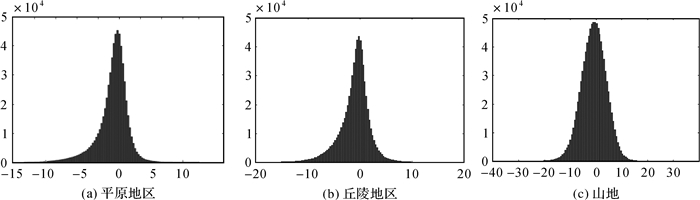
2.3.2 ZY-3生成的DSM精度分析为进一步定量评价本文方法生成DSM的绝对精度,选取资源三号影像上平原、丘陵和山地区域的DSM与参考DSM进行误差对比分析,绝对值误差分布见图 13-图 15,图 16为误差直方图统计结果。

|
| 图 13 平原地区DSM绝对值误差分布图 Fig. 13 The absolute error map of DSM in plain area |

|
| 图 14 丘陵地区DSM绝对值误差分布图 Fig. 14 The absolute error map of DSM in hill area |

|
| 图 15 山地区域DSM绝对值误差分布图 Fig. 15 The absolute error map of DSM in mountain area |
|
| 图 16 不同试验区域下的高程误差直方图 Fig. 16 Elevation error histogram under different experimental areas |
从图 13-图 15绝对值误差分布可以看出,本文方法获取的DSM在大部分区域内误差较小,绝对值误差均值最大的为山区,这主要是由于山体阴影处匹配误差较大。对图 16中误差进行统计分析,剔除不符合正态分布的误差后,计算一定范围内误差的均值、绝对值均值和均方根误差来定量评定本文方法生成的DSM精度,结果如表 4所示。从DSM的均方根误差结果可以看出,本文方法生成的DSM在平原地区均方根误差较小,精度较高,在山区接近于1.5倍GSD;从误差的平均值可以看出,3个地区的误差均值均表现为负值,推测其原因可能是影像定向结果中存在一定的系统误差,从而传递到了最终生成的DSM中。
| m | |||
| 试验区域 | 高程精度 | ||
| 平均误差 | 绝对值均值误差 | 均方根误差 | |
| 平原 | -1.6 | 2.71 | 3.69 |
| 丘陵 | -1.71 | 3.22 | 4.66 |
| 山区 | -1.18 | 3.96 | 5.62 |
2.4 计算效率和内存开销对比分析
为定量评价本文密集匹配算法的性能,在相同的硬件测试环境下将本文方法和Envi与ERDAS密集匹配方法进行计算效率和内存开销的对比分析,其中计算效率通过计算时间来反映,内存开销通过比较计算过程中内存稳定时的最大值,结果见表 5。
| WV3立体像对12 984×12 928 | 输入 | 模块功能 | 输出 | 内存大小/GB | 计算时间/min |
| 本文方法 | 区域网平差后的立体像对 | 密集匹配+前方交会 | 密集点云 | 5.46 | 11 |
| Envi | 原始立体像对 | 区域网平差+密集匹配+前方交会 | 密集点云+DSM影像 | 5.69 | 9 |
| ERDAS | 区域网平差后的立体像对 | 密集匹配+前方交会 | 密集点云 | 4.47 | 19 |
由于本文方法和ERDAS的输入输出数据相同,因此具有较好的对比性,由表 5的对比结果可以看出,本文方法的计算效率要高于ERDAS,但计算时的内存开销也相对较多。与Envi对比后发现,本文方法计算效率要略低于Envi,但在内存开销上要优于Envi,由于Envi的密集匹配模块自带了区域网平差功能,因此综合计算效率要高于本文方法。从整体上看,本文方法在计算效率和内存开销方面有较好的平衡。
3 结论本文提出了一种基于改进半全局匹配的高分辨率遥感影像DSM生成方法,针对影像定向模型中存在的系统误差,利用影像间连接点几何约束关系对有理函数模型系统误差进行了补偿,获得了亚像素级的定位精度;生成核线影像的过程中,通过对原始影像分块后基于投影轨迹法获取到了0.3个像素精度的核线影像;在密集匹配阶段,为了减小代价空间大小和计算时间,对影像建立金字塔后逐层进行半全局匹配,匹配过程中引入顾及影像纹理信息的视差图膨胀腐蚀算法约束视差搜索范围,更好地保留地物的边缘特性;最后,采用加权中值滤波算法对视差图进行滤波,基于前方交会原理得到DSM。利用WorldView 3和资源三号立体影像进行了试验,结果表明:本文算法获取的DSM无论在高程精度或地物边缘特性的保留上都有较好的结果,计算效率和内存开销方面也具有较好的平衡。
| [1] | SCHARSTEIN D, SZELISKI R. A Taxonomy and Evaluation of Dense Two-frame Stereo Correspondence Algorithms[J]. International Journal of Computer Vision, 2002, 47(1-3): 7–42. |
| [2] | KOLMOGOROV V, MONASSE P, TAN P. Kolmogorov and Zabih's Graph Cuts Stereo Matching Algorithm[J]. Image Processing on Line, 2014(4): 220–251. |
| [3] | FELZENSZWALB P F, HUTTENLOCHER D P. Efficient Belief Propagation for Early Vision[C]//Proceedings of 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington, DC, USA: IEEE, 2004: 261-268. |
| [4] | HIRSCHMULLER H. Accurate and Efficient Stereo Processing By Semi-global Matching and Mutual Information[C]//Proceedings of 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego, CA, USA: IEEE, 2005: 807-814. |
| [5] | D'ANGELO P. Improving Semi-global Matching:Cost Aggregation and Confidence Measure[J]. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2016, XLI-B1: 299–304. DOI:10.5194/isprsarchives-XLI-B1-299-2016 |
| [6] | WENZEL K. Dense Image Matching for Close Range Photogrammetry[D]. Stuttgart: University of Stuttgart, 2016. |
| [7] | ROTHERMEL M, WENZEL K, FRITSCH D, et al. SURE: Photogrammetric Surface Reconstruction From Imagery[C]//Proceedings of LC3D Workshop. Berlin: [s.n.], 2012. |
| [8] | KUSCHK G, D'ANGELO P, QIN R, et al. DSM Accuracy Evaluation for the ISPRS Commission Ⅰ Image Matching Benchmark[J]. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2014, XL-1: 195–200. DOI:10.5194/isprsarchives-XL-1-195-2014 |
| [9] | D'ANGELO P. Evaluation of ZY-3 for DSM and Ortho Image Generation[J]. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2013, XL-1/W1: 57–61. DOI:10.5194/isprsarchives-XL-1-W1-57-2013 |
| [10] | GHUFFAR S. Satellite Stereo Based Digital Surface Model Generation Using Semi Global Matching in Object and Image Space[J]. ISPRS Annals of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2016(Ⅲ-1): 63–68. |
| [11] | BETHMANN F, LUHMANN T. Semi-global Matching in Object Space[J]. ISPRS-international Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2015, XL-3/W2: 23–30. DOI:10.5194/isprsarchives-XL-3-W2-23-2015 |
| [12] | LUHMANN T, BETHMANN F, HASTEDT H. Dense Pointclouds from Combined Nadir and Oblique Imagery by Object-based Semi-global Multi-image Matching[D]. Oldenburg: Jade University of Applied Sciences, 2017. |
| [13] | HIRSCHMULLER H. Stereo Processing By Semiglobal Matching and Mutual Information[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(2): 328–341. DOI:10.1109/TPAMI.2007.1166 |
| [14] | TATAR N, SAADATSERESHT M, AREFI H, et al. Quasi-epipolar Resampling of High Resolution Satellite Stereo Imagery for Semi Global Matching[J]. ISPRS-International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2015, XL-1-W5: 707–712. DOI:10.5194/isprsarchives-XL-1-W5-707-2015 |
| [15] |
张春森, 吕佩育, 郭丙轩.
基于控制点约束影像的密集匹配及其在考古发掘中的应用[J]. 武汉大学学报(信息科学版), 2015, 40(12): 1575–1581.
ZHANG Chunsen, LÜ Peiyu, GUO Bingxuan. Based GCP-SGM Algorithm and Its Application in Scene 3D Reconstruction of Archaeological Excavation Site[J]. Geomatics and Information Science of Wuhan University, 2015, 40(12): 1575–1581. |
| [16] |
张彦峰.利用多条件约束的航空影像逐像素密集匹配算法研究[D].北京: 中国测绘科学研究院, 2014. ZHANG Yanfeng. Pixel-wise Dense Matching of Aerial Images with Multi-conditional Constraints[D]. Beijing: Chinese Academy of Surveying and Mapping, 2014. http://cdmd.cnki.com.cn/Article/CDMD-86001-1014330447.htm |
| [17] | ROTHERMEL M. Development of A SGM-based Multi-view Reconstruction Framework for Aerial Imagery[D]. Stuttgart: University of Stuttgart, 2016. |
| [18] | GONG K, FRITSCH D. A Detailed Study about Digital Surface Model Generation Using High Resolution Satellite Stereo Imagery[J]. ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2016, Ⅲ-1: 69–76. |
| [19] |
闫利, 费亮, 陈长海, 等.
利用网络图进行高分辨率航空多视影像密集匹配[J]. 测绘学报, 2016, 45(10): 1171–1181.
YAN Li, FEI Liang, CHEN Changhai, et al. A Multi-view Dense Matching Algorithm of High Resolution Aerial Images Based on Graph Network[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(10): 1171–1181. DOI:10.11947/j.AGCS.2016.20160068 |
| [20] |
刘军, 张永生, 王冬红.
基于RPC模型的高分辨率卫星影像精确定位[J]. 测绘学报, 2006, 35(1): 30–34.
LIU Jun, ZHANG Yongsheng, WANG Donghong. Precise Positioning of High Spatial Resolution Satellite Images Based on RPC Models[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(1): 30–34. DOI:10.3321/j.issn:1001-1595.2006.01.007 |
| [21] |
李德仁, 张过, 江万寿, 等.
缺少控制点的SPOT-5 HRS影像RPC模型区域网平差[J]. 武汉大学学报(信息科学版), 2006, 31(5): 377–381.
LI Deren, ZHANG Guo, JIANG Wanshou, et al. SPOT-5 HRS Satellite Imagery Block Adjustment Without GCPS or with Single GCP[J]. Geomatics and Information Science of Wuhan University, 2006, 31(5): 377–381. |
| [22] | MORGAN M, KIM K O, JEONG S, et al. Epipolar Resampling of Space-borne Linear Array Scanner Scenes Using Parallel Projection[J]. Photogrammetric Engineering & Remote Sensing, 2006, 72(11): 1255–1263. |
| [23] |
张过, 潘红播, 江万寿, 等.
基于RPC模型的线阵卫星影像核线排列及其几何关系重建[J]. 国土资源遥感, 2010, 22(4): 1–5.
ZHANG Guo, PAN Hongbo, JIANG Wanshou, et al. Epipolar Resampling and Epipolar Geometry Reconstruction of Linear Array Scanner Scenes Based on RPC Model[J]. Remote Sensing for Land & Resources, 2010, 22(4): 1–5. |
| [24] | HIRSCHMULLER H, SCHARSTEIN D. Evaluation of Cost Functions for Stereo Matching[C]//Proceedings of 2007 IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis, MN, USA: IEEE, 2007: 1-8. |
| [25] | HUMENBERGER M, ENGELKE T, KUBINGER W. A Census-based Stereo Vision Algorithm Using Modified Semi-global Matching and Plane Fitting to Improve Matching Quality[C]//Proceedings of 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition workshops. San Francisco, CA, USA: IEEE, 2010: 77-84. |
| [26] | SPANGENBERG R, LANGNER T, ADFELDT S, et al. Large Scale Semi-global Matching on the CPU[C]//Proceedings of 2014 IEEE Intelligent Vehicles Symposium. Dearborn, MI, USA: IEEE, 2014: 195-201. |
| [27] |
袁修孝, 曹金山.
高分辨率卫星遥感精确对地目标定位理论与方法[M]. 北京: 科学出版社, 2012: 182-183.
YUAN Xiuxiao, CAO Jinshan. Theory and Method of Precise Object Positioning of High Resolution Satellite Imagery[M]. Beijing: Science Press, 2012: 182-183. |



