线特征是立体场景的重要组成之一, 以线特征作为描述基元可简化目标结构的三维表示且更符合人类视觉感知的特点。在传统的三维重建过程中, 由影像匹配所得的同名点基本不定位在边缘, 这使得重建结果缺失了场景的几何和结构信息。相比之下, 线特征对于目标轮廓的描述优势明显, 且具有丰富的语义信息。融入线特征匹配结果可弥补现有匹配方式的不足, 在强化目标结构表达的同时拓展影像匹配的方法和模式。
如今, 点特征匹配技术已相对成熟[1-5], 而线特征匹配技术仍面临着线特征提取不完全、端点不固定、断裂线阻碍匹配等诸多问题。对于直线匹配, 经典方法多利用直线的固有属性进行匹配, 如直线的长度、夹角、邻域信息、端点位置等[6-9]。文献[10]提出利用颜色特征结合拓扑滤波的方式进行直线匹配, 对于纹理匮乏场景中的匹配具有优越性, 但需迭代求解, 因此消耗较大。文献[11]引入不同高程的投影平面作为约束, 通过联合像方与物方的相似性共同确定同名直线, 保证了匹配的可靠性。文献[12]认为相邻线特征的共面概率高, 并以此为先验利用相邻直线构造V字形连接点进而实现直线匹配。文献[13-14]利用直线与其邻域内同名点的几何关系建立投影、仿射不变量作为描述子进行直线匹配, 此类方法对于误匹配点及共面条件具有较强的容错性, 匹配正确率较高。文献[15]利用已知同名点生成虚拟直线, 再通过虚拟直线与目标直线的交点构造交比不变量, 有效实现了直线匹配及三维重建。文献[16-17]通过一些直线共有特征进行编组, 依据组直线间的拓扑关系进行整体匹配, 此类方法抗噪性好, 但也存在计算复杂度高, 对图像的视点变换及几何变形适应性不强等问题。
直线易于参数化描述, 匹配可利用的约束条件也更多, 而曲线则不具备这些优势, 匹配难度相对较大。文献[18]利用几何互相关约束的方法对线上关键点进行匹配, 进而实现了曲线的多视匹配及重建。文献[19]对曲线的描述进行了探索, 提出了链码描述、几何性质描述、线段分割序列描述等, 但多是基于曲线形态的全局描述符, 对曲线的完整性要求很高。文献[20]利用曲线上的特征点构造弦高比来描述曲线, 此法对断裂线特征匹配有一定的效果, 但对曲线变形十分敏感。文献[21]依据线支持区中的像素亮度关系进行子区域划分, 设计了基于亮度序的均值标准差描述符以完成曲线匹配, 此法受线支持区变化的影响较大, 且不具有尺度不变性。
为解决线特征因遮挡、变形及提取算法限制等带来的匹配问题, 本文联合点特征匹配的优势, 通过对线特征进行离散化描述并结合同名点约束进而实现线特征匹配。算法具有应对复杂匹配问题的能力, 保证了匹配的可靠性。
1 航空影像线特征匹配由于缺少严格的约束条件和稳定的描述符, 线特征匹配技术仍面临着极大挑战。在航空影像中, 线特征经常出现遮挡、断裂及变形等情况, 因而难以利用基于形态的全局描述符对其进行描述和匹配。为此, 本文首先采用“以点代线”的方式, 将线看作离散点集, 通过统计线上同名点的分布情况来确定线特征的初匹配结果; 然后再根据已知同名点, 利用点、线间的距离关系构造仿射不变量对匹配结果进行核验, 从而增强匹配的可靠性。综上, 本文算法主要包括3部分内容:①线特征提取与候选线特征确定; ②线上离散点匹配及线特征初匹配; ③基于点线距离关系的匹配结果核验。算法的整体流程如图 1所示。
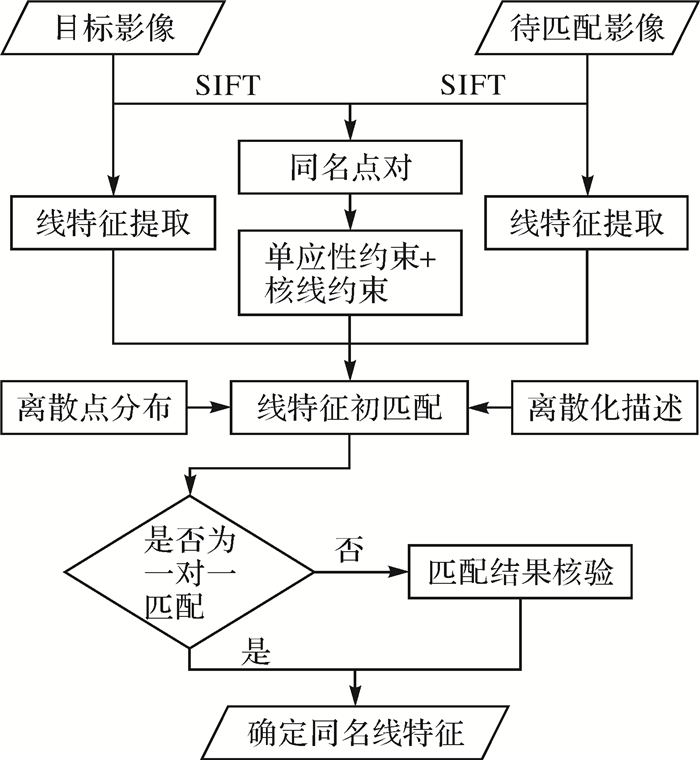
|
| 图 1 线特征匹配算法流程 Fig. 1 Flow chart of line matching |
1.1 线上离散点匹配 1.1.1 单应性约束
单应性为两平面间的映射关系。由于航空影像摄影时的航高较高, 对于存在地形起伏的区域, 物方虽不能看作平面, 但仍可利用单应性矩阵进行匹配区域限定, 实现对应线特征之间的位置约束。两平面之间的对应关系可表示为
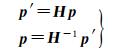 (1)
(1)
式中, p与p′为两幅影像中的对应点; 单应性矩阵H为3阶矩阵。根据式(1), 利用4对及以上同名点即可确定H。接着再通过H将目标图像中的边缘点映射到待匹配图像中, 并将与映射点距离小于Td的区域设置为感兴趣区域, 以限制搜索范围。
1.1.2 核线约束利用核线约束可将匹配的搜索空间由二维降至一维, 从而提高匹配效率和可靠性。从目标影像上一点到待匹配影像上对应核线的映射矩阵被称为基础矩阵。设p为影像中一点, 则p与其对应核线l′p间的关系可表示为
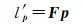 (2)
(2)
式中, 基础矩阵F是秩为2的3阶矩阵。由于点p的同名点p′一定位于核线l′p上, 因此有
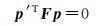 (3)
(3)
本文利用文献[22]所述方法计算基础矩阵, 进而求得目标影像中的点在待匹配影像中的对应核线。结合单应性矩阵与核线约束的线上离散点的匹配约束如图 2所示。其中IL代表目标影像, IL中l1为目标线特征, p为l1上一点; IR为待匹配影像, IR中线E代表p所对应的核线, p′为p由单应性矩阵映射得到的对应点, 虚线圆为单应性矩阵的约束范围, l′1、l′2、l′3是由约束确定的候选线特征, 点p1、p2、p3是p的候选同名点。
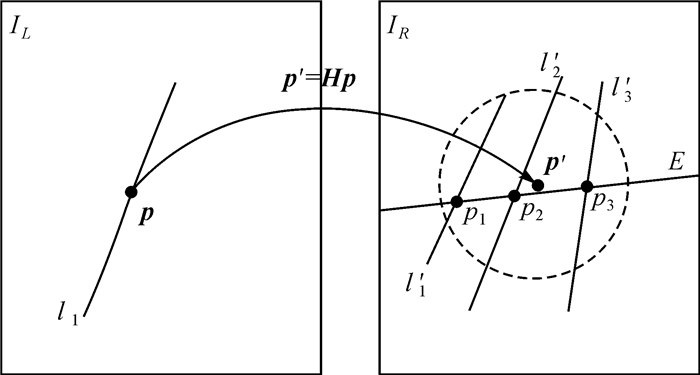
|
| 图 2 线上离散点的匹配约束 Fig. 2 Matching constraints of the discrete points on the line |
1.1.3 线上离散点匹配
线上离散点的匹配结果直接影响线特征匹配的正确率。当视点变换时, 线特征非共面一侧的纹理可能发生变化。为使算法具有适应复杂匹配条件的能力, 本文采用如下方法来构造描述符并匹配:
(1) 主方向确定。将线特征的方向作为离散点的主方向可使描述符具备旋转不变性且不易受噪声和区域变形等因素的影响。以直线为例, 设直线方程为ax+by+c=0, 则其方向V可定义为
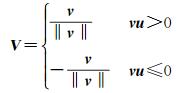 (4)
(4)
式中, 向量u为线上各点平均梯度方向; 向量v=(b, -a)T。在确定目标线特征的方向V后, 待匹配线特征的方向可通过影像间的映射关系将目标线特征的方向向量映射到待匹配影像中, 并选择与此向量夹角较小的待匹配线特征方向作为线上离散点的主方向。
(2) 尺度选择。为使描述符具备尺度不变性, 需确定影像间的尺度关系。由于尺度变换对邻域梯度计算和形状特征描述没有太大影响, 因此, 本文将图像尺度变换等价于比例变化。文献[23]证明了图像缩放对相等比例的局部邻域内对应点的梯度具有不变性。由此, 可以通过已知同名点间的单应性关系来确定描述子间的相对尺度sr。设目标点所在尺度为s′, 则尺度s可确定为
 (5)
(5)
(3) 描述符构建。将坐标轴旋转至离散点的主方向, 对两幅图像建立其在尺度s的图像; 以离散点为中心选取16×16的窗口并计算窗口内每个像素的梯度, 通过高斯窗口对其进行加权运算, 再将窗口合并为4×4的子块并统计每个子块在8个方向的梯度累加值[1]; 利用直线两侧的4×2子块分别生成64维描述子, 将向量归一化即可去除光照影响, 形成两个离散点的描述符。
(4) 描述符匹配。以欧氏距离作为相似性测度对两侧描述符分别进行匹配, 选取相似性测度较大的一侧作为离散点的匹配结果。
1.2 线特征匹配 1.2.1 线特征初匹配对于目标线特征上的点, 通过1.1节所述匹配方法将相似性测度最大的点确定为同名点, 进而确定同名点所在的线特征。本文采用线上点逐像素匹配的方法, 即离散点以整像素的形式逐一进行匹配, 并建立累计分布矩阵统计线上同名点的分布情况。由于各组线特征的重叠区域大小各不相同, 选择利用同名点数量在重叠区域中所占比重Tr来确定线特征初匹配结果。Tr越大即代表该组为同名线特征的概率越大。图 3为线特征匹配过程示意图。图 3(a)中虚线连接的点为匹配所得的线上同名点, 箭头所指为该对同名点对累计分布矩阵(图 3(b))的相应位置进行投票; 当影像中所有的线上同名点投票完毕后, 由其分布情况所确定的匹配结果如图 3(c)所示。可以看出, 累计分布矩阵可以保留所有可能的匹配结果, 有效实现了断裂线特征的多对多匹配。
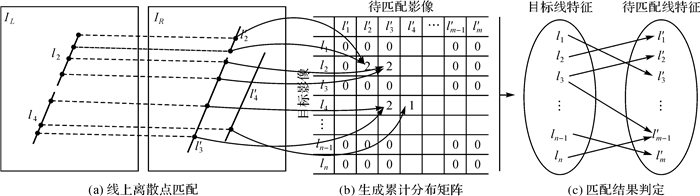
|
| 图 3 线特征匹配过程示意图 Fig. 3 Schematic figure of line matching process |
1.2.2 匹配结果核验
基于邻域信息的线特征匹配算法难以消除相似特征、重复纹理等产生的误匹配问题。由于影像中的点特征匹配结果易于获得也相对可靠, 因此, 可利用线特征及其支持区内的同名点构造仿射不变量, 通过点、线间的距离关系来验证初匹配结果的正确性[14]。由一组直线(l, l′)及两组同名点(X1, X′1)、(X2, X′2)可得
 (6)
(6)
式中, 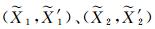
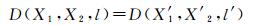 (7)
(7)
式中, D(X, X, l)即为仿射不变量, 此不变量可用于匹配结果的核验。由于线支持区内的多组同名点中可能存在误匹配, 这将导致不变量构建失败。为解决这一问题, 首先选取一组同名点作为基础点, 利用剩余的同名点作为参考点依次与其组成不变量并计算相似性
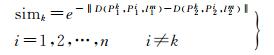 (8)
(8)
通过式(8), 一对基础点即可计算一组相似性判别结果。为减小误匹配点带来的影响, 选择这组相似性的中位数作为该基础点对应的计算结果。接着逐一替换基础点, 由此可得各基础点所对应的中位数, 并将这组中位数的最大值作为同名点所在一侧的相似性。由于无法预先确定共面一侧, 因此对线特征两侧分别计算相似性, 选择相似性大的一侧作为最终结果以降低误判概率。
在直线段两侧分别设定中垂线方向两倍于直线段长度的矩形为线支持区。构建不变量所需的同名点在支持区中很容易找到, 此种方法在含有一定误匹配点的情况下仍能得到正确的匹配结果。由于线的误匹配问题大多存在于非一对一匹配中, 因此本文仅对非一对一匹配结果进行核验, 若两直线满足上述仿射不变关系, 即两不变量的相似性大于阈值Tc, 则确定为同名线特征, 否则将视为误匹配被剔除。
1.3 曲线匹配曲线在实际应用中更为常见, 本文所提线特征匹配算法也可扩展到曲线匹配层面。由于初匹配过程是将线离散为点再进行匹配, 对于线特征形态没有要求, 因此, 仅需对误匹配剔除策略做相应调整即可实现曲线匹配。直线的误匹配剔除是利用与直线邻域内两点到直线的距离构造不变量。对于曲线匹配, 本文采用构造虚拟直线的方法, 首先通过核线约束确定初匹配同名线特征重叠区域中的同名点, 利用距离最远两点连线所得虚拟直线段来代替曲线构造不变量, 可达到同样的误匹配剔除效果。由于曲线与核线的交点可能不止一个, 在此, 只利用交点唯一的离散点来确定虚拟直线。图 4为虚拟直线构造示意图。影像IL和IR中确定了同名线特征l1和l′1; 通过核线可以确定重叠区域中一一对应的同名点, 选取其中间隔距离最远的两对点(B, F)、(C, G)以构造虚拟直线BC和FG来代替曲线计算不变量, 即可实现曲线匹配。

|
| 图 4 虚拟直线构造示意图 Fig. 4 Virtual line selection |
试验中, 由于少量曲线过于卷曲, 因而难以确定虚拟直线, 而多条面与面的交线所组成的曲线也会导致所构造的虚拟直线找不到共面同名点, 最终产生误判。为解决上述问题, 选择在一次匹配之后将长度较长的曲线在其高曲率点打断后再进行一次匹配。由于此类曲线的数量较少, 因此一次迭代仅需较小的计算代价即可实现。
2 试验结果及分析为验证所提线特征匹配算法的有效性, 本文采用AMC580相机系统获得的航空影像进行匹配试验。试验环境为Core i5 2.5 GHz, 内存8 GB, Windows操作平台, 编程平台为Visual Studio 2010, 编程语言为C++。AMC580相机系统是由垂直和倾斜成像的5部相机组合而成; 试验采用该系统于2016年在郑州地区获取的影像作为原始数据, 成像区域均为包含建筑物的城市区域, 摄影航高1000 m; 6组试验影像如图 5所示, 影像中分别存在亮度变换、旋转变换、尺度变换、相似纹理、部分遮挡及视点变换等复杂匹配问题。

|
| 图 5 试验航空影像 Fig. 5 Aerial image sets |
2.1 匹配参数设置
匹配过程中涉及一些参数。其中部分参数主要影响线特征提取数量, 其波动对匹配结果没有太大影响, 可依照实际需求进行设置。此外, 算法还需要初始同名点作为先验来计算单应性矩阵、基础矩阵及进行匹配结果核验, 所需同名点均为SIFT特征匹配所得, 参数依照文献[1]建议值设置。而对于线特征匹配, 参数Td、Tr、Tc对算法的可用性有较大影响。本文针对试验影像, 对上述参数的取值情况进行分析。
(1) 阈值Td的设定。Td是限定单应性约束范围的阈值, 用于精简候选线特征数量。Td越大则候选线特征数量越多, 匹配时间也随之上升。但受地面起伏的影响, 当Td过小时则限定区域中可能未包含正确的匹配结果。结合试验影像的特点及城市区域的起伏状况, 最终设定Td为70像素, 实际应用中Td应分块确定为宜。
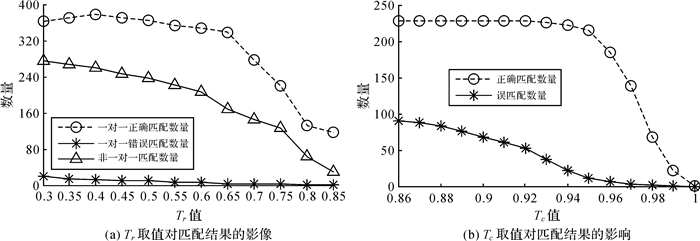
(2) 阈值Tr的设定。Tr用于衡量线上同名点数量占重叠区域的比重, 主要影响初匹配结果。初匹配需保证一对一匹配的正确率。利用图 5(a)组影像进行试验, 通过统计Tr变化对匹配结果的影响以确定参数取值(采用2.2节所述方法进行直线提取和匹配, 下同)。为降低偶然因素的影响, 只有当线上同名点数量多于5个才认为是候选线特征。Tr从0.3到0.85间隔0.05采样, 所得正确匹配数量, 误匹配数量及非一对一匹配数量随参数变化情况如图 6(a)所示。观察可知, 当Tr取值大于0.65时, 一对一正确匹配数量下降明显, 而一对一错误匹配和非一对一匹配的数量也不断减少。为保证一对一匹配的数量和正确率, 选择将Tr设置为0.65。
|
| 图 6 匹配参数设置 Fig. 6 Parameters selection |
(3) 阈值Tc的设定。Tc用于判别不变量的相似度。可见Tc值越大则误匹配筛选越严格。为确定Tc的取值, 选取图 5(f)组影像, 统计Tc不同取值对匹配正确率的影响, 设定Tc从0.86至1.0间隔0.1采样。由图 6(b)可以看出, 当Tc在大于0.94时线特征的误匹配较少。为在减少误匹配的同时尽可能保留正确的匹配结果, 本文将Tc设置为0.95。
2.2 直线匹配LSD是一种直线段检测器[24], 可得到子像素级的直线提取结果并具有较高的检测准确率。本文以LSD算法提取的直线段为基元进行匹配试验。为了减少误检直线对匹配的影响, 在此仅利用20像素以上的直线进行匹配。试验影像的匹配结果如图 7所示。其中, 线特征被随机标记为红、绿、蓝3种颜色, 同名线特征的颜色相同。

|
| 图 7 直线匹配结果 Fig. 7 Results of line matching |
可以看出, 本文算法在应对复杂匹配条件时表现出较好的稳健性。算法继承了点特征描述符的不变性, 可避免因直线提取不完整造成支持区不一致的问题, 且在直线存在部分遮挡时也表现出较好的适应性。同时, 通过引入点线距离关系作为约束对非一对一匹配结果进行验证, 对于非一对一匹配可得到满足局部特征和点线距离关系双重约束的匹配结果, 降低了误匹配概率。为评价本文算法的匹配效果, 选取文献[6, 14]所提直线匹配算法进行对比试验, 3种算法针对试验图像的匹配结果对比见表 1。
| 试验影像 | 提取线特征数目 | 本文算法 | 文献[6]算法 | 文献[14]算法 | ||||||||||
| 左影像 | 右影像 | 匹配总数 | 正确匹配数量 | 匹配正确率/(%) | 匹配总数 | 正确匹配数量 | 匹配正确率/(%) | 匹配总数 | 正确匹配数量 | 匹配正确率/(%) | ||||
| 图 5(a) | 1070 | 910 | 435 | 406 | 93.3 | 342 | 290 | 84.8 | 377 | 350 | 92.8 | |||
| 图 5(b) | 1205 | 1144 | 626 | 577 | 92.2 | 481 | 409 | 85.0 | 613 | 566 | 92.3 | |||
| 图 5(c) | 1177 | 929 | 474 | 444 | 93.7 | 336 | 189 | 56.3 | 404 | 373 | 92.3 | |||
| 图 5(d) | 1205 | 1054 | 610 | 579 | 94.9 | 468 | 377 | 80.6 | 527 | 499 | 94.7 | |||
| 图 5(e) | 243 | 456 | 160 | 146 | 91.3 | 142 | 121 | 85.2 | 149 | 135 | 90.6 | |||
| 图 5(f) | 885 | 1430 | 358 | 323 | 90.2 | 301 | 209 | 69.4 | 323 | 293 | 90.7 | |||
文献[6]算法利用线支持区来构造整条线的描述符, 并通过归一化克服了直线长度变化对匹配的影响。该算法在应对旋转和亮度变换时具有一定的适用性, 但在视点变换的情况下, 线支持区非共面一侧的纹理发生变化会使匹配受到一定影响。此外, 该算法在影像尺度变换的情况下也会导致误匹配。本文针对线特征邻域特性设计局部不变描述符, 降低了周围纹理变化带来的影响, 也令匹配算法具有一定尺度不变性。再通过结合点线不变量对非一对一匹配进行核验, 降低了误匹配概率, 稳定性明显优于文献[6]算法。
文献[14]算法利用直线邻域内的特征点到直线的距离比建立仿射不变描述子, 再通过距离比的最大值和中位数判断匹配结果。由于本文所用误匹配剔除策略的核心与此相同, 因此本文算法可以看作该算法的改进。由表 1可知, 本文算法对于试验影像的平均匹配正确率略高于文献[14]算法, 在匹配数量上也多于该算法。这是因为本文算法融入了线特征的邻域相似性判别并将匹配结果区别开来进行误匹配剔除, 使得算法的匹配准确率更高, 加之利用累计分布矩阵提取得到了所有可能的匹配结果, 因此获得的匹配结果数量更多。
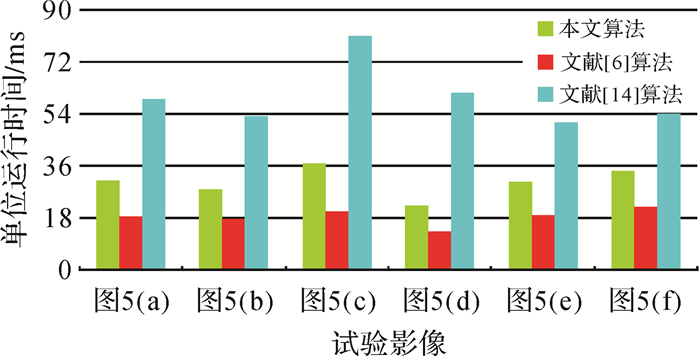
图 8为3种匹配算法的单位运行时间(线特征匹配时间与匹配总数之比)对比柱状图。由于本文算法仅对非一对一匹配结果进行误匹配检验, 而文献[14]算法则需不断地循环计算描述符并计算相似性, 因此本文算法在匹配效率上优于文献[14]算法。相比文献[6]算法, 本文算法所需的单位运行时间略高。本文算法所用的匹配约束条件有效精简了候选线特征数量, 加快了匹配速度, 但误匹配剔除相对耗时。相对而言, 文献[6]算法的匹配稳定性难以适应复杂的匹配条件, 而本文算法的可用性强, 在保证匹配可靠性的同时实现了线特征的快速匹配。
|
| 图 8 直线匹配的单位运行时间对比 Fig. 8 Unit running time comparison of line matching |
2.3 曲线匹配
本文利用Canny算子[25]提取影像中的曲线并匹配。为消除提取结果中的交叉线, 首先遍历所有边缘点, 判断每个点的八邻域内是否存在互不相邻的不少于3个方向的延伸线, 若存在则认为该点为交叉线连接点, 并将其所连接的线特征由此断开。另外, 对闭合环采取在高曲率点打断的方式再进行整理。考虑到长度较短或较为卷曲的线特征在重建过程中的作用不大, 故仅利用最小外接矩边长最大值大于18像素的曲线进行匹配。匹配结果中, 若高曲率点打断曲线的其中一部分匹配成功, 则整条曲线均视为匹配成功。
对于曲线匹配, 针对图 5中6组试验影像的匹配正确率与所提直线匹配算法相当, 较好地实现了曲线匹配。在实际应用中, 由于一些人工地物的边缘不能用直线完全表示, 因此, 曲线匹配是更具普适性的方法。图 9展示了一组城市区域影像利用本文所述的直线与曲线匹配算法所得的结果对比, 图中同色矩形框标记的即为直线与曲线匹配的不同之处。可以看出, 直线可以覆盖大部分人工地物的边缘, 但无法描述和匹配部分不规则地物的轮廓。相比之下, 曲线匹配技术则对匹配基元的形态没有要求, 算法的适用性更广。

|
| 图 9 直线匹配与曲线匹配 Fig. 9 Comparison of lines matching with curve matching |
线特征匹配的目的是为了重建目标地物的边缘结构, 而曲线从边缘表达完整性和普适性的角度讲都是较优的匹配基元, 曲线匹配的研究更具实际意义。本文所述算法仅是对曲线匹配的一种探索, 在应对卷曲曲线的匹配问题时仍存在不足, 且匹配结果也较为稀疏。随着线特征提取与匹配技术的发展, 曲线对地物边缘结构表达的优势会进一步显现。
3 结语本文提出一种结合离散化描述与同名点约束的线特征匹配方法, 通过统计线上同名点的分布情况判定线特征初匹配结果, 并利用点线之间的距离关系对匹配结果进行核验, 减少了因线特征断裂、变形带来的匹配问题。试验结果表明, 本文方法在应对多种复杂匹配条件时表现均衡, 稳健性强。相应的, 算法也存在一定的局限性, 如匹配可靠性仍受到点特征匹配的影响, 在难以获得初始同名点的区域, 算法的适用性不强; 对于纹理匮乏地区的线特征匹配问题仍有待于进一步的探索。单一特征(点或线)的重建模型均有着各自的优势, 而本文仅对线特征匹配技术进行了探索, 因此, 多特征相结合的高精度DSM生成技术将是下一步的研究方向。
| [1] | LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91–110. |
| [2] | BAY H, TUYTELAARS T, VAN GOOL L. SURF: Speeded up Robust Features[M]//LEONARDIS A, BISCHOF H, PINZ A. Computer Vision. Berlin, Heidelberg: Springer, 2006. |
| [3] | TOLA E, LEPETIT V, FUA P. DAISY:An Efficient Dense Descriptor Applied to Wide-baseline Stereo[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(5): 815–830. DOI:10.1109/TPAMI.2009.77 |
| [4] | RUBLEE E, RABAUD V, KONOLIGE K, et al. ORB: An Efficient Alternative to SIFT or SURF[C]//Proceedings of 2011 IEEE International Conference on Computer Vision. Barcelona: IEEE, 2011: 2564-2571. |
| [5] | REVAUD J, WEINZAEPFEL P, HARCHAOUI Z, et al. Deep Matching:Hierarchical Deformable Dense Matching[J]. International Journal of Computer Vision, 2016, 120(3): 300–323. |
| [6] | WANG Zhiheng, WU Fuchao, HU Zhanyi. MSLD:A Robust Descriptor for Line Matching[J]. Pattern Recognition, 2009, 42(5): 941–953. DOI:10.1016/j.patcog.2008.08.035 |
| [7] |
黄良明, 彭立中, 程民德.
利用几何代数进行线段模型匹配和运动估计[J]. 中国图象图形学报, 2001, 6(3): 270–274.
HUANG Liangming, PENG Lizhong, CHENG Minde. Matching and Estimating Motion of Line Model Using Geometric Algebra[J]. Journal of Image and Graphics, 2001, 6(3): 270–274. DOI:10.3969/j.issn.1006-8961.2001.03.013 |
| [8] | SUN Yanbiao, ZHAO Liang, HUANG Soudong, et al. Line Matching Based on Planar Homography for Stereo Aerial Images[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015(104): 1–17. |
| [9] | BAILLARD C, SCHMID C, ZISSERMAN A, et al. Automatic Line Matching and 3D Reconstruction of Buildings from Multiple Views[C]//ISPRS Conference on Automatic Extraction of GIS Objects from Digital Imagery. Munich: International Archives of Photogrammetry and Remote Sensing, 1999: 69-80. |
| [10] | BAY H, FERRARI V, VAN GOOL L. Wide-baseline Stereo Matching with Line Segments[C]//Proceedings of 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego: IEEE, 2005: 329-336. |
| [11] |
王竞雪, 宋伟东, 王伟玺.
同名点及高程平面约束的航空影像直线匹配算法[J]. 测绘学报, 2016, 45(1): 87–95.
WANG Jingxue, SONG Weidong, WANG Weixi. Line Matching Algorithm for Aerial Image Based on Corresponding Points and Z-plane Constraints[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 87–95. DOI:10.11947//j.AGCS.2016.20140527 |
| [12] | LI Kai, YAO Jian, LU Xiaohu, et al. Hierarchical Line Matching Based on Line-junction-line Structure Descriptor and Local Homography Estimation[J]. Neurocomputing, 2016, 184: 207–220. DOI:10.1016/j.neucom.2015.07.137 |
| [13] | JIA Qi, GAO Xinkai, FAN Xin, et al. Novel Coplanar Line-points Invariants for Robust Line Matching Across Views[C]//Proceedings of the 14th European Conference on Computer Vision. Amsterdam: Springer, 2016: 599-611. |
| [14] | FAN Bin, WU Fuchao, HU Zhanyi. Robust Line Matching Through Line-point Invariants[J]. Pattern Recognition, 2012, 45(2): 794–805. DOI:10.1016/j.patcog.2011.08.004 |
| [15] | RAMALINGAM S, ANTUNES M, SNOW D, et al. Line-sweep: Cross-ratio for Wide-baseline Matching and 3D Reconstruction[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 2015: 1238-1246. |
| [16] |
张跃强, 苏昂, 朱遵尚, 等.
结合局部描述和拓扑约束的直线段匹配算法[J]. 国防科技大学学报, 2014, 36(6): 25–30.
ZHANG Yueqiang, SU Ang, ZHU Zunshang, et al. A Line Matching Algorithm Combining Local Description with Topological Constraint[J]. Journal of National University of Defense Technology, 2014, 36(6): 25–30. |
| [17] | KIM H, LEE S. Simultaneous Line Matching and Epipolar Geometry Estimation Based on the Intersection Context of Coplanar Line Pairs[J]. Pattern Recognition Letters, 2012, 33(10): 1349–1363. DOI:10.1016/j.patrec.2012.03.014 |
| [18] | ZHANG Li, GRUEN A. Multi-image Matching for DSM Generation from IKONOS Imagery[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 60(3): 195–211. DOI:10.1016/j.isprsjprs.2006.01.001 |
| [19] |
胡海霞.视觉运动分析中的线特征提取与匹配方法研究[D].南昌: 南昌航空大学, 2009: 53-68. HU Haixia. Research on Extraction and Matching of Linear and Curvilinear Features in Vision Motion Analysis[D]. Nanchang: Nanchang Hangkong University, 2009: 53-68. |
| [20] |
张桂梅, 熊逸文, 马珂.
基于仿射不变性的轮廓曲线局部描述符[J]. 模式识别与人工智能, 2012, 25(6): 972–978.
ZHANG Guimei, XIONG Yiwen, MA Ke. Contour Curve Descriptor Based on Affine Invariance[J]. Pattern Recognition and Artificial Intelligence, 2012, 25(6): 972–978. DOI:10.3969/j.issn.1003-6059.2012.06.012 |
| [21] |
王志衡, 智珊珊, 刘红敏.
基于亮度序的均值标准差描述子[J]. 模式识别与人工智能, 2013, 26(4): 409–416.
WANG Zhiheng, ZHI Shanshan, LIU Hongmin. Intensity Order Based Mean-standard Deviation Descriptor[J]. Pattern Recognition and Artificial Intelligence, 2013, 26(4): 409–416. DOI:10.3969/j.issn.1003-6059.2013.04.012 |
| [22] |
彭科举.基于序列图像的三维重建算法研究[D].长沙: 国防科学技术大学, 2012: 34-37. PENG Keju. 3D Reconstruction Using Image Sequences[D]. Changsha: National University of Defense Technology, 2012: 34-37. http://cdmd.cnki.com.cn/Article/CDMD-90002-1013047617.htm |
| [23] |
缪君, 储珺, 张桂梅.
一种仿射不变的直线描述子与直线匹配[J]. 电子学报, 2015, 43(12): 2505–2512.
MIAO Jun, CHU Jun, ZHANG Guimei. An Affine Invariant Line Descriptor and Line Matching[J]. Acta Electronica Sinica, 2015, 43(12): 2505–2512. DOI:10.3969/j.issn.0372-2112.2015.12.024 |
| [24] | VON GIOI R G, JAKUBOWICZ J, MOREL J M, et al. LSD:A Line Segment Detector[J]. Image Processing on Line, 2012, 2(4): 35–55. |
| [25] | CANNY J. A Computational Approach to Edge Detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, 8(6): 679–698. |



