高分辨率遥感卫星在军用和民用方面都具有极其重要的价值,其发展和应用得到了各国的高度重视。卫星平台的姿态稳定性,是决定高分辨率卫星几何定位精度和辐射质量的关键因素之一,然而卫星在轨运行期间,外部空间环境的变化和内部机械的振动等会导致姿态存在不稳定和周期性微小振动现象,即卫星平台颤振现象,如果不进行有效处理会大幅影响卫星的测图精度和成像质量[1]。随着成像传感器分辨率的提高,平台颤振对高分卫星影像几何精度的影响愈发显著。因此,卫星平台颤振是高分辨率对地观测系统和智能化摄影测量处理亟须解决的难题之一。
卫星平台震颤是高分辨率卫星在轨运行普遍存在的复杂现象,国内外学者在卫星平台颤振分析方面已开展了相关研究。目前,采用卫星影像或产品数据来反演颤振信息已成为了热门方法,与传统的基于地面密集控制和姿态数据的探测方法相比,该方法具有便捷高效和探测能力强等优点[2]。基于影像间密集视差变化的视差法颤振探测已经成功应用于ASTER、PLEIADES-HR、UK-DMC、天绘一号和资源三号等国内外卫星和传感器的颤振处理分析[3-7]。实现高精度稳健的密集匹配是视差法颤振探测的基础,选择有效的匹配方法来获取影像间颤振导致的相对视差变化是决定卫星平台颤振探测质量的关键之一。相位相关匹配算法因其高精度、高计算效率和对比度不敏感等特点,已广泛应用于视差法颤振探测框架[5-7]。
相位相关是一种基于傅里叶变换的区域影像匹配方法,利用频率域的影像信息和操作来精确估计影像间的偏移量,与归一化互相关等其他常用影像相关方法相比,能够保证更高的精度和稳定度[8-9],已经在遥感影像配准[10]、窄基线立体重建[11]和地表动态监测[12]等智能处理方面得到了广泛关注和应用。相位相关的理论基础是傅里叶变换的平移特性,亚像素的相位相关算法研究主要分为两类,第1类算法通过确定互功率谱逆傅里叶变换后精确的峰值位置来获取偏移量,第2类算法通过直接估计互功率谱的线性相位差来获取偏移量[12-13]。在第1类算法的研究方面,文献[13]假设影像间的亚像素偏移通过存在整像素偏移的高分辨率图像降采样获得,利用sinc函数近似Dirichlet核,理论上推导了亚像素计算的解析形式。文献[14]根据一维sinc函数拟合推导出peak evaluation formula(PEF)方法,采用主相关峰及其两侧不同距离的位置组成的多组三元组,根据推导公式,通过非迭代的最小二乘法来估计亚像素偏移。在第2类算法的研究方面,针对非缠绕的相位角理论上是一个二维平面这一特性,文献[15]提出利用最小二乘估计来拟合平面参数,平面的斜率对应亚像素的偏移值。文献[16]提出利用奇异值分解对互功率谱进行子空间分解,通过拟合奇异值向量对应的相位角斜率来获取亚像素偏移值。
视差法颤振探测需要选择两幅或多幅不同时间成像的影像来进行相互匹配,选择的影像间由于成像时间差异或谱段差异不可避免地存在复杂的辐射差异。因此,保证匹配算法的辐射稳健性对卫星平台颤振探测的质量相当重要。相位相关匹配在频域进行了归一化处理并只利用了影像的相位信息,因此对影像强度变化特别是亮度和对比度的全局线性变化并不非常敏感。然而,关于局部和非线性等复杂辐射差异对亚像素相位相关匹配精度影响和相应有效改进的研究非常少。因此,为了进一步提高亚像素相位相关算法对影像间辐射差异的稳健性,本文从影像表达方式入手,提出一种基于局部频率分析的改进亚像素相位相关算法,结合相位一致性和局部平均相位生成辐射不变的影像表达,从而保证亚像素相位相关算法在复杂辐射差异情况下的精度优势。将提出的亚像素相位相关算法融入视差法颤振探测框架,可以在存在噪声和复杂辐射差异等干扰情况下精确获取影像间的颤振视差,从而提高颤振探测的精度,扩展用于颤振探测影像的选择,增加从影像中反演颤振信息的可信度。
1 基于亚像素相位相关的视差法颤振探测 1.1 基于局部频率分析的亚像素相位相关算法 1.1.1 相位相关理论基础相位相关的理论基础是傅里叶变换的平移特性,即空域下的平移在频域下显示为线性相位差。假设两幅影像f(x, y)和g(x, y)存在水平方向偏移x0和垂直方向偏移y0,其对应傅里叶变换表示为G(u, v)和F(u, v),傅里叶变换的平移特性表示为
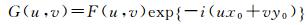 (1)
(1)
式中,i表示虚数。计算两幅影像间的归一化互功率谱矩阵来提取相位信息
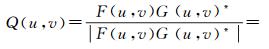
 (2)
(2)
式中,*表示复共轭。在实际离散影像情况下,采用快速傅里叶变换,归一化互功率谱进行逆傅里叶变换后理论上可以得到一个二维脉冲函数,通过获取峰值的位置可以求取整像素级的匹配结果[13]。
1.1.2 辐射不变的影像表达为了减少辐射差异对影像匹配和配准结果的影响,局部结构特征常被采纳加入影像匹配配准框架[17]。通过局部频率分析计算局部相位信息被证实符合人类对影像特征的视觉感知[18],相当于提取影像内在的局部结构特性,在不同光照条件和不同模态下保持一致,与梯度和局部熵等其他结构特征相比,受影像强度变化和噪声的影响相对更小[19]。因此,本文借鉴文献[19-20]的方法通过局部频率分析提取相位一致性和局部平均相位信息来构造辐射稳健的结构影像表达。
相位一致性来源于局部能量模型,此模型认为影像中能够被人眼感知的特征存在于傅里叶分量同相性最大的位置,即感知的特征是各傅里叶分量相位一致性最高的点。文献[21]采用log Gabor小波来计算相位一致性并提出了一种新的相位一致性计算公式。以Mne和Mno分别表示尺度n下的偶对称滤波器和奇对称滤波器,滤波器对的响应向量表示为
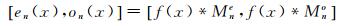 (3)
(3)
在特定尺度n下,局部幅值和相位为
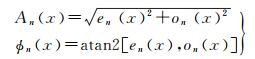 (4)
(4)
局部平均相位可以计算为
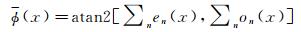 (5)
(5)
考虑噪声补偿、频率宽度和相位差,相位一致性计算公式定义为[21]
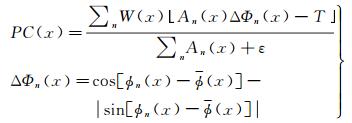 (6)
(6)
式中,T为噪声阈值;ε为避免分母为0的小量;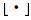
为了分析影像的局部频率信息,需要从一维情况扩展到二维。可以利用单演信号理论来实现二维相位一致性的计算[19-20]。
结合局部平均相位和相位一致性可以得到辐射不变的影像表达为
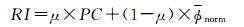 (7)
(7)
式中,μ为加权参数,通过计算影像的熵来自适应确定[19],较低的图像熵意味较少的纹理信息,因此需要较大的加权参数。前一部分通过计算相位一致性生成边缘保持表达EPM,提供结构信息,后一部分归一化局部平均相位得到纹理保持表达TPM,提供纹理信息。如图 1所示,不同曝光设置拍摄的影像间存在显著的辐射差异,而通过局部频率分析生成的影像表达明显减少了辐射差异。

|
| 图 1 不同曝光影像生成的辐射不变影像表达 Fig. 1 Illumination-invariant image representations from images with different exposures |
1.1.3 改进的亚像素相位相关算法
将基于局部频率分析生成的结构影像表达融入亚像素相位相关匹配框架可以得到辐射稳健的亚像素相位相关算法。生成新影像表达的改进方式是通用的,从本质上减少辐射差异对亚像素偏移值估计的影响。因其高效率与高可信度,本文结合PEF算法[14]提出改进的亚像素相位相关算法。
PEF算法根据多组三元组拟合一维sinc函数来确定亚像素偏移值。根据文献[13]的推导,亚像素的相位相关生成了一个二维Dirichlet核,分解为一维情况,可以用一维sin c函数来近似
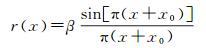 (8)
(8)
式中,β表示峰值大小;r(x)为逆傅里叶变换后的相关函数。对于一个三元组r(p-d)、r(p)和r(p+d)满足
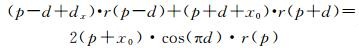 (9)
(9)
调整后可得
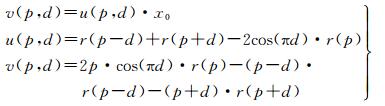 (10)
(10)
式中,p和d取值确定三元组的位置,根据相关函数峰值整像素位置附近的多组三元组利用最小二乘法拟合可估计出亚像素偏移值。
通过结合基于局部频率分析的影像表达和相位相关匹配,本文方法充分利用了影像的局部和全局相位信息来确保在噪声和辐射差异等干扰因素影响下亚像素偏移值估计的精度和稳定性。提出的亚像素相位相关算法流程为:
(1) 对于输入影像,根据式(7)计算辐射不变影像表达,附加Tukey窗减弱边缘效应的影响。
(2) 对生成的影像表达进行傅里叶变换,根据式(2)计算归一化互功率谱矩阵。
(3) 利用高斯函数对互功率谱进行频域滤波,减弱噪声和混叠的影响,并进行逆傅里叶变换,计算二维相关函数。
(4) 采用奇异值分解计算秩一近似将相关函数分离成一维情况。
(5) 根据式(10)估计亚像素偏移值。
1.2 视差法颤振探测方法理论上,如果空间分辨率和成像质量足够高,卫星平台任何微小的振动都会影响CCD传感器的成像并记录在生成的影像中。从影像中反演卫星平台颤振信息,可以采用视差法颤振探测方法,根据短时间相隔成像的线阵CCD间的视差变化来估计颤振引起的随时间变化的像移[3-7]。视差法颤振探测方法大致可以分为密集匹配,视差颤振转换和频谱分析3个步骤。其中,高精度的密集匹配是视差法颤振探测的基础,匹配精度决定颤振探测的能力。为了提高存在辐射差异和噪声等影响情况下的匹配精度,保证卫星平台颤振探测的可信度和可用性,将提出的局部频率分析亚像素相位相关算法融入常规的视差法颤振探测框架,来估计影像间的颤振视差。
改进的视差法颤振探测方法具体流程如下:
(1) 对影像进行预处理,包括影像增强和初始配准。初始配准目的是为了消除了两幅影像间较大的变形和差异,减少影像密集匹配时误匹配点的可能性。
(2) 通过等间隔匹配的方式,利用提出的局部频率,分析亚像素相位相关算法对参考影像和待匹配影像进行密集匹配,获取待匹配影像各像素相对于参考影像的颤振视差图。
(3) 根据计算的相关系数约束,剔除误匹配点,并以行为单位,对该行影像的所有有效视差取均值,获取颤振视差曲线。
(4) 通过单频率分量的空域转换方式或多频率分量的频域转换方式实现视差到颤振的转换[7]。
(5) 利用傅里叶频谱分析的方法分析获取的平台颤振的频率成分,计算颤振频率和幅值等特性参数。
2 试验与分析本文的试验部分包括以下两部分内容:
(1) 通过存在实际辐射差异的已知真实偏移的数据集,开展亚像素相位相关算法对比,验证本文局部频率分析亚像素相位相关算法的可信度。
(2) 采用改进的视差法颤振探测方法估计资源三号卫星颤振特性,验证其有效性。
2.1 亚像素相位相关算法对比通过两组存在实际辐射差异的影像数据集来验证提出的亚像素相位相关方法在辐射变化情况下的效果提升,模拟生成影像间的亚像素偏移,以便直接计算不同方法的匹配精度,开展光源变化和曝光变化情况下的亚像素相位相关算法对比。
模拟试验数据以Middlebury Stereo Datasets[22]中的两幅实际辐射差异影像为基础影像生成,对于每幅影像,分别通过3种不同曝光设置和3种不同光源配置来进行拍摄。为了分析光源变化的影响,固定拍摄的曝光设置,变化光源配置,共有3种组合:I1/I2,I1/I3和I2/I3。为了分析曝光变化的影响,固定拍摄的光源配置,变化曝光设置,同样共有3种组合:E1/E2,E1/E3和E2/E3。对于每个组合,采用文献[9]相似的低通滤波和降采样方式来生成128对已知亚像素偏移值的模拟影像对,并添加微量的零均值高斯噪声以求更加符合实际影像情况和分析不同干扰因素与辐射变化的综合影响。图 2为模拟试验的示例影像,根据I1/I3组合影像和E1/E3组合影像以x和y方向0.5个像素的偏移值生成。

|
| 图 2 模拟试验示例影像 Fig. 2 Sample images in the simulated test |
根据上述试验数据,将提出的基于局部频率分析影像表达的算法与其他主流的亚像素相位相关算法对比,以验证提出算法的可信度。对比算法包括Foroosh算法[13]、PEF算法[14]、Stone算法[15]和Hoge算法[16]。对每一光照和曝光组合,通过总共128对影像根据真实偏移值来计算各方法x方向和y方向综合匹配误差的平均值和均方根作为评价测度。
图 3绘制了不同光源或曝光设置组合下,各亚像素傅里叶影像相关方法计算的绝对误差的均值和均方根结果。从图 3中可以发现,无论是光源变化引起的局部辐射差异还是曝光变化引起的全局辐射差异,对亚像素傅里叶影像相关匹配的精度都有一定程度的影响,而且随着辐射差异的增大,各方法计算的匹配误差整体趋势上增大。相对比其他4种主流的相位相关算法,本文提出的基于局部频率分析的亚像素算法在不同影像组合下取得了一致的更优和更稳定的效果,匹配误差的均值和均方根最小,验证了基于局部频率分析提取的辐射不变影像表达的可信度,以及用于减小辐射差异对亚像素相位相关算法影响的可行性。即使存在明显辐射差异和噪声等的影响,本文亚像素相位相关算法仍能达到0.05个像素的匹配精度。

|
| 图 3 模拟试验亚像素相位相关算法对比 Fig. 3 Comparison of different subpixel phase correlation methods in the simulated test |
2.2 资源三号卫星平台颤振探测
本文采用资源三号卫星多光谱影像来进行平台颤振探测试验,试验影像为2012年拍摄的河南区域影像。颤振探测方法采用本文提出的局部频率分析亚像素相位相关算法,适用于采用存在明显辐射差异影像的颤振探测,例如采用多光谱可见光波段和近红外波段影像。扩展颤振探测影像的谱段,一方面可以完善颤振信息的提取,提供相互验证手段,另一方面有助于避免视差法颤振探测的盲点频率[4]。资源三号卫星的多光谱传感器包含红(B1)、绿(B2)、蓝(B3)和近红外(B4)4个波段,本文选取B1与B4以及B1与B2的波段组合。
密集匹配后逐行平均得到的垂轨方向颤振视差曲线结果如图 4所示,从中可以看出,两组波段组合计算得到的颤振视差曲线都出现了由颤振引起的随时间周期性变化的波动,并且具有相似的变化趋势。

|
| 图 4 垂轨方向卫星颤振视差曲线结果 Fig. 4 Jitter disparity curve in the cross-track direction |
为了验证获取颤振探测结果的准确性,通过视差颤振转换和频谱分析获取颤振的频率与幅值特性[7],并与从姿态数据反演的颤振特性进行对比分析。表 1列出了利用两组波段组合计算的颤振频率和幅值,以及从姿态数据反演的颤振频率与幅值,可以看出资源三号卫星存在频率约0.66 Hz的周期性平台颤振,从不同波段组合影像计算出的颤振频率和幅值与从姿态数据得到的结果相似,表明了基于局部频率分析亚像素相位相关算法的视差法颤振探测方法的有效性。
| 类别 | 频率/Hz | 幅值/(″) |
| B1与B2 | 0.665 | 2.113 |
| B1与B4 | 0.662 | 2.098 |
| 姿态数据 | 0.667 | 2.036 |
3 结论
卫星平台颤振的精密探测和反演对保证高分辨率卫星的测图精度和成像质量至关重要,是摄影测量领域亟须解决的难题之一。本文结合高精度机器视觉,提出了基于局部频率分析亚像素相位相关的高分辨率卫星平台颤振精密探测方法。针对从影像反演颤振对匹配算法精度和不受辐射差异影响的要求,提取相位一致性和局部平均相位构造辐射不变的结构影像表达来改进亚像素相位相关算法,结构影像表达考虑了影像的内在信息,在不同光照条件和不同模态下保持一致,并将改进的相位相关算法融入视差法颤振探测框架,实现稳健高效的卫星平台颤振精密探测。利用实际辐射变化的数据集开展了相位相关算法对比试验,本文亚像素相位相关算法的效果优于其他4种主流亚像素算法,在辐射差异和噪声等影响情况下,匹配精度达到0.05个像素。采用本文颤振探测方法对资源三号卫星平台颤振的特性进行了有效地反演,与姿态数据估计结果对比验证了其可信度。笔者的后续工作将尝试将提出的颤振精密探测方法应用于更多高分辨率卫星的颤振分析。
| [1] | TONG Xiaohua, YE Zhen, XU Yusheng, et al. Framework of Jitter Detection and Compensation for High Resolution Satellites[J]. Remote Sensing, 2014, 6(5): 3944–3964. DOI:10.3390/rs6053944 |
| [2] | IWASAKI A. Detection and Estimation Satellite Attitude Jitter Using Remote Sensing Imagery[M]//HALL J. Advances in Spacecraft Technologies. Rijeka, Croatia: In-Tech, 2011, 257-272. |
| [3] | TESHIMA Y, IWASAKI A. Correction of Attitude Fluctuation of Terra Spacecraft Using ASTER/SWIR Imagery with Parallax Observation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(1): 222–227. DOI:10.1109/TGRS.2007.907424 |
| [4] | AMBERG V, DECHOZ C, BERNARD L, et al. In-flight Attitude Perturbances Estimation: Application to PLEIADES-HR Satellites[C]//Proceedings Volume 8866, Earth Observing Systems XVⅢ. San Diego, California: SPIE, 2013, 8866: 886612. |
| [5] | MUMTAZ R, PALMER P. Attitude Determination by Exploiting Geometric Distortions in Stereo Images of DMC Camera[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(3): 1601–1625. DOI:10.1109/TAES.2013.6558007 |
| [6] | SUN Tao, LONG Hui, LIU Baocheng, et al. Application of Attitude Jitter Detection Based on Short-time Asynchronous Images and Compensation Methods for Chinese Mapping Satellite-1[J]. Optics Express, 2015, 23(2): 1395–1410. DOI:10.1364/OE.23.001395 |
| [7] | TONG Xiaohua, XU Yusheng, YE Zhen, et al. Attitude Oscillation Detection of the ZY-3 Satellite by Using Multispectral Parallax Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(6): 3522–3534. DOI:10.1109/TGRS.2014.2379435 |
| [8] | ZITOVÁ B, FLUSSER J. Image Registration Methods:A Survey[J]. Image and Vision Computing, 2003, 21(11): 977–1000. DOI:10.1016/S0262-8856(03)00137-9 |
| [9] | TONG Xiaohua, YE Zhen, XU Yusheng, et al. A Novel Subpixel Phase Correlation Method Using Singular Value Decomposition and Unified Random Sample Consensus[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(8): 4143–4156. DOI:10.1109/TGRS.2015.2391999 |
| [10] |
林卉, 梁亮, 杜培军, 等.
利用Fourier-Mellin变换的遥感图像自动配准[J]. 武汉大学学报(信息科学版), 2012, 37(6): 649–652.
LIN Hui, LIANG Liang, DU Peijun, et al. Image Registration Based on Fourier-Mellin Transform[J]. Geomatics and Information Science of Wuhan University, 2012, 37(6): 649–652. |
| [11] | LI Jie, LIU Yiguang, DU Shuangli, et al. Hierarchical and Adaptive Phase Correlation for Precise Disparity Estimation of UAV Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(12): 7092–7104. DOI:10.1109/TGRS.2016.2595861 |
| [12] | LEPRINCE S, BARBOT S, AYOUB F, et al. Automatic and Precise Orthorectification, Coregistration, and Subpixel Correlation of Satellite Images, Application to Ground Deformation Measurements[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(6): 1529–1558. DOI:10.1109/TGRS.2006.888937 |
| [13] | FOROOSH H, ZERUBIA J B, BERTHOD M. Extension of Phase Correlation to Subpixel Registration[J]. IEEE Transactions on Image Processing, 2002, 11(3): 188–200. DOI:10.1109/83.988953 |
| [14] | NAGASHIMA S, AOKI T, HIGUCHI T, et al. A Subpixel Image Matching Technique Using Phase-only Correlation[C]//Proceedings of 2006 International Symposium on Intelligent Signal Processing and Communications. Tottori, Japan: IEEE, 2006: 701-704. |
| [15] | STONE H S, ORCHARD M T, CHANG E C, et al. A Fast Direct Fourier-based Algorithm for Subpixel Registration of Images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(10): 2235–2243. DOI:10.1109/36.957286 |
| [16] | HOGE W S. A Subspace Identification Extension to the Phase Correlation Method[MRI Application][J]. IEEE Transactions on Medical Imaging, 2003, 22(2): 277–280. DOI:10.1109/TMI.2002.808359 |
| [17] | YE Yuanxin, SHAN Jie, BRUZZONE L, et al. Robust Registration of Multimodal Remote Sensing Images Based on Structural Similarity[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(5): 2941–2958. DOI:10.1109/TGRS.2017.2656380 |
| [18] | MORRONE M C, OWENS R A. Feature detection from local energy[J]. Pattern Recognition Letters, 1987, 6(5): 303–313. DOI:10.1016/0167-8655(87)90013-4 |
| [19] | LI Zhang, MAHAPATRA D, TIELBEEK J A W, et al. Image Registration Based on Autocorrelation of Local Structure[J]. IEEE Transactions on Medical Imaging, 2016, 35(1): 63–75. DOI:10.1109/TMI.2015.2455416 |
| [20] | MOUATS T, AOUF N, RICHARDSON M A. A Novel Image Representation Via Local Frequency Analysis for Illumination Invariant Stereo Matching[J]. IEEE Transactions on Image Processing, 2015, 24(9): 2685–2700. DOI:10.1109/TIP.2015.2426014 |
| [21] | KOVESI P. Image Features from Phase Congruency[J]. Videre:Journal of Computer Vision Research, 1999, 1(3): 1–26. |
| [22] | HIRSCHMULLER H, SCHARSTEIN D. Evaluation of Stereo Matching Costs on Images with Radiometric Differences[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(9): 1582–1599. DOI:10.1109/TPAMI.2008.221 |


