随着各类空间大地测量技术的迅猛发展, 毫米级地球参考框架正逐步地建立并应用于大地测量领域中。温度变化被发现为GPS测站垂向周年变化作出了一定比例的毫米量级贡献[1-3];季节性温度变化引发的测站水泥墩与基岩的热胀冷缩被发现与测站周年变化存在很强的正相关性, 会造成测站高程方向的季节性变化[2-8];大气负荷、水文负载、非潮汐海洋负载等负载变化是引起测站垂向周年变化的主要因素[9-17];高阶电离层延迟是造成中纬度测站垂向周年, 东西方向半周年以及低纬测站垂向半周年运动的主要原因之一[18-20];文献[21]统计了全球492个GPS测站坐标时间序列的周期项, 发现周年项在全球具有普遍性;文献[22]发现了南北半球周年项初始相位存在约180°的系统差。由于GPS测站的非线性变化成因复杂, 目前国际上还未建立包含多种机制影响的非线性变化理论改正模型。若基于现有全球GPS实测数据, 分析测站垂向坐标时间序列中周期项的全球分布规律, 并根据此规律构建全球测站垂向非线性变化统计改正模型, 将会从整体上削弱全球测站垂向非线性运动, 并为从全球角度研究测站垂向非线性变化提供参考。
本文在全球范围内选取了461个连续观测时段在2年以上的GPS测站(其中北半球357个, 南半球104个), 提取了测站垂向周年项的振幅与初始相位, 分析得出了周年项振幅与初始相位的全球分布规律函数, 基于此函数构建了全球GPS测站垂向周年变化统计改正模型, 并对模型的改正效果进行了测试与评估。
1 数据源与提取周期项 1.1 数据源本文采用的测站坐标残差数据可通过ITRF2008官方网站(http://itrf.ensg.ign.fr/ITRF_solutions/2008/)下载。为了便于后续数据分析, 本文对原始数据进行了粗差剔除与零均值化处理。
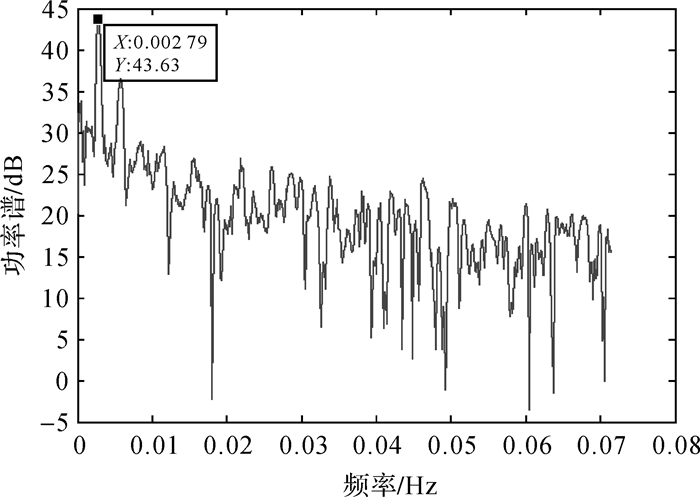
1.2 周期项提取根据谐波分析的基本思想, 含有若干周期项的时间序列可以看成由一系列不同频率的周期波叠加而成, 因此只需要确定某一周期波的准确频率以及参考历元, 就能计算出其对应的振幅和初始相位[3]。本文采用周期图法对测站垂向坐标残差时间序列进行了频谱分析, 探测并统计了周期项。鉴于篇幅, 只列出了BJFS站垂向坐标残差时间序列的频谱图, 如图 1所示。
|
| 图 1 BJFS站垂直方向坐标时间序列的频率谱 Fig. 1 Frequency spectrum of vertical coordinates time series of BJFS station |
图 1中能量最高频点的频率为0.002 79 Hz, 可以得出所对应的周期为358.4 d, 接近于一周年。确定了周期项所对应的频率后, 可以利用最小二乘拟合的方法得出周期项的振幅和初始相位[23]。
1.3 全球GPS测站垂向时间序列周期项统计本文对全球461个GPS测站垂向时间序列所包含的各类周期项进行了统计, 如表 1所示。
| 参数 | 周期项/a | |||||
| 0.5 | 1 | 1.5 | 2 | 3 | 4 | |
| 测站个数 | 314 | 461 | 194 | 228 | 160 | 157 |
| 所占比例/(%) | 68 | 100 | 42 | 49 | 35 | 34 |
在实际探测中, 发现测站时间序列中很少存在严格的周年项, 主要为类周年项, 因此本文在提取周年振幅与初始相位时, 将周期介于350~380 d之间的周期项都视为周年项[21-24]。
从表 1可以看出, 周年项在全球具有普遍性, 因此研究周年项振幅与初始相位的全球分布规律, 是建立全球测站垂向非线性变化统计改正模型的重要手段。
2 全球测站周年项分布规律建立基于周年项的统计改正模型, 需要分析周年项振幅与初始相位的全球分布规律。考虑到南北半球存在以下差异:①南北半球存在非对称构造变化[25]。②南北半球的海洋与陆地面积比例不同, 导致南北半球的气候变化、气象条件、GPS测站部署有所差异[26]。因此, 分别对南北半球测站垂向周年项的全球分布规律进行研究。
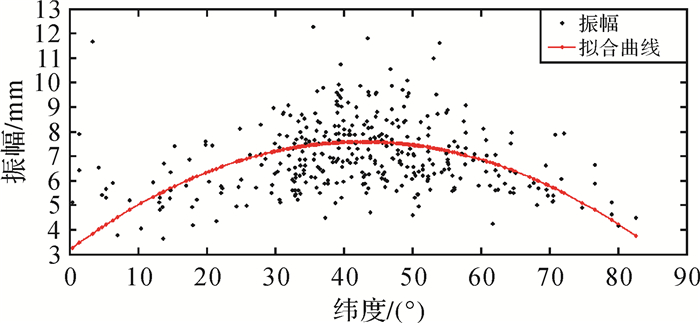
2.1 周年项振幅全球分布规律图 2和图 3分别展示了北半球、南半球测站垂向周年项振幅随纬度的分布规律。从中可看出, 南北半球垂向周年项振幅随纬度的总体变化趋势都呈现了单一的凹凸性, 且总体趋势较为平缓。由于二次项函数的凹凸性单一, 不存在拐点, 且函数值随着横坐标的变化不会出现剧烈的震荡, 结合振幅随纬度的分布特征, 对垂向周年项振幅全球分布规律进行建模时, 用二次项拟合的方法最合适;考虑到函数在赤道处的连续性, 使用分段拟合的方法, 最终得出了南北半球振幅的分布规律函数。北半球垂向周年项振幅分布规律函数为
|
| 图 2 北半球垂向周年项振幅随纬度分布规律 Fig. 2 Distribution law of vertical annual terms' amplitudes of northern hemisphere with latitude |

|
| 图 3 南半球垂向周年项振幅随纬度分布规律 Fig. 3 Distribution law of vertical annual terms' amplitudes of southern hemisphere with latitude |
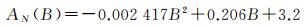 (1)
(1)
式中, B为纬度, 下同。
南半球垂向周年项振幅分布规律函数为
 (2)
(2)
对南北半球的振幅分布规律函数进行了t检验(显著性水平为0.05, 零假设为拟合函数值与振幅值来自同一分布), 检验结果如表 2所示。
| 结果 | H | P | 置信区间 |
| 北半球检验结果 | 0 | 0.650 1 | [-0.21, 0.13] |
| 南半球检验结果 | 0 | 0.262 1 | [-0.46, 0.13] |
经过显著性检验, 在显著性水平为0.05的条件下, 南北半球振幅拟合函数的H值都为0, 则接受零假设, 即模型拟合值与真实振幅值为同一分布, 说明二次项拟合函数能准确刻画振幅的分布特征。
从图 2和图 3中可以看出两个明显的现象:①随着纬度的增加, 南北半球测站垂向周年项振幅呈现先增大后减小的规律;②北半球的垂向周年项振幅普遍高于南半球。
针对第1个现象, 由于环境负载与测站垂向坐标季节性温度变化存在强相关性[15], 对于季节性变化剧烈的中纬度地区的GPS测站, 其环境负载导致的垂向位移普遍高于其他地区;同时, 环境负载是引起测站垂向周年变化的主要因素[9]。因此, 中纬度地区的周年振幅高于低、高纬度测站。
针对第2个现象, 由于地表环境负载是引起测站垂向周年变化的主要因素, 同时北半球测站环境负载的垂向绝对平均坐标值普遍高于南半球测站[9], 因此导致北半球测站的周年项振幅普遍高于南半球测站。
2.2 周年项初始相位全球分布规律研究提取周年项的初始相位时, 需要统一各测站垂向时间序列的参考历元[3]。在兼顾时间序列长度与测站数目的基础上, 本文选用2002年1月1日为参考历元。由于部分测站时间序列的观测时段不包含参考历元, 因此参与初始相位全球分布规律分析的北半球、南半球测站分别为298、89个, 测站数目总和占全球测站数目的84%。
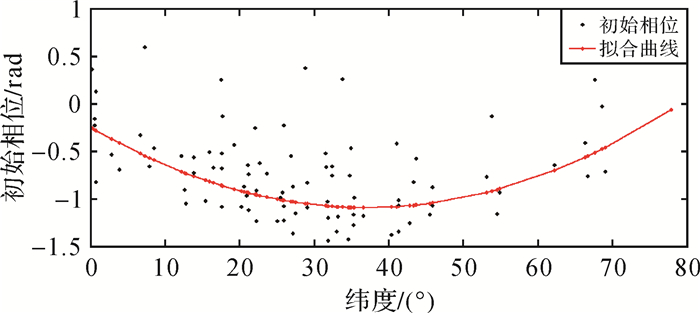
图 4和图 5分别展示了北半球、南半球测站垂向周年项初始相位随纬度的分布规律。

|
| 图 4 北半球垂向周年初始相位随纬度分布规律 Fig. 4 Distribution law of vertical annual terms' initial phases of northern hemisphere with latitude |
|
| 图 5 南半球垂向周年项初始相位随纬度分布规律 Fig. 5 Distribution law of vertical annual terms' initial phases of southern hemisphere with latitude |
根据南北半球垂向周年项初始相位的分布特征, 同2.1节, 使用分段二项式拟合的方法得出了垂向周年项初始相位的全球分布规律函数。北半球垂向周年项初始相位分布规律函数为
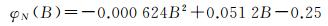 (3)
(3)
南半球垂向周年项初始相位分布规律函数为
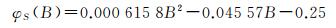 (4)
(4)
对南北半球的初始相位分布规律函数进行了t检验(显著性水平为0.05, 零假设为拟合函数值与振幅值来自同一分布), 检验结果如表 3所示。
| 结果 | H | P | 置信区间 |
| 北半球检验结果 | 0 | 0.245 2 | [-0.10, 0.03] |
| 南半球检验结果 | 0 | 0.185 7 | [-0.04, 0.18] |
根据表 3可知, 模型拟合值与真实初始相位值为同一分布, 说明二次项拟合函数能准确刻画初始相位的分布特征。
图 5、图 6之间最大的差异在于拟合曲线的凹凸。在中纬度地区, 南北半球测站垂向周年项初始相位之间存在约180°的系统差, 即垂向周年位移趋势相反。由于南北半球测站的季节性温度变化相反, 测站环境负载与测站季节性温度变化存在强相关性[15], 且环境负载是导致测站垂向周年变化的主要因素[9], 因此在同一时间段内, 季节性温度变化最剧烈的中纬度地区会呈现南北半球测站垂向周年位移趋势相反的现象, 低、高纬度地区测站的季节性变化相对较弱, 因此其垂向周年位移不会呈现明显的相反趋势。
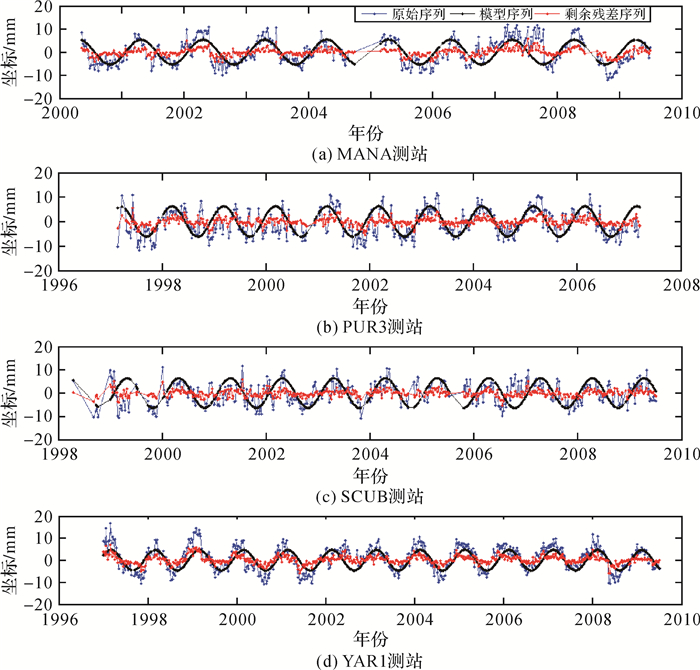
|
| 图 6 低纬度测站改正效果 Fig. 6 Correction effect of stations located in low latitudes |
3 建模及改正效果分析 3.1 建立统计改正模型
在只考虑周年项的条件下, 统计改正模型时间序列M(t)为
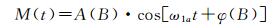 (5)
(5)
GPS测站时间序列采样周期为7 d/次, 可以得出周年角频率ω1a
 (6)
(6)
根据全球GPS测站垂向周年项振幅与初始相位的全球分布规律函数, 建立了全球GPS测站垂向周年变化统计改正模型。北半球的GPS测站垂向周年变化统计改正模型为
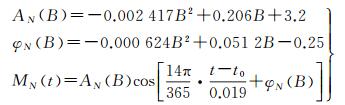 (7)
(7)
式中, B为测站纬度;t0为测站时间序列的起始历元;t为拟合值所对应的历元, 下同。
南半球的GPS测站垂向周年变化统计改正模型为
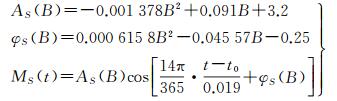 (8)
(8)
利用建立的统计改正模型对全球461个测站的垂向时间序列进行了改正, 并且根据时间序列的RMS对改正效果进行了评价。
设原始时间序列为O(t), 模型序列为M(t), 改正后的剩余残差序列为R(t), 原始时间序列所包含历元数为n。则原始时间序列O(t)的RMS为
 (9)
(9)
改正模型序列M(t)的RMS为
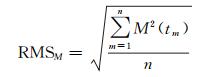 (10)
(10)
剩余残差序列R(t)的RMS为
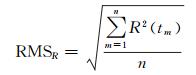 (11)
(11)
本文利用了模型改正比例km及剩余残差比例kr, 评估模型改正效果
 (12)
(12)
本文在全球低、中、高纬度各选取了具代表性的4个测站, 分别统计了模型改正比例及剩余残差比例, 如表 4所示。
| 测站 | 纬度/(°) | 原始序列RMS/mm | 模型序列RMS/mm | 剩余残差序列RMS/mm | 模型改正比例/(%) | 平均模型改正比例/(%) | 剩余残差比例/(%) | 平均剩余残差比例/(%) | |
| 低纬度测站 | MANA | 12.15(N) | 5.1 | 3.8 | 1.6 | 75 | 31 | ||
| PUR3 | 18.46(N) | 4.8 | 4.4 | 1.6 | 92 | 78 | 33 | 33 | |
| SCUB | 20.01(N) | 4.1 | 3.4 | 1.4 | 83 | 34 | |||
| YAR1 | 29.05(S) | 5.2 | 3.3 | 1.8 | 63 | 35 | |||
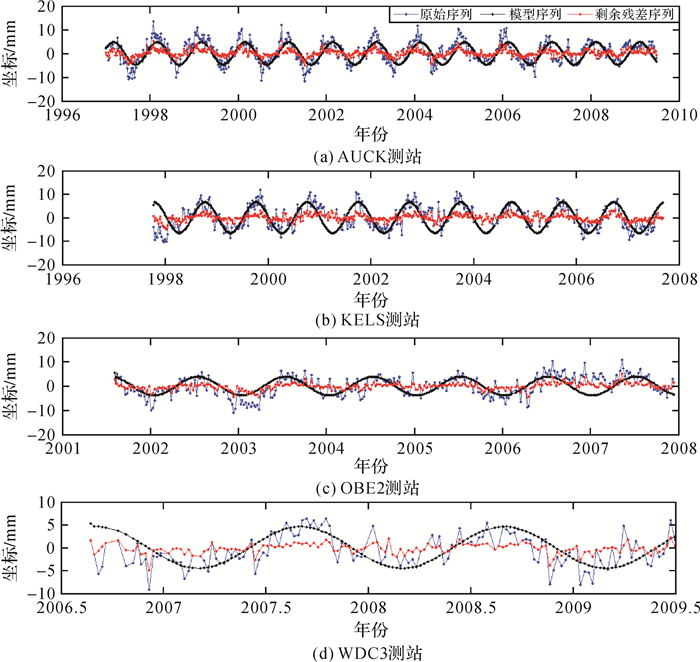
| 中纬度测站 | AUCK | 36.60(S) | 4.4 | 3.3 | 1.4 | 75 | 32 | ||
| KELS | 46.12(N) | 4.3 | 3.9 | 1.3 | 91 | 83 | 30 | 32 | |
| OBE2 | 48.09(N) | 3.9 | 2.7 | 1.3 | 69 | 33 | |||
| WDC3 | 38.92(S) | 3.3 | 3.2 | 1.1 | 97 | 33 | |||
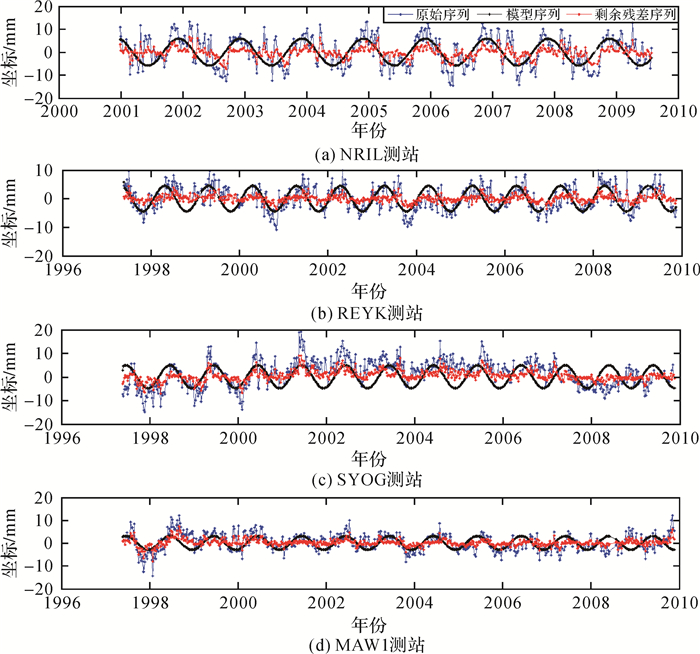
| 高纬度测站 | NRIL | 69.36(N) | 6.2 | 4.2 | 2.4 | 68 | 39 | ||
| REYK | 64.19(N) | 3.7 | 3.2 | 1.2 | 86 | 70 | 38 | 40 | |
| SYOG | 69.00(S) | 5.4 | 3.5 | 2.2 | 65 | 41 | |||
| MAW1 | 67.60(S) | 3.6 | 2.2 | 1.5 | 61 | 42 | |||
图 6是低纬度4个测站的改正效果(其中蓝色线表示原始时间序列, 黑色线表示模型改正序列, 红色线表示剩余残差序列, 下同)。图 7是中纬度4个测站的改正效果。图 8是高纬度4个测站的改正效果。
|
| 图 7 中纬度测站改正效果 Fig. 7 Correction effect of stations located in middle latitudes |
|
| 图 8 高纬度测站改正效果 Fig. 8 Correction effect of stations located in high latitudes |
结合表 4与图 6-图 8, 可以看出中纬度测站的平均模型改正比例最大, 平均剩余残差比例最小, 总体改正效果最好;低、高纬度测站的改正效果均不如中纬度测站。可能有以下两点原因:①中纬度地区由于季节性温度效应较为明显[6-7], 环境负载、热膨胀效应等因素与季节性温度变化存在强相关性[7-9], 且环境负载是导致测站垂向周年运动的主要因素[9], 因此垂向周年变化是中纬度地区测站垂向位移的主要周期性变化;低、高纬度测站由于受季节性温度效应影响较小, 其他周期性变化在测站垂向位移中的占比高, 导致中纬度测站垂向周年振幅随纬度的分布比低、高纬度测站更为集中, 改正效果更好。②与原因①同理, 中纬度测站垂向周年初始相位值分布比低、高纬度测站分布更为集中, 因此与低、高纬度测站相比, 中纬度测站的改正效果更好。
从图 6-图 8可看出, 测站原始时间序列的主周期变化与模型序列中的周年变化并不完全契合, 因此原始序列中非线性变化的不是严格的周年变化, 而是类周年变化, 印证了文献[27]的结论。
本文统计了全球461个GPS测站的改正效果, 如图 9和图 10所示。

|
| 图 9 全球GPS测站模型改正比例统计 Fig. 9 Statistics of model correction ratio of global GPS stations |
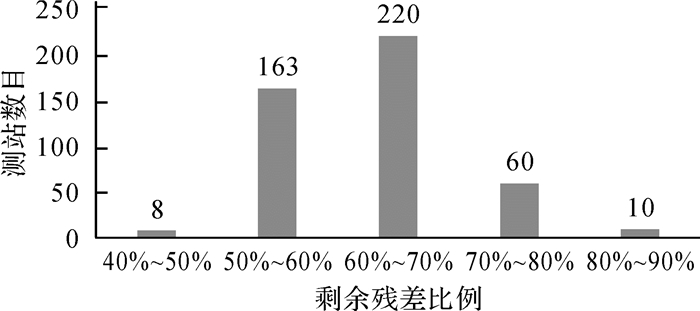
|
| 图 10 全球GPS测站剩余残差比例统计 Fig. 10 Statistics of residuals ratio of global GPS stations |
根据统计结果, 在所有测站中, 剩余残差比例达50%~70%的测站占多数, 可知统计改正模型能削弱多数测站30%~50%的垂向坐标残差。在模型改正比例达30%~40%的测站中, 存在一部分模型改正比例达到130%~140%的测站, 是因为此类测站的垂向周年项振幅小于模型拟合值。综合分析统计结果, 改正模型能大幅度削弱GPS测站的垂向坐标残差并提升大规模测站数据处理效率。
3.3 统计改正模型评价 3.3.1 模型优点(1) 本文建立的统计改正模型能削弱全球多数测站30%~50%的垂向坐标残差, 精确分离测站的线性与非线性运动。
(2) 模型能统一对全球测站垂向坐标进行改正, 提高了数据处理效率。
(3) 模型能直观地显示测站垂向周年项振幅以及初始相位的全球分布规律, 为研究全球范围内周年性地球物理运动提供参考。
3.3.2 模型缺点(1) 由于全球测站所处地区的地球物理条件各异, 引起周年项的因素复杂, 部分测站的周年项振幅与模型拟合值相差较大, 导致其改正效果不理想。
(2) 二次曲线受局部异常值影响较大, 异常值的存在会影响二项式拟合效果。
(3) 由于数据观测时段限制, 有16%的测站不包含用于提取初始相位的参考历元, 导致建模时数据利用率降低, 影响此类测站的改正效果。
3.3.3 模型改进展望(1) 半周年项也较为普遍地存在于全球GPS测站垂向坐标残差时间序列中。总结半周年项的全球分布规律, 优化现有统计改正模型, 对一些含有半周年项的测站将有更好的改正效果。
(2) 研究测站水平方向非线性变化项的全球分布规律, 建立GPS测站三维非线性变化统计改正模型。
(3) 由于二项式拟合对异常值较为敏感, 今后改进模型时, 可以考虑使用抗差性更好的方法进行更精确的拟合。
(4) 对全球GPS测站数据使用最新的精密数据处理策略进行重新处理, 使所有测站的坐标时间序列中包含相同的参考历元, 得出更精确的周年项初始相位分布规律函数, 精化全球GPS测站垂向周年变化统计改正模型。
4 结论本文基于实测数据, 研究发现了全球GPS测站垂向坐标残差时间序列中周年项的全球分布规律, 建立了全球GPS测站垂向周年变化统计改正模型, 分析了模型的改正效果, 得出如下结论。
(1) 周年项是全球GPS测站中普遍存在的周期项, 南北半球周年项振幅、北半球周年项初始相位随纬度的增加呈现先增后减的规律, 南半球周年项初始相位的变化规律与北半球相反, 南北半球中纬度地区测站周年项初始相位之间存在约180°的系统差, 低、高纬度地区测站的周年项初始相位之间则不存在明显系统差。
(2) 本文建立的统计改正模型能削弱全球多数测站30%~50%的垂向坐标残差, 可以精确分离测站的线性与非线性运动, 说明建立统计改正模型是必要且可行的。
(3) 测站周年项的周期并不严格等于一周年, 各个测站周年项的真实周期存在微小偏差。
| [1] | DONG D, FANG P, BOCK Y, et al. Anatomy of Apparent Seasonal Variations from GPS-derived Site Position Time Series[J]. Journal of Geophysical Research, 2002, 107(4): 1–7. |
| [2] | YAN Haoming, CHEN Wu, ZHU Yaozhong, et al. Contributions of Thermal Expansion of Monuments and Nearby Bedrock to Observed GPS Height Changes[J]. Geophysical Research Letters, 2009, 36(13): L13301. DOI:10.1029/2009GL038152 |
| [3] |
闫昊明, 陈武, 朱耀仲, 等.
温度变化对我国GPS台站垂直位移的影响[J]. 地球物理学报, 2010, 53(4): 825–832.
YAN Haoming, CHEN Wu, ZHU Yaozhong, et al. Thermal Effects on Vertical Displacement of GPS Stations in China[J]. Chinese Journal of Geophysics, 2010, 53(4): 825–832. DOI:10.3969/j.issn.0001-5733.2010.04.007 |
| [4] | PRAWIRODIRDJO L, BEN-ZION Y, BOCK Y. Observation and Modeling of Thermoelastic Strain in Southern California Integrated GPS Network Daily Position Time Series[J]. Journal of Geophysical Research, 2006, 111(B2): B02408. |
| [5] | ROMAGNOLI C, ZERBINI S, LAGO L, et al. Influence of Soil Consolidation and Thermal Expansion Effects on Height and Gravity Variations[J]. Journal of Geodynamics, 2003, 35(4-5): 521–539. DOI:10.1016/S0264-3707(03)00012-7 |
| [6] |
谭伟杰, 许雪晴, 董大南, 等.
温度变化对中国大陆三维周年位移的影响[J]. 测绘学报, 2017, 46(9): 1080–1087.
TAN Weijie, XU Xueqing, DONG Danan, et al. Thermoelastic Seasonal Deformation in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(9): 1080–1087. DOI:10.11947/j.AGCS.2017.20160628 |
| [7] |
姜卫平, 王锴华, 邓连生, 等.
热膨胀效应对GNSS基准站垂向位移非线性变化的影响[J]. 测绘学报, 2015, 44(5): 473–480.
JIANG Weiping, WANG Kaihua, DENG Liansheng, et al. Impact on Nonlinear Vertical Variation of GNSS Reference Stations Caused by Thermal Expansion[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(5): 473–480. DOI:10.11947/j.AGCS.2015.20140296 |
| [8] |
孙付平, 田亮, 门葆红, 等.
GPS测站周年运动与温度变化的相关性研究[J]. 测绘学报, 2012, 41(5): 723–728.
SUN Fuping, TIAN Liang, MEN Baohong, et al. Study on Correlation of Temperature Changes with GPS Station's Non-linear Movement[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 723–728. |
| [9] | JIANG Weiping, LI Zhao, VAN DAM T, et al. Comparative Analysis of Different Environmental Loading Methods and Their Impacts on the GPS Height Time Series[J]. Journal of Geodesy, 2013, 87(7): 687–703. DOI:10.1007/s00190-013-0642-3 |
| [10] | FARRELL W E. Deformation of the Earth by Surface Loads[J]. Reviews of Geophysics, 1972, 10(3): 761–797. DOI:10.1029/RG010i003p00761 |
| [11] | SUN H P, DUCARME B, DEHANT V. Effect of the Atmospheric Pressure on Surface Displacements[J]. Journal of Geodesy, 1995, 70(3): 131–139. DOI:10.1007/BF00943688 |
| [12] | VAN DAM T M, BLEWITT G, HEFLIN M B. Atmospheric Pressure Loading Effects on Global Positioning System Coordinate Determinations[J]. Journal of Geophysical Research, 1994, 99(B12): 23939–23950. DOI:10.1029/94JB02122 |
| [13] |
姜卫平, 李昭, 刘鸿飞, 等.
中国区域IGS基准站坐标时间序列非线性变化的成因分析[J]. 地球物理学报, 2013, 56(7): 2228–2237.
JIANG Weiping, LI Zhao, LIU Hongfei, et al. Cause Analysis of the Non-linear Variation of the IGS Reference Station Coordinate Time Series Inside China[J]. Chinese Journal of Geophysics, 2013, 56(7): 2228–2237. |
| [14] | VAN DAM T M, WAHR J, MILLY P C D, et al. Crustal Displacements due to Continental Water Loading[J]. Geophysical Research Letters, 2001, 28(4): 651–654. DOI:10.1029/2000GL012120 |
| [15] |
张诗玉, 钟敏.
地表流体变化对我国地壳垂直形变的影响[J]. 武汉大学学报(信息科学版), 2007, 32(5): 458–461.
ZHANG Shiyu, ZHONG Min. Vertical Crustal Displacements in China due to Surface Fluid Changes[J]. Geomatics and Information Science of Wuhan University, 2007, 32(5): 458–461. |
| [16] |
张诗玉, 钟敏, 唐诗华.
我国GPS基准站地壳垂直形变的大气负荷效应[J]. 武汉大学学报(信息科学版), 2006, 31(12): 1090–1093.
ZHANG Shiyu, ZHONG Min, TANG Shihua. Vertical Crustal Displacements due to Atmospheric Loading Effects at GPS Fiducial Stations in China[J]. Geomatics and Information Science of Wuhan University, 2006, 31(12): 1090–1093. |
| [17] | ZHANG Jie, BOCK Y, JOHNSON H, et al. Southern California Permanent GPS Geodetic Array:Error Analysis of Daily Position Estimates and Site Velocities[J]. Journal of Geophysical Research, 1997, 102(B8): 18035–18055. DOI:10.1029/97JB01380 |
| [18] | CHEN Wu, GAO Shan, HU Congwei, et al. Effects of Ionospheric Disturbances on GPS Observation in Low Latitude Area[J]. GPS Solutions, 2008, 12(1): 33–41. DOI:10.1007/s10291-007-0062-z |
| [19] | KEDAR S, HAJJ G A, WILSON B D, et al. The Effect of the Second Order GPS Ionospheric Correction on Receiver Positions[J]. Geophysical Research Letters, 2003, 30(16): 1829. DOI:10.1029/2003GL017639 |
| [20] |
姜卫平, 李昭, 邓连生, 等.
高阶电离层延迟对GPS坐标时间序列的影响分析[J]. 科学通报, 2014, 59(10): 913–923.
JIANG Weiping, LI Zhao, DENG Liansheng, et al. Impact of Higher Order Ionospheric Delay on Continuous GPS Coordinate Time Series[J]. Chinese Science Bulletin, 2014, 59(10): 913–923. |
| [21] |
田亮, 刘武凤, 张建东, 等.
基于GPS坐标残差序列的全球测站非线性变化规律统计[J]. 地理空间信息, 2013, 11(4): 70–71, 75.
TIAN Liang, LIU Wufeng, ZHANG Jiandong, et al. Statistics and Analysis of Global GPS Non-linear Movement Based on GPS Coordinate Residual Series[J]. Geospatial Information, 2013, 11(4): 70–71, 75. DOI:10.11709/j.issn.1672-4623.2013.04.026 |
| [22] |
田亮, 孙付平, 牛冬梅.
全球GNSS测站坐标周年非线性变化相位规律分析[J]. 大地测量与地球动力学, 2016, 36(2): 154–157.
TIAN Liang, SUN Fuping, NIU Dongmei. The Study on Phase Rule of Global GNSS Coordinate Annual Non-linear Motion[J]. Journal of Geodesy and Geodynamics, 2016, 36(2): 154–157. |
| [23] |
王振龙, 胡永宏.
应用时间序列分析[M]. 北京: 科学出版社, 2007: 79-82.
WANG Zhenlong, HU Yonghong. Application of Time Series Analysis[M]. Beijing: Science Press, 2007: 79-82. |
| [24] |
刘伟, 李昭, 邓连生, 等. GPS高程时间序列的季节性变化分析周期项提取与残差时间序列模型建立[C]//第三届中国卫星导航学术年会电子文集——S08卫星导航模型与方法.广州: 中国卫星导航学术年会组委会, 2012. LIU Wei, LI Zhao, DENG Liansheng, et al. Seasonal Changes Analysis of GPS Elevation Times Series[C]//The 3rd Chinese Satellite Navigation Conference on electronic S08 Satellite Navigation Model and Method. Guangzhou: Organizing Committee of China Satellite Navigation Academic Annual Meeting, 2012. |
| [25] |
孙付平, 赵铭, 宁津生, 等.
用空间大地测量数据检测地球的非对称性全球构造变化[J]. 科学通报, 2000, 45(7): 639–643.
SUN Fuping, ZHAO Ming, NING Jinsheng, et al. Detection of Unsymmetrical Global Tectonic Change by Using Space Geodetic Data[J]. Chinese Science Bulletin, 2000, 45(7): 639–643. |
| [26] |
孙家抦.
遥感原理与应用[M]. 武汉: 武汉大学出版社, 2003: 10-13.
SUN Jiabing. Principles and Applications of Remote Sensing[M]. Wuhan: Wuhan University Press, 2003: 10-13. |
| [27] | RAY J, ALTAMIMI Z, COLLILIEUX X, et al. Anomalous Harmonics in the Spectra of GPS Position Estimates[J]. GPS Solutions, 2008, 12(1): 55–64. DOI:10.1007/s10291-007-0067-7 |



