精密单点定位(precise point positioning, PPP)仅靠单台接收机便可高精度确定位置,在形变监测、工程测量、地球动力学等方面得到了广泛应用[1]。但由于受到未校准相位延迟(uncalibrated phase delays, UPD)的影响,PPP中模糊度通常表现为实数,而准确固定模糊度有利于提高定位的收敛速度和精度[2-3]。国内外学者为实现固定解PPP,提出了小数周偏差(fractional cycle bias, FCB)法、整数钟法、去耦钟差法等方法[4-6],且已有研究证明了上述方法的等价性[7-8]。其中,FCB方法提出最早且应用较广:文献[9]最早估计了星间单差的FCB,但限于当时星历的精度,仅能有效分离出宽巷模糊度的小数部分;文献[4]采用IGS(International GNSS Service)参考网数据,成功获得宽巷和窄巷的FCB,实现了单差的固定解PPP;文献[10]引入模糊度基准后生成非差FCB参数,进行了非差的固定解PPP;文献[11-16]也围绕FCB的生成与应用展开了研究。
根据是否进行星间差分可将FCB的解算方法分为非差和单差两种。非差方法假设接收机宽巷FCB足够稳定,利用非差模糊度构建观测方程,同时解算接收机和卫星的FCB。研究表明接收机宽巷FCB单天最大变化可达0.3周,并且接收机重启后宽巷FCB会重新赋值[17],而非差方法每天仅估计一组卫星宽巷FCB,故非差FCB会受到接收机端FCB的不利影响。单差方法则通过星间单差消除了接收机FCB的不利影响,仅估计卫星FCB,无需平差解算,计算量小。但由于一颗卫星无法与所有卫星直接构成单差观测,因此单参考星FCB的作用范围有限,需播发多个参考星的单差FCB才能保证全球范围的可用性,这将大幅增加传输的数据量。受限于此,单差FCB多用于进行区域参考网内的固定解PPP解算,为保证全球范围的可用性,目前公开发布的FCB参数,均采用非差FCB估计方法。
针对这一问题,本文提出一种单参考星下全星座单差FCB估计方法。该方法利用差分传递的思想,将不同卫星对的单差FCB转换到统一的参考星下。采用与整数无关的抗差初值消除转换后FCB值域边界跳变的影响,采用抗差估计合并FCB。为解决宽巷差异引起的窄巷FCB跳变,解算时先使用合并后宽巷FCB解算各卫星的窄巷FCB,再合并得到改进后的窄巷单差FCB。最后,分别利用静态和车载动态数据验证了改进FCB用于固定解PPP的性能。
1 单差FCB估计方法星间单差消除了接收机影响,只需估计卫星的FCB。采用无电离层(ionosphere-free, IF)组合解算PPP,将IF模糊度分解为具有整数特性的宽巷和窄巷模糊度,分别固定后得到对应的FCB参数。
1.1 宽巷FCB估计由MW(Melbourne-Wubbena)组合可得宽巷模糊度浮点解为
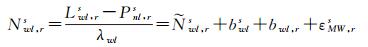 (1)
(1)
式中:r和s为测站和卫星;Lwl, rs为载波宽巷;Pnl, rs为伪距窄巷;λwl为宽巷波长。Nwl, rs由整数部分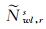
设s1和s2为共视卫星对,经星间单差可消除bwl, r影响,且按高度角加权平滑后可消除噪声影响,得到平滑后的单差宽巷模糊度
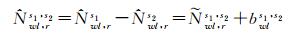 (2)
(2)
其包括整数部分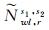
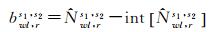 (3)
(3)
平均所有测站的FCB,可得该卫星对宽巷FCB的均值估计bwls1, s2及估计量的标准差
 (4)
(4)
式中,〈·〉表示测站间取平均;nsta为参与解算的测站数。
1.2 窄巷FCB估计在k历元时,由IF组合PPP可得单差IF模糊度(NIF, rs1, s2)k,宽巷FCB改正宽巷模糊度浮点解(Nwl, rs1, s2)k后可得固定解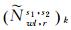
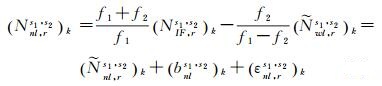 (5)
(5)
(Nnl, rs1, s2)k由整数部分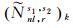
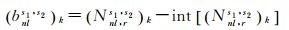 (6)
(6)
测站间平均后可得该卫星对在k历元的窄巷FCB平均估值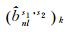
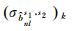
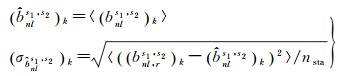 (7)
(7)
单参考星的单差FCB无法涵盖全时段的所有卫星,需经差分传递将其他参考星的FCB转换到同一个参考星下。设s1-s3、s2-s3为共视卫星对,已知s1、s2以s3为参考星的FCB、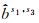
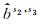
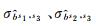
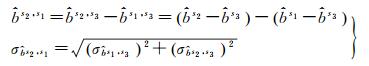 (8)
(8)
据式(8)可知,标准差随转换次数的增加而累积,故为限制误差传播仅进行一次转换。
转换后,新参考星下每颗卫星可获取多组单差FCB(6~24组),获取方法有直接法和传递法两种:直接法仅可应用于两星直接共视时;而传递法则可应用于借助中间星构成的间接共视。表 1列出了以s1为目标参考星时,卫星对s1-s2对应的单差FCB获取方法及标准差。理论上获取的多组FCB应当相等,但误差影响会导致其存在差异,窄巷FCB所受影响更大。
| 获取方法 | 单差FCB | 原参考星 | 标准差 |
| 直接法 | 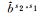 |
s1 | 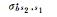 |
| 传递法 |  |
sx(x≠1, 2) | 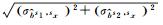 |
2.2 转换后FCB的合并估计 2.2.1 基于GPHASE初值的抗差估计
为削弱不同来源FCB间差异与粗差的影响,提高估计精度,采用IGG Ⅲ定权方案下的抗差估计对参考星转换后的FCB参数进行合并估计[18-19]。抗差估计中采用估计初值确定初始残差,初值的好坏直接影响抗差结果,偏差较大的初值甚至会导致估计发散,通常采用中位数或均值作为抗差估计的初值[20]。作为UPD的小数部分,FCB的值域为(-0.5, +0.5]。当FCB真值在值域边界附近时,由不同参数星转换得到的FCB估值为
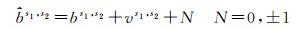 (9)
(9)
式中,bs1, s2为FCB真值;vs1, s2为FCB的误差影响;N是为保证估值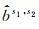
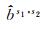

|
| 图 1 值域边界附近的FCB序列 Fig. 1 The FCB sequence near boundaries of the range |
为消除值域边界跳变对FCB合并的影响,采用文献[21]提出的与整数无关的GPHASE函数计算抗差估计的初值。该函数利用三角函数消除FCB整数部分的影响,再用反三角函数得到非整部分,其值域为(-0.5, +0.5],函数式如下
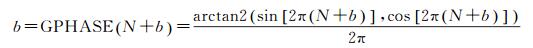 (10)
(10)
式中,(N+b)为FCB估值,N和b分别为整数和非整部分;arctan2(·)是求向量方向角的函数,值域为(-π,π]。其拓展后可用于求取FCB估值序列(Ni+bi)的合并估计结果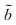
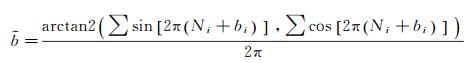 (11)
(11)
转换后FCB合并时取Ni为零,并将式(9)中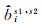
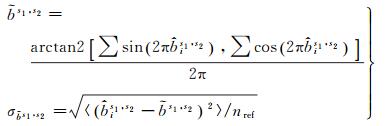 (12)
(12)
式中,nref为参与合并的FCB估值总数。如图 1所示,GPHASE合并结果不受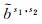
需要说明的是,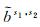
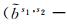
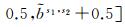
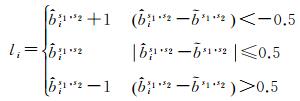 (13)
(13)
转换后FCB在合并时有两种解算顺序:一是先采用单差法分别解算出所有参考星的宽巷和窄巷FCB,再分别将宽窄巷FCB转换到目标参考星后进行合并;二是在生成单差宽巷FCB后,先合并得到目标参考星的宽巷FCB,再用合并后宽巷FCB生成单差窄巷FCB,最后对窄巷FCB进行合并。理论上两种方案是等价的,但值域边界跳变会使方案1的窄巷FCB在转换后分布在相差约0.5周的两组中,从而影响到窄巷FCB估值的准确估计。
宽巷FCB发生边界跳变后分布在(-0.5, -0.5+Δ1]和[0.5-Δ2, 0.5]内(Δ1和Δ2为小量)。此时若采用方案1,不同参考星宽巷FCB的差异会使固定的
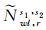
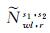
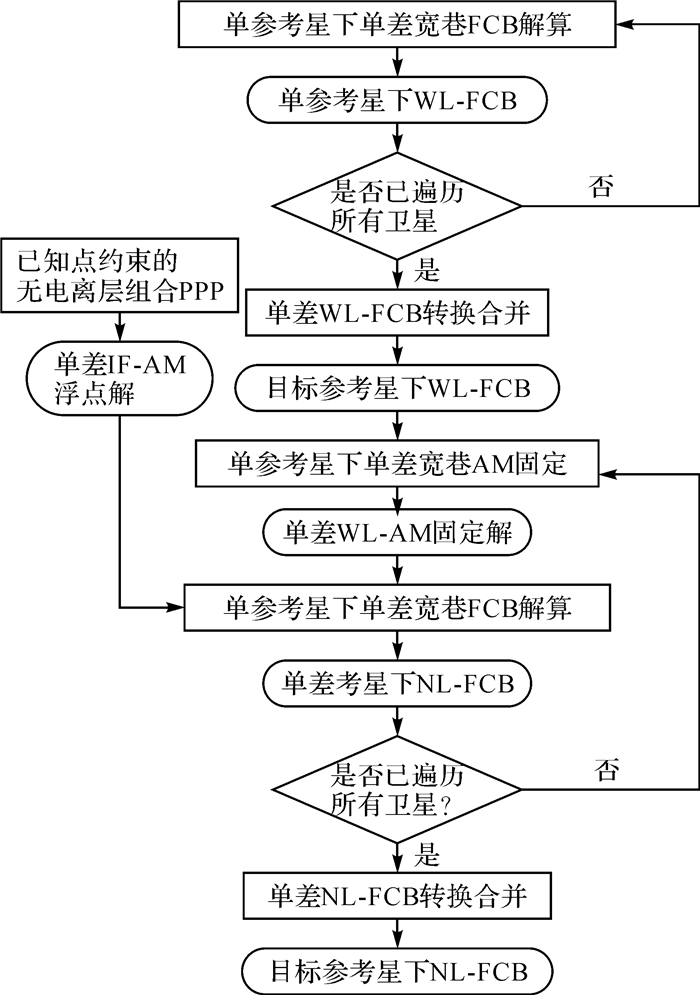
参照单差FCB估计方法,结合参考星转换与方案2的FCB合并顺序,得到单参考星下全星座单差FCB的生成流程,如图 2所示。
|
| 图 2 改进后单差FCB生成流程 Fig. 2 The generation process of improved single-difference FCB |
3 改进后单差FCB试验
试验解算了2016年1月10日至24日共15 d的改进后FCB,选取全球180个IGS观测站采样间隔为30 s的数据。按照宽巷一天一组,窄巷每15 min一组估计FCB;宽巷FCB求解时连续弧段长度不小于20 min;参考星转换时要求FCB的标准差小于0.2周;单参考星和转换后FCB的参考星皆为G01星。转换后FCB在合并中,IGGⅢ方案的调和系数为k0=1.5、k1=3.0,收敛阈值10-3。解算窄巷FCB时,为加快无电离层模糊度收敛,在PPP中将测站坐标固定至已知值,其他参数与误差设置如表 2所示。
| 类别 | 项目 | 处理策略 |
| 参数估计 | 接收机位置, 模糊度 | 逐历元估计 |
| 接收机钟差 | 白噪声模型 | |
| 电离层延迟 | 无电离层组合 | |
| 对流层延迟 | 估计ZTD参数 | |
| 解算方法 | 扩展卡尔曼滤波 | |
| 高度角 | 截止角10°, 高度角加权 | |
| 误差处理 | 轨道及钟差 | IGS精密星历:15 min轨道, 30 s钟差 |
| 周跳探测, 钟跳修复 | GF-MW组合, 历元间差分 | |
| 天线相位中心改正 | igs08.atx | |
| 固体潮、海潮 | 模型改正 | |
| DCB改正 | CODE发布的P1C1.dcb | |
| 相位缠绕 | 模型改正 | |
| 相对论效应 | 模型改正 |
3.1 宽巷FCB分析
单差宽巷FCB的结果如图 3所示:左侧为转换后的FCB合并值,右侧为单参考星的单差解。其中G01星为参考星、G04星无观测数据,共有30组单差结果,图中不同颜色曲线分别代表各卫星结果。因无法与G01星直接共视,单星结果中缺少G05、G20、G21、G29星数据;改进方法则可经间接共视获得所有卫星的单差宽巷FCB;除子图(c)中的G32星FCB在解算周期内显著增大,两组宽巷FCB15 d内的变化都小于0.1周。

|
| 图 3 宽巷FCB时间序列 Fig. 3 Time series of wide-lane FCB |
武汉大学发布了基于多种星历和钟差的非差的宽巷和窄巷FCB产品[11],法国国家太空研究中心(CNES)在其整数钟产品中也包含了非差宽巷FCB[22]。将上述非差FCB转换到G01星为参考后作外符合基准,对比可得本文FCB的偏差。数据无缺失时,一天共30对宽巷FCB,15 d共450对,定义宽巷FCB的可用率为有值的FCB总数占450对的比例。两组宽巷FCB的统计结果如表 3所示。
| 类型 | 单星结果 | 合并结果 |
| FCB总数/对 | 390 | 450 |
| 可用率/(%) | 86.70 | 100 |
| 标准差均值 | 0.020 8 | 0.007 7 |
| 与武汉大学的平均偏差/周 | 0.030 5 | 0.022 4 |
| 与CNES的平均偏差/周 | 0.038 2 | 0.029 6 |
相比传统结果,改进后宽巷FCB的可用性与稳定性更佳。其中,合并后宽巷FCB全时段可用,平均标准差减小63.0%,与已有产品的差异均值小于0.03。对比CNES和武汉大学的宽巷FCB产品可知,G32星在观测期间内宽巷FCB都存在一致的增长趋势。根据IGS发布的卫星状态信息可知原G32星为BLOCK ⅡA卫星且于2016年1月25日终止了工作[23],故推测可能因星上设备老化导致其宽巷FCB稳定性劣于其他卫星。
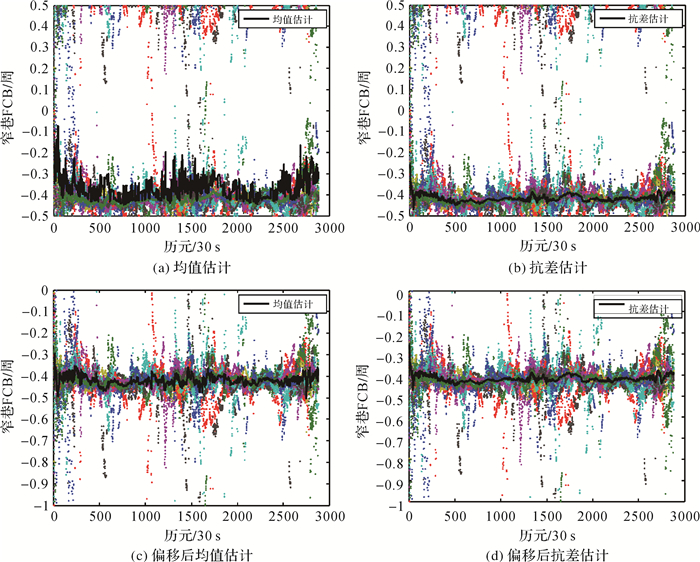
3.2 窄巷FCB分析 3.2.1 窄巷FCB合并方法比较窄巷波长较短,其FCB受误差影响较大,且考虑值域边界跳变,因此采用GPHASE初值进行抗差估计。图 4以2016年1月10日的G11星为例,比较了窄巷FCB的各合并方法,其中彩色散点为转换后FCB序列,黑色曲线为合并估值。对比图 4(a)与(b),值域边界跳变使均值估计偏离真值,波动变大;而GPHASE初值下抗差估计能较稳定地收敛到真值。图 4(c)和(d)中先对FCB观测序列进行偏移,以消除边界跳变影响,此时两种估计都能收敛到真值,但均值估计的标准差为0.021,抗差估计则为0.015,稳定性更好。对比图 4(b)与(d),可知GPHASE初值下抗差估计不受值域边界跳变影响。
|
| 图 4 不同合并方法下的G11窄巷FCB Fig. 4 The narrow-lane FCB of G11 using different combining methods |
3.2.2 窄巷FCB生成方案差异分析
估计转换后FCB时应选择方案二的解算顺序,以消除窄巷FCB间可能存在的半周差异。为分析该差异的影响,以2016年1月10日G03星观测数据为例,其合并后宽巷FCB为-0.493,将参考星转换到G01后集中在值域边界附近,如图 5所示。
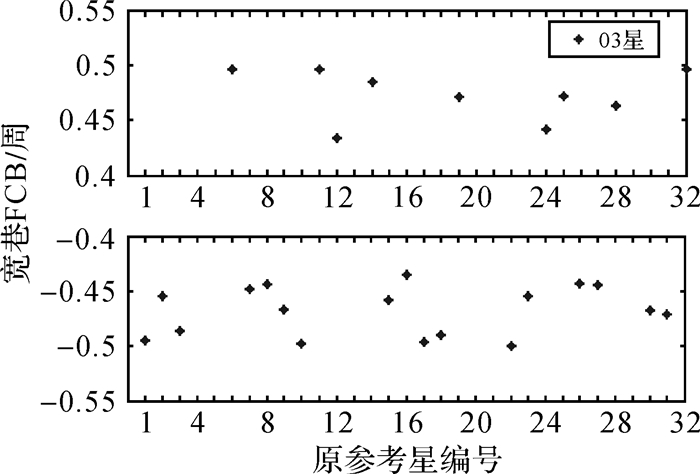
|
| 图 5 转换后G03的宽巷FCB序列 Fig. 5 The wide-lane FCB of G03 after conversion |
分别采用方案1和2生成G03的窄巷FCB,转换到G01后利用GPHASE函数得到估计初值,图 6中彩色散点为不同参考星转换参考星后的窄巷FCB序列,黑色曲线为GPHASE估值。方案1中FCB转换后分布在相差约半周的两组,而GPHASE函数只能消除整周影响,因此方案一中GPHASE初值无法真实反映真值,将影响抗差估计的结果。方案2则不会产生窄巷FCB的半周差异。

|
| 图 6 转换后G03星窄巷FCB Fig. 6 The narrow-lane FCB of G03 after conversion |
3.2.3 合并后窄巷FCB特性分析
相比单参考星结果,合并后窄巷FCB的稳定性与连续性更优。经历元间平滑后生成15 min一组的合并后窄巷FCB,作为对照也计算了传统方法下单G01星的单差FCB。图 7为2016年1月10日的窄巷FCB变化图,左图为合并结果,右侧为单星结果。单星的窄巷FCB不具备全天的完整结果,序列稳定性较差且存在跳变,日最大变化可达0.4周;而抗差合并的FCB序列全天连续且更稳定,变化小于0.2周。
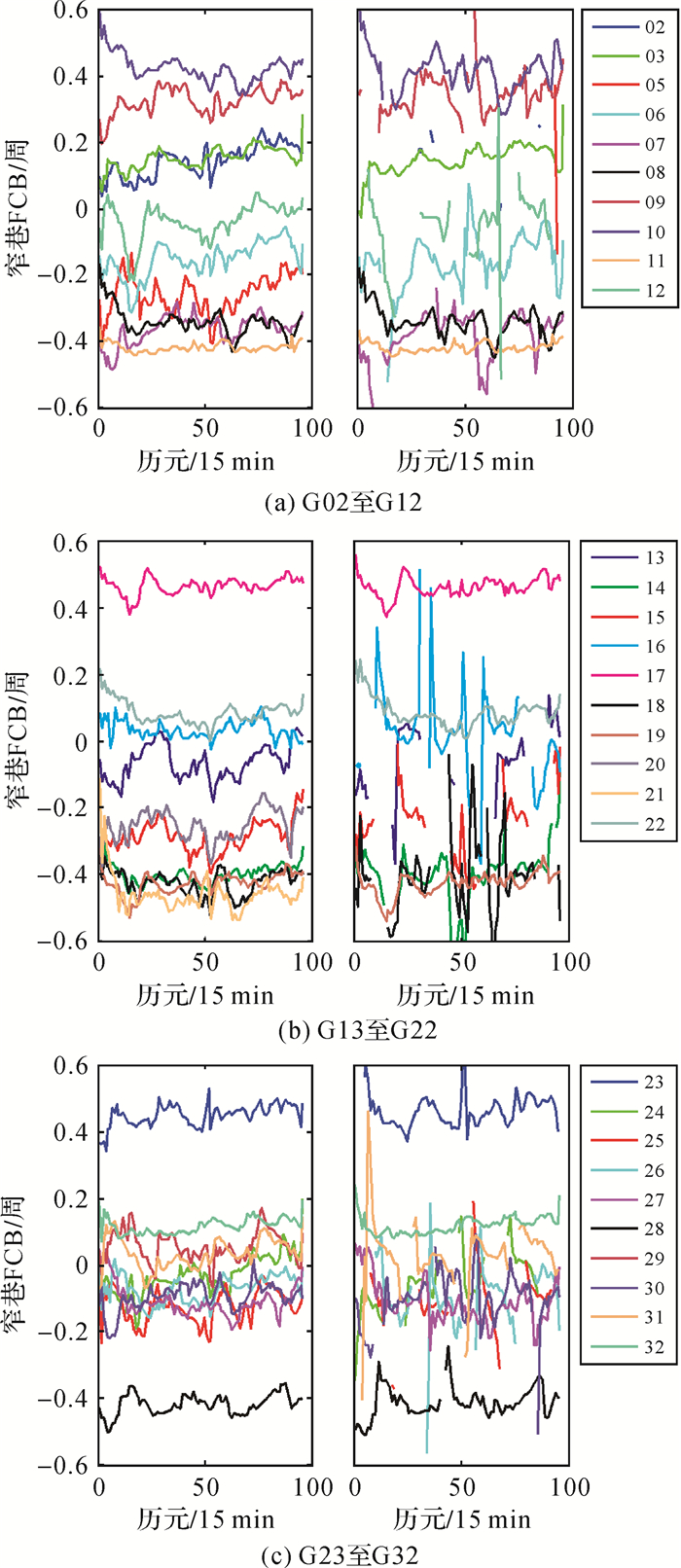
|
| 图 7 窄巷FCB时间序列 Fig. 7 Time series of narrow-lane FCB |
合并后FCB的标准差显著小于单参考星结果。图 8对比了单星与合并窄巷FCB各历元标准差的均值,其中,单星结果中缺少G20、G21与G29的结果。由于合并后FCB整合了更多观测信息,且抗差估计削弱了粗差影响,故可获得更为可靠的FCB估值。
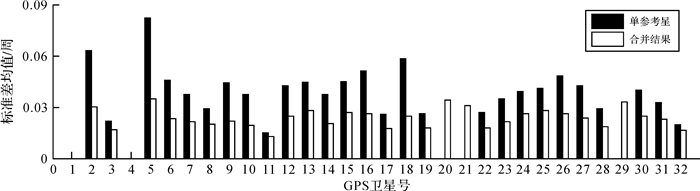
|
| 图 8 窄巷FCB平均标准差 Fig. 8 Average standard errors of narrow-lane FCB |
相比于单星结果,合并结果与外符合精度基准的一致性更好。选取由武汉大学发布且与本文采用相同星历、钟差和DCB参数的非差窄巷FCB,将其参考星转换到G01下并消除窄巷FCB半周差异后,作为外符合精度评判基准。统计单星和合并后FCB与其相比的偏差,结果如图 9所示。合并后FCB的偏差小于单星结果,且均不超过0.05周。
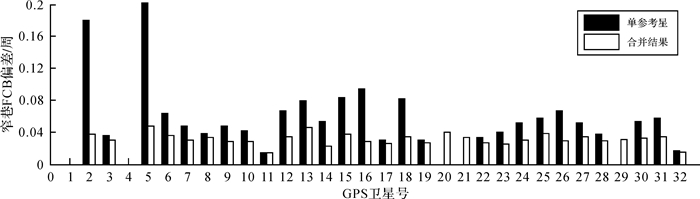
|
| 图 9 窄巷FCB平均偏差 Fig. 9 Average errors of narrow-lane FCB |
在无数据缺失时,单颗参考星下一天共应有2880对窄巷FCB,则窄巷FCB的可用率为可用结果在应有总数中的比例。表 4统计了窄巷FCB的各项特性,结合图 6-图 8可得:改进后的窄巷FCB全天可用,其标准差和偏差的均值相比于单星结果分别改善了42.9%和50.8%。
| 类型 | 单星结果 | 合并结果 |
| 总数/对 | 2066 | 2880 |
| 可用率/(%) | 71.7 | 100 |
| 标准差均值/周 | 0.042 | 0.024 |
| 偏差均值/周 | 0.063 | 0.031 |
3.3 基于改进FCB的固定解PPP验证
为验证改进后单差FCB的定位性能,分别选取IGS站的静态数据和车载动态数据进行了固定解PPP验证,其参数估计与误差处理策略采用表 2的设置。固定模糊度时,使用Bootstraping成功率和Ratio-test进行检核,阈值分别为0.999和3.0[4];为确保固定正确率,在连续5历元通过检核、标准差小于0.15 m后才更新固定解结果。若固定解偏差大于0.15 m且超出浮点解偏差的1.5倍,则认为模糊度未能正确固定。
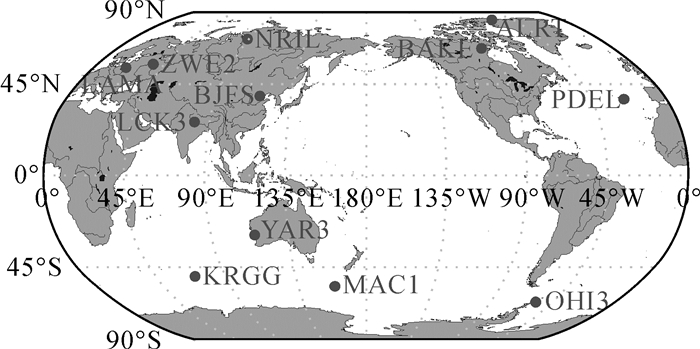
3.3.1 静态验证静态验证时采用图 10所示的12个未参与FCB生成的IGS测站,将2016年1月10日至24日的观测数据分为360段,分别采用3种方案进行PPP静态小时解:①浮点解;②采用单参考星FCB的固定解;③采用合并后FCB的固定解。以IGS周解坐标为参考值,评估各方案下北、东、天(north east up, NEU)方向及三维的偏差,方案2和3中只统计正确固定的时段。图 11为各测站方案1到3的NEU方向位置偏差。
|
| 图 10 静态验证测站分布 Fig. 10 The distribution of stations used in static experiments |

|
| 图 11 各测站位置偏差 Fig. 11 Position errors of each station |
相比浮点解,固定解定位精度显著提升,E方向改进最明显;固定解中,两种FCB的PPP在固定后定位精度相近,但合并后FCB的固定率更高。表 5给出了各方案的定位精度的统计结果:方案3中E方向误差相比方案1减小了72.1%,三维偏差减小了1.61 cm;方案2固定后的精度与方案3相近。单参考星FCB由于缺失部分卫星的改正数,仅能正确固定64.9%的时段,而改进后的合并单差FCB可固定97.2%的时段,可用性显著提升。
| cm | ||||
| 方案 | 平均定位误差 | |||
| N | E | U | 3D | |
| 1 | 0.95 | 1.90 | 2.17 | 3.44 |
| 2 | 0.76 | 0.71 | 1.67 | 2.19 |
| 3 | 0.50 | 0.53 | 1.48 | 1.83 |
3.3.2 动态验证
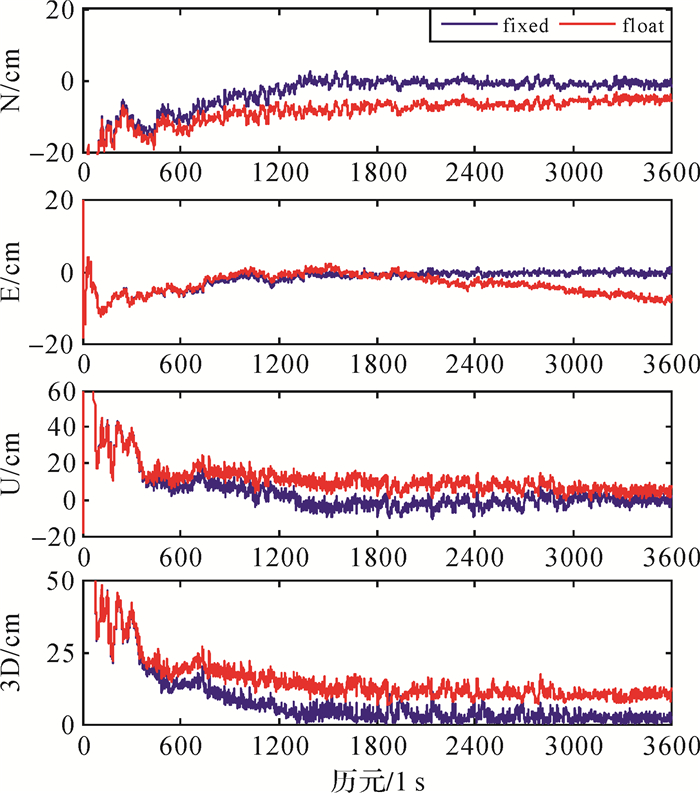
采用2017年12月27日的车载动态数据进行固定解PPP的动态验证,所用接收机为Trimble NetR9,数据采样率为1 Hz,时长为1 h,运动轨迹如图 12所示。在评估动态PPP的定位精度时,以短基线的双差固定解为参考[24]。图 13为动态PPP各方向位置偏差的变化曲线,其中蓝色曲线为采用改进后FCB的固定解,红色曲线为浮点解。

|
| 图 12 动态试验的运动轨迹 Fig. 12 The track of dynamic experiment |
|
| 图 13 动态PPP的位置偏差 Fig. 13 Position errors of kinematic PPP |
定义动态PPP收敛的条件为NEU方向偏差均小于10 cm,且保持超过20个历元[25]。如图 13所示,动态验证中PPP浮点解需22.9 min才能收敛,且收敛过程中位置偏差存在波动;而固定解的收敛时间缩短了37.5%,仅需14.3 min便可收敛,收敛后不但精度更高且更为稳定。表 6给出了收敛后动态PPP的平均定位偏差和均方根误差(root mean square, RMS),为保持一致性,固定解和浮点解均从22.9 min后开始统计。由表 6的统计结果可见:动态情况下,固定解PPP在收敛后精度可达5 cm以内,三维定位误差相比浮点解减小了61.4%。
| cm | |||||||||
| 参数 | 浮点解 | 固定解 | |||||||
| E | N | U | 3D | E | N | U | 3D | ||
| 平均偏差 | 3.03 | 7.13 | 8.66 | 12.22 | 1.00 | 1.52 | 3.20 | 3.97 | |
| RMS | 3.83 | 7.33 | 9.47 | 12.57 | 1.29 | 2.25 | 4.10 | 4.85 | |
4 结论
本文改进了单差FCB生成方法,经差分传递转换了单差FCB的参考星,利用GPHASE初值下的抗差估计对转换后FCB进行合并,并采用先合并宽巷再生成窄巷的解算顺序避免窄巷FCB间的半周差异。采用IGS全球网生成改进后的全星座单差FCB,并进行固定解PPP验证,得出:
(1) 参考星转换后的合并FCB可保证全时段可用,其数据量小于传统单差法,与非差法相当。而传统单差法中单颗参考星的宽巷和窄巷FCB的可用率仅有86.70%和71.7%。
(2) 合并后FCB在准确性和稳定性等方面均优于单参考星结果。其中,合并后宽巷FCB在15天内的变化小于0.1周,窄巷FCB单天内变化不超过0.2周;与现有产品相比,宽窄巷FCB的平均偏差都在0.04周内。
(3) 利用合并后FCB进行PPP固定解,定位精度相比浮点解显著提升,固定率相比单星FCB大幅提高。静态解算时,NEU方向精度分别提高了0.45 cm、1.37 cm和0.69 cm,3D偏差减少了46.8%;应用改进的单差FCB进行固定解PPP的固定率相比单星FCB提升了32.3%,固定后位置偏差减少了16.4%。动态PPP解算时,固定解平均收敛时间为14.32 min,相比浮点解加快了37.5%,收敛后RMS为4.85 cm,减少了61.4%。
| [1] | ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research Solid Earth, 1997, 102(B3): 5005–5017. DOI:10.1029/96JB03860 |
| [2] | TEUNISSEN P J G, KHODABANDEH A. Review and Principles of PPP-RTK Methods[J]. Journal of Geodesy, 2015, 89(3): 217–240. DOI:10.1007/s00190-014-0771-3 |
| [3] |
宋超.精密单点定位快速收敛技术与方法研究[D].郑州: 信息工程大学, 2015: 1-164. SONG Chao. Technologies and Methods on Rapid Convergence of Precise Point Positioning[D]. Zhengzhou: Information Engineering University, 2015: 1-164. |
| [4] | GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS Carrier-phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations[J]. Journal of Geodesy, 2008, 82(7): 389–399. DOI:10.1007/s00190-007-0187-4 |
| [5] | LAURICHESSE D, MERCIER F, BERTHIAS J P, et al. Integer Ambiguity Resolution on Undifferenced GPS Phase Measurements and Its Application to PPP and Satellite Precise Orbit Determination[J]. Navigation, 2009, 56(2): 135–149. DOI:10.1002/navi.2009.56.issue-2 |
| [6] | COLLINS P, BISNATH S, LAHAYE F, et al. Undifferenced GPS Ambiguity Resolution Using the Decoupled Clock Model and Ambiguity Datum Fixing[J]. Navigation, 2010, 57(2): 123–135. DOI:10.1002/navi.2010.57.issue-2 |
| [7] | ODIJK D, ZHANG B, KHODABANDEH A, et al. On the Estimability of Parameters in Undifferenced, Uncombined GNSS Network and PPP-RTK User Models by Means of S-system Theory[J]. Journal of Geodesy, 2016, 90(1): 15–44. DOI:10.1007/s00190-015-0854-9 |
| [8] | SHI Junbo, GAO Yang. A Comparison of Three PPP Integer Ambiguity Resolution Methods[J]. GPS Solutions, 2014, 18(4): 519–528. DOI:10.1007/s10291-013-0348-2 |
| [9] | GABOR M J, NEREMR S. GPS Carrier Phase Ambiguity Resolution Using Satellite-Satellite Single Differences[C]//Proceedings of the 12th International Technical Meeting of the Satellite Division of the Institute of Navigationion Nashville, TNUS, : ION, 1999, pp: 1569-1578. |
| [10] |
张小红, 李星星.
非差模糊度整数固定解PPP新方法及实验[J]. 武汉大学学报(信息科学版), 2010, 35(6): 657–660.
ZHANG Xiaohong, LI Xingxing. A New Method for Zero-differenced Interger Ambiguity Resolution and Its Application to PPP[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 657–660. |
| [11] |
李盼. GNSS精密单点定位模糊度快速固定技术和方法研究[D].武汉: 武汉大学, 2016: 1-134. LI Pan. Research on Methodology of Rapid Ambiguity Resolution for GNSS Precise Point Positioning[D]. Wuhan: Wuhan University, 2016: 1-134. http://cdmd.cnki.com.cn/Article/CDMD-10486-1016113506.htm |
| [12] | GENG Jianghui, TEFERLE F N, SHI C, et al. Ambiguity Resolution in Precise Point Positioning with Hourly Data[J]. GPS Solutions, 2009, 13(4): 263–270. DOI:10.1007/s10291-009-0119-2 |
| [13] | LI Xingxing, GE Maorong, ZHANG Hongping, et al. A Method for Improving Uncalibrated Phase Delay Estimation and Ambiguity-fixing in Real-time Precise Point Positioning[J]. Journal of Geodesy, 2013, 87(5): 405–416. DOI:10.1007/s00190-013-0611-x |
| [14] |
潘宗鹏, 柴洪洲, 刘军, 等.
基于部分整周模糊度固定的非差GPS精密单点定位方法[J]. 测绘学报, 2015, 44(11): 1210–1218.
PAN Zongpeng, CHAI Hongzhou, LIU Jun, et al. GPS Partial Ambiguity Resolution Method for Zero-difference Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(11): 1210–1218. DOI:10.11947/j.AGCS.2015.20150056 |
| [15] | LI Yihe, GAO Yang, SHI Junbo. Improved PPP Ambiguity Resolution by COES FCB Estimation[J]. Journal of Geodesy, 2016, 90(5): 437–450. DOI:10.1007/s00190-016-0885-x |
| [16] |
李林阳, 崔阳, 王宇谱, 等.
窄巷FCB估计方法改进及时变特性分析[J]. 测绘学报, 2017, 46(1): 34–43.
LI Linyang, CUI Yang, WANG Yupu, et al. Improvement of Narrow-lane Fractional Cycle Bias Estimation and Analysis of Its Time-varying Property[J]. Acta Geodaetica et Cartogr-aphica Sinica, 2017, 46(1): 34–43. DOI:10.11947/j.AGCS.2017.20160222 |
| [17] |
张小红, 李盼, 李星星, 等.
宽巷载波相位模糊度小数偏差时变特性分析[J]. 测绘学报, 2013, 42(6): 798–803, 809.
ZHANG Xiaohong, LI Pan, LI Xingxing, et al. An Analysis of Time-varying Property of Wide-lane Carrier Phase Ambiguity Fractional Bias[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6): 798–803, 809. |
| [18] |
黄维彬.
近代平差理论及其应用[M]. 北京: 解放军出版社, 1992: 1-525.
HUANG Weibin. Modern Adjustment Theory and Its Application[M]. Beijing: PLA Publishing House, 1992: 1-525. |
| [19] |
杨元喜.
自适应抗差最小二乘估计[J]. 测绘学报, 1996, 25(3): 206–211.
YANG Yuanxi. Adaptively Robust Least Squares Estimation[J]. Acta Geodaetica et Cartographica Sinica, 1996, 25(3): 206–211. DOI:10.3321/j.issn:1001-1595.1996.03.009 |
| [20] |
杨玲, 沈云中, 楼立志.
基于中位参数初值的等价权抗差估计方法[J]. 测绘学报, 2011, 40(1): 28–32.
YANG Ling, SHEN Yunzhong, LOU Lizhi. Equivalent Weight Robust Estimation Method Based on Median Parameter Estimates[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 28–32. |
| [21] | GABOR M J, NEREM R S. Satellite-satellite Single-difference Phase Bias Calibration as Applied to Ambiguity Resolution[J]. Navigation, 2002, 49(4): 223–242. DOI:10.1002/navi.2002.49.issue-4 |
| [22] | LOYER S, PEROSANZ F, MERCIER F, et al. Zero-difference GPS Ambiguity Resolution at CNES-CLS IGS Analysis Center[J]. Journal of Geodesy, 2012, 86(11): 991–1003. DOI:10.1007/s00190-012-0559-2 |
| [23] | International GNSS Service (IGS). Igs08_1930. atx[DB/OL]. (2017-01-07)[2017-09-05]. ftp://igs.org/pub/station/general/. |
| [24] |
刘帅, 孙付平, 郝万亮, 等.
整数相位钟法精密单点定位模糊度固定模型及效果分析[J]. 测绘学报, 2014, 43(12): 1230–1237.
LIU Shuai, SUN Fuping, HAO Wanliang, et al. Modeling and Effects Analysis of PPP Ambiguity Fixing Based on Integer Phase Clock Method[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1230–1237. DOI:10.13485/j.cnki.11-2089.2014.0195 |
| [25] | ZHANG Xiaohong, LI Pan, GUO Fei. Ambiguity Resolution in Precise Point Positioning with Hourly Data for Global Single Receiver[J]. Advances in Space Research, 2013, 51(1): 153–161. DOI:10.1016/j.asr.2012.08.008 |



