2. 武汉大学测绘学院, 湖北 武汉 430079;
3. 武汉大学地球空间环境与大地测量教育部重点实验室, 湖北 武汉 430079
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
3. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China
GNSS定位过程中由于非色散效应影响,对流层延迟不能采用频率组合的方式消除,因此其延迟量是影响定位精度的主要误差源之一[1]。天顶方向对流层延迟影响一般能达到2~3 m左右,当高度角在10°以下时,倾斜对流层误差影响可达20 m以上[2-3]。目前常采用模型改正的方法来削弱对流层延迟影响,即将信号传播路径上的对流层延迟通过映射函数投影到天顶方向,然后对天顶对流层延迟(zenith tropospheric delay,ZTD)进行建模[4-5]。
传统的对流层气象参数模型如文献[6-8]提出的模型改正精度可达厘米级,但模型计算要求输入实测气象参数。由于实测气象参数难以获得,又发展出一系列不依赖实测气象参数的对流层经验模型。文献[9-10]建立了UNB系列模型,UNB3m模型精度已达到4.9 cm;文献[11]指出,欧盟星基广域增强系统(The European Geostationary Navigation Overlay Service, EGNOS)采用EGNOS模型,平均精度约为5 cm;文献[12]构建了IGGtrop模型,虽然精度有所改进,但是参数数量太多;文献[13]建立了TropGrid模型,以格网形式提供气象元素的时序变化特征参数;而后文献[14]对该模型进行了简化,提出了TropGrid2格网模型;文献[15]建立了基于球谐函数表达的全球非气象参数模型GZTD,计算简便且精度较高。文献[16]在文献[17]提出的GPT2模型的基础上,增加了大气加权平均温度Tm和水汽压垂直梯度λ两个参数,建立了GPT2w模型,可同时获得计算ZHD和ZWD所需的气象元素,是目前精度最高、使用较为广泛的对流层延迟模型[18]。GPT2w模型采用ECMWF(European Center for Medium-range Weather Forecast)提供的2001-2010年共10年的高质量的ERA-37数据进行建模,气象参数可由式(1)[18]计算得到
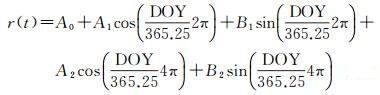 (1)
(1)
式中,r(t)为气象参数;DOY为年积日;A0为平均值;(A1,B1)为年周期振幅;(A2,B2)为半年周期振幅。
式(1)得到的气象参数是相对地面测站高度的,其他高度上是通过地面数值进行高度归算得到的,如式(2)所示[19](http://ggosatm.hg.tuwien.ac.at/DELAY/SOURCE/GPT2w/)
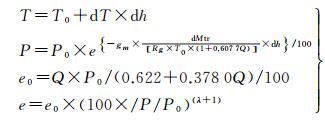 (2)
(2)
式中,T0、P0、e0分别为格网点处温度、气压、水汽压; dT为温度递减率; dh为高度; T、P、e分别为格网点对应高度为dh处的温度、气压、水汽压; gm为重力,gm=9.806 65 m/s2; dMtr为干空气的摩尔质量;dMtr=28.965×10-3 kg/mol; Rg为气体常数,Rg=8.314 3 J/K/mol; O为比湿; λ为水汽压垂直梯度。
对流层延迟由天顶静力学延迟(zenith hydrostatic delay,ZHD)和天顶湿延迟(zenith wet delay,ZWD)组成,一般而言,ZHD可利用Saastamoinen模型[20]精确计算得出
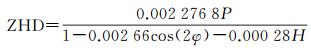 (3)
(3)
式中,P、φ、H分别代表格网点处总气压、纬度和正高。
而GPT2w模型计算ZWD可由加权平均温度、水汽压及其垂直梯度[16]通过式(4)得到
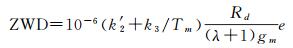 (4)
(4)
式中,Tm为加权平均温度;Rd为液态水密度(103 kg/m3); gm为水汽气体常数(461 J·kg-1·K-1),k′2、k3为大气折射常数, 本文中, 取k′2=16.48 K·hPa-1, k3=(3.776±0.014)×105 K2hPa-1; e为水汽压; λ为水汽压垂直梯度。
进而可得到对流层延迟
 (5)
(5)
从式(1)可以看到,GPT2w模型气象参数变化周期项仅考虑到年周期项和半年周期项,没有考虑更短周期变化,如季节周期,日周期项。文献[21]指出,GPT2w模型提供的气压、温度、水汽压在全球范围内均具有很高的精度和稳定性,但在南北极地区精度仍然较低。文献[16]利用全球341个IGS站对GPT2w模型进行了精度评估,发现其在全球范围具有很好的精度,但是统计过程中南极区域IGS测站分布较少且不均匀。文献[22-24]对比了目前的对流层延迟模型,指出GPT2w模型较其他模型精度高,与IGS站得到的对流层延迟最为接近。文献[25]指出,GPT2w模型得到的气压等参数由于没有考虑其日周期项,在寒冷季节存在较大误差,可能更适用于热带地区。
南极地区地理位置特殊,气象条件不同于地球其他区域,目前专门研究GPT2w在南极区域精度评价的文章较少,而随着后勤保障的巨大改善,在南极地区开展的大地测量科学研究日趋增多,因此有必要对GPT2w模型在南极地区的精度进行评估。另外,由于GPT2w模型没有考虑日周期项,本文利用中国第33次南极科考实测探空数据进一步检验了模型在短时间尺度下的精度状况。
1 数据来源及数据处理方法无线电探空数据可以提供垂直气象元素(如气压、温度、水汽压等)的剖面信息,且垂直分辨率和精度较高,经常被作为参考(真值),用来评估其他方式获取的气象元素的精度[26-27]。本文选取两种类型的探空数据来对GPT2w模型提供的气压、温度、水汽压进行精度评估:一是全球站点无线电探空资料数据集(the integrated global radiosonde archive,IGRA)中南极探空站数据,二是中国第33次南极科考期间施放的探空气球实测数据。
美国国家气候数据中心(NCDC)研制的IGRA包含全球1538个探空站点自1938年至今的多层次、多要素逐日探空资料。该数据是目前全球范围内时空密度最高、资料最为完整的一套高质量探空站点资料数据集[28]。探空站施放探空气球的时间为世界时每天的00时和12时,但由于天气、设备故障等原因,会导致数据缺失。
IGRA探空站能直接提供气压、温度、水汽压等气象参数。南极科考期间施放的探空气球数据只能提供气压和温度,不能直接获得水汽压,可通过露点温度对水汽压进行求解[29],具体公式如下
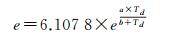 (6)
(6)
式中,a、b为常数:温度高于0℃时,a=17.26,b=237.29;温度低于-40℃时,a=21.87, b=265.49;若温度介于两者之间,a、b用线性内插获得。
为了对GPT2w模型在高度上的精度进行评估,本文按照气球上升高度进行分层,以探究模型随高度的精度变化。由于对流层及平流层没有明显的分层特性,结合数据的垂直分布特点采用不均匀分层[30],共分为9层,分层高度见表 1,其中高度表示离地面高度。
| 层数 | 1层 | 2层 | 3层 | 4层 | 5层 | 6层 | 7层 | 8层 | 9层 |
| 高度/km | 0~1 | 1~2 | 2~3 | 3~5 | 5~7 | 7~9 | 9~10 | 10~15 | 15及以上 |
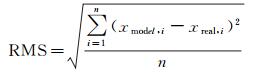
采用偏差(Bias)和均方根误差(RMS)作为精度评定标准,分别对分层数据进行评估。Bias和RMS分别由式(7)和式(8)计算得到
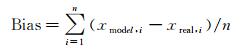 (7)
(7)
 (8)
(8)
式中,xmodel, i表示模型计算值;xreal, i表示探空数据气象元素(本文视为真值);n为数据总个数。
2 GPT2w模型南极地区精度检验及分析 2.1 利用IGRA探空站数据进行模型气象参数精度分析取南极地区探空站2016年全年数据作为参考值,共选取14个具有可用数据的探空站,与GPT2w模型计算的气压、温度、水汽压进行分层对比。探空站坐标信息见表 2。由于南极特殊的地理位置,全年仅分为寒、暖两季,4月-10月是寒季,11月-次年3月是暖季。取1月和7月分别作为暖季、寒季代表月份,对模型精度的季节性特征进行初步分析,并分层分季节统计Bias和RMS。
| 测站名 | 纬度 | 经度 | 海拔/m |
| AYM00089002 | -70.666 7 | -8.250 0 | 50.0 |
| AYM00089009 | -90.000 0 | 0.000 0 | 2 835.0 |
| AYM00089022 | -75.445 0 | -26.218 1 | 30.0 |
| AYM00089062 | -67.566 1 | -68.129 7 | 3.0 |
| AYM00089512 | -70.767 8 | 11.831 7 | 118.9 |
| AYM00089532 | -69.005 3 | 39.581 1 | 18.4 |
| AYM00089564 | -67.601 7 | 62.875 3 | 9.9 |
| AYM00089571 | -68.574 4 | 77.967 2 | 18.0 |
| AYM00089592 | -66.551 9 | 93.014 7 | 43.4 |
| AYM00089611 | -66.282 5 | 110.523 1 | 40.0 |
| AYM00089625 | -75.101 7 | 123.411 9 | 3 233.0 |
| AYM00089642 | -66.663 1 | 140.001 1 | 43.0 |
| AYM00089662 | -74.695 8 | 164.092 2 | 92.0 |
| AYM00089664 | -77.850 0 | 166.666 7 | 24.0 |
表 3和表 4为GPT2w模型气压、温度、水汽压的分层分季节Bias和RMS统计结果。从表中可以看出,随着层数(高度)的增加,三者的Bias和RMS均呈现增大的趋势;当到达第7、8层左右,随着高度增加,气压的Bias有减小趋势,其Bias最大出现在第8层(10~15 km)左右,数值为7月的41 mb左右;温度的Bias逐渐减小为负数,但其绝对值仍远大于地面附近数值,其Bias绝对值最大出现在第9层(15 km以上),数值为7月的-45 K左右;水汽压的Bias和RMS也有增加趋势,但是没有气压和温度变化显著,其Bias最大出现在第9层(15 km以上),数值为7月的38 mb。对比发现,在全年时间尺度上,GPT2w在地面附近精度较高,但是随高度增加,精度大致呈下降趋势。GPT2w模型一般提供地面高度的气象参数初值,其他高度气象参数的计算都是从地面进行归算的,随着高度增加,误差会累积,从而导致精度降低。
| 层数 | 气压/mb | 温度/K | 水汽压/mb | |||||
| Bias | RMS | Bias | RMS | Bias | RMS | |||
| 1层 | 2.385 | 7.179 | -7.967 | 8.184 | -1.247 | 1.457 | ||
| 2层 | 0.427 | 5.972 | -6.401 | 6.749 | -0.722 | 0.991 | ||
| 3层 | 0.510 | 5.548 | -5.456 | 6.063 | -0.337 | 0.555 | ||
| 4层 | 3.168 | 7.062 | -3.733 | 5.650 | -0.120 | 0.269 | ||
| 5层 | 9.453 | 12.323 | 2.473 | 8.020 | 1.659 | 2.069 | ||
| 6层 | 18.713 | 19.111 | 9.081 | 12.707 | 7.718 | 8.938 | ||
| 7层 | 22.417 | 23.971 | 6.604 | 14.879 | 8.610 | 11.735 | ||
| 8层 | 25.436 | 25.574 | -4.620 | 24.274 | 7.57 | 9.109 | ||
| 9层 | 14.600 | 14.705 | -44.525 | 74.687 | 7.942 | 9.102 | ||
| 层数 | 气压/mb | 温度/K | 水汽压/mb | |||||
| Bias | RMS | Bias | RMS | Bias | RMS | |||
| 1层 | 2.655 | 11.266 | 6.816 | 8.781 | 0.750 | 0.937 | ||
| 2层 | 6.226 | 11.410 | 4.602 | 6.755 | 0.354 | 0.576 | ||
| 3层 | 9.617 | 13.097 | 3.214 | 5.755 | 0.191 | 0.387 | ||
| 4层 | 14.572 | 17.194 | 7.369 | 9.203 | 2.258 | 3.848 | ||
| 5层 | 22.673 | 24.322 | 12.252 | 13.456 | 7.301 | 8.692 | ||
| 6层 | 31.640 | 32.500 | 19.842 | 23.275 | 18.394 | 33.369 | ||
| 7层 | 32.785 | 37.619 | 23.275 | 23.596 | 33.369 | 35.183 | ||
| 8层 | 40.638 | 40.811 | 19.754 | 22.548 | 34.345 | 36.571 | ||
| 9层 | 28.547 | 28.814 | -12.550 | 31.492 | 39.361 | 39.837 | ||
对比1月与7月统计结果,气压、温度和水汽压精度整体1月精度数值小于7月,说明1月精度较7月高,即GPT2w模型精度在南极区域呈现出季节性特征。
2.2 利用南极探空气球实测数据进行模型气象参数精度分析本文选取2016年11月到2017年4月第33次南极考察期间施放的环南极18颗探空气球获得的实测探空气象数据,通过高度分层对比其与GPT2w模型计算的气温、气压、水汽压,对模型在南极地区的短时间尺度精度进行进一步分析。由于探空气球是在航行过程中施放的,每个特定位置施放一个,达到既定高度气球会自行爆炸,因此每颗气球只能记录当天的一组数据,共有18组数据,分布在不同时间和地点。表 5为施放探空气球的坐标信息。
| 气球编号 | 纬度 | 经度 | 海拔/m |
| 15187632 | -42.075 6 | 114.154 2 | 114.15 |
| 15181841 | -45.178 3 | 107.534 4 | 107.53 |
| 15181812 | -63.049 2 | 50.815 83 | 50.82 |
| 14162920 | -63.757 8 | -4.876 67 | -4.88 |
| 15187636 | -59.925 | -42.438 1 | -42.44 |
| 15194012 | -61.108 3 | -53.760 6 | -53.76 |
| 15194055 | -62.440 3 | -58.573 9 | -58.57 |
| 13111476 | -55.948 9 | -66.324 2 | -66.32 |
| 15188307 | -71.033 9 | -121.616 | -121.62 |
| 15188344 | -74.499 2 | -157.081 | -157.08 |
| 15185715 | -74.511 9 | 168.483 9 | 168.48 |
| 15185729 | -77.668 3 | 165.896 9 | 165.90 |
| 15185721 | -65.211 9 | 154.918 1 | 154.92 |
| 12470630 | -63.947 8 | 112.563 6 | 112.56 |
| 14013343 | -69.111 9 | 76.378 61 | 76.38 |
| 14018724 | -60.526 4 | 73.553 61 | 73.55 |
| 14014934 | -43.995 | 74.338 61 | 74.34 |
| 15191244 | -35.034 4 | 75.064 44 | 75.06 |
2.2.1 利用ECMWF气压分层数据验证气球实测数据
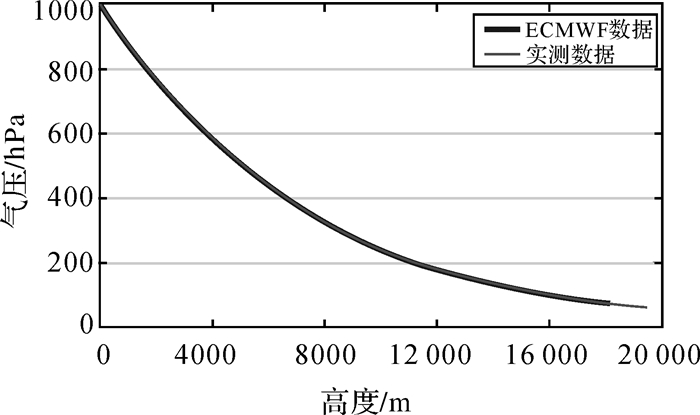
欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF)是全球数值天气预报组织,可提供高精度的ERA-Interim产品,在全球范围内包括南北极地区都具有很高的精度[20]。本文选取ECMWF气压分层数据,与探空气球实测气压数据进行对比,来验证气球气象数据的可靠性,以15185729号探空气球数据为例,选取与其时间及地点对应的ECMWF气压分层数据,两者随高度的变化如图 1所示。可以看到,两者符合较好,说明南极探空气球实测数据具有较高的可靠性,可以用来对GPT2w模型精度进行评估。
|
| 图 1 ECMWF气压分层数据与气球实测气压数据对比 Fig. 1 Comparison between ECMWF pressure data and measured pressure data from sounding balloons |
2.2.2 利用探空气球实测数据对模型气象参数进行精度分析
表 6为Bias和RMS统计结果。可以看出,对于气压和温度而言,其趋势与探空站统计结果类似,表现为地面精度最高,随高度增加,精度下降。当到达第7、8层左右时,气压的Bias有减小趋势,Bias最大出现在第8层(10~15 km),数值为31 mb左右;温度的Bias逐渐减小为负数,但其绝对值仍远大于地面附近数值,Bias绝对值最大出现在第9层(15 km以上),数值为-60 K左右;而水汽压的Bias和RMS都比较小,在0附近波动,保持在基本稳定状态,这是由于实测数据与GPT2w模型的水汽压均是利用指数模型计算得来的,两者之间差异较小。
| 层数 | 气压/mb | 温度/K | 水汽压/mb | |||||
| Bias | RMS | Bias | RMS | Bias | RMS | |||
| 1层 | -3.852 | 8.321 | -5.344 | 5.792 | -1.171 | 1.859 | ||
| 2层 | -3.847 | 8.506 | -6.121 | 6.677 | -0.713 | 1.221 | ||
| 3层 | -1.860 | 8.335 | -7.498 | 7.872 | -0.208 | 0.956 | ||
| 4层 | 3.406 | 9.258 | -8.778 | 9.450 | 0.010 | 0.503 | ||
| 5层 | 12.402 | 14.227 | -8.925 | 11.082 | 0.077 | 0.222 | ||
| 6层 | 21.897 | 22.151 | -8.676 | 13.044 | 0.046 | 0.095 | ||
| 7层 | 28.114 | 28.144 | -14.094 | 22.309 | 0.031 | 0.038 | ||
| 8层 | 31.061 | 31.476 | -32.235 | 33.911 | 0.011 | 0.014 | ||
| 9层 | 28.495 | 18.502 | -59.646 | 18.502 | 0.001 | 0.001 | ||
与2.1节相比,虽然GPT2w没有考虑日周期项,但是温度和气压的天内精度与月统计精度在地面附近精度相当。但是垂直高度上,天内精度与月统计精度相比有所下降,特别是与1月精度对比,随着高度的增加精度在下降,可见未考虑日周期变化项对模型精度有所影响。
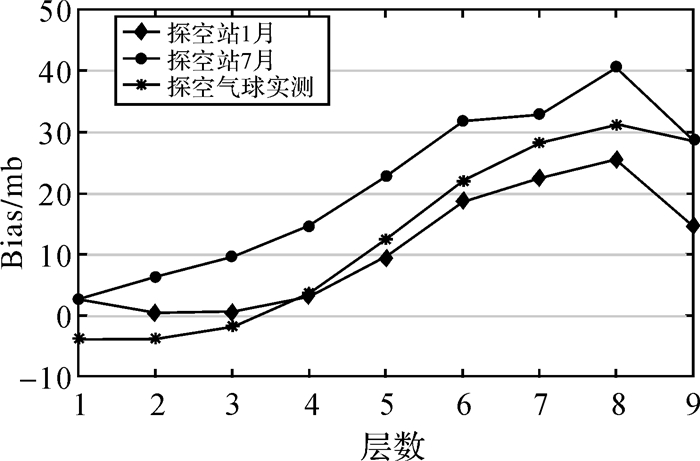
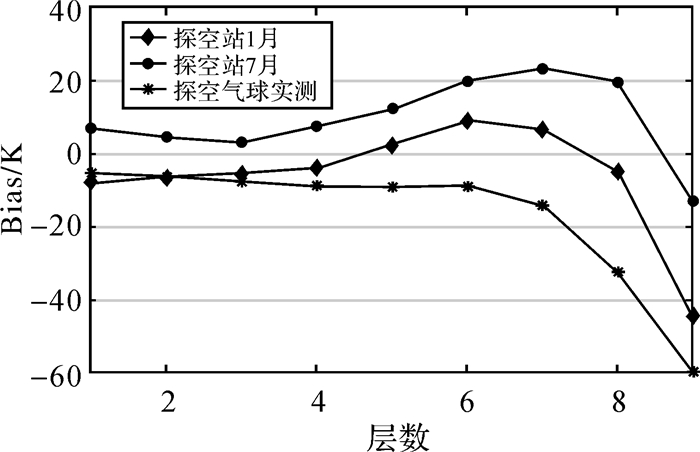
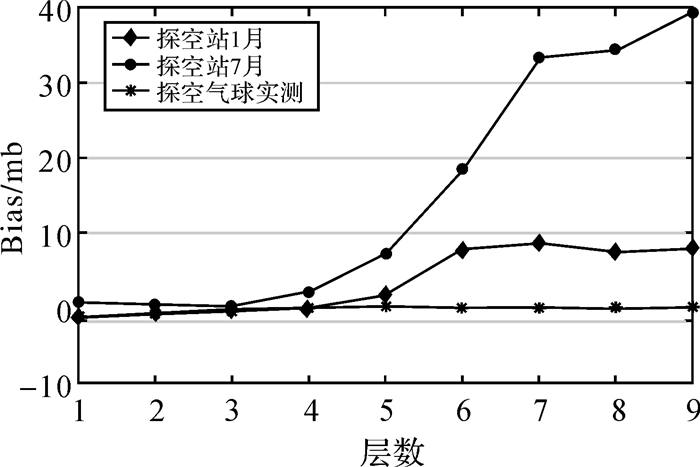
图 2、图 3、图 4是GPT2w模型分别与探空站1月、7月及气球实测数据对比得到的气压、温度、水汽压的Bias,图中给出了各层的Bias分布。对于气压和温度,三者的趋势有一致性,表现为地面附近精度较高,随着高度增加精度下降;本文使用的实测数据采集于2016年11月至2017年4月,对应于2.1节统计的暖季区间,整体而言,GPT2w模型与实测数据的精度对比结果差于探空站1月对比精度,而优于7月对比精度,与2.1节得到的暖季精度略优于寒季精度的结果相符。而与探空站水汽压增幅较大不同,气球实测数据的水汽压较小且波动不大。
|
| 图 2 GPT2w模型与探空站1月、7月及气球实测气压数据对比的Bias Fig. 2 Comparison of pressure between GPT2w and the radiosonde stations in January and July and sounding balloons, respectively |
|
| 图 3 GPT2w模型与探空站1月、7月及气球实测温度数据对比的Bias Fig. 3 Comparison of temperature between GPT2w and the radiosonde stations in January and July and sounding balloons, respectively |
|
| 图 4 GPT2w模型与探空站1月、7月及气球实测水汽压数据对比的Bias Fig. 4 Comparison of water vapor pressure between GPT2w and the radiosonde stations in January and July and sounding balloons, respectively |
2.3 利用探空数据进行模型对流层延迟精度分析 2.3.1 利用探空数据计算对流层延迟的方法及原理
探空数据计算对流层延迟是根据其定义进行求解的。GPS卫星信号在对流层中的延迟为[31]
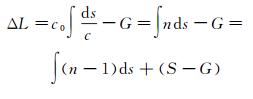 (9)
(9)
式中,c0是真空中的光速;c代表实际光速;S代表卫星信号传播的实际长度;G代表卫星和GPS接收机间之间的几何距离;∫(n-1)ds代表对流层延迟;(S-G)表示卫星信号弯曲所引起的路径增长部分,其值比较小,约占总延迟量的0.1%,所以忽略不计。
因此,ΔL可以进一步表示为
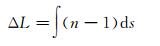 (10)
(10)
或
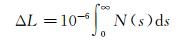 (11)
(11)
式中,N=(n-1)·106表示大气折射率。
大气折射率计算公式为[32]
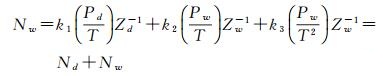 (12)
(12)
式中,k1=77.604、k2=64.790、k3=3.776,分别表示与大气折射率有关的常数;T表示绝对温度;Nd、Nw分别代表干折射率和湿折射率;Pd、Pw为水汽压, Zd-1、Zw-1分别为干空气和水汽的压缩因子,计算公式如式(13)、式(14)所示
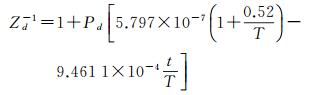 (13)
(13)
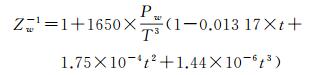 (14)
(14)
将对流层延迟继续沿高度进行积分,则得到GPS信号穿过对流层天顶方向的总延迟
 (15)
(15)
利用上述计算方法,分别计算GPT2w模型与探空数据计算得到的对流层延迟,结果见表 7、表 8。
| m | |||||||
| GPT2w模型 | 探空站 | ||||||
| 测站 | ZHD | ZWD | ZTD | ZHD | ZWD | ZTD | |
| AYM00089002 | 2.231 1 | 0.026 4 | 2.257 5 | 2.263 | 0.037 3 | 2.300 3 | |
| AYM00089009 | 1.540 5 | 0.004 5 | 1.545 0 | 1.573 6 | 0.006 9 | 1.580 5 | |
| AYM00089022 | 2.235 1 | 0.024 5 | 2.259 6 | 2.267 0 | 0.057 0 | 2.324 0 | |
| AYM00089062 | 2.245 7 | 0.043 6 | 2.289 3 | 2.243 0 | 0.033 6 | 2.276 6 | |
| AYM00089512 | 2.217 2 | 0.021 1 | 2.238 3 | 2.238 0 | 0.066 0 | 2.304 0 | |
| AYM00089532 | 2.243 3 | 0.026 5 | 2.269 8 | 2.260 9 | 0.040 2 | 2.303 3 | |
| AYM00089564 | 2.254 0 | 0.023 1 | 2.277 1 | 2.274 8 | 0.040 1 | 2.314 9 | |
| AYM00089571 | 2.242 2 | 0.025 4 | 2.267 6 | 2.272 4 | 0.027 2 | 2.299 6 | |
| AYM00089611 | 2.223 3 | 0.029 8 | 2.253 1 | 2.252 3 | 0.040 8 | 2.293 1 | |
| AYM00089625 | 1.461 2 | 0.003 9 | 1.465 1 | 1.490 1 | 0.004 2 | 1.494 3 | |
| AYM00089642 | 2.224 5 | 0.026 2 | 2.250 7 | 2.254 5 | 0.040 9 | 2.295 4 | |
| AYM00089662 | 2.206 4 | 0.015 3 | 2.221 7 | 2.244 3 | 0.041 6 | 2.286 | |
| AYM00089664 | 2.224 6 | 0.017 8 | 2.242 4 | 2.262 2 | 0.040 0 | 2.302 2 | |
| 数据对比时段:2017-01-16 | |||||||
| m | |||||||
| GPT2w模型 | 实测数据 | ||||||
| 气球编号 | ZHD | ZWD | ZTD | ZHD | ZWD | ZTD | |
| 15187632 | 2.294 7 | 0.094 1 | 2.388 8 | 2.291 1 | 0.066 7 | 2.357 8 | |
| 15181841 | 2.286 1 | 0.088 2 | 2.374 3 | 2.283 6 | 0.099 4 | 2.383 0 | |
| 15181812 | 2.241 6 | 0.039 7 | 2.281 3 | 2.250 5 | 0.010 8 | 2.261 3 | |
| 14162920 | 2.237 7 | 0.037 9 | 2.275 6 | 2.254 9 | 0.052 2 | 2.307 1 | |
| 15187636 | 2.260 9 | 0.049 9 | 2.310 8 | 2.261 5 | 0.061 5 | 2.323 1 | |
| 15194012 | 2.257 0 | 0.050 8 | 2.307 8 | 2.258 3 | 0.066 7 | 2.325 1 | |
| 15194055 | 2.253 2 | 0.049 5 | 2.302 8 | 2.213 8 | 0.075 3 | 2.289 2 | |
| 13111476 | 2.268 6 | 0.069 3 | 2.337 9 | 2.254 1 | 0.089 2 | 2.343 3 | |
| 15188307 | 2.212 6 | 0.036 8 | 2.249 4 | 2.256 1 | 0.077 1 | 2.333 2 | |
| 15188344 | 2.205 8 | 0.028 8 | 2.234 6 | 2.251 2 | 0.085 7 | 2.336 9 | |
| 15185715 | 2.225 7 | 0.018 2 | 2.243 9 | 2.242 1 | 0.066 3 | 2.308 4 | |
| 15185729 | 2.229 7 | 0.017 8 | 2.247 4 | 2.255 4 | 0.053 2 | 2.308 6 | |
| 15185721 | 2.220 8 | 0.038 7 | 2.259 5 | 2.235 1 | 0.062 4 | 2.297 5 | |
| 12470630 | 2.224 9 | 0.037 8 | 2.262 7 | 2.252 6 | 0.069 6 | 2.322 3 | |
| 14013343 | 2.246 7 | 0.024 9 | 2.271 6 | 2.231 4 | 0.066 0 | 2.297 4 | |
| 14018724 | 2.240 0 | 0.042 8 | 2.282 8 | 2.216 8 | 0.073 5 | 2.290 3 | |
| 14014934 | 2.309 6 | 0.097 8 | 2.407 4 | 2.322 6 | 0.109 0 | 2.431 6 | |
| 15191244 | 2.325 4 | 0.122 4 | 2.447 8 | 2.331 3 | 0.074 2 | 2.405 5 | |
由两表可以看出,由GPT2w模型及探空数据计算得到的ZTD差距约为几个厘米,这与其他学者验证得到的GPT2w模型对流层延迟在全球范围内精度为厘米级的结论是一致的[16]。同时可以看出,ZWD数值较小,仅为几个厘米,一般来说,在大气中,ZHD占90%左右,ZWD占10%左右,而南极处于高纬度地区,水汽含量很少,故ZWD相对来说更小。且两者ZWD相差最多在气球编号为15188344处,约为5.7 cm,数值较小。
在探空数据计算结果作为真值的情况下,统计模型ZWD和ZTD的Bias及RMS,结果见表 9。可以看出,GPT2w得到的对流层延迟与探空数据计算得到的对流层延迟较为接近,Bias及RMS均处于厘米级,说明该模型可用于一般定位等对流层延迟的求解。但在精密定位中,仍需对该模型进行精化。
| m | ||||
| ZWD | ZTD | |||
| 数据类型 | Bias | RMS | Bias | RMS |
| 模型与探空站数据 | -0.014 4 | 0.020 2 | -0.041 3 | 0.046 0 |
| 模型与气球实测数据 | -0.017 4 | 0.032 0 | -0.024 2 | 0.045 1 |
3 结果讨论及分析 3.1 结果分析
一般认为,探空气球在上升过程中,只有高度发生变化,经纬度不发生变化。
(1) 由上述分析可知,在南极地区,Bias和RMS随着高度的增加而发生变化,GPT2w模型在地面附近精度最高;用ECMWF气压分层数据对实测气压数据进行检验,两者符合较好,说明了实测数据具有可靠的测量精度,Bias和RMS随高度变差主要是由于GPT2w模型本身误差造成的。
(2) GPT2w模型中,气压和温度的计算均与高度有关,气压采用高度的指数函数拟合,温度采用高度的线性函数拟合得到,而水汽压的计算与气压相关。因此,高度的变化,会导致模型精度的变化。GPT2w模型一般用来提供地面高度的气象参数初值,其他高度的参数值模型内部进行了函数改正,即高度归算,而这种改正本身存在一定误差。且会随着高度增加,空气成分及其他因素的变化,进一步导致模型精度下降,从而导致模型值与实测值出现较大不符。
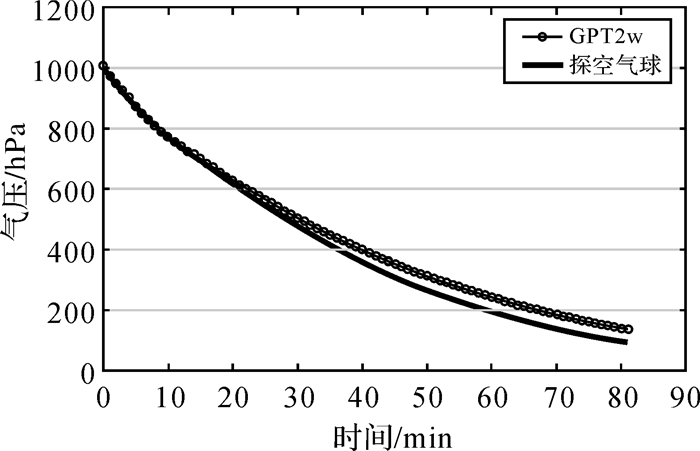
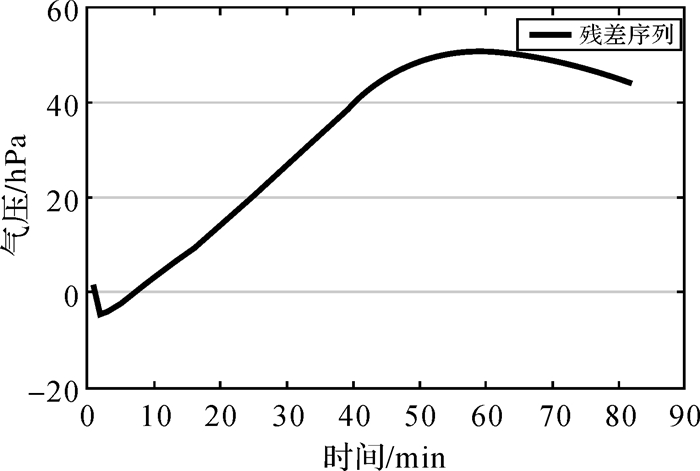
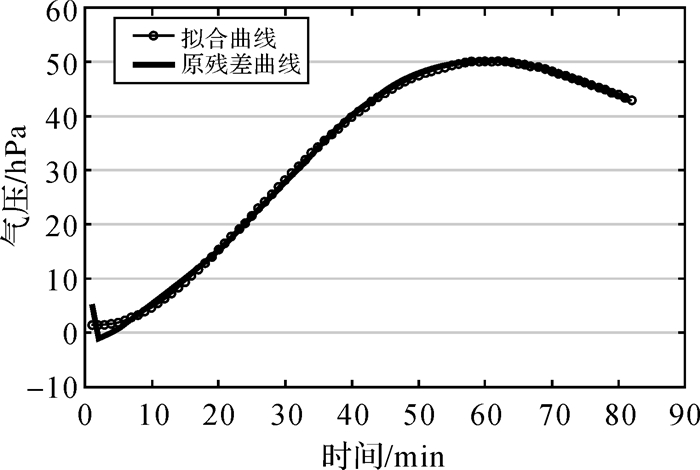
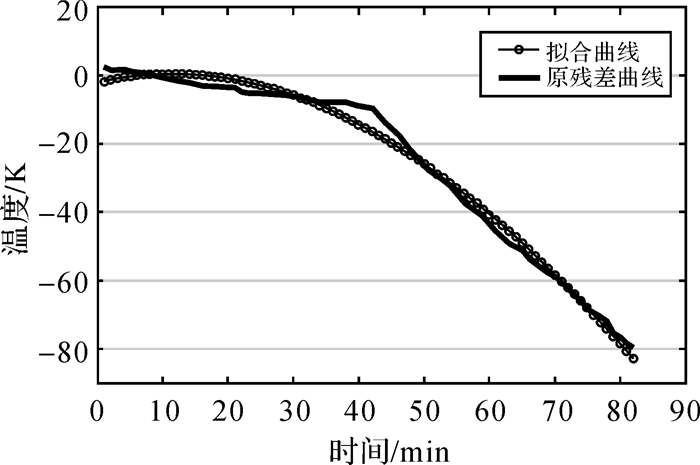
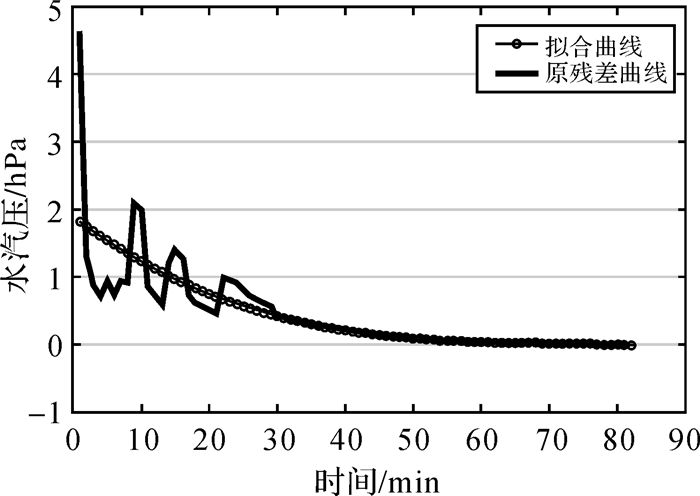
3.2 残差拟合GPT2w模型计算的气象参数值与实测数据在高度上存在较大的差异,本节对两者之间的差异作进一步的分析。以15187632号探空气球数据为例,图 5给出的是实测气压与GPT2w模型计算气压随时间变化对比图。从图中可以看出,在地面附近,两者相差不大,随着高度的增加,两者之间的差异在增大,在最高处略有下降。从两者的残差图(图 6)也可以看出这一现象。图 6中开始时段异常是由于探空气球是在走航期间施放的,开始时段气球运动处于不稳定的上下浮动状态。对两者残差进行初步拟合,如图 7所示,可以看到,用三次多项式就可以较好的拟合两者之间的差异。通过对温度和水汽压进行类似计算,可以得到相同的结论,如图 8、图 9所示。
|
| 图 5 气球实测气压数据与模型计算气压对比 Fig. 5 Comparison of pressure between results calculated by GPT2w and results measured by sounding balloons |
|
| 图 6 气球实测气压数据与模型计算气压残差 Fig. 6 Residual of pressure between results calculated by GPT2w and results measured by sounding balloons |
|
| 图 7 气压残差三阶多项式拟合 Fig. 7 Three-order polynomial fitting of pressure's residual |
|
| 图 8 温度残差三阶多项式拟合 Fig. 8 Three-order polynomial fitting of temperature's residual |
|
| 图 9 水汽压残差三阶多项式拟合 Fig. 9 Three-order polynomial fitting of water vapor pressure's residual |
因此,下一步可以对GPT2w模型在高度上与实测数据的差异进行模型拟合改正,进而对该模型在南极地区乃至全球垂直方向上的精度进行改进。
4 结论本文通过探空站和探空气球提供的气象数据对GPT2w模型在南极区域计算的气压、温度、水汽压进行精度检验,结果表明,该模型在地面附近精度可达到与全球其他区域精度一致的水平,但随着高度的增加,Bias和RMS有不同程度的增加,精度有所下降。由模型计算得到的对流层延迟可达到厘米级精度,可用于一般定位等方面的对流层延迟改正。得到如下结论:
(1) GPT2w一般用于地面气象参数的计算,本文分析显示,在地面附近,模型在南极地区精度与全球其他位置精度一致;且在南极区域,模型精度表现出季节性。
(2) 通过与实测数据对比发现,GPT2w模型虽然没有考虑日周期项,但是对于南极区域而言,在地面高度上,计算的气象参数天内精度与月平均精度相当。但是随着高度的增加,精度较1月精度有所下滑,而略优于7月精度。
(3) 随着高度的增加,模型值与探空数据差异增加,除了气球升空过程中产生漂移等原因外,主要原因是模型本身计算气象元素时所使用的高度归算函数存在一定误差。同时可以发现,残差规律性较强,因此,可以在考虑季节性因素的基础上,对其GPT2w模型加以改进,使其在垂直高度上精度得以改善。
(4) 总体而言,由GPT2w模型计算的ZTD在南极地区有较高的精度,Bias和RMS均在厘米级,与全球其他地区得到的ZTD精度较为一致。
| [1] | SCHUELER T, HEIN G W, EISSFELLER B. A New Tropospheric Correction Model for GNSS Navigation[C]//Proceedings of GNSS. Sevilla, Spain: [s.n.], 2001: 8-11. |
| [2] | ZHANG J, LCHAPELLE, G. Precise Estimation of Residual Tropospheric Delays Using a Regional GPS Network for Real-time Kinematic Applications[J]. Journal of Geodesy, 2001, 75(5-6): 255–266. DOI:10.1007/s001900100171 |
| [3] | CHEN Qinming, SONG Shuli, ZHU Wenyao. An Analysis for the Accuracy of Tropospheric Zenith Delay Calculated from ECMWF/NECP Data over Asia[J]. Chinese Journal of Geophysics, 2012, 55(3): 275–283. DOI:10.1002/cjg2.v55.3 |
| [4] |
姚宜斌, 胡羽丰, 张豹.
利用多源数据构建全球天顶对流层延迟模型[J]. 科学通报, 2016, 61(24): 2730–2741.
YAO Yibin, HU Yufeng, ZHANG Bao. Establishment of a Global Zenith Tropospheric Delay Model Using Multi-source Data[J]. Chinese Science Bulletin, 2016, 61(24): 2730–2741. |
| [5] |
赵祥伟, 陈正宇.
全球天顶对流层延迟模型新修正方法[J]. 测绘科学, 2018, 43(5): 18–22, 61.
ZHAO Xiangwei, CHEN Zhengyu. The New Correction Method of Global Zenith Total Delay Model[J]. Science of Surveying and Mapping, 2018, 43(5): 18–22, 61. |
| [6] | HOPFIELD H S. Tropospheric Effect on Electromagnetically Measured Range:Prediction from Surface Weather Data[J]. Radio Science, 1971, 6(3): 357–367. DOI:10.1029/RS006i003p00357 |
| [7] | SAASTAMOINEN J H. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging Satellites[M]//HENRIKSEN S W, MANCINI A, CHOVITZ B H.The Use of Artificial Satellites for Geodesy.Washington, DC: American Geophysical Union, 1972: 247-251. |
| [8] | BLACK H D. An Easily Implemented Algorithm for the Tropospheric Range Correction[J]. Journal of Geophysical Research:Solid Earth (1978-2012), 1978, 83(B4): 1825–1828. DOI:10.1029/JB083iB04p01825 |
| [9] | LAMANCE J, COLLINS P, LANGLEY R. Limiting Factors in Tropospheric Propagation Delay Error Modelling for GPS Airborne Navigation[C]//Proceedings of the Institute of Navigation 52nd Annual Meeting.Cambridge, MA: [s.n.], 1996: 519-528. |
| [10] | LEANDRO R, SANTOS M C, LANGLEY R B. UNB Neutral Atmosphere Models: Development and Performance[C]//Proceedings of the 2006 National Technical Meeting of the Institute of Navigation.Monterey, California, USA: [s.n.], 2006: 564-573. |
| [11] | PENNA N, DODSON A, CHEN Wu. Assessment of EGNOS Tropospheric Correction Model[J]. Journal of Navigation, 2001, 54(1): 37–55. DOI:10.1017/S0373463300001107 |
| [12] | LI Wei, YUAN Yunbin, OU Jikun, et al. New Versions of the BDS/GNSS Zenith Tropospheric Delay Model IGGtrop[J]. Journal of Geodesy, 2015, 89(1): 73–80. DOI:10.1007/s00190-014-0761-5 |
| [13] | KRUEGER E, SCHUELER T, ARBESSER-RASTBURG B. The Standard Tropospheric Correction Model for the European Satellite Navigation System Galileo[C]//Proceeding of General Assembly URSI.[s.l.]: [s.n.], 2005. |
| [14] | SCHÜLER T. The TropGrid2 Standard Tropospheric Correction Model[J]. GPS Solutions, 2014, 18(1): 123–131. DOI:10.1007/s10291-013-0316-x |
| [15] |
姚宜斌, 何畅勇, 张豹, 等.
一种新的全球对流层天顶延迟模型GZTD[J]. 地球物理学报, 2013, 56(7): 2218–2227.
YAO Yibin, HE Changyong, ZHANG Bao, et al. A New Global Zenith Tropospheric Delay Model (GZTD)[J]. Chinese Journal of Geophysical, 2013, 56(7): 2218–2227. |
| [16] | BÖHM J, MÖLLER G, SCHINDELEGGER M, et al. Development of an Improved Empirical Model for Slant Delays in the Troposphere (GPT2w)[J]. GPS Solutions, 2015, 19(3): 433–441. DOI:10.1007/s10291-014-0403-7 |
| [17] | LAGLER K, SCHINDELEGGER M, BÖHM J, et al. GPT2:Empirical Slant Delay Model for Radio Space Geodetic Techniques[J]. Geophysical Research Letters, 2013, 40(6): 1069–1073. DOI:10.1002/grl.50288 |
| [18] |
胡羽丰.高分辨率全球天顶对流层延迟模型研究[D].武汉: 武汉大学, 2015. HU Yufeng. Research on Global Zenith Tropospheric Delay Model with High Resolution[D]. Wuhan: Wuhan University, 2015. |
| [19] |
姚宜斌, 张豹, 严凤, 等.
两种精化的对流层延迟改正模型[J]. 地球物理学报, 2015, 58(5): 1492–1501.
YAO Yibin, ZHANG Bao, YAN Feng, et al. Two New Sophisticated Models for Tropospheric Delay Corrections[J]. Chinese Journal of Geophysical, 2015, 58(5): 1492–1501. |
| [20] | BEVIS M, BUSINGER S, HERRING T A, et al. GPS Meteorology:Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research, 1992, 97(D14): 15787–15801. DOI:10.1029/92JD01517 |
| [21] |
姚宜斌, 曹娜, 许超钤, 等.
GPT2模型的精度检验与分析[J]. 测绘学报, 2015, 44(7): 726–733.
YAO Yibin, CAO Na, XU Chaoqian, et al. Accuracy Assessment and Analysis for GPT2[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(7): 726–733. |
| [22] | ISIOYE O A, COMBRINCK L, BOTAI J. Performance Evaluation of Blind Tropospheric Delay correction Models over Africa[J]. South African Journal of Geomatics, 2015, 4(4): 502–525. DOI:10.4314/sajg.v4i4.10 |
| [23] | LIU Jiye, CHEN Xihong, SUN Jizhe, et al. An Analysis of GPT2/GPT2w+Saastamoinen Models for Estimating Zenith Tropospheric Delay over Asian Area[J]. Advances in Space Research, 2017, 59(1): 824–832. |
| [24] | ZHANG Di, GUO Jiming, CHEN Ming, et al. Quantitative Assessment of Meteorological and Tropospheric Zenith Hydrostatic Delay Models[J]. Advances in Space Research, 2016, 58(6): 1033–1043. DOI:10.1016/j.asr.2016.05.055 |
| [25] | WANG Xiaoming, ZHANG Kefei, WU Suqin, et al. Determination of Zenith Hydrostatic Delay and Development of New Global Long-term GNSS-derived Precipitable Water Vapor[J]. Atmospheric Measurement Techniques Discussions, 2016. DOI:10.5194/amt-2016-264 |
| [26] | CHEN Biyan, LIU Zhizhao. Voxel-optimized Regional Water Vapor Tomography and Comparison with Radiosonde and Numerical Weather Model[J]. Journal of Geodesy, 2014, 88(7): 691–703. DOI:10.1007/s00190-014-0715-y |
| [27] | NIELL AE, COSTER AJ, SOLHEIM FS, et al. Comparison of Measurements of Atmospheric Wet Delay by Radiosonde, Water Vapor Radiometer, GPS, and VLBI[J]. Journal of Atmospheric Oceanic Technology, 2001, 18(6): 830–850. DOI:10.1175/1520-0426(2001)018<0830:COMOAW>2.0.CO;2 |
| [28] |
陈哲, 高杰, 杨旭.
IGRA全球站点探空数据集及其资料质量状况分析[J]. 气象与环境学报, 2013, 29(5): 106–111.
CHEN Zhe, GAO Jie, YANG Xu. Introduction of IGRA Dataset and Analysis of Its Data Quality[J]. Journal of Meteorology and Environment, 2013, 29(5): 106–111. DOI:10.3969/j.issn.1673-503X.2013.05.017 |
| [29] |
赵庆志.地基GPS大气可降水量估计及水汽层析研究[D].徐州: 中国矿业大学, 2014. ZHAO Qingzhi. Study on Atmospheric Precipitable Water Estimation Using Ground-based GPS and Water Vapor Tomography[D]. Xuzhou: China University of Mining and Technology, 2014. http://www.bigengculture.com/kejilunwen/dizhicehuilunwen/458144.html |
| [30] |
陈宏斌, 熊永良, 陈志胜, 等.
垂直不均匀分层的地基GPS层析水汽研究[J]. 测绘工程, 2015, 24(5): 11–14, 18.
CHEN Hongbin, XIONG Yongliang, CHEN Zhisheng, et al. Research on Tomography of Ground-based GPS Water Vapor With Uneven Vertical Stratification[J]. Engineering of Surveying and Mapping, 2015, 24(5): 11–14, 18. DOI:10.3969/j.issn.1006-7949.2015.05.003 |
| [31] |
薛骐.地基GPS水汽反演及水汽层析研究[D].重庆: 西南交通大学, 2017. XUE Qi. Research on Ground-based GPS Atmospheric Water Vapor Retrieval and Water Vapor Tomography[D]. Chongqing: Southwest Jiaotong University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10613-1017142301.htm |
| [32] | THAYER G D. An Improved Equation for the Radio Refractive Index of Air[J]. Radio Science, 1974, 9(10): 803–807. DOI:10.1029/RS009i010p00803 |



