当观测值不含粗差、观测误差服从零均值的分布时,经典最小二乘估计具有最优无偏性。然而,在实际的数据采集中经常会出现粗差,由于最小二乘不具有抗差性,对粗差观测值十分敏感,少量的粗差就可能对最小二乘估计结果产生破坏性影响[1-6]。因此,在粗差干扰出现的情况下,选择适当的估计方法,尽量降低或者去除粗差对参数估值的影响,得出正常模式下的最优或接近最优的参数估值,即为测量数据处理领域稳健估计的基本思想。对于现代空间测量技术如GNSS、摄影测量与遥感等,利用稳健估计处理自动化采集、海量的测量数据中混入的粗差具有重要的理论和实际意义。
1953年,文献[7]首次提出了稳健估计(又称为抗差估计)这一专业术语。文献[8]提出了污染分布模式。文献[9]阐述了定位参数的抗差估计。文献[10]提出了影响函数和崩溃点的概念。这些都为稳健估计理论奠定了基础。1980年,文献[11]将稳健估计理论引入测量界,提出了著名的“丹麦法”。此外,国内学者在稳健估计方面也取得重大突破,如文献[12]提出等价权的概念;文献[13]提出自适应的稳健估计算法等。目前,稳健估计可以分为3大类:M估计、L估计、R估计。其中,M估计是经典极大似然估计的推广,是测量数据处理中稳健估计最重要的估计方法。
稳健估计的选权迭代算法属于M估计,在测量中应用广泛。基本原理为:首先采用最小二乘法得到观测值的估计残差;根据残差确定各观测值新的权因子,进行下一轮平差计算;反复迭代,直至前后两次估计值的变化值小于限差为止。算法每次迭代求解法方程均需进行矩阵的求逆运算,矩阵求逆的复杂度是其维数的三次方。因此,平差模型的待估参数多,即法方程正交矩阵维数高,算法的计算量和计算时间急剧上升,算法效率难以满足现代测量中大规模测量方案、海量数据及平差模型实时解算等要求。
本文基于矩阵逆的运算法则,提出了一种有效改进现有选权迭代算法的方法。迭代计算中,仅需计算由前一次残差确定的新权阵下的模型未知参数估计值的变化量,避免了法方程正交矩阵的求逆,显著提高了算法的效率,并能保持原稳健权函数的抗差性。本文以水准网为例,通过增加估计参数的数量和粗差数量,验证了当模型的估计量增加时,改进的选权迭代算法的计算效率要远高于经典选权迭代算法。
1 经典选权迭代算法设平差的线性函数模型和随机模型为
 (1)
(1)
式中,l为观测值向量;B为系数矩阵并且列满秩;x为未知参数向量;Δ为误差向量;D为对角方差-协方差矩阵;σ0为单位权中误差;Q为对角协因数矩阵;P为对角权阵。
独立不等权观测情况下的M估计准则为
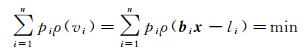 (2)
(2)
式中,bi=[bi1 bi2 … bit];li表示第i个观测值,相应的误差方程为
 (3)
(3)
对式(2)中x求导,记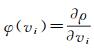
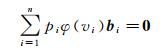 (4)
(4)
令pi=piwi,
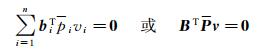 (5)
(5)
式中,P为等价权阵;pi为等价权元素;wi为权因子[12]。
将式(3)代入式(5),得到M估计下的法方程
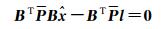 (6)
(6)
解式(6)得
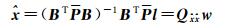 (7)
(7)
式中,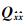
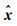
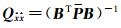
根据残差v确定各观测值新的权因子,再进行下一轮平差,反复迭代直至前后两次估计值的变化小于限差,计算结束。算法的核心是确定权函数ρ(或φ),即由每次迭代的残差估计值确定新的权阵,以保证估值的抗差性和效率[13]。以下介绍几种常见的权函数。
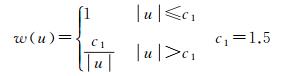
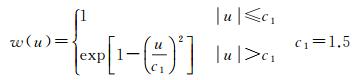
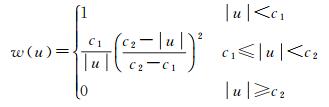
c1=1.5, c2=3.0
以上权函数中,w(u)为权函数,c1和c2为相应的调和系数。
2 改进选权迭代算法经典选权迭代算法中,每次由残差v的估计值确定新的权阵计算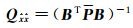
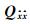
选权迭代算法中,每次迭代运算确定了观测值新的权值后(每次仅改变一个权值),将其增量记为对角矩阵dP,则待估参数新的协因数阵
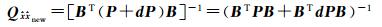 (8)
(8)
式中
 (9)
(9)
将式(9)代入式(8)得
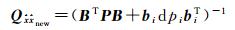 (10)
(10)
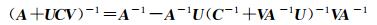 (11)
(11)
将式(10)展开
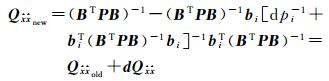 (12)
(12)
式中,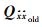

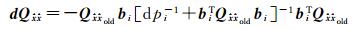 (13)
(13)
式(7)中,令wold、wnew分别表示权阵更新前后的权阵,则
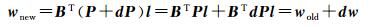 (14)
(14)
式中,dw为
 (15)
(15)
令
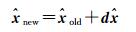 (16)
(16)
式中,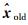

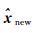
由式(12)—式(16)得
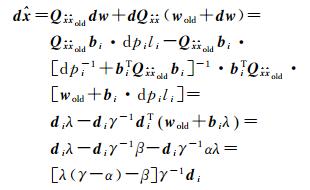 (17)
(17)
式中,
则式(13)可表示为
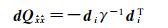 (18)
(18)
改进选权迭代算法步骤总结如下:
(1) 估计最小二乘初值:
根据平差模型的输入量l、B、P(Q),采用最小二乘估计初值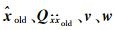
(2) 选权迭代计算:
由v和式(15)计算权阵更新后的dw,式(18)计算
由式(16)、式(17)计算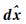

直到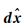
改进选权迭代算法每次迭代只需计算增量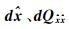
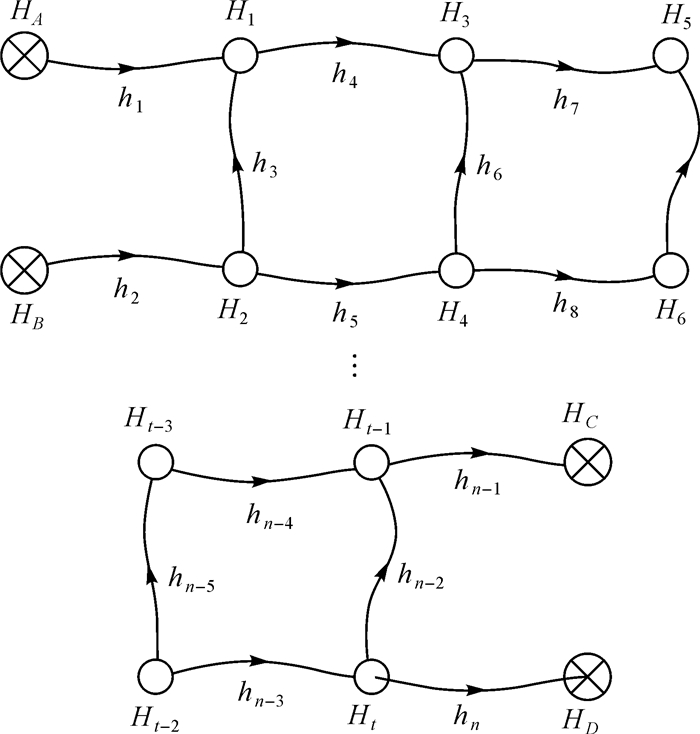
为了从数值上说明改进选权迭代算法在计算效率上的优势,笔者设计了一个条状、结构规整的水准网实例,如图 1所示。点A、B、C、D为已知控制点,其余为未知点,未知点个数为t(t为偶数),观测值个数为n, 且n=1.5t+2。
|
| 图 1 模拟的水准网 Fig. 1 Simulated leveling network |
水准网设计试验数据数据说明如下:
控制点高程:HA=1 m, HB=0 m, HC=1.5 m, HD=0.5 m
高差观测值:
h1=h2=h7=h8=…=(0.5+Δ)m
h4=h5=h10=h11=…=(-0.5+Δ)m
h3=h6=h9=h12=…=(1+Δ)m
式中,Δ为符合正态分布(μ=0,σ=0.005)的随机误差,设计粗差的量级约为1 m。
当水准网包含不同数量级的未知点t=100、500、1000、5000、10 000时,且分别包含1到5个粗差的情况下,笔者采用Matlab编程对改进选权迭代算法与经典算法的计算效率进行了比较。程序采用Matlab自带的tic/toc函数,记录了算法改进前后程序运行所需时间,试验结果见表 1。
| s | ||||||||||||||
| 未知点个数t | 1个粗差 | 2个粗差 | 3个粗差 | 4个粗差 | 5个粗差 | |||||||||
| 改进前 | 改进后 | 改进前 | 改进后 | 改进前 | 改进后 | 改进前 | 改进后 | 改进前 | 改进后 | |||||
| 100 | 0.003 | 0.001 | 0.004 | 0.001 | 0.006 | 0.002 | 0.008 | 0.002 | 0.009 | 0.002 | ||||
| 500 | 0.182 | 0.028 | 0.311 | 0.033 | 0.437 | 0.039 | 0.566 | 0.044 | 0.689 | 0.050 | ||||
| 1000 | 1.395 | 0.176 | 2.347 | 0.200 | 3.422 | 0.229 | 4.390 | 0.254 | 5.351 | 0.278 | ||||
| 5000 | 124.413 | 13.218 | 207.168 | 13.828 | 319.313 | 14.389 | 388.992 | 15.222 | 476.952 | 15.743 | ||||
| 10 000 | 828.569 | 99.679 | 1 557.476 | 101.935 | 2 084.277 | 104.629 | 2 608.107 | 105.823 | 3 284.699 | 108.993 | ||||
试验结果表明:
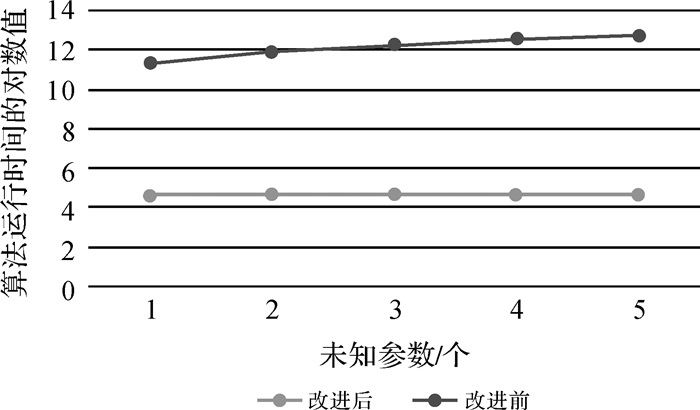
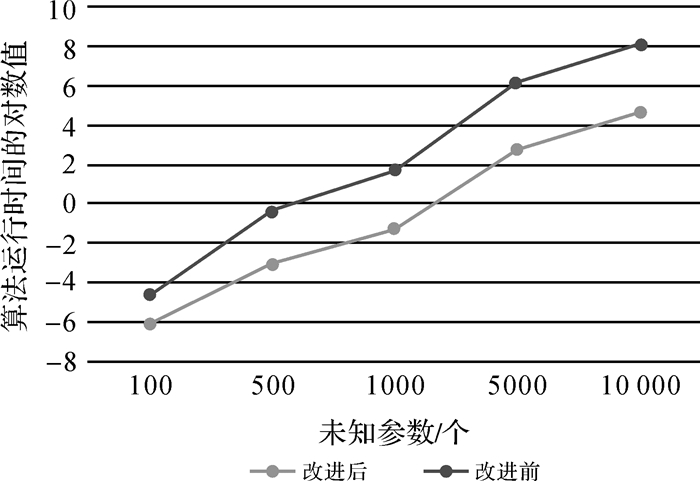
(1) 改进算法计算效率要高于经典选权迭代算法(图 2、图 3),尤其是在平差模型中待求参数个数t较大或者多个粗差的情况下,计算效率显著提升。当未知数个数t=10 000且含5个粗差时,改进算法所需计算时间仅为经典算法的1/30。
|
| 图 2 改进前后运行时间比较(未知点数为10 000) Fig. 2 Computational cost comparison when the unknown parameters is 10 000 |
|
| 图 3 改进前后运行时间比较(误差数为5) Fig. 3 Computational cost comparison when there are 5 errors |
(2) 改进算法的计算效率取决于采用最小二乘估计初值的计算时间,迭代计算无需求逆,当粗差个数增加时,计算时间仅有微小增长。例如,当未知数个数t=10 000,粗差从1个增长到5个时,经典算法计算时间急剧增长,由829 s增加4倍,达到3285 s;而改进算法从100 s仅增加到109 s,改进算法对于处理多个粗差情况非常高效。
4 结论经典选权迭代算法属于M估计,是当前运用最为广泛的稳健估计方法之一。本文采用矩阵逆运算法则,提出了一种改进的选权迭代算法。改进算法在迭代过程中,仅需计算新权阵下的最小二乘估计改正值,避免了经典算法中每步对平差模型法方程的求逆运算,显著提高了算法的计算效率。改进选权迭代算法适用于现代空间测量技术下对自动观测的海量数据的实时或者准实时的处理需求,如GNSS、遥感等观测数据,当这些数据含有一定数量的粗差时,改进算法可以大大降低经典选权迭代算法的计算时间。本文算法基于独立不等精度观测值的情况,笔者下一步的研究目标是针对海量数据,讨论如何提高相关观测值[5, 17, 26]的选权迭代算法的计算效率。
| [1] | HUBER P J. Robust Statistics[M]. New York: John Wiley and Sons, 1981. |
| [2] | AMIRI-SIMKOOEI A. Formulation of L1 Norm Minimization in Gauss-Markov Models[J]. Journal of Surveying Engineering, 2003, 129(1): 37–43. DOI:10.1061/(ASCE)0733-9453(2003)129:1(37) |
| [3] |
彭军还, 李淑慧, 师芸, 等.
不等式约束M估计的均方误差矩阵和解的改善条件[J]. 测绘学报, 2010, 39(2): 129–134.
PENG Junhuan, LI Shuhui, SHI Yun, et al. The Mean Squares Error Matrix of Inequality Constrained M-estimate and the Conditions for Improving Solutions[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 129–134. |
| [4] |
欧吉坤.
一种三步抗差方案的设计[J]. 测绘学报, 1996, 25(3): 173–179.
OU Jikun. Design of a New Scheme of Robust Estimation by Three Steps[J]. Acta Geodaetica et Cartographica Sinica, 1996, 25(3): 173–179. DOI:10.3321/j.issn:1001-1595.1996.03.003 |
| [5] | GUO Jianfeng, OU Jikun, WANG Haitao. Robust Estimation for Correlated Observations:Two Local Sensitivity-based Downweighting Strategies[J]. Journal of Geodesy, 2010, 84(4): 243–250. DOI:10.1007/s00190-009-0361-y |
| [6] |
王新洲, 陶本藻, 邱卫宁, 等.
高等测量平差[M]. 北京: 测绘出版社, 2006.
WANG Xinzhou, TAO Benzao, QIU Weining. Advanced Surveying Adjustment[M]. Beijing: Surveying and Mapping Press, 2006. |
| [7] | TUKEY J W. A Survey of Sampling from Contaminated Distribution[M]//GLESER L J, PERLMAN M D, PRESS S J, et al. Contributions to Probability and Statistics. California: Stanford University Press, 1960. |
| [8] | BOX G E P. Non-normality and Tests on Variances[J]. Biometrika, 1953, 40(3-4): 318–335. DOI:10.1093/biomet/40.3-4.318 |
| [9] | HUBER P J. Robust Estimation of a Location Parameter[J]. The Annals of Mathematical Statistics, 1964, 35(1): 73–101. DOI:10.1214/aoms/1177703732 |
| [10] | HAMPEL F R. Contributions to the Theory of Robust Estimation[D]. Berkeley: University of California, 1968. |
| [11] | KRARUP T, JUHL J, KUBIK K. Gotterdammerung over Least Squares Adjustment[C]//Proceedings of the 14th Congress of International Archives of Photogrammetry. Hamburg: [s.n.], 1980. |
| [12] |
周江文.
经典误差理论与抗差估计[J]. 测绘学报, 1989, 18(2): 115–120.
ZHOU Jiangwen. Classical Theory of Errors and Robust Estimation[J]. Acta Geodaetica et Cartographica Sinica, 1989, 18(2): 115–120. DOI:10.3321/j.issn:1001-1595.1989.02.005 |
| [13] |
杨元喜.
自适应抗差最小二乘估计[J]. 测绘学报, 1996, 25(3): 206–211.
YANG Yuanxi. Adaptively Robust Least Squares Estimation[J]. Acta Geodaetica et Cartographica Sinica, 1996, 25(3): 206–211. DOI:10.3321/j.issn:1001-1595.1996.03.009 |
| [14] | BASELGA S. Global Optimization Solution of Robust Estimation[J]. Journal of Surveying Engineering, 2007, 133(3): 123–128. DOI:10.1061/(ASCE)0733-9453(2007)133:3(123) |
| [15] |
杨元喜, 柴洪洲, 宋力杰.
污染分布的逼近及应用[J]. 测绘学报, 1999, 28(3): 209–214.
YANG Yuanxi, CHAI Hongzhou, SONG Lijie. Approximation for Contaminated Distribution and Its Applications[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(3): 209–214. DOI:10.3321/j.issn:1001-1595.1999.03.005 |
| [16] | GUI Q, ZHANG J. Robust Biased Estimation and Its Applications in Geodetic Adjustments[J]. Journal of Geodesy, 1998, 72(7-8): 430–435. DOI:10.1007/s001900050182 |
| [17] | YANG Y, SONG L, XU T. Robust Estimator for Correlated Observations Based on Bifactor Equivalent Weights[J]. Journal of Geodesy, 2002, 76(6-7): 353–358. DOI:10.1007/s00190-002-0256-7 |
| [18] | KNIGHT N L, WANG Jinling. A Comparison of Outlier Detection Procedures and Robust Estimation Methods in GPS Positioning[J]. The Journal of Navigation, 2009, 62(4): 699–709. DOI:10.1017/S0373463309990142 |
| [19] |
李德仁.
利用选择权迭代法进行粗差定位[J]. 武汉测绘学院学报, 1984(1): 46–48.
LI Deren. Gross Error Location by Means of the Iteration Method with Variable Weights[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1984(1): 46–48. |
| [20] |
葛永慧.
再生权最小二乘法稳健估计[M]. 北京: 科学出版社, 2015.
GE Yonghui. Self-born Weighted Robust Least Squares Estimation[M]. Beijing: Science Press, 2015. |
| [21] |
杨元喜.
抗差估计理论及其应用[M]. 北京: 八一出版社, 1993.
YANG Yuanxi. Theory of Robust Estimation and Its Application[M]. Beijing: "August 1st" Publishing House, 1993. |
| [22] |
杨元喜, 宋力杰, 徐天河.
双因子方差膨胀抗差估计[J]. 解放军测绘研究所学报, 2001, 21(2): 1–5.
YANG Yuanxi, SONG Lijie, XU Tianhe. Robust Parameter Estimation for Correlated Observations by Variance-Covariance Inflating[J]. Journal of the Institute of Surveying and Mapping of the PLA, 2001, 21(2): 1–5. |
| [23] | YANG Yuanxi. Robust Estimation for Dependent Observations[J]. Manuscripta Geodaetica, 1994, 19(1): 10–17. |
| [24] |
李德仁, 袁修孝.
误差处理与可靠性理论[M]. 2版. 武汉: 武汉大学出版社, 2012.
LI Deren, YUAN Xiuxiao. Error Processing and Reliability Theory[M]. 2nd ed. Wuhan: Press of Wuhan University, 2012. |
| [25] | KOCH K R. Parameter Estimation and Hypothesis Testing in Linear Models[M]. Berlin: Springer-Verlag, 1999. |
| [26] | XU Peiliang. On Robust Estimation with Correlated Observations[J]. Bulletin Géodésique, 1989, 63(3): 237–252. DOI:10.1007/BF02520474 |



