2. 西安测绘研究所, 陕西 西安 710054
2. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China
我国目前采用的1985国家高程基准是由青岛大港验潮站处平均海平面定义的[1-3]。平均海面的重力位是我国高程基准的重要基础数据,也是实现我国高程基准与世界高程基准统一的重要依据[4-7]。
全球高程基准由大地水准面定义,大地水准面是全球范围内平均海面最佳拟合的重力等位面。IERS规定,全球大地水准面重力位W0=62 636 856.0 m2s-2±0.5 m2s-2,是由文献[8-11]利用T/P卫星的全球观测资料确定的,是大地水准面重力位的平均值。由于海面地形、局部地质环境等因素的影响,局部地区验潮站的平均海平面与大地水准面并不重合,存在一定的差异[10]。因此,局部高程基准与全球高程基准的垂直偏差,实质上是局部地区验潮站的平均海平面与大地水准面之间的重力位差。
对于我国高程基准相对大地水准面的垂直偏差,不少学者作了探索和研究。文献[12-14]利用EGM96模型和GPS/水准数据采用异常位法、高程异常等方法获得我国高程相对大地水准面的垂直偏差0.26 m;文献[15]利用EGM2008模型和全国GPS/水准数据获得我国高程基准相对大地水准面的垂直偏差0.32 m;文献[16-18]对我国高程基准与全球高程基准统一从理论、方法和实际问题等方面做出了一系列研究。但是,因验潮站平均海平面位置特殊,直接测量其坐标程序和工作比较复杂,至今尚未有直接采用验潮站平均海平面处的坐标计算获得的我国高程基准的垂直偏差。
为了获得我国高程基准的第一手资料(曾获得过概略经纬度,与本文测量结果相差十几米),笔者进行了相关测量,然后进行高程基准偏差计算。基本思路是:直接通过大港验潮站坐标利用重力场模型计算我国高程基准的重力位,将计算得到的重力位与IERS给出的大地水准面重力位作差,从而得出我国高程基准的垂直偏差。
本文首先给出通过大港验潮站坐标确定我国高程基准垂直偏差的基本原理,然后介绍测定大港验潮站平均海面坐标的方法及过程,接下来通过重力场模型计算出大港验潮站重力位,进而推算出我国高程基准的垂直偏差,并与我国东部地区GPS/水准数据的计算结果进行了比较,最后给出几点结论。
1 通过大港验潮站坐标确定我国高程基准的垂直偏差假定已知高程基准处的坐标,可以通过重力场模型直接计算该处的重力位W′0[12-13, 15]
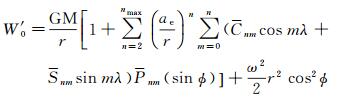 (1)
(1)
式中,GM是地心引力常数;r是地心向径,r=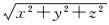
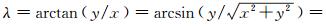
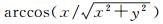
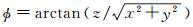
得到高程基准面的重力位后,即可由式(2)得到高程基准的垂直偏差[12-13, 15]
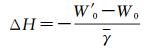 (2)
(2)
式中,W0是大地水准面重力位,W0=62 636 856.0 m2s-2±0.5 m2s-2[19];γ为大港验潮站平均正常重力。理论上大地水准面是全球平均海面最佳拟合的等位面,其重力位W0是时变的,与观测的历元和所选用的大地坐标系统有关。但是,因确定大地水准面重力位涉及多方面因素,例如不同的海面高模型、重力场模型、椭球参数等,是近年研究的热点,也有不同的计算结果。IERS作为参考系统中的标准典范,具有一定的规范性,众多学者将其定义的W0作为全球高程基准重力位[12-15],因此本文也采用此数值。
式(1)表明,W′0的误差与重力场模型和三维位置误差有关。相关文献表明,EGM2008模型计算我国点位平均高程异常的误差为0.2 m[20],EIGEN-6C2模型比EGM2008模型精度高2~3 cm[21](EIGEN-6C4与之相当),由此推断EGM2008模型计算我国点位平均重力位的误差约为2 m2/s2,EIGEN-6C4模型计算我国点位平均重力位的误差约为1.7 m2/s2,已知大地水准面重力位的误差为0.5 m2/s2,则EGM2008模型计算的高程基准的垂直偏差误差约为0.21 m,EIGEN-6C4模型计算的垂直偏差误差略小一点。文献[22]表明,三维位置中仅有大地高的误差对高程偏差的影响较大,以1:1比例传播,若验潮站位置误差在厘米量级,相比重力位误差,此误差影响可以忽略不计。
2 大港验潮站平均海面坐标的测定图 1为大港验潮站示意图,验潮井口近似圆形,上面盖以格网铁盘,井口上两个验潮仪连接绿色和黄色两根线,这两根摆线与平均海平面处的交点即为1985国家高程基准的零点。井口两侧有两个水准墩,两水准墩连接一根铜线,铜线距离水准零点6 m,1985国家高程基准的平均海面距离水准零点2.429 m[2]。
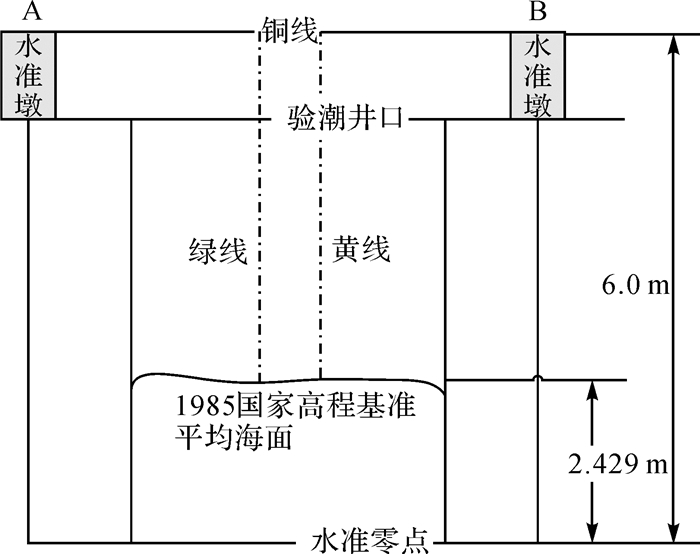
|
| 图 1 大港验潮站示意图 Fig. 1 Dagang Tidal Gauge |
高程基准的零点坐标无法进行直接测量,只能通过联测得到。
选取验潮站北20 m草地处已有GPS点作为主控点QDYC,在码头灯塔附近选取方位点YCF1和YCF2,在验潮站门口处选取两个过渡点P1、P2,这5个点组成控制网,见图 2。
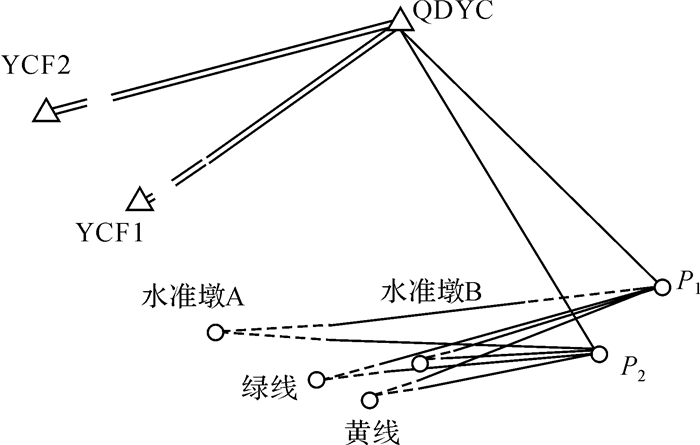
|
| 图 2 验潮站坐标测量示意图 Fig. 2 Measurement for the coordinates of Dagang Tidal Gauge |
控制网测量采用GPS测量方法实施,使用3台Topcon GPS接收机同步观测,其中主控点QDYC、方位点YCF2按照B级要求进行同步观测,方位点YCF1测量按照C级要求与主控点进行同步观测。
通过水平角测量、距离测量将主控点和方位点平面坐标通过P1、P2、水准墩A和B归算到绿线和黄线处;然后通过高差测量获得主控点和方位点与水准墩A和B之间的高差。
采用Gamit软件、利用4个国际IGS站(BJFS、SUWN、SHAO、WUHN)的观测数据和坐标解算出主控点QDYC和方位点YCF2的坐标;使用Pinnacle软件,利用主控点QDYC和方位点YCF2的坐标解算出方位点YCF1的坐标;使用平差之星2007软件中水准网平差模块,解算出水准墩A和B的大地高;使用平差之星2007软件中网平差模块,解算出黄线、绿线、水准墩A和B的平面坐标;根据水准墩A和B铜线的大地高,减去3.571 m(6 m-2.429 m),即得到黄线、绿线在平均海面处的大地高,从而获得大港验潮站平均海面处的坐标。
GPS网平差解算获得的内符合精度在水平方向分别为1.6 mm、1.5 mm,高程方向为2.2 mm。根据长基线网平差结果统计,外符合精度水平方向1~2 cm,高程2~3 cm,归心测量和水准测量的精度都是毫米级,可以认为通过本文方法测量获得的验潮站坐标精度优于5 cm。
3 结果及分析采用EGM2008模型和EIGEN-6C4模型分别计算大港验潮站重力位,两个模型的有关参数[23-25]见表 1。这里需要说明的是,我国采用CGCS2000参考椭球,椭球参数与EGM2008模型和EIGEN-6C4模型相差甚微,引起的重力位计算差异小于0.05 m2/s2,可以忽略。
| EGM2008 | EIGEN-6C4 | |
| GM/m3s-2 | 3 986 004.415×108 | 3 986 004.415×108 |
| ae/m | 6 378 136.3 | 6 378 136.46 |
| ω/rad s-1 | 7 292 115.0×10-11 | 7 292 115.0×10-11 |
| nmax | 2190 | 2190 |
验潮站平均海面处黄绿摆线非常接近(东西向相差0.13 m,南北向相差0.003 m,高度没有差异),所以采用其中一点坐标计算重力位W′0。计算结果列于表 2。
| m2s-2 | ||
| 参数 | EGM2008 | EIGEN-6C4 |
| W′0 | 62 636 852.637 | 62 636 853.642 |
为了检验计算结果的准确性,本文采用全国均匀分布的936个GPS/水准数据通过式(3)计算我国高程基准的重力位W′0[6-7, 9]
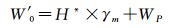 (3)
(3)
式中,WP为地面任一点的重力位,用式(1)重力位模型计算获得;H*是P点的正常高;γm是P点的平均正常重力,由式(4)获得[9]
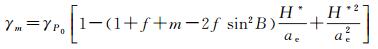 (4)
(4)
式中,γP0表示P点在椭球面上的正常重力;f表示椭球扁率;B表示P点的大地纬度,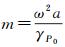
将936个GPS/水准数据划分为两组计算:
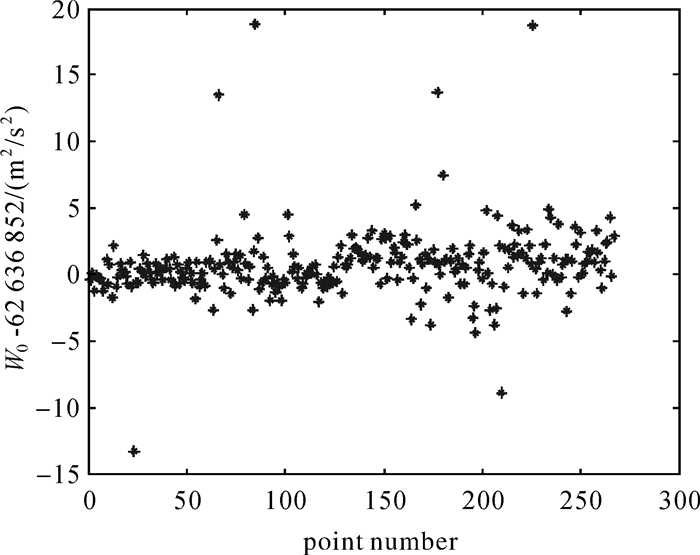
组1:我国东部GPS/水准数据(经度大于117°E,共计267个点),如图 3所示。
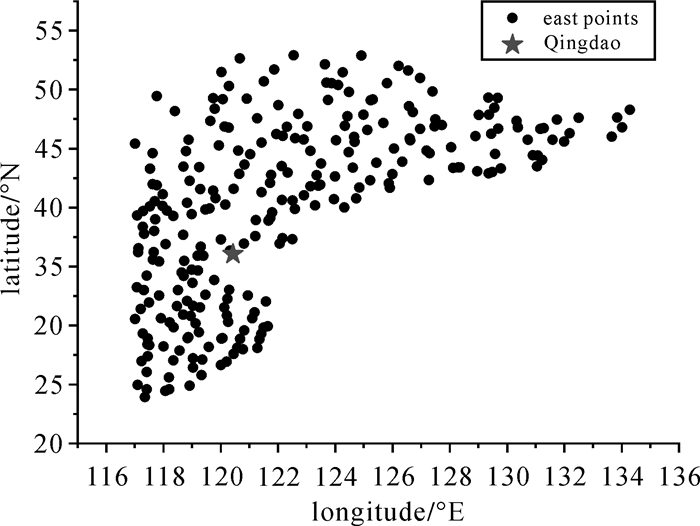
|
| 图 3 东部GPS/水准数据 Fig. 3 GPS/Leveling data from eastern area |
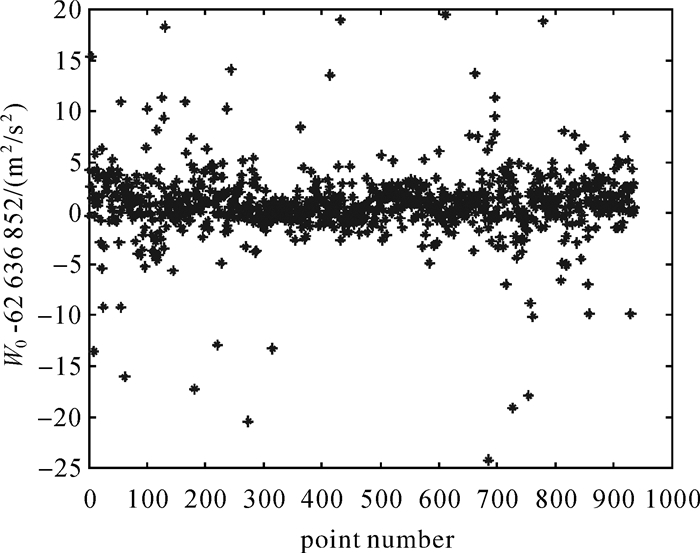
组2:全部GPS/水准数据(936个点)。
图 4和图 5给出利用式(3)采用EGM2008模型计算的W′0,EIGEN-6C4模型的计算结果与之类似。表 3列出采用两种模型计算的W′0的平均值、离散度和标准差。
|
| 图 4 组1数据计算得到的W′0 Fig. 4 W′0 obtained from group 1 data |
|
| 图 5 组2数据计算得到的W′0 Fig. 5 W′0 obtained from group 2 data |
| m2s-2 | |||||
| 组 | 模型 | 点数 | W′0 | 离散度 | 标准差 |
| 组1 | EGM2008 | 267 | 62 636 852.721 | 2.731 | 0.167 |
| EIGEN-6C4 | 62 636 852.676 | 2.635 | 0.161 | ||
| 组2 | EGM2008 | 936 | 62 636 852.835 | 3.337 | 0.109 |
| EIGEN-6C4 | 62 636 852.861 | 2.890 | 0.094 | ||
所采用的这些GPS/水准数据是在20世纪观测的,其中少数点的三维位置坐标存在较大误差,按照3倍中误差剔除异常值,结果如表 4所示。
| m2s-2 | |||||
| 组 | 模型 | 点数 | W′0 | 离散度 | 标准差 |
| 组1 | EGM2008 | 261 | 62 636 852.578 | 1.631 | 0.101 |
| EIGEN-6C4 | 261 | 62 636 852.546 | 1.473 | 0.091 | |
| 组2 | EGM2008 | 912 | 62 636 852.909 | 2.214 | 0.073 |
| EIGEN-6C4 | 916 | 62 636 852.952 | 1.845 | 0.061 | |
采用同样的GPS/水准数据,文献[12]曾用EGM96模型计算得到W′0=62 636 853.39 m2/s2。文献[15]用EGM2008模型计算得到的W′0与文中计算结果一致。从表 4中可以看出,EGM2008模型计算得到W′0的离散度为1.6~2.3 m2/s2,EIGEN-6C4模型计算得到W′0的离散度为1.4~1.9 m2/s2,EIGEN-6C4模型要比EGM2008模型计算结果精度略高,这与之前的误差分析结果是一致的。
以上数据得到的平均W′0的标准差为0.06~0.11 m2s-2,实际上这只是形式精度。从离散度来看,东部因接近大港验潮站且地势平坦,其离散度较小,且剔除的异常值较少(6个),而西部地区离大港验潮站较远且地势起伏较大,其离散度较大,且剔除的异常值较多(24个或20个)。利用验潮站坐标计算的W′0,尽管仅用一点,但是这相当于直接测定重力位,具有更重要的意义和更高的可信度。
表 5给出在验潮站直接测定和用东部GPS/水准数据得到的我国高程基准相对大地水准面的垂直偏差。从表 5可看出,尽管EIGEN-6C4模型的计算精度要好于EGM2008模型,但是用该模型计算的垂直偏差与用东部GPS/水准数据计算的结果相差较大,而利用EGM2008模型的计算结果与东部GPS/水准数据的计算结果相差较小,因此认为利用EGM2008模型的计算结果更加可靠。
| m | ||
| 模型 | 验潮站 | 东部GPS/水准数据 |
| EGM2008 | 0.344 | 0.349±0.010 |
| EIGEN-6C4 | 0.241 | 0.353±0.009 |
利用EGM2008模型和验潮站坐标获得的偏差值是0.344 m,利用东部261个GPS/水准点数据计算获得的偏差值是0.350 m,两者相差0.006 m。
4 结论本文通过大港验潮站坐标分别采用EGM2008模型和EIGEN-6C4模型计算得到的我国高程基准相对大地水准面的垂直偏差,并与我国东部261个GPS/水准点数据的计算结果进行了比较,得出如下结论:
(1) 尽管EIGEN-6C4模型精度要高于EGM2008模型,但是利用EGM2008模型和验潮站坐标计算的我国高程基准的垂直偏差与其他数据的计算结果相差较小,因此认为利用EGM2008模型的计算结果要更可靠一些(此结论依赖于已有的GPS/水准数据的计算结果,读者可以有不同的见解,但是文中的计算结果是忠实于数据的)。
(2) 将GPS/水准数据分成东部数据和全国数据两类,东部地区相较于西部地区的得到的重力位更加可靠。
(3) 利用EGM2008模型和大港验潮站坐标计算获得的我国高程基准相对于大地水准面的偏差为0.344 m,比利用东部261个GPS/水准点数据得到的偏差值小约0.006 m。
致谢: 感谢有关单位对大港验潮站进行的GPS测量、水平角测量、距离测量和水准测量,并进行数据处理。
| [1] |
陈宗镛.
计算平均海面的方法[J]. 山东海洋学院学报, 1960(1): 65–73.
CHEN Zongyong. The Method of Calculating the Mean Sea Level[J]. Journal of Ocean Institute of Shandong, 1960(1): 65–73. |
| [2] |
陈宗镛.
潮汐学[M]. 北京: 科学出版社, 1980.
CHEN Zongyong. Tide[M]. Beijing: Science Press, 1980. |
| [3] |
陈宗镛, 周天华, 于宜法, 等.
1985国家高程基准的研究[J]. 青岛海洋大学学报, 1988, 18(1): 9–14.
CHEN Zongyong, ZHOU Tianhua, YU Yifa, et al. A Study on the 1985 National Datum Level of Altitude[J]. Journal of Ocean University of Qingdao, 1988, 18(1): 9–14. |
| [4] | YANG Yuanxi, WEN Yuannan, XIONG Jie, et al. Robust Estimation for a Dynamic Model of the Sea Surface[J]. Survey Review, 1999, 35(271): 2–10. DOI:10.1179/sre.1999.35.271.2 |
| [5] |
陈俊勇.
对我国建立现代大地坐标系统和高程系统的建议[J]. 测绘通报, 2002(8): 1–5.
CHEN Junyong. On the Chinese Modern Geodetic Coordinate System and Height System[J]. Bulletin of Surveying and Mapping, 2002(8): 1–5. DOI:10.3969/j.issn.0494-0911.2002.08.001 |
| [6] |
陈俊勇.
建设我国现代大地测量基准的思考[J]. 武汉大学学报(信息科学版), 2003, 28(S1): 1–6.
CHEN Junyong. Thinking on the Establishment of Modern Geodetic Datum of China[J]. Geomatics and Information Science of Wuhan University, 2003, 28(S1): 1–6. |
| [7] |
文援兰, 杨元喜.
我国近海平均海面及其变化的研究[J]. 武汉大学学报(信息科学版), 2001, 26(2): 127–132.
WEN Yuanlan, YANG Yuanxi. Research on Sea Level and Rising Trend of Coastal Waters in China[J]. Geomatics and Information Science of Wuhan University, 2001, 26(2): 127–132. |
| [8] | BURŠA M, KOUBA J, RADĚJ K, et al. Mean Earth's Equipotential Surface from TOPEX/Poseidon Altimetry[J]. Studia Geophysica et Geodaetica, 1998, 42(4): 459–466. DOI:10.1023/A:1023356803773 |
| [9] | BURŠA M, KOUBA J, KUMAR M, et al. Geoidal Geopotential and World Height System[J]. Studia Geophysica et Geodaetica, 1999, 43(4): 327–337. DOI:10.1023/A:1023273416512 |
| [10] | BURŠA M, KOUBA J, MÜLLER A, et al. Determination of Geopotential Differences between Local Vertical Datums and Realization of a World Height System[J]. Studia Geophysica et Geodaetica, 2001, 45(2): 127–132. DOI:10.1023/A:1021860126850 |
| [11] | BURŠA M, KENYON S, KOUBA J, et al. A Global Vertical Reference Frame Based on Four Regional Vertical Datums[J]. Studia Geophysica et Geodaetica, 2004, 48(3): 493–502. DOI:10.1023/B:SGEG.0000037468.48585.e6 |
| [12] |
焦文海, 魏子卿, 马欣, 等.
1985国家高程基准相对于大地水准面的垂直偏差[J]. 测绘学报, 2002, 31(3): 196–200.
JIAO Wenhai, WEI Ziqing, MA Xin, et al. The Origin Vertical Shift of National Height Datum 1985 with Respect to the Geoidal Surface[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(3): 196–200. DOI:10.3321/j.issn:1001-1595.2002.03.003 |
| [13] |
郭海荣, 焦文海, 杨元喜, 等.
1985国家高程基准的系统差[J]. 武汉大学学报(信息科学版), 2004, 29(8): 715–719.
GUO Hairong, JIAO Wenhai, YANG Yuanxi, et al. Systematic Error of the 1985 National Height Datum[J]. Geomatics and Information Science of Wuhan University, 2004, 29(8): 715–719. |
| [14] |
郭海荣, 焦文海, 杨元喜.
1985国家高程基准与全球似大地水准面之间的系统差及其分布规律[J]. 测绘学报, 2004, 33(2): 100–104.
GUO Hairong, JIAO Wenhai, YANG Yuanxi. The Systematic Difference and Its Distribution between the 1985 National Height Datum and the Global Quasigeoid[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(2): 100–104. DOI:10.3321/j.issn:1001-1595.2004.02.002 |
| [15] |
翟振和, 魏子卿, 吴富梅, 等.
利用EGM2008位模型计算中国高程基准与大地水准面间的垂直偏差[J]. 大地测量与地球动力学, 2011, 31(4): 116–118.
ZHAI Zhenhe, WEI Ziqing, WU Fumei, et al. Computation of Vertical Deviation of Chinese Height Datum from Geoid by Using EGM2008 Model[J]. Journal of Geodesy and Geodynamics, 2011, 31(4): 116–118. |
| [16] |
赫林, 李建成, 褚永海.
1985国家高程基准与全球高程基准之间的垂直偏差[J]. 测绘学报, 2016, 45(7): 768–774.
HE Lin, LI Jiancheng, CHU Yonghai. The Vertical Shift between 1985 National Height Datum and Global Vertical Datum[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(7): 768–774. DOI:10.11947/j.AGCS.2016.20160029 |
| [17] |
李建成, 褚永海, 徐新禹.
区域与全球高程基准差异的确定[J]. 测绘学报, 2017, 46(10): 1262–1273.
LI Jiancheng, CHU Yonghai, XU Xinyu. Determination of Vertical Datum offset between the Regional and the Global Height Datum[J]. Acta Geodaetica et Cartographica Sinica, 2017, 46(10): 1262–1273. DOI:10.11947/j.AGCS.2017.20170538 |
| [18] |
褚永海, 李建成.
联合全球重力场模型和海面高模型确定平均海面位常数[J]. 大地测量与地球动力学, 2012, 32(5): 58–62.
CHU Yonghai, LI Jiancheng. Determination of Mean Sea Level Geotential from Global Gravity Field Model and Global Sea Surface Height Model[J]. Journal of Geodesy and Geodynamics, 2012, 32(5): 58–62. |
| [19] | PETIT G, LUZUM B. IERS Conventions (2010)[R]. Frankfurt am Main: Verlag des Bundesamts für Kartographie und Geodäsie, 2010. |
| [20] |
章传银, 郭春喜, 陈俊勇, 等.
EGM 2008地球重力场模型在中国大陆适用性分析[J]. 测绘学报, 2009, 38(4): 283–289.
ZHANG Chuanyin, GUO Chunxi, CHEN Junyong, et al. EGM 2008 and Its Application Analysis in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 283–289. DOI:10.3321/j.issn:1001-1595.2009.04.001 |
| [21] |
赵德军, 张敏利, 王强, 等.
EIGEN-6c2重力场模型在中国大陆的精度分析[J]. 大地测量与地球动力学, 2014, 34(5): 21–24.
ZHAO Dejun, ZHANG Minli, WANG Qiang, et al. Accuracy Analyses of EIGEN-6c2 Geopotential Model in China Mainland[J]. Journal of Geodesy and Geodynamics, 2014, 34(5): 21–24. |
| [22] |
吴富梅, 魏子卿.
利用GNSS和EGM2008模型进行跨海高程传递[J]. 武汉大学学报(信息科学版), 2016, 41(5): 698–703.
WU Fumei, WEI Ziqing. Height Transfer from Land to Island Based on GNSS and EGM2008 Model[J]. Geomatics and Information Science of Wuhan University, 2016, 41(5): 698–703. |
| [23] | PAVLIS N K, HOLMES S A, KENYON S C, et al. An Earth Gravitational Model to Degree 2160: EGM2008[C]//Proceedings of 2008 General Assembly of the European Geosciences Union. Vienna, Austria: National Geospatial-Intelligence Agency, 2008. |
| [24] | PAVLIS N K, HOLMES S A, KENYON S C, et al. The Development and Evaluation of the Earth Gravitational Model 2008(EGM2008)[J]. Journal of Geophysical Research:Solid Earth, 2012, 117(B4): B04406. |
| [25] | FÖRSTE C, BRUINSMA S L, ABRIKOSOV O, et al. EIGEN-6C4 the Latest Combined Global Gravity Field Model Including GOCE Data up to Degree and Order 2190 of GFZ Potsdam and GRGS Toulouse[R].[S.l.]: International Centre for Global Earth Models, 2014. |


