2. 武汉大学资源与环境科学学院, 湖北 武汉 430079
2. School of Resource and Environment Sciences, Wuhan University, Wuhan 430079, China
相对于全色影像,多光谱各波段的波谱范围较窄,传感器所能接收到的辐射能量较少,为了维持一定的图像信噪比,会损失一定的空间分辨率[1]。因此,一般的光学遥感卫星提供较高分辨率的全色影像与较低分辨率的多光谱影像。空间信息与光谱信息是遥感解译、地物判别等后续处理的重要依据。全色-多光谱融合用于获得高分辨率的多光谱影像,一直是遥感领域较为关注的一个问题。
针对全色-多光谱融合问题,根据作用域的不同可以分为空间域方法和频率域方法两类。空间域方法可进一步分为系数增强与成分变换。系数增强是利用全色波段生成一个调制系数来对多光谱波段进行锐化、细节增强,典型方法有SFIM[2-3](smoothing filter-based intensity modulation)、Pansharp[4-5]、Brovey[6]等。SFIM利用邻域滤波后的全色影像生成调制系数,该方法存在空间信息融入度不足的问题;Pansharp利用多光谱影像加权模拟出的全色影像来生成系数,存在局部光谱畸变的问题;Brovey利用多光谱影像的色彩权重对全色影像进行模拟分光,存在色彩严重畸变的问题。成分变换是将多光谱影像转换到另一个坐标系,将其中具备大部分空间信息的分量用全色波段进行代替,从而达到提高多光谱影像分辨率的目的,典型方法有HIS(hue, intensity, saturation)[7-8]、Gram-Schmidt[9-10]、PC(principal components)[11]等。HIS是将RGB色彩空间转为HIS色彩空间,该方法只能对3个波段进行融合,也存在光谱畸变的问题;Gram-Schmidt将图像进行正交变换,用全色影像替换第1分量,但算法复杂度较高,不适合大范围影像处理;PC是主成分变换,用全色影像替换信息量最多的第1分量,但因第1分量信息量过于集中,使得融合结果存在较大的光谱畸变。频率域典型方法有高通滤波[12]、小波变换[13-14]、Contourlet[15]变换等,具有较好的光谱保持特性,但计算量较大,在商业软件中使用较少。
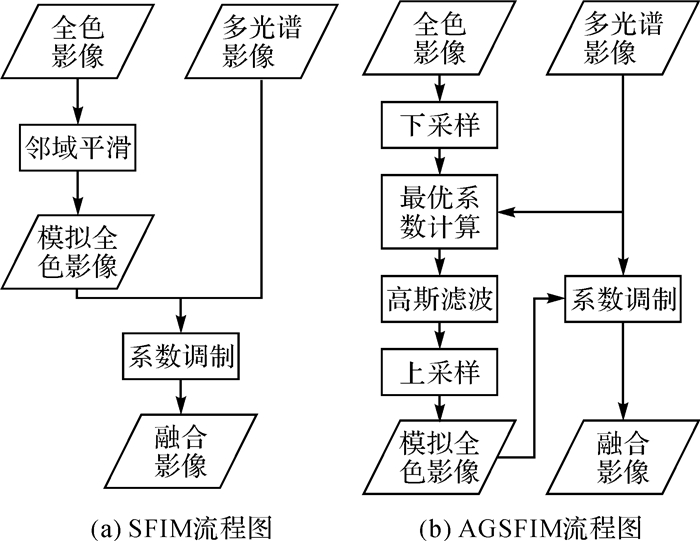
全色-多光谱融合问题的关键在于如何在光谱特征改变最小的情况下,最大限度地提高空间分辨率[16]。对于高分辨率遥感影像,大多数融合方法会造成比较严重的光谱畸变。SFIM是一种光谱保真效果较好的影像融合方法,但是存在着空间信息融入不足的缺点。本文提出一种自适应高斯滤波与SFIM模型相结合的融合方法(AGSFIM),可以在光谱信息保持良好的前提下,较好地提高空间信息融入度,改善融合影像的综合质量。SFIM与AGSFIM之间的差别在于模拟全色影像的获取方式。如图 1所示,SFIM是将全色影像进行邻域平滑从而得到模拟全色影像。AGSFIM则是通过以下步骤得到模拟全色影像:①对全色影像进行下采样;②根据下采样全色影像和多光谱影像的图像信息计算最优参数;③依据最优参数进行高斯滤波;④上采样得到模拟全色影像。
|
| 图 1 SFIM与AGSFIM流程对比 Fig. 1 Process flows comparison between SFIM and AGSFIM |
1 SFIM模型
SFIM是一种高保真的影像融合方法[2, 17]。对于一幅波段为λ的光学遥感影像,其DN(digital number)值大小与辐照度E(λ)及地物的地表反射率ρ(λ)有关[18],即
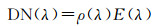 (1)
(1)
SFIM模型定义为
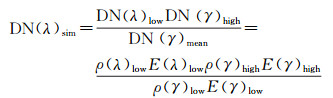 (2)
(2)
如果太阳辐射是给定不变的,那么地表反射值只和地形有关。如果两幅图像被量化为同样的DN值区间,对于相同分辨率的图像,就可以假设E(λ)≈E(γ)[19],则E(λ)low与E(γ)low就可以相互抵消。同时因为不同分辨率图像的地表反射率没有明显变化,就可以假设ρlow≈ρhigh,则ρ(γ)low与ρ(γ)high就可以相互抵消。式(2)可以转化为
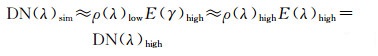 (3)
(3)
针对全色-多光谱融合问题,式(2)可以简化为
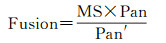 (4)
(4)
式中,MS是多光谱影像;Pan是全色影像;Pan′是低分辨率全色影像;Fusion是融合结果。Pan和Pan′的比值只保留了高分辨率图像的边缘细节信息,而基本消除了光谱与对比度信息。SFIM模型可以视为是在低分辨率图像中添加了高分辨率细节[20],其融合结果与高分辨率图像的光谱差异无关。假设存在理想的低分辨率全色影像Pan′idea,它应当具备两个特点:①空间信息特征与原始多光谱影像MS保持一致,这一点可以确保抵消多光谱影像MS的空间信息;②光谱特征应与原始全色影像Pan一致,这一点可以确保抵消全色影像Pan的光谱特征。
SFIM和Pansharp[4-5]在融合模型上是一致的,两者的区别在于怎样获取低分辨率全色影像Pan′。SFIM是通过对Pan进行降质(邻域滤波)来得到Pan′。这一操作相当于降低了全色影像的空间分辨率,而基本没有改变图像的光谱特征,满足上述的第二个特点。所以SFIM融合结果光谱畸变较小,但空间信息融入度低,使得融合结果清晰度不佳。
Pansharp是通过多光谱影像的加权拟合来获取Pan′的,基于最小二乘法测算多光谱各波段的权重并拟合得到Pan′。此操作是多光谱各波段的加权叠加过程,所得到的Pan′空间信息和MS相比没有发生改变,满足上述的第一个特点。所以Pansharp融合结果的空间信息融入程度较好,图像较为清晰,但光谱畸变较SFIM严重。综合而言,基于SFIM的改进方法主要是为了提高融合结果清晰度;基于Pansharp的改进方法则主要是为了降低融合结果的光谱畸变。
因为Pansharp是基于最小二乘法来计算各波段权重,当图幅较大时,单个系数存在局部描述不准确的弊端;此外当图幅中存在云、海等过亮或过暗地物时,系数会因这些极端灰度区域的存在而失真。以上情况会加剧Pansharp的光谱畸变;而SFIM只与图像邻域相关,不必考虑图像整体情况,可以有效避免上述弊端。基于以上理由,本文选择SFIM算法作为改进基础。
2 改进方法 2.1 改进原理对SFIM的改进主要是着眼于怎样得到空间信息特征与多光谱影像一致,光谱特征与全色影像一致的低分辨率全色影像Pan′。因为在融合过程中,MS需要重采样,使其图像大小与Pan保持一致,所以相应的,理想低分辨率全色影像Pan′idea的下采样图像Pan′idea_ds(下采样全色影像记为Pands,下标ds表示下采样)应当具有与多光谱影像类似的图像空间特征,主要表现在两者的图像清晰度应当是相似的。图 2是一组同一分辨率下的全色与多光谱影像的对比,其中图 2(a)是通过最近邻域法下采样得到的全色影像,图 2(b)是多光谱影像的第1波段。

|
| 图 2 同一分辨率的全色与多光谱影像 Fig. 2 Panchromatic and multi-spectral image of same spatial resolution |
如图 2所示,Pands的清晰度明显优于MS,其细节更为锐利,地物特征更为明显,图像中的线条、边角更为突出,像素间的反差更大。为了使Pands具有与MS相似的空间信息结构,需要利用低通滤波器消去Pands的部分高频信息。因为高斯滤波可以通过调整参数σ以控制卷积核的锐利程度,从而控制滤波后的图像清晰度,所以本文选择高斯滤波作为调整Pands清晰度的工具。高斯算子如下所示
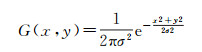 (5)
(5)
卷积核的平滑程度会随着参数σ的变化而渐次变化,进而改变滤波后图像的清晰度。定性而言,σ越大,滤波后图像的清晰度越低。因此必然存在一个最优的σ值,使得模糊处理后得到的Pan′ds与MS的清晰度最为相似。因为最优参数的条件是Pan′ds与MS清晰度最为相似,那么其关键问题就是怎样定量测量不同辐射特征下的图像清晰度。
方差(variance)可以衡量图像整体灰度值的偏离程度,在一定程度上可以反映图像清晰度,但容易受到噪声干扰,从而造成指标失真;平均梯度(average gradient, AG)反映的是图像局部灰度变化率,反映了图像微小细节反差变化的速率,可以用于衡量图像清晰度[21]。方差定义为
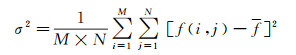 (6)
(6)
式中,f是图像均值。平均梯度定义为
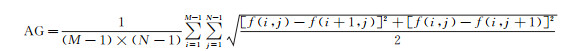 (7)
(7)
因为多光谱与全色影像是由不同的传感器成像的,其模-数转换方式不同,同时全色影像与多光谱各波段之间的光谱响应范围也不一致,造成各波段之间存在整体灰度差异。方差与平均梯度都依靠图像DN值进行计算,但是如果图像均值不同,那么方差与平均梯度就只是一个相对数值,无法横向比较各波段之间的清晰度情况。因此需要在图像均值相同的情况下来计算方差与平均梯度。
以全色影像的均值作为标准,则多光谱各波段只要乘上一个均值调整系数μ就可以使其均值与全色影像相同,均值调整系数μ定义为
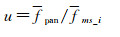 (8)
(8)
式中,fpan是全色影像的均值;fms_i是多光谱第i波段的均值。由方差与平均梯度的定义可知
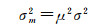 (9)
(9)
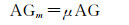 (10)
(10)
式中,σm2、AGm是经过均值调整后的方差和平均梯度。
试验发现,平均梯度更适合定量评价图像清晰度,其具体试验与分析过程见3.2节。最优参数σ的计算步骤如下:①计算全色及多光谱影像各波段的平均梯度与均值;②以全色影像的均值为标准,调整多光谱各波段的平均梯度;③从1开始,直到0.5,每隔0.1设置一次σ值,以不同的σ值进行高斯滤波得到Pan′ds并计算其平均梯度;④对采样数据进行二次多项式拟合,得到σ与Pan′ds平均梯度的函数关系;⑤以调整后的多光谱整体平均梯度作为标准代入拟合方程中,计算出最优参数。
2.3 影像融合对Pands进行模糊处理得到Pan′ds之后,再将Pan′ds与多光谱影像MS上采样至与全色影像Pan一样大小,上采样方法选用双线性内插法(bilinear interpolation),最后依照SFIM模型进行融合即可,其整体流程见图 1(b)。
3 试验与分析试验与分析包括3个部分。第1部分是最优参数计算,证明了以多光谱整体平均梯度作为计算最优参数的标准更为合理。第2部分试验下采样全色影像Pands的清晰度与融合结果之间的关系,证明了最优参数可以得到最优的融合结果。第3部分是AGSFIM与其他一些融合算法的比较结果。
本文选用Beijing-2和ZY-3 02等两颗卫星的影像作为试验数据。Beijing-2星座系统设计寿命为7年,由3颗推扫式光学遥感卫星组成,提供1 m分辨率的全色影像、4 m分辨率的四波段多光谱影像,Beijing-2数据由二十一世纪空间技术应用股份有限公司提供。ZY-3 02是民用三线阵光学遥感卫星,装备有下视、前视、后视及多光谱4台相机,下视相机提供2.1 m分辨率的全色影像,前后视相机提供2.5 m全色影像,多光谱相机提供5.8 m分辨率的4波段多光谱影像。ZY-3 02数据由中国资源卫星应用中心提供。
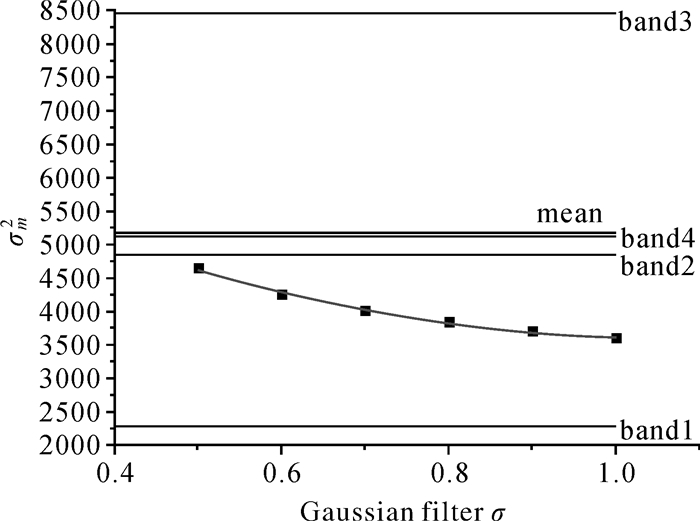
3.1 最优参数计算图 3是经过不同模糊处理后得到的Pan′ds,其中图 3(a)—(d)是多光谱的1—4波段,图 3(e)和(f)是分别经过窗口大小为3×3和5×5的均值滤波后的全色影像,图 3(g)—(l)是经过窗口大小为5×5,σ分别等于1—0.5的高斯滤波后的全色影像。图 4是模糊图像方差与高斯滤波参数σ的关系图,图 5是模糊图像平均梯度与σ的关系图。

|
| 图 3 模糊处理对比图 Fig. 3 Comparison of different blur processed images |
|
| 图 4 各影像方差 Fig. 4 Variances of images |
|
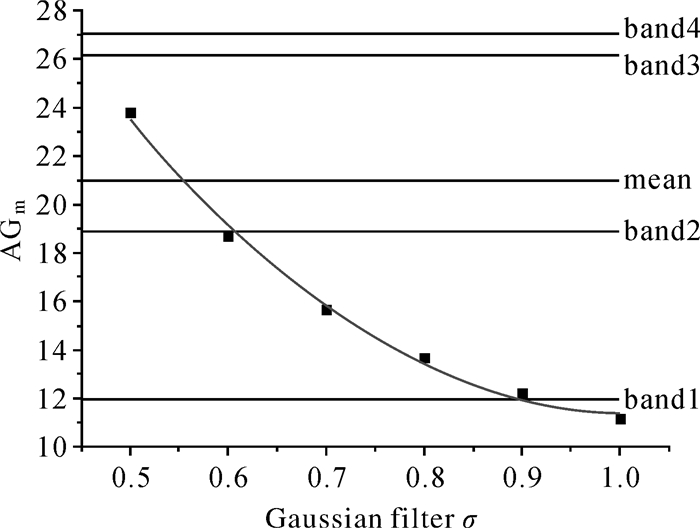
| 图 5 各影像平均梯度 Fig. 5 Average gradient of images |
依据图 3进行目视判断,多光谱第1波段的清晰度与(j)较为接近;第2、3、4波段的清晰度介于图 3(k)—(l)之间。图 4中以高斯滤波的σ值作为x轴,以模糊图像的方差作为y轴。通过对数据进行二次多项式拟合,两者的关系可以描述为
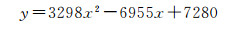 (11)
(11)
当拟合曲线达到多光谱4个波段的整体方差时,σ=0.365。
图 5中以高斯滤波的σ值作为x轴,以模糊图像的平均梯度作为y轴。通过对数据进行二次多项式拟合,两者的关系可以描述为
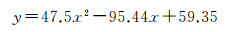 (12)
(12)
当拟合曲线达到多光谱4个波段的整体平均梯度时,σ=0.554 6。
在上文的目视判断中,多光谱各波段的清晰度整体上应当介于(j)—(k)之间,即σ∈[0.5, 0.6]。以平均梯度作为清晰度标准计算得到的最优σ值与目视判别的结果一致,因此用平均梯度作为清晰度的标准来对图像进行模糊处理较为准确与适当。就这组试验数据而言,将高斯滤波的σ设为0.554 6,可以得到与多光谱影像清晰度最为相似的下采样全色影像。
3.2 模糊处理对融合结果的影响由上文的分析中可知,影响SFIM融合效果的主要因素是Pan′的清晰度。以经过不同模糊处理得到的Pan′ds的上采样图像作为Pan′来进行融合。表 1记录了不同清晰度的Pan′ds所得到的融合结果的评价参数,图 6是Pan′ds的平均梯度与融合影像评价参数之间的关系。结果评价主要从空间信息融入度与光谱信息保真度两方面展开[22-23]。利用平均梯度(average gradient, AG)及信息熵(information entropy, IE)来评价空间信息融入度,利用相关系数(correlation coefficient, CC)与偏差指数(deviation index, DI)来评价光谱信息保真度[24-25]。
| Image | AG of Pan′ds | AG | IE | CC | DI |
| Mean Filter(3×3) | 13.02 | 73.383 9 | 1 688.813 1 | 7.837 1 | 6.890 2 |
| Mean Filter(5×5) | 7.84 | 74.536 3 | 2 197.093 3 | 8.338 4 | 7.001 8 |
| Gaussian Filter(σ=1) | 11.16 | 7.745 5 | 6.895 9 | 0.884 9 | 0.141 8 |
| Gaussian Filter(σ=0.9) | 12.23 | 7.638 6 | 6.879 5 | 0.888 5 | 0.136 9 |
| Gaussian Filter(σ=0.8) | 13.67 | 7.509 1 | 6.861 3 | 0.892 8 | 0.131 2 |
| Gaussian Filter(σ=0.7) | 15.66 | 7.352 3 | 6.841 4 | 0.898 0 | 0.124 6 |
| Gaussian Filter(σ=0.6) | 18.70 | 7.165 3 | 6.820 2 | 0.904 2 | 0.116 7 |
| Gaussian Filter(σ=0.5) | 23.82 | 6.965 0 | 6.799 3 | 0.910 8 | 0.107 2 |
|
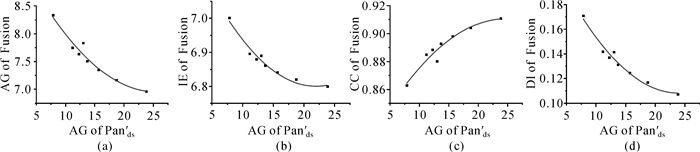
| 图 6 融合影像评价指标与Pan′ds平均梯度的关系 Fig. 6 Relationship between evaluate indexes and average gradient of pan′ds |
图 6(a)记录了Pan′ds平均梯度与融合结果平均梯度之间的关系;图 6(b)记录了Pan′ds平均梯度与融合结果信息熵之间的关系;图 6(c)记录了Pan′ds平均梯度与融合结果相关系数之间的关系;图 6(d)记录了Pan′ds平均梯度与融合结果偏差指数之间的关系。从图 6中的拟合曲线来看,融合结果的空间信息融入度与光谱信息保真度并不是线性变化的。随着Pan′ds平均梯度的下降,融合图像的空间信息融入度会加速上升,而光谱信息保真度会加速下降。因为空间信息融入度和光谱信息保真度是相互矛盾的一组性质,所以有必要寻找其最有搭配,即找到Pan′ds平均梯度的最优参数。该试验佐证了上文中的结论,即就这组数据而言,将高斯滤波的σ设为0.554 6,可以得到与多光谱影像清晰度最为相似的Pan′ds,从而得到空间信息融入度和光谱信息保真度最为平衡的融合图像。
3.3 AGSFIM与其他算法的比较为了比较与其他融合方法的差别,本文使用SFIM、AGSFIM、Pansharp、Gram-Schmidt、Brovey、PC 6种融合方法对Bejing-2及ZY-3 02星数据进行处理,分别得到图 7与图 8所示结果。其中图 7(a)是全色影像;图 7(b)是上采样多光谱影像;图 7(c)是SFIM融合结果;图 7(d)是AGSFIM融合结果,其中对于Beijing-2数据σ=0.554 6,对于ZY-3 02星试验数据σ=0.751;图 7(e)是Pansharp融合结果;图 7(f)Brovey融合结果;图 7(g)是PC融合结果;图 7(h)Gram-Schmidt融合结果。表 2、表 3分别是Beijing-2和ZY-3 02融合结果的评价参数。

|
| 图 7 “北京2号”融合结果比较 Fig. 7 Comparison of Beijing-2 fusion results |

|
| 图 8 “资源三号”02星融合结果比较 Fig. 8 Comparison of ZY-3 02 fusion results |
| Image | AG | EI | CC | DI |
| Pan | 15.172 1 | 7.714 3 | — | — |
| Up-sampled MS | 2.039 5 | 6.678 1 | — | — |
| SFIM | 4.976 9 | 6.693 6 | 0.978 3 | 0.047 8 |
| AGSFIM | 7.072 8 | 6.810 4 | 0.907 2 | 0.112 6 |
| Pansharp | 7.067 1 | 6.740 1 | 0.896 8 | 0.118 9 |
| Gram-Schmidt | 5.776 0 | 6.613 0 | 0.903 0 | 0.156 1 |
| Brovey | 4.869 4 | 6.164 2 | 0.894 7 | 0.325 6 |
| PC | 5.758 0 | 6.566 9 | 0.907 2 | 0.144 8 |
| Image | AG | EI | CC | DI |
| Pan | 2.997 3 | 7.000 3 | — | — |
| Up-sampled MS | 1.229 3 | 6.484 8 | — | — |
| SFIM | 2.140 0 | 6.544 2 | 0.996 5 | 0.009 0 |
| AGSFIM | 3.091 6 | 6.672 2 | 0.969 6 | 0.026 4 |
| Pansharp | 3.312 6 | 6.846 7 | 0.912 3 | 0.053 1 |
| Gram-Schmidt | 2.540 0 | 6.718 9 | 0.964 3 | 0.046 5 |
| Brovey | 0.847 9 | 5.415 1 | 0.483 2 | 0.556 4 |
| PC | 3.015 0 | 7.044 1 | 0.479 1 | 0.228 7 |
平均梯度与信息熵是用于衡量空间信息融入度的指标。对于这两组数据的空间信息融入度而言,这6种方法可以大致分为3档,SFIM与Brovey效果最差,Gram-Schmidt和PC居中,Pansharp与AGSFIM效果最好。相关系数与偏差指数是用于衡量光谱信息保真度的指标。对于这两组数据的光谱信息保真度而言,这6种方法可以大致分为3档,Brovey、PC效果最差,Gram-Schmidt、Pansharp与AGSFIM较好,SFIM最好。
试验与分析表明,相较于经典SFIM算法,AGSFIM较好地提高了空间信息融入度。Beijing-2融合结果平均梯度从4.976 9提高到了7.072 8,信息熵从6.693 6提高到了6.810 4,平均梯度与信息熵在所有方法中均排第一。ZY-3 02融合结果平均梯度从2.14提高到3.091 6,信息熵从6.544 2提高到6.672 2。与此同时,AGSFIM依然保持了较好的光谱信息保真度,其光谱保持能力仅次于SFIM。Beijing-2融合结果相关系数为0.907 2,偏差指数为0.112 6。ZY-3 02融合结果相关系数为0.969 6,偏差指数为0.026 4。
4 结论本文首先介绍与分析了SFIM融合模型的原理与方法,指出造成SFIM与Pansharp融合结果具有不同空间信息融入度与光谱信息保真度的原因在于模拟全色影像Pan′的获取方式不同,并就此提出了改进方向。之后,提出在理想状态下,全色影像的下采样图Pands应当具有与多光谱影像相同清晰度这一观点,并提出以均值调整后的多光谱平均梯度作为标准,自适应地设置最优σ值,利用高斯滤波调整Pands的清晰度。最后,以Beijing-2及ZY-3 02影像作为数据进行试验,并与SFIM、Pansharp、PC、Gram-Schmidt、Brovey等方法进行了对比,试验表明,AGSFIM可以在较好光谱信息保真度的前提下,有效改善融合结果的空间信息融入度,提高整体效果。
| [1] |
李春华, 徐涵秋.
高分辨率遥感图像融合的光谱保真问题[J]. 地球信息科学, 2008, 10(4): 520–526.
LI Chunhua, XU Hanqiu. Spectral Fidelity in High-resolution Remote Sensing Image Fusion[J]. Geo-Information Science, 2008, 10(4): 520–526. |
| [2] | LIU J G. Smoothing Filter-based Intensity Modulation: A Spectral Preserve Image Fusion Technique for Improving Spatial Details[J]. International Journal of Remote Sensing, 2000, 21(18): 3461–3472. DOI:10.1080/014311600750037499 |
| [3] |
何贵青, 齐敏, 赵海涛, 等.
一种基于SFIM和IHS变换的图像融合算法[J]. 西北工业大学学报, 2008, 26(1): 41–46.
HE Guiqing, QI Min, ZHAO Haitao, et al. A New and Better Image Fusion Algorithm based on SFIM Model and IHS Transform[J]. Journal of Northwestern Polytechnical University, 2008, 26(1): 41–46. |
| [4] | ZHANG Yun. Problems in the Fusion of Commercial High-Resolution Satellites Images as well as LANDSAT 7 Images and Initial Solutions[C]//Proceedings of the International Archives of Photogrammetry and Remote Sensing. Ottawa, 2002: 9-12. |
| [5] | ZHANG Yuri. A New Automatic Approach for Effectively Fusing Landsat 7 as well as IKONOS Images[C]//Proceedings of the IEEE International Geoscience and Remote Sensing Symposium. Toronto, Ontario, Canada: IEEE, 2002: 2429-2431. |
| [6] | VRABEL J. Multispectral Imagery Advanced Band Sharpening Study[J]. Photogrammetric Engineering and Remote Sensing, 2000, 66(1): 73–80. |
| [7] | HAYDN R, DALKE G W, HENKEL J, et al. Application of the IHS Color Transform to the Processing of Multisensor Data and Image Enhancement[C]//Proceedings of the International Symposium on Remote Sensing of Environment, First Thematic Conference: Remote Sensing of Arid and Semi-Arid Lands. Ann Arbor MI: Environmental Research Institute of Michigan, 1982. |
| [8] |
楚恒, 王汝言, 朱维乐.
DCT域遥感影像融合算法[J]. 测绘学报, 2008, 37(1): 70–76.
CHU Heng, WANG Ruyan, ZHU Weile. Remote Sensing Image Fusion Algorithm in the DCT Domain[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 70–76. DOI:10.3321/j.issn:1001-1595.2008.01.013 |
| [9] | AIAZZI B, BARONTI S, SELVA M, et al. Enhanced Gram-Schmidt Spectral Sharpening Based on Multivariate Regression of MS and Pan Data[C]//IEEE International Symposium on Geoscience and Remote Sensing. Denver, CO, USA: IEEE, 2006: 3806-3809. |
| [10] |
张涛, 刘军, 杨可明, 等.
结合Gram-Schmidt变换的高光谱影像谐波分析融合算法[J]. 测绘学报, 2015, 44(9): 1042–1047.
ZHANG Tao, LIU Jun, YANG Keming, et al. Fusion Algorithm for Hyperspectral Remote Sensing Image Combined with Harmonic Analysis and Gram-Schmidt Transform[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(9): 1042–1047. DOI:10.11947/j.AGCS.2015.20140637 |
| [11] | SHETTIGARA V K. A Generalized Component Substitution Technique for Spatial Enhancement of Multispectral Images Using A Higher Resolution Data Set[J]. Photogrammetric Engineering and Remote Sensing, 1992, 58(5): 561–567. |
| [12] | SCHOWENGERDT R A. Reconstruction of Multispatial, Multispectral Image Data Using Spatial Frequency Content[J]. Photogrammetric Engineering and Remote Sensing, 1980, 46(10): 1325–1334. |
| [13] | MALLAT S G. A Theory for Multiresolution Signal Decomposition: The Wavelet Representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(7): 674–693. DOI:10.1109/34.192463 |
| [14] | ZHANG Yun, HONG Gang. An IHS and Wavelet Integrated Approach to Improve Pan-Sharpening Visual Quality of Natural Colour IKONOS and QuickBird Images[J]. Information Fusion, 2005, 6(3): 225–234. DOI:10.1016/j.inffus.2004.06.009 |
| [15] | POHL C, VAN GENDEREN J L. Review Article Multisensor Image Fusion in Remote Sensing: Concepts, Methods and Applications[J]. International Journal of Remote Sensing, 1998, 19(5): 823–854. DOI:10.1080/014311698215748 |
| [16] |
杨景辉. 遥感影像像素级融合通用模型及其并行计算方法[D]. 武汉: 武汉大学, 2014. YANG Jinghui. The Generalized Model and Parallel Computing Methods for Pixel-Level Remote Sensing Image Fusion[J]. Wuhan: Wuhan University, 2014. |
| [17] |
韩冰, 赵银娣.
一种改进的SFIM高光谱图像融合算法[J]. 遥感信息, 2012, 27(5): 44–47, 54.
HAN Bing, ZHAO Yindi. An Improved Smoothing Filter-based Intensity Modulation Algorithm for Hyperspectral Image Fusion[J]. Remote Sensing Information, 2012, 27(5): 44–47, 54. |
| [18] | ELACHI C, ZIMMERMAN P D. Introduction to the Physics and Techniques of Remote Sensing[J]. Physics Today, 1988, 41(11): 126–126. |
| [19] | GUO Liujian, MOORE J M, HAIGH J D. Simulated Reflectance Technique for ATM Image Enhancement[J]. International Journal of Remote Sensing, 1997, 18(2): 243–254. DOI:10.1080/014311697219042 |
| [20] |
李艳雯, 杨英宝, 程三胜.
基于亮度平滑滤波调节(SFIM)的SPOT5影像融合[J]. 遥感信息, 2007(1): 63–66.
LI Yanwen, YANG Yingbao, CHENG Sansheng. The SPOT-5 Image Fusion by Smoothing Filter-based Intensity Modulation (SFIM)[J]. Remote Sensing Information, 2007(1): 63–66. |
| [21] |
陈超, 江涛, 徐文学.
基于平均梯度的多聚焦图像融合方法研究[J]. 山东建筑大学学报, 2009, 24(2): 133–137.
CHEN Chao, JIANG Tao, XU Wenxue. Research on Multi-Focus Image Fusion Methods based on Mean Gradient[J]. Journal of Shandong Jianzhu University, 2009, 24(2): 133–137. |
| [22] |
赵鲁燕, 尹君.
图像融合效果评价方法研究[J]. 遥感信息, 2005(4): 16–17.
ZHAO Luyan, YIN Jun. Study on the Effect Evaluation of Image Fusion[J]. Remote Sensing Information, 2005(4): 16–17. |
| [23] |
苏媛媛, 李英杰, 周志峰.
遥感图像融合算法与质量评价探讨[J]. 工程勘察, 2012, 40(12): 70–74.
SU Yuanyuan, LI Yingjie, ZHOU Zhifeng. Remote Sensing Image Fusion Methods and Their Quality Evaluation[J]. Geotechnical Investigation & Surveying, 2012, 40(12): 70–74. |
| [24] | SHANNON C E. A Mathematical Theory of Communication[J]. ACM SIGMOBILE Mobile Computing and Communications Review, 2001, 5(1): 3–55. DOI:10.1145/584091 |
| [25] |
贠培东, 曾永年, 历华.
不同遥感影像融合方法效果的定量评价研究[J]. 遥感信息, 2007(4): 40–45.
YUN Peidong, ZENG Yongnian, LI Hua. Quantitative Assessment of Image Fusion Methods[J]. Remote Sensing Information, 2007(4): 40–45. |



