多模态遥感影像能够弥补单一影像源的不足,提高影像的信息量。有效利用多模态遥感影像的关键是影像配准技术。影像配准技术是多模态遥感影像融合、目标识别、变化检测等应用必需的前期工作,是各类问题提高精度和有效性的瓶颈[1]。由于不同传感器的成像机理不同,获取影像的时间、角度、环境也不同,多模态影像的配准研究领域中还存在着很多的困难,特别是图像或数据类别差异大(如光学与SAR影像)、波段差异大(如可见光与中波红外影像)等情况下的影像高精度、自动配准技术的实现,更是存在较大的困难。
对于多模态遥感影像,灰度特性会发生非线性甚至非函数的变化,影像之间的灰度关系存在统计相关性及几何结构的相似性。传统的遥感影像配准工作量大、自动化程度低。一般的基于灰度的配准方法(如相关函数[2])无法成功实现配准。特征描述符在多模态遥感影像中不具有相同的稳健性[3],基于特征的配准方法(如轮廓特征[4-5]、SUSAN算子[6]、SIFT[7]特征、基于相位一致性的特征[8-9]、扩展SURF描述符[10])也面临着特征重复性探测和模态不变特征描述两方面的挑战。而基于统计依赖性的区域配准方法适用于多模态影像配准。最常用的互信息[11-13]主要利用影像之间灰度特性的统计相关性,最早用于医学影像配准,后引入到多模态图像配准中。归一化互信息[14]改进了互信息对于影像重叠率变化敏感的缺点。高维互信息[15]、区域互信息[16]、特征互信息[17]存在数据维度高,计算复杂等缺陷。交叉累积剩余熵(CCRE)[18]将累积剩余熵引入互信息,具有较强的抗噪性和稳定性。除此之外,基于互信息的配准方法还引入了小波变换[19],实现红外与光学遥感影像逐级由粗到精的配准。但这些方法的配准精度无法达到像素级,且均未顾及影像的梯度信息。多模态影像的地物边缘属于几何特征,具有一定的相似性和不变性,梯度信息能很好地表示影像的边缘特征,从而使影像配准结果更加准确。
因此,本文研究了一种顾及灰度和梯度信息的多模态影像自动配准算法,且满足空间精度的要求。充分利用多模态影像的图像信息进行相似性测量,并采用基于马尔科夫随机场(MRF)的非参数化配准模型,配准变换满足微分同胚保持影像的拓扑结构[20]。模型上同时考虑了灰度及梯度统计信息,求解方法上对值空间进行离散化,提高收敛速度。试验表明该算法能较好地完成多模态遥感影像的自动配准。
1 顾及灰度和梯度信息的多模态影像配准本文研究的顾及灰度和梯度信息的多模态影像配准算法是马尔科夫随机场(MRF)和B样条插值策略的综合。算法的整体框架是马尔科夫随机场(MRF)模型,通过最小化能量函数来估计最佳变换。首先,将影像进行网格划分形成均匀控制点网格,考虑影像的灰度和梯度信息进行代价计算,根据马尔科夫随机模型通过最优化解算(Fast PD算法[21-22])得到控制网格节点的位移量,再利用B样条插值策略计算每个像素点的位移控制图像变形实施配准。
在图像配准的具体情况下,MRF模型定义如下[23]:节点p∈V(具有空间位置xp)对应于均匀B样条网格中的控制点,对于每个节点,存在一组离散标签;离散标签的集合L对应于解空间的量化,表示允许的离散位移量,L≡d。标签集L={l1, …l4n+1}的基数为4n+1,由沿x、y轴和对角线均匀采样n个标签加上原点构建;随机变量对应于控制点的位移量;优化的能量函数由两个项组成:数据代价项Dp(lp),采用块匹配对源影像及其梯度影像进行相似性测度;正则代价项Ppq(lp, lq),引入变形场平滑约束的先验知识,λ是一个标量值,用于权衡正则项的影响。图像配准的目标是为每个控制网格节点分配一个最佳标签l,使得以下能量函数最小化
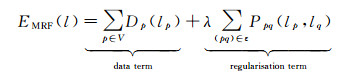 (1)
(1)
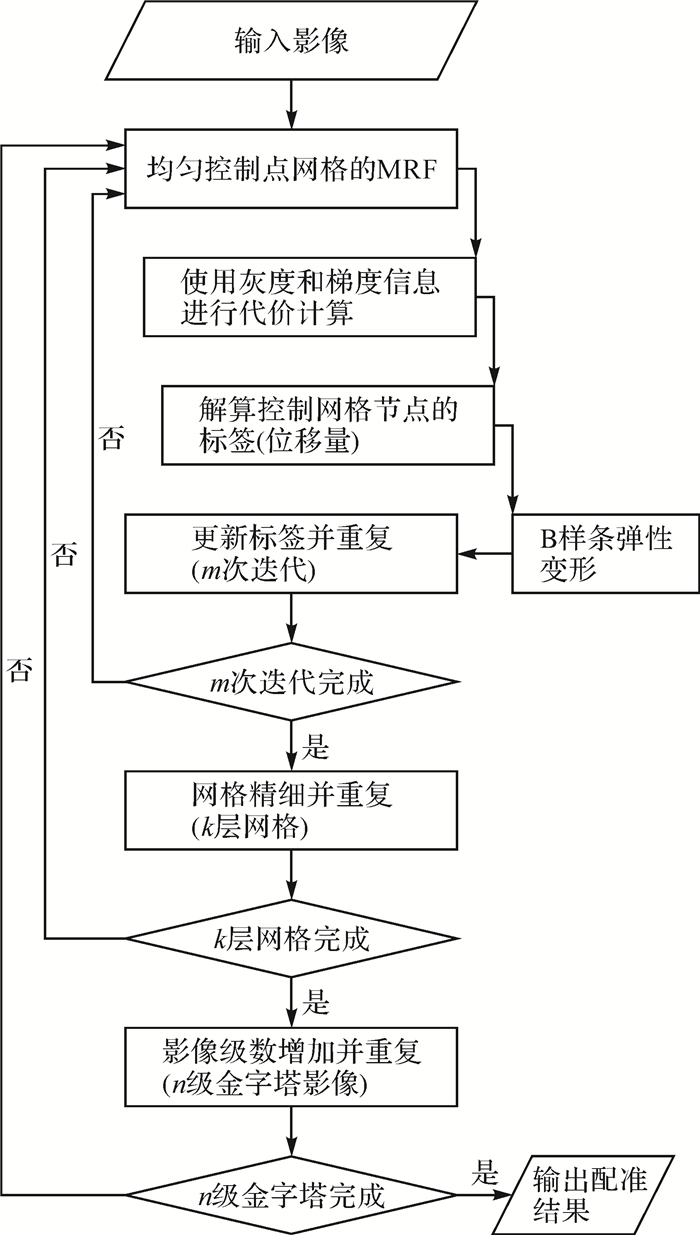
与此同时,本文算法结合影像高斯金字塔与变形网格模型的多尺度,高斯金字塔能够降低计算成本,变形网格模型的多尺度通过将控制点的间距减半来增加变形网格的分辨率,因此,可以恢复较大的位移,逐步改善配准结果。对于各层影像金字塔下的各级网格,使用迭代方案来提高离散标签的效率。保持标签空间的基数合理,并在每次迭代时优化标签,并利用上一次迭代的结果来改进配准影像以捕获较小的位移。配准流程概述如图 1所示。
|
| 图 1 多模态影像配准流程概述 Fig. 1 Overview of presented approach for multimodel image registration |
1.1 均匀控制点网格划分与代价计算
本文研究的配准模型是基于MRF的非参数化配准模型。将影像进行网格划分形成均匀控制点网格G:[1,K]×[1,L](K和L显著小于图像尺寸;控制点之间的距离为δ),利用多模态影像的灰度及梯度信息根据MRF模型进行均匀控制网格节点的代价计算。其中能量函数由两部分组成。第1项为数据代价项,用于评估将所有允许的位移应用于每个随机变量的最大似然。对于数据代价项,采用块匹配[24]进行相似性测度,即以每个控制网格节点为中心的分块及其梯度影像来进行相似性度量
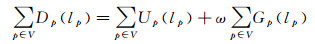 (2)
(2)
 (3)
(3)
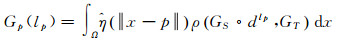 (4)
(4)
式中,
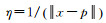
本文采用形态学梯度提取多模态影像的梯度信息。将形态学的腐蚀、膨胀、开运算以及闭运算等基本运算用于图像处理,可构成形态学梯度算子。常见的形态学梯度算子如下
 (5)
(5)
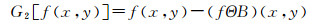 (6)
(6)
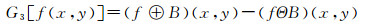 (7)
(7)
形态学梯度是膨胀图与腐蚀图之差,可以检测图像边缘,提取特征信息,在配准时明显减少相似性测度的计算,同时改善局部极值问题。
相似性测度ρ可以选用对光照变化不敏感的互信息[25]。两张影像的互信息是通过它们的熵以及联合熵来反映它们之间信息的相互包含程度。hI1、hI2、hI1, I2可以用于块匹配策略的相似性测度计算
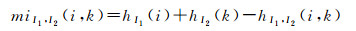 (8)
(8)
式中,hI1, I2可由相应灰度的联合概率分布PI1, I2计算。相应像素的数量为n。与2D高斯(由
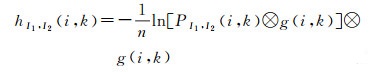 (9)
(9)
相应的,计算hI1, hI2可类似于hI1, I2
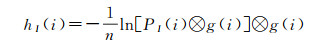 (10)
(10)
对于正则代价项,引入变形场平滑约束的先验知识,即假设控制点的位移场是平滑的,紧密相关的变量p和q应该分配给类似的标签。采用标签之间的向量差异的简单策略,并通过网格距离δ进行归一化
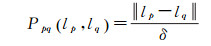 (11)
(11)
模型上同时考虑了灰度以及梯度统计信息,同时采用适用于多模态遥感数据集的块匹配策略,可以局部评估配准图像之间的差异,提高计算效率。求解方法上,对值空间进行离散化,提高收敛速度。代价计算是利用多模态影像的灰度及梯度信息计算基于互信息(MI)的控制网格节点的匹配成本,其流程图如图 2所示。其中,代价计算的中间数值可线性缩放实现可视化,越深的点表示越大的值。

|
| 图 2 代价计算流程图 Fig. 2 Overview of cost calculation visualization |
1.2 B样条的弹性变形模型
通过优化MRF模型可以解算控制网格节点的标签即位移量。采用基于网格的B样条的弹性变形模型,可以提供一对一和可逆转换。变形模型的基本思想是通过叠加均匀变形网格G:[1,K]×[1,L],可以通过控制网格的节点的位移量并使用插值策略来计算图像域的其余像素点的位移量来使底层图像变形
 (12)
(12)
式中,T(x)为目标影像;d表示一个控制点的位移;η对应于控制网格节点ij对图像点x的影响的内插或加权函数。图像点越近,控制点的影响越大。控制点在图像上均匀分布行为网格,网格间距为δ。
插值策略采用均匀三次B样条函数。令F2为(m+3)×(n+3)控制格网定义的2D均匀三次B样条函数。函数F2由m×n个2D面片组成,每个面片由R2中的4×4控制点决定。通过面片f2来表示二维均匀三次B样条函数[27]
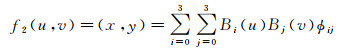 (13)
(13)
式中,0≤u, v≤1;B0、B1、B2和B3为均匀立方B样条基函数;ϕij为控制点的位移量。
2 试验与分析 2.1 试验数据本文共设置3组多模态影像配准试验,具体试验数据如表 1所示。配准前,将影像叠加在一起,以棋盘格的方式交替分块显示。图 3显示了3组多模态影像叠加时的棋盘格,观察棋盘格的每个分块边缘,将未重合的区域用红色圆圈突出表示,并从中选择3个未重合区域作局部放大显示。
| 试验数据 | 影像类型 | 影像大小/像素 | 影像介绍 | 最大视差/像素 | 平均视差/像素 |
| 1 | 中波红外影像 | 3072×4096 | 湖北省荆门市漳河测区航拍影像。测区飞行范围约为11 km2 | 39 | 22 |
| 可见光正射影像 | 3072×4096 | ||||
| 2 | Terra SAR影像 | 2048×2048 | 江苏省常州市测区卫星影像 | 54 | 23 |
| 光学影像 | 2048×2048 | ||||
| 3 | worldview-3近红外波段 | 1536×2048 | 湖北省武汉市东西湖测区卫星影像 | 29 | 10 |
| worldview-3多光谱波段 | 1536×2048 |

|
| 图 3 配准前多模态影像的棋盘格叠加显示及其局部图 Fig. 3 Chessboard overlay and local graphs of multimodel images before registration |
2.2 多模态影像配准
为了验证本文算法的性能优劣,以3组多模态影像为研究对象,共进行3组对比试验:①人工选取10对同名点利用多项式模型进行配准;②只考虑灰度信息的基于MRF的非参数化配准[23];③顾及灰度和梯度信息的基于MRF的非参数化配准。
本文使用了以下试验配置:三级高斯金字塔,三级变形网格,初始控制点网格间距δ为128像素,其他两个层级的距离分别设置为64和32像素。对于各层金字塔下各级网络,使用5次迭代方案,采用归一化互信息作为相似性测度,形态学梯度保留物体的边缘轮廓。标签集的基数为41(沿x、y轴和对角线均匀采样10个标签加上原点构建标签集)。在第1次迭代中,采样的最大位移等于0.4×δ,满足微分同胚要求从而保证影像的拓扑结构不发生改变[20]。在以下迭代中,最大采样位移对应于前一次迭代的最大位移的0.67。ω的初始值为1。λ为经验选择,取值在10左右是稳健的。面片尺寸等于2δ×2δ。本文研究算法对于中波红外影像与可见光正射影像配准计算耗时控制在30 min之内;对于Terra SAR影像与光学影像配准计算耗时在12 min左右;对于Worldview-3近红外与多光谱影像配准计算耗时在9 min左右。与只考虑灰度信息的基于MRF的非参数化配准方法相比,计算耗时相差不多于1~2 min。
2.2.1 配准结果定性评价本文通过棋盘格叠加显示及兴趣区域的局部图定性评价3种方法的配准效果。将配准后的多模态遥感影像叠加在一起,以棋盘格的方式交替分块显示。图 4、图 5、图 6分别显示了中波红外影像与可见光正射影像、Terra SAR影像与光学影像、Worldview-3近红外与多光谱影像配准叠加时的棋盘格。与此同时,在棋盘格叠加显示结果上选取3个相同的兴趣区域(黄色矩形圈中显示)作局部放大显示,便于比较分析。其中,(A)代表基于人工刺点的多项式模型配准结果;(B)代表只考虑灰度信息的基于MRF的非参数化配准结果;(C)代表顾及灰度和梯度信息的基于MRF的非参数化配准结果;(D)代表 3种方法的局部区域对比图,每一行表示相同区域不同方法的配准结果,每一列表示同一方法不同区域的配准结果。观察多模态影像叠加显示的棋盘格的分块边缘,可以发现:

|
| 图 4 中波红外影像与可见光正射影像配准后棋盘格叠加显示及其局部图 Fig. 4 Chessboard overlay and local graph of mid-infrared image and visible orthophoto after registration |

|
| 图 5 Terra SAR影像与光学影像配准后棋盘格叠加显示及其局部图 Fig. 5 Chessboard overlay and local graph of Terra SAR image and optical image after registration |

|
| 图 6 Worldview-3近红外与多光谱影像配准后棋盘格叠加显示及其局部图 Fig. 6 Chessboard overlay and local graph of worldview-3 near infrared and multi-spectral images after registration |
(1) 对于中波红外影像与可见光正射影像配准、Worldview-3近红外与多光谱影像配准,基于人工刺点的多项式模型效果最差,而顾及灰度和梯度信息的基于MRF的非参数化配准效果与只考虑灰度信息的基于MRF的非参数化配准效果较好,且配准结果大致相当。
(2) 对于Terra SAR影像与光学影像配准,基于人工刺点的多项式模型与只考虑灰度信息的基于MRF的非参数化配准方法均不能实现成功配准,而顾及灰度和梯度信息的基于MRF的非参数化配准结果的棋盘格分块边缘均整齐地重合,配准效果远优于其他两种方法。
综上所述,本文算法的棋盘可视化结果最优。
2.2.2 配准结果定量评价为准确地评价3种方法的配准效果,本文通过15组同名点对的像素坐标的差异定量评价3种方法的配准效果(表 2)。可以发现:
| 试验影像 | 中波红外影像与可见光正射影像 | Terra SAR影像与可见光正射影像 | worldview-3近红外波段与多光谱波段 | |||||||
| 试验方法 | 人工刺点+多项式模型 | 灰度信息+MRF | 灰度和梯度信息+MRF | 人工刺点+多项式模型 | 灰度信息+MRF | 灰度和梯度信息+MRF | 人工刺点+多项式模型 | 灰度信息+MRF | 灰度和梯度信息+MRF | |
| 平均配准 误差/像素 |
X | -3.808 | 1.444 | 0.977 | 5.771 | 8.877 | 0.721 | 3.107 | -0.911 | 0.108 |
| Y | -4.954 | 1.359 | 0.874 | -8.961 | 10.231 | 0.763 | 4.251 | -1.817 | 0.130 | |
| 最大误差 /像素 |
X | -4.535 | 4.027 | -1.933 | 6.520 | 13.564 | -1.396 | 4.268 | -2.08 | 0.364 |
| Y | -8.753 | 2.748 | -1.903 | -9.414 | 11.344 | -1.72 | 6.632 | -2.364 | 0.232 | |
(1) 从同名点对的匹配精度来看,基于人工刺点的多项式模型配准方法的精度最差,而顾及灰度及梯度信息的基于MRF的非参数化配准模型的精度最优,3组多模态影像的x、y方向的平均配准误差均小于1个像素,最大误差小于2个像素。
(2) 本文算法对于3组多模态影像的配准精度均有明显改进,尤其是Terra SAR影像与光学影像的配准。在其余两种方法均不能实现成功配准的情况下,本文研究的算法针对Terra SAR影像与光学影像可达到像素级的配准精度。
综上所述,对于多组多模态影像的配准,本文研究的算法最优且满足像素级配准精度要求。
2.3 大形变影像的配准试验上述试验中,多模态影像的初始最大视差约为50个像素,为了进一步验证本文研究的算法的适应性,即测试本文算法针对较大视差的多模态影像是否有效,将配准前的中波红外影像进行人工平移,对较大初始视差的中波红外数据进行了试验。
根据位移离散空间的最大标签值和金字塔影像级数,本文设置如图 7所示的3组试验:对中波红外影像进行x方向、y方向、对角线方向各200个像素的平移,将平移后的中波红外影像与可见光正射影像进行配准。试验配置与上述试验相同,采用归一化互信息作为相似性测度。配准前的平移后的中波红外影像及配准后的棋盘格叠加显示如图 7所示,配准精度见表 3。

|
| 图 7 平移后的中波红外影像及配准结果 Fig. 7 Mid-infrared image after translation and the registration chessboard overlay |
| 像素 | ||||
| 平移方向 | x | y | 对角线 | |
| 平均配准误差 | X | 0.897 | 0.997 | 0.533 |
| Y | 0.799 | 0.968 | 0.893 | |
| 最大误差 | X | -1.934 | -1.857 | 1.962 |
| Y | 1.670 | 1.867 | 1.998 | |
由配准结果可知,棋盘格分块的边缘均整齐地重合。从同名检查点的匹配精度来看,x、y方向的平均配准精度均小于1像素,最大误差小于2个像素。相比与较小形变的多模态影像配准,同名点对的匹配精度基本相当。因此针对较大形变的多模态影像,本文研究的算法也具有较好的配准效果,配准精度满足需求。由此说明本文研究的算法针对较大形变的多模态影像配准也具有一定的适用性,利用高精度的POS定向数据与快速拼接能够满足大部分多模态影像的配准要求。
3 结论本文研究的基于MRF的非参数化配准模型同时考虑了灰度以及梯度统计信息,能够实现多种多模态图像的自动配准,具有较好的稳定性和配准精度。文中进行了多组多模态影像配准试验,试验结果证明:本文算法的平均配准误差小于1个像素,最大配准误差小于2个像素。该算法利用互信息进行相似性测度时需要计算多模态影像的联合概率分布,因此待配准影像的初始视差范围是有限的,对于具有显著旋转、尺度变化和视差的多模态数据的配准,有待进一步研究。
| [1] |
倪国强, 刘琼.
多源图像配准技术分析与展望[J]. 光电工程, 2004, 31(9): 1–6.
NI Guoqiang, LIU Qiong. Analysis and Prospect of Multi-Source Image Registration Techniques[J]. Opto-Electronic Engineering, 2004, 31(9): 1–6. |
| [2] | BROWN L G. A Survey of Image Registration Techniques[J]. ACM Computing Surveys, 1992, 24(4): 325–376. DOI:10.1145/146370.146374 |
| [3] | FANBin, HUO Chunlei, PAN Chunhong, et al. Registration of Optical and SAR Satellite Images by Exploring the Spatial Relationship of the Improved SIFT[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(4): 657–661. DOI:10.1109/LGRS.2012.2216500 |
| [4] | LI Hui, MANJUNATH B S, MITRA S K. A Contour-Based Approach to Multisensor Image Registration[J]. IEEE Transactions on Image Processing, 1995, 4(3): 320–334. DOI:10.1109/83.366480 |
| [5] | LI HH, ZHOU Yitong. Automatic Visual/IR Image Registration[J]. Optical Engineering, 1996, 35(2): 391–400. DOI:10.1117/1.600908 |
| [6] |
张迁, 刘政凯, 庞彦伟, 等.
基于SUSAN算法的航空影像的自动配准[J]. 测绘学报, 2003, 32(3): 245–250.
ZHANG Qian, LIU Zhengkai, PANG Yanwei, et al. Automatic Registration of Aerophotos Based on SUSAN Operator[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(3): 245–250. |
| [7] | KELMANA, SOFKA M, STEWART C V. Keypoint Descriptors for Matching Across Multiple Image Modalities and Non-Linear Intensity Variations[C]//Proceedings of 2007 IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis, MN, USA: IEEE, 2007. |
| [8] | KOVESI P. Image Featuresfrom Phase Congruency[J]. Videre: Journal of Computer Vision Research, 1999, 1(3): 1–26. |
| [9] | WONG A, CLAUSI D A. AISIR: Automated Inter-Sensor/Inter-Band Satellite Image Registration Using Robust Complex Wavelet Feature Representations[J]. Pattern Recognition Letters, 2010, 31(10): 1160–1167. DOI:10.1016/j.patrec.2009.05.016 |
| [10] |
罗楠, 孙权森, 耿蕾蕾, 等.
一种扩展SURF描述符及其在遥感图像配准中的应用[J]. 测绘学报, 2013, 42(3): 383–388.
LUO Nan, SUN Quansen, GENG Leilei, et al. An Extended SURF Descriptor and Its Application in Remote Sensing Images Registration[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 383–388. |
| [11] | VIOLA P, WELLS Ⅲ W M. Alignment by Maximization of Mutual Information[J]. International Journal of Computer Vision, 1997, 24(2): 137–154. DOI:10.1023/A:1007958904918 |
| [12] | COLLIGNONA, MAES F, DELAERE D, et al. Automated Multi-Modality Image Registration based on Information Theory[C]//Proceedings of the International Conference on Information Processing in Medical Imaging. Ile de Berder, France: Kluwer Academic Publishers, 1995. |
| [13] | MAES F, COLLIGNON A, VANDERMEULEN D, et al. Multimodality Image Registration by Maximization of Mutual Information[J]. IEEE Transactions on Medical Imaging, 1997, 16(2): 187–198. DOI:10.1109/42.563664 |
| [14] | STUDHOLME C, HILL D L G, HAWKES D J. An Overlap Invariant Entropy Measure of 3D Medical Image Alignment[J]. Pattern Recognition, 1999, 32(1): 71–86. DOI:10.1016/S0031-3203(98)00091-0 |
| [15] | RUECKERT D, CLARKSONM J, HILL D L G, et al. Non-Rigid Registration Using Higher-Order Mutual Information[C]//Proceedings of SPIE-Medical Imaging 2000: Image Processing. San Diego, CA, United States: SPIE, 2000: 438-447. |
| [16] | RUSSAKOFF D B, TOMASI C, ROHLFING T, et al. Image Similarity Using Mutual Information of Regions[C]//Proceedings of the 8th European Conference on Computer Vision. Prague, Czech Republic: Springer, 2004: 596-607. |
| [17] | TOMAŽEVIČ D, LIKAR B, PERNUŠ F. Multi-Feature Mutual Information Image Registration[J]. Image Analysis and Stereology, 2012, 31(1): 43–53. DOI:10.5566/ias.v31.p43-53 |
| [18] | WANG Fei, VEMURI B C. Non-Rigid Multi-Modal Image Registration Using Cross-CumulativeResidual Entropy[J]. International Journal of Computer Vision, 2007, 74(2): 201–215. DOI:10.1007/s11263-006-0011-2 |
| [19] | FAN Xiaofeng. Automatic Registration of Multi-Modal Airborne Imagery[D]. Rochester: Rochester Institute of Technology, 2011. |
| [20] |
闫德勤, 刘彩凤, 刘胜蓝, 等.
大形变微分同胚图像配准快速算法[J]. 自动化学报, 2015, 41(8): 1461–1470.
YAN Deqin, LIU Caifeng, LIU Shenglan, et al. A Fast Image Registration Algorithm for DiffeomorphicImage with Large Deformation[J]. ActaAutomaticaSinica, 2015, 41(8): 1461–1470. |
| [21] | STREKALOVSKIY E, CREMERS D. Real-Time Minimization of the Piecewise Smooth Mumford-Shah Functional[C]//Proceedings of the 13th European Conference on Computer Vision. Zurich, Switzerland: Springer, 2014: 127-141. |
| [22] | KOMODAKIS N, TZIRITAS G, PARAGIOS N. Performance vs Computational Efficiency for Optimizing Single and Dynamic MRFs: Setting the State of the Art with Primal-Dual Strategies[J]. Computer Vision and Image Understanding, 2008, 112(1): 14–29. DOI:10.1016/j.cviu.2008.06.007 |
| [23] | KARANTZALOSK, SOTIRAS A, PARAGIOS N. Efficient and Automated Multimodal Satellite Data Registration through MRFs and Linear Programming[C]//Proceedings of 2014 IEEE Conference on Computer Vision and Pattern Recognition Workshops. Columbus, OH, USA: IEEE, 2014. |
| [24] |
张剑清, 潘励, 王树根.
摄影测量学[M]. 2版.武汉: 武汉大学出版社, 2009.
ZHANG Jianqing, PAN Li, WANG Shugen. Photogrammetry[M]. 2nd ed. Wuhan: Wuhan University Press, 2009. |
| [25] | HIRSCHMULLERH. Stereo Processing by Semiglobal Matching and Mutual Information[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(2): 328–341. DOI:10.1109/TPAMI.2007.1166 |
| [26] | KIM J, KOLMOGOROV V, ZABIH R. Visual Correspondence Using Energy Minimization and Mutual Information[C]//Proceedings of the 9th IEEE International Conference on Computer Vision. Nice, France: IEEE, 2003. |
| [27] | CHOIY, LEE S. Injectivity Conditions of 2D and 3D Uniform Cubic B-Spline Functions[J]. Graphical Models, 2000, 62(6): 411–427. DOI:10.1006/gmod.2000.0531 |


