ITRF(international terrestrial reference frame)的解算是综合应用全球导航卫星系统GNSS、甚长基线干涉测量VLBI(very long baseline interferometry)、卫星激光测距SLR(satellite laser ranging)和多普勒定轨与无线电定位技术DORIS(doppler orbit determination and radio positioning integrated on satellite)4种空间大地测量技术的观测数据和并址站归心基线[1-4]。并址站归心基线作为联系ITRF中各观测技术的主要约束条件,已成为限制ITRF解算精度的关键因素之一。即使各观测技术的数据质量有了很大的提高,如果归心基线的精度没有相应地提高,ITRF解的精度也会受到一定程度的影响[5-6]。
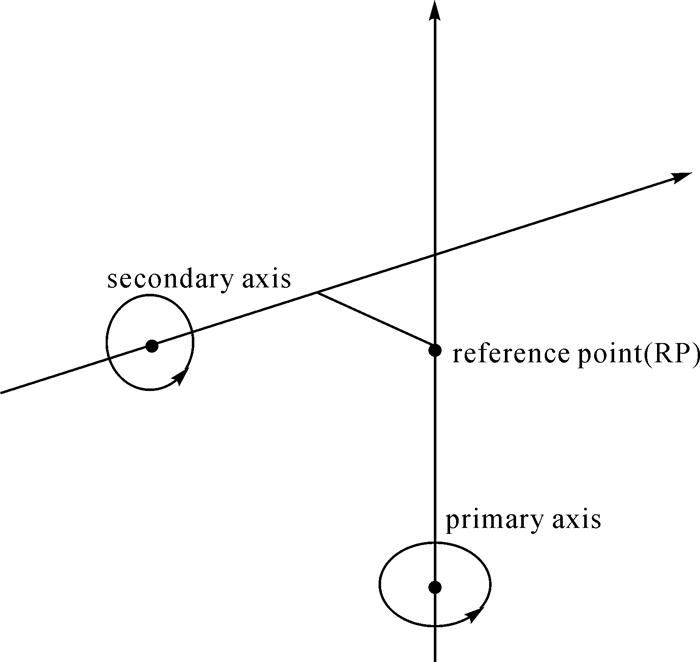
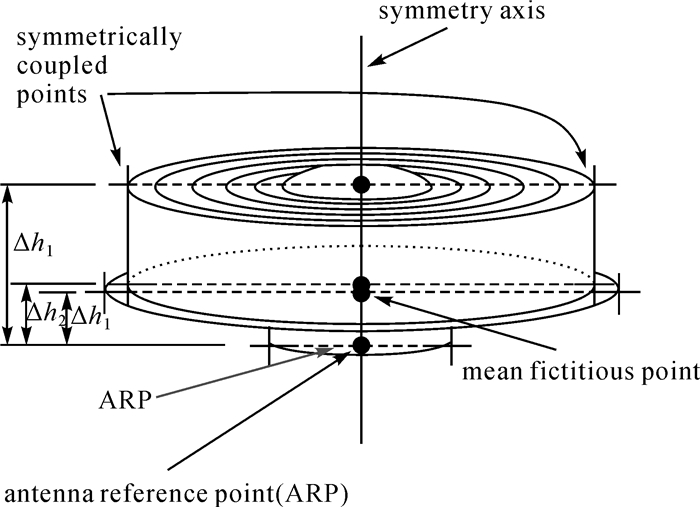
并址站归心测量的实质就是获取ITRF中各观测设备参考点RP(reference point)的坐标及其协方差阵[7-9]。SLR望远镜的RP为绕垂直轴p的旋转中心与水平轴s和垂直轴p之间的最短距离的交点,如图 1所示。GNSS的RP为其接收机天线的几何中心(如图 2所示),可以直接测定。而SLR望远镜的RP为其望远镜的旋转中心,并非一个可以直接观测到的实体点,因此必须设法以间接的方式得到。
对于SLR望远镜参考点的测定,通常是先在SLR望远镜周围布设控制点,采用常规三维控制测量精确测定各控制点坐标,通过极坐标法或前方交会测定固定在SLR望远镜上标志点的坐标[10-13],也有在并址站设备上安装GNSS天线,通过静态或动态技术获取标志点的坐标[14-15],以标志点坐标为虚拟观测量解算SLR望远镜参考点的坐标及其方差阵,目前解算方法主要有两种:分步解算方式和构建坐标转换模型的方式。分步解法主要有:①将标志点的三维空间直角坐标转换为站心坐标,通过曲线拟合求出绕垂直轴和绕水平轴旋转中心的站心坐标,再将旋转中心的站心坐标逆变换得到三维空间直角坐标[10-12, 16-18];②以标志点三维空间直角坐标作为虚拟观测量,建立两类约束条件获取参考的位置,具体可参考文献[13];③为了提高解算精度,可引入额外的约束条件,如距离相等条件、旋转平面一致性条件、共线性条件、半径相等条件、旋转中心距离相等条件、旋转轴正交性条件、轴偏差相等[7, 19-20];④利用参考点与绕垂直轴和水平轴旋转中心之间的空间向量关系,获取参考点的位置,间接得到两轴之间的偏差[21]。
除分步解法外,目前最新的解算方法是通过构建包括参考点、轴偏差等未知参数的并址站设备的独立坐标系统与地面坐标系统之间的转换模型间接得到并址站参考点位置[15, 20, 22, 24],但这种方法同样是在独立坐标系中进行分步解算,而且解算时需要知道一些参数的值(绕垂直轴和水平轴的旋转角)等。
总结以上文献,仍存在着以下方面的特点与不足:①将观测量和确定参考点和两轴偏差分开计算,存在站心系和空间直角坐标系多次换算的问题,造成最终结果的不准确和最终精度的损失;②忽略或是未考虑观测标志与参考点或几何设备所应满足的几何约束条件,如忽略两轴偏差的影响,将会造成结果0.5 mm的精度损失[19];③虽然可以建立坐标转换模型获取参考点的位置,但同样需要进行分步解算,而且事先需要提供一些参数的值。
不同的文献有着不同的解算方法,不同的方法所得出结果各有不同,因此本文力图在一个坐标框架(ITRF)中,将SLR望远镜的参考点、两轴偏差等参数视为未知参数,联合GNSS基线和地面网观测数据,引入满足条件的各种几何约束条件方程,提出并址站归心基线的“一步解”。“一步解”经平差后可直接得到并址站归心基线及其方差协方差阵。
1 “一步解”的数学模型 1.1 地面观测量和GNSS基线网的观测方程 1.1.1 地面观测量的观测方程地面观测量一般是指经全站仪通过极坐标法、前方交会等方法测量的水平方向、垂直角和边长。通过建立站心坐标可以实现与空间直角坐标之间的转换,可以将地面观测量归算至空间直角坐标系中。
根据法线站心坐标和空间直角之间的转换关系,测点j在以测站i为原点的站心坐标系中的坐标向量xj和空间直角坐标向量xi和xj关系为
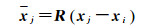 (1)
(1)
式中,xj=(Nj, Ej, Uj),Nj、Ej、Uj为站心坐标分量;同样,xi=(Xi, Yi, Zi), xj=(Xj, Yj, Zj),Xi, Yi, Zi和Xj, Yj, Zj为测站i和测点j的空间直角坐标分量,本文后面的坐标分量统一以坐标向量的形式表示。其中,R为旋转矩阵
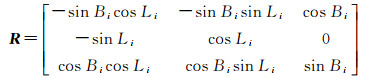 (2)
(2)
式中,(Bi, Li)为测站i的纬度和经度。
由极坐标和站心坐标之间的关系可以得到测站i至测点j的水平方向αij、垂直角βij和边长Sij在站心系中的观测方程为
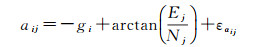 (3)
(3)
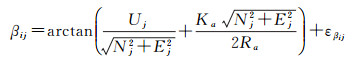 (4)
(4)
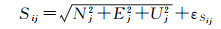 (5)
(5)
式中,(εαij, εβij, εSij)为αij、βij和Sij的观测误差;gi为测站i的定向角;Ka为测站的大气折光;Ra为地球曲率。
对式(3)—式(5)进行线性化后可以得到αij、βij和Sij在空间直角坐标系中的观测方程见式(6)—式(8)
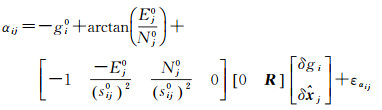 (6)
(6)
式中,变量上方带0均表示近似值;δ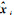
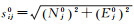
特别说明的是,旋转矩阵R中3列向量对应的是δ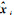
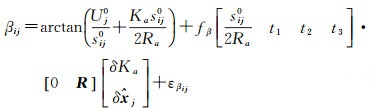 (7)
(7)
式中,δKa为大气折光参数的改正数。其中
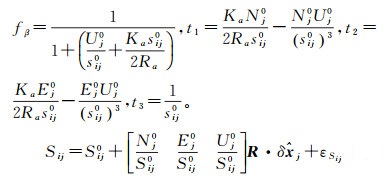 (8)
(8)
式中,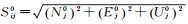
经GNSS软件解算后的基线网向量视为观测量,则GNSS基线ij的观测方程为
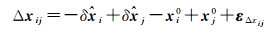 (9)
(9)
式中,Δxij和εΔxij为基线ij的坐标向量及其误差,Δxij=(ΔXij, ΔYij, ΔZij),εΔx=(εXij, εYij, εZij),(ΔXij, ΔYij, ΔZij)和(εXij, εYij, εZij)为基线ij在X, Y, Z方向的3个分量及其观测误差;xi0=(Xi0, Yi0, Zi0),xj0=(Xj0, Yj0, Zj0)。
式(6)—式(9)以向量形式表示的观测方程为
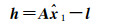 (10)
(10)
式中,x1为4类观测方程中所包括的未知参数向量改正数;A为4类观测方程系数阵组成的系数向量,l为4类观测方程常数组成的向量。
1.2 约束条件 1.2.1 观测标志所满足的条件观测标志绕某一旋转轴旋转一周时,可构成一个球面和平面方程。当观测标志k绕垂直轴p旋转构成的平面法向量和球面半径分别为np和rp,同样绕水平轴s旋转构成的平面法向量和球面半径分别为ns和rs,则得到的两组平面和球面方程分别为
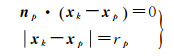 (11)
(11)
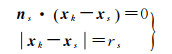 (12)
(12)
式中,xk为观测标志k的坐标向量;xp和xs为垂直轴p和水平轴s旋转中心的坐标向量。
1.2.2 距离和半径相等条件在旋转过程中,安装在SLR望远镜上的两个观测标志之间的距离是保持不变的。如:当观测标志1和2绕旋转轴第k1和k2次旋转时分别构成的距离相等
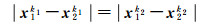 (13)
(13)
同样,同一观测标志绕同一旋转轴多次旋转时具有相同的中心和半径,如:观测标志1和2绕垂直轴p第k1次和k2次旋转时,构成的球面半径相等。则有
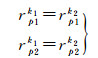 (14)
(14)
同样,绕水平轴s进行旋转时,得到
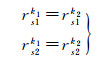 (15)
(15)
不同的观测标志绕同一旋转轴旋转时构成的平面法向量相等。如标志1和2绕垂直轴p构成的法向量np1、np2和水平轴s构成的法向量ns1、ns2分别相等,且为单位向量
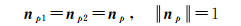 (16)
(16)
 (17)
(17)
同样,同一标志绕同一旋转轴多次旋转构成的法向量也相等。如:绕p轴和s轴进行第k1次和k2次旋转构成的法向量分别相等。
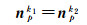 (18)
(18)
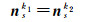 (19)
(19)
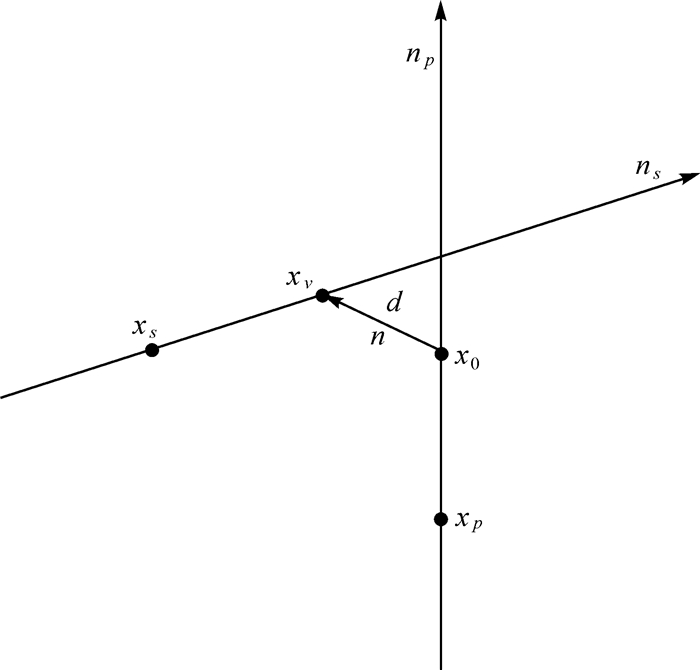
如图 3所示,x0为参考点RP的坐标向量,xv为RP至s轴的最短距离与s轴交点的坐标向量,d为两轴的偏差。当绕垂直轴p旋转时可构成线性条件为
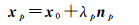 (20)
(20)
|
| 图 3 参考点与两轴偏差之间的关系 Fig. 3 The relationship between the reference point and two axes offsets |
同样,绕水平轴s旋转时也可构成线性条件为
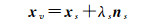 (21)
(21)
式中,λp和λs为垂直轴p和水平轴s的比例参数。
垂直轴p和水平轴s之间的最短距离必正交于两轴,因此,两轴之间的法向量n同时垂直于p和s,得出
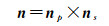 (22)
(22)
由于x0和xv具有同一个法向量,得出线性关系
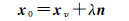 (23)
(23)
同样,两轴的偏差向量d为参考点x0和投影点的xv的关系为
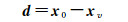 (24)
(24)
式(13)—(21)和式(23)—(24)经过线性化后,这些约束条件可以表示为
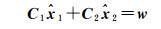 (25)
(25)
式中,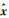
在观测方程式(10)中引入约束方程式(25),经过最小二乘平差后可得到参考点的坐标及其方差阵。联立式(10)和式(25),得
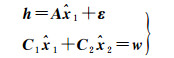 (26)
(26)
式(26)中涉及GNSS基线观测量、水平方向和垂直角、边长共3类观测量,对于不同类观测量采用经验公式定权是不够准确的。为了提高这3类观测量的方差协方差Σh估计的精度,本文采用赫尔默特方差分量验后估计定权法。具体的计算公式和步骤可参考广义测量平差的内容。
根据附有约束条件的间接平差可得法方程为
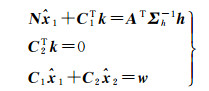 (27)
(27)
式中,N=ATΣh-1A。则未知参数向量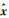
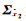
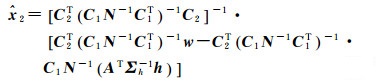 (28)
(28)
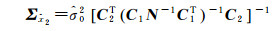 (29)
(29)
式中,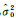
假设式(26)中有u个未知参数,其中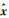
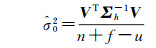 (30)
(30)
由于每一个SLR望远镜周围附近都有一个IGS站,因此可利用IGS站的ITRF2014成果作为基准约束,可将式(27)的平差成果计算至ITRF2014中。
2 成果计算与分析本文采用“一步解”处理了2011年笔者实际观测的“陆态网络”北京(BJFS-SLR)、昆明(KUNM-SLR)和西安(XIAA-SLR)3个并址站归心测量数据,获取了3个并址站的归心基线及其协方差阵,SLR并址站外业观测方案具体可参考文献[12 -13 ]。GNSS基线网和地面观测量的定权采用方差分量估计法,具体可参考文献[25]。计算步骤如下:
首先用GAMIT软件解算出SLR望远镜周围GNSS强制观测墩构成控制网的基线向量;其次列出GNSS网基线向量、地面三维观测量的观测方程,再引入本文总结的多类约束条件方程,利用式(28)和式(29)解算出“陆态网络”3个SLR并址站的归心基线及其协方差矩阵。解算结果如下:
表 1给出3个并址站的归心基线及其中误差;表 2、表 3和表 4为3个并址站归心基线的方差协方差阵;表 5给出与文献[12]的比较结果;表 6给出与ITRF2014的比较结果;表 7和表 8分别给出两个并址站的两轴偏差及其中误差。
| 站点 | ΔX/m | ΔY/m | ΔZ/m | MX/mm | MY/mm | MZ/mm |
| SLR-BJFS | -16.516 7 | 118.317 6 | -146.283 5 | 0.5 | 1.0 | 0.9 |
| SLR-KUNM | -20.214 4 | -18.854 3 | 45.779 9 | 2.1 | 1.4 | 1.9 |
| SLR-XIAA | -14.864 7 | 14.690 6 | -28.080 2 | 1.0 | 0.3 | 0.3 |
| 注:BJFS和KUNM为SLR站并址的IGS站。XIAA为“陆态网络”站点。 | ||||||
| m2 | |||
| 站点 | σΔX2/σΔYΔX/σΔZΔX | σΔXΔY/σΔY2/σΔZΔY | σΔXΔZ/σΔYΔZ/σΔZ2 |
| SLR-BJFS | 2.150 160 970 185 56e-7 | -1.037 761 723 447 34e-7 | 7.004 956 010 966 25e-8 |
| -1.037 761 723 447 35e-7 | 9.275 691 969 902 75e-7 | -6.075 994 832 041 38e-7 | |
| 7.004 956 010 966 27e-8 | -6.075 994 832 041 36e-7 | 7.406 431 134 424 57e-7 | |
| 注:σΔX2、σΔY2、σΔZ2分别为归心基线向量各分量的方差;σΔXΔY、σΔXΔZ、σΔYΔZ、σΔYΔX、σΔZΔX、σΔZΔY分别为归心基线分量各分量间的协方差。 | |||
| m2 | |||
| 站点 | σΔX2/σΔYΔX/σΔZΔX | σΔXΔY/σΔY2/σΔZΔY | σΔXΔZ/σΔYΔZ/σΔZ2 |
| SLR-KUNM | 4.566 126 520 890 61e-6 | 4.823 167 320 632 08e-7 | 2.968 767 370 758 03e-7 |
| 4.823 167 320 632 09e-7 | 1.917 000 385 453 36e-6 | -1.199 157 128 944 03e-6 | |
| 2.968 767 370 758 03e-7 | -1.199 157 128 944 04e-6 | 3.793 812 635 793 69e-6 | |
| m2 | |||
| 站点 | σΔX2/σΔYΔX/σΔZΔX | σΔXΔY/σΔY2/σΔZΔY | σΔXΔZ/σΔYΔZ/σΔZ2 |
| SLR-XIAA | 9.882 988 436 035 68e-7 | -2.405 885 801 693 21e-7 | 2.432 668 170 971 15e-7 |
| -2.405 885 801 693 24e-7 | 9.337 905 643 218 07e-8 | -5.645 340 637 193 09e-8 | |
| 2.432 668 170 971 15e-7 | -5.645 340 637 193 04e-8 | 9.278 541 016 649 78e-8 | |
| mm | |||
| 站点 | 差值 | ||
| ΔX | ΔY | ΔZ | |
| SLR-BJFS | -3.5 | 9.8 | -0.3 |
| SLR-KUNM | 19.6 | -32.3 | -19.1 |
| SLR-XIAA | — | — | — |
| mm | ||||
| 并址站 | dX | dY | dZ | d |
| 北京SLR | 3.5 | 0.8 | 1.0 | 3.8 |
| 昆明SLR | 0.1 | 0.3 | -0.6 | 0.7 |
| 西安SLR | 1.5 | 2.2 | -2.4 | 3.6 |
| mm | ||||
| 并址站 | dX | dY | dZ | d |
| 北京SLR | 0.5 | 1.0 | 0.6 | 1.3 |
| 昆明SLR | 0.8 | 0.5 | 0.9 | 1.2 |
| 西安SLR | 1.0 | 0.8 | 0.3 | 1.3 |
由以上的结果可知:
(1) 3个并址站归心基线中误差基本位于2 mm左右,其中误差最大为2.1 mm。
(2) 本文“一步解”得出的归心基线与Gong的结果相比,基线向量的差值分量小于2 mm,差值最大为1.7 mm。出现差值的主要原因是Gong采用分步解法,而且未考虑两轴偏差、观测标志与参考点满足的各种几何条件,因此从理论上本文的算法更加严密,结果更加可靠。
(3) 与ITRF2014参考值相比,差值普遍较大,其中差值最大为32.3 mm。主要原因在于IFRF2014解算时未考虑GNSS、VLBI、SLR、DORIS这4种技术之间的系统偏差,导致本文测定的并址站归心基线与ITRF2014采用值的差异较大。
(4) 3个SLR望远镜两轴之间的偏差最大为3.5 mm,其中中误差最大不超过2.0 mm。
3 结论针对已有的并址站归心基线解算中需要分步解算、涉及多次坐标转换和未充分考虑多种约束条件等问题,本文提出了并址站归心基线的“一步解”。“一步解”是将SLR望远镜参考点和轴偏差引入至约束方程中,按照附有约束条件的间接平差直接获取归心基线及其协方差阵,理论严密、数学模型简单、易于程序设计,经与已有算法的结果相比,差值基本在2 mm左右;利用北京、昆明和西安SLR望远镜的实测数据,计算出两轴的偏差,偏差分别为3.8、0.7、3.6 mm,本文的解算方法和结果对ITRF解算具有一定的参考价值。
| [1] | ALTAMIMI Z, SILLARD P, BOUCHER C. ITRF2000: A New Release of The International Terrestrial Reference Frame for Earth Science Applications[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B10): ETG 2-1–ETG 2-19. DOI:10.1029/2001JB000561 |
| [2] | ALTAMIMI Z, COLLILIEUX X, LEGRAND J, et al. ITRF2005: A New Release of the International Terrestrial Reference Frame Based on Time Series of Station Positions and Earth Orientation Parameters[J]. Journal of Geophysical Research: Solid Earth, 2007, 112(B9): B09401. |
| [3] | ALTAMIMI Z, COLLILIEUX X, MÉTIVIER L. ITRF2008: An Improved Solution of the International Terrestrial Reference Frame[J]. Journal of Geodesy, 2011, 85(8): 457–473. DOI:10.1007/s00190-011-0444-4 |
| [4] | ALTAMIMI Z, REBISCHUNG P, MÉTIVIER L, et al. ITRF2014: A New Release of the International Terrestrial Reference Frame Modeling Nonlinear Station Motions[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(8): 6109–6131. DOI:10.1002/2016JB013098 |
| [5] | ANGERMANN D, DREWES H, GERSTL M, et al. ITRF Combination-Status and Recommendations for the Future[M]. Berlin: Springer, 2005: 3-8. |
| [6] |
刘经南, 魏娜, 施闯.
国际地球参考框架(ITRF)的研究现状及展望[J]. 自然杂志, 2013, 35(4): 243–250.
LIU Jingnan, WEI Na, SHI Chuang. Status and Prospects of the International Terrestrial Reference Frame (ITRF)[J]. Chinese Journal of Nature, 2013, 35(4): 243–250. |
| [7] | SARTI P, SILLARD P, VITTUARI L. Surveying Co-located Space-geodetic Instruments for ITRF Computation[J]. Journal of Geodesy, 2004, 78(3): 210–222. DOI:10.1007/s00190-004-0387-0 |
| [8] | ALTAMIMI Z, ROTHACHER M. ITRF and Co-location Sites[C]//Proceedings of IERS Workshop on Site Co-location. Matera, Italy: [s. n. ], 2005: 8-15. |
| [9] | LÖSLER M. New Mathematical Model for Reference Point Determination of An Azimuth-elevation Type Radio Telescope[J]. Journal of Surveying Engineering, 2009, 135(4): 131–135. DOI:10.1061/(ASCE)SU.1943-5428.0000010 |
| [10] |
王解先, 季善标, 施一民.
上海天文台的VLBI、SLR、GPS站的空间归心测量[J]. 解放军测绘学院学报, 1997, 14(1): 7–10.
WANG Jiexian, JI Shanbiao, SHI Yimin. The Determination of Space Coordinate Differences Among VLBI, SLR and GPS Stations of Shanghai Observatory[J]. Journal of the PLA Institute of Surveying and Mapping, 1997, 14(1): 7–10. |
| [11] |
沈云中, 陈廷武.
上海天文台并址站的空间归心测量[J]. 同济大学学报(自然科学版), 2006, 34(2): 217–220.
SHEN Yunzhong, CHEN Tingwu. Determination of Space Coordinate Differences of Co-location Sites in Shanghai Observatory[J]. Journal of Tongji University (Natural Science), 2006, 34(2): 217–220. |
| [12] | GONG Xiuqiang, SHEN Yunzhong, WANG Jiexian, et al. Surveying Colocated GNSS, VLBI, and SLR Stations in China[J]. Journal of Surveying Engineering, 2014, 140(1): 28–34. DOI:10.1061/(ASCE)SU.1943-5428.0000118 |
| [13] |
马下平, 沈云中, 王解先, 等.
卫星激光测距与甚长基线干涉测量的天线旋转中心的直接解法[J]. 测绘学报, 2014, 43(3): 257–262.
MA Xiaping, SHEN Yunzhong, WANG Jiexian, et al. Direct Solution of SLR and VLBI Antenna Rotation Center[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(3): 257–262. DOI:10.13485/j.cnki.11-2089.2014.0037 |
| [14] | KALLIO U, POUTANEN M. Can We Really Promise A mm-Accuracy for the Local Ties on A Geo-VLBI Antenna[M]//KENYON S, PACINO M C, MARTI U. Geodesy for Planet Earth. Berlin, Heidelberg: Springer, 2012: 35-42. |
| [15] | NING T, HAAS R, ELGERED G. Determination of the Local Tie Vector Between the VLBI and GNSS Reference Points at Onsala Using GPS Measurements[J]. Journal of Geodesy, 2015, 89(7): 711–723. DOI:10.1007/s00190-015-0809-1 |
| [16] |
潘国荣, 谷川, 施贵刚.
空间圆形物体检测方法与数据处理[J]. 大地测量与地球动力学, 2007, 27(3): 28–30.
PAN Guorong, GU Chuan, SHI Guigang. Test Method and Data Processing for 3D Circular Object[J]. Journal of Geodesy and Geodynamics, 2007, 27(3): 28–30. |
| [17] |
李金岭, 乔书波, 刘鹏, 等.
2008年佘山25m射电天线归心测量[J]. 武汉大学学报(信息科学版), 2010, 35(12): 1387–1391.
LI Jinling, QIAO Shubo, LIU Peng, et al. Site Survey at Sheshan 25m Radio Telescope in 2008[J]. Geomatics and Information Science of Wuhan University, 2010, 35(12): 1387–1391. |
| [18] | ABBONDANZA C, ALTAMIMI Z, SARTI P, et al. Local Effects of Redundant Terrestrial and GPS-based Tie Vectors in ITRF-like Combinations[J]. Journal of Geodesy, 2009, 83(11): 1031–1040. DOI:10.1007/s00190-009-0321-6 |
| [19] | DAWSON J, SARTI P, JOHNSTON G M, et al. Indirect Approach to Invariant Point Determination for SLR and VLBI Systems: An Assessment[J]. Journal of Geodesy, 2007, 81(6-8): 433–441. DOI:10.1007/s00190-006-0125-x |
| [20] | LEINEN S, BECKER M, DOW J, et al. Geodetic Determination of Radio Telescope Antenna Reference Point and Rotation Axis Parameters[J]. Journal of Surveying Engineering, 2007, 133(2): 41–51. DOI:10.1061/(ASCE)0733-9453(2007)133:2(41) |
| [21] | SHEN Yunzhong, YOU Xinzhao, WANG Jiexian, et al. Mathematical Model for Computing Precise Local Tie Vectors for CMONOC Co-located GNSS/VLBI/SLR Stations[J]. Geodesy and Geodynamics, 2015, 6(1): 1–6. DOI:10.1016/j.geog.2014.12.001 |
| [22] | LÖSLER M, HENNES M. An Innovative Mathematical Solution for a Time-efficient IVS Reference Point Determination[C]//Proceedings of the 13th FIG International Symposium on Deformation Measurements and Analysis, 4th IAG Symposium on Geodesy for Geotechnical and Structural Engineering. Lisbon: [s. n. ], 2008: 12-15. |
| [23] | LI Jinling, XIONG Fuwen, YU Chenglei, et al. Precise Determination of the Reference Point Coordinates of Shanghai Tianma 65-m Radio Telescope[J]. Chinese Science Bulletin, 2014, 59(21): 2558–2567. DOI:10.1007/s11434-014-0349-8 |
| [24] | LÖSLER M, HAAS R, ESCHELBACH C. Terrestrial Monitoring of A Radio Telescope Reference Point Using Comprehensive Uncertainty Budgeting[J]. Journal of Geodesy, 2016, 90(5): 467–486. DOI:10.1007/s00190-016-0887-8 |
| [25] |
马下平, 游为.
附加垂线偏差参数的地面常规网与GNSS基线网联合平差[J]. 武汉大学学报(信息科学版), 2017, 42(4): 550–557.
MA Xiaping, YOU Wei. Combined Adjustment of Terrestrial Network and GNSS Network with Additional Parameters of Vertical Deflection[J]. Geomatics and Information Science of Wuhan University, 2017, 42(4): 550–557. |