2. 信息工程大学, 河南 郑州 450001;
3. 卫星导航工程中心, 北京 100000
2. Information Engineering University, Zhengzhou 450001, China;
3. Satellite Navigation Engineering Center, Beijing 100000, China
电离层层析成像技术是一种能够有效反演电离层电子密度的电离层三维探测技术,也是研究电离层三维空间结构的重要方法。该技术克服了传统电离层单层模型的局限,不但为大尺度电离层电子密度空间变化监测提供支撑,而且特别适合研究电子密度在太阳活动异常状态下的扰动特性[1-3]。但是,电离层层析技术严重受观测数据的制约,观测站的数量和分布情况直接影响层析反演精度,以目前全球测站分布情况来看,观测站最为密集的区域在电子密度反演过程中仍然存在严重的不适定问题[4-6]。为了解决电离层层析成像中由于观测数据不充分而引起的不适定问题,国内外众多学者先后提出了相应的解决方法,有效克服了重构过程中不适定问题。文献[7-9]针对电子密度反演过程中的不适定问题分别提出了相应的解决方法,将总电子含量(total electron content,TEC)实测值与投影重构值之间的误差按截距所占的权重比进行分配,但该方法仅以射线截距作为误差分配的唯一依据,未考虑电子密度值大小对迭代模型的影响。随后,文献[10-11]在迭代过程中引入电子密度参数作为修正值,提高了反演电子密度垂直结构相对背景值的稳定性,但是在电离层扰动异常的情况下有可能使电子密度反演的结构发生畸变[12-14]。此外,现有的层析迭代算法中的松弛因子通常取为固定的常数,导致噪声误差在不同电子密度值的像素格网内的传播不平衡,影响电离层层析反演电子密度的精度[15-17]。
针对上述问题,本文提出一种自适应乘法代数重构算法(adaptive multiplicative algebraic reconstruction techniques, AMART),在MART算法的基础上,考虑电子密度值对TEC投影重建值和实测值之间误差分配的影响,增加自适应松弛因子,提高电子密度反演精度。在试验论证阶段,本文采用GIM数据在垂直方向对电子密度进行反演,验证算法的单射线垂直迭代精度;采用国际GNSS服务组织(IGS)观测站的GPS双频观测数据,验证算法的多射线综合迭代精度。
1 电离层层析原理电离层层析是利用实测电离层TEC反演所在路径上的电子密度的方法[18-22],见式(1)
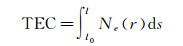 (1)
(1)
式中,TEC为总电子含量;Ne为电子密度;r为经度、纬度和高度组成的位置方向向量;l0为路径起始位置;l为路径的终点。
在电离层层析过程中,考虑到实际情况,将反演的电离层空间离散化为一个个的立体格网,称为像素,以像素中心点的电子密度值代表该像素的电子密度。这样射线穿过每个像素的电子含量值可以表示为射线在该像素内截距与电子密度的乘积,该路径上的总电子含量为各个像素电子含量的总和。对于离散的层析模型,选取像素指标函数bj作为基函数,如果射线穿过该像素则bj取值为1,否则bj取值为0。因此,离散化的电子密度表达式如下
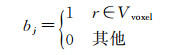 (2)
(2)
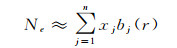 (3)
(3)
式中,n为层析区域像素总数量;xj(j=0, 1, 2,…,n)为对应像素中心点的电子密度,每条射线上对应TEC表达式为
 (4)
(4)
式中,m为TEC观测总数;aij为第i条射线中第j个像素内的截距;lj0为第j个像素内射线的起点;lj1为第j个像素内射线的终点。考虑到观测噪声和离散误差的影响,式(4)用矩阵的形式表示为
 (5)
(5)
式中,y为TEC观测值组成的m为向量;A为m行n列截距组成的系数矩阵;x为待反演的电子密度向量;ε为误差向量,由观测噪声和离散误差组成。
2 AMART算法原理 2.1 MART算法MART算法作为一种常用的电离层层析算法,目前已被广泛地应用于电离层电子密度的反演过程中[23]。利用IRI2012经验模型获取电子密度初值,然后釆用迭代的方式逐步改善待重构图像的初始估计[24]。每一步迭代对应于电离层中的一次斜距TEC测量,即针对一个方程进行,每n(总GPS射线数)步迭代称之为一轮迭代,修正的依据是利用第k步迭代计算的电离层电子密度求出的斜距TEC与实际观测求出的斜距TEC之比,对电离层电子密度分布图像做相应的修正,使结果收敛。在第k步迭代中,MART方法的修正公式为
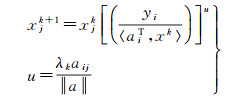 (6)
(6)
式中,xjk+1是第j个像素中电子密度的第k+1步迭代值;aiT是射线在对应像素内的截距构成向量的第i行转置(即第i条射线);λk是松弛因子,取值范围为0 < λk < 1。该算法的优点是迭代速度快,并可以保证反演结果为正值。
2.2 AMART算法从式(6)中可以看出,MART算法将TEC实测值与反演值的误差以比值的形式给出,以乘积的形式对电子密度误差进行分配,在分配误差的过程中完全取决于截距值,这样分配误差没有考虑到电子密度值的实际情况,会对误差起放大的作用。此外,松弛因子在MART算法中被视为常数代入方程,而松弛因子的作用是调节反演电子密度精度与结果的平滑程度。松弛因子取较大,则反演电子密度较为平滑,电离层局部变化特征将会被掩盖;而松弛因子取较小时,又会受到噪声的干扰[25]。因此,本文针对乘法代数重构算法在迭代系数和松弛因子方面进行改进。采用射线通过像素的截距值与电子密度的乘积(像素电子含量)作为自变量,构造新的G-MRAT迭代模型,在不同电子密度的像素格网内重新分配TEC实测值与反演值之间的误差。提出的AMART迭代算法表达式如下
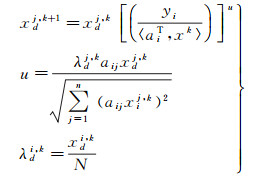 (7)
(7)
式中,N为常数,用于控制迭代次数,其取值视实际情况而定,且N>max(xdi, k);d表示有射线穿过的格网中由地面到卫星方向的格网数;xdj, k表示第j条射线在第d个格网内电子密度的第k次迭代值;λdi, k为第d个格网所对应的松弛因子。图 1给出了一条射线穿越电离层层析格网时的示意图。

|
| 图 1 GPS射线穿越电离层层析格网 Fig. 1 The GPS ray passing through ionospheric tomography grid |
3 数据来源及预处理
本文试验研究分为两部分,第一部分利用GIM数据验证AMART算法单射线垂直迭代精度,数据采用2015年5月28日CODE发布的GIM格网VTEC数据,经纬度分辨率为5°×2.5°,时间分辨率为1 h;第二部分利用IGS发布的GPS双频观测数据验证AMART算法整体迭代精度,数据采用2015年5月28日欧洲区域43个GPS观测站的双频载波相位平滑数据,计算出各个观测站在卫星方向的STEC值,卫星截至高度角选取20°。为了得到充足的观测数据,选取测站40 min的数据反演一个时刻的电子密度。
本文电离层层析区域经度范围为10°E~30°E,纬度范围为45°N~55°N,高度范围为100~1000 km;在选定区域进行空间离散化时,选择经度5°、纬度2.5°和高度50 km的空间间隔为一个像素点范围。各像素点的电子密度初值由电离层IRI2012模型提供。为了验证新算法的可靠性,选取欧洲Pruhonice观测站(14.6°E,50°N)电离层测高仪数据获得的电子密度剖面信息并与新算法反演的电子密度剖面结果进行比较。
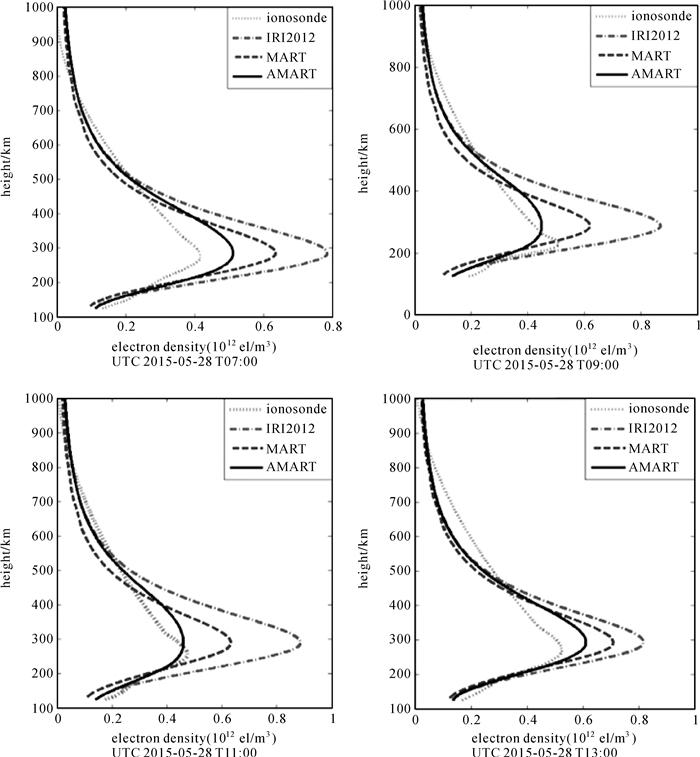
4 结果分析 4.1 基于GIM数据反演电子密度精度分析本节利用GIM提供的VTEC数据,通过对比AMART算法和MART算法在垂直方向的反演精度验证新算法的可行性。采用电离层垂直探测仪提供的电子密度剖面数据作为评价值,对比IRI模型、MART算法和AMART算法反演得到的电子密度与评价值的差异,分析AMART算法与MART算法反演精度。图 2给出了UTC 2015年5月28日07:00、09:00、11:00和13:00共4个时刻欧洲Pruhonice观测站(14.6°E,50°N)上空电子密度沿高度变化结果。其中电离层探测仪主要提供电子密度峰值以及峰值以下的数据,峰值以上数据由数学方法外推得到。因此,在研究AMART算法反演精度时重点比较峰值以及峰值以下的电子密度反演情况。
|
| 图 2 基于GIM数据的MART和AMART算法反演结果与IRI模型和电离层垂直探测仪电子密度数据比较 Fig. 2 Comparison of the reconstructed results of MART and AMART algorithm based on GIM data with the electron density obtained by IRI model and ionosondes |
由图 2可以看出,与电离层垂直探测仪结果相比,IRI模型计算的电子密度初值精度较低,而MART和AMART算法反演精度均较IRI模型有较大的提高。同时,本文提出的AMART算法反演精度明显高于传统的MART算法,尤其在11:00时刻,反演电子密度值与电离层探测仪数据基本吻合。这表明单条射线在垂直方向上,新算法反演电子密度精度比MART算法反演电子密度精度高。侧面反映出在观测数据相同的情况下,AMART算法反演电子密度更加接近真实值。由于GIM提供的VTEC数据精度有限,且不能提供水平方向信息,因此下节采用GPS双频观测数据进行电子密度反演。
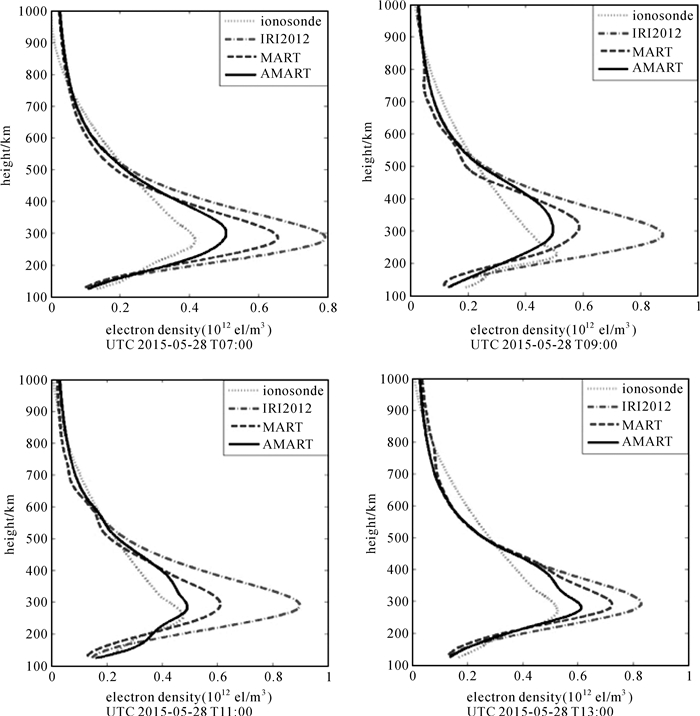
4.2 基于GPS双频观测数据反演电子密度精度分析为了进一步验证AMART相对于传统MART算法的优越性,采用与4.1节相同时刻的GPS双频数据反演电子密度,图 3给出了对应时刻的电子密度剖面图。
|
| 图 3 基于GPS观测数据的MART和AMART算法反演结果与IRI模型和电离层垂直探测仪电子密度数据比较 Fig. 3 Comparison of the reconstructed results of MART and AMART algorithm based on GPS data with the electron density obtained by IRI model and ionosondes |
从图 3可以看出,在Pruhonice站上空,本文提出的AMART算法得到的峰值处电子密度与电离层测高仪观测获得的结果较MART算法更为接近,尤其是在11:00与13:00两个时刻,新算法反演的峰值电子密度和峰值高度与电离层测高仪给出的结果十分接近。但是,新方法和传统方法都不能摆脱对电子密度初值的依赖,当电子密度初值精度较差时,两种方法反演电子密度精度随之降低。总体来看,本文提出的AMART算法较传统的MART算法有明显的优越性。
为了进一步统计不同时刻两种方法反演电子密度峰值处误差值和峰值以下误差值,现将电子密度峰值误差绝对值和峰值以下误差的均方根误差(RMS)统计见表 1。
| el/m3 | ||||
| 时间 | 峰值电子密度误差 绝对值 | 峰值以下电子密度 均方根误差(RMS) | ||
| MART | AMART | MART | AMART | |
| 07:00 | 0.233 92 | 0.080 08 | 0.128 62 | 0.056 55 |
| 09:00 | 0.059 47 | 0.113 25 | 0.090 64 | 0.079 89 |
| 11:00 | 0.084 28 | 0.015 05 | 0.053 04 | 0.032 64 |
| 13:00 | 0.176 52 | 0.081 58 | 0.074 65 | 0.074 65 |
从表 1中可以看出,AMART算法反演的电子密度在峰值处的误差绝对值在07:00、11:00和13:00明显小于MART算法的反演结果,而在09:00误差值超过MART算法的误差。结合图 2结果可以发现该时刻IRI模型提供的电子密度的峰值与垂直探测仪偏差较大,可以判定AMART模型误差来源于IRI模型提供的电子密度初值。通过对比峰值以下电子密度RMS值,可以确定AMART算法相对于MART算法具有优越性。
由于电离层探测仪在测区分布数量有限,且只能分析其上方垂直电子密度变化情况,为了更好地对比AMART算法与MART算法的反演效果,基于GPS双频观测数据得到的电子密度反演结果,下文对不同时间、经纬度和高度的电子密度分布情况进行更加详细的分析。
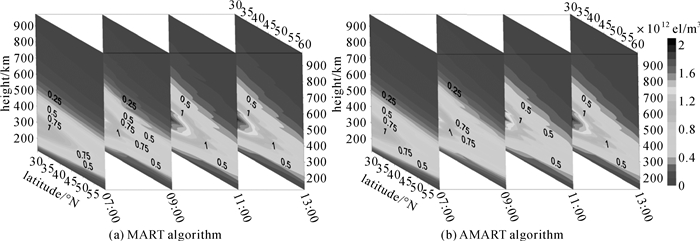
4.3 不同时间电子密度随纬度和高度变化情况分析考虑电离层垂直探测仪所在位置为(14.6°E,50°N),图 4给出了经度15°E平面内电子密度随高度和纬度的变化的剖面反演结果,本节仍然采用2015年5月28日07:00、09:00、11:00和13:00共4个时刻IGS提供的GPS观测数据进行分析。反演纬度范围为30°N~60°N,高度范围为100~1000 km,电子密度单位为1012el/m3。反演时刻的Dst指数均在-17~0 nt之间,地磁处于平静阶段;F10.7指数为88,太阳活动水平较弱,因此本文试验结果可以基本忽略地磁和太阳活动的影响。
|
| 图 4 MART和AMART算法反演电子密度随高度和纬度变化情况分析 Fig. 4 The variation analysis of electron density reconstructed by MART and AMART algorithm in a height versus latitude plane |
从图 4中分别采用两种算法对4个时刻电子密度随高度和纬度的变化情况反演,对比图 4(a)和图 4(b)可以发现,两种算法在电子密度峰值区域(200~400 km)电子密度反演结果随时间变化呈逐渐增大的趋势,变化趋势相似。随纬度的增加,利用AMART算法反演的电子密度值在峰值附近变化程度比MART算法反演的电子密度在峰值处的变化程度大,呈逐渐减小的趋势,尤其是在11:00变化尤为明显,这与图 3中反映出的Pruhonice观测站上空利用AMART算法反演的电子密度比MART算法反演的电子密度小且更接近电离层测高仪观测结果相一致。综上所述,本文提出的AMART算法可以更好地反映电子密度随高度在不同时间的变化情况。
5 结论本文提出一种电离层层析AMART新算法,相对于传统的MART算法,该方法充分考虑了电子密度值对迭代精度的影响,克服了传统MART算法只依赖截距值分配TEC实测值与投影重构值之间的差异,有效提高电子密度反演的精度。采用GIM数据验证新算法的可行性;采用GPS双频观测数据对新算法优越性进行验证,结果表明新算法更加准确地反映电子密度分布特征。
| [1] | YAO Y B, CHEN P, ZHANG S, et al. Temporal and Spatial variations in Ionospheric Electron Density Profiles over South Africa During Strong Magnetic Storms[J]. Natural Hazards and Earth System Sciences, 2013, 13(2): 375–384. DOI:10.5194/nhess-13-375-2013 |
| [2] | JIN Shuanggen, LUO O F, PARK P. GPS Observations of the Ionospheric F2-Layer Behavior During the 20th NOVEMBER 2003 Geomagnetic Storm over South Korea[J]. Journal of Geodesy, 2008, 82(12): 883–892. DOI:10.1007/s00190-008-0217-x |
| [3] | POKHOTELOV D, JAYACHANDRAN P T, MITCHELL C N, et al. Gps Tomography in the Polar Cap: Comparison with Ionosondes and in Situ Spacecraft Data[J]. GPS Solutions, 2011, 15(1): 79–87. DOI:10.1007/s10291-010-0170-z |
| [4] | CHARTIER A T, SMITH N D, MITCHELL C N, et al. The Use of Ionosondes in GPS Ionospheric Tomography at Low Latitudes[J]. Journal of Geophysical Research, 2012, 117(A10): A10326. DOI:10.1029/2012JA018054 |
| [5] | NESTEROV I A, KUNITSYN V E. GNSS Radio Tomography of the Ionosphere: The Problem with Essentially Incomplete Data[J]. Advances in Space Research, 2011, 47(10): 1789–1803. DOI:10.1016/j.asr.2010.11.034 |
| [6] | WEN Debao, WANG Yong, NORMAN R. A New Two-Step Algorithm for Ionospheric Tomography Solution[J]. GPS Solutions, 2012, 16(1): 89–94. DOI:10.1007/s10291-011-0211-2 |
| [7] | AUSTEN J R, FRANKE S J, LIU C H. Ionospheric Imaging Using Computerized Tomography[J]. Radio Science, 1988, 23(3): 299–307. DOI:10.1029/RS023i003p00299 |
| [8] | BUST G S, MITCHELL C N. History, Current State, and Future Directions of Ionospheric Imaging[J]. Reviews of Geophysics, 2008, 46(1): RG1003. DOI:10.1029/2006RG000212 |
| [9] | PRYSE S E, KERSLEY L, RICE D L, et al. Tomographic Imaging of the Ionospheric Mid-Latitude Trough[J]. Annales Geophysicae, 1993, 11(2-3): 144–149. |
| [10] | MITCHELL C N, KERSLEY L, HEATON J A T, et al. Determination of the Vertical Electron-Density Profile in Ionospheric Tomography: Experimental Results[J]. Annales Geophysicae, 1997, 15(6): 747–752. DOI:10.1007/s00585-997-0747-1 |
| [11] | WEN Debao, YUAN Yunbin, OU Jikun, et al. Three-Dimensional Ionospheric Tomography by An Improved Algebraic Reconstruction Technique[J]. GPS Solutions, 2007, 11(4): 251–258. DOI:10.1007/s10291-007-0055-y |
| [12] | DAS S K, SHUKLA A K. Two-Dimensional Ionospheric Tomography over the Low-Latitude Indian Region: An Intercomparison of Art and Mart Algorithms[J]. Radio Science, 2011, 46(2): RS2005. DOI:10.1029/2010RS004350 |
| [13] | FOUGERE P F. Ionospheric Radio Tomography Using Maximum Entropy 1. Theory and Simulation Studies[J]. Radio Science, 1995, 30(2): 429–444. DOI:10.1029/94RS03164 |
| [14] | QU Gangrong, WANG Caifang, JIANG Ming. Necessary and Sufficient Convergence Conditions for Algebraic Image Reconstruction Algorithms[J]. Advances in Mathematics, 2007, 36(3): 379–381. |
| [15] | AHN S, FESSLER J A, BLATT D, et al. Convergent Incremental Optimization Transfer Algorithms: Application to Tomography[J]. IEEE Transactions on Medical Imaging, 2006, 25(3): 283–296. DOI:10.1109/TMI.2005.862740 |
| [16] | BYRNE C L, GRAHAM-EAGLE J. Convergence Properties of the Algebraic Reconstruction Technique (ART)[C]//Proceedings of the Conference Record of the 1992 IEEE Nuclear Science Symposium and Medical Imaging Conference. Orlando, FL: IEEE, 1992: 1240-1242. |
| [17] | KAK A C, SLANEY M, WANG Ge. Principles of Computerized Tomographic Imaging[J]. Medical Physics, 2002, 29(1): 107. |
| [18] |
陈鹏.
GNSS电离层层析及震前电离层异常研究[J]. 测绘学报, 2013, 42(3): 474.
CHEN Peng. Research on GNSS-Based Ionospheric Tomography and Pre-Earthquake Ionospheric Anomaly[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 474. |
| [19] |
汤俊.
GNSS三维电离层层析算法及电离层扰动研究[J]. 测绘学报, 2015, 44(1): 117.
TANG Jun. Studies on Three-Dimension Ionospheric Tomography Using GNSS Measurements and Ionospheric Disturbances[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(1): 117. DOI:10.11947/j.AGCS.2015.20140398 |
| [20] |
姚宜斌, 汤俊, 张良, 等.
电离层三维层析成像的自适应联合迭代重构算法[J]. 地球物理学报, 2014, 57(2): 345–353.
YAO Yibin, TANG Jun, ZHANG Liang, et al. An Adaptive Simultaneous Iteration Reconstruction Technique for Three-Dimensional Ionospheric Tomography[J]. Chinese Journal of Geophysics, 2014, 57(2): 345–353. DOI:10.6038/cjg20140201 |
| [21] |
闻德保, 吕慧珠, 张啸.
电离层层析重构的一种新算法[J]. 地球物理学报, 2014, 57(11): 3611–3616.
WEN Debao, LÜ Huizhu, ZHANG Xiao. A New Method of Ionospheric Tomographic Reconstruction[J]. Chinese Journal of Geophysics, 2014, 57(11): 3611–3616. DOI:10.6038/cjg20141114 |
| [22] |
吴寒, 姚宜斌, 陈鹏, 等.
GNSS电离层层析成像算法研究[J]. 武汉大学学报(信息科学版), 2013, 38(12): 1405–1408.
WU Han, YAO Yibin, CHEN Peng, et al. Investigation of GNSS-Based Ionospheric Tomographic Algorithms[J]. Geomatics and Information Science of Wuhan University, 2013, 38(12): 1405–1408. |
| [23] |
汤俊, 姚宜斌, 张良.
一种适用于电离层层析成像的TV-MART算法[J]. 武汉大学学报(信息科学版), 2015, 40(7): 870–876.
TANG Jun, YAO Yibin, ZHANG Liang. A TV-Mart Algorithm Applied to Computerized Ionospheric Tomography[J]. Geomatics and Information Science of Wuhan University, 2015, 40(7): 870–876. |
| [24] |
闻德保, 张啸, 张光胜, 等.
基于选权拟合法的电离层电子密度层析重构[J]. 地球物理学报, 2014, 57(8): 2395–2403.
WEN Debao, ZHANG Xiao, ZHANG Guangsheng, et al. Tomographic Reconstruction of Ionospheric Electron Density Based on the Fitting Method by Selection of the Parameter Weights[J]. Chinese Jounal of Geophysics, 2014, 57(8): 2395–2403. DOI:10.6038/cjg20140801 |
| [25] |
霍星亮, 袁运斌, 欧吉坤, 等.
顾及电离层变化的层析反演新算法[J]. 地球物理学报, 2016, 59(7): 2393–2401.
HUO Xingliang, YUAN Yunbin, OU Jikun, et al. A New Ionospheric Tomographic Algorithm Taking Into Account The Variation of the Ionosphere[J]. Chinese Journal of Geophysics, 2016, 59(7): 2393–2401. DOI:10.6038/cjg20160706 |


