2. 地壳运动监测工程研究中心, 北京 100045
2. National Earthquake Infrastructure Service, Beijing 100045, China
截至2012年12月28日,北斗卫星导航系统(BDS)已有5颗地球静止轨道卫星、5颗倾斜地球同步轨道卫星和4颗中圆地球轨道卫星,共14颗卫星,已经初步形成了亚太地区的导航定位服务能力[1-2]。自2015年至2016年6月12日,BDS又连续发射了7颗卫星,其中5颗为新一代导航卫星,两颗为区域服务备份卫星,这7颗卫星成为现有系统的有力支撑,但目前并没有入网运行(http://www.beidou.gov.cn/fbh2016.html)。
随着BDS的逐步完善和发展,其高精度大地测量的实际能力受到了国内外学者的关注。基于“北斗卫星观测试验网”观测数据和武汉大学自主研制的高精度GNSS数据处理软件PANDA,文献[3]较好地实现了BDS的定轨与定位,研究结果显示BDS静态精密单点定位精度已达到厘米级。文献[4]利用相同的观测数据在单系统定位的基础上实现了BDS/GPS融合定位研究,结果显示BDS单系统静态精密单点定位精度能够达到厘米级,BDS/GPS融合动态定位能够促进PPP收敛时间。文献[5]利用国内7个跟踪站,研究了BDS静态和动态定位精度,结果显示BDS的PPP定位可以实现静态厘米级、动态分米级的定位精度。文献[6]与文献[7]利用不同的观测数据不同方法分析了当前BDS的轨道精度,结果均显示BDS轨道在径向上都能达到分米级。文献[8]梳理和分析了不同定轨方法得到的BDS轨道精度,结果显示BDS单系统定轨法与利用GPS辅助的两步定轨法得到的轨道精度相当,定轨精度均能达到分米级。文献[9]对比分析了多家IGS分析中心的BDS、GPS、GLONASS和Galileo四星座轨道和钟差产品精度,认为BDS的GEO、IGSO与MEO卫星的轨道精度分别能达到分米级、分米级和厘米级。另外,随着多系统的融合定位的发展[10-13],已有研究结果显示BDS/GPS融合定位在获取地表强震运动速度方面较单独的GPS动态定位有所提升[13]。
需要指出的是,上述BDS静态PPP定位精度均显示为厘米级,但这些结果都是基于短时间内观测资料的单天定位结果得到的结论,难免会受到特定时间段内轨道和钟差产品精度的影响[6-9]。同时,BDS在定位与定轨方面已经有众多研究成果[3-13],然而并没有相关研究讨论BDS在高精度地壳运动监测中的实际应用能力。因此,本文将利用6个连续台站2 a以上的GNSS观测数据来分析BDS的精密单点定位精度及其稳定性,并进而通过与GPS基线和速度场结果的对比分析,来更加全面、客观地探讨目前BDS在地壳运动监测中的应用能力。
1 观测数据本文所用的观测数据来源于分布在中国大陆的7个GNSS观测站,分别位于宁夏盐池(BDYC)、河北唐山(BDTS)、北斗荣成(BDRC)、山东荣成(SDRC)、四川筠连(SCGU)、山西太原(SXTY)和湖北武汉(WUHN)。站点分布如图 1所示,其中3个观测站架设了国产GNSS接收机UNICORECOMM UR370,4个站点来自于其他观测网络的基准站,GNSS接收机类型为TRMBLE NETR9,天线均采用的是扼流圈天线。图中, 三角为布设有国产接收机的站点,圆圈为其他连续站点。台站具体参数及观测时间见表 1。

|
| 图 1 GNSS站点分布图 Fig. 1 Distribution of GNSS sites |
| 台站 | 经度/(°E) | 纬度/(°N) | GNSS接收机类型 | 天线类型 | 连续观测时间 |
| 宁夏盐池(BDYC) | 107.44 | 37.78 | UNICORECOMM UR370 | TRM59800.00 | 2013-02-12—2015-03-19 |
| 河北唐山(BDTS) | 118.20 | 39.61 | UNICORECOMM UR370 | TRM59800.00 | 2013-02-12—2016-11-05 |
| 北斗荣成(BDRC) | 122.42 | 37.17 | UNICORECOMM UR370 | TRM59800.00 | 2013-02-12—2016-11-05 |
| 四川筠连(SCGU) | 105.90 | 32.42 | TRIMBLE NETR9 | TRM59900.00 | 2014-12-18—2016-11-05 |
| 山东荣成(SDRC) | 122.42 | 37.17 | TRIMBLE NETR9 | TRM59900.00 | 2014-01-01—2016-11-05 |
| 山西太原(SXTY) | 112.43 | 37.71 | TRIMBLE NETR9 | TRM59900.00 | 2014-01-01—2016-11-05 |
| 湖北武汉(WUHN) | 114.36 | 30.53 | TRIMBLE NETR9 | TRM59900.00 | 2014-01-01—2016-11-05 |
从表 1可以看到,布设国产接收机的站点中,BDTS和BDRC站点的观测时间跨度约有3.5 a,BDYC站点观测时间长度为2 a;其他4个站点观测时间跨度大于2.5 a,且均为TRIMBLE NETR9接收机。这7个观测站都能接收到BDS和GPS信号,为BDS与GPS定位精度的对比分析提供了基础数据。基准站SDRC与北斗观测站BDRC空间距离约为5 m,这为站点稳定性的对比及短基线精度衡量提供了可能;同时,这7个站点在空间上的分布比较均匀,也为分析讨论BDS与GPS所得速度场的差异性提供了条件。
2 精密单点定位处理方法本文利用PANDA软件中的PPP模块,分别处理了上述BDS和GPS观测数据。PANDA软件由武汉大学卫星导航定位技术研究中心研发,包含了多卫星导航系统精密定道、精密钟差确定、精密定位及动态融合定位等多个模块[3-4, 7-10]。
数据处理过程中解算的主要参数包括坐标、接收机钟差、天顶对流层延迟及模糊度等,采用了IGS武汉大学分析中心(WHU)提供的精密轨道和钟差产品(WUM)[9],该产品可以从IGS数据中心下载得到(ftp://cddis.gsfc.nasa.gov/pub/gps/products/mgex),精密轨道和钟差都是基于ITRF08框架下的产品。
这里的精密单点定位,以每24 h的数据解算得到一个单日解。具体解算过程为:对数据采样间隔为30 s的GPS和BDS数据,分别采用无电离层线性组合观测值消除电离层延迟一阶项影响,之后利用TurboEdit方法来检测主要的周跳和消除主要粗差[14],其次用残差编辑法来检测小的周跳和消除剩余粗差。另外,解算过程中采用的卫星截止高度角为7°,对坐标参数给予了10 m的约束,同时对固体潮、极潮及海潮都采用了IERS2010协议模型进行了改正,对流层延迟的干分量采用Sasstamonion模型计算得到[15],并对残余湿分量每2 h估计一个参数,之后使用GMF投影函数[16-17]将对流层延迟投影到传播路径上。
在处理GPS数据过程中,笔者改正了卫星端及接收机端的天线相位中心偏移(PCO)和天线相位中心变化(PCV);而在BDS处理过程中,由于目前IGS只提供了BDS卫星端粗略的PCO改正,且没有其他机构发布卫星端PCV及接收机端PCO与PCV改正信息,因此对BDS无法进行精确的天线相位中心改正[18]。
3 结果分析考虑到这7个站点在观测时间段内并没有受到地震、滑坡等因素的影响,本文利用线性回归模型来研究其坐标时间序列的重复性精度。
在原始时间序列中,所有观测站的BDS结果在某些天同时出现了较大的波动,而GPS并未受到明显的影响,这是由北斗轨道或钟差的不稳定性所造成;同时,个别站点还出现GPS和BDS结果同时波动的现象,这可能是由于数据观测质量本身所引起的。由于这些波动数据容易对精度评估结果造成一定的偏差,所以本文在后续结果分析中去除了这些粗差。
去除粗差的具体步骤为:首先利用线性回归方法拟合时间序列,得到拟合残差及其RMS值;然后,去除残差大于3倍RMS的观测值;最后,对去除粗差后的时间序列再次进行线性回归拟合并计算RMS值[19]。在此基础上讨论BDS和GPS单日解的重复性精度、基线时间序列变化趋势及速度场的一致性。
3.1 时间序列结果分析表 2给出了BDS与GPS观测结果在ENU方向上的RMS。可以发现BDS在南北向的RMS要明显小于东西向,GPS虽然也有这种特征但并不明显,这与导航系统在南北向的精度要优于东西向相一致。这种特征在BDS中表现得更明显的原因是目前BDS卫星星座并没有完全建成,可用的MEO和IGSO卫星较少,受到GEO卫星轨道精度影响较大[6, 9]。对比7个观测站的RMS值可以发现,SCGU台站的BDS和GPS的RMS值在三分量上都要明显大于其他站点,这可能与该站的观测环境有关。通过TEQC检测SCGU数据观测质量,发现该台站受到较强的多路径效应影响,从而引起解算过程中不确定性增加[20-21],最终导致该站时间序列结果的RMS值增大。除SCGU台站外,其他6个台站的BDS在E、N、U三分量上的RMS值分别约为7、5.4和20 mm,GPS在E、N、U三分量上的RMS值分别约为3.3、3.1和7.0 mm。考虑如果拟合残差服从正态分布,置信水平为95%时的置信区间为[-2RMS 2RMS],将2倍RMS作为解算精度,可以得到BDS的PPP定位精度在水平和垂向分别约为17和40 mm,GPS的PPP定位精度在水平和垂向分别约为9和14 mm,对比BDS与GPS的PPP定位精度可以发现,前者水平向精度要低于后者1倍,垂向精度低于后者2倍。
| mm | |||||||
| Site | BDS RMS E-W | BDS RMS N-S | BDS RMS U-D | GPS RMS E-W | GPS RMS N-S | GPS RMS U-D | 接收机类型 |
| BDYC | 6.8 | 6.7 | 19.0 | 3.2 | 2.4 | 6.2 | UNICORECOMM UR370 |
| BDTS | 7.0 | 6.2 | 21.2 | 2.9 | 3.1 | 6.7 | UNICORECOMM UR370 |
| BDRC | 6.6 | 5.6 | 18.0 | 3.0 | 2.7 | 6.3 | UNICORECOMM UR370 |
| SCGU | 18.0 | 9.0 | 35.7 | 6.7 | 4.0 | 10.7 | TRIMBLE NETR9 |
| SDRC | 6.6 | 4.3 | 17.2 | 3.0 | 2.9 | 6.0 | TRIMBLE NETR9 |
| SXTY | 7.8 | 5.3 | 19.0 | 4.2 | 4.0 | 7.5 | TRIMBLE NETR9 |
| WUHN | 6.8 | 4.4 | 24.5 | 3.8 | 3.5 | 9.3 | TRIMBLE NETR9 |
由表 2可知,BDYC、BDTS和BDRC台站的接收机是UNICORECOMM UR370,这3个台站BDS结果在E、N、U方向上的RMS均值分别为:6.8、6.1和19.4 mm,GPS结果为:3、2.7和6.4 mm;其他4个台站的接收机是TRIMBLE NETR9,除SCGU外,另外3个台站BDS结果在E、N、U方向上的RMS均值分别为:7.1、4.7和20.2 mm,GPS结果为:3.7、3.5和7.6 mm。两种接收机BDS结果在N、E、U方向上的RMS均值差值最大为1.4 mm,GPS结果为1.2 mm,这一结果在观测误差范围之内,并不显著。总体来说,根据这6个站点的结果可以得出接收机的差异并未引起BDS与GPS定位精度的显著性差异。
3.2 基线时间序列结果分析在考察基线时,笔者主要选取了两条基线来详细讨论BDS与GPS结果之间的差异性。其中由BDRC与SDRC这两个站组成的基线较短,约为5 m,由BDRC与BDTS两个站组成的基线较长,约为457 km。
图 2给出了BDRC与BDTS基线时间序列结果,从基线的长度及其变化率来看,BDS与GPS得到基线的绝对长度的参考值是一致的,且两者基线长度都以1.8 mm/a的速率在缩短。从基线时间序列的拟合残差RMS值来看,GPS得到该基线时间序列的拟合残差RMS值要比BDS小,这说明GPS的观测精度要优于BDS,但BDS也能够准确反映这两个站点间的基线长度与变化速率特征,即BDS可以用来监测站点间基线的线性变化速率。图 2中粗线为最小二乘拟合线,细线为2倍RMS值波动范围。
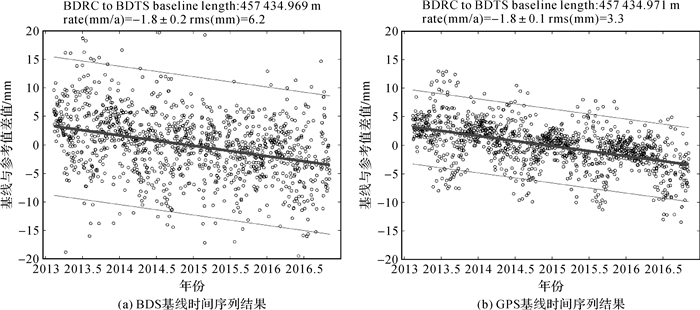
|
| 图 2 BDRC与BDTS基线时间序列结果 Fig. 2 The result of baseline between BDRC and BDTS |
从图 2中还可以看到,GPS观测到两个站点间基线在年中时间段出现了残差波动较大的情况,这可能与季节性变化或模型误差有关。而在BDS中并没有这种季节性变化的信号,这是由于BDS信号的基线残差幅度与GPS信号观测到的季节性波动幅度相当,所以很难在BDS信号中检测出这一季节性信号的变化。BDS检测弱信号能力要低于GPS系统的主要原因在于目前BDS卫星星座和各种模型尚不完善,以及其卫星精密轨道与钟差产品的精度比GPS稍低等。
图 3给出了BDRC与SDRC站点间BDS和GPS基线时间序列结果,两个系统得到的基线长度结果基本一致,但线性速率相差1 mm/a,造成这一差异的原因是BDS定位精度与噪声等带来的偏差[22-23]。对比图 2与图 3中的RMS值,可以发现短基线的RMS明显比长基线的RMS要小,这说明短基线可以消除一些共模误差[23],得到精度更高的结果。图 3中,粗线为最小二乘拟合线,细线为1.96倍RMS值波动范围。
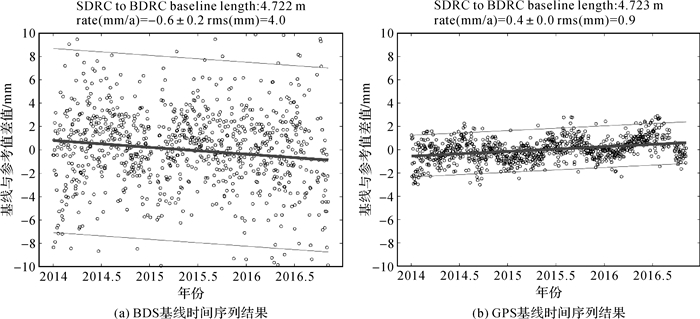
|
| 图 3 SDRC与BDRC基线时间序列结果 Fig. 3 The result of baseline between BDRC and SDRC |
统计除SCGU外其他6个站点间的15条基线,结果显示,BDS与GPS基线速率的平均误差分别为:0.4和0.2 mm/a。在置信水平为95%时,BDS与GPS监测基线速率的精度分别为0.8和0.4 mm/a。图 4显示出基线速率误差与基线长度成正相关性,这进一步说明BDS与GPS能更好地监测短基线的速率变化。在基线不超过500 km时,BDS与GPS能够监测基线变化率的精度分别为:0.4和0.2 mm/a,且两者的精度都将随基线缩短而进一步提高。

|
| 图 4 基线速率误差与基线长度相关图 Fig. 4 The correlation of baseline rate and baseline length |
3.3 速度场结果分析
本文利用线性回归方法得到7个台站BDS和GPS结果在ITRF08框架下的速度场,从图 5(a)中可以看出两者在水平方向上无论是大小还是方向都很一致,图 5(b)给出了两套速度场的差异。对比表 3两套速度场结果,发现其在水平向的差异约为1~2 mm/a,在垂向的差异约为10~15 mm/a。
| mm/a | ||||||
| site | BDS N | BDS E | BDS U | GPS N | GPS E | GPS U |
| BDYC | 31.1 | -7.4 | 14.1 | 31.7 | -8.4 | -2.5 |
| BDTS | 27.6 | -14.1 | 16.6 | 29.5 | -13.7 | 2.4 |
| BDRC | 28.5 | -10.5 | 12.4 | 30.0 | -10.7 | 1.0 |
| SCGU | 31.8 | -11.4 | -8.7 | 33.6 | -8.6 | -0.7 |
| SDRC | 28.9 | -11.0 | 9.2 | 29.3 | -10.5 | 0.7 |
| SXTY | 37.4 | -7.4 | 12.2 | 34.8 | -6.3 | 1.0 |
| WUHN | 31.4 | -11.3 | 9.7 | 32.7 | -10.3 | 0.3 |
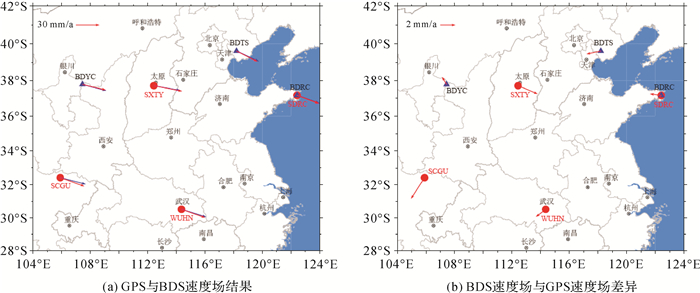
|
| 图 5 BDS与GPS速度场对比图 Fig. 5 The comparison of BDS and GPS velocity field |
图 5(b)给出的7个站点在水平方向的速度场差异没有明显的整体性运动,而表 3中,除SCGU站点外所有站点的BDS与GPS之间的垂向速度差都有上升趋势,为了分析这一差异的来源,笔者以除SCGU站外的其他6个台站的GPS时间序列为参考,利用七参数转换法将BDS时间序列转换到GPS参考框架下,得到转换参数的时间序列,如图 6所示。

|
| 图 6 BDS与GPS之间七参数转换时间序列 Fig. 6 The seven parameters transformation time series between BDS and GPS |
从图 6中的平移和旋转参数来看,BDS与GPS时间序列结果之间不存在明显的整体性的旋转和平移特征,而尺度因子不仅有~10-8整体性偏移,且在2014.6年前后还存在明显的趋势性转折,这说明BDS与GPS的时间序列结果所在参考框架有一定的差异性。通过计算发现,尺度因子的偏移并不影响水平和垂向速度场,而尺度因子的趋势性变化主要影响垂向速度场。因此,笔者认为BDS与GPS垂向速度场差异是框架尺度因子波动所带来的误差。
另外,BDS目前星座并不完善,虽然能对亚太地区提供很好的定位服务[1, 2],但其地面跟踪站点只分布在亚太地区,且BDS卫星端和接收端天线相位中心等相关改正模型的不完善,这都有可能造成框架实现时尺度因子或框架原点的偏离[24, 25]。这一情况将随着卫星星座的完善、地面跟踪站在全球逐步建设及BDS相关改正模型的完善而得到改善。
4 结论本文利用PANDA软件的PPP模块,对7个GNSS台站连续2 a以上的BDS和GPS观测资料进行了处理,通过对两种系统处理结果在位置时间序列重复性精度、基线时间序列变化特征及速度场差异的对比分析,主要得到以下几点认识:
(1) 在当前BDS星座尚未部署完全的情况下,可用的MEO和IGSO卫星较少,由于受到GEO卫星的影响较大,BDS在中国大陆的华北和华南大区域范围内,南北向定位精度要显著优于东西向,GPS虽也有这种特征但并不显著。
(2) 考虑如果时间序列拟合残差服从正态分布,在置信水平为95%时的置信区间为[-2RMS2RMS],在此以两倍RMS作为解算精度,则目前BDS的PPP定位精度在水平和垂向分别约为17和40 mm,GPS的PPP定位精度在水平和垂向分别约为9和14 mm。两者相比,前者水平向精度要低于后者1倍,垂向精度低于后者两倍。
(3) 由于目前BDS卫星星座尚不完善,地面跟踪站点亦比较稀疏,再加之其卫星精密轨道与钟差产品的精度也低于GPS以及各种模型的不完善等因素,造成BDS的定位精度要弱于GPS,因此BDS对于检测弱信号的变化也要弱于GPS。
(4) 虽然BDS的PPP定位精度要弱于GPS,但还是能够较好地反映站点间的基线长度与变化速率特征,在基线不超过500 km时,BDS能够监测基线变化率的精度为0.4 mm/a,而这一精度将随基线的缩短进一步提高,即BDS可以用来监测短基线毫米级线性变化速率。
(5) BDS与GPS之间的水平速度场不存在系统性差异,而垂向速度场的偏差,是由当前BDS轨道框架尺度因子波动所致。
总体来说,当前BDS的PPP定位精度要弱于GPS,但其能够准确监测到站点区域的水平速度场及基线速率变化特征,虽然其监测到的垂向速度场误差较大,但这将随着北斗系统星座的完善、地面跟踪站点的加密建设以及各种模型的改进等而减弱,届时BDS的定位精度将得到进一步提高,从而促进BDS在地壳运动监测中的广泛应用。
| [1] |
杨元喜, 李金龙, 徐君毅, 等.
中国北斗卫星导航系统对全球PNT用户的贡献[J]. 科学通报, 2011, 56(26): 2813–2819.
YANG Yuanxi, LI Jinlong, XU Junyi, et al. Contribution of the Compass Satellite Navigation System to Global PNT Users[J]. Chinese Science Bulletin, 2011, 56(26): 2813–2819. |
| [2] |
杨元喜, 李金龙, 王爱兵, 等.
北斗区域卫星导航系统基本导航定位性能初步评估[J]. 中国科学:地球科学, 2014, 44(1): 72–81.
YANG Yuanxi, LI Jinlong, WANG Aibing, et al. Preliminary Assessment of the Navigation and Positioning Performance of Beidou Regional Navigation Satellite System[J]. Science China: Earth Sciences, 2014, 44(1): 72–81. |
| [3] |
施闯, 赵齐乐, 李敏, 等.
北斗卫星导航系统的精密定轨与定位研究[J]. 中国科学:地球科学, 2012, 42(6): 854–861.
SHI Chuang, ZHAO Qile, LI Min, et al. Precise Orbit Determination of Beidou Satellites with Precise Positioning[J]. Science China: Earth Sciences, 2012, 42(6): 854–861. |
| [4] | LI Min, QU Lizhong, ZHAO Qile, et al. Precise Point Positioning with the BeiDou Navigation Satellite System[J]. Sensors, 2014, 14(1): 927–943. |
| [5] |
朱永兴, 冯来平, 贾小林, 等.
北斗区域导航系统的PPP精度分析[J]. 测绘学报, 2015, 44(4): 377–383.
ZHU Yongxing, FENG Laiping, JIA Xiaolin, et al. The PPP Precision Analysis Based on BDS Regional Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(4): 377–383. DOI:10.11947/j.AGCS.2015.20140082 |
| [6] | STEIGENBERGER P, HUGENTOBLER U, HAUSCHILD A, et al. Orbit and Clock Analysis of Compass GEO and IGSO Satellites[J]. Journal of Geodesy, 2013, 87(6): 515–525. DOI:10.1007/s00190-013-0625-4 |
| [7] | ZHAO Qile, GUO Jing, LI Min, et al. Initial Results of Precise Orbit and Clock Determination for COMPASS Navigation Satellite System[J]. Journal of Geodesy, 2013, 87(5): 475–486. DOI:10.1007/s00190-013-0622-7 |
| [8] | LOU Yidong, LIU Yang, SHI Chuang, et al. Precise Orbit Determination of BeiDou Constellation: Method Comparison[J]. GPS Solutions, 2016, 20(2): 259–268. DOI:10.1007/s10291-014-0436-y |
| [9] | GUO Jing, XU Xiaolong, ZHAO Qile, et al. Precise Orbit Determination for Quad-constellation Satellites at Wuhan University: Strategy, Result validation, and Comparison[J]. Journal of Geodesy, 2016, 90(2): 143–159. DOI:10.1007/s00190-015-0862-9 |
| [10] | LOU Yidong, ZHENG Fu, GU Shengfeng, et al. Multi-GNSS Precise Point Positioning with Raw Single-frequency and Dual-frequency Measurement Models[J]. GPS Solutions, 2016, 20(4): 849–862. DOI:10.1007/s10291-015-0495-8 |
| [11] |
陈良, 耿长江, 周泉.
北斗/GPS实时精密卫星钟差融合解算模型及精度分析[J]. 测绘学报, 2016, 45(9): 1028–1034.
CHEN Liang, GENG Changjiang, ZHOU Quan. Estimation Model and Accuracy Analysis of Beidou/GPS Real-time Precise Satellite Clock Error Integrated Resolving[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(9): 1028–1034. DOI:10.11947/j.AGCS.2016.20150296 |
| [12] | GENG Jianghui, JIANG Peng, LIU Jingnan. Integrating GPS with GLONASS for High-Rate Seismogeodesy[J]. Geophysical Research Letters, 2017, 44(7): 3139–3146. DOI:10.1002/2017GL072808 |
| [13] | GENG Tao, XIE Xin, FANG Rongxin, et al. Real-time Capture of Seismic Waves Using High-Rate Multi-GNSS Observations: Application to the 2015Mw 7.8 Nepal Earthquake[J]. Geophysical Research Letters, 2016, 43(1): 161–167. DOI:10.1002/2015GL067044 |
| [14] | BLEWITT G. An Automatic Editing Algorithm for GPS Data[J]. Geophysical Research Letters, 1990, 17(3): 199–202. DOI:10.1029/GL017i003p00199 |
| [15] | SAASTAMOINEN J. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging Satellites[M]//HENRIKSEN S W, MANCINI A, CHOVITZ B H. The Use of Artificial Satellites for Geodesy. Washington: American Geophysical Union, 1972: 247-251. |
| [16] | NIELL A E. Global Mapping Functions for the Atmosphere Delay at Radio Wavelengths[J]. Journal of Geophysical Research: Solid Earth, 1996, 101(B2): 3227–3246. DOI:10.1029/95JB03048 |
| [17] | BÖHM J, HEINKELMANN R, SCHUH H. Short Note: A Global Model of Pressure and Temperature for Geodetic Applications[J]. Journal of Geodesy, 2007, 81(10): 679–683. DOI:10.1007/s00190-007-0135-3 |
| [18] |
张小红, 左翔, 李盼, 等.
BDS/GPS精密单点定位收敛时间与定位精度的比较[J]. 测绘学报, 2015, 44(3): 250–256.
ZHANG Xiaohong, ZUO Xiang, LI Pan, et al. Convergence Time and Positioning Accuracy Comparison between BDS and GPS Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(3): 250–256. DOI:10.11947/j.AGCS.2015.20130771 |
| [19] |
王阅兵, 游新兆, 金红林, 等.
北斗导航系统与GPS精密单点定位精度的对比分析[J]. 大地测量与地球动力学, 2014, 34(4): 110–116.
WANG Yuebing, YOU Xinzhao, JIN Honglin, et al. Accuracy Compariison of Precise Point Positioning of BeiDou Navigation System with GPS[J]. Journal of Geodesy and Geodynamics, 2014, 34(4): 110–116. |
| [20] |
石强, 戴吾蛟, 曾凡河, 等.
BDS多路径效应特征及其对静态基线解精度的影响[J]. 大地测量与地球动力学, 2016, 36(10): 874–878.
SHI Qiang, DAI Wujiao, ZENG Fanhe, et al. The Characteristics of BDS Carrier Phase Multipath and Its Effects on Static Baseline Solution[J]. Journal of Geodesy and Geodynamics, 2016, 36(10): 874–878. |
| [21] |
黄声享, 李沛鸿, 杨保岑, 等.
GPS动态监测中多路径效应的规律性研究[J]. 武汉大学学报(信息科学版), 2005, 30(10): 877–880.
HUANG Shengxiang, LI Peihong, YANG Baocen, et al. Study on the Characteristics of Multipath Effects in GPS Dynamic Deformation Monitoring[J]. Geomatics and Information Science of Wuhan University, 2005, 30(10): 877–880. |
| [22] |
黄立人.
GPS基准站坐标分量时间序列的噪声特性分析[J]. 大地测量与地球动力学, 2006, 26(2): 31–33, 38.
HUANG liren. Noise Properties in Time Series of Coordinate Component at GPS fiducial stations[J]. Journal of Geodesy and Geodynamics, 2006, 26(2): 31–33, 38. |
| [23] |
田云锋, 沈正康.
GPS坐标时间序列中非构造噪声的剔除方法研究进展[J]. 地震学报, 2009, 31(1): 68–81.
TIAN Yunfeng, SHEN Zhengkang. Progress on Reduction of Non-Tectonic Noise in GPS Position Time Series[J]. Acta Seismologica Sinica, 2009, 31(1): 68–81. |
| [24] |
魏娜, 施闯, 刘经南.
地表负载及GPS测站分布对参考框架转换的影响分析[J]. 地球物理学报, 2016, 59(2): 484–493.
WEI Na, SHI Chuang, LIU Jingnan. Effects of Surface Loading and Heterogeneous GPS Network on Helmert Transformation[J]. Chinese Journal of Geophysics, 2016, 59(2): 484–493. DOI:10.6038/cjg20160208 |
| [25] | ALTAMIMI Z, MÉTIVIER L, COLLILIEUX X. ITRF2008 Plate Motion Model[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 2012, 117(B7): B07402. |


