2. 海军大连舰艇学院海洋测绘工程军队重点实验室, 辽宁 大连 116018;
3. 地理信息工程国家重点实验室, 陕西 西安 710054;
4. 海军出版社, 天津 300450
2. Key Laboratory of Hydrographic Surveying and Mapping of PLA, Dalian Naval Academy, Dalian 116018, China;
3. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China;
4. Navy Press, Tianjin 300450, China
当前,多波束测深系统已成为海底地形探测的主要设备,但在测量过程中由于仪器自噪声、海况因素、设备参数设置不合理及海中生物的影响,导致多波束测深数据不可避免地存在较多粗差,严重影响了海底地形的真实表达[1-2]。为了提高多波束测深数据的精度,需要对其进行滤波处理。依据多波束测深数据粗差探测手段的不同,多波束测深数据滤波方法可大致划分为交互式滤波和自动滤波两类[2-3]。交互式滤波是一个主观识别和标定错误的过程,即在三维可视的环境下,由作业人员人工标定测深数据中的异常值,滤波效率相对较低,且严重依赖作业人员的主观经验;为克服交互式滤波的缺点,国内外学者通过将数理统计、误差处理、地形分析等理论和方法融入粗差探测技术中,提出了诸多自动滤波方法[4]。文献[5]提出了一种基于加权平均移动模型的深度滤波方法,在假设海底地形连续的条件下识别多波束条带内标准偏差异常高于平均值的水深点,并运用2σ或3σ准则对多波束数据进行滤波。文献[6]将趋势面滤波的思想引入到多波束测深数据异常值判定中,利用一定范围内的水深值z和平面坐标(x, y)进行多项式趋势面拟合,并结合2σ或3σ准则对异常值进行判定。文献[2]针对基于函数/统计推值的比较判别法在检验异常数据时出现的异常值“遮蔽”现象,将抗差估计理论引入到检验异常值的推值比较法中,提出了一种基于抗差估计的选权迭代插值比较检验法,采用简单加权平均数模型作为判别异常值的推值模型,在被检测点邻域内选取正确观测数据,拒绝不正确或者带有粗差的数据,提高了检测方法的抗差性。文献[7-12]提出了一种基于不确定度理论的多波束测深数据滤波算法-CUBE(combined uncertainty and bathymetry estimator)算法,该算法主要利用测深数据的深度信息和不确定度信息,通过卡尔曼滤波方法剔除数据中可能存在的粗差,滤波效果较为理想。文献[3]提出了一种基于中值滤波、局部方差检测和小波分析理论的联合滤波方法,该方法中的局部方差检测模型避免了中值滤波对海底地形细节的破坏,小波分析理论增强了数据的抗差性和算法的可靠性。文献[13]引入了观测值识别变量的概念,构建了识别变量均值漂移模型,提出了一种基于识别变量后验概率的粗差探测Bayes方法。在此基础上,文献[14]将该粗差探测Bayes方法应用于多波束测深数据异常值探测中,通过构造水深观测识别变量判别模型对异常值的后验概率进行分析,判断和识别水深观测数据中的异常值。文献[15]针对最小二乘支持向量机(LS-SVM)在构造海底趋势面过程中存在的数值解稀疏性较差以及样本数据偏差引起的拟合曲面形态失真等问题,提出了一种基于水深不确定度调控的趋势面滤波方法,利用水深不确定度调控模型对训练样本数据进行形态优化,构造出反映海底实际变化的趋势面,实现对测深异常值的有效剔除。
在诸多自动滤波方法中,由于趋势面滤波法设计思想简单、预设参数较少、易于并行计算等特点,受到了海洋测绘学者的广泛关注[7, 14-17]。然而由于海底地形的复杂多变以及局部曲面拟合范围的不确定性,趋势面滤波法存在其固有的技术缺陷,主要体现在:①由于海底地形复杂多变,局部曲面拟合范围不易确定,单一的曲面拟合函数无法全面反映海底的实际地形,极易出现粗差滤除不彻底或误将正常水深判定为粗差点进而被滤除的情况;②当局部曲面拟合范围内存在较大的突变粗差点时,将会导致正常水深点与所拟合的趋势面之间产生较大偏差,进而影响正常水深点的判定结论,当局部曲面拟合范围内存在的粗差点相对集中且成簇出现时,趋势面滤波法将无法检测出所有粗差点,相反可能出现将粗差点误判为正常水深点保留,而将正常水深点误判为粗差点滤除的情况;③趋势面滤波法的构建前提是海底地形的连续性,当海底出现断裂点(如断崖)或障碍物(如暗礁或沉船)时,趋势面滤波法可能导致断裂点或障碍物被不合理滤除的情况。为解决上述问题,本文提出了一种基于自然邻点影响域的多波束测深数据趋势面滤波改进算法。该算法在引入散乱水深点局部最小范围-自然邻点影响域的概念的基础上,通过构造影响域内特定局部坐标系下的统一曲面拟合函数,进行传递式迭代趋势面滤波,逐步滤除影响正常水深点判定的粗差数据,并针对突变地形边界点难以确定的问题,根据边界点在其相邻邻域地形内连续性不一致的特性,建立了面向突变地形边界点的判断准则,最后通过实验验证了改进算法的有效性。
1 传统趋势面滤波法及其存在问题 1.1 传统趋势面滤波法构建原理趋势面滤波法是一种以曲面拟合函数为数值分析基础的误差处理算法[16-18]。其算法构建原理为:依据波束脚印的深度值和平面位置坐标,构造出反映海底地形变化趋势的多项式曲面函数,计算和统计实测水深值与所构造趋势面间的深度偏离量,结合误差处理理论建立粗差数据的判定准则,实现多波束测深数据的自动滤波[16-18]。趋势面滤波法中曲面拟合函数的一般形式为[19]
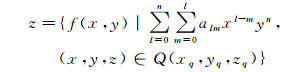 (1)
(1)
式中,z表示波束脚印的深度值;(x, y)表示波束脚印的平面位置坐标;alm表示各多项式系数;n表示多项式总阶数;Q(xq, yq, zq)表示以待检测点q(xq, yq, zq)为中心的曲面拟合函数f(x, y)的局部曲面拟合范围。趋势面滤波法的关键在于多项式总阶数n与局部曲面拟合范围Q的选择[4]。相关研究表明:局部曲面拟合范围Q选择过小且多项式总阶数n选择过高,可能存在粗差点未被有效滤除的情况;范围Q过大且总阶数n过低,可能引起海底有效地形信息的丢失[4]。一般情况下,多项式总阶数n与局部曲面拟合范围Q由拟合范围内的海底地形复杂度f来确定[4]。
在假设局部海底地形复杂度适中且变化不大的前提下,局部曲面拟合范围Q可以待检测点q(xq, yq, zq)为中心且包含20~30个水深点的区域范围代替,多项式总阶数n控制在3阶以内(1≤n≤3)[15, 20-21]。为更好地说明问题,本文以多项式总阶数n=2为例,阐述趋势面滤波法的滤波原理。
将n=2代入式(1),并将其改写为AX=L的误差方程形式,其中
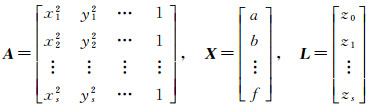 (2)
(2)
根据最小二乘条件: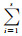
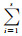
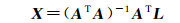 (3)
(3)
根据局部曲面拟合范围Q内的平面坐标(xi, yi)和水深值zi拟合出趋势面后,趋势面滤波的异常值判断准则为[4]
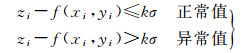 (4)
(4)
式中,k=2或3;σ表示局部曲面拟合范围Q内各实测水深值与所构造趋势面间的深度偏离量均方差。
1.2 传统趋势面滤波法存在的主要问题由1.1的分析可知,趋势面滤波法的关键在于多项式总阶数n与局部曲面拟合范围Q的匹配。传统趋势面滤波法中上述相关参数的经验取值尽管在一定程度上简化了算法的分析过程,提高了多波束测深数据的滤波效率,但不同经验参数的取值将引起局部曲面拟合范围Q内水深点位分布与数量的较大差异,进而导致曲面拟合函数与实际海底地形匹配的不确定性问题。因此,定量分析多项式总阶数n与局部曲面拟合范围Q之间的匹配关系,建立顾及海底地形复杂度的多项式曲面函数,将是该滤波法改进方向之一。
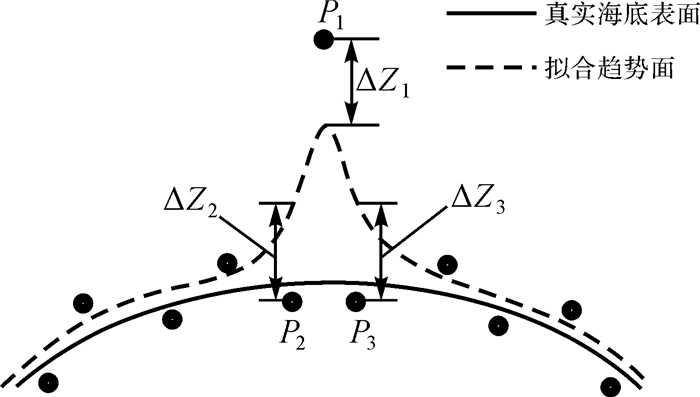
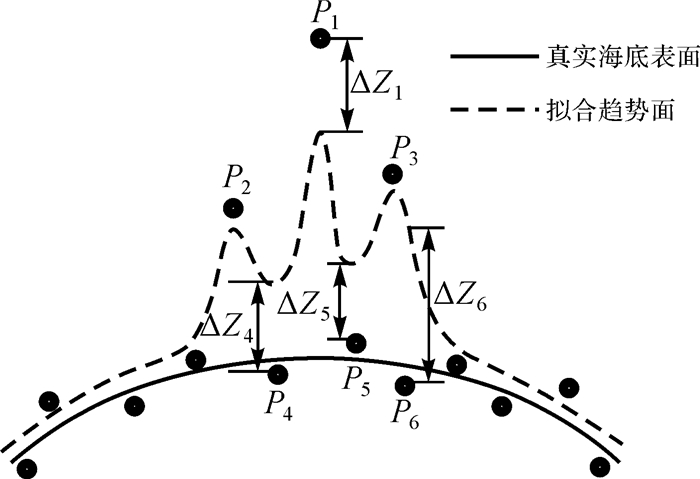
其次,传统趋势面滤波法在构造趋势面过程中所采用的拟合数据可能含有粗差,该粗差数据点可能单个出现,也可能多个成簇出现[19, 21]。如图 1和图 2所示,图 1为粗差点单个出现的情况,假设P1点为局部曲面拟合范围Q内的单个粗差点且其粗差值较大,则由范围Q内的水深点所构造的趋势面将在P1点处产生较大的形态突变,使P2和P3点与所构造的趋势面间产生较大的偏差ΔZ2和ΔZ3,从而误将正常点P2和P3判定为粗差点;图 2为粗差点多个成簇出现的情况,假设P1、P2和P3点为局部曲面拟合范围Q内的多个成簇出现的粗差点群且P1点的粗差值远大于P2和P3点的粗差值,则所构造的趋势面将在P1点处产生较大的形态突变,可能造成P2和P3点与趋势面间的偏差小于限差,被误判为正常点,而正常点P4、P5和P6与所构造的趋势面间产生较大的偏差ΔZ4、ΔZ5和ΔZ6,从而误将正常点P4、P5和P6判定为粗差点。这些问题产生的原因在于拟合海底地形表面的点中含有粗差,拟合出的趋势面不能合理反映海底地形变化。因此,研究如何从所选范围内选取可信度较高的水深点,拒绝不正确或带有粗差的可疑点,以此来拟合地形趋势面,将是该滤波法改进的另一方向。
|
| 图 1 单个粗差点影响滤波示意图 Fig. 1 The situation of single gross error point |
|
| 图 2 多个粗差点成簇影响滤波示意图 Fig. 2 The situation of conglomerate multiple gross error points |
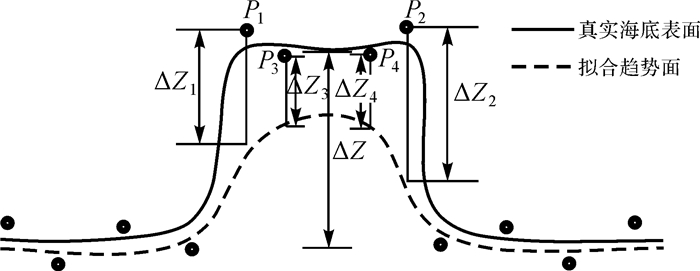
最后,由于传统趋势面滤波法是在假设海底地形连续的前提下进行的,当海底出现局部突变地形(断崖或障碍物)且其偏差大于限差时,可能出现突变地形整体或部分水深点被不合理剔除的情况。如图 3所示,P1和P2点为突变地形的边界点,P3和P4点为突变地形上的局部连续点。当局部曲面拟合范围Q大于突变地形点群时,若突变地形点群占局部曲面拟合范围Q内总点数的比重较小,对所构造的趋势面影响较小,可能使得P1-P4点与所构造的趋势面间的偏差ΔZ1—ΔZ4均大于限差,则突变地形点群将被误当作成簇出现的粗差点群,导致突变地形被不合理剔除;若突变地形点群占拟合范围Q内总点数的比重较大,对所构造的趋势面影响较大,可能使得突变地形中部的P3和P4点与所构造的趋势面间的偏差ΔZ3和ΔZ4小于限差,而P1和P2点与所构造的趋势面间的偏差ΔZ1和ΔZ2大于限差,导致突变地形的边界点P1和P2被不合理剔除,使海底地形不能精确地被表达。因此,有效区分和辨别成簇出现的粗差点群和突变地形点群及保留海底突变地形中的边界点,进一步提高海底地形表达精度,将是该滤波法改进的又一方向。
|
| 图 3 突变地形点群影响滤波示意图 Fig. 3 The situation of point group on the mutation terrain |
2 趋势面滤波改进算法 2.1 局部曲面拟合范围及拟合函数的确定 2.1.1 局部曲面拟合范围的确定
参照文献[23],对于曲面S中任意一点p处的局部曲面规范形式定义为
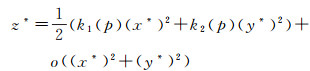 (5)
(5)
式中,(x*,y*,z*)为局部曲面在局部坐标系的三维坐标;k1(p)和k2(p)分别为p点相应的两个主曲率;该局部坐标系以p点为原点,以两主曲率的方向为x轴和y轴的方向,以局部曲面的法向量为z轴方向,o((x*)2+(y*)2)为高阶无穷小量。
对式(5)分析可知,当k1(p)和k2(p)同号且均不为零时,局部曲面近似为椭圆抛物面;当k1(p)和k2(p)异号且均不为零时,局部曲面近似为双曲抛物面;当k1(p)和k2(p)有且只有一个为零时,局部曲面近似为抛物柱面。因此,任意曲面S在点p处的局部曲面为一个二次抛物曲面。
鉴于曲面S中任意一点p处的局部曲面规范形式相对简单,且严格微分意义下的局部曲面地形复杂度近似为零,若采用任意一点周围的若干点所组成的局部拟合范围近似代表微分意义下的局部曲面,则该局部离散点拟合范围应具有最小的地形复杂度。根据文献[19]中对地形复杂度f与间距为d的所有地形点的自相关系数R(d)间关系的描述可知,自相关系数R(d)越大,地形复杂度f越小。自相关系数R(d)的曲线可由高斯函数来描述,其公式为
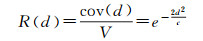 (6)
(6)
式中,cov(d)是间距为d的所有地形点之间的协方差;V为由所有地形点计算得到的方差;c为cov(d)接近零时的相关间距。
由式(6)可知,自相关系数R(d)与各点间的间距d有关,d越小,R(d)越大。因此,为了降低拟合范围内的地形复杂度f,可在待检测点q处选择各方向距离最近的点组成局部曲面拟合范围Q,该拟合范围内的地形复杂度f最小。而在Voronoi图非结构化网格中,q点各方向距离最近的点为其对应的Voronoi单胞的邻接离散点,被称为自然邻点[24-27],由每一离散点的自然邻点所构成的局部范围可称为该点的自然邻点影响域。根据多波束测深系统海底跟踪控制技术的相关知识可知,一般认为在任意方向至少有连续记录的3~5个测深点才可以判断海底是否存在凹(凸)地形[27],因此自然邻点影响域也可认为是海底地形表达的最小局部范围。因此,由自然邻点影响域组成的拟合范围可近似代表微分意义下的局部曲面。对于如何快速确定任意离散点的自然邻点影响域,可参照文献[28]或文献[29]中描述的方法,根据Delaunay三角网构建基本原则-最大最小角准则或空外接圆特性来快速寻找局部范围内任意一点的自然邻点。
由上述分析可知,若采用自然邻点影响域作为趋势面拟合范围,可将复杂多变的海底地形表面分割成若干个由自然邻点影响域构成的局部简单地形,且地形形态单一,均可采用算法相对简单的低阶固定多项式曲面函数进行拟合。此外,自然邻点影响域作为海底地形表达的最小局部范围,使得海底地形易于精细化表达,更有利于海底微地貌或微小障碍物(如暗礁或沉船)的识别和判定。
2.1.2 曲面拟合函数的确定通常自然邻点影响域范围内的点数较少(4≤m < 27)[21],若仍采用完整的二次多项式来拟合自然邻点影响域内的二次抛物面,将因点数不够而导致拟合过程终止。为解决此问题,需要减少曲面拟合函数中的多项式系数,对自然邻点影响域范围内的曲面拟合函数进行统一确定。
当局部曲面所在的局部坐标系的各坐标轴方向按照式(6)定义后,曲面拟合函数可以被简化成z*=a(x*)2+b(y*)2的形式,但在实际操作过程中,局部曲面的两个主曲率方向很难直接确定,而其法向量方向可直接近似获得,若在p点建立以p点为原点,以局部曲面的法向量为z轴方向,x轴和y轴方向任意设置的新局部坐标系,假设新局部坐标系下的三维坐标为(x′, y′, z′),则两个局部坐标系各点的关系为
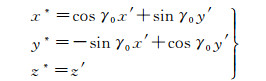 (7)
(7)
式中,γ0为z轴旋转角度。
不考虑式(5)中的高阶无穷小量,将式(7)代入式(5)中,可得任意离散点的自然邻点影响域内的局部曲面在所构建的新局部坐标系下的二次抛物面多项式函数为
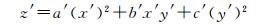 (8)
(8)
式中,a′、b′、c′表示整理后的各多项式系数,为待求参数。
由于式(8)所采用的新局部坐标系与多波束测深数据所采用的全局坐标系存在差异,因此,需要将多波束测深数据转换至新局部坐标系下的数据,才可采用式(8)进行曲面拟合。
对于空间坐标系转换可采用变换矩阵来描述。假设全局坐标系为A(x, y, z),局部坐标系为B(x*, y*, z*),p点坐标为(x0,y0,z0),坐标系转换过程为将全局坐标系A的原点平移至p点,使两坐标系原点重合,绕局部坐标系原点p旋转A的坐标轴,使其z轴与B的z轴重合即可[30]。整个过程的数学描述为
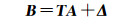 (9)
(9)
式中,Δ为坐标系平移矩阵;T为坐标系旋转矩阵,T=Tx×Ty×Tz,各矩阵的计算公式详见文献[30]。
在旋转过程中,z轴不进行旋转,而对于x轴和y轴的旋转角度α和β,可采用局部曲面的法向量来求得。首先对自然邻点影响域内的数据用最小二乘法进行平面拟合,用拟合平面的法向量N(nx, ny, nz)来近似代替p点的法向量,则可得旋转角度α和β为
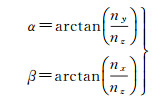 (10)
(10)
最后采用式(8)进行曲面拟合,由于曲面拟合过程中只存在3个未知数,因此,自然邻点影响域内的点数(m≥4)完全满足曲面拟合要求。
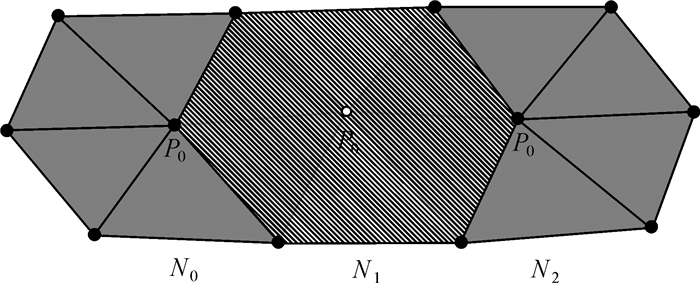
2.2 传递式迭代趋势面滤波方法针对拟合数据中含有粗差而导致所构造的趋势面与实际地形趋势面之间存在较大偏差这一问题,借鉴抗差M估计滤波方法[2],本文提出传递式迭代趋势面滤波的方法。如图 4所示,由离散点集N0、N1和N2所组成的范围分别是以P0、P1和P2点为中心点的连续3个自然邻点影响域,假设N0点集的自然邻点影响域已进行趋势面滤波处理,以N1点集的自然邻点影响域为例,所提传递式迭代趋势面滤波法的具体过程如下:
|
| 图 4 迭代趋势面滤波过程示意图 Fig. 4 The process of iterative trend surface filtering |
(1) 首先将N0点集中已经确定含有粗差的水深点利用其拟合的趋势面进行改正,这样可保证N0∩N1点集中的水深点不含粗差。
(2) 然后用N1点集的自然邻点影响域内所有的水深点来拟合地形表面,找出其中大于2倍(或3倍)中误差的水深点,将其存入可疑点集Ω中。
(3) 用(N1-Ω)点集的水深点继续拟合,重复步骤(2),直到无水深点存入可疑点集Ω中,用(N1-Ω)点集所拟合的地形趋势面达到稳定状态,得到最终的海底地形趋势面。
(4) 最后计算可疑点集Ω中的水深点与最终海底地形趋势面之间的最大偏差,以2倍(或3倍)中误差为判断标准,从可疑点集Ω中得出最终的粗差点集Ω′。
如图 4所示,通过步骤(1)可使得N0∩N1点集中的水深点不含粗差,这样可以保证N1点集内至少有4个不含粗差的水深点(m≥4),因此在迭代过程中将不会出现由于点数不够而导致拟合过程终止情况的发生。
2.3 突变地形边界点判断准则当海底出现突变地形(断崖或障碍物)且其偏差大于限差时,可能出现突变地形点群被误认为是成簇出现的粗差点群或者突变地形中的边界点被不合理剔除等情况。对于突变地形点群被误认为是成簇出现的粗差点群这种情况,由于改进算法采用自然邻点影响域作为趋势面拟合范围,而自然邻点影响域又是海底地形表达的最小局部范围,其可将突出点群表面分割成若干个自然邻点影响域范围,通过判断突出点群表面是否为局部连续的真实地形来区分成簇出现的粗差点群和突变地形点群,进而完整保留突变地形点群上的局部连续点。但对于突变地形中的边界点,由于其既具有突变地形点群局部连续的特性,又具有粗差点群单点突变的特性,采用上述改进算法进行滤波时,仍然将突变地形边界点误判为粗差点滤除,导致突变地形的完整性受损。
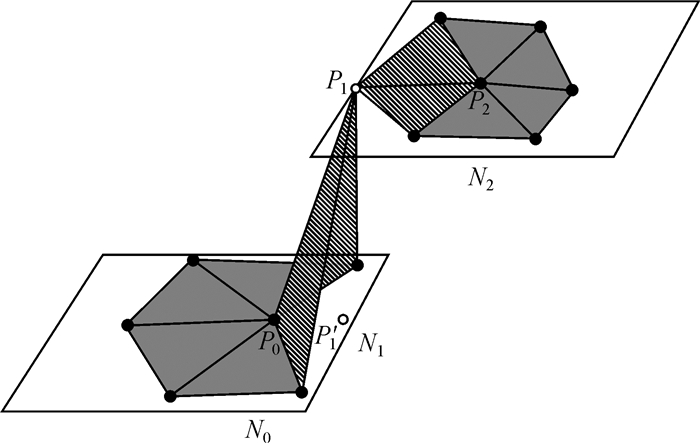
针对这一问题,本文在上述趋势面滤波改进算法中加入突变地形边界点判断准则,避免了突变地形边界点被不合理剔除。如图 5所示,在上述迭代趋势面滤波方法的滤波过程中,假设N0点集的自然邻点影响域在正常的海底地形上,N1点集的自然邻点影响域为正常地形到突变地形的过渡区域,P1点为突变地形边界点,N2点集的自然邻点影响域在突变海底地形上,P2点为突变地形上的局部连续点,所提突变地形边界点的判断准则如下:
|
| 图 5 突变地形边界点判断准则示意图 Fig. 5 The boundary point of mutation terrain detection |
(1) 在N0点集的自然邻点影响域内进行滤波时,将设定P1点为粗差点并将其改正为P′1。
(2) 在N1点集的自然邻点影响域内进行滤波时,将会形成一个曲率变化较大的趋势面,以保证海底地形的连续性。
(3) 在N2点集的自然邻点影响域内进行滤波时,由于N2点集的自然邻点影响域已在突变的海底地形上,应将改正后的P′1点再次设定为粗差点并对其进行改正。
这样在三次趋势面滤波中对于改正前后的P1点是否为粗差点的判定便形成矛盾,而造成这一矛盾的原因是P1点为突变地形边界点,因此根据边界点在其相邻邻域地形内连续性不一致这一特性,可对滤波过程中出现的矛盾点设定为突变地形边界点,对其进行保留操作。
3 试验结果与分析为验证上述改进算法的有效性,本文通过VC++编程实现了基于自然邻点影响域的趋势面滤波改进算法及传统趋势面滤波法,分别采用传统趋势面滤波法、基于自然邻点影响域的趋势面滤波改进算法和当前应用较多的CUBE算法(HIPS & SIPS 6.1软件自带滤波算法)对包含粗差的实测数据和模拟数据进行滤波试验。试验环境为Inter(R)core(TM)i3处理器,主频为3.4 GHz,内存为2 GB,最后利用Surfer8.0软件对试验结果进行了可视化显示及对比分析。
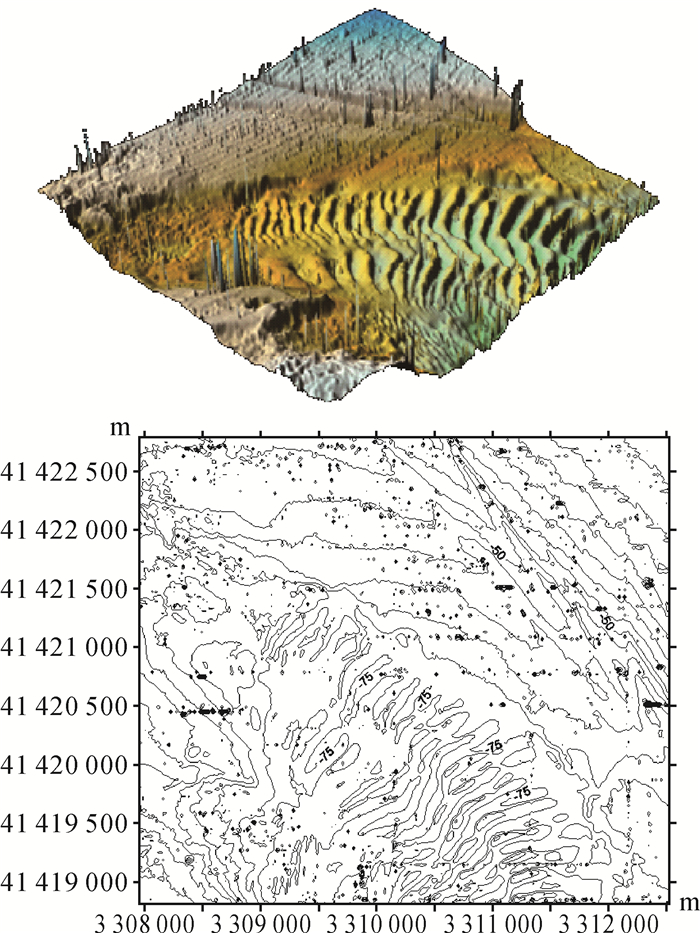
3.1 实测算例实测试验所采用的数据为我国东海某海区的多波束数据,由于边缘波束的数据质量较差,所以只选取靠近中央波束的数据进行拼接,数据共包含716 516个水深点。在算法参数设置中,对于传统趋势面滤波法,采用完整的二次多项式,范围半径根据多波束测深数据密度保证所选范围包含大约30个水深点,粗差判断准则中的k为2;对于其改进算法,k同样设定为2。两种滤波方法耗时分别为2414 s和2643 s,CUBE算法耗时为78 s。最后利用Surfer8.0软件中的反距离加权内插法,对原始多波束测深数据、经传统趋势面滤波法、改进算法和CUBE算法滤波后的多波束测深数据进行插值处理,形成229×200的格网,分别绘制各数据的海底地形表面及等深距为5 m的等深线图,试验结果如图 6、图 7、图 8和图 9所示。此外,还对实测原始多波束数据(A)、经传统趋势面滤波算法(B)、改进算法(C)和CUBE算法(D)滤波后的实测多波束数据中的水深极大值、水深极小值、水深标准方差和数据点数进行了统计分析,结果见表 1。
| 水深值统计 | (A) | (B) | (C) | (D) |
| 极小值/m | -103.33 | -92.550 | -98.838 | -98.260 |
| 极大值/m | -1.55 | -11.244 | -11.136 | -11.126 |
| 标准方差/m | 18.51 | 15.24 | 16.92 | 16.30 |
| 数据点数 | 716 516 | 578 840 | 682 691 | 627 862 |
|
| 图 6 实测原始数据的海底地形表面及等深线图 Fig. 6 The submarine surface and contour map from the measured original data |
|
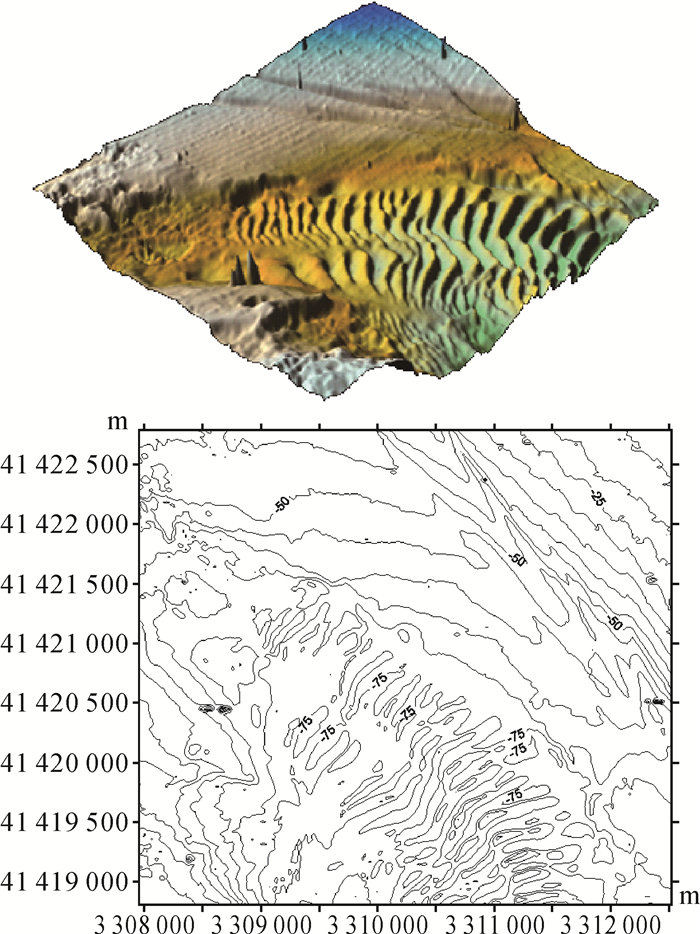
| 图 7 传统趋势面滤波法滤波后的实测数据海底地形表面及等深线图 Fig. 7 The submarine surface and contour map from the measured data after trend surface filtering |
|
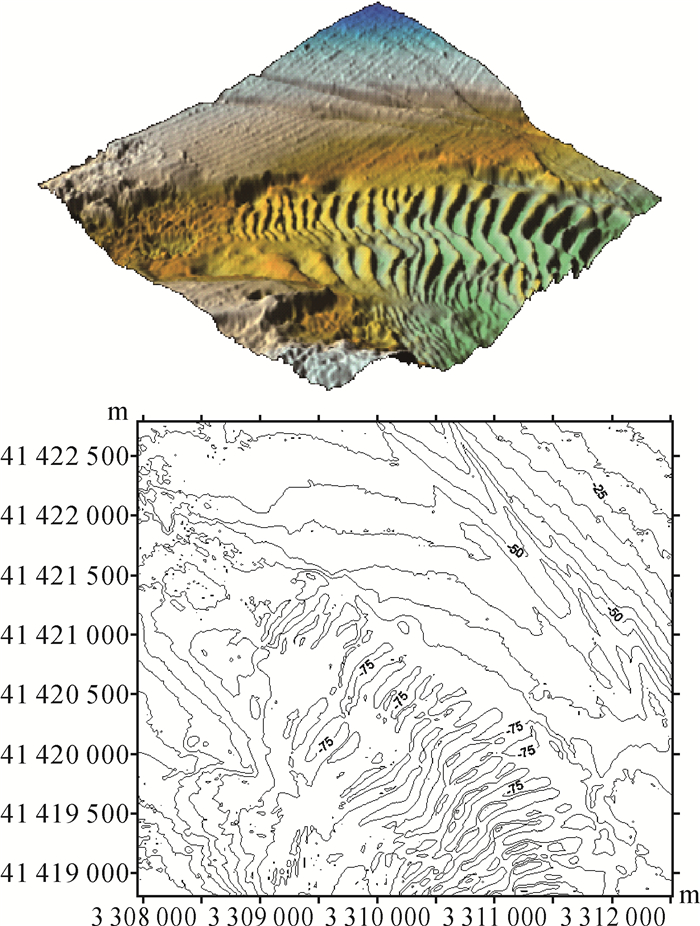
| 图 8 改进算法滤波后的实测数据海底地形表面及等深线图 Fig. 8 The submarine surface and contour map from the measured data after the improved filtering |
|
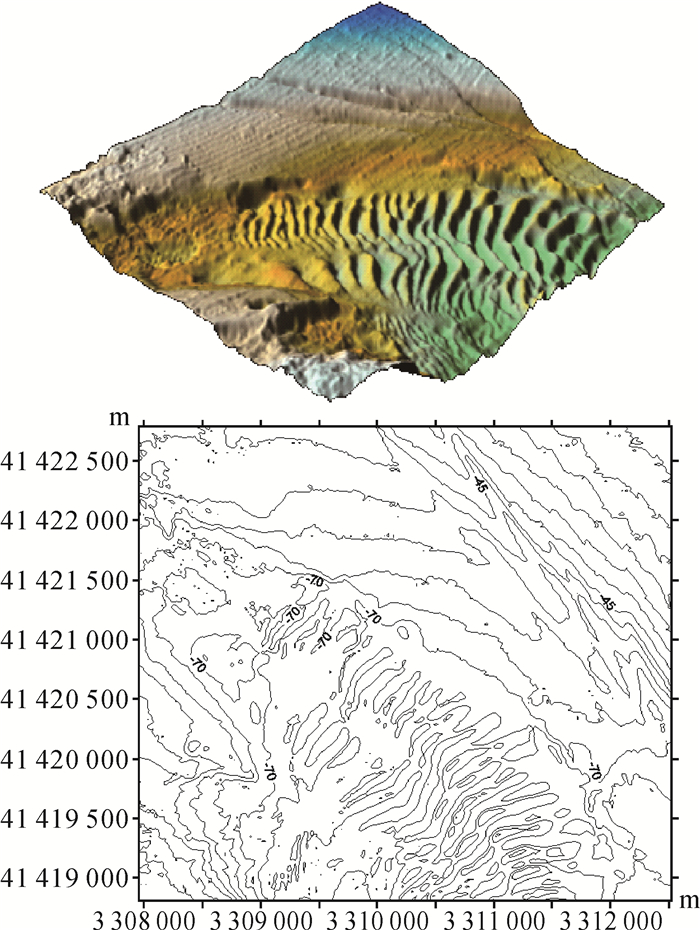
| 图 9 CUBE算法滤波后的实测数据海底地形表面及等深线图 Fig. 9 The submarine surface and contour map from the measured data after the method of CUBE |
由实测算例试验结果对比分析可知:①改进算法和CUBE算法的滤波效果较好,而经传统趋势面滤波法处理后的测深数据仍然包含部分粗差点,这些粗差点主要集中在复杂地区和粗差点成簇出现的区域;②经传统趋势面滤波法、改进算法和CUBE算法处理后的测深数据的水深值范围均小于实测原始数据的水深值范围,说明3种滤波方法均滤掉实测原始数据中的较大粗差点,而传统趋势面滤波法处理后的测深数据仍保留了一部分相对较小的粗差点,这主要是由于传统趋势面滤波法的抗差性较弱,较大粗差点严重影响所构造的趋势面,而产生的异常值“遮蔽”现象;③相比于改进算法,传统趋势面滤波法和CUBE算法处理后的测深数据的海底地形表面相对更加平滑,对应等深线图中代表微小地貌的细部弯曲多数被滤除,相关统计数据诸如水深值范围、标准方差和数据点数的数值表现均相对较小。
需要指出,在无法预先获得真实海底地形的前提下,此类海底地形的相对平滑并不能代表各滤波算法的优劣。主要原因在于平滑处理的海底地形信息低频分量无法确定其是否为水深异常值。尤其在海底地形存在微小地貌的情况下,过度平滑可能造成海底地形表达精度的丢失。本文算法采用自然邻点影响域作为趋势面拟合范围,且其又是海底地形表达的最小局部范围,保证了微小地貌的准确识别,传递式迭代滤波思想的应用更是保证了算法的抗差性。尽管表 1中的试验结论不足以验证改进算法在保留微小地貌方面的优势,但数值统计规律表明改进算法具有识别和保留海底地形信息低频分量的特性。
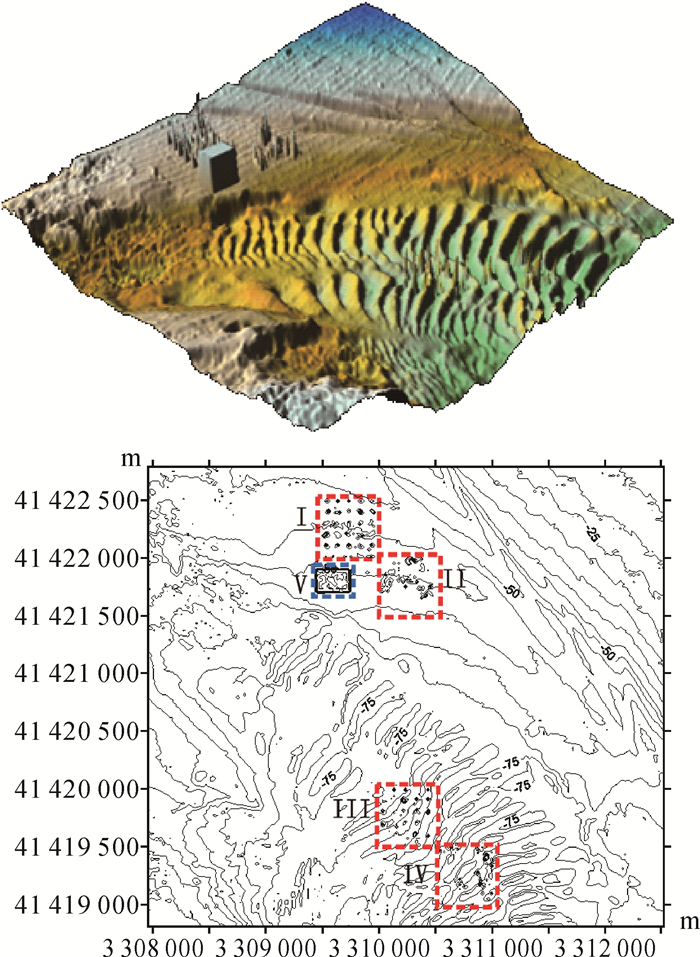
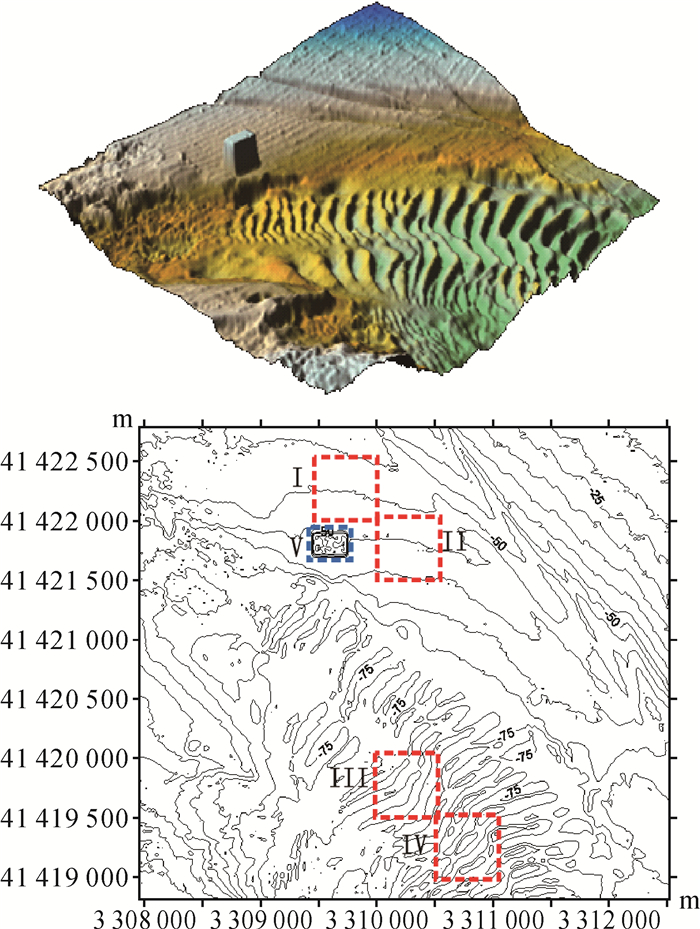
3.2 模拟算例为进一步验证改进算法所具有的海底地形信息低频分量保持特性,以及验证其在突变地形边界点保留方面的优势,本文在上述海区人为设置粗差点及突变地形并进行模拟滤波试验。首先,对上述海区的测深数据以2σ作为粗差判断准则进行人工逐点检查滤波处理,然后,选择测区中的4块小区域(长宽均为500 m),对各小区域内的400个水深点随机加入大小为3σ~10σ不等的异常值各50个并进行模拟滤波试验。如图 11所示,对4个等大的小区域(红框区域)进行编号,分别为Ⅰ~Ⅳ,其中Ⅰ和Ⅱ区域为平坦地形,Ⅲ和Ⅳ区域为复杂地形,在Ⅰ和Ⅲ区域内均匀选取400个水深点并随机加入异常值,以模拟平坦地形和复杂地形的拟合范围内单个粗差点出现的情况;在Ⅱ和Ⅳ区域内随机选取25个水深点,在每个水深点的拟合范围内随机加入大小为3σ~10σ不等的异常值各两个,以模拟平坦地形和复杂地形的拟合范围内多个粗差点成簇出现的情况。此外,为了验证突变地形边界点判断准则的可行性,在平坦区域设置了一个凸起的长方体(蓝框区域,长为300 m,宽为200 m,水深值为-35 m)作为突变地形,编号为Ⅴ。最后利用Surfer8.0软件绘制人工处理后的原始数据(A)、加粗差后的模拟数据(B)、经传统趋势面滤波法(C)、改进算法(D)和CUBE算法(E)滤波后的模拟多波束测深数据的海底地形表面及等深距为5 m的等深线图,试验结果如图 10-图 14所示。此外,还对各小区域内的水深极大值、水深极小值、水深标准方差、数据点数和各方法粗差检测正确率进行了统计,结果见表 2和表 3所示。
| 水深值统计 | 极小值/m | 极大值/m | 标准方差/m | 数据点数 |
| A(Ⅰ) | -54.10 | -43.90 | 2.64 | 8820 |
| B(Ⅰ) | -54.10 | -38.20 | 5.84 | 8820 |
| C(Ⅰ) | -54.10 | -44.30 | 2.15 | 6694 |
| D(Ⅰ) | -54.10 | -43.90 | 2.51 | 8267 |
| E(Ⅰ) | -54.10 | -44.04 | 2.36 | 8021 |
| A(Ⅱ) | -61.64 | -49.36 | 2.62 | 9085 |
| B(Ⅱ) | -61.64 | -29.38 | 5.75 | 9085 |
| C(Ⅱ) | -57.82 | -42.67 | 2.24 | 6275 |
| D(Ⅱ) | -61.64 | -49.23 | 2.56 | 8521 |
| E(Ⅱ) | -58.94 | -48.67 | 2.39 | 8143 |
| A(Ⅲ) | -86.27 | -73.57 | 3.35 | 8945 |
| B(Ⅲ) | -86.27 | -54.15 | 6.57 | 8945 |
| C(Ⅲ) | -84.53 | -76.42 | 2.39 | 6095 |
| D(Ⅲ) | -86.27 | -73.95 | 2.89 | 8370 |
| E(Ⅲ) | -85.04 | -73.69 | 2.54 | 7901 |
| A(Ⅳ) | -90.30 | -74.14 | 3.51 | 8822 |
| B(Ⅳ) | -90.30 | -58.16 | 6.49 | 8822 |
| C(Ⅳ) | -88.04 | -70.31 | 2.32 | 5211 |
| D(Ⅳ) | -90.30 | -73.96 | 2.86 | 8164 |
| E(Ⅳ) | -89.42 | -73.21 | 2.58 | 7902 |
| B(Ⅴ) | -35.0 | -35.0 | 0 | 2363 |
| C(Ⅴ) | -35.0 | -35.0 | 0 | 821 |
| D(Ⅴ) | -35.0 | -35.0 | 0 | 2287 |
| E(Ⅴ) | -35.0 | -35.0 | 0 | 1852 |
| (%) | ||||||||
| 粗差值 | 3σ | 4σ | 5σ | 6σ | 7σ | 8σ | 9σ | 10σ |
| C(Ⅰ) | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| D(Ⅰ) | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| E(Ⅰ) | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| C(Ⅱ) | 38 | 74 | 98 | 100 | 100 | 100 | 100 | 100 |
| D(Ⅱ) | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| E(Ⅱ) | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| C(Ⅲ) | 68 | 86 | 100 | 100 | 100 | 100 | 100 | 100 |
| D(Ⅲ) | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| E(Ⅲ) | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| C(Ⅳ) | 22 | 52 | 84 | 100 | 100 | 100 | 100 | 100 |
| D(Ⅳ) | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| E(Ⅳ) | 94 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
|
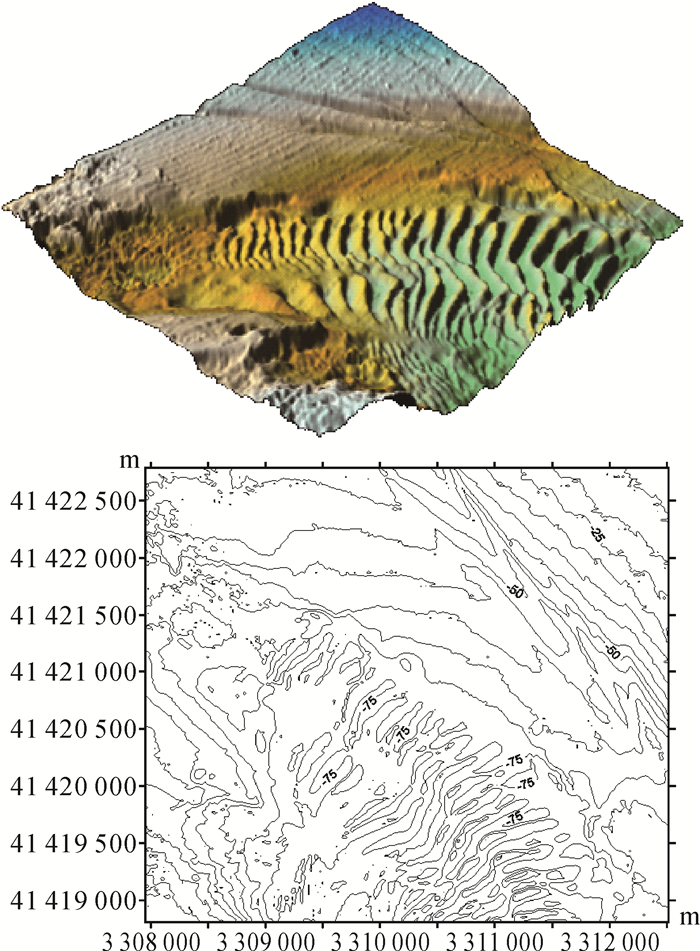
| 图 10 人工处理后的测深数据海底地形表面及等深线图 Fig. 10 The submarine surface and contour map from the measured original data after manual handling |
|
| 图 11 模拟原始数据的海底地形表面及等深线图 Fig. 11 The submarine surface and contour map from the simulative original data |
|
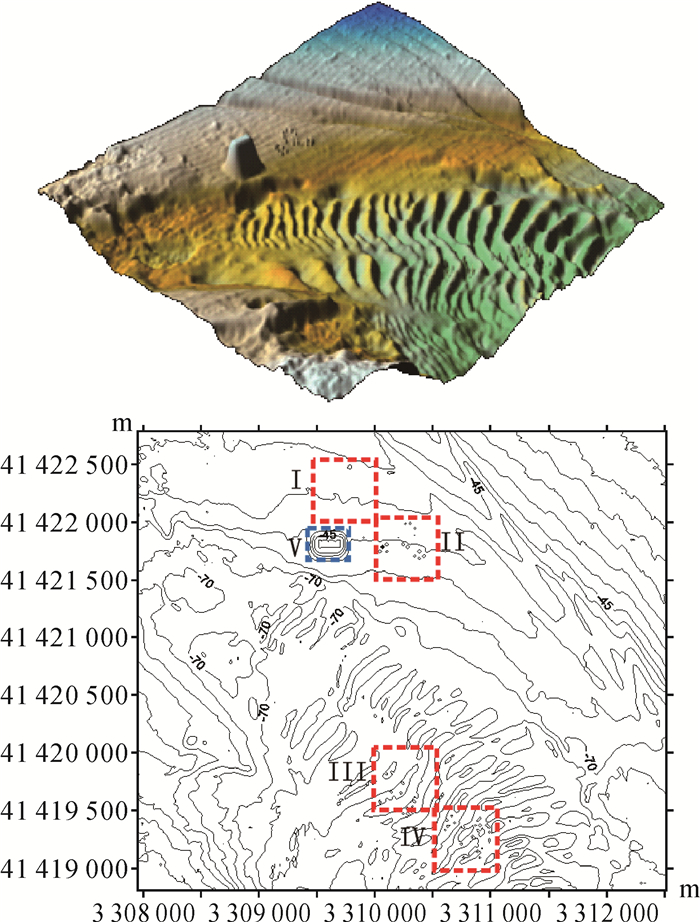
| 图 12 传统趋势面滤波法滤波后的模拟数据海底地形表面及等深线图 Fig. 12 The submarine surface and contour map from the simulative data after trend surface filtering |
|
| 图 13 改进算法滤波后的模拟数据海底地形表面及等深线图 Fig. 13 The submarine surface and contour map from the simulative data after the improved filtering |
|
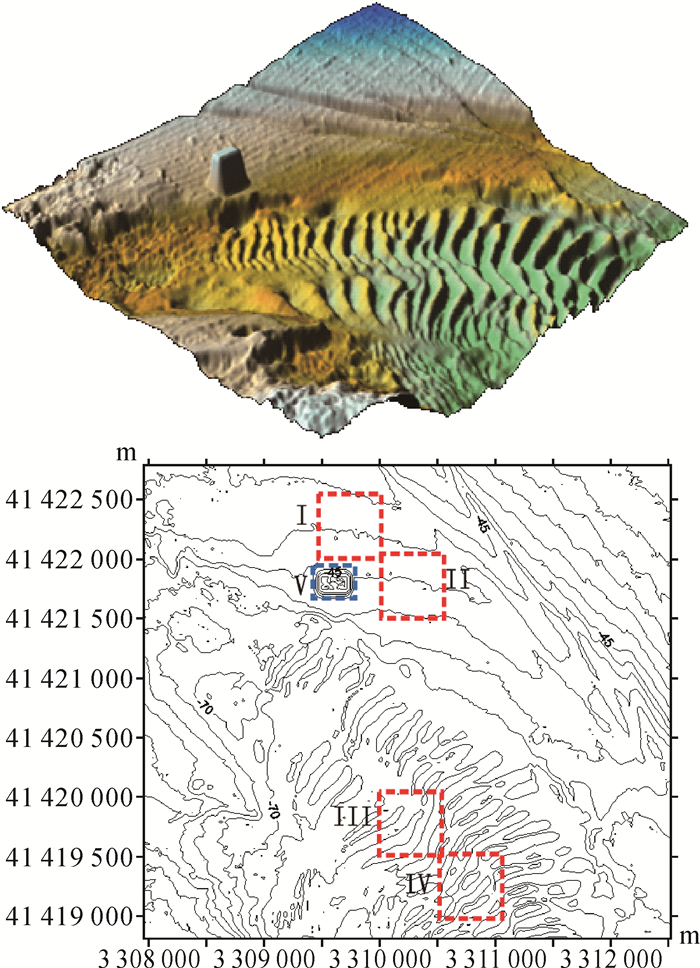
| 图 14 CUBE算法滤波后的模拟数据海底地形表面及等深线图 Fig. 14 The submarine surface and contour map from the simulative data after the method of CUBE |
由模拟算例试验结果对比分析可进一步看出:
(1) 对于平坦海底处单个出现的粗差点(Ⅰ区域),由于海底地形较为简单,各滤波方法所构造的趋势面与真实海底地形之间的偏差较小,3种滤波方法对不同程度的粗差点均具有较好的识别能力。
(2) 对于平坦海底处多个成簇出现的粗差点(Ⅱ区域),由于传统趋势面滤波法未考虑粗差数据对趋势面构造的影响,导致滤波后的多波束测深数据中仍有小部分粗差值较小的粗差点未被剔除,而改进算法和CUBE算法在算法设计上增加了对测深数据的抗差性,减弱了粗差数据对趋势面构造的影响,滤波效果较好。
(3) 对于复杂海底处出现的单个和多个成簇出现的粗差点(Ⅲ和Ⅳ区域),由于传统趋势面滤波法在复杂地区局部范围内所构造的趋势面不能合理反映真实海底地形,导致多波束测深数据中的粗差点剔除不彻底,尤其在复杂海底处多个成簇出现的粗差点(Ⅳ区域)滤除情况最差;而CUBE算法运用水深信息局部相关性原则为每一个水深节点确定水深估值,所构造的CUBE曲面为规则网格曲面,其与真实海底地形在微小地貌处仍存在一定的差异,特别在复杂海底处多个粗差点成簇出现的区域(Ⅳ区域),可能出现少量粗差值较小的粗差点被保留;本文所提改进算法采用自然邻点影响域作为其拟合范围,所构造的趋势面可以反映各种复杂程度的真实海底地形,特别对于复杂海底处多个成簇出现的粗差点,改进算法滤波效果最好。
(4) 在Ⅰ~Ⅳ 4个区域中,经改进算法滤波后的测深数据的水深值范围、标准方差和数据点数均大于传统趋势面滤波法和CUBE算法滤波后的测深数据,且与人工处理后的测深数据的各水深值统计数据较为接近,这说明经改进算法滤波后的测深数据的水深值波动相对于海底地形的变化较小,相比于传统趋势面滤波法和CUBE算法,保留了较多的正常水深点。造成上述差异的主要原因在于传统趋势面滤波法在复杂地区局部范围内所构造的趋势面不能合理反映真实海底地形且未考虑粗差数据对趋势面构造的影响,导致大量正常水深点误判为粗差点而被滤除;而CUBE算法是在设定的格网节点下选择水深,并对测区格网节点处进行水深及其相关误差估计,最终拟合的CUBE曲面与实际海底地形曲面存在一定的差异,将会导致一部分正常点被滤除。
(5) 在Ⅴ区域中,由各算法滤波后的测深数据点数可以看出,改进算法对突变地形的保留效果最好,CUBE算法次之,传统趋势面滤波法最差。对比图 12和图 14,CUBE算法和传统趋势面滤波法滤除的突变地形点主要为突变地形边界点和突变地形边缘以内的部分局部连续点。造成这一现象的主要原因在于传统趋势面滤波法和CUBE算法是在假设海底地形连续的前提下进行的,均无法有效识别突变地形点群。传统趋势面滤波法将突变地形点群视为海底连续地形的一部分,滤除掉与所构造趋势面之间偏差较大的水深点,导致出现突变地形边界点和突变地形边缘以内的部分局部连续点被剔除的结果;CUBE算法运用水深信息局部相关性原则为每一个水深节点确定水深估值,对于突变地形边缘以内的局部连续点,由于其局部连续性,得到最大限度的保留,但突变地形边界点具有粗差单点突变的特性,由其邻近水深节点构成的CUBE曲面与突变地形边界点仍存在较大差异,最终导致出现突变地形边界点和少量的突变地形局部连续点被剔除的结果;而改进算法采用自然邻点影响域作为拟合范围,由于其是海底地形表达的最小局部范围,较好地保留了突变地形上的局部连续点,通过引入突变地形边界点判断准则,有效识别了突变地形的边界点,较好地刻画了海底突变地形的实际形状。
4 结论通过理论分析及试验比对得结论如下:
(1) 改进算法和CUBE算法的粗差点识别能力优于传统趋势面滤波法,特别是在海底地形复杂区域或粗差点成簇连续出现的区域,改进算法可有效识别并剔除粗差点。
(2) 传统趋势面滤波法和CUBE算法在滤波过程中均有较多正常点被剔除掉,而改进算法则对这些正常水深点进行了保留,提高了海底地形表达的精度。
(3) 传统趋势面滤波法和CUBE算法由于在假设海底地形连续的前提下进行的,均无法有效识别突变地形点群,导致突变地形部分局部连续点和全部边界点被不合理剔除,而改进算法采用自然邻点影响域作为拟合范围和引入突变地形边界点判断准则,有效识别了突变地形点群,保证了海底突变地形的完整性。
本文对传统趋势面滤波法的改进主要集中于海底实际趋势面的构建,而对粗差判断准则未进行讨论,仍然采用2倍(或3倍)中误差判断准则作为改进算法的粗差判断准则,这可能会导致部分正常水深点被不合理删除和一些较小粗差被保留下来,下一步可针对粗差判断准则进行研究及改进。此外,改进算法与CUBE算法在效率方面相差较大,下一步可在自然邻点快速搜索、数据分块处理和算法并行运算等方面进行研究。
| [1] |
刘雁春, 肖付民, 暴景阳, 等.
海道测量学概论[M]. 北京: 测绘出版社, 2006: 132-138.
LIU Yanchun, XIAO Fumin, BAO Jingyang, et al. Introduction to Hydrogrophy[M]. Beijing: Surveying and Mapping Press, 2006: 132-138. |
| [2] |
黄谟涛, 翟国君, 王瑞, 等.
海洋测量异常数据的检测[J]. 测绘学报, 1999, 28(3): 269–277.
HUANG Motao, ZHAI Guojun, WANG Rui, et al. The Detection of Abnormal Data in Marine Survey[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(3): 269–277. DOI:10.3321/j.issn:1001-1595.1999.03.015 |
| [3] |
阳凡林, 刘经南, 赵建虎.
多波束测深数据的异常检测和滤波[J]. 武汉大学学报(信息科学版), 2004, 29(1): 80–83.
YANG Fanlin, LIU Jingnan, ZHAO Jianhu. Detecting Outliers and Filtering Noises in Multi-beam Data[J]. Geomatics and Information Science of Wuhan University, 2004, 29(1): 80–83. |
| [4] |
赵建虎, 刘经南.
多波束测深及图像数据处理[M]. 武汉: 武汉大学出版社, 2008: 205-210.
ZHAO Jianhu, LIU Jingnan. Multi-beam Sounding and Image Data Processing[M]. Wuhan: Wuhan University Press, 2008: 205-210. |
| [5] | WARE C, KNIGHT W, WELLS D. Memory Intensive Statistical Algorithms for Multibeam Bathymetric Data[J]. Computers & Geosciences, 1991, 17(7): 985–993. |
| [6] |
朱庆, 李德仁.
多波束测深数据的误差分析与处理[J]. 武汉测绘科技大学学报, 1998, 23(1): 1–4, 46.
ZHU Qing, LI Deren. Error Analysis and Processing of Multibeam Soundings[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1998, 23(1): 1–4, 46. |
| [7] | CALDER B R, MAYER L A. Automatic Processing of High-rate, High-density Multibeam Echosounder Data[J]. Geochemistry Geophysics Geosystems, 2003, 4(6): 1048. |
| [8] | VÁSQUEZ M E. Tuning the CARIS Implementation of CUBE for Patagonian Waters[D]. New Brunswick: University of New Brunswick, 2007. |
| [9] | MALLACE D, ROBERTSON P. Alternative Use of CUBE: How to Fit a Square Peg in a Round Hole[C]//Proceedings of US Hydrographic Conference. Norfolk, Virginia: [s. m. ], 2007. |
| [10] | LCDR Aluizio Maciel de Oliveira Junior, CDR Izabel King Jeck. Multibeam Processing for Nautical Charts (Using CUBE and "Surface Filter" to Enhance Multibeam Processing)[J]. International Hydrographic Review, 2009(2): 61–71. |
| [11] |
王德刚, 叶灿银.
CUBE算法及其在多波束数据处理中的应用[J]. 海洋学研究, 2008, 26(2): 82–87.
WAND Degang, YE Canyin. The Theory of CUBE Algorithm and Its Application in the Processing of Multi-beam Data[J]. Journal of Marine Sciences, 2008, 26(2): 82–87. |
| [12] |
黄谟涛, 翟国君, 柴洪洲, 等.
检测多波束测深异常数据的CUBE算法模型解析[J]. 海洋测绘, 2011, 31(4): 1–4.
HUANG Motao, ZHAI Guojun, CHAI Hongzhou, et al. Analysis on the Mathematical Models of CUBE Algorithm for the Detection of Abnormal Data in Multibeam Echosounding[J]. Hydrographic Surveying and Charting, 2011, 31(4): 1–4. |
| [13] |
李新娜, 归庆明, 许阿裴.
基于识别变量的粗差探测Bayes方法[J]. 测绘学报, 2008, 37(3): 355–360, 366.
LI Xinna, GUI Qingming, XU Apei. Bayesian Method for Detection of Gross Errors Based on Classification Variables[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3): 355–360, 366. DOI:10.3321/j.issn:1001-1595.2008.03.015 |
| [14] |
黄贤源, 隋立芬, 翟国君, 等.
利用Bayes估计进行多波束测深异常数据探测[J]. 武汉大学学报(信息科学版), 2010, 35(2): 168–171.
HUANG Xianyuan, SUI Lifen, ZHAI Guojun, et al. Outliers Detection of Multi-beam Data Based on Bayes Estimation[J]. Geomatics and Information Science of Wuhan University, 2010, 35(2): 168–171. |
| [15] |
黄贤源, 翟国君, 黄谟涛, 等.
利用水深不确定度探测测深异常值的方法[J]. 测绘科学技术学报, 2011, 28(1): 70–74, 78.
HUANG Xianyuan, ZHAI Guojun, HUANG Motao, et al. The Approach on Detecting Outliers of Multi-beam Data by Uncertainty[J]. Journal of Geomatics Science and Technology, 2011, 28(1): 70–74, 78. |
| [16] |
董江, 任立生.
基于趋势面的多波束测深数据滤波方法[J]. 海洋测绘, 2007, 27(6): 25–28.
DONG Jiang, REN Lisheng. Filter of MBS Sounding Data Based on Trend Surface[J]. Hydrographic Surveying and Charting, 2007, 27(6): 25–28. |
| [17] |
王海栋, 柴洪洲, 宋国大, 等.
多波束测深趋势面系数的主成分估计[J]. 海洋测绘, 2009, 29(5): 5–7.
WANG Haidong, CHAI Hongzhou, SONG Guoda, et al. Principal Components Estimation of Trend Surface Coefficients in Multibeam Bathymetry[J]. Hydrographic Surveying and Charting, 2009, 29(5): 5–7. |
| [18] |
王海栋, 柴洪洲, 翟天增, 等.
多波束测深异常的两种趋势面检测算法比较[J]. 海洋通报, 2010, 29(2): 182–186.
WANG Haidong, CHAI Hongzhou, ZHAI Tianzeng, et al. Comparison of Two Trend Surface Detection Algorithms of Multibeam Bathymetry Outlier[J]. Marine Science Bulletin, 2010, 29(2): 182–186. |
| [19] |
李志林, 朱庆.
数字高程模型[M]. 2版. 武汉: 武汉大学出版社, 2008: 17-133.
LI Zhilin, ZHU Qing. Digital Elevation Model[M]. 2nd ed. Wuhan: Wuhan University Press, 2008: 17-133. |
| [20] | YANG Xunnian, WANG Guozhao. Planar Point Set Fairing and Fitting by Arc Splines[J]. Computer-Aided Design, 2001, 33(1): 35–43. DOI:10.1016/S0010-4485(00)00059-2 |
| [21] |
陈曦. 反求工程中基于点云的特征挖掘技术研究[D]. 杭州: 浙江大学, 2005: 38-39. CHEN Xi. Study on Feature Mining Technology Based on Point Cloud in Reverse Engineering[D]. Hangzhou: Zhejiang University, 2005: 38-39. http://cdmd.cnki.com.cn/Article/CDMD-10335-2006175642.htm |
| [22] |
汤国安, 刘学军, 闾国年.
数字高程模型及地学分析的原理与方法[M]. 北京: 科学出版社, 2005: 63-65.
TANG Guoan, LIU Xuejun, LÜ Guonian. Principle and Method of Digital Elevation Model and Geological Analysis[M]. Beijing: Science Press, 2005: 63-65. |
| [23] |
王幼宁, 刘继志.
微分几何讲义[M]. 北京: 北京师范大学出版社, 2011: 116-117.
WANG Youning, LIU Jizhi. Differential Geometry Notes[M]. Beijing: Beijing Normal University Press, 2011: 116-117. |
| [24] |
陈军, 赵仁亮, 乔朝飞.
基于Voronoi图的GIS空间分析研究[J]. 武汉大学学报(信息科学版), 2003, 28(S1): 32–37.
CHEN Jun, ZHAO Renliang, QIAO Chaofei. Voronoi Diagram-based GIS Spatial Analysis[J]. Geomatics and Information Science of Wuhan University, 2003, 28(S1): 32–37. |
| [25] |
董箭, 彭认灿, 郑义东, 等.
局部动态最优Voronoi图的NNI算法及其在格网数字水深模型中的应用[J]. 测绘学报, 2013, 42(2): 284–289, 303.
DONG Jian, PENG Rencan, ZHENG Yidong, et al. An algorithm of Natural Neighbor Interpolation Based on local Dynamic Optimal Voronoi Diagram and Its Application in Grid Digital Depth Model[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2): 284–289, 303. |
| [26] |
郭艳军, 潘懋, 燕飞, 等.
自然邻点插值方法在三维地质建模中的应用[J]. 解放军理工大学学报(自然科学版), 2009, 10(6): 650–655.
GUO Yanjun, PAN Mao, YAN Fei, et al. Application of Natural Neighbor Interpolation Method in Three-Dimensional Geological Modeling[J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2009, 10(6): 650–655. |
| [27] |
吴英姿. 多波束测深系统地形跟踪与数据处理技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2001: 59-79. WU Yingzi. A Study on Multi-Beam Sounding System Seafloor Tracking & Data Processing Techniques[D]. Harbin: Harbin Engineering University, 2001: 59-79. |
| [28] |
蔡永昌, 朱合华.
基于局部搜索算法的自然邻接点方法[J]. 力学学报, 2004, 36(5): 623–628.
CAI Yongchang, ZHU Hehua. Natural Neighbour Method Based on the Algorithm of Local Search[J]. Acta Mechanica Sinica, 2004, 36(5): 623–628. |
| [29] |
董箭, 彭认灿, 郑义东.
利用局部动态最优Delaunay三角网改进逐点内插算法[J]. 武汉大学学报(信息科学版), 2013, 38(5): 613–617.
DONG Jian, PENG Rencan, ZHENG Yidong. An Improved Algorithm of Point-by-point Interpolation by Using Local Dynamic Optimal Delaunay Triangulation Network[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 613–617. |
| [30] |
吕志平, 魏子卿, 李军, 等.
我国CGCS2000高精度坐标转换格网模型的建立[J]. 测绘学报, 2013, 42(6): 791–797.
LÜ Zhiping, WEI Ziqing, LI Jun, et al. The Establishment of High Precise Coordinate Transformation Grid Model of CGCS2000[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6): 791–797. |



